Mathematical Modeling of the Concentrated Energy Flow Effect on Metallic Materials
Abstract
:1. Introduction
2. Mathematical Models of Electron-Beam Effect on Metallic Materials
2.1. Thermal Model
2.2. Model of Thermoelastic Waves Generation
2.3. The Diffusion Model of Dissolution Refractory Inclusions in Metals under Concentrated Flows of Energy Action
3. Modeling of Subsurface Nanostructure Formation
4. Conclusions
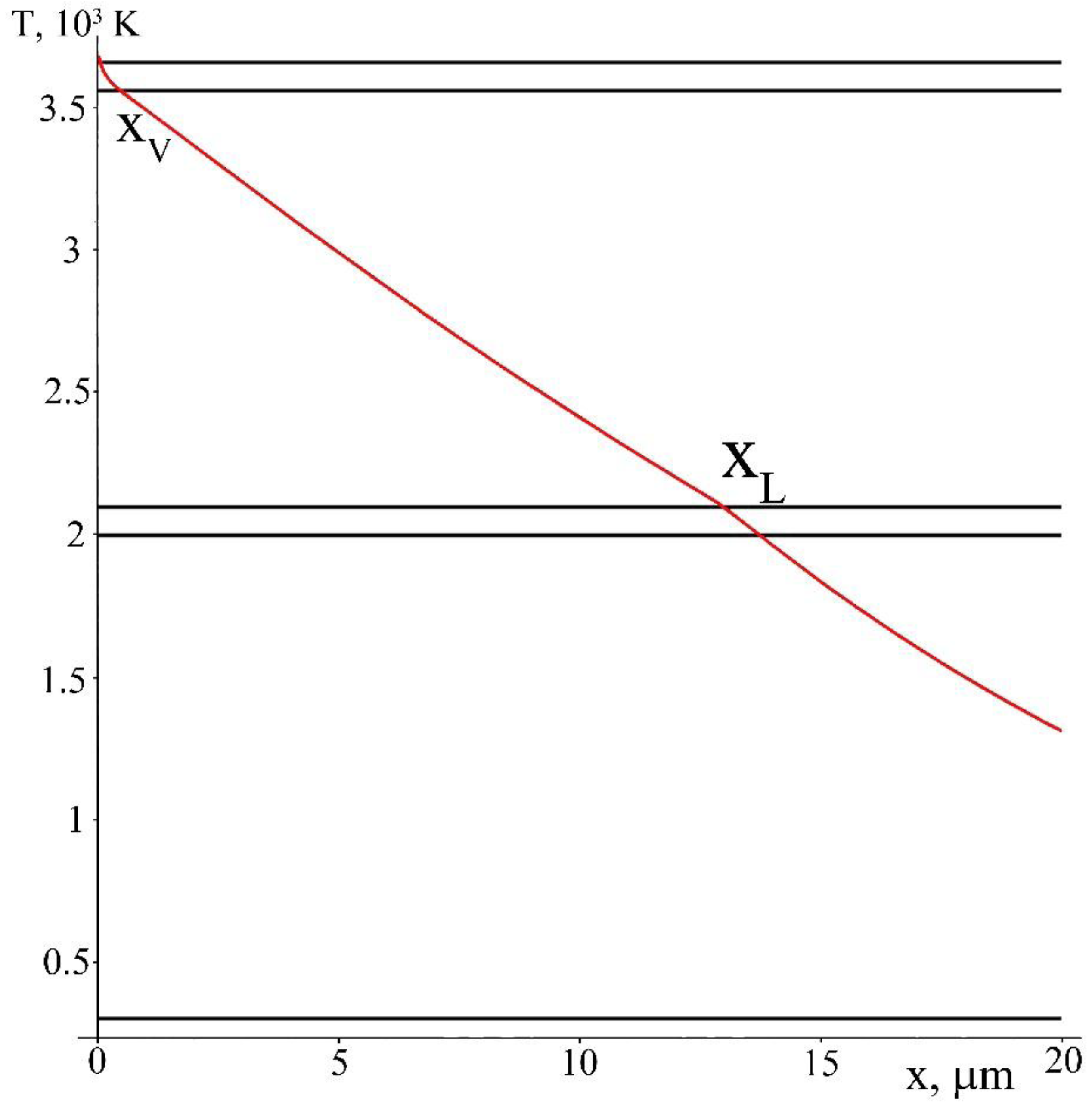
- A thermal mathematical model, which considers vaporization from the surface of the material, has been presented. The dependence of penetration depth vs. energy surface density is obtained. Its linear character has been shown. When comparing penetration depths determined computationally with the experimental data their satisfactory fit has been determined. The period of vaporization has been determined without solving the gas-dynamic problem.
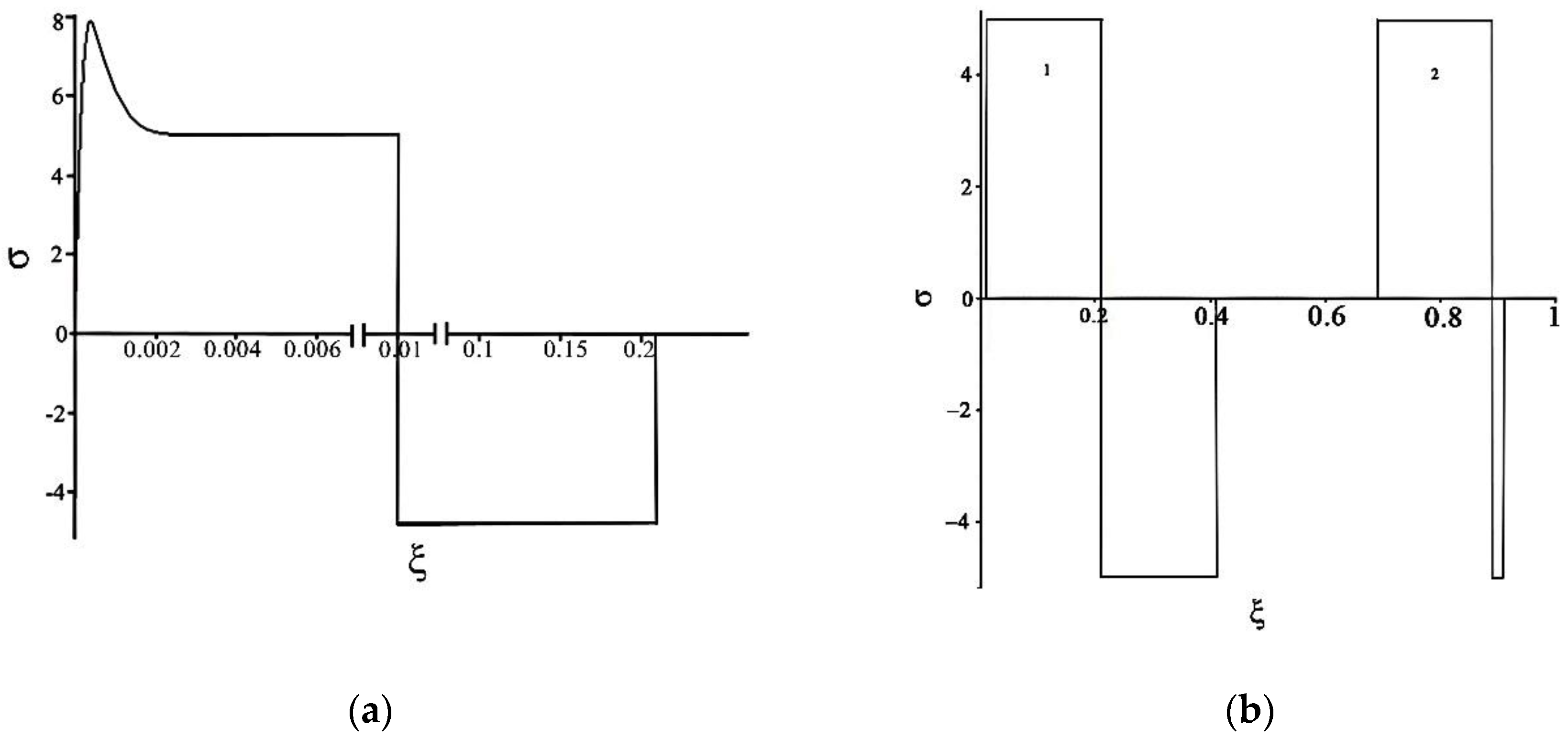
- The mechanism of bipolar thermo-elastic wave generation has been revealed on the basis of being solved analytically, not on the basis of the uncoupled thermo-elasticity problem. The matter of it is that tension and compression in the thermo-elastic wave are caused by an increase and a subsequent drop of temperature on the edge.
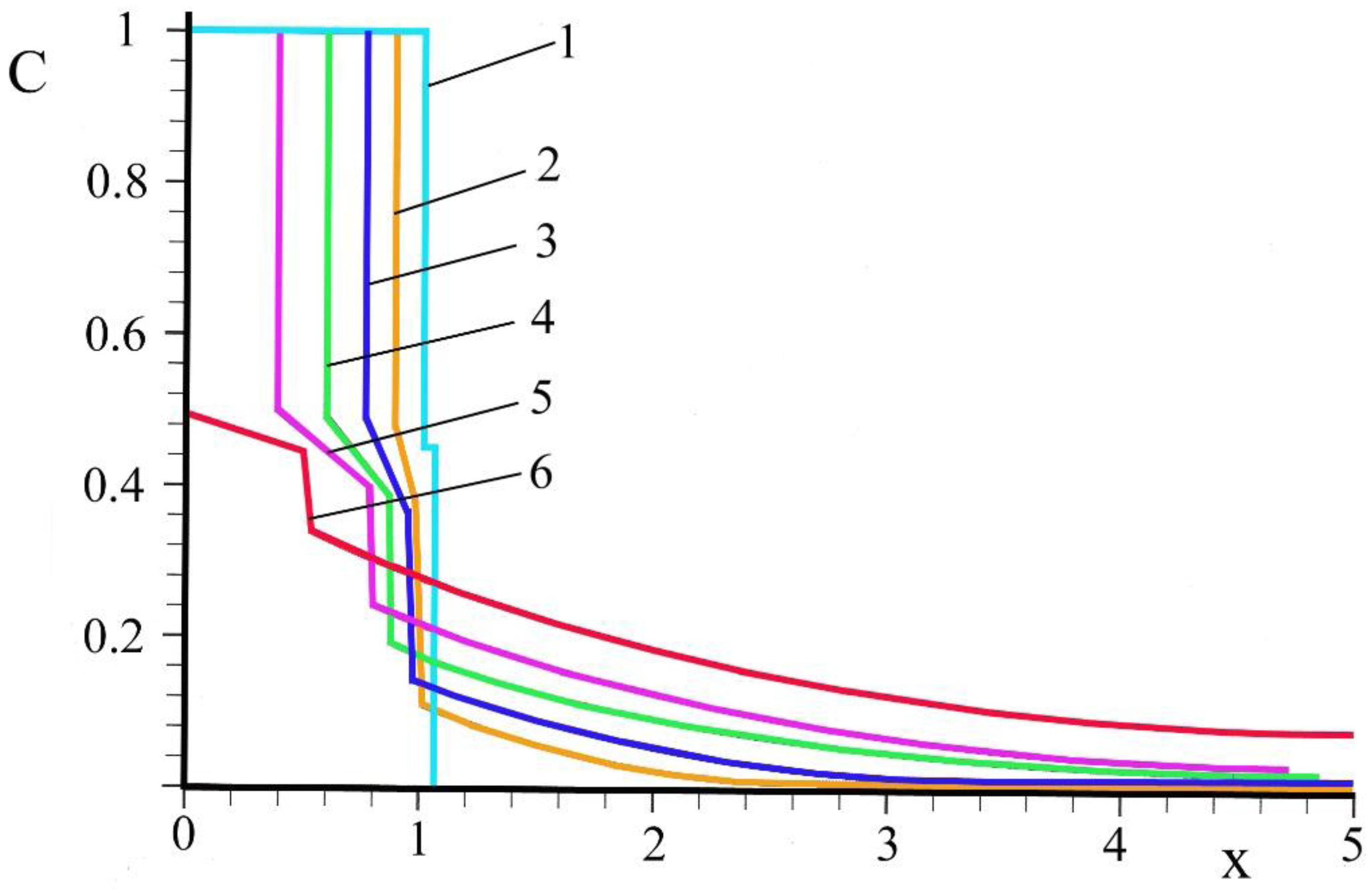
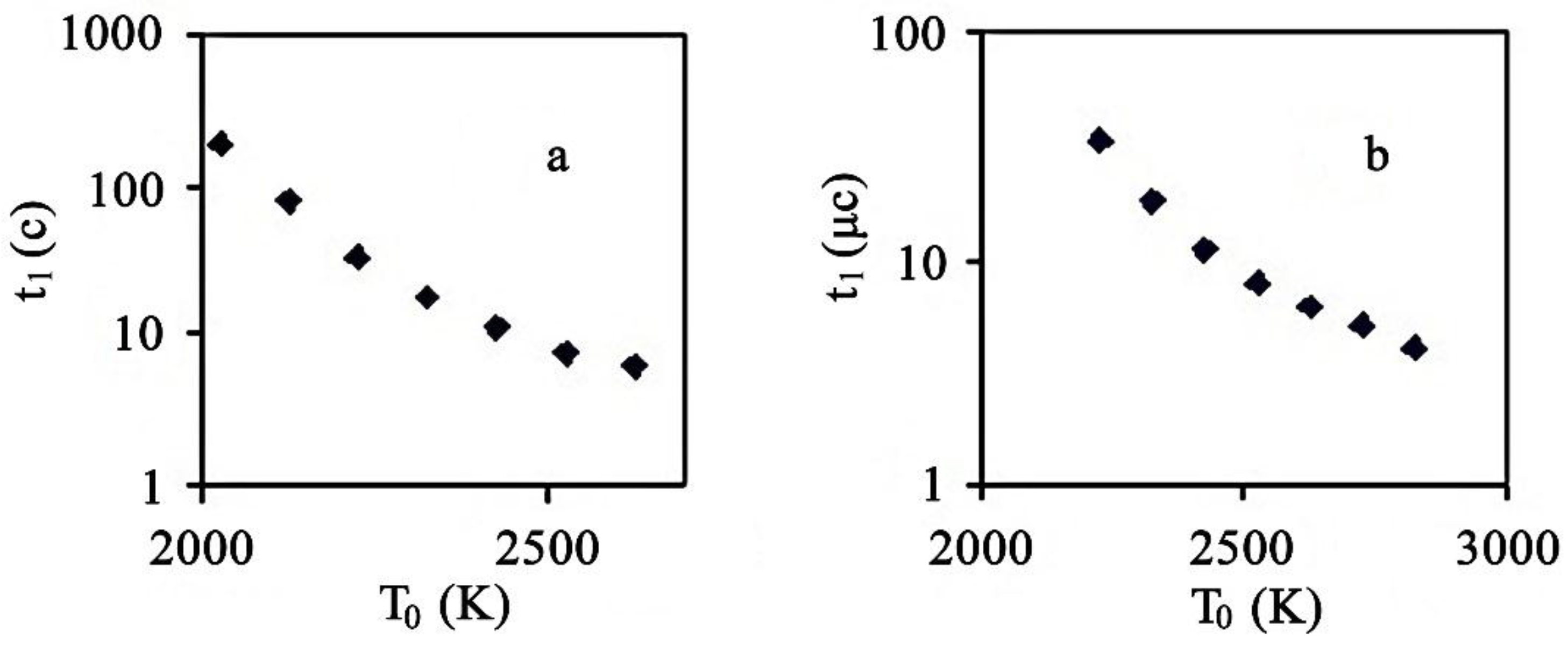
- A model of the dissolution of carbon particles in titanium has been analyzed under the action of electron beams. It has been stated that micrometer-dimensional carbon particles get dissolved for about 10 s. This time significantly exceeds the time of concentrated energy flow impact on the material. If particles are nanometer-dimensional ones, the time of dissolution is 10 μs in order of magnitude. In this case carbon particles get dissolved as long as they are impacted by electron beams.
- Formation of internal nano-structural layers has been analyzed under the action of heterogeneous plasma flows. Instability increment dependence on the wavelength with two maximums—in nano- and micro- ranges—have been developed.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ilyuschenko, A.P.; Shevtsov, A.I.; Astashynski, V.M.; Kuzmitski, A.M.; Gromyko, G.F.; Chumakov, A.N.; Bosak, N.A.; Buikus, K.V. Friction and wear of powder coatings produced by using high-energy pulsed flows. High Temp. Mater. Process. 2015, 19, 141–152. [Google Scholar] [CrossRef]
- Huang, Z.-T.; Suo, H.-B.; Yang, G.; Yang, F.; Dong, W. Effect of heat treatment on microstructure and property of TC18 titanium alloy prepared by electron beam rapid manufacturing. Trans. Mater. Heat Treat. 2015, 36, 50–54. [Google Scholar]
- Da Silva, M.R.; Gargarella, P.; Gustmann, T.; Filho, W.J.B.; Kiminami, C.S.; Eckert, J.; Pauly, S.; Bolfarini, C. Laser surface remelting of a Cu-Al-Ni-Mn shape memory alloy. Mater. Sci. Eng. A 2016, 66, 161–167. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Fang, Y.; Madigan, B.; Xu, G.; Zhou, J. Investigation of microstructures and residual stresses in laser peened Incoloy 800H weldments. Opt. Laser Technol. 2014, 57, 159–164. [Google Scholar] [CrossRef]
- Hu, J.; Chai, L.; Xu, H.; Ma, C.; Deng, S. Microstructural modification of brush-plated nanocrystalline Cr by high current pulsed electron beam irradiation. J. Nano Res. 2016, 41, 87–95. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, B.; Xiao, H.; Tu, J.; Chai, L.; Huang, W.; Hu, J. Microstructure and properties of CuFe10 alloys treated by high current pulsed electron beam. High Power Laser Part. Beams. 2015, 27, 024105. [Google Scholar] [CrossRef]
- Devyatkov, V.N.; Koval, N.N.; Schanin, P.M.; Grigoryev, V.P.; Koval, T.V. Generation and propagation of high-current low-energy electron beams. Laser Part. Beams 2003, 21, 243–248. [Google Scholar] [CrossRef]
- Sosnin, K.V.; Raykov, S.V.; Vaschuk, E.S.; Budovskikh, E.A.; Gromov, V.E.; Ivanov, Y.F. Morphology of the surface of technically pure titanium VT1-0 after electroexplosive carbonization with a weighed zirconium oxide powder sample and electron beam treatment. In Proceedings of the International Conference on Physical Mesomechanics of Multilevel Systems, Tomsk, Russia, 3–5 September 2014.
- Sosnin, K.V.; Raikov, S.V.; Gromov, V.E.; Ivanov, Y.F.; Budovskikh, E.A.; Vashchuk, E.S. Formation of a microcomposite structure in the surface layer of yttrium-doped titanium. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2015, 9, 377–382. [Google Scholar] [CrossRef]
- Ivanov, Yu.F.; Teresov, A.D.; Petrikova, E.A.; Raikov, S.V.; Goryushkin, V.F.; Budovskikh, E.A. Surface layer of commercially pure VT1-0 titanium after electric-explosion alloying and subsequent treatment by a high-intensity pulsed electron beam. Steel Transl. 2013, 43, 798–802. [Google Scholar] [CrossRef]
- Markov, A.B.; Rotshtein, V.P. Calculation and experimental determination of hardening and tempering zones in quenched U7A steel irradiated with a pulsed electron beam. Nucl. Instrum. Methods Phys. Res. Sect. B 1997, 132, 79–86. [Google Scholar] [CrossRef]
- Markov, A.B.; Ivanov, Yu.F.; Proskurovsky, D.I.; Rotshtein, V.P. Mechanisms for hardening of carbon steel with a nanosecond high-energy, high-current electron beam. Mater. Manuf. Process. 1999, 14, 205–216. [Google Scholar] [CrossRef]
- Leyvi, A.Ya.; Talala, K.A.; Krasnikov, V.S.; Yalovets, A.P. Modification of the Constructional Materials with the Intensive Charged Particle Beams and Plasma Flows. Ser. Mech. Eng. Ind. 2016, 16, 28–55. (In Russian) [Google Scholar]
- Mazhukin, V.I.; Mazhukin, A.V.; Lobok, M.G. Mathematical modeling of dynamics of fast phase transitions and overheated metastable states during nano- and femtosecond laser treatment of metal targets. Math. Model. Comput. Simul. 2010, 2, 396–405. [Google Scholar] [CrossRef]
- Bleykher, G.A.; Krivobokov, V.P.; Yuryeva, A.V. Thermal Processes and Emission of Atoms from the Liquid Phase Target Surface of a Magnetron Sputtering System. Russ. Phys. J. 2015, 58, 431–437. [Google Scholar] [CrossRef]
- Yalovets, A.P. Calculation of flows of a medium induced by high-power beams of charged particles. J. Appl. Mech. Tech. Phys. 1997, 38, 137–150. [Google Scholar] [CrossRef]
- Khaimzon, B.B.; Sarychev, V.D.; Gromov, V.E. Temperature distribution produced by pulsed energy fluxes, with evaporation of the target. Steel Transl. 2013, 43, 55–58. [Google Scholar] [CrossRef]
- Maier, A.E.; Yalovets, A.P. Mechanical stresses in an irradiated target with a disturbed surface. Tech. Phys. 2006, 51, 459–465. [Google Scholar] [CrossRef]
- Chumakov, Yu.A.; Knyazeva, A.G. Interrelated processes of heat mass transfer and stress evolution in a disk with an inclusion under the action of high density energy flow. Phys. Mesomech. 2013, 16, 85–91. [Google Scholar]
- Sarychev, V.D.; Voloshina, M.S.; Gromov, V.E. Mathematical model of generation of the thermoplastic waves under action of concentrated energy fluxes at the materials. Basic Probl. Mater. Sci. 2011, 8, 71–76. (In Russian) [Google Scholar]
- Lyubov, B.Ya. Diffusion Processes in Nonhomogeneous Solid State; Nauka: Moscow, Russia, 1981. (In Russian) [Google Scholar]
- Bukrina, N.V.; Knyazeva, A.G. Numerical solution algorithm for non-isothermal diffusion problems in surface treatment processes. Phys. Mesomech. 2006, 9, 55–62. (In Russian) [Google Scholar]
- Knyazeva, A.G.; Krukova, O.N.; Bukrina, O.V.; Sorokova, S.N. Simulation issues of surface treatment and coating materials using high energy sources. Izv. TPU 2010, 317, 93–101. (In Russian) [Google Scholar]
- Merzhanov, A.G.; Averson, A.E. The present state of the thermal ignition theory: An invited review. Combust. Flame 1971, 16, 89–124. [Google Scholar] [CrossRef]
- Nekrasov, E.A.; Smolyakov, V.K.; Maksimov, Yu.M. Adiabatic heating in the titanium-carbon system. Combust. Explos. Shock Waves 1981, 17, 305–311. [Google Scholar] [CrossRef]
- Khina, B.B. Combustion Synthesis of Advanced Materials; Nova Science Publishers Inc.: New York, NY, USA, 2010. [Google Scholar]
- Aleksandrov, V.V.; Korchagin, M.A. Mechanism and macrokinetics of reactions accompanying the combustion of SHS systems. Combust. Explos. Shock Waves 1987, 23, 557–564. [Google Scholar] [CrossRef]
- Sarychev, V.D.; Khaimzon, B.B.; Gromov, V.E. Mathematical model of dissolution of particles of carbon in the titan at influence of the concentrated streams of energy. Titan 2012, 1, 4–8. (In Russian) [Google Scholar]
- Sarychev, V.D.; Mochalov, S.P.; Budovskikh, E.A.; Vashchuk, E.S.; Gromov, V.E. Formation of convective structures in metals and alloys under the action of pulsed multiphase plasma jets. Steel Transl. 2010, 40, 531–536. [Google Scholar] [CrossRef]
- Granovskii, A.Yu.; Sarychev, V.D.; Gromov, V.E. Model of formation of inner nanolayers in shear flows of material. Tech. Phys. 2013, 58, 1544–1547. [Google Scholar] [CrossRef]
- Inogamov, N.A.; Zhakhovsky, V.V.; Khokhlov, V.A.; Petrov, Y.V.; Migdal, K.P. Solitary nanostructures produced by ultrashort laser pulse. Nanoscale Res. Lett. 2016, 11, 177. [Google Scholar] [CrossRef] [PubMed]
- Suh, K.Y.; Jeong, H.E.; Kim, D.-H.; Singh, R.A.; Yoon, E.-S. Capillarity-assisted fabrication of nanostructures using a less permeable mold for nanotribological applications. J. Appl. Phys. 2006, 100, 034303. [Google Scholar] [CrossRef]
- Prokoshev, V.G.; Parfionov, S.D.; Obgadze, T.A. Mathematical modelling of the temperature fields induced under the laser processing material. In Proceedings of the International conference on laser assisted net shape engineering LANE 2001, Erlangen, Germany, 28–31 March 2001; pp. 185–190.
- Galkin, A.F.; Abramov, D.V.; Savina, L.D.; Fedotova, O.Yu.; Prokoshev, V.G.; Arakelian, S.M. Laser-induced hydrodynamics waves on the surface of melt. In Proceedings of the Laser-induced hydrodynamics waves on the surface of melt, Vladimir/Suzdal, Russia, 21 September 2000; Volume 4429, pp. 101–104.
- Lee, P.D.; Quested, P.N.; McLean, M. Modelling of Marangoni effects in electron beam melting. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1998, 356, 1027–1043. [Google Scholar] [CrossRef]
- Lukashov, E.A.; Radkevich, E.V.; Yakovlev, N.N. Structurization of the instability zone and crystallization. J. Math. Sci. 2011, 179, 491–514. [Google Scholar] [CrossRef]
- Kuznetsov, V.P.; Smolin, I.Y.; Dmitriev, A.I.; Tarasov, S.Y.; Gorgots, V.G. Toward control of subsurface strain accumulation in nanostructuring burnishing on thermostrengthened steel. Surf. Coat. Technol. 2016, 285, 171–178. [Google Scholar] [CrossRef]
- Sarychev, V.D.; Nevskii, S.A.; Konovalov, S.V.; Komissarova, I.A.; Cheremushkina, E.V. Thermocapillary model of formation of surface nanostructure in metals at electron beam treatment. IOP Conf. Ser. Mater. Sci. Eng. 2015, 91, 012028. [Google Scholar] [CrossRef]
- Sarychev, V.D.; Nevskii, S.A.; Sarycheva, E.V.; Konovalov, S.V.; Gromov, V.E. Viscous Flow Analysis of the Kelvin–Helmholtz Instability for Short Waves. In Proceedings of the International Conference on Advanced Materials with Hierarchical Structure for New Technologies and Reliable Structures 2016, Tomsk, Russia, 19–23 September 2016; Volume 1783.
- Samarskii, A.A.; Babishchevich, P.N. Vychislitel’naya Teploperedacha (Computational Heat Transmission); Editorial URSS: Moscow, Russia, 2003. [Google Scholar]
- Cheynet, B.; Dubois, J.-D.; Milesi, M. Données thermodynamiques des éléments chimiques. Tech. Ing. Traité Mater. Metall. 1993, M64-1–M64-22. [Google Scholar]
- Missenard, A. Conductivite Thermique des Solides, Liquides, Gaz et Leurs Melanges; Editions Eyrolles: Paris, France, 1965. [Google Scholar]
- Iesan, D.; Antonio, S. Thermoelastic Deformations; Springer: Berlin, Germany, 1996. [Google Scholar]
- Awrejcewicz, J.; Krysko, V.A. Nonclassical Thermoelastic Problems in Nonlinear Dynamics of Shells; Springer: Berlin, Germany, 2003. [Google Scholar]
- Three-Dimensional Problems of the Mathematical Theory of Elasticity and Thermoelasticity; Kupradze, V.D. (Ed.) Elsevier: Amsterdam, The Netherlands, 1976.
- Proskurovsky, D.I.; Rotshtein, V.P.; Ozur, G.E.; Ivanov, Y.F.; Markov, A.B. Physical foundations for surface treatment of materials with low energy, high current electron beams. Surf. Coat. Technol. 2000, 125, 49–56. [Google Scholar] [CrossRef]
- Paul, T.; Vuorinen, V.; Divinski, S.V.; Laurila, T. Thermodynamics, Diffusion and the Kirkendall Effect in Solids; Springer: Berlin, Gemany, 2014. [Google Scholar]
- Mehrer, H. Diffusion in Solids; Springer: Berlin, Germany, 2007. [Google Scholar]
- Bagautdinov, A.Ya.; Tsvirkun, O.A.; Budovskikh, E.A.; Ivanov, Yu.F.; Gromov, V.E. Gradient state of the surface layers of iron and nickel after electro-explosive alloying. Metallurgist 2007, 51, 151–158. [Google Scholar] [CrossRef]
- Glezer, A.M.; Permyakova, I.E. Melt-Quenched Nanocrystals; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Bazylev, B.; Janeschitz, G.; Landman, I.; Loarte, A.; Klimov, N.S.; Podkovyrovd, V.L.; Safronov, V.M. Experimental and theoretical investigation of droplet emission from tungsten melt layer. Fusion Eng. Des. 2009, 84, 441–445. [Google Scholar] [CrossRef]
- Forsythe, W.E. Smithsonian Physical Tables; Knovel: Norwich, NY, USA, 2003. [Google Scholar]
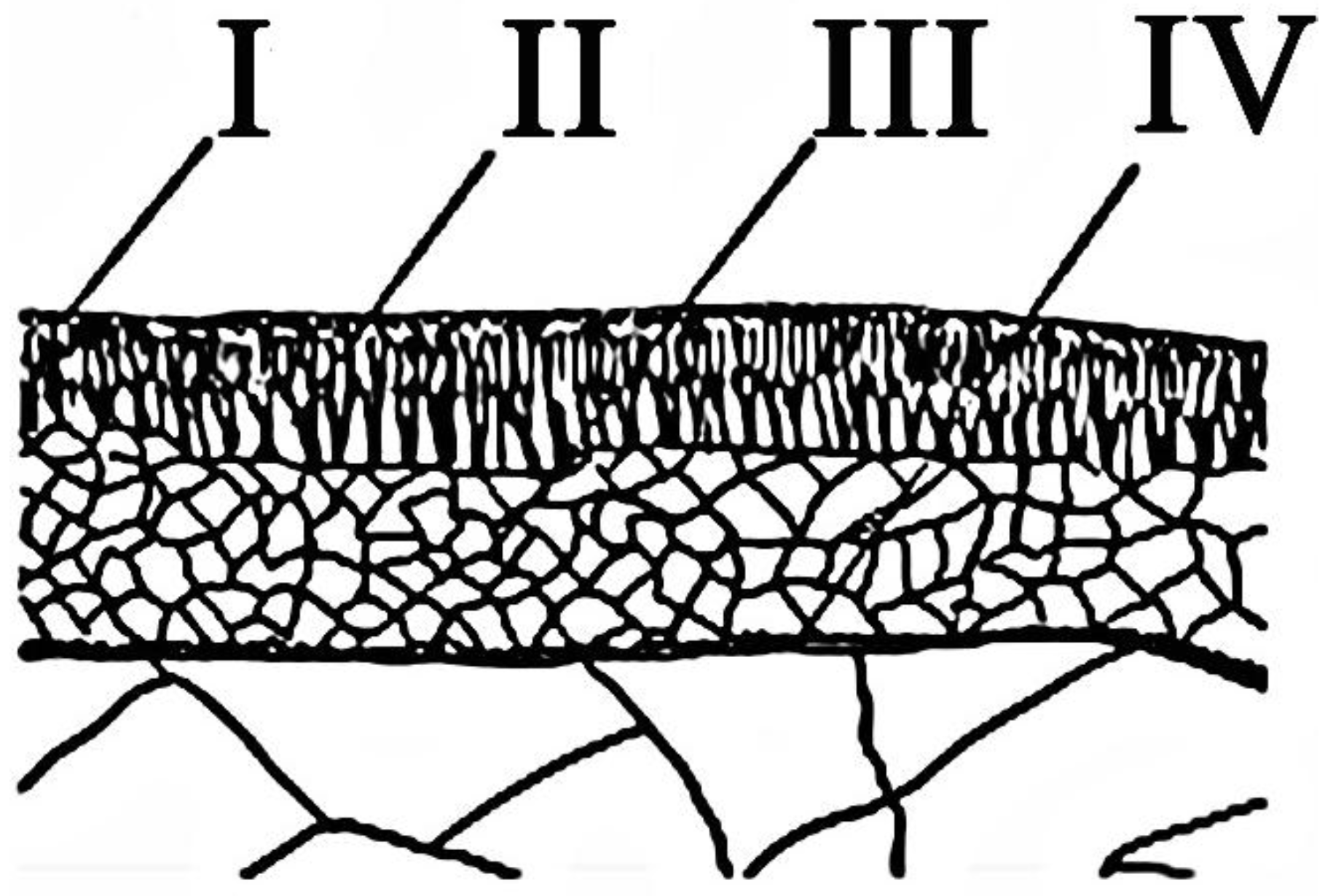
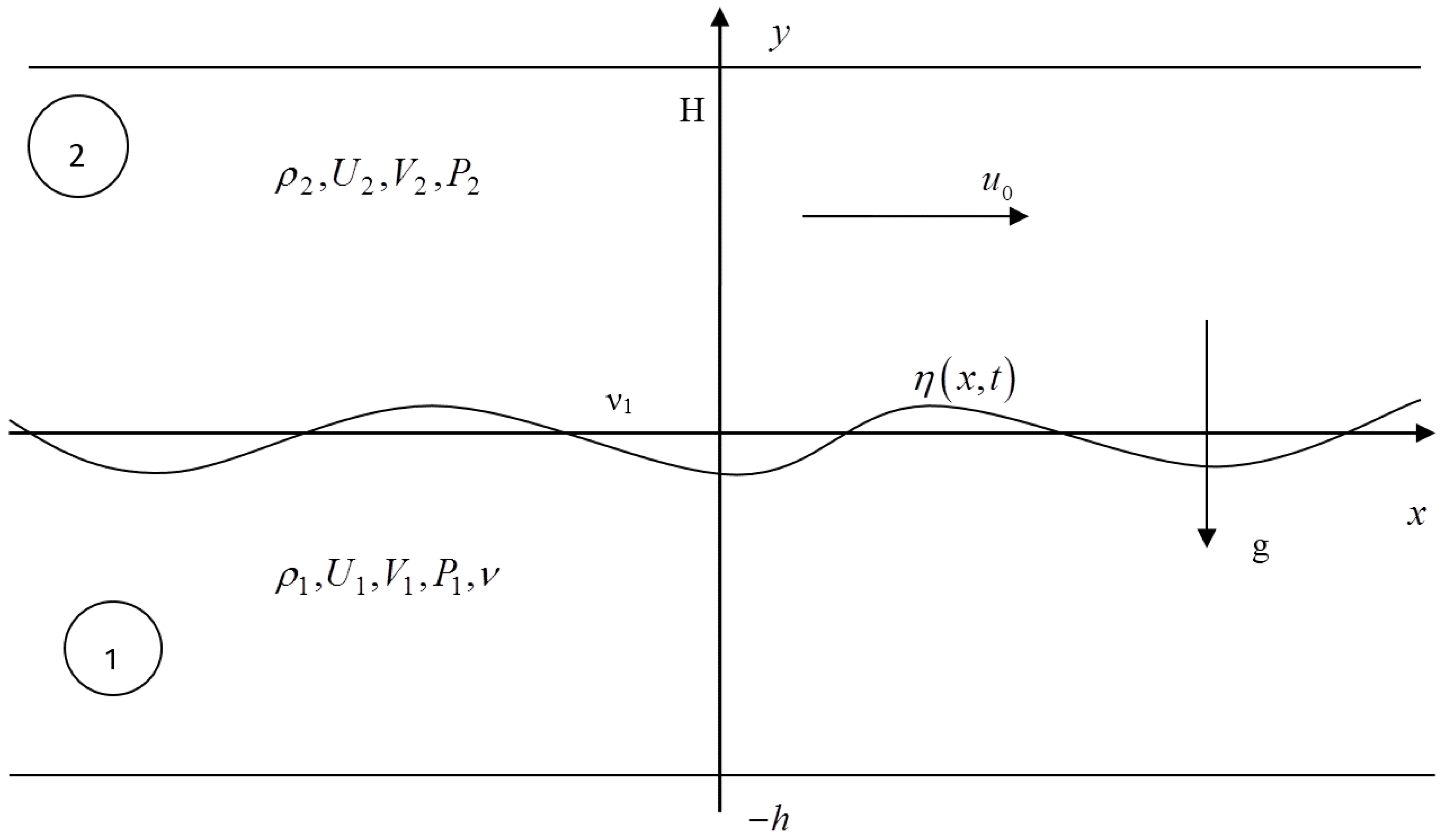

| ES, J/cm2 | t0, μs | hmelt, μm | |
|---|---|---|---|
| Experimental | Estimated | ||
| 18 | 50 | 6 | 7 |
| 21 | 50 | 8 | 8 |
| 25 | 50 | 13 | 15 |
| 45 | 100 | 31.1 | 31.2 |
| 50 | 100 | 36 | 35.0 |
| 60 | 100 | 50.1 | 50 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalov, S.; Chen, X.; Sarychev, V.; Nevskii, S.; Gromov, V.; Trtica, M. Mathematical Modeling of the Concentrated Energy Flow Effect on Metallic Materials. Metals 2017, 7, 4. https://doi.org/10.3390/met7010004
Konovalov S, Chen X, Sarychev V, Nevskii S, Gromov V, Trtica M. Mathematical Modeling of the Concentrated Energy Flow Effect on Metallic Materials. Metals. 2017; 7(1):4. https://doi.org/10.3390/met7010004
Chicago/Turabian StyleKonovalov, Sergey, Xizhang Chen, Vladimir Sarychev, Sergey Nevskii, Victor Gromov, and Milan Trtica. 2017. "Mathematical Modeling of the Concentrated Energy Flow Effect on Metallic Materials" Metals 7, no. 1: 4. https://doi.org/10.3390/met7010004
APA StyleKonovalov, S., Chen, X., Sarychev, V., Nevskii, S., Gromov, V., & Trtica, M. (2017). Mathematical Modeling of the Concentrated Energy Flow Effect on Metallic Materials. Metals, 7(1), 4. https://doi.org/10.3390/met7010004







