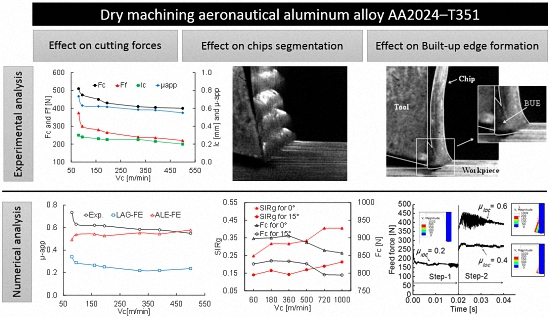
Dry Machining Aeronautical Aluminum Alloy AA2024-T351: Analysis of Cutting Forces, Chip Segmentation and Built-Up Edge Formation
Abstract
:1. Introduction
2. Experimental and Modelling Aspects
2.1. Experimental Aspects
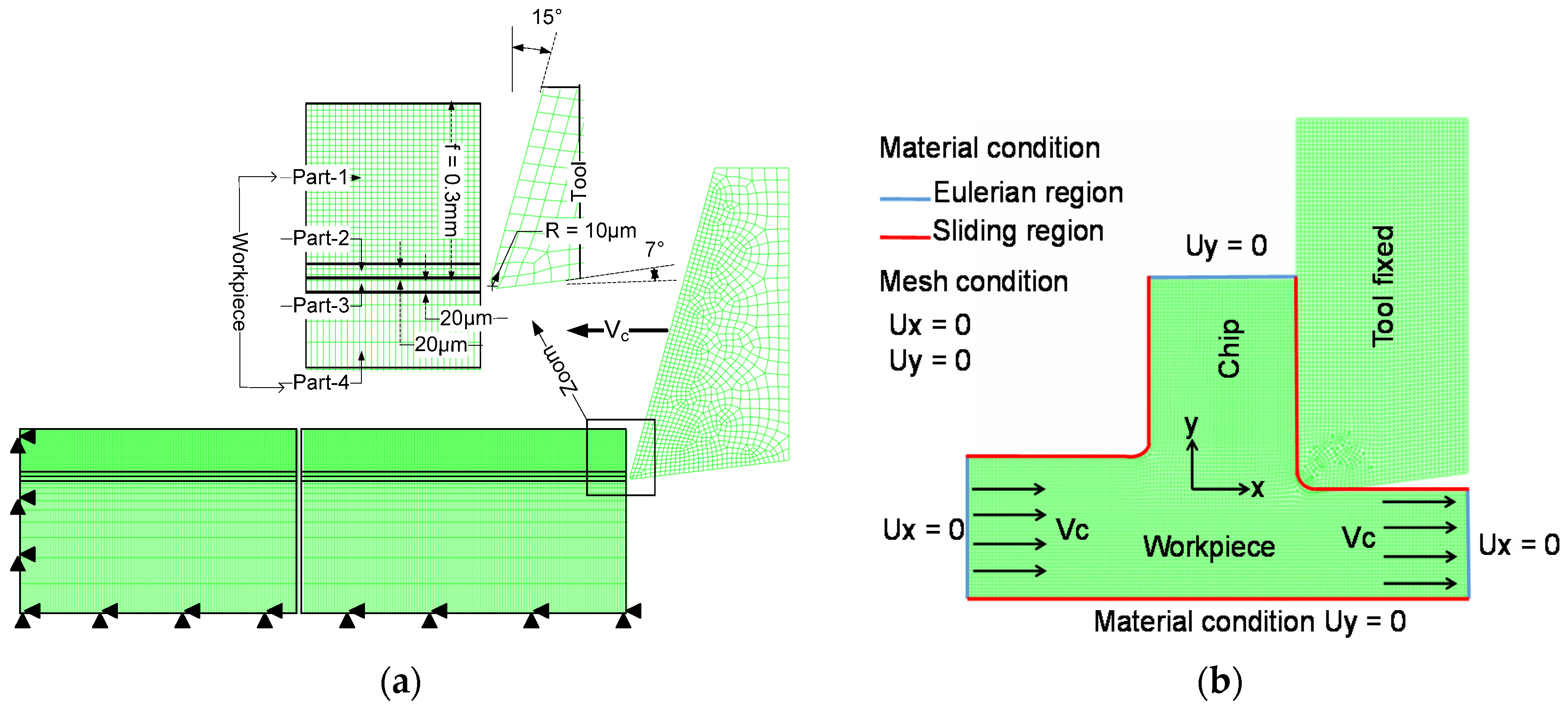
2.2. Modelling Aspects
3. Results and Discussion
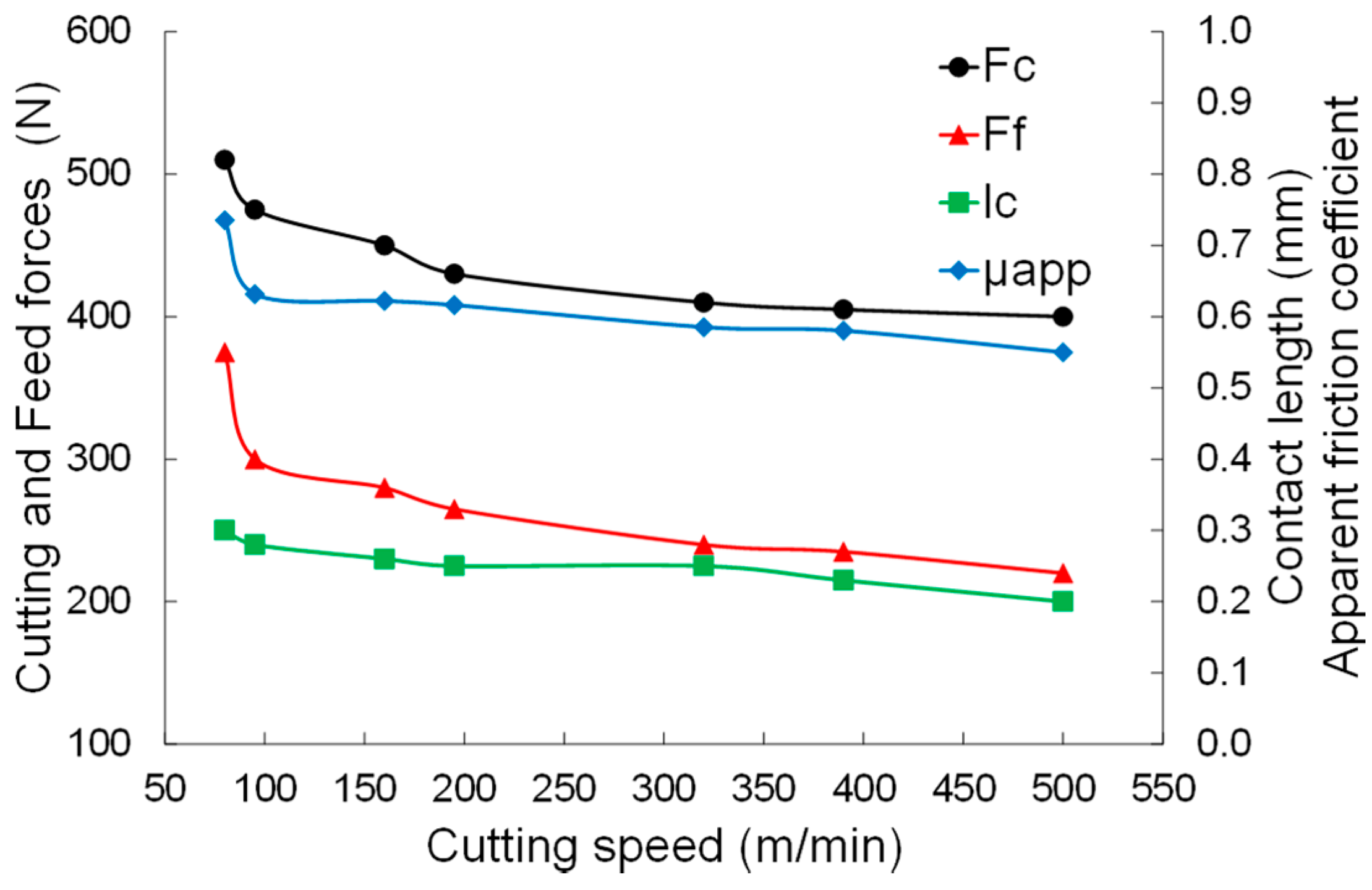
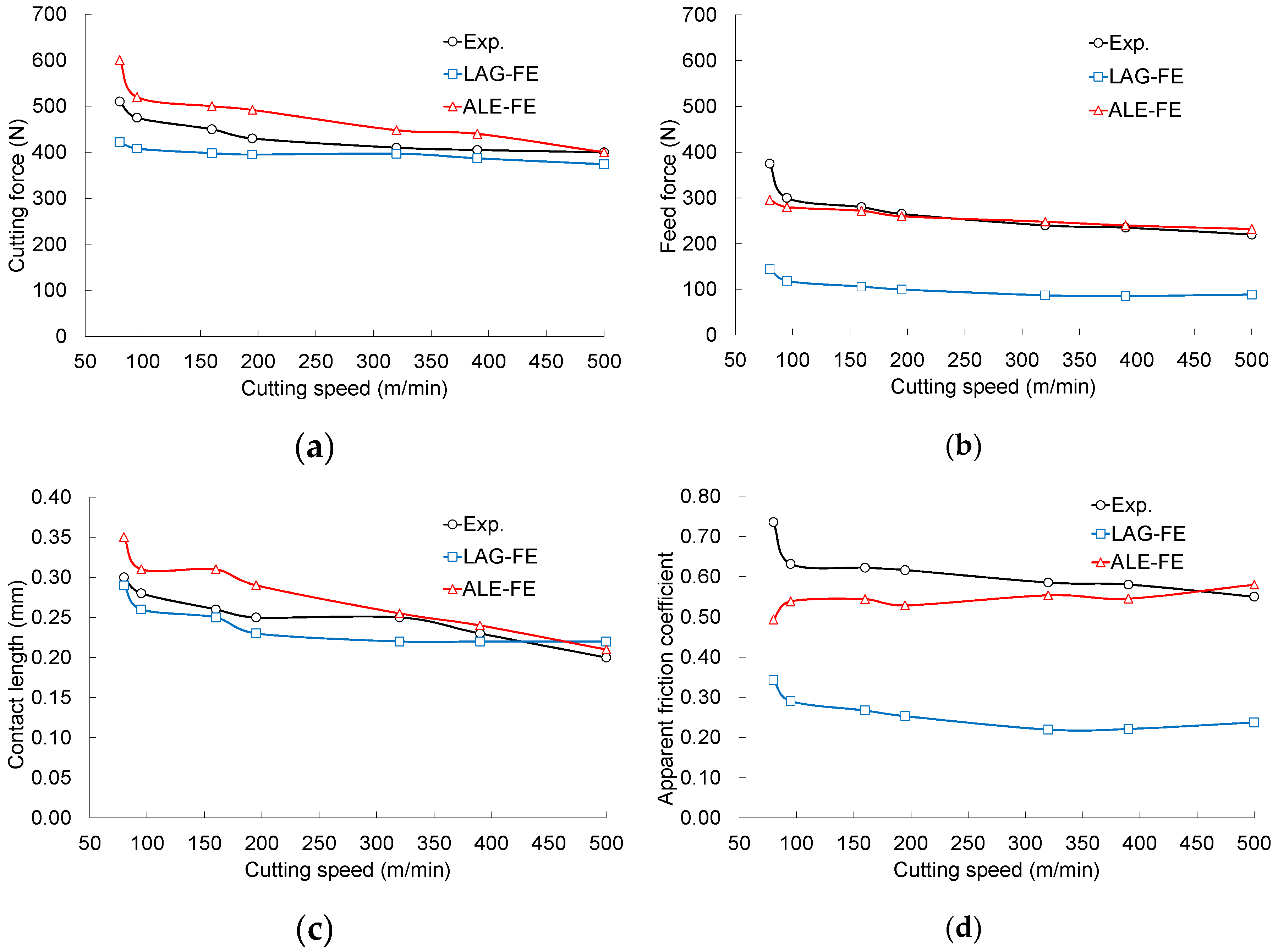
3.1. Cutting Forces Analysis
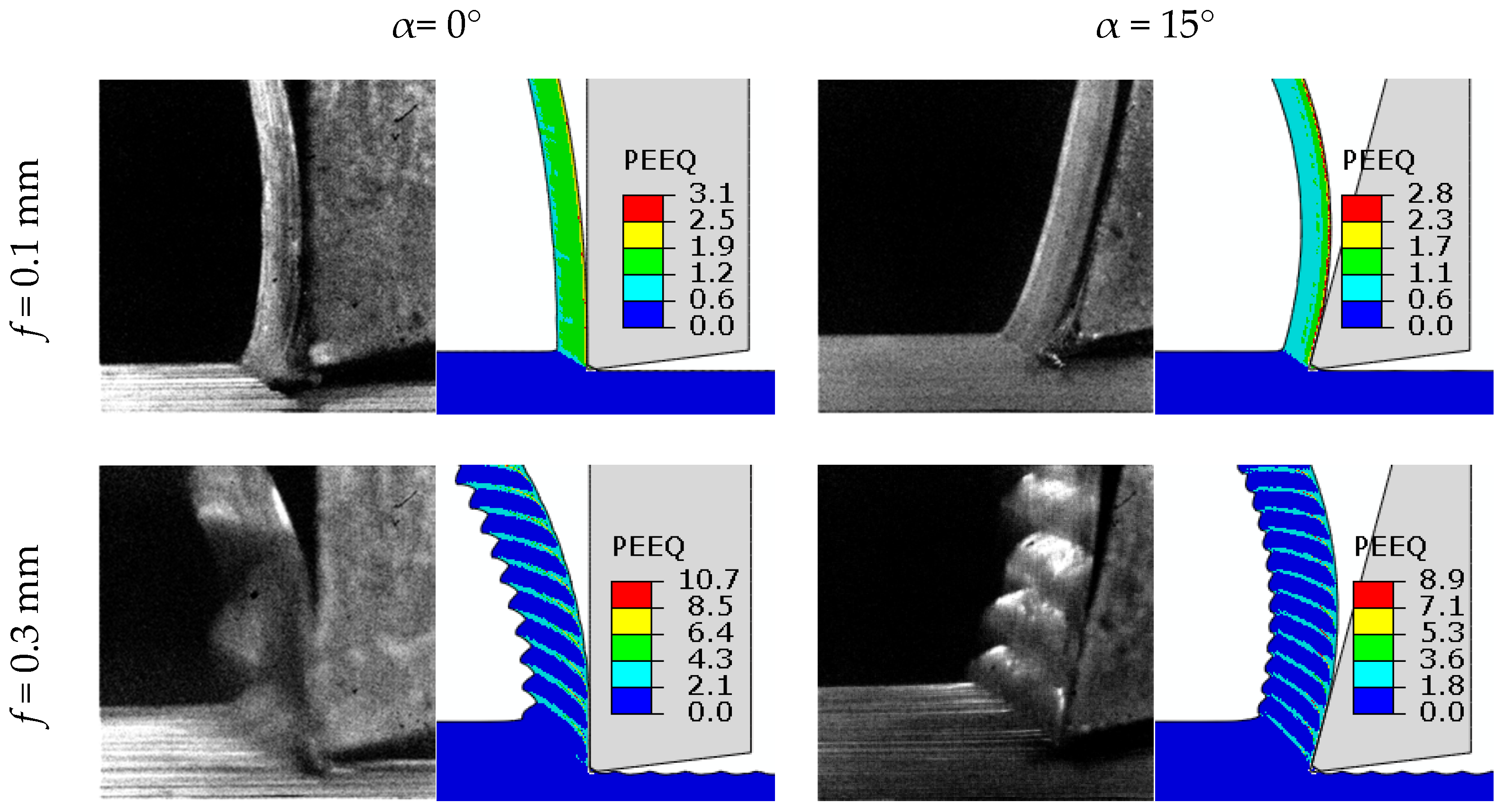
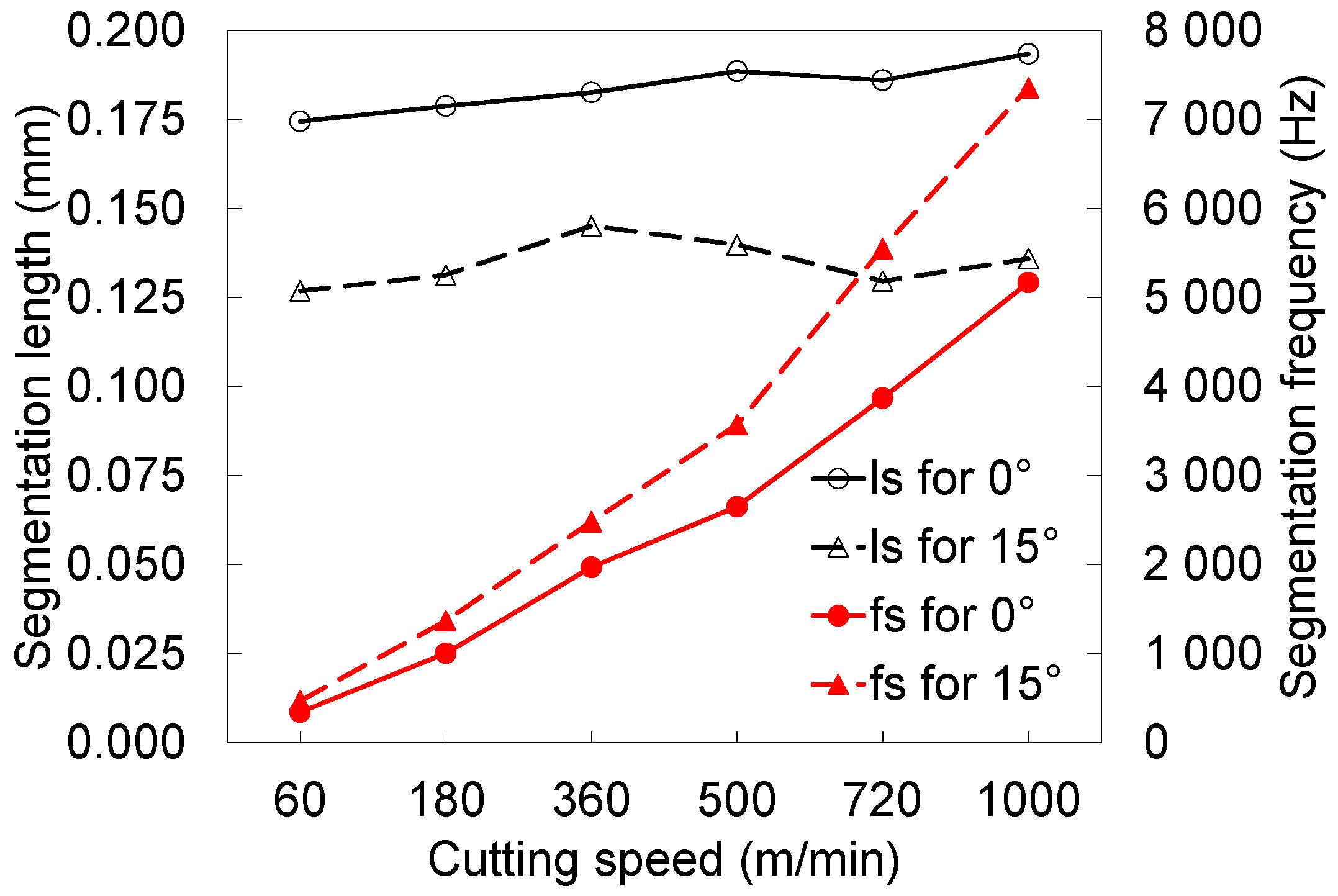
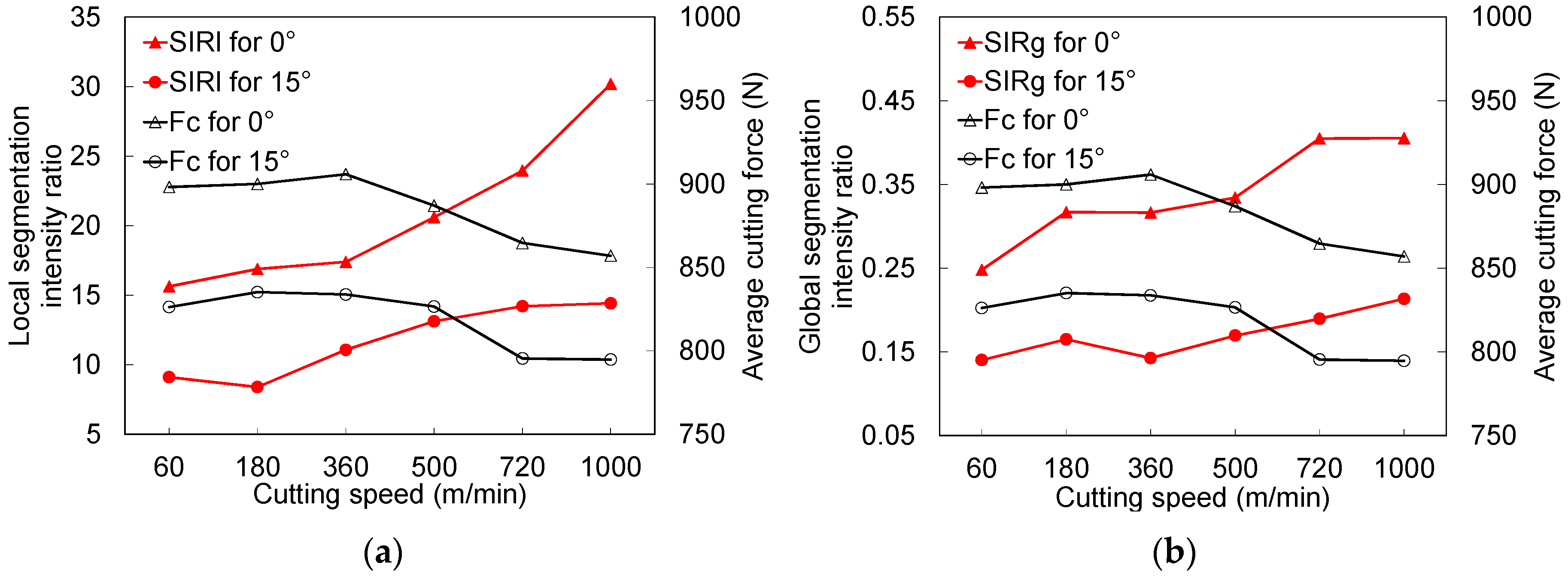
3.2. Chip Morphology-Segmented vs. Continuous Chip
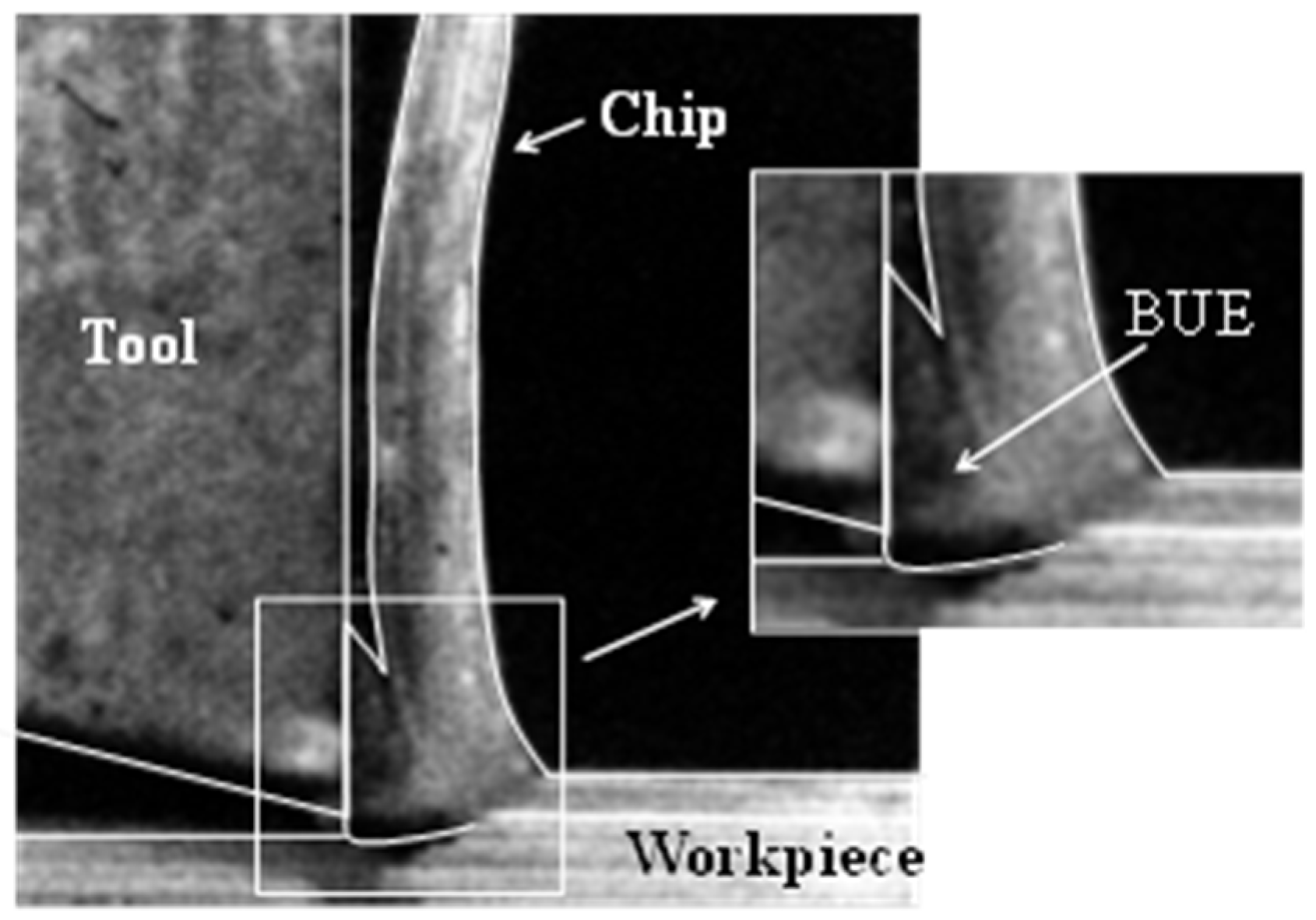
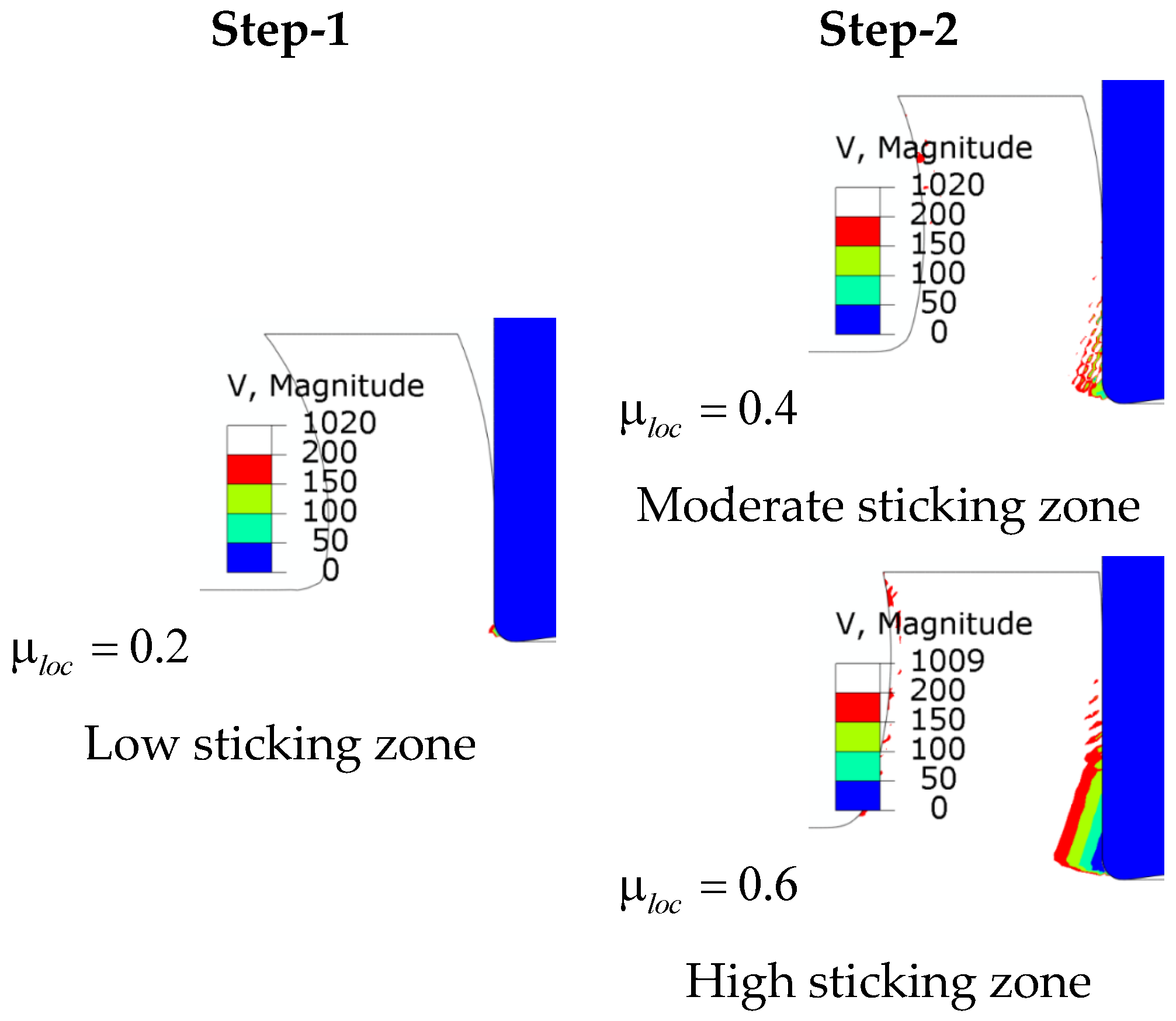
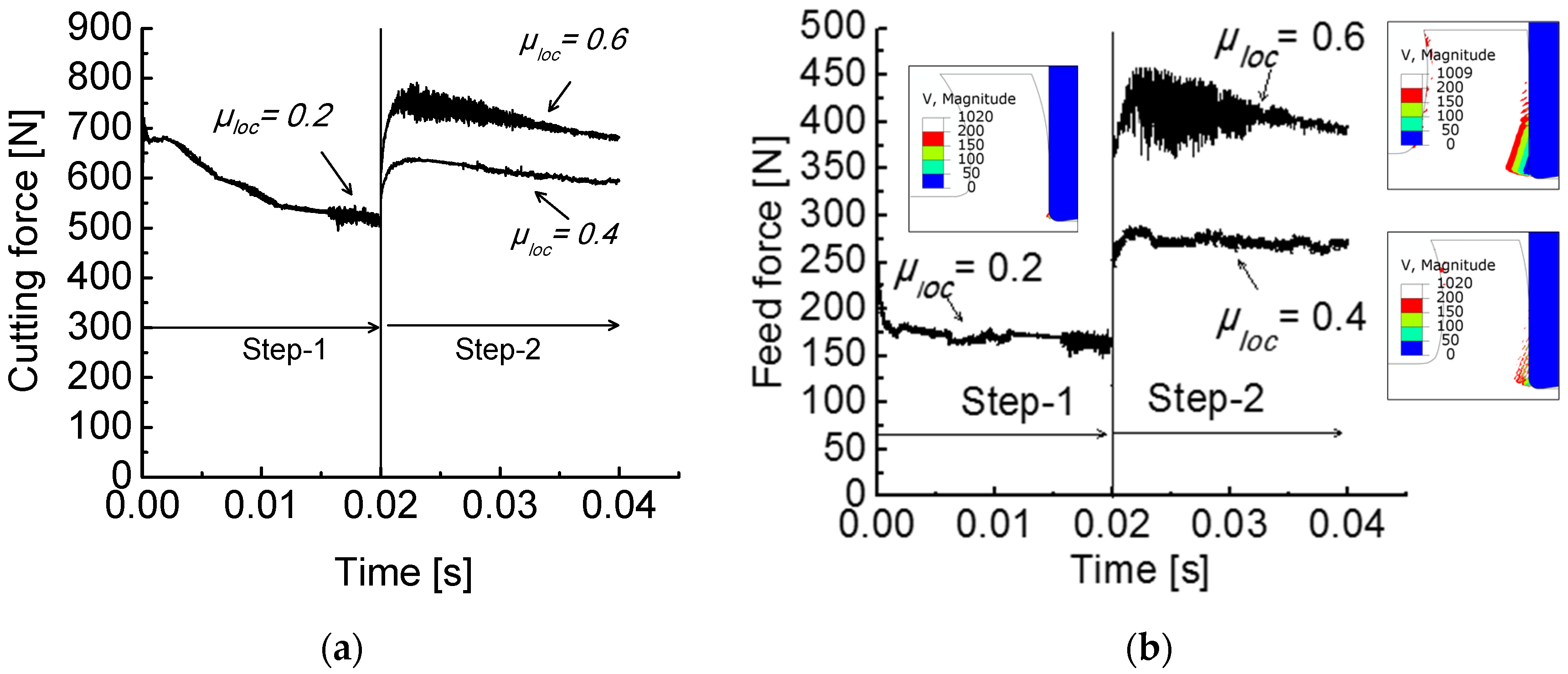
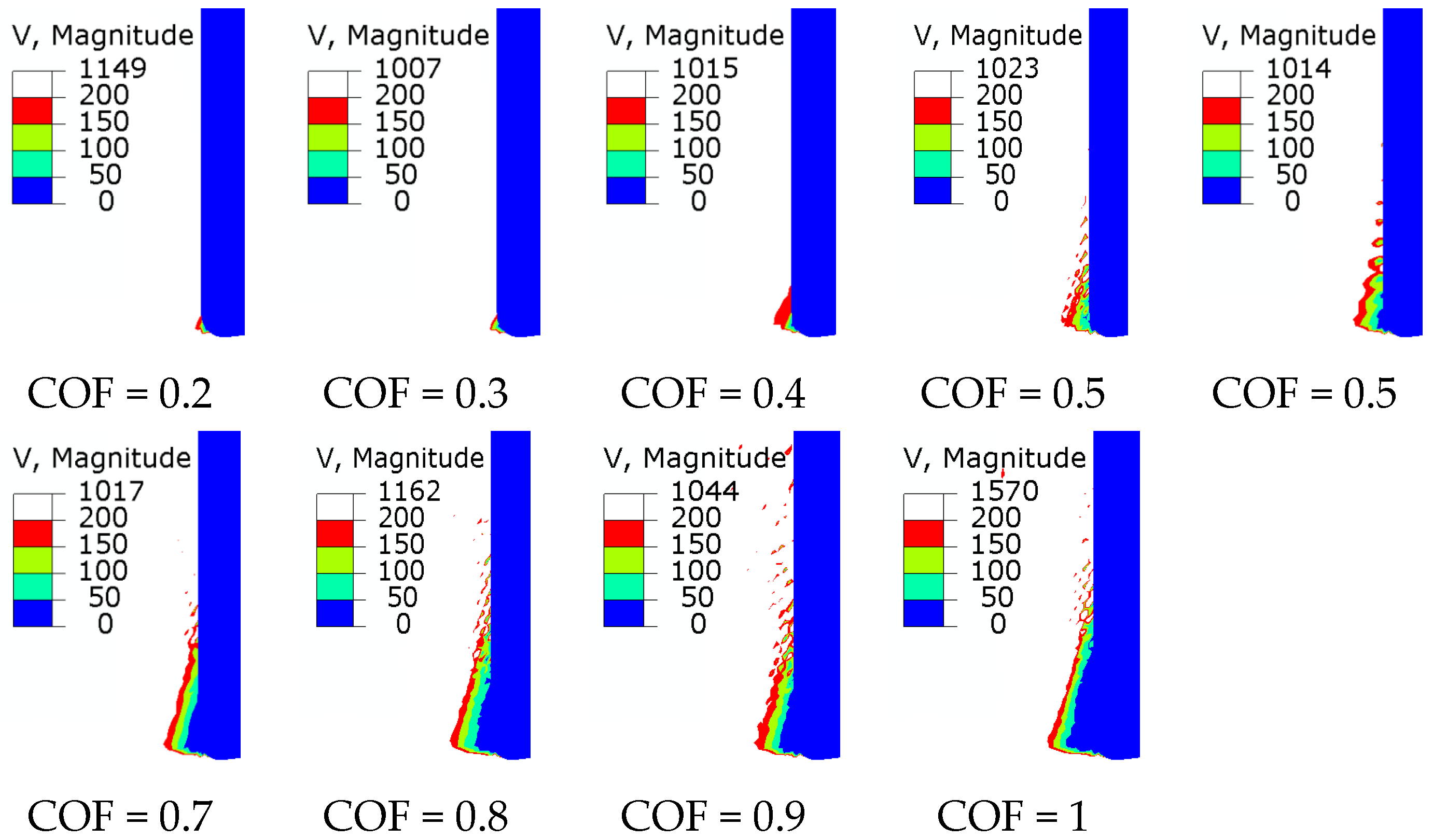
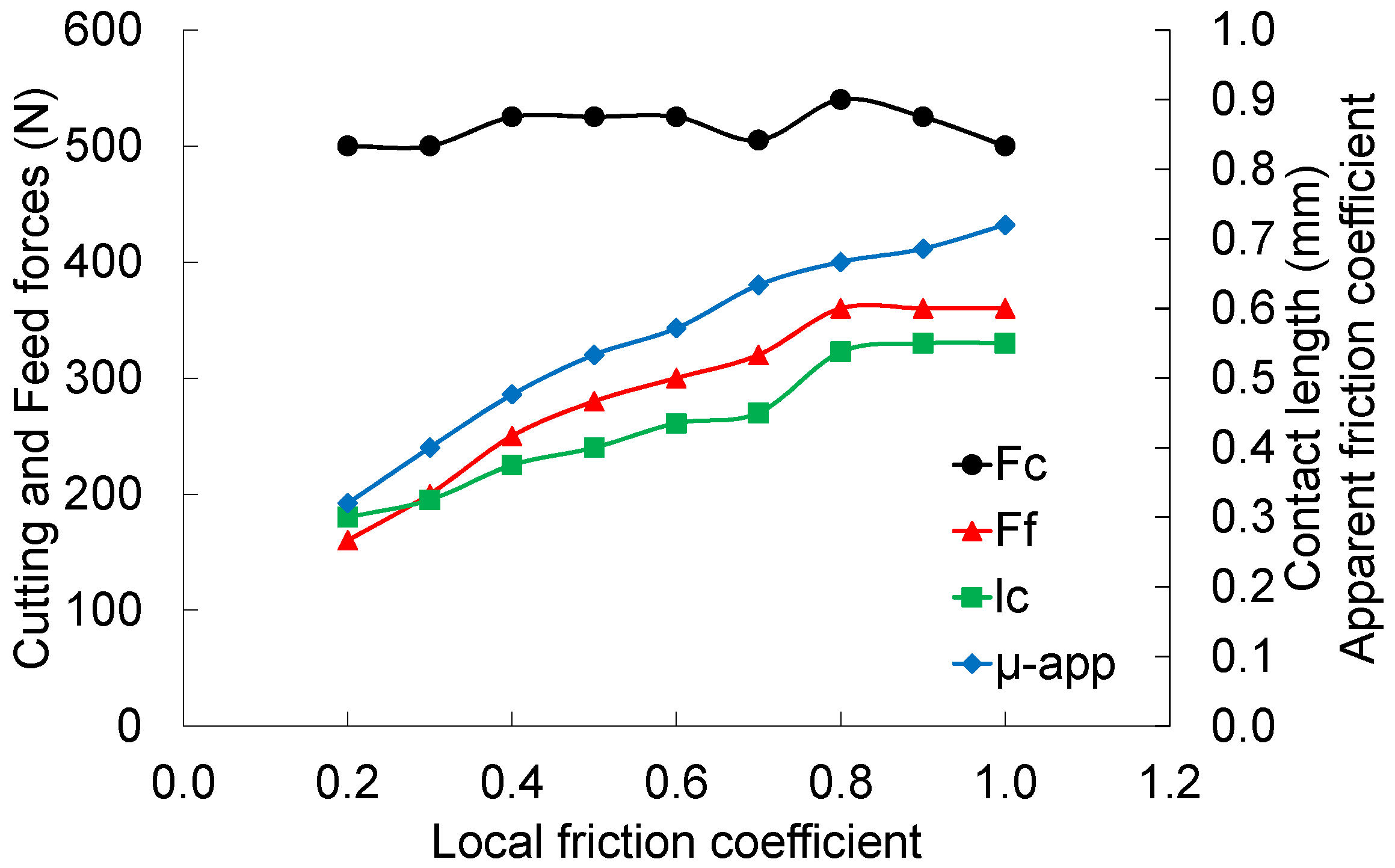
3.3. Built-Up Edge Formation-Time-Dependent Friction
4. Conclusions
- (1)
- Measured cutting forces evolve highly at low cutting speeds for fixed feed and tend to stabilize rapidly at about 100 m/min. LAG-FE and ALE-FE models predict well cutting force, but LAG-FE model fails to predict feed force.
- (2)
- Chip segmentation depends highly on the tool rake angle and the uncut chip thickness.
- (3)
- Using LAG-FE model, it is shown that there is a close link between cutting forces evolution and chip segmentation intensity. So, chip segmentation phenomenon reduces the average cutting forces, but its fluctuation increases.
- (4)
- The BUE can be explained by the contact/friction change at the tool–work material interface during cutting. The ductility of aluminum alloy AA2024-T351 also promotes BUE formation.
- (5)
- The BUE can be modeled by making the friction coefficient time-dependent. This is done in the ALE-FE model. So, the sticking zone becomes larger with the increase of friction coefficient. This condition promotes the BUE formation, but there is no unique scenario of friction evolution as BUE occurs.
Author Contributions
Conflicts of Interest
Abbreviations
| cutting speed (m/min) | |
| feed (mm) | |
| , | tool-rake and clearance angles (°) |
| , | cutting and feed forces (N) |
| contact length (mm) | |
| contact length (mm) | |
| maximum chip thickness | |
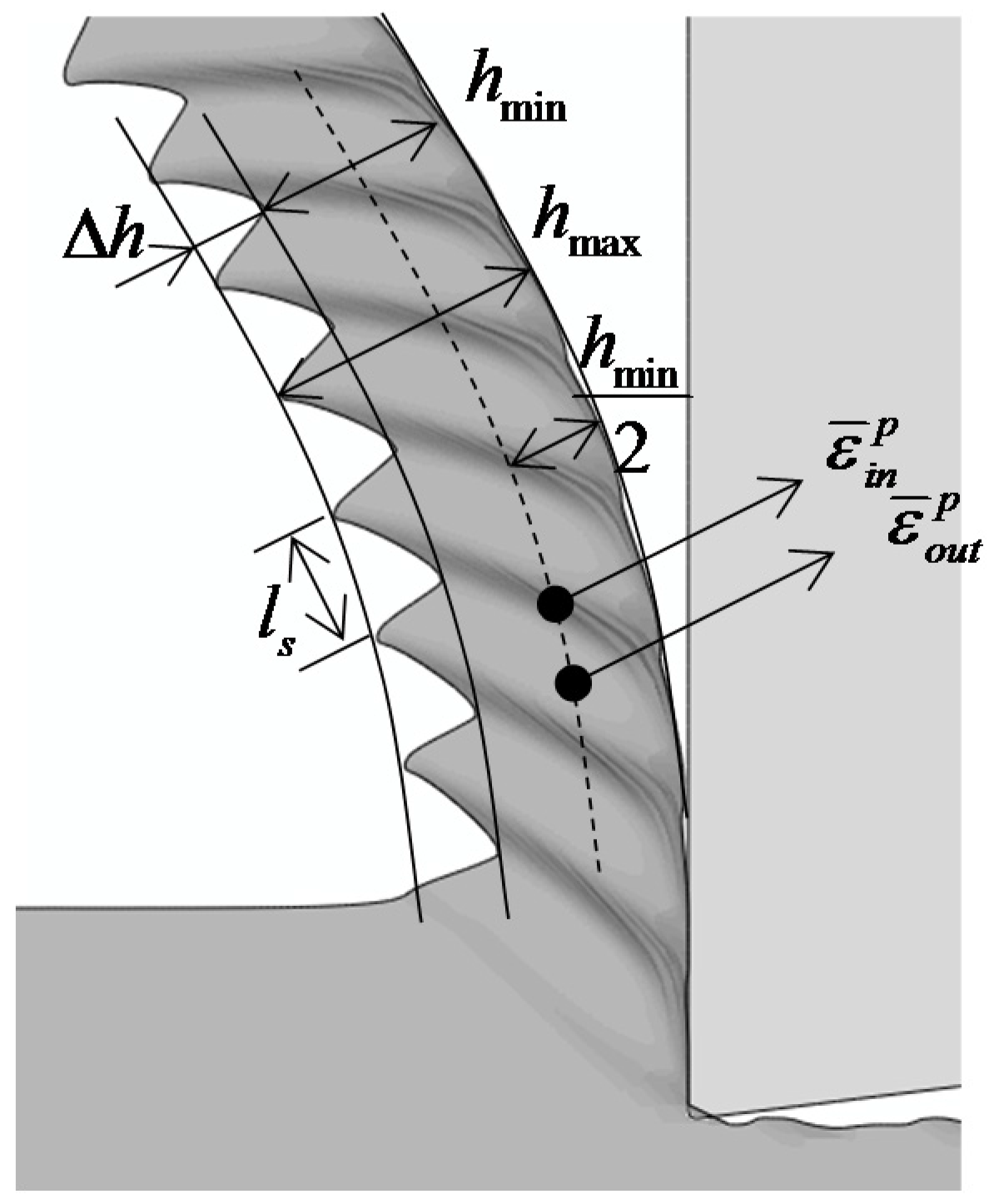
| chip segmentation length | |
| chip segmentation frequency | |
| global segmentation intensity ratio | |
| local segmentation intensity ratio | |
| Cauchy stress tensor (MPa) | |
| effective stress tensor (not affected by damage) | |
| material density (kg/m3) | |
| , | Young modulus (GPa) and Poisson’s ratio |
| , , , , | Johnson-Cook flow stress parameters |
| von Mises equivalent plastic strain | |
| von Mises equivalent plastic strain-rate | |
| Reference equivalent plastic strain-rate | |
| von Mises equivalent stress (MPa) | |
| damage initiation criterion | |
| damage variable | |
| fracture strain energy | |
| contact pressure (MPa) | |
| friction stress (MPa) | |
| COF | local friction coefficient |
| µ-app | apparent friction coefficient |
| shear stress limit (MPa) | |
| sliding velocity at the tool-workpiece interface (m/s) | |
| temperature (°C) | |
| reference ambient temperature (°C) | |
| melting temperature (°C) | |
| tool temperature at the tool-workpiece interface (°C) | |
| workpiece temperature of at the tool-workpiece interface (°C) | |
| thermal conductivity (W/m/°C) | |
| specific heat capacity (J/kg/°C) | |
| thermal expansion (µm/m/°C) | |
| plastic work conversion factor (Taylor-Quinney factor) | |
| frictional work conversion factor | |
| heat partition coefficient | |
| heat transfer coefficient (kW/m2/°C) | |
| volumetric heat generation due to plastic work (W/m3) | |
| heat conduction flux at the tool-workpiece interface (W/m2) | |
| heat flux going into the tool at the tool-workpiece interface (W/m2) | |
| heat flux going into the workpiece at the tool-workpiece interface (W/m2) | |
| Exp. | experiment |
| Num. | Numerical |
| Err. | error (%) |
| Max. | Maximum |
References
- Pauze, N. Fatigue Corrosion dans le Sens Travers Court de Tôles d’aluminium 2024-T351 Présentant des Défauts de Corrosion Localisée. Ph.D. Thesis, Ecole Nationale Supérieure des Mines de Saint-Etienne, Saint-Etienne, France, 2008. [Google Scholar]
- Komanduri, R.; Brown, R.H. On the mechanics of chip segmentation in machining. J. Eng. Ind. 1981, 103, 33–51. [Google Scholar] [CrossRef]
- Bayoumi, A.E.; Xie, J.Q. Some metallurgical aspects of chip formation in cutting Ti-6 wt. % Al-4 wt. % V alloy. Mater. Sci. Eng. A 1995, 190, 173–180. [Google Scholar] [CrossRef]
- Barry, J.; Byrne, G. The mechanisms of chip formation in machining hardened steels. J. Manuf. Sci. Eng. 2002, 124, 528–535. [Google Scholar] [CrossRef]
- Komanduri, R.; von Turkovich, B.F. New observations on the mechanism of chip formation when machining titanium alloys. Wear 1981, 69, 179–188. [Google Scholar] [CrossRef]
- Atlati, S.; Haddag, B.; Nouari, M.; Zenasni, M. Analysis of a new segmentation intensity ratio “SIR” to characterize the chip segmentation process in machining ductile metals. Int. J. Mach. Tools Manuf. 2011, 51, 687–700. [Google Scholar] [CrossRef]
- Kouadri, S.; Necib, K.; Atlati, S.; Haddag, B.; Nouari, M. Quantification of the chip segmentation in metal machining: Application to machining the aeronautical aluminium alloy AA2024-T351 with cemented carbide tools WC-Co. Int. J. Mach. Tools Manuf. 2013, 64, 102–113. [Google Scholar] [CrossRef]
- Ernst, H.; Martellotti, M. The formation of the built-up edge. ASME Mech. Eng. 1938, 57, 487–498. [Google Scholar]
- Shaw, M.C.; Usui, E.; Smith, P.A. Free Machining Steel: III—Cutting Forces; Surface Finish and Chip Formation. J. Eng. Ind. 1961, 83, 181–192. [Google Scholar] [CrossRef]
- Philip, P.K. Built-up edge phenomenon in machining steel with carbide. Int. J. Mach. Tool Des. Res. 1971, 11, 121–132. [Google Scholar] [CrossRef]
- List, G.; Nouari, M.; Géhin, D.; Gomez, S.; Manaud, J.-P.; LePetitcorps, Y.; Girot, F. Wear behaviour of cemented carbide tools in dry machining of aluminium alloy. Wear 2005, 259, 1177–1189. [Google Scholar] [CrossRef]
- List, G. Etude des Mécanismes D’endommagement des Outils Carbure WC-Co par la Caractérisation de l’interface Outil Copeau: Application à l’usinage à sec de l’alliage d’aluminium Aéronautique AA2024-T351. Ph.D. Thesis, Ecole Nationale Supérieure des Arts et Métiers of Bordeaux, Saint-Etienne, France, 2004. [Google Scholar]
- Abaqus/Explicit®. Dassault Systemes 2015. Available online: http://www.3ds.com/products-services/simulia/products/abaqus/abaqusexplicit (accessed on 17 August 2016).



| Al | Cr | Cu | Fe | Mg | Mn | Si | Ti | Zn |
|---|---|---|---|---|---|---|---|---|
| Balanced | Max. 0.1 | 3.8–4.9 | Max. 0.5 | 1.2–1.8 | 0.3–0.9 | Max. 0.5 | Max. 0.15 | Max. 0.25 |
| Cutting Speed (m/min) | Cutting Force (N) | Feed Force (N) | Contact Length (mm) |
|---|---|---|---|
| 80 | 510 | 375 | 0.30 |
| 95 | 475 | 300 | 0.28 |
| 160 | 450 | 280 | 0.26 |
| 195 | 430 | 265 | 0.25 |
| 320 | 410 | 240 | 0.25 |
| 390 | 405 | 235 | 0.23 |
| 500 | 400 | 220 | 0.20 |
| Physical Parameter | Workmaterial (AA2024-T351) | Tool (WC-Co) |
|---|---|---|
| Density, ρ (kg/m3) | 2700 | 11,900 |
| Elastic modulus, E (GPa) | 73 | 534 |
| Poisson’s ratio, ν | 0.33 | 0.22 |
| Specific heat, (J/kg/°C) | 400 | |
| Thermal conductivity, λ (W/m/C) | 50 | |
| Thermal expansion, α (µm·m/°C) | - | |
| Tm (°C) | 520 | - |
| T0 (°C) | 25 | 25 |
| Viscoplastic Parameters | ||||||||
| (Mpa) | (Mpa) | |||||||
| 352 | 440 | 0.42 | 0.0083 | 1 | ||||
| Damage Parameters | ||||||||
| (MPa·m1/2) | (MPa·m1/2) | |||||||
| 0.13 | 0.13 | 1.5 | 0.011 | 0 | 37 | 26 | ||
| Vc (m/min) | Fc (N) | Ff (N) | Lc (mm) | µapp | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | Exp. | Num. | Err. (%) | Exp. | Num. | Err. (%) | Exp. | Num. | Err. (%) | Exp. | Num. | Err. (%) |
| 80 | 510 | 422 | 17 | 375 | 145 | 61 | 0.30 | 0.29 | 3 | 0.74 | 0.34 | 53 |
| 95 | 475 | 408 | 14 | 300 | 118 | 61 | 0.28 | 0.26 | 7 | 0.63 | 0.29 | 54 |
| 160 | 450 | 398 | 12 | 280 | 106 | 62 | 0.26 | 0.25 | 4 | 0.62 | 0.27 | 57 |
| 195 | 430 | 395 | 8 | 265 | 100 | 62 | 0.25 | 0.23 | 8 | 0.62 | 0.25 | 59 |
| 320 | 410 | 397 | 3 | 240 | 87 | 64 | 0.25 | 0.22 | 12 | 0.59 | 0.22 | 62 |
| 390 | 405 | 387 | 4 | 235 | 86 | 64 | 0.23 | 0.22 | 4 | 0.58 | 0.22 | 62 |
| 500 | 400 | 374 | 7 | 220 | 89 | 60 | 0.20 | 0.22 | 10 | 0.55 | 0.24 | 57 |
| Vc (m/min) | Fc (N) | Ff (N) | Lc (mm) | µapp | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | Exp. | Num. | Err. (%) | Exp. | Num. | Err. (%) | Exp. | Num. | Err. (%) | Exp. | Num. | Err. (%) |
| 80 | 510 | 600 | 18 | 375 | 296 | 21 | 0.30 | 0.35 | 17 | 0.74 | 0.49 | 33 |
| 95 | 475 | 520 | 9 | 300 | 280 | 7 | 0.28 | 0.31 | 11 | 0.63 | 0.54 | 15 |
| 160 | 450 | 500 | 11 | 280 | 272 | 3 | 0.26 | 0.31 | 19 | 0.62 | 0.54 | 13 |
| 195 | 430 | 492 | 14 | 265 | 260 | 2 | 0.25 | 0.29 | 16 | 0.62 | 0.53 | 14 |
| 320 | 410 | 448 | 9 | 240 | 248 | 3 | 0.25 | 0.26 | 2 | 0.59 | 0.55 | 5 |
| 390 | 405 | 440 | 9 | 235 | 240 | 2 | 0.23 | 0.24 | 4 | 0.58 | 0.55 | 6 |
| 500 | 400 | 400 | 0 | 220 | 232 | 5 | 0.20 | 0.21 | 5 | 0.55 | 0.58 | 5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddag, B.; Atlati, S.; Nouari, M.; Moufki, A. Dry Machining Aeronautical Aluminum Alloy AA2024-T351: Analysis of Cutting Forces, Chip Segmentation and Built-Up Edge Formation. Metals 2016, 6, 197. https://doi.org/10.3390/met6090197
Haddag B, Atlati S, Nouari M, Moufki A. Dry Machining Aeronautical Aluminum Alloy AA2024-T351: Analysis of Cutting Forces, Chip Segmentation and Built-Up Edge Formation. Metals. 2016; 6(9):197. https://doi.org/10.3390/met6090197
Chicago/Turabian StyleHaddag, Badis, Samir Atlati, Mohammed Nouari, and Abdelhadi Moufki. 2016. "Dry Machining Aeronautical Aluminum Alloy AA2024-T351: Analysis of Cutting Forces, Chip Segmentation and Built-Up Edge Formation" Metals 6, no. 9: 197. https://doi.org/10.3390/met6090197
APA StyleHaddag, B., Atlati, S., Nouari, M., & Moufki, A. (2016). Dry Machining Aeronautical Aluminum Alloy AA2024-T351: Analysis of Cutting Forces, Chip Segmentation and Built-Up Edge Formation. Metals, 6(9), 197. https://doi.org/10.3390/met6090197