Differential Scanning Calorimetry and Thermodynamic Predictions—A Comparative Study of Al-Zn-Mg-Cu Alloys
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
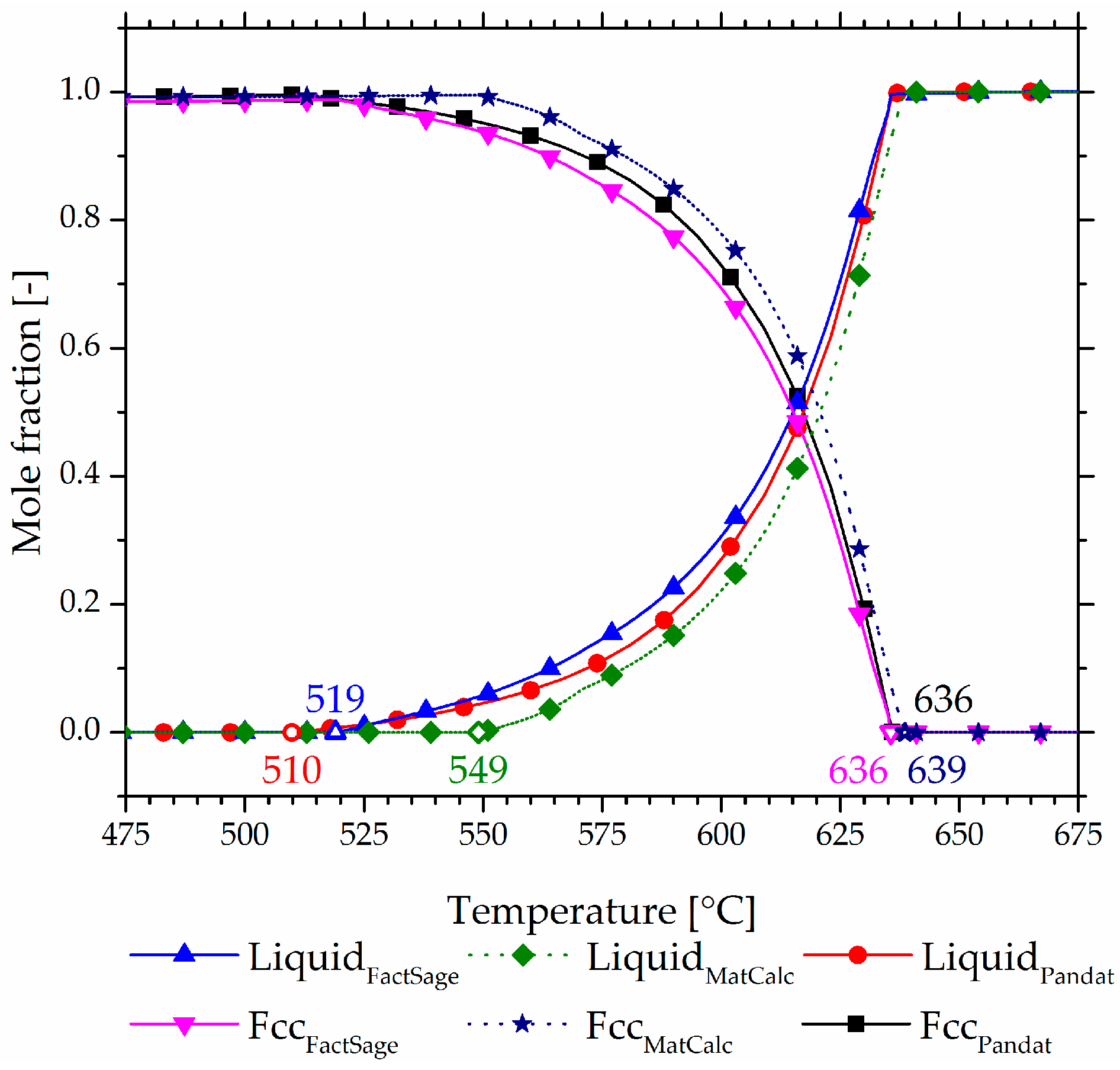
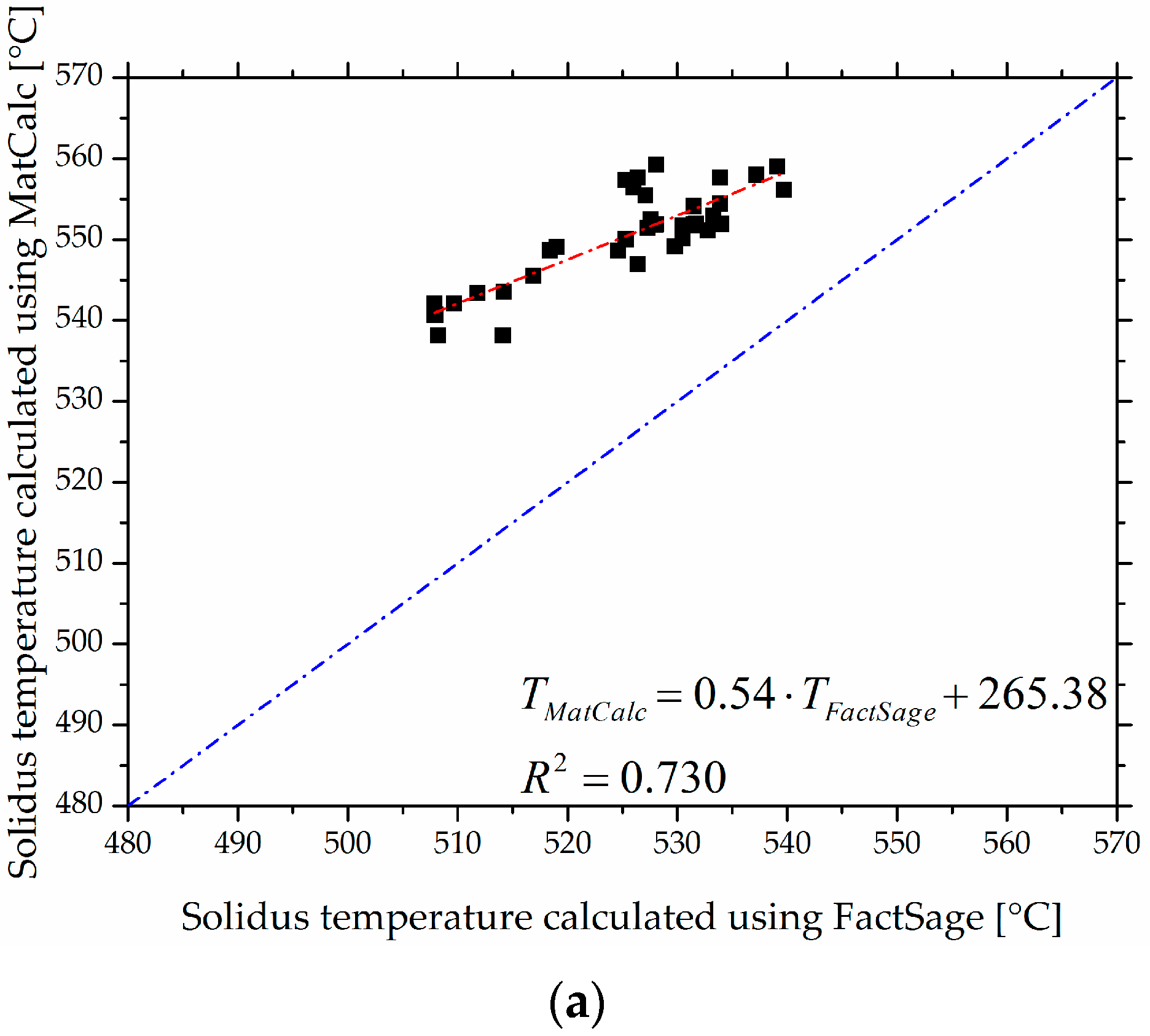
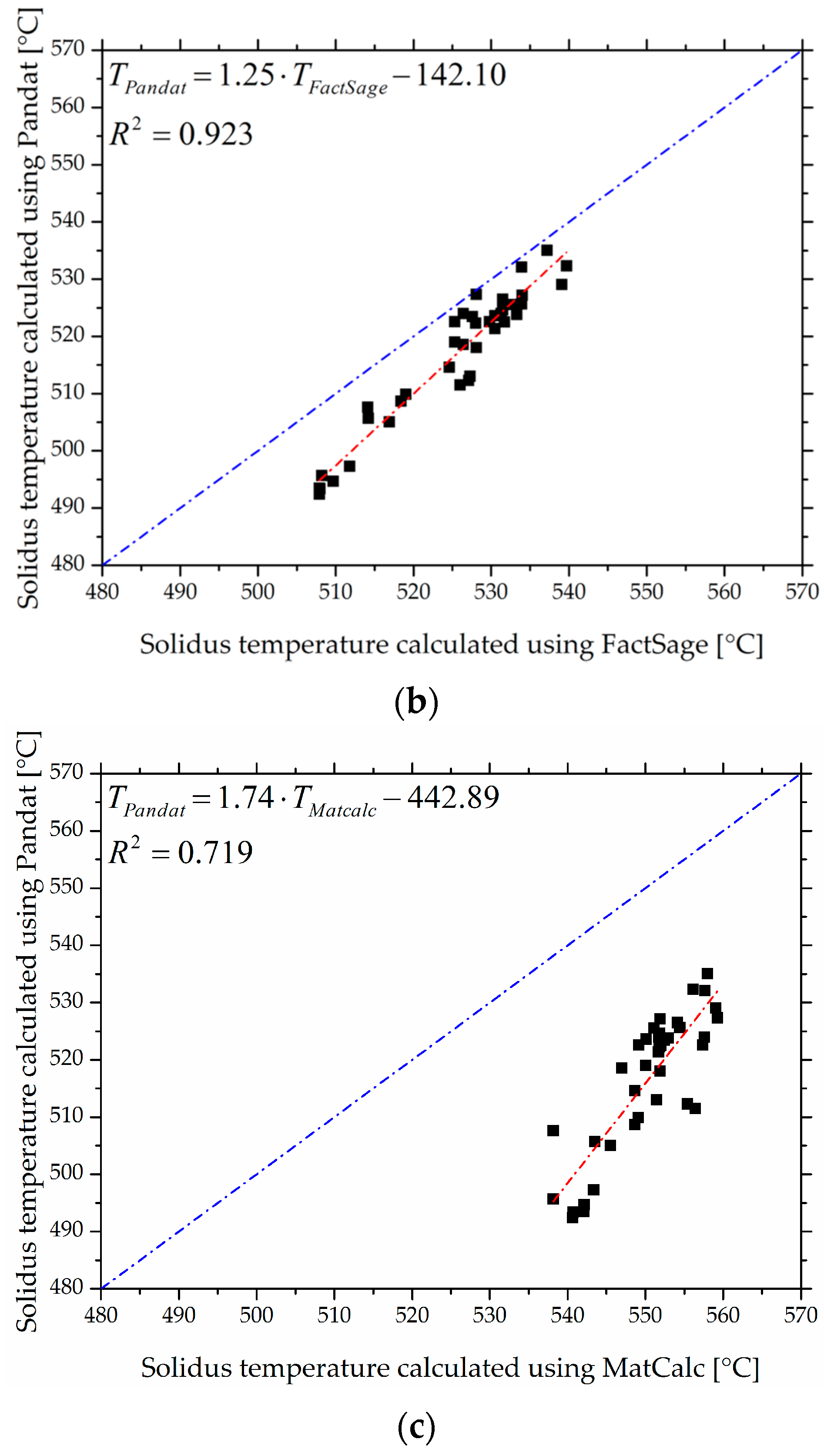
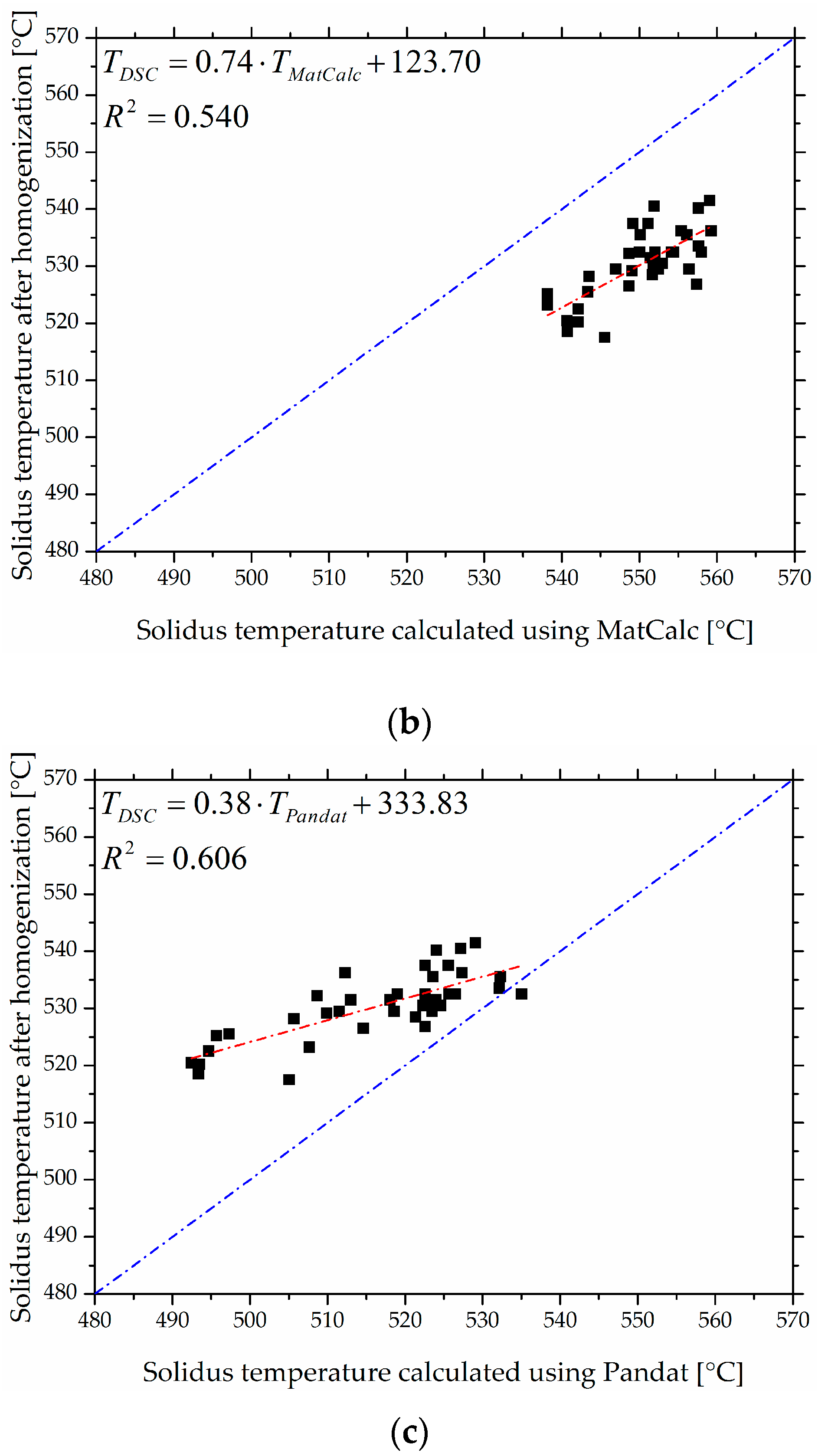
- The CALPHAD tools FactSage®, Pandat™ and MatCalc predict correlated solidus temperature values, although within a maximum observed absolute temperature deviation of 49 °C for various Al-Zn-Mg-Cu alloys.
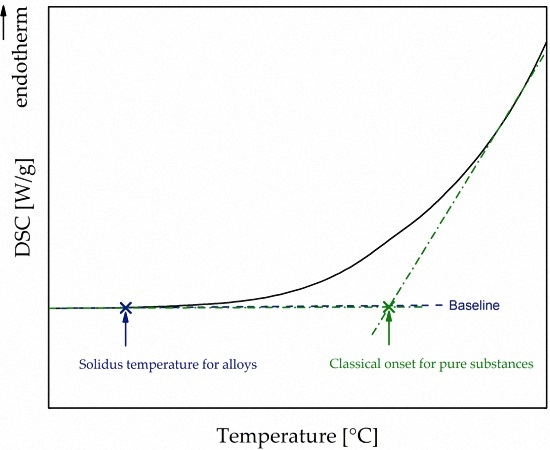
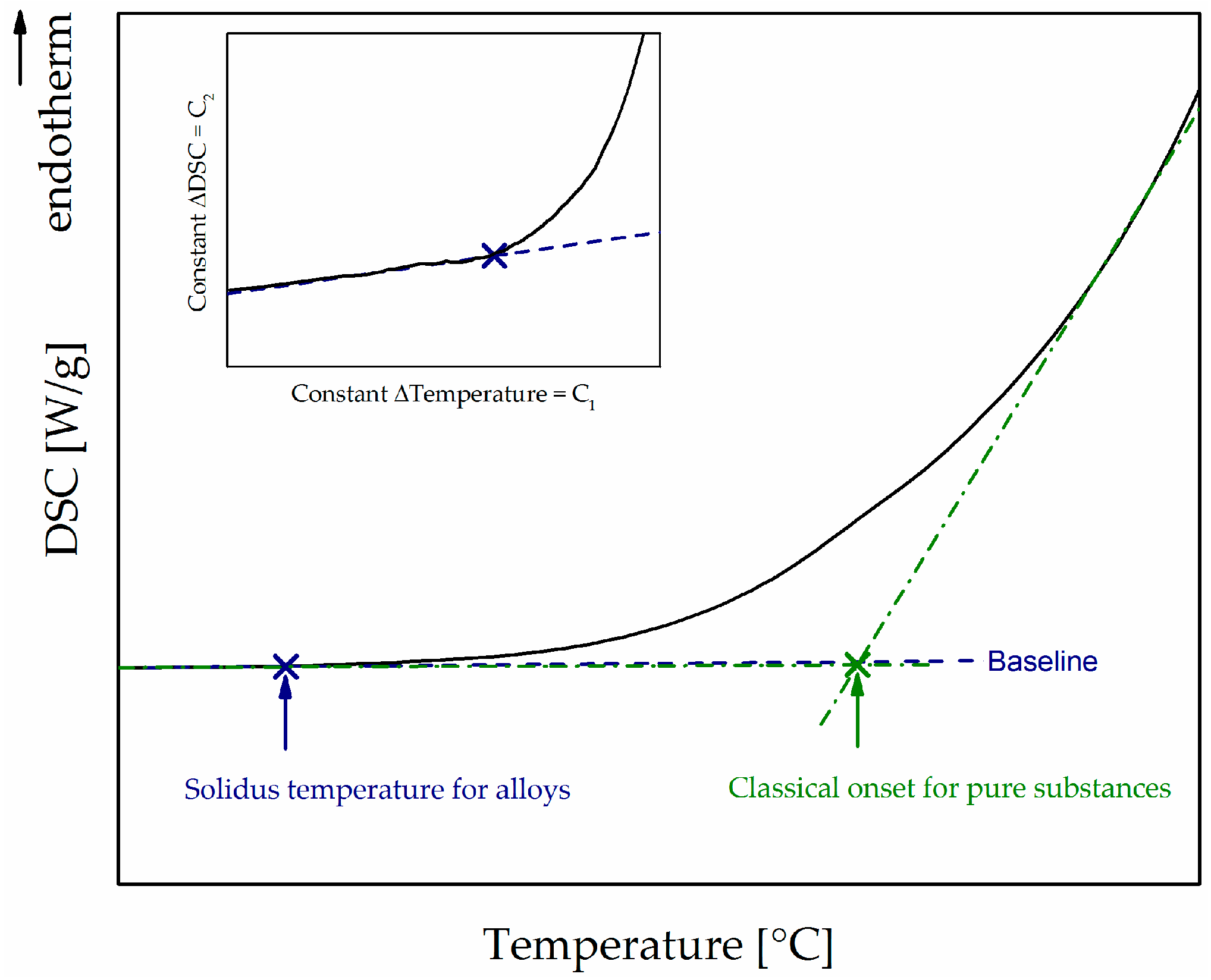
- To compare simulated solidus temperatures to data from DSC measurements, a user-defined method for estimating the solidus temperature for alloys with a broad melting interval was introduced.
- Experimentally determined solidus temperatures agree with the predictions and deviate no more than the predictions of different CALPHAD tools themselves.
Acknowledgments
Author contributions
Conflicts of interest
References
- Dursun, T.; Soutis, C. Recent developments in advanced aircraft aluminium alloys. Mater. Des. 2014, 56, 862–871. [Google Scholar] [CrossRef]
- Heinz, A.; Haszler, A.; Keidel, C.; Moldenhauer, S.; Benedictus, R.; Miller, W.S. Recent development in aluminium alloys for aerospace applications. Mater. Sci. Eng. A 2000, 280, 102–107. [Google Scholar] [CrossRef]
- Lang, P.; Wojcik, T.; Povoden-Karadeniz, E.; Falahati, A.; Kozeschnik, E. Thermo-kinetic prediction of metastable and stable phase precipitation in Al-Zn-Mg series aluminium alloys during non-isothermal DSC analysis. J. Alloy. Compd. 2014, 609, 129–136. [Google Scholar] [CrossRef]
- Deschamps, A.; Livet, F.; Bréchet, Y. Influence of predeformation on ageing in an Al-Zn-Mg alloy—I. Microstructure evolution and mechanical properties. Acta Mater. 1998, 47, 281–292. [Google Scholar] [CrossRef]
- Berg, L.; Gjønnes, J.; Hansen, V.; Li, X.; Knutson-Wedel, M.; Waterloo, G.; Schryvers, D.; Wallenberg, L. GP-zones in Al-Zn-Mg alloys and their role in artificial aging. Acta Mater. 2001, 49, 3443–3451. [Google Scholar] [CrossRef]
- Lim, S.T.; Eun, I.S.; Nam, S.W. Control of Equilibrium Phases (M,T,S) in the Modified Aluminum Alloy 7175 for Thick Forging Applications. Mater. Trans. 2003, 44, 181–187. [Google Scholar] [CrossRef]
- Höhne, G.W.H.; Hemminger, W.F.; Flammersheim, H.-J. Differential Scanning Calorimetry; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Schmitz, S.M. Phasenseparation und Einfuss von Mikrolegierungselementen in Systemen mit metallischer Glasbildung. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, April 2012. [Google Scholar]
- Hillert, M. Partial Gibbs energies from Redlich-Kister polynomials. Thermochim. Acta 1988, 129, 71–75. [Google Scholar] [CrossRef]
- Kattner, U.R. The thermodynamic modeling of multicomponent phase equilibria. JOM 1997, 49, 14–19. [Google Scholar] [CrossRef]
- Das, K.N.; Habibullah, M.; Ghosh, M.; AkberHossain, N. Regression alternative to the redlich-kister equation in the determination of the excess partial molar volumes of the constituents in a binary mixture. Phys. Chem. Liq. 2004, 42, 89–94. [Google Scholar] [CrossRef]
- Dos Santos, I.A.; Klimm, D.; Baldochi, S.L.; Ranieri, I.M. Thermodynamic modeling of the LiF-YF3 phase diagram. J. Cryst. Growth 2012, 360, 172–175. [Google Scholar] [CrossRef]
- Dos Santos, I.A.; Klimm, D.; Baldochi, S.L.; Ranieri, I.M. Experimental evaluation and thermodynamic assessment of the LiF-LuF3 phase diagram. Thermochim. Acta 2013, 552, 137–141. [Google Scholar] [CrossRef]
- Luo, A.A. Material design and development: From classical thermodynamics to CALPHAD and ICME approaches. Calphad 2015, 50, 6–22. [Google Scholar] [CrossRef]
- Bale, C.W.; Chartrand, P.; Degterov, S.A.; Eriksson, G.; Hack, K.; Mahfoud, R.B.; Melançon, J.; Pelton, A.D.; Petersen, S. FactSage thermochemical software and databases. Calphad 2002, 26, 189–228. [Google Scholar] [CrossRef]
- CompuTherm LLC. Software package for calculating phase diagrams and thermodynamic properties of multi-component alloys. Available online: http://www.computherm.com (accessed on 21 May 2016).
- Riesen, R. Wahl der Basislinien. Available online: https://at.mt.com/dam/mt_ext_files/Editorial/Simple/0/basislinien_ta_usercom25ds0106.pdf (accessed on 29 July 2016).
- Hydrate web. DSC. Available online: http://www.hydrateweb.org/dsc (accessed on 9 May 2016).
- Rometsch, P.A.; Zhang, Y.; Knight, S. Heat treatment of 7xxx series aluminium alloys—Some recent developments. Trans. Nonferr. Met. Soc. China 2014, 24, 2003–2017. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. CALPHAD (Calculation of Phase Diagrams). A Comprehensive Guide; Pergamon: Oxford, UK, 1998. [Google Scholar]


| Alloy | Composition (Mass Fraction × 102) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| # | Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
| 1 | 0.40 | 0.40 | 1.69 | 0.26 | 1.37 | 0.24 | 4.15 | 0.13 | Bal. |
| 2 | 0.39 | 0.37 | 1.70 | 0.25 | 1.35 | 0.23 | 6.20 | 0.14 | Bal. |
| 3 | 0.35 | 0.34 | 1.47 | 0.25 | 2.07 | 0.23 | 5.81 | 0.13 | Bal. |
| 4 | 0.18 | 0.10 | 1.26 | 0.10 | 1.87 | 0.16 | 4.73 | 0.05 | Bal. |
| 5 | 0.18 | 0.10 | 1.29 | 0.10 | 2.01 | 0.17 | 5.30 | 0.04 | Bal. |
| 6 | 0.18 | 0.09 | 1.19 | 0.10 | 2.17 | 0.18 | 5.67 | 0.05 | Bal. |
| 7 | 0.18 | 0.10 | 1.29 | 0.10 | 2.22 | 0.16 | 5.96 | 0.04 | Bal. |
| 8 | 0.15 | 0.10 | 1.17 | 0.09 | 2.12 | 0.20 | 5.24 | 0.04 | Bal. |
| 9 | 0.15 | 0.11 | 1.21 | 0.10 | 1.81 | 0.20 | 5.28 | 0.04 | Bal. |
| 10 | 0.16 | 0.11 | 1.31 | 0.10 | 1.88 | 0.20 | 5.64 | 0.04 | Bal. |
| 11 | 0.16 | 0.11 | 1.28 | 0.10 | 1.83 | 0.20 | 5.86 | 0.04 | Bal. |
| 12 | 0.16 | 0.11 | 1.27 | 0.10 | 1.80 | 0.21 | 5.98 | 0.04 | Bal. |
| 13 | 0.14 | 0.02 | 1.19 | 0.10 | 2.36 | 0.16 | 4.97 | 0.04 | Bal. |
| 14 | 0.13 | 0.02 | 1.16 | 0.10 | 2.25 | 0.16 | 5.11 | 0.04 | Bal. |
| 15 | 0.13 | 0.02 | 1.13 | 0.10 | 2.12 | 0.16 | 5.32 | 0.04 | Bal. |
| 16 | 0.13 | 0.02 | 1.16 | 0.10 | 2.14 | 0.16 | 5.73 | 0.04 | Bal. |
| 17 | 0.13 | 0.02 | 1.22 | 0.10 | 2.16 | 0.16 | 5.91 | 0.04 | Bal. |
| 18 | 0.13 | 0.12 | 1.33 | 0.11 | 2.22 | 0.21 | 5.10 | 0.05 | Bal. |
| 19 | 0.13 | 0.12 | 1.32 | 0.11 | 1.83 | 0.21 | 5.28 | 0.05 | Bal. |
| 20 | 0.14 | 0.12 | 1.33 | 0.10 | 1.84 | 0.21 | 5.65 | 0.05 | Bal. |
| 21 | 0.13 | 0.11 | 1.34 | 0.10 | 1.85 | 0.21 | 6.01 | 0.05 | Bal. |
| 22 | 0.13 | 0.11 | 1.30 | 0.10 | 1.79 | 0.21 | 6.29 | 0.06 | Bal. |
| 23 | 0.13 | 0.12 | 1.34 | 0.10 | 1.80 | 0.21 | 6.51 | 0.05 | Bal. |
| 24 | 0.12 | 0.12 | 1.21 | 0.11 | 3.04 | 0.18 | 5.47 | 0.06 | Bal. |
| 25 | 0.13 | 0.12 | 1.30 | 0.11 | 2.89 | 0.17 | 5.75 | 0.05 | Bal. |
| 26 | 0.12 | 0.12 | 1.37 | 0.11 | 2.64 | 0.16 | 6.30 | 0.05 | Bal. |
| 27 | 0.12 | 0.12 | 1.25 | 0.11 | 2.41 | 0.18 | 6.33 | 0.05 | Bal. |
| 28 | 0.14 | 0.13 | 1.37 | 0.11 | 2.47 | 0.16 | 6.79 | 0.05 | Bal. |
| 29 | 0.44 | 0.27 | 1.55 | 0.29 | 2.40 | 0.22 | 5.00 | 0.12 | Bal. |
| 30 | 0.07 | 0.14 | 1.31 | 0.11 | 2.07 | 0.20 | 5.64 | 0.11 | Bal. |
| 31 | 0.08 | 0.14 | 1.19 | 0.10 | 2.93 | 0.17 | 5.97 | 0.11 | Bal. |
| 32 | 0.06 | 0.03 | 1.33 | 0.10 | 2.38 | 0.17 | 6.02 | 0.08 | Bal. |
| 33 | 0.06 | 0.03 | 1.39 | 0.10 | 2.32 | 0.17 | 6.74 | 0.08 | Bal. |
| 34 | 0.06 | 0.03 | 1.30 | 0.10 | 2.20 | 0.17 | 6.65 | 0.09 | Bal. |
| 35 | 0.07 | 0.13 | 1.24 | 0.11 | 2.09 | 0.20 | 5.57 | 0.11 | Bal. |
| 36 | 0.07 | 0.15 | 1.27 | 0.11 | 2.05 | 0.20 | 6.04 | 0.10 | Bal. |
| 37 | 0.06 | 0.13 | 1.19 | 0.11 | 2.65 | 0.20 | 5.57 | 0.10 | Bal. |
| 38 | 0.07 | 0.13 | 1.21 | 0.11 | 2.50 | 0.20 | 5.85 | 0.10 | Bal. |
| Alloy # | Ts DSC"homogenized" (°C) | Ts FactSage® (°C) | Ts MatCalc (°C) | Ts Pandat™ (°C) |
|---|---|---|---|---|
| 1 | 542 | 539 | 559 | 529 |
| 2 | 532 | 527 | 551 | 513 |
| 3 | 530 | 526 | 556 | 512 |
| 4 | 536 | 540 | 556 | 532 |
| 5 | 531 | 533 | 553 | 524 |
| 6 | 529 | 531 | 552 | 521 |
| 7 | 527 | 525 | 549 | 515 |
| 8 | 533 | 534 | 554 | 526 |
| 9 | 533 | 537 | 558 | 535 |
| 10 | 533 | 532 | 552 | 523 |
| 11 | 532 | 531 | 552 | 524 |
| 12 | 531 | 532 | 552 | 525 |
| 13 | 536 | 531 | 550 | 524 |
| 14 | 538 | 533 | 551 | 526 |
| 15 | 541 | 534 | 552 | 527 |
| 16 | 538 | 530 | 549 | 523 |
| 17 | 530 | 526 | 547 | 519 |
| 18 | 532 | 528 | 552 | 518 |
| 19 | 534 | 534 | 558 | 532 |
| 20 | 533 | 532 | 554 | 527 |
| 21 | 531 | 528 | 552 | 522 |
| 22 | 530 | 528 | 552 | 524 |
| 23 | 533 | 525 | 550 | 519 |
| 24 | 526 | 512 | 543 | 497 |
| 25 | 523 | 510 | 542 | 495 |
| 26 | 521 | 508 | 541 | 493 |
| 27 | 518 | 517 | 546 | 505 |
| 28 | 519 | 508 | 541 | 493 |
| 29 | 536 | 527 | 555 | 512 |
| 30 | 540 | 526 | 558 | 520 |
| 31 | 520 | 508 | 542 | 494 |
| 32 | 528 | 514 | 544 | 506 |
| 33 | 525 | 508 | 538 | 496 |
| 34 | 523 | 514 | 538 | 508 |
| 35 | 536 | 528 | 559 | 527 |
| 36 | 527 | 525 | 557 | 523 |
| 37 | 532 | 518 | 549 | 509 |
| 38 | 529 | 519 | 549 | 510 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolb, G.K.-H.; Scheiber, S.; Antrekowitsch, H.; Uggowitzer, P.J.; Pöschmann, D.; Pogatscher, S. Differential Scanning Calorimetry and Thermodynamic Predictions—A Comparative Study of Al-Zn-Mg-Cu Alloys. Metals 2016, 6, 180. https://doi.org/10.3390/met6080180
Kolb GK-H, Scheiber S, Antrekowitsch H, Uggowitzer PJ, Pöschmann D, Pogatscher S. Differential Scanning Calorimetry and Thermodynamic Predictions—A Comparative Study of Al-Zn-Mg-Cu Alloys. Metals. 2016; 6(8):180. https://doi.org/10.3390/met6080180
Chicago/Turabian StyleKolb, Gernot K.-H., Stefanie Scheiber, Helmut Antrekowitsch, Peter J. Uggowitzer, Daniel Pöschmann, and Stefan Pogatscher. 2016. "Differential Scanning Calorimetry and Thermodynamic Predictions—A Comparative Study of Al-Zn-Mg-Cu Alloys" Metals 6, no. 8: 180. https://doi.org/10.3390/met6080180
APA StyleKolb, G. K.-H., Scheiber, S., Antrekowitsch, H., Uggowitzer, P. J., Pöschmann, D., & Pogatscher, S. (2016). Differential Scanning Calorimetry and Thermodynamic Predictions—A Comparative Study of Al-Zn-Mg-Cu Alloys. Metals, 6(8), 180. https://doi.org/10.3390/met6080180