Onset Frequency of Fatigue Effects in Pure Aluminum and 7075 (AlZnMg) and 2024 (AlCuMg) Alloys
Abstract
:1. Introduction
1.1. Influence of the Loading Frequency on the Fatigue Response of Metals
1.2. Influence of Temperature on the Fatigue Response of Al Alloys
1.3. Influence of the Microstructure on the Fatigue Response of Al Alloys
2. Materials and Methods
3. Results and Discussion
3.1. Storage Modulus
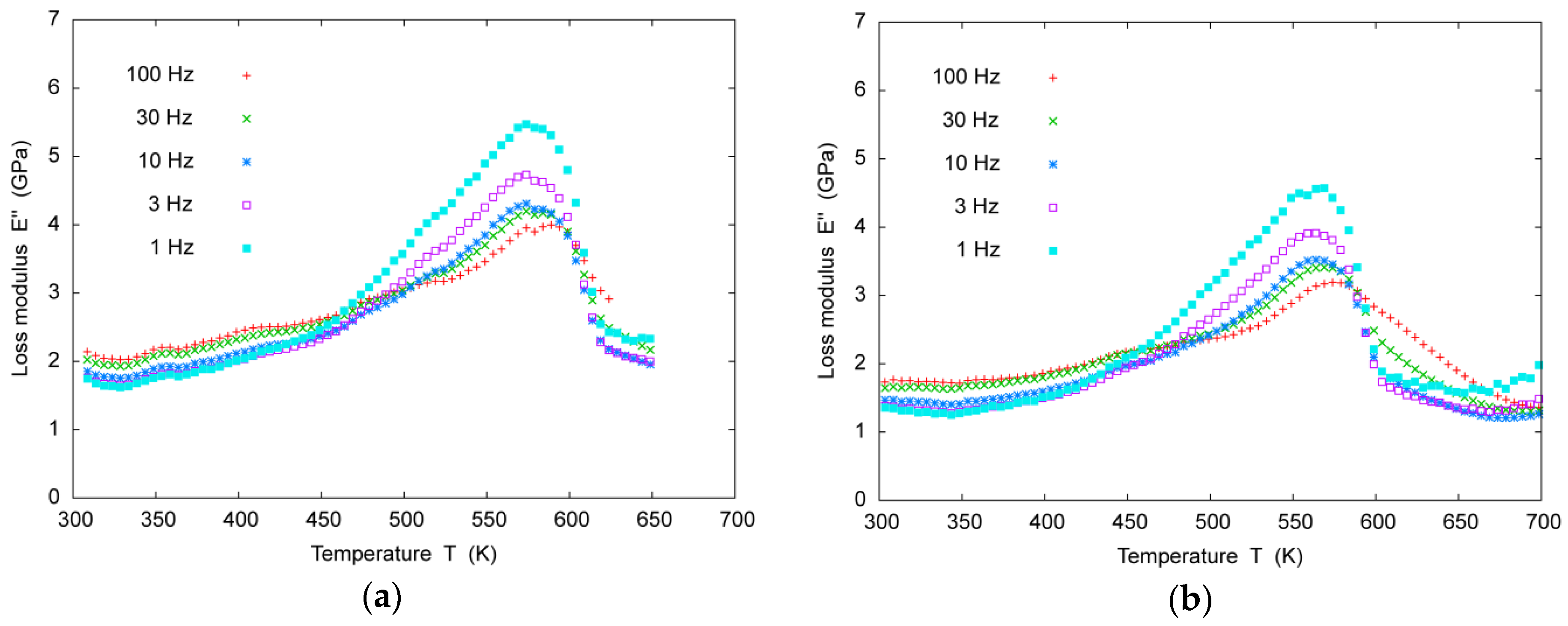
3.2. Loss Modulus
3.3. Temperature Dependence of the Storage Modulus
3.4. Effect of Internal Friction on Fatigue Strength
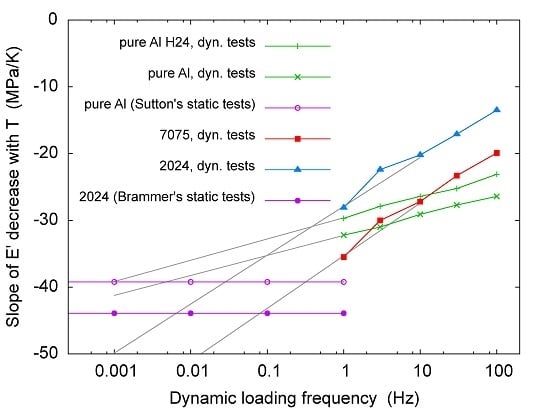
3.5. Onset Frequency of Fatigue Effects
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AA | Aluminum alloy(s) |
| bcc | Body-centered cubic |
| CFCG | Creep-fatigue crack growth |
| CCG | Creep crack growth |
| DMA | Dynamic-mechanical analyzer |
| fcc | Face-centered cubic |
| FCG | Fatigue crack growth |
| GPBZ | Guinier–Preston–Bagariastkij zones |
| GPZ | Guinier–Preston zones |
| HCF | High cycle fatigue |
| RT | Room temperature |
| VHCF | Very high cycle fatigue |
References
- Callister, W.D.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering, 4th ed.; John Wiley & Sons, Ltd.: Singapore, Singapore, 2013; pp. 1–910. [Google Scholar]
- Van Kranenburg, C. Fatigue Crack Growth in Aluminium Alloys; Technische Universiteit Delft: Delft, The Netherlands, 2010; Volume 1, pp. 1–194. [Google Scholar]
- Srivatsan, T.S.; Kolar, D.; Magnusen, P. Influence of temperature on cyclic stress response, strain resistance, and fracture behavior of aluminum alloy 2524. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2001, 314, 118–130. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. Life prediction of metals undergoing fatigue load based on temperature evolution. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2010, 527, 1555–1559. [Google Scholar] [CrossRef]
- Rojas, J.I.; Aguiar, A.; Crespo, D. Effect of temperature and frequency of dynamic loading in the viscoelastic properties of aluminium alloy 7075-T6. Phys. Status Solidi C 2011, 8, 3111–3114. [Google Scholar] [CrossRef]
- Rojas, J.I.; Crespo, D. Modeling of the effect of temperature, frequency and phase transformations on the viscoelastic properties of AA 7075-T6 and AA 2024-T3 aluminum alloys. Metall. Mater. Trans. A 2012, 43, 4633–4646. [Google Scholar] [CrossRef]
- Nowick, A.S.; Berry, B.S. Anelastic Relaxation in Crystalline Solids, 1st ed.; Academic Press: New York, NY, USA, 1972; pp. 1–677. [Google Scholar]
- Starke, E.A.; Staley, J.T. Application of modern aluminum alloys to aircraft. Prog. Aerosp. Sci. 1996, 32, 131–172. [Google Scholar] [CrossRef]
- Hong, Y.; Zhao, A.; Qian, G. Essential characteristics and influential factors for very-high-cycle fatigue behavior of metallic materials. Acta Metall. Sin. 2009, 45, 769–780. [Google Scholar]
- Braun, R. Transgranular environment-induced cracking of 7050 aluminium alloy under cyclic loading conditions at low frequencies. Int. J. Fatigue 2008, 30, 1827–1837. [Google Scholar] [CrossRef]
- Nikitin, I.; Besel, M. Effect of low-frequency on fatigue behaviour of austenitic steel AISI 304 at room temperature and 25 °C. Int. J. Fatigue 2008, 30, 2044–2049. [Google Scholar] [CrossRef]
- Furuya, Y.; Matsuoka, S.; Abe, T.; Yamaguchi, K. Gigacycle fatigue properties for high-strength low-alloy steel at 100 Hz, 600 Hz, and 20 kHz. Scr. Mater. 2002, 46, 157–162. [Google Scholar] [CrossRef]
- Papakyriacou, M.; Mayer, H.; Pypen, C.; Plenk, H.; Stanzl-Tschegg, S. Influence of loading frequency on high cycle fatigue properties of b.c.c. and h.c.p. metals. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2001, 308, 143–152. [Google Scholar] [CrossRef]
- Zhu, X.; Jones, J.W.; Allison, J.E. Effect of frequency, environment, and temperature on fatigue behavior of E319 cast aluminum alloy: Stress-controlled fatigue life response. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2008, 39A, 2681–2688. [Google Scholar] [CrossRef]
- Mayer, H.; Papakyriacou, M.; Pippan, R.; Stanzl-Tschegg, S. Influence of loading frequency on the high cycle fatigue properties of AlZnMgCu1.5 aluminium alloy. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2001, 314, 48–54. [Google Scholar] [CrossRef]
- Liaw, P.K.; Wang, H.; Jiang, L.; Yang, B.; Huang, J.Y.; Kuo, R.C.; Huang, J.G. Thermographic detection of fatigue damage of pressure vessel steels at 1000 Hz and 20 Hz. Scr. Mater. 2000, 42, 389–395. [Google Scholar] [CrossRef]
- Urabe, N.; Weertman, J. Dislocation mobility in potassium and iron single-crystals. Mater. Sci. Eng. 1975, 18, 41–49. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T. Factors influencing the mechanism of superlong fatigue failure in steels. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 581–590. [Google Scholar] [CrossRef]
- Mayer, H. Fatigue crack growth and threshold measurements at very high frequencies. Int. Mater. Rev. 1999, 44, 1–34. [Google Scholar] [CrossRef]
- Laird, C.; Charsley, P. Ultrasonic Fatigue, 1st ed.; The Metallurgical Society of AIME: Philadelphia, PA, USA, 1982. [Google Scholar]
- Yan, N.; Wang, Q.Y.; Chen, Q.; Sun, J.J. Influence of loading frequency on fatigue behavior of high strength steel. Prog. Fract. Strength Mater. Struct. 2007, 353–358, 227–230. [Google Scholar] [CrossRef]
- Verkin, B.I.; Grinberg, N.M. Effect of vacuum on the fatigue behavior of metals and alloys. Mater. Sci. Eng. 1979, 41, 149–181. [Google Scholar] [CrossRef]
- Menan, F.; Henaff, G. Influence of frequency and waveform on corrosion fatigue crack propagation in the 2024-T351 aluminium alloy in the S-L orientation. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2009, 519, 70–76. [Google Scholar] [CrossRef]
- Benson, D.K.; Hancock, J.R. Effect of strain rate on cyclic response of metals. Metall. Trans. 1974, 5, 1711–1715. [Google Scholar] [CrossRef]
- Nikbin, K.; Radon, J. Prediction of fatigue interaction from static creep and high frequency fatigue crack growth data. In Advances in Fracture Research, Proceedings of the 9th International Conference in Fracture (ICF9), Sydney, Australia, 1–5 April 1997; Karihaloo, B.L., Mai, Y.W., Ripley, M.I., Ritchie, R.O., Eds.; Pergamon Press, Ltd.: Kidlington, UK, 1997; Volume 1–6, p. 429. [Google Scholar]
- Henaff, G.; Odemer, G.; Benoit, G.; Koffi, E.; Journet, B. Prediction of creep-fatigue crack growth rates in inert and active environments in an aluminium alloy. Int. J. Fatigue 2009, 31, 1943–1951. [Google Scholar] [CrossRef]
- Botny, R.; Kaleta, K.; Grzebien, W.; Adamczewski, W. A method for determining the heat energy of the fatigue process in metals under uniaxial stress: Part 2. Measurement of the temperature of a fatigue specimen by means of thermovision camera-computer system. Int. J. Fatigue 1986, 8, 35–38. [Google Scholar] [CrossRef]
- Luong, M.P. Fatigue limit evaluation of metals using an infrared thermographic technique. Mech. Mater. 1998, 28, 155–163. [Google Scholar] [CrossRef]
- Chung, T.E.; Faulkner, R.G. Parametric representation of fatigue in alloys and its relation to microstructure. Mater. Sci. Technol. 1990, 6, 1187–1192. [Google Scholar] [CrossRef]
- Rojas, J.I.; Lopez-Ponte, X.; Crespo, D. Effect of temperature, frequency and phase transformations on the viscoelastic behavior of commercial 6082 (Al-Mg-Si) alloy. J. Alloys Compd. in preparation.
- Jeong, H.T.; Kim, J.H.; Kim, W.T.; Kim, D.H. The mechanical relaxations of a Mm55Al25Ni10Cu10 amorphous alloy studied by dynamic mechanical analysis. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2004, 385, 182–186. [Google Scholar] [CrossRef]
- Belhas, S.; Riviere, A.; Woirgard, J.; Vergnol, J.; Defouquet, J. High-temperature relaxation mechanisms in Cu-Al solid-solutions. J. Phys. 1985, 46, 367–370. [Google Scholar] [CrossRef]
- Riviere, A.; Gerland, M.; Pelosin, V. Influence of dislocation networks on the relaxation peaks at intermediate temperature in pure metals and metallic alloys. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2009, 521–522, 94–97. [Google Scholar] [CrossRef]
- Mondino, M.; Schoeck, G. Coherency loss and internal friction. Phys. Status Solidi A Appl. Res. 1971, 6, 665–670. [Google Scholar] [CrossRef]
- Brammer, J.A.; Percival, C.M. Elevated-temperature elastic moduli of 2024-aluminum obtained by a laser-pulse technique. Exp. Mech. 1970, 10, 245–250. [Google Scholar] [CrossRef]
- Sutton, P.M. The variation of the elastic constants of crystalline aluminum with temperature between 63 K and 773 K. Phys. Rev. 1953, 91, 816–821. [Google Scholar] [CrossRef]
- Kamm, G.N.; Alers, G.A. Low temperature elastic moduli of aluminum. J. Appl. Phys. 1964, 35, 327–330. [Google Scholar] [CrossRef]
- Varshni, Y.P. Temperature dependence of the elastic constants. Phys. Rev. B 1970, 2, 3952–3958. [Google Scholar] [CrossRef]
- Wolfenden, A.; Wolla, J.M. Mechanical damping and dynamic modulus measurements in alumina and tungsten fiber-reinforced aluminum composites. J. Mater. Sci. 1989, 24, 3205–3212. [Google Scholar] [CrossRef]
- Granato, A.; Lucke, K. Theory of mechanical damping due to dislocations. J. Appl. Phys. 1956, 27, 583–593. [Google Scholar] [CrossRef]
- Zhang, Y.; Godfrey, A.; Jensen, D.J. Local boundary migration during recrystallization in pure aluminium. Scr. Mater. 2011, 64, 331–334. [Google Scholar] [CrossRef]

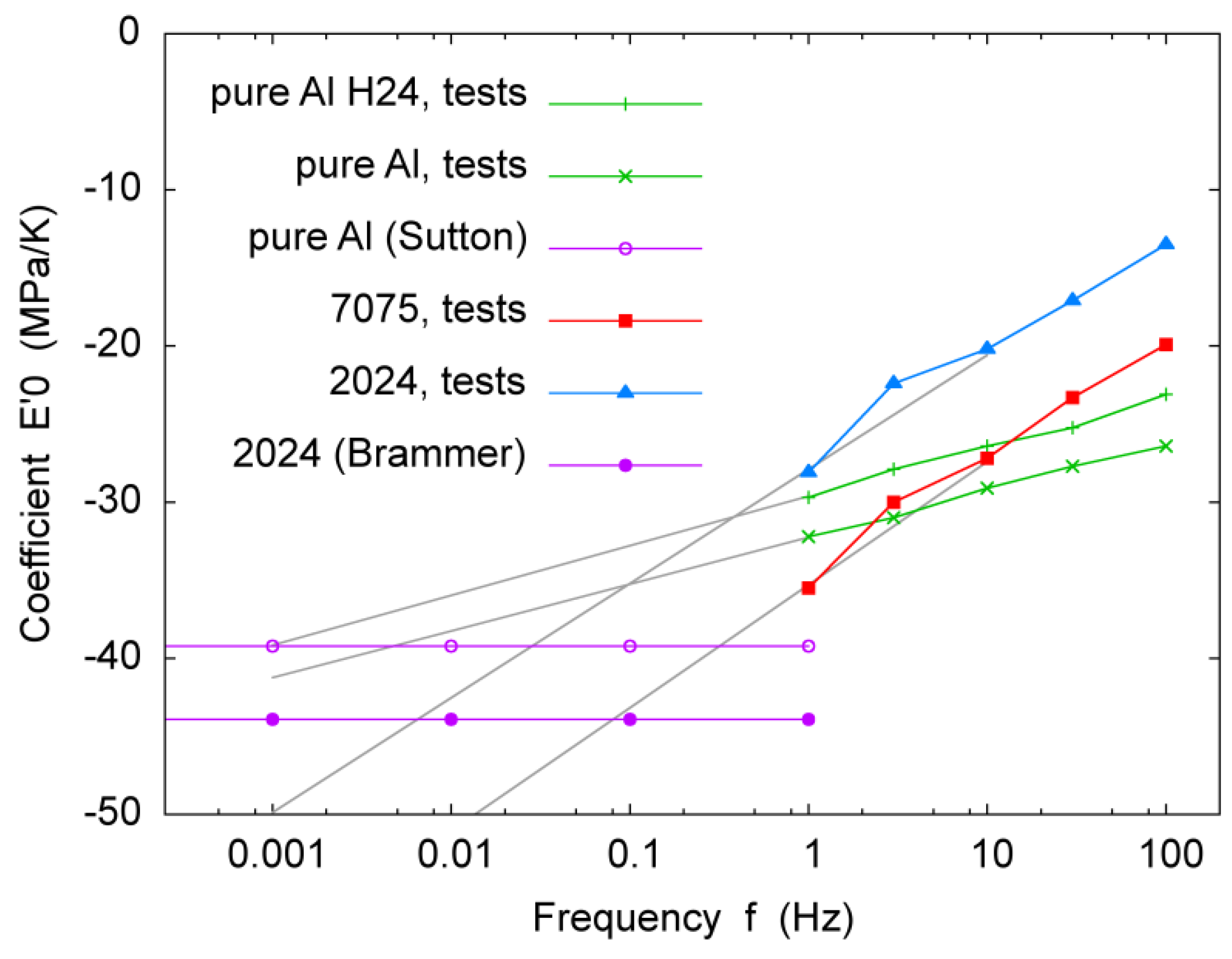
| Loading Frequency (Hz) | E0’ (Pure Al in H24 Temper) (MPa·K−1) | E0’ (Pure Al) (MPa·K−1) |
|---|---|---|
| 100 | −23.1 | −26.4 |
| 30 | −25.2 | −27.7 |
| 10 | −26.4 | −29.1 |
| 3 | −27.9 | −31.0 |
| 1 | −29.7 | −32.2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojas, J.I.; Crespo, D. Onset Frequency of Fatigue Effects in Pure Aluminum and 7075 (AlZnMg) and 2024 (AlCuMg) Alloys. Metals 2016, 6, 50. https://doi.org/10.3390/met6030050
Rojas JI, Crespo D. Onset Frequency of Fatigue Effects in Pure Aluminum and 7075 (AlZnMg) and 2024 (AlCuMg) Alloys. Metals. 2016; 6(3):50. https://doi.org/10.3390/met6030050
Chicago/Turabian StyleRojas, Jose I., and Daniel Crespo. 2016. "Onset Frequency of Fatigue Effects in Pure Aluminum and 7075 (AlZnMg) and 2024 (AlCuMg) Alloys" Metals 6, no. 3: 50. https://doi.org/10.3390/met6030050
APA StyleRojas, J. I., & Crespo, D. (2016). Onset Frequency of Fatigue Effects in Pure Aluminum and 7075 (AlZnMg) and 2024 (AlCuMg) Alloys. Metals, 6(3), 50. https://doi.org/10.3390/met6030050