Deformation in Metallic Glasses Studied by Synchrotron X-Ray Diffraction
Abstract
:1. Introduction
2. Synchrotron X-Ray Diffraction Measurement under Stress
2.1. Anisotropic PDF Analysis
2.2. Procedure of Determining Anisotropic PDF
2.2.1. Sample Preparation
- 1)
- Prepare a cylindrical or rectangular sample of bulk metallic glass of chosen composition. Make sure that the two end surfaces are smooth and parallel to each other.
- 2)
- Subject the sample to uniaxial stress, and raise the temperature to Ta, which has to be below the glass transition temperature, Tg. One has to be careful to keep the stress level below the yield stress at that temperature, because the yield stress is strongly temperature dependent, particularly near Tg.
- 3)
- Cool the sample down to room temperature with the stress still applied.
- 4)
- Remove the stress, and cut a sample thin enough for X-ray diffraction (~0.5 mm) from the crept sample. The cut should be made parallel to the stress axis so that, in transmission geometry, the scattering vector Q probes the direction parallel and normal to the applied stress.
- 5)
- The reference sample annealed in the same conditions (same temperature and time) should be prepared with a similar thickness. In general, the thickness is chosen in reference to absorption of X-rays (tμ < 0.2, t is the thickness and μ is the absorption coefficient) and samples containing heavy elements should be thinner.
2.2.2. Diffraction Measurement
- 6)
- Set-up the beam line for a high-energy PDF experiment with a 2D detector. The detector should be placed at a distance that covers enough Q space for reliable normalization and Fourier transformation, up to 18–25 Å−1.
- 7)
- Place the sample with the plane normal to the beam and the stress axis aligned vertically to the ground.
- 8)
- Turn on the X-ray and take data for a sufficiently long time, typically 5–15 min (Data Set #1). The data should be in the form of I(Q, θ), where θ is the azimuthal angle. The counting time and number of exposures depend on specifics of the detector and X-ray beam intensity. Ideally we want to have ~106 counts per inverse Å after integration over θ, at high Q.
- 9)
- Turn the sample by 90° around the beam so that the stress axis is horizontal, and repeat the measurement (Data Set #2). This step is useful because the sensitivity and background of the 2D detector are usually not isotropic. It is helpful to have a sample holder that can rotate the sample by 90° without changing its distance to the detector.
- 10)
- Rotate Data Set #2 by 90° and subtract it from Data Set #1, to remove the effect of the efficiency, and the flat field anisotropy of the 2D detector.
- 11)
- Determine S(Q, θ) from the raw data, I(Q, θ), by correcting for absorption, background, Compton intensity and the atomic scattering factor, <f(Q)>2, and normalizing to unity at Q → ∞.
2.2.3. Data Processing
- 12)
- Ideally the isotropic and anisotropic S(Q) is obtained by:However, as we noted, we make measurements with two sample orientations to compensate for the anisotropy of detector efficiency, and obtain two sets of data, Data Sets #1 and #2. The method of obtaining S20(Q) from the two sets of data is as follows.
- 13)
- The anisotropic part of Data Set #1 has the form:On the other hand, for Data Set #2, the stress is along the x-axis, so that:Thus, the difference is:Therefore:Then:because the second term in Equation (17) integrates out to zero using this integration. Usually, S20(Q) is much smaller thanS00(Q), and thus requires a higher precision to determine. By taking the difference in Equation (16), the background and the Compton scattering intensity are automatically removed, making the result more accurate.
- 14)
- Carry out the Bessel transformation to obtain the isotropic and anisotropic PDF:
- 15)
- Calculate the anisotropic PDF for affine deformation using Equation (11).
- 16)
- Sometimes it is not possible to rotate the sample by 90°, for instance when we carry out an in situ measurement using a heavy mechanical testing machine. In such a case, we use an isotropic sample, such as a metallic glass, well annealed and relaxed at a temperature close to Tg, to determine the S20(Q) of the detector using the step 12), and subtract the detector S20(Q) from the result.
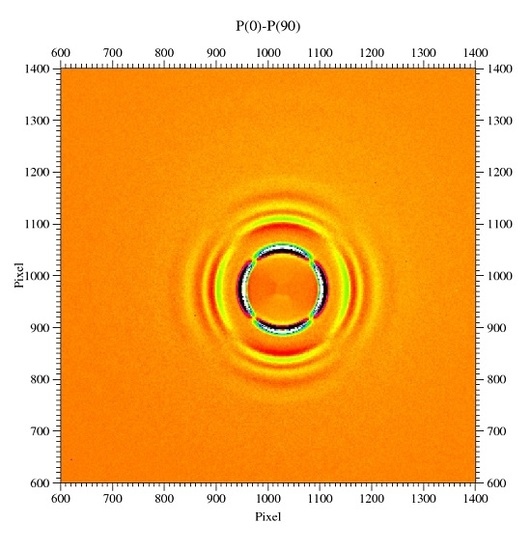
3. Results




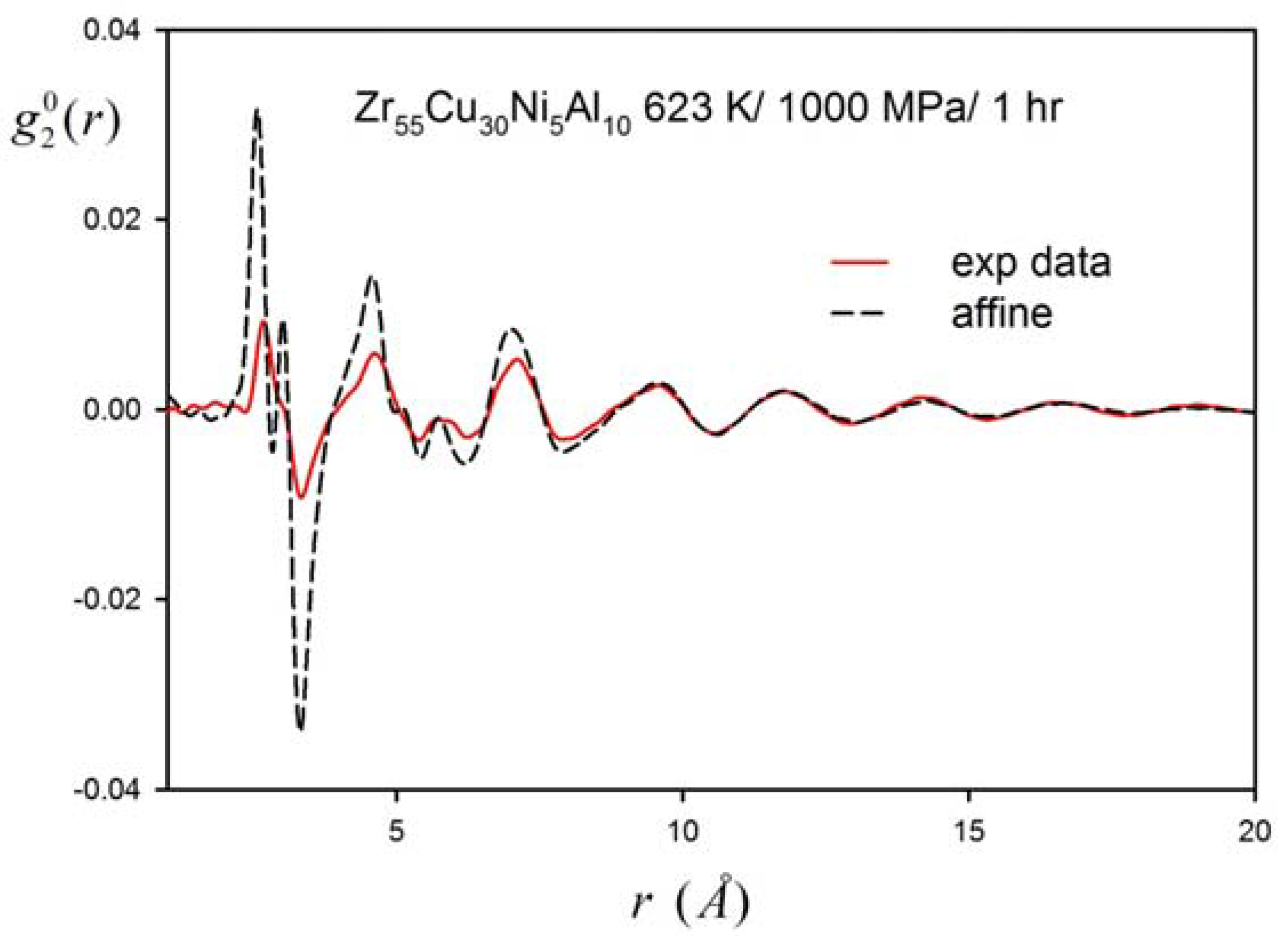

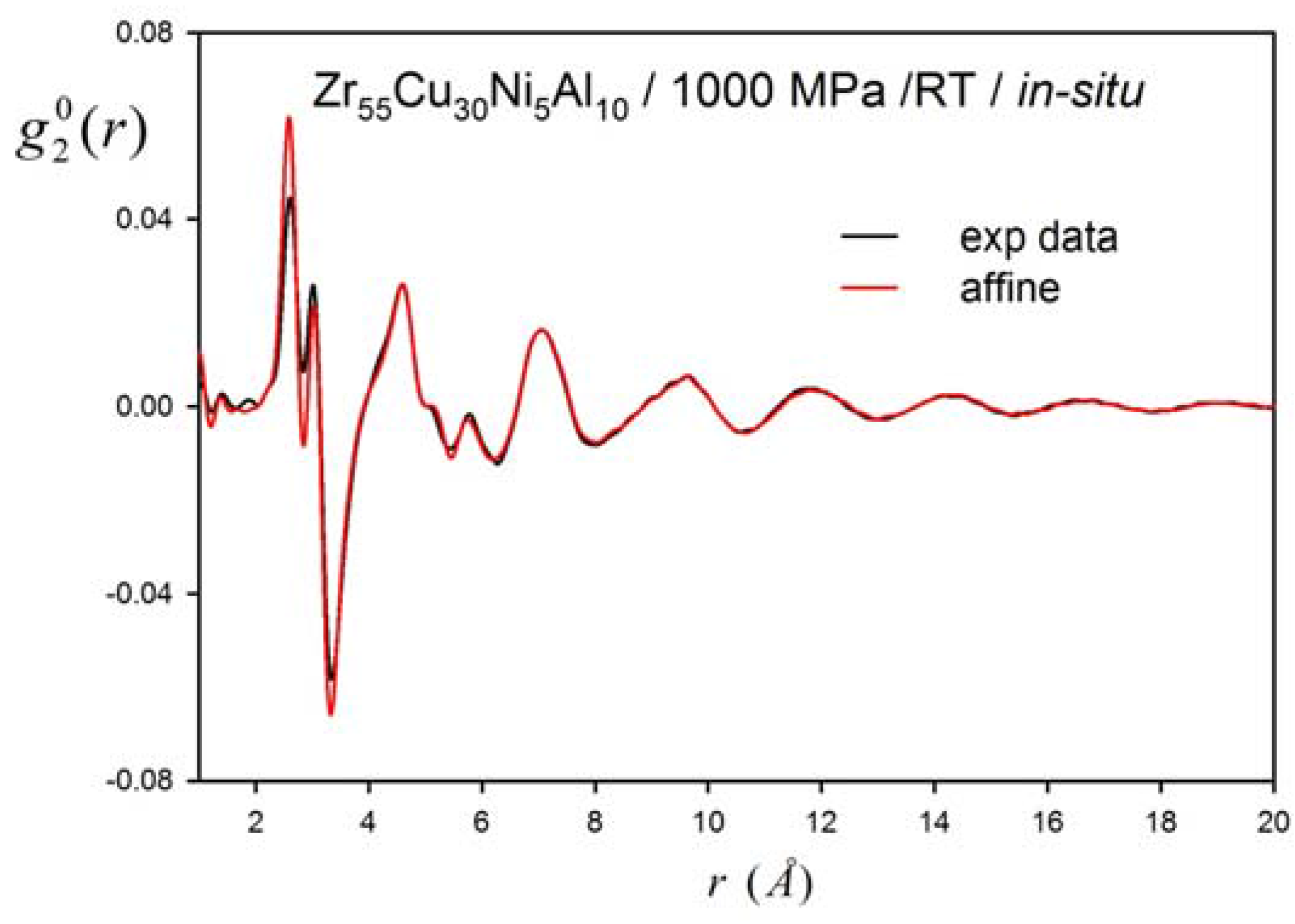
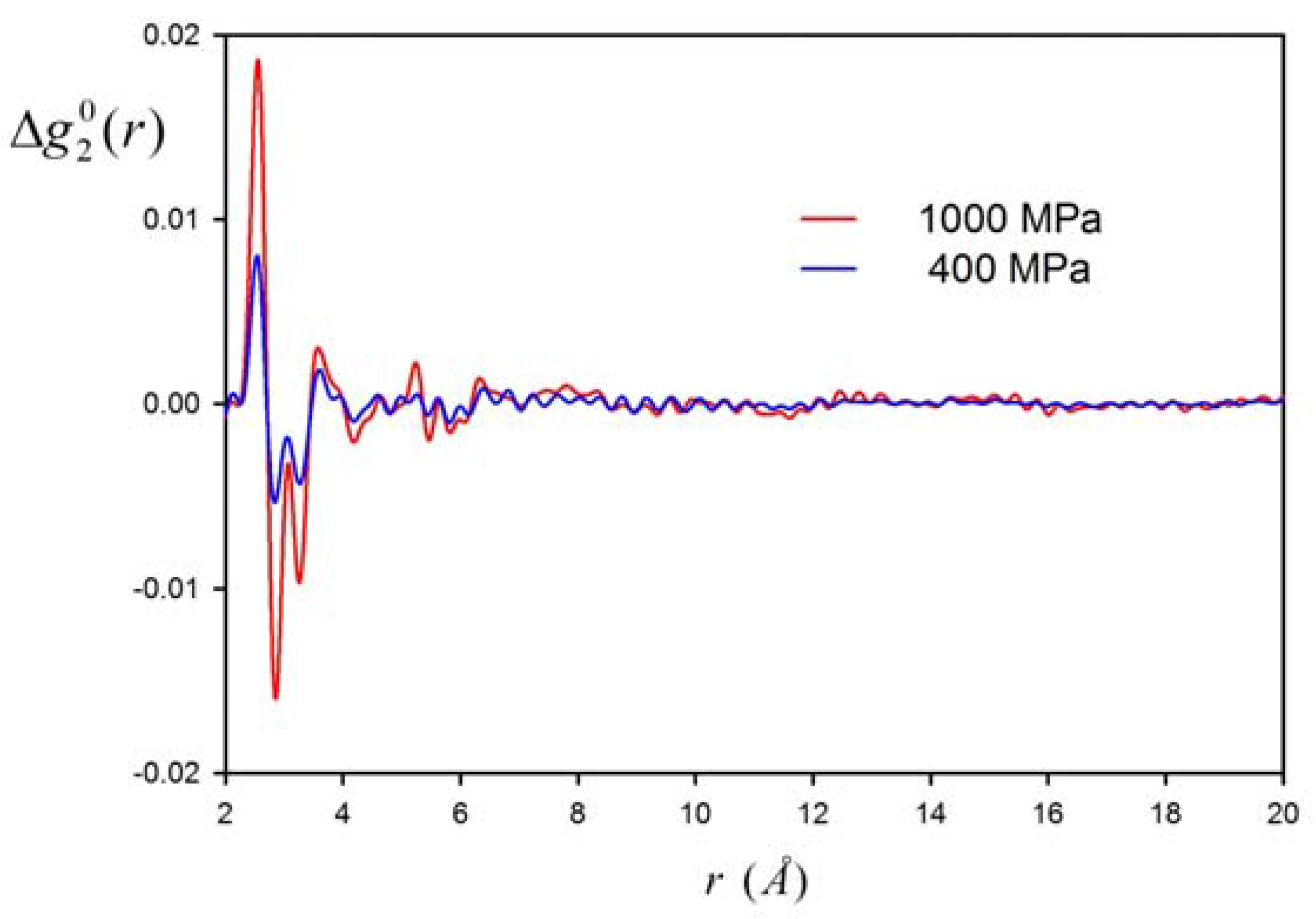
4. Discussion
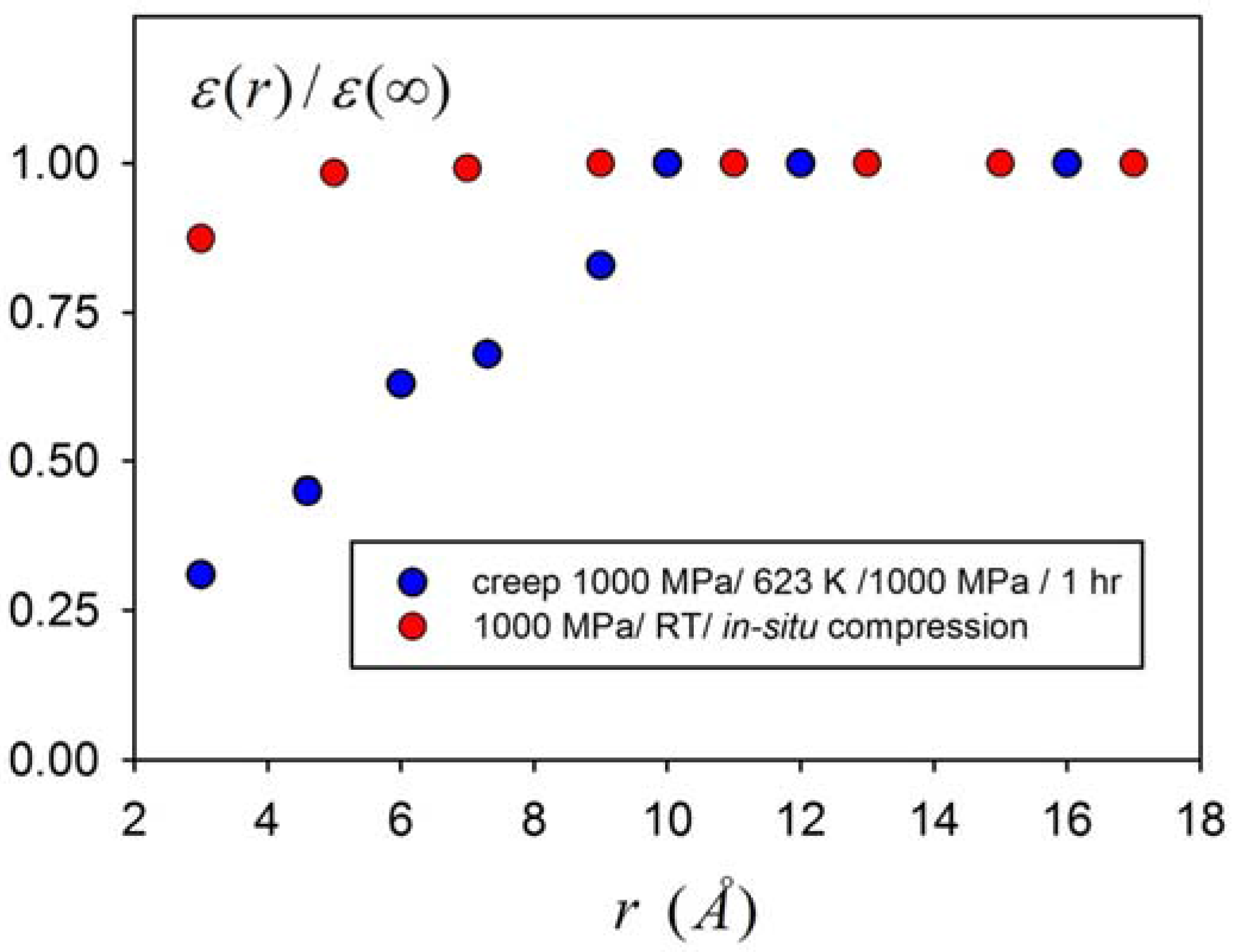
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Greer, A.L. Metallic glasses. Science 1995, 267, 1947–1953. [Google Scholar] [CrossRef] [PubMed]
- Argon, A.S. Mechanisms of inelastic deformation in metallic glasses. J. Phys. Chem. Solids 1982, 43, 945–961. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192–7205. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Dover Publications: New York, NY, USA, 1969. [Google Scholar]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials, 2nd ed.; Pergamon Materials Series, Elsevier: Amsterdam, The Netherland, 2012. [Google Scholar]
- Chupas, P.J.; Qiu, X.; Hanson, J.C.; Lee, P.L.; Grey, C.P.; Billinge, S.J.L. Rapid-acquisition pair distribution function (RA-PDF) analysis. J. Appl. Cryst. 2003, 36, 1342–1347. [Google Scholar] [CrossRef]
- Suzuki, Y.; Haimovich, J.; Egami, T. Bond‑orientational anisotropy in metallic glasses observed by X-ray diffraction. Phys. Rev. B 1987, 35, 2162–2168. [Google Scholar] [CrossRef]
- Yokoyama, Y.; Inoue, K.; Fukaura, K. Pseudo Float melting state in ladle arc-melt-type furnace for preparing crystalline inclusion-free bulk amorphous alloy. Mater. Trans. 2002, 43, 2316–2320. [Google Scholar] [CrossRef]
- Dmowski, W.; Egami, T. Observation of structural anisotropy in metallic glasses induced by mechanical deformation. J. Mater. Res. 2007, 22, 412–418. [Google Scholar] [CrossRef]
- Suzuki, Y.; Egami, T. Shear deformation of glassy metals: Breakdown of Cauchy relationship and anelasticity. J. Non-Cryst. Solids 1985, 75, 361–366. [Google Scholar] [CrossRef]
- Dmowski, W.; Iwashita, T.; Chuang, C.-P.; Almer, J.; Egami, T. Elastic heterogeneity in metallic glasses. Phys. Rev. Lett. 2010. [Google Scholar] [CrossRef] [PubMed]
- Egami, T.; Iwashita, T.; Dmowski, W. Mechanical properties of metallic glasses. Metals 2013, 3, 77–113. [Google Scholar] [CrossRef]
- Waire, D.; Ashby, M.F.; Logan, J.; Weis, J. On the use of pair potentials to calculate the properties of amorphous metals. Acta Metall. 1971, 19, 779–788. [Google Scholar] [CrossRef]
- Maloney, C.E.; Lemaître, A. Amorphous systems in athermal, quasistatic shear. Phys. Rev. E 2006. [Google Scholar] [CrossRef] [PubMed]
- Poulsen, H.F.; Wert, J.A.; Neuefeind, J.; Honkimäki, V.; Daymond, M. Measuring strain distributions in amorphous materials. Nat. Mater. 2005, 4, 33–36. [Google Scholar] [CrossRef]
- Hufnagel, T.C.; Ott, R.T.; Almer, J. Structural aspects of elastic deformation of a metallic glass. Phys. Rev. B 2006. [Google Scholar] [CrossRef]
- Wang, X.D.; Bednarcik, J.; Saksl, K.; Franz, H.; Cao, Q.P.; Jiang, J.Z. Tensile behavior of bulk metallic glasses by in situ X-ray diffraction. Appl. Phys. Lett. 2007. [Google Scholar] [CrossRef]
- Mattern, N.; Bednarcik, J.; Pauly, S.; Wang, G.; Das, J.; Eckert, J. Structural evolution of Cu-Zr metallic glasses under tension. Acta Mater. 2009, 57, 4133–4139. [Google Scholar] [CrossRef]
- Vempati, U.K.; Valavala, P.K.; Falk, M.L.; Almer, J.; Hufnagel, T.C. Length-scale dependence of elastic strain from scattering measurements in metallic glasses. Phys. Rev. B 2012. [Google Scholar] [CrossRef]
- Qu, D.D.; Liss, K.-D.; Sun, Y.J.; Reid, M.; Almer, J.D.; Yan, K.; Wang, Y.B.; Liao, X.Z.; Shen, J. Structural origins for the high plasticity of a Zr-Cu-Ni-Al bulk metallic glass. Acta Mater. 2013, 61, 321–330. [Google Scholar] [CrossRef]
- Schuh, C.A.; Lund, A.C.; Nieh, T.G. New regime of homogeneous flow in the deformation map of metallic glasses: Elevated temperature nanoindentation experiments and mechanistic modeling. Acta Mater. 2004, 52, 5879–5891. [Google Scholar] [CrossRef]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Natl. Acad. Sci. USA 2008, 105, 14769–14772. [Google Scholar] [CrossRef] [PubMed]
- Ju, J.D.; Jang, D.; Nwankpa, A.; Atzmon, M. An atomically quantized hierarchy of shear transformation zones in a metallic glass. J. Appl. Phys. 2011. [Google Scholar] [CrossRef]
- Choi, I.-C.; Zhao, Y.; Yoo, B.-G.; Kim, Y.-J.; Suh, J.-Y.; Ramamurty, U.; Jiang, J. Estimation of the shear transformation zone size in a bulk metallic glass through statistical analysis of the first pop-in stresses during spherical nanoindentation. Scr. Mater. 2012, 66, 923–926. [Google Scholar] [CrossRef]
- Fan, Y.; Iwashita, T.; Egami, T. How thermally activated deformation starts in metallic glass. Nat. Commun. 2014. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Iwashita, T.; Egami, T. Crossover from Localized to Cascade Relaxations in Metallic Glasses. Phys. Rev. Lett. 2015. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Iwashita, T.; Dmowski, W.; Bei, H.; Yokoyama, Y.; Egami, T. Structural Rejuvenation in Bulk Metallic Glasses. Acta Mater. 2015, 86, 240–248. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egami, T.; Tong, Y.; Dmowski, W. Deformation in Metallic Glasses Studied by Synchrotron X-Ray Diffraction. Metals 2016, 6, 22. https://doi.org/10.3390/met6010022
Egami T, Tong Y, Dmowski W. Deformation in Metallic Glasses Studied by Synchrotron X-Ray Diffraction. Metals. 2016; 6(1):22. https://doi.org/10.3390/met6010022
Chicago/Turabian StyleEgami, Takeshi, Yang Tong, and Wojciech Dmowski. 2016. "Deformation in Metallic Glasses Studied by Synchrotron X-Ray Diffraction" Metals 6, no. 1: 22. https://doi.org/10.3390/met6010022
APA StyleEgami, T., Tong, Y., & Dmowski, W. (2016). Deformation in Metallic Glasses Studied by Synchrotron X-Ray Diffraction. Metals, 6(1), 22. https://doi.org/10.3390/met6010022