Next Article in Journal
Stress-Corrosion Interactions in Zr-Based Bulk Metallic Glasses
Next Article in Special Issue
The Effect of Grinding and Roasting Conditions on the Selective Leaching of Nd and Dy from NdFeB Magnet Scraps
Previous Article in Journal
The Promising Features of New Nano Liquid Metals—Liquid Sodium Containing Titanium Nanoparticles (LSnanop)
Previous Article in Special Issue
“High-Throughput” Evaluation of Polymer-Supported Triazolic Appendages for Metallic Cations Extraction
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 5
Issue 3
10.3390/met5031241
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental Simulation of Long Term Weathering in Alkaline Bauxite Residue Tailings

by
Talitha C. Santini
1,2,3,*,
Martin V. Fey
4 and
Robert J. Gilkes
3
1
School of Geography, Planning, and Environmental Management, the University of Queensland, Brisbane, QLD 4072, Australia
2
Centre for Mined Land Rehabilitation, the University of Queensland, Brisbane, QLD 4072, Australia
3
School of Earth and Environment, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
4
Department of Plant Production and Soil Science, University of Pretoria, Private Bag X20, Hatfield, Pretoria 0002, South Africa
*
Author to whom correspondence should be addressed.
Metals 2015, 5(3), 1241-1261; https://doi.org/10.3390/met5031241
Submission received: 18 June 2015 / Revised: 6 July 2015 / Accepted: 7 July 2015 / Published: 14 July 2015
(This article belongs to the Special Issue Hydrometallurgy)
Browse Figures
Versions Notes

Abstract

:
Bauxite residue is an alkaline, saline tailings material generated as a byproduct of the Bayer process used for alumina refining. Developing effective plans for the long term management of potential environmental impacts associated with storage of these tailings is dependent on understanding how the chemical and mineralogical properties of the tailings will change during weathering and transformation into a soil-like material. Hydrothermal treatment of bauxite residue was used to compress geological weathering timescales and examine potential mineral transformations during weathering. Gibbsite was rapidly converted to boehmite; this transformation was examined with in situ synchrotron XRD. Goethite, hematite, and calcite all precipitated over longer weathering timeframes, while tricalcium aluminate dissolved. pH, total alkalinity, and salinity (electrical conductivity) all decreased during weathering despite these experiments being performed under “closed” conditions (i.e., no leaching). This indicates the potential for auto-attenuation of the high alkalinity and salinity that presents challenges for long term environmental management, and suggests that management requirements will decrease during weathering as a result of these mineral transformations.

1. Introduction

1.1. Tailings as a Soil Parent Material

Tailings are the residual mixture of solids and liquids remaining after extraction of a mineral or energy resource from its ore. Around 7 Gt of tailings are produced worldwide each year, with almost half of this total derived from copper extraction alone [1]. Tailings have typically been treated solely as waste materials; however, tailings are increasingly being recognized as substrates for soil development [2,3,4]. The annual mass of tailings produced globally is approximately one-third of the mass of soil lost through erosion globally [1,5]. Understanding how tailings materials weather into soils over extended timescales is therefore important not only for managing long term environmental impacts associated with tailings (e.g., acid mine drainage), but also for predicting future ecosystem properties and land use capabilities given the substantial and growing contribution of tailings to parent material inputs for global soil development.
Bauxite residue is an alkaline, saline-sodic byproduct of the Bayer process for alumina refining. Most economic reserves of bauxite worldwide are hosted in deeply weathered lateritic deposits [6], and the bauxite residues produced during the Bayer process contain a characteristic mineral assemblage dominated by weathering-resistant minerals, such as quartz (SiO2), goethite (FeOOH), hematite (Fe2O3), anatase (TiO2) and rutile (TiO2). Precipitates formed during the Bayer process, such as the desilication products sodalite (Na8(AlSiO4)6Cl2) and cancrinite (Na6Ca2(AlSiO4)6(CO3)2), calcite (CaCO3), tricalcium aluminate (Ca3Al2(OH)12), and perovskite (CaTiO3), also report to the residue fraction during processing, as well as minor amounts of undigested aluminium oxides (gibbsite (Al(OH)3) and boehmite (AlOOH)). Each year, 120 Mt of bauxite residue are produced globally, adding to the 3 Gt already stored in tailings facilities [7]. After deposition in tailings storage facilities, management tasks include collection and treatment of alkaline, saline leachates, and rehabilitation of the bauxite residue surface. Rehabilitation aims to stabilize the surface and improve visual amenity by establishing a vegetation cover. Insofar as the objective of rehabilitation is to establish a vegetation cover, rehabilitation strategies aim to accelerate pedogenesis (soil formation) in bauxite residue and enhance natural mechanisms of alkalinity and salinity attenuation such as precipitation, dissolution, and leaching. The weathering trajectory of bauxite residue, therefore, needs to be determined in order to identify any attenuation mechanisms that can be targeted by applied treatments. Furthermore, an understanding of the potential weathering trajectories of bauxite residue may aid in minimizing amounts and types of applied treatments. Refinery scale Bayer processing commenced in 1894, which gives 120 years exposure to weathering in the very oldest residue deposits [7]. The longest weathering timeframe for bauxite residue reported in studies to date was 40 years under a tropical climate in Guyana, in which dissolution of sodalite and calcite were observed [3]. This reflects the fact that weathering of primary minerals, an essential part of soil formation, can be a slow process in the field which is partially constrained by reaction kinetics. Limited evidence of mineral weathering has also been reported in other studies of soil development in bauxite residue [8,9]. Laboratory simulation of weathering is therefore essential in order to understand how this material behaves over longer weathering timescales and ensure that management strategies are effectively designed to minimize adverse environmental impacts over the long term.

1.2. Laboratory Simulation of Weathering

Compressing the geological timescales over which mineral weathering occurs requires manipulation of environmental conditions to accelerate reaction rates. Increasing temperature and/or pressure can accelerate attainment of chemical equilibrium according to the modified Arrhenius Equation (Equation (1)):
K = A (exp (−(Ea + PΔV)/RT))
where K is reaction rate (s−1; for a first-order reaction), A is the pre-exponential factor (s−1; for a first-order reaction), Ea is activation energy (J·mol−1), P is partial pressure of reactant (mol·cm−3), ΔV is activation volume (cm3·mol−1), R is the universal gas constant (8.314 J·mol−1·K−1) and T is temperature (°K).
Soxhlet extractors have been used to simulate weathering for a variety of geological materials [10,11,12,13,14]; however, the very fine texture of bauxite residue (median particle diameter 130 μm for bauxite residue used in this study; [15]) inhibited leaching. Furthermore, the Soxhlet extraction procedure is slow and labour intensive when conducting experiments at multiple temperatures to investigate reaction kinetics. Pressure vessels (also known as pressure bombs, Teflon bombs, Parr bombs) have been used to accelerate reactions and rapidly bring materials to chemical equilibrium, because they apply both elevated temperatures and pressures to the material under investigation. Their previous use in weathering studies has mostly concerned the alteration of single minerals during pedogenesis [16,17,18]. Reaction kinetics can be derived from these experiments and extrapolated to predict reaction rates under field conditions [17,19]. The drawback of pressure vessels compared to Soxhlet extractors for weathering simulations is that they do not allow for the effect of leaching, being a “closed” system. Allowing reaction products to accumulate may create a local equilibrium which slows further reactions. Different equilibrium states could therefore be identified for the same material under various leaching conditions. Bauxite residue has a very low hydraulic conductivity [20], which limits leaching; and under low leaching rates, equilibration with pore water may proceed to chemical equilibrium. The use of pressure vessels to predict the long term equilibrium composition of bauxite residue may therefore be a reasonable representation of reactions that occur under field conditions.
The aims of this study were to: (a) analyse the chemical and mineralogical composition of bauxite residue over time under simulated weathering conditions in pressure vessels; (b) extrapolate results from the pressure vessel studies to temperatures and pressures typical of field conditions in bauxite residue deposit areas (tailings storage facilities); and (c) determine whether pressure vessels provide a suitable method for rapidly determining potential weathering trajectories of bauxite residue under field conditions. Under hydrothermal conditions, we expected to observe some conversion of mineral phases that are commonly associated with Bayer process conditions, such as conversion of gibbsite to boehmite [21], goethite to hematite [22], tricalcium aluminate to calcite [23], and quartz to desilication products [24]. Dissolution of sodalite and calcite has been observed during weathering under leaching conditions [3,25,26]. However, dissolution of these minerals was not expected within this experiment because no leaching was possible.

2. Experimental Section

2.1. Study Design

This study used pressure vessels to elevate temperature and pressure in order to rapidly determine the likely weathering trajectory of bauxite residue. Two types of pressure vessels were used: PTFE-lined stainless steel pressure vessels; and fused silica capillaries, sealed and pressurized with N2 to avoid boiling. These vessels were used in two experiments to provide complementary information. The stainless steel pressure vessels allowed sampling and analysis of both solid and liquid phases, but required 90 min to reach the required temperature in an oven. This limited temporal resolution, and complete transformation of some minerals (e.g., gibbsite to boehmite) was observed between the initial (t = 0) and second (t = 90 min) sampling times. Use of the fused silica capillary reaction vessels at the Australian Synchrotron Powder Diffraction beamline 10BM1 resolved this problem, as they heated quickly (less than 40 s in our experiment) and full X-ray diffraction (XRD) patterns can be collected in situ on a rapid basis (20 s in this experiment) with the Mythen detector array. Results are unreplicated; that is, only one sample was analysed for each time and temperature combination. This is common in mineral dissolution and precipitation studies where reaction rates are studied in response to variables, such as temperature or pH [17,22,27,28,29,30,31,32,33,34] to derive reaction kinetics. A single time and temperature combination in the pressure vessel experiments (100 °C, 909 h) was conducted in triplicate to estimate variability; this approach has also been used elsewhere [35].

2.2. Bauxite Residue Sample

Bauxite residue was sourced from Alcoa of Australia Limited’s Kwinana refinery. Iron oxides (goethite and hematite) were the major mineral phases present, with smaller amounts of quartz, and calcite and sodalite formed during the Bayer process (Table 1). In 1:1 bauxite residue to water suspensions, initial pH was 13.07, electrical conductivity (EC) was 15.52 dS·m−1, and total alkalinity (TA) was 7.35 g/L CaCO3.

2.3. Stainless Steel Pressure Vessel Experiment

Five hydrothermal treatment temperatures (100, 140, 165, 200 and 235 °C) were employed in order to extract kinetic data for observed reactions. Subsamples (4 g) of bauxite residue were added to 5 mL of ultrapure deionised water to create bauxite residue slurries inside 25 cm3 internal volume PTFE-lined stainless steel pressure vessels (Parr Instrument Company, Moline, IL, USA) and heated to the designated temperature in a rotating oven. One vessel was removed after 1.5, 3.75, 21, 28, and 48 h and allowed to cool to room temperature. Additional samples of the 100 °C treatment were also collected at 170, 336 and 909 h. Slurry samples were taken from each vessel after cooling (<2 h).
Table
Table 1. Mineral concentrations in bauxite residue prior to hydrothermal treatment, as determined by quantitative mineral analysis by Rietveld refinement of an X-ray diffraction pattern.
Table 1. Mineral concentrations in bauxite residue prior to hydrothermal treatment, as determined by quantitative mineral analysis by Rietveld refinement of an X-ray diffraction pattern.
MineralFormulaConcentration (% Weight) a
GoethiteFeOOH41
HematiteFe2O311
CalciteCaCO311
QuartzSiO29.4
BoehmiteAlOOH8.4
MuscoviteKAl2Si3AlO10(OH)28.4
GibbsiteAl(OH)33.4
SodaliteNa8(AlSiO4)6Cl22.8
AnataseTiO21.7
IlmeniteFeTiO31.7
Tricalcium aluminateCa3Al2(OH)120.4
Amorphous/unidentified-0.8
a X-ray diffraction analysis was performed as described for hydrothermally-treated samples in Section 2.4. using Rietveld refinement implemented in TOPAS-Academic (v. 4.1; [36] Coelho Software, Brisbane, Australia) without running in sequential refinement mode.
Cooled slurries were centrifuged at 3000 rpm for 5 min to separate liquid and solid phases. Supernatants were immediately filtered through a 0.2 μm cellulose acetate filter and analysed for pH, EC, and total alkalinity by titration with 0.1 M HCl to endpoints pH 8.5 and 4.5 [37]. Subsamples of supernatants were diluted 1:10, acidified with HCl to pH < 2 and stored at 4 °C prior to analysis by Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES; Optima 5300DV, PerkinElmer, Waltham, MA, USA) to determine Al, Ca, Fe, K, Na, Si, and Ti concentrations.
Treated solids were shaken with acetone in an end-over-end shaker for 90 min and then centrifuged at 3000 rpm for 5 min. The supernatant was decanted and the solids allowed to dry at ambient laboratory temperature for 48 h. Dried solids were hand ground with an agate mortar and pestle and then packed into 0.3 mm internal diameter glass capillaries for XRD analysis (wavelength 0.8271 Å, collection time 5 min) at the Powder Diffraction beamline (10BM1) at the Australian Synchrotron, Victoria, Australia. Peak locations and areas for selected minerals were then calculated using Traces [38]. Anatase, which is naturally present in the bauxite residue, was used as an internal standard for the purpose of comparing peak areas of selected minerals between XRD patterns. Anatase has been found to be only sparingly soluble in the presence of Bayer liquor at 90 °C under ambient pressure [39].

2.4. Fused Silica Capillary Pressure Vessel Experiment

In situ XRD experiments were conducted at the Australian Synchrotron’s beamline 10BM1, with slurries heated in Norby cells [40], consisting of fused silica capillaries (internal diameter: 0.8 mm; wall thickness: 0.1 mm, typical working volume: 0.02 mL) heated with a hot air blower, continuously rotated through 270° along the longitudinal axis of the capillary, and held under N2 pressure during heating to various temperatures (140–170 °C) to avoid boiling. The N2 regulator could not provide sufficient pressure to avoid boiling above 170 °C. Slurries were prepared <2 h before analysis at the same bauxite residue: Deionised water ratio as in the stainless steel pressure vessel experiments (44% wt solids). Diamond powder was added to the dry bauxite residue at 5% wt (2.2% wt in slurries) as an internal standard for the purposes of quantitative phase analysis by Rietveld refinement. Diamond was selected for its low reactivity under the experimental conditions, and for its few diffraction peaks within the 2θ angular range of interest, which minimizes overlaps with other phases. Diffraction patterns were collected continuously every twenty seconds using the Mythen microstrip detector, capable of collecting 80° 2θ simultaneously, to allow calculation of mineral transformation kinetics. XRD patterns were collected first at ambient temperature with the required N2 pressure applied, during heating, and for the duration of the experiment. Operating temperature was reached in 20–40 s. Run times varied between 1.5 h and 4 h, depending on factors such as loss of synchrotron beam, capillary failure, and observed reaction rates.
To quantify changes in mineral concentrations and amorphous content during this experiment, quantitative mineral analysis of X-ray diffractograms was conducted using TOPAS-Academic (v. 4.1; [36] Coelho Software, Brisbane, Australia) for Rietveld refinement. Compared with the peak area based data analysis approach, Rietveld refinement removes the potential for errors from peak overlaps, reports mineral concentrations on an absolute rather than relative scale, and allows quantification of amorphous content. Data were analysed using a sequential refinement approach, which used the refined (output) mineral concentrations for dataset x as the input mineral concentrations for the Rietveld refinement of dataset x + 1, where x is any dataset in the collected sequence of XRD patterns for bauxite residue at a particular temperature. Reported mineral concentrations (on a percent weight basis) were corrected for amorphous content (including X-ray amorphous solids, fused silica capillary, and water in the slurry) using the diamond internal standard and Equations (2) and (3):
Absi = (wiSTDtrue)/(STDmeas)
w amorph = 1 − ( ∑ i = 1 n Ab s i )
where Absi is the absolute weight fraction of phase i, wi is the weight fraction of phase i determined by Rietveld refinement, STDtrue is the known weight fraction of the diamond standard, STDmeas is the calculated weight fraction of the diamond standard by Rietveld refinement and wamorph is the total absolute weight fraction of amorphous and unidentified phases.

2.5. Reaction Kinetics Calculations

An extent of reaction parameter, α, was calculated from either peak areas (stainless steel pressure vessel experiment) or mineral concentrations (fused silica capillary experiment), where It was the observed peak area or mineral concentration at a sampling time, t, and Imax was the maximum peak area or mineral concentration attained (Equation (4)):
α = (It)/(Imax)
Kinetic data was then extracted using an approach identical to that detailed by Murray et al. [22]. The Sharp-Hancock equation (Equation (5); [41]), a linearised version of the Avrami-Erofe’ev Equation (Equation (6); [42,43,44,45]), was used to calculate kinetic parameters n (reaction order) and k (reaction rate) by plotting ln(−ln(1 − α)) against ln(t) and fitting a least-squares linear equation.
ln(−ln(1 − α)) = n ln(t − t0) + n ln(k)
α = 1 − exp(−k (t − t0))n
Nucleation time (t0) was assumed to be zero as no new minerals were formed and growth sites therefore existed for all phases. Values for ln(k) were then plotted against 1/T in an Arrhenius plot to determine activation energy, Ea, and the pre-exponential factor, A.

3. Results and Discussion

3.1. Supernatant Chemistry

Decreases in pH, EC, and total alkalinity (TA) were observed over time in bauxite residue in the 200 °C and 235 °C treatments (Figure 1), indicating a potential for “auto-attenuation” of alkalinity and salinity within the bauxite residue. This is in sharp contrast with the weathering trajectories of tailings derived from sulfidic ores, in which initially low pH and high salinity are exacerbated during weathering due to oxidation of residual iron sulfides [2,4]. Some increases in EC and TA were observed in 100 °C and 135 °C treatments whereas EC and TA initially increased and then sharply decreased in the 165 °C, 200 °C, and 235 °C treatments. This suggests that the lower temperature hydrothermal treatments progress along the same reaction trajectory as the higher temperature treatments, with slower reaction rates in the lower temperature treatments.
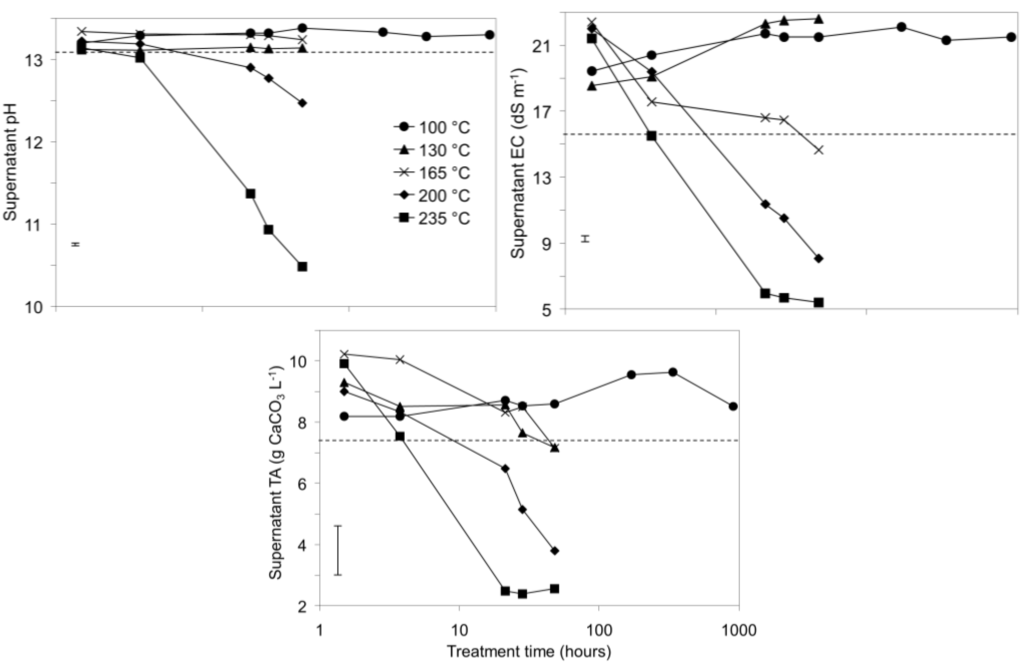
Metals 05 01241 g001 1024
Figure 1. pH, EC, and total alkalinity (TA) of supernatants from bauxite residue during pressure vessel treatments at various temperatures. Dashed lines indicate t = 0 values. Note that treatment time (X axis) is graphed on a logarithmic scale. Error bars indicate 95% confidence interval for the mean of the 100 °C treatment at 909 h.
Figure 1. pH, EC, and total alkalinity (TA) of supernatants from bauxite residue during pressure vessel treatments at various temperatures. Dashed lines indicate t = 0 values. Note that treatment time (X axis) is graphed on a logarithmic scale. Error bars indicate 95% confidence interval for the mean of the 100 °C treatment at 909 h.
Metals 05 01241 g001
Supernatant concentrations of Al, K, Na, and S all decreased over time to below initial concentrations in the 200 and 235 °C treatments, suggesting removal from solution by mineral precipitation. Concentrations of Al, Na, and S increased and then decreased to concentrations slightly above or below initial concentrations in the 165 °C treatment. This suggests that similar reactions are responsible for observed changes in concentrations of Al, Na, and S at temperatures from 165 to 235 °C, and that reaction rates decrease with decreasing temperature. At 100 and 130 °C, Al, K, Na, and S concentrations increased and remained above initial concentrations during hydrothermal treatment; this suggests that precipitation reactions occur very slowly or do not occur at all at lower temperatures. Silicon concentrations in the supernatant increased over time in all but the 235 °C treatment. This could be a result of dissolution of reactive Si (from muscovite or finely divided quartz), with precipitation of sodalite or cancrinite only occurring to an appreciable extent at 235 °C. Iron concentrations in solution remained near or below the detection limit for all treatment temperatures except 235 °C (Figure 2). The assumption of anatase insolubility was supported by ICP-OES data, which indicated that little Ti was released to solution, except at 235 °C. Titanium and iron concentrations increased simultaneously and were present in solution at an approximate Fe:Ti molar ratio of 8:1, which is inconsistent with ilmenite dissolution and rather may indicate dissolution of a minor titanium-substituted iron oxide phase, such as titanohematite. Ca concentrations were below detection limits (0.35 mg/L) in all samples and are therefore not shown in Figure 2.
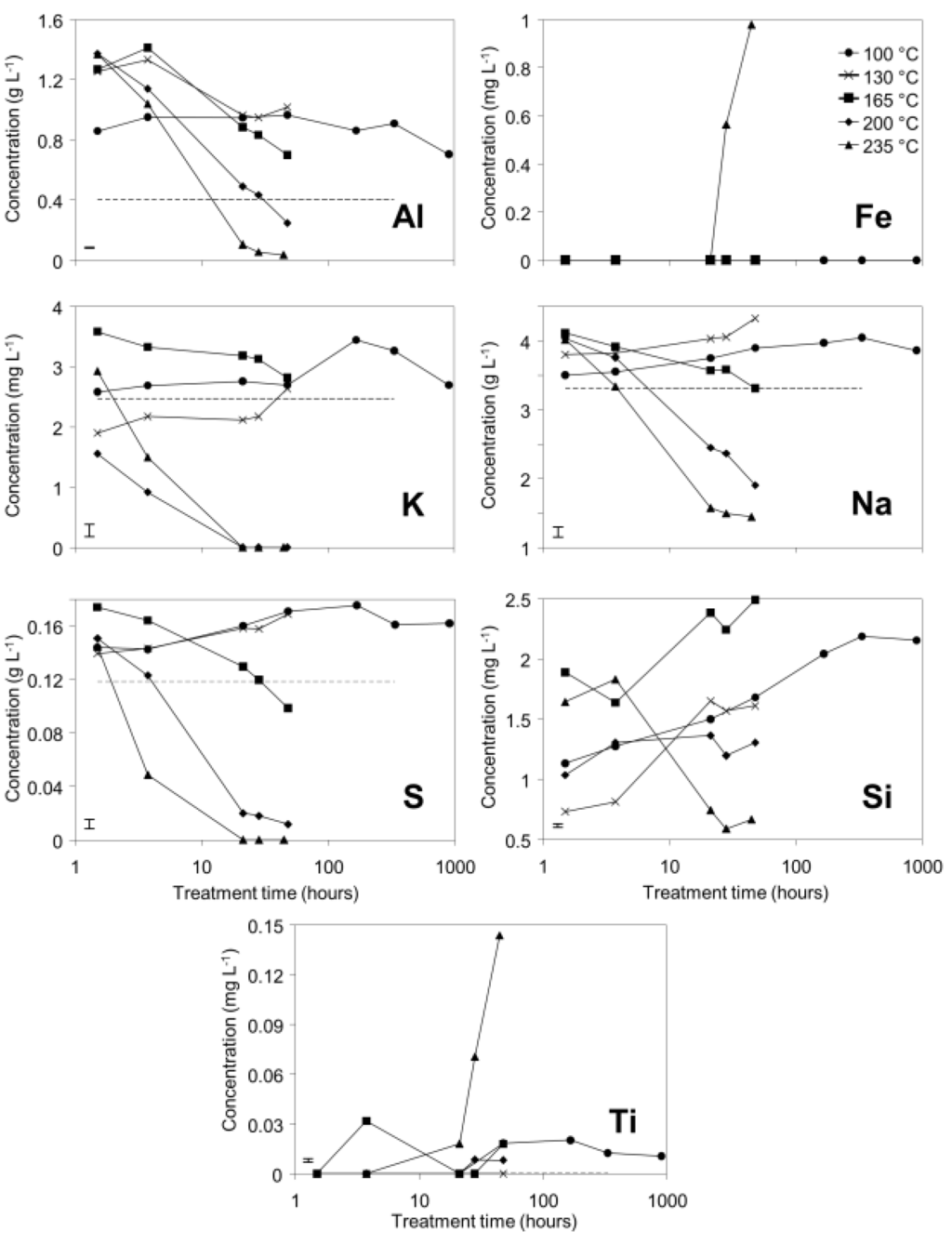
Metals 05 01241 g002 1024
Figure 2. Concentrations of selected elements (mg or g·L−1) in supernatant from bauxite residue after treatment in pressure vessels. Dashed lines indicate concentrations at t = 0. Where no dashed line is visible, concentrations at t = 0 were below detection limits. Note that treatment time (X axis) is graphed on a logarithmic scale. Error bars indicate 95% confidence interval for the mean of the 100 °C treatment at 909 h.
Figure 2. Concentrations of selected elements (mg or g·L−1) in supernatant from bauxite residue after treatment in pressure vessels. Dashed lines indicate concentrations at t = 0. Where no dashed line is visible, concentrations at t = 0 were below detection limits. Note that treatment time (X axis) is graphed on a logarithmic scale. Error bars indicate 95% confidence interval for the mean of the 100 °C treatment at 909 h.
Metals 05 01241 g002

3.2. Solids Mineralogy

The rapid collection of XRD patterns from the bauxite residue slurry in fused silica capillary reaction vessels allowed construction of time sequence graphs which illustrate the temperature dependent transformation of gibbsite to boehmite over short timescales (Figure 3, Figure 4, Figure 5 and Figure 6). Gibbsite and boehmite dynamics reflect a dissolution-precipitation mechanism based on observed rates of transformation in Figure 3, Figure 4, Figure 5 and Figure 6, and previous studies of hydrothermal conversion [46,47]. This would aid in lowering pH, EC, and TA by diluting the supernatant (Equation (7)). No Al would be released to the supernatant, although some Al initially present in solution may also be precipitated as boehmite.
Al(OH)3(s) → AlOOH(s) + H2O(l)
The gibbsite to boehmite reaction could only be observed by in situ synchrotron XRD because the transformation time (<50 min at 165–170 °C) was faster than the required time for the stainless steel pressure vessels to heat to temperature. The gibbsite to boehmite transformation is known to occur above 100 °C [22]. Transformation of gibbsite to boehmite was very slow at temperatures ≤150 °C in this study and increased markedly above this temperature. Elevated pressure slows the transformation, because the sum of the molar volumes of the products is greater than that of the reactants (Equation (7)). At lower temperatures, the inhibitory effect of elevated pressure is likely to have slowed the transformation; however, this effect appeared to have less influence on reaction rates at higher temperatures. A similar conclusion was drawn by Mehta and Kalsotra [48], who observed conversion of gibbsite to boehmite under hydrothermal conditions only at temperatures ≥190 °C. Higher alumina to caustic ratios (A/C; Al2O3:Na2O ratio (g/L) in the supernatant) also raise the minimum transformation temperature [49,50]; the alumina:caustic ratio was consistently below 0.5 in this experiment and was therefore unlikely to have inhibited transformation of gibbsite to boehmite.
Goethite precipitated to a minor extent at 170 °C (Figure 6). Anatase concentrations appeared stable according to quantitative mineral analysis graphs (Figure 3, Figure 4, Figure 5 and Figure 6), which supports interpretations based on Ti concentrations in the supernatants (Figure 2). Amorphous content was stable during the transformation of gibbsite to boehmite; given that calculated amorphous content includes contributions from water in the slurry, amorphous content was expected to increase as a result of the water released during this transformation. The water released during transformation of gibbsite (present in the bauxite residue slurry at approximately 2% wt) to boehmite may have been insufficient to increase the amorphous content detectable within the error of the Rietveld-based quantification approach. The quality of the diffractograms was compromised by the short collection time; this hindered accurate quantification of gibbsite concentrations below 0.5% wt, and quantification of tricalcium aluminate and ilmenite concentrations. Diffractogram quality may also have been too poor to detect small changes in amorphous content of the solid phase. Longer collection times (1–2 min) are required for complex mineral assemblages if quantification of minor phases, or small changes in concentration of major phases are of interest.
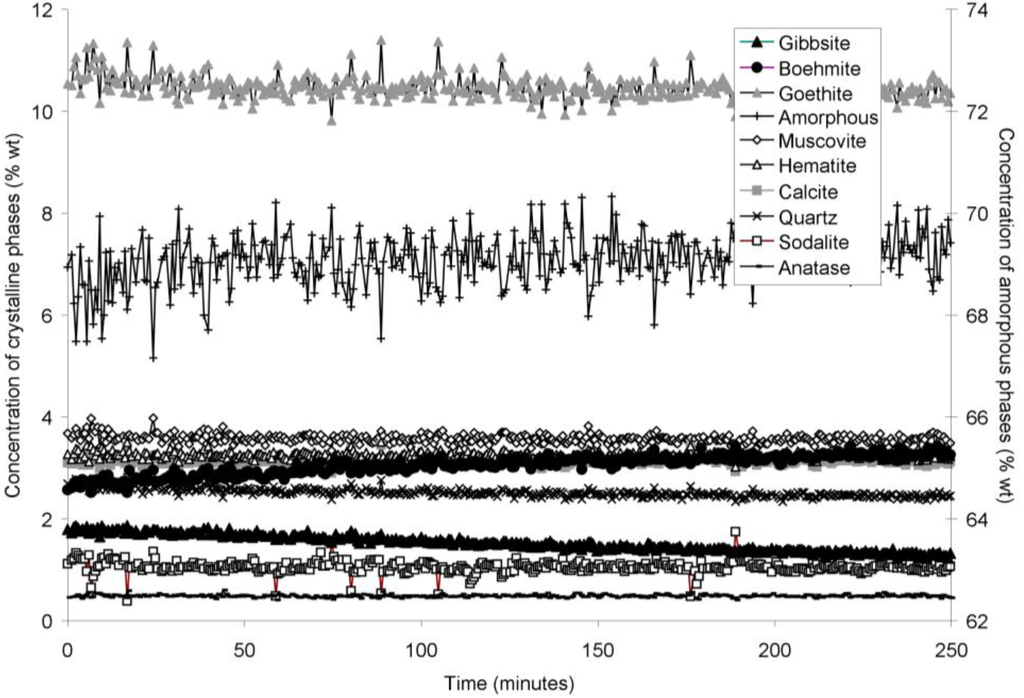
Metals 05 01241 g003 1024
Figure 3. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 140 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary.
Figure 3. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 140 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary.
Metals 05 01241 g003
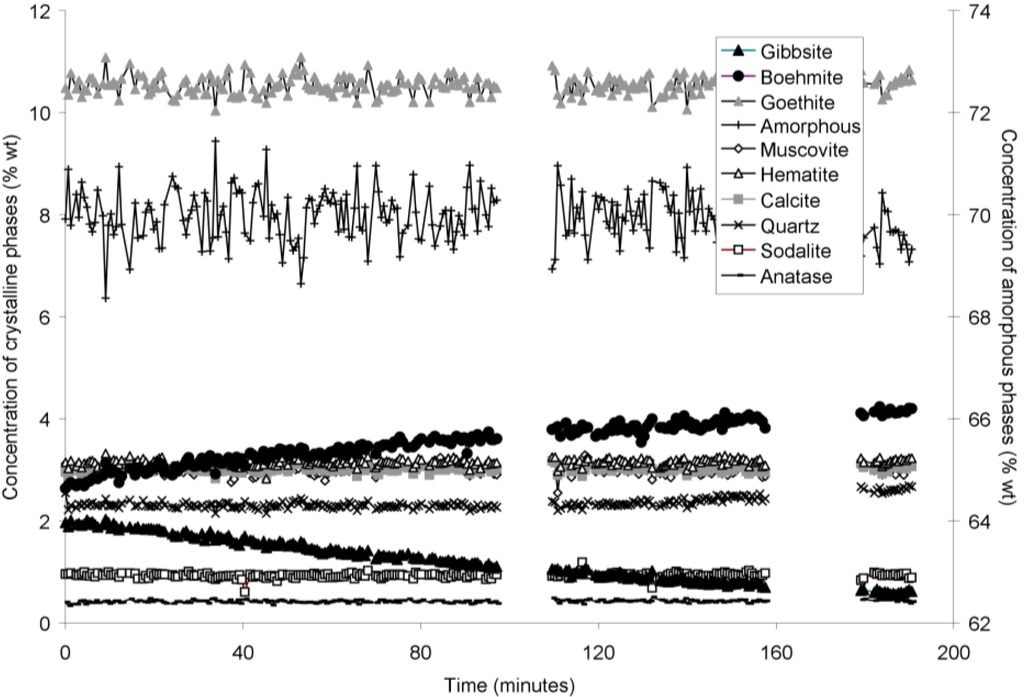
Metals 05 01241 g004 1024
Figure 4. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 150 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary. Gaps in data from 100–110, and 160–180 min were caused by beam loss at the synchrotron. Heating of the slurry continued during beam loss.
Figure 4. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 150 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary. Gaps in data from 100–110, and 160–180 min were caused by beam loss at the synchrotron. Heating of the slurry continued during beam loss.
Metals 05 01241 g004
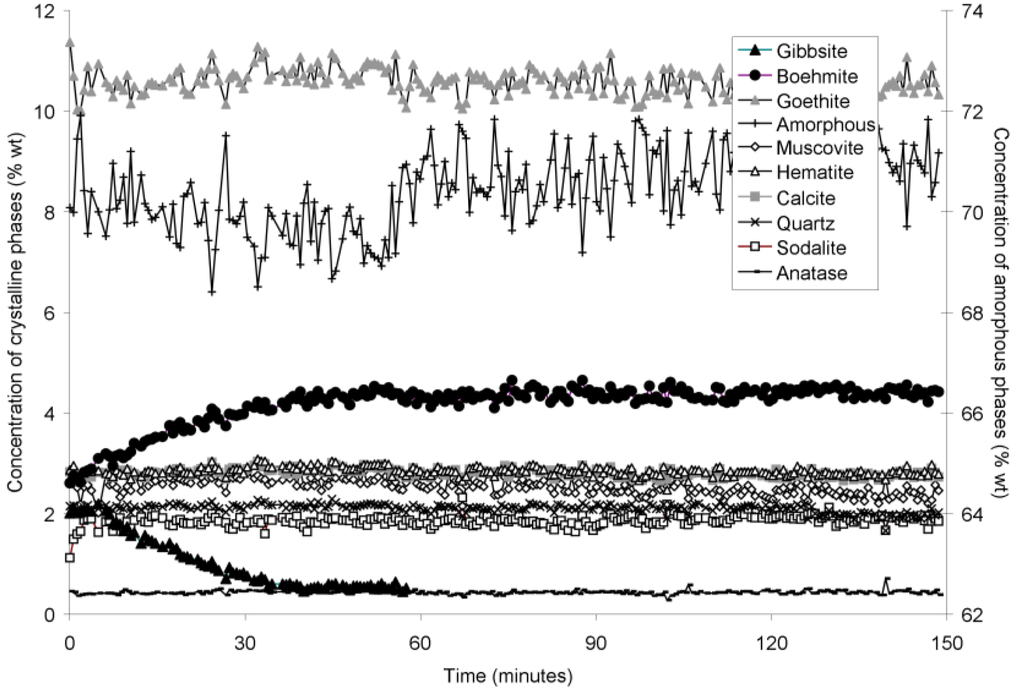
Metals 05 01241 g005 1024
Figure 5. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 165 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary.
Figure 5. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 165 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary.
Metals 05 01241 g005
Metals 05 01241 g006 1024
Figure 6. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 170 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary.
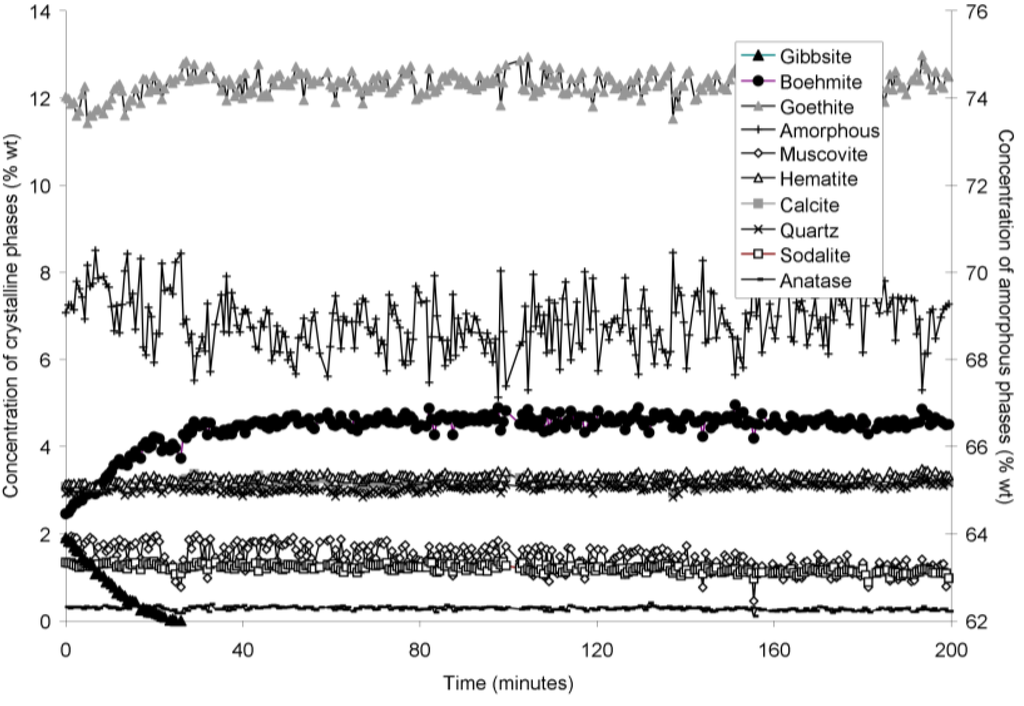
Figure 6. Concentration of crystalline and amorphous phases in bauxite residue slurry in capillary reaction vessels as a function of treatment time at 170 °C, as determined by Rietveld-based quantitative mineral analysis of X-ray diffractograms. Note that amorphous content is plotted on the secondary Y axis and represents contributions from X-ray amorphous minerals in bauxite residue, water in the slurry, and the fused silica capillary.
Metals 05 01241 g006
During extended hydrothermal treatment in stainless steel pressure vessels, boehmite, goethite, hematite, and calcite appeared to precipitate (Figure 7; Table 2), along with minor precipitation of sodalite; whereas gibbsite and tricalcium aluminate dissolved (Figure 7). As discussed above, gibbsite is likely converted to boehmite during hydrothermal treatment. Although conversion of goethite to hematite has been observed under Bayer process conditions [22], goethite dissolution was not observed during this experiment, perhaps due to the inhibitory effect of anatase [22]. The precipitation of both goethite and hematite was likely limited by low dissolved Fe concentrations. Fe(OH)4−(aq) is thermodynamically predicted to be the dominant form of dissolved iron at pH values observed in these experiments, and goethite and hematite precipitation would therefore have a minimal effect upon pH, EC, and TA (Equations (8) and (9)) even if precipitation occurred to a greater extent:
Fe(OH)4−(aq) → FeOOH(s) + H2O(l) + OH−(aq)
2Fe(OH)4−(aq) + 2H+(aq) → Fe2O3(s) + 5H2O(l)
Tricalcium aluminate dissolved more slowly than gibbsite and the majority of Al and Ca supplied to solution from dissolution of both minerals is likely to have been precipitated as boehmite and calcite given that Al and Ca concentrations did not increase substantially during dissolution (Equation (10); Figure 2). This conclusion is consistent with the conversion mechanisms described elsewhere [23,46,47].
Ca3Al2(OH)12(s) + 3CO32−(aq) → 3CaCO3(s) + 2AlOOH(s) + 10OH−(aq)
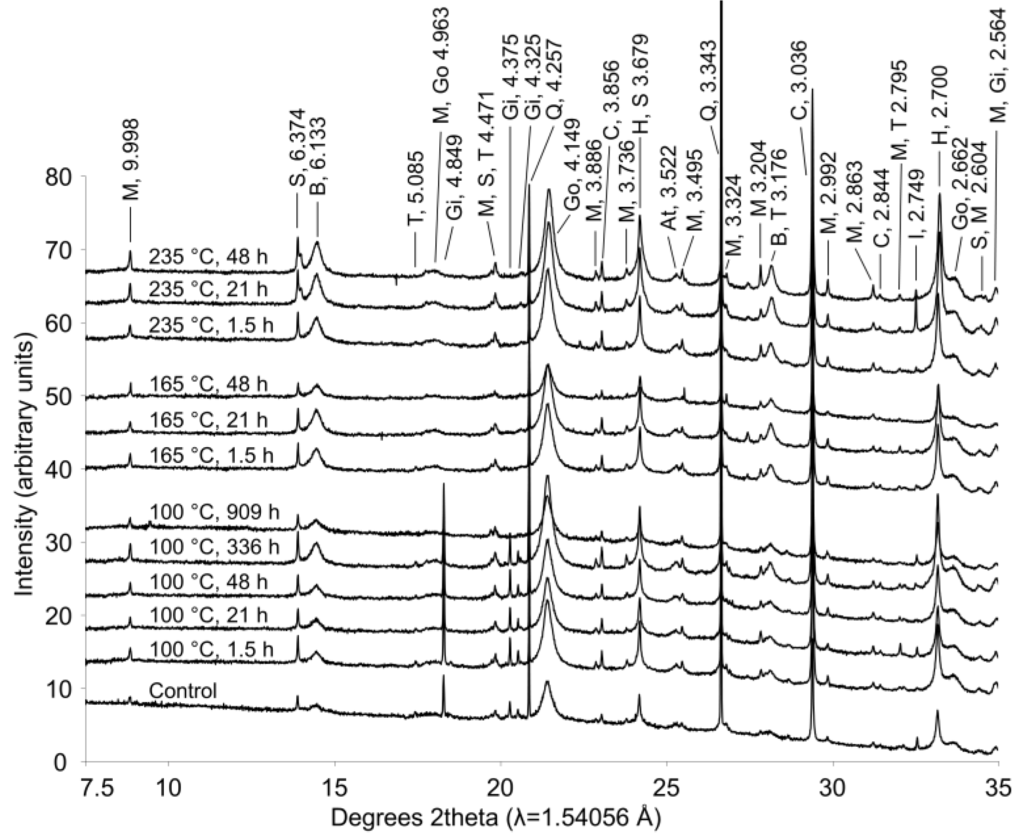
Metals 05 01241 g007 1024
Figure 7. X-ray diffraction patterns from bauxite residue before and after hydrothermal treatment. Treatment time and temperature are indicated for each pattern. Peaks between 7.5°–35° 2θ are labeled with d-spacings (Å) and abbreviations for minerals as follows: M—muscovite; S—sodalite; B—boehmite; T—tricalcium aluminate; Go—goethite; Gi—gibbsite; Q—quartz; C—calcite; H—hematite; At—natase; I—ilmenite.
Figure 7. X-ray diffraction patterns from bauxite residue before and after hydrothermal treatment. Treatment time and temperature are indicated for each pattern. Peaks between 7.5°–35° 2θ are labeled with d-spacings (Å) and abbreviations for minerals as follows: M—muscovite; S—sodalite; B—boehmite; T—tricalcium aluminate; Go—goethite; Gi—gibbsite; Q—quartz; C—calcite; H—hematite; At—natase; I—ilmenite.
Metals 05 01241 g007
Calcite and sodalite precipitation were not observed in the fused silica capillary experiments; changes in calcite:anatase ratio in Table 2 indicate that this is a slower reaction and smaller in magnitude than the boehmite precipitation reaction. Precipitation of calcite may have only occurred to a minor extent during the fused silica capillary experiments, and therefore may not have been detected. A similar explanation may account for the observations of goethite and hematite precipitation in the longer term stainless steel pressure vessel experiment. Both minerals precipitated more slowly and to a lesser extent than boehmite (Table 2), and precipitation may therefore not have been detectable over timescales of 150–250 min at temperatures of 140–165 °C.
Muscovite appeared to dissolve at 165–170 °C in the fused silica capillary experiments but was stable in the stainless steel pressure vessel experiments. As the only K-bearing mineral in bauxite residue, muscovite behaviour could be expected to mirror supernatant K concentrations (Figure 2), dissolving at temperatures ≤165 °C and precipitating at temperatures ≥200 °C. This is not fully supported by the XRD data from the fused silica capillary or the stainless steel pressure vessel experiments. All XRD patterns were collected from powders or slurries that were rotated during collection of XRD patterns; preferred orientation is therefore unlikely to cause changes in peak areas between patterns. Muscovite has been observed to dissolve under alkaline conditions [28,31], although dissolution rates decrease as aqueous Al and Si concentrations increase [32]. The minor dissolution observed in fused silica capillary experiments at 165–170 °C may be due to decreases in aqueous Al in supernatant solution at temperatures ≥165 °C (Figure 2). It is unclear why muscovite dissolution was not observed by ex situ XRD of hydrothermally treated solids.
Table
Table 2. Percentage change in mineral:anatase ratio during hydrothermal treatment of bauxite residue, relative to untreated bauxite residue. Ratio was calculated from primary peak areas of each mineral from synchrotron XRD scans. Mineral names are abbreviated as follows: Gi—gibbsite; T—tricalcium aluminate; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite. Mineral:anatase ratios of muscovite, anatase, and quartz did not indicate dissolution or precipitation in response to temperature or treatment time.
Table 2. Percentage change in mineral:anatase ratio during hydrothermal treatment of bauxite residue, relative to untreated bauxite residue. Ratio was calculated from primary peak areas of each mineral from synchrotron XRD scans. Mineral names are abbreviated as follows: Gi—gibbsite; T—tricalcium aluminate; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite. Mineral:anatase ratios of muscovite, anatase, and quartz did not indicate dissolution or precipitation in response to temperature or treatment time.
Temperature (°C)Treatment Time (h)Mineral
GiTBCGoHS
1001.554418230471547
10021472410243482962
1004846−215344523064
10033643−23138810789106
1651.5−100−1430053715568
16521−100−10046895119109118
16548−100−100584106138117190
2351.5−100−35348859990123
2353.75−100−10052688114119150
23521−100−10058794141177294
23548−100−100643111156198389

3.3. Reaction Kinetics

Peak areas of minerals in XRD patterns of residues from the 100, 165, and 235 °C treatments in the stainless steel pressure vessel experiment (Table 2) were used to calculate extents of reaction (α) and kinetic parameters (Equations (4)–(6)). The rapid dissolution of gibbsite and tricalcium aluminate precluded calculation of reaction kinetics for these phases from the stainless steel pressure vessel experiment data. Fused silica capillary reaction vessel data were used for the calculation of gibbsite reaction kinetics, at hydrothermal treatment temperatures of 140, 150, 165, and 170 °C, using absolute mineral concentration as calculated by Rietveld refinement of XRD patterns rather than peak area of minerals relative to the internal standard. The quality of the XRD patterns from the fused silica capillary experiment was insufficient to allow accurate quantification of tricalcium aluminate and reaction kinetics were therefore not calculated for this mineral.
Sharp-Hancock analysis of mineral transformations within these experiments indicated that the plots of ln(−ln(1 − α)) against ln(t) were well described by linear functions because r2 values were generally >0.80 (Table 3), except for goethite at 100 °C. This indicates that a single reaction mechanism dominated over the course of the dissolution or precipitation reactions for most minerals. The n values of 0.8–1.2 observed for gibbsite dissolution (Table 4) are consistent with first-order reaction kinetics (n = 1). Contracting area kinetics, with an n value of 1.04, and contracting volume kinetics, with an n value of 1.08, would also be feasible explanations for the observed n values and are consistent with the transformation of gibbsite to boehmite as a dissolution-precipitation mechanism [46,47].
Table
Table 3. Coefficients of determination (r2) for Sharp-Hancock lines of best fit (ln(−ln(1 − α)) vs. ln(t)) to mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Table 3. Coefficients of determination (r2) for Sharp-Hancock lines of best fit (ln(−ln(1 − α)) vs. ln(t)) to mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Temperature (°C)GiTemperature (°C)BCGoHS
1400.901000.860.840.640.910.91
1500.981650.940.990.990.990.92
1650.942350.861.001.001.000.97
1700.99
Table
Table 4. Reaction orders (n) derived from Sharp-Hancock lines of best fit (ln(−ln(1 − α)) vs. ln(t)) to mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Table 4. Reaction orders (n) derived from Sharp-Hancock lines of best fit (ln(−ln(1 − α)) vs. ln(t)) to mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Temperature (°C)GiTemperature (°C)BCGoHS
1400.8041000.2890.2810.2000.3630.162
1501.0721650.3570.4410.3610.3010.331
1650.9912350.4030.0960.3140.4990.508
1701.185
The Ea value calculated from this study (Table 5) match well with values from Mehta and Kalsotra’sstudy [48] of boehmite precipitation under hydrothermal, alkaline conditions for boehmite (Ea 69.63–73.46 kJ·mol−1). Under alkaline, heated (60–85 °C) conditions, at ambient pressure, the Ea for gibbsite dissolution is 107 kJ·mol−1 [51]. This is lower than the value observed in this study (Table 5), which suggests that pressure inhibited the gibbsite-boehmite transformation [21] The Ea value determined from this study for sodalite precipitation (Table 5) was much higher than that determined in other studies for first-order reaction kinetics involving precipitation from solution (38.2–48.4 kJ·mol−1; [52,53]). This suggests that sodalite is not directly precipitated from solution, but that precipitation is reliant upon the dissolution or transformation of another mineral. A similar elevation in activation energy for cancrinite precipitation under Bayer conditions was observed when cancrinite formed from sodalite rather than directly precipitating from solution [54]. Muscovite or quartz could be sources of reactive silica for sodalite precipitation; however, neither were observed to dissolve to an appreciable extent within this study. No values for activation energies of precipitation of calcite, goethite, or hematite under similar reaction conditions were available in the literature.
The low values of n returned from Sharp-Hancock analysis (0.10 < n < 0.85) for minerals other than gibbsite suggest that precipitation of minerals proceeded via three-dimensional (3D) diffusion controlled reaction mechanisms (Table 3), because these reactions occur with an ideal n value of 0.57 [55]. However, the activation energies calculated from Arrhenius plots of ln(k) against 1/T ranged from 76–131 kJ·mol−1 (Table 5). These activation energies are far higher than expected for diffusion controlled reactions (generally <21 kJ·mol−1; [56]), and therefore suggest that precipitation reactions were in fact surface controlled.
Table
Table 5. Activation energies (Ea; kJ·mol−1), pre-exponential (“frequency”) factors (A; s−1), and reaction rates at 165 °C (k; s−1) calculated from Arrhenius plots for mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Table 5. Activation energies (Ea; kJ·mol−1), pre-exponential (“frequency”) factors (A; s−1), and reaction rates at 165 °C (k; s−1) calculated from Arrhenius plots for mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
ParameterGiBCGoHS
Ea190.7988.0399.5875.5475.71131.15
ln A49.0012.8018.459.798.3821.07
log(k), 165 °C−1.47−4.94−3.86−4.76−5.39−6.50
In an attempt to distinguish which kinetic models best describe observed behaviour, lines were fitted to the reaction data for [ln(1 − α)] against t, which should result in a straight line with gradient k if the reaction is controlled by first-order kinetics, and [1 − (1 − α)1/3]2 against t, which should result in a straight line with gradient k if the reaction is controlled by 3D diffusion [55]. Gibbsite data was also fitted to [1 − (1 − α)1/2] against t, which should result in a straight line with gradient k if the reaction proceeds at a decelerating rate proportional to remaining mineral surface area (contracting area), and [1 − (1 − α)1/3] against t, which should result in a straight line with gradient k if the reaction proceeds at a decelerating rate proportional to remaining mineral volume (contracting volume). Coefficient of determination values (r2) were used to compare the linear fits achieved by each model. Fits achieved were similar, although r2 values for first-order reaction models were generally better than r2 values for 3D diffusion models for precipitating minerals (Table 6). The gibbsite dissolution rate appears to be constant at 140 and 150 °C (Figure 3 and Figure 4), but appears to decelerate at 165 and 170 °C (Figure 5 and Figure 6). However, the first-order, contracting area, and contracting volume models fit gibbsite dissolution at 150 and 170 °C equally well (Table 6). Overall, the fits to first-order, contracting area, and contracting volume models for gibbsite dissolution were almost identical, which does not allow the most appropriate model amongst these three to be identified.
Reaction half lives (time required for half of the reactant(s) in a chemical reaction to be consumed), as predicted by the Avrami-Erofe’ev Equation and using the values of n expected for first-order surface controlled and 3D diffusion controlled reactions, were compared with observed reaction half lives, calculated by interpolation of Sharp-Hancock lines of best fit. Precipitation reaction half lives were predicted far more accurately by the first-order surface control model (Table 7). This information, combined with the high activation energies which are inconsistent with the 3D diffusion mechanism, suggests that the rates of these precipitation reactions were controlled by first-order surface kinetics. It also seems unlikely that 3D diffusion would control reaction rates in a continuously stirred system. However, there was more than an order of magnitude difference between observed and predicted reaction half lives for boehmite, goethite, muscovite, and sodalite using first-order kinetics, which suggests that first-order kinetics do not accurately model reaction kinetics in all cases.
Table
Table 6. Coefficient of determination (r2) values for least square lines fitted to mineral precipitation or dissolution data under a first-order surface control kinetic model (FO), 3D diffusion control kinetic model (3D), contracting area model (CA), and contracting volume model (CV). Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Table 6. Coefficient of determination (r2) values for least square lines fitted to mineral precipitation or dissolution data under a first-order surface control kinetic model (FO), 3D diffusion control kinetic model (3D), contracting area model (CA), and contracting volume model (CV). Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
MineralKinetic ModelTemperature (°C)
100165235
BFO0.9850.9980.785
3D0.9990.9890.813
CFO0.9950.9890.938
3D0.9960.9940.944
GoFO0.9940.9850.988
3D0.9910.9960.992
HFO0.9920.8190.994
3D0.9950.8540.999
SFO0.9630.9930.999
3D0.9890.9620.998
MineralKinetic ModelTemperature (°C)
140150165170
GiFO0.9070.9870.9480.976
3D0.8900.9540.9370.916
CA0.9070.9860.9390.986
CV0.9070.9870.9430.984
Table
Table 7. Reaction half lives (t1/2) as calculated by interpolation of Sharp-Hancock lines of best fit to observed data (OB) and the Avrami-Erofe’ev equation predicted for first-order surface control (FO) and 3D diffusion control (3D) for mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
Table 7. Reaction half lives (t1/2) as calculated by interpolation of Sharp-Hancock lines of best fit to observed data (OB) and the Avrami-Erofe’ev equation predicted for first-order surface control (FO) and 3D diffusion control (3D) for mineral transformations in bauxite residue. Mineral names are abbreviated as follows: Gi—gibbsite; B—boehmite; C—calcite; Go—goethite; H—hematite; S—sodalite.
TemperatureKinetic ModelGiBCGoHS
165°C (h)OB0.00612221783
FO0.005716.781.401147595
3D0.0570678708693241241698635509858
25 °C (years)FO320981646121941513193
Using the kinetic data presented in Table 4 and Table 5, and assuming that reactions are controlled by a first-order surface mechanism (i.e., n = 1), reaction rates were extrapolated to determine reaction half lives at field conditions (1 atm pressure, 25 °C). Calcite, boehmite, goethite and hematite reach their reaction half lives within two centuries; however, gibbsite and sodalite take substantially longer to reach their half lives. Boehmite precipitation was predicted to occur more rapidly than gibbsite dissolution at field conditions, which indicates that gibbsite dissolution would control the gibbsite to boehmite transformation. Although auto-attenuation of residue alkalinity and salinity under closed system conditions is theoretically possible, it would take millions of years under field conditions if controlled by these mineral reactions. No mineral transformations or reactions were observed during simulated weathering that would be potentially deleterious to rehabilitation and long term environmental management, although the slow dissolution of calcite and sodalite (which precipitated to a minor extent under closed system conditions) during rainfall leaching would contribute to the maintenance of high alkalinity and salinity in bauxite residue pore water and leachates. Given the mineral transformations observed here, the soil forming from bauxite residue is likely to have similar mineralogical properties to deeply weathered soils characteristic of tropical environments, such as Nitisols and Ferralsols [57], owing to the dominance of iron oxides and absence of high-activity clay minerals. These soils are not alkaline or saline so substantial leaching of residue would be required to remove soluble salts, especially sodium which remains in pore water at substantial concentrations (≥1.5 g·L−1) even at the highest treatment temperature.
The reactions observed in this experiment may not occur under field conditions. Non-linearity in the response of activation energies and reaction rates to temperature and pressure can occur due to different reaction mechanisms being favoured [56], which hinders the use of observed activation energies and rates to predict behaviour outside the observed range. Diffusion does not appear to be a significant rate limiting process in the observed reactions, but is dependent on pressure, and the direction of this dependence (and thus the effect of pressure on reaction rates according to Equation (1)) cannot be predicted without determining activation volumes of the reactions. The effect of pressure on reaction rates is considered to be small relative to temperature for pressures found in the Earth’s crust (1–10,000 kbar) [56], and is, therefore, unlikely to cause substantial variation between observed and predicted reaction half lives within this study. However, the effect of temperature on activation energies, rates, and reaction mechanisms could result in a different suite of reactions occurring in bauxite residue within storage areas under ambient temperature and pressure compared to those observed at elevated temperatures and pressures. Results from this study illustrate a potential weathering trajectory for bauxite residue; but this would need to be validated against observations of mineral transformations in the long term for field weathered bauxite residues to confirm that the predicted reactions occur in the field. Further, trace element speciation and mobility, which were beyond the scope of this study, also merit evaluation under both simulated laboratory weathering and field weathering scenarios to ensure that the weathering reactions observed here do not result in pulses of elements, such as As, Se, Mo, and V, being released.

4. Conclusions

Hydrothermal treatment of bauxite residue slurry resulted in a decrease in pH, EC, and total alkalinity, as well as decreases in concentrations of Al, K, Na, and S, in the liquid component of the slurry; these decreases were inversely related to treatment temperature and time. Conversion of gibbsite to boehmite, and the dilution from water released to solution during this reaction, appeared to be the main mechanism responsible for decreases in pH, EC, TA, and element concentrations. Dissolution and precipitation kinetics were adequately described by first-order kinetics. Extrapolation of reaction rates and activation energies from hydrothermal conditions imposed in this study to standard temperature and pressure indicated that calcite, goethite, hematite, and boehmite precipitation could be expected to occur within a few centuries; but that dissolution of gibbsite and precipitation of sodalite would take substantially longer. Auto-attenuation of alkalinity and salinity in bauxite residue under closed conditions is theoretically possible according to the reaction kinetics determined in this study, although it would occur over lengthy timescales. Based on the observed mineral transformations, soil developing from bauxite residue is likely to have characteristics associated with Nitisols or Ferralsols. Extrapolation of reaction kinetics observed under hydrothermal conditions to standard temperatures and pressures may be invalid because of different reaction mechanisms being favoured at different temperatures and pressures. Temperature is likely to be more important than pressure in this regard. Validation of observed mineral behaviour in this study against field weathered residues is required to determine if mineral transformations observed under hydrothermal conditions provide an accurate representation of weathering reactions under field conditions.

Acknowledgments

The authors thank Stephen Leavy, Tina Matheson, and Alan Jones (Alcoa of Australia Limited) for assistance with the stainless steel reaction vessel experiment; Michael Smirk (University of Western Australia) and Bree Morgan (Monash University) for assistance with the fused silica capillary reaction vessel experiment; and Ian Madsen (CSIRO) and Matthew Rowles (Curtin University) for assistance with Rietveld refinement of X-ray diffractograms. Part of this research was undertaken on the Powder Diffraction beamline (10BM1) at the Australian Synchrotron, Victoria, Australia, and the authors would like to thank Kia Wallwork for assistance with the fused silica capillary reaction vessel experiment. This research was supported by an Australian Postgraduate Award, and funding from the Minerals and Energy Research Institute of Western Australia, Alcoa of Australia Ltd., and BHP Billiton Worsley Alumina Pty Ltd.

Author Contributions

T.S. and M.F. conceived the experiments; T.S. designed experiments with contributions from M.F. and R.G.; T.S. performed experiments, data analysis and interpretation, and wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest. This study was supported by funding from Alcoa of Australia Ltd. and BHP Billiton Worsley Alumina Ltd.; however, funders had no role in the design of the study or interpretation of results.

References

  1. Mudd, G.M.; Boger, D.V. The ever growing case for paste and thickened tailings—Towards more sustainable mine waste management. J. Aust. Inst. Min. Metall. 2013, 2, 56–59. [Google Scholar]
  2. Uzarowicz, L.; Skiba, A. Technogenic soils developed on mine spoils containing iron sulphides: Mineral transformations as an indicator of pedogenesis. Geoderma 2011, 163, 95–108. [Google Scholar] [CrossRef]
  3. Santini, T.C.; Fey, M.V. Spontaneous vegetation encroachment upon bauxite residue (red mud) as an indication and facilitator of in situ remediation processes. Environ. Sci. Technol. 2013, 47, 12089–12096. [Google Scholar] [CrossRef] [PubMed]
  4. Hayes, S.M.; Root, R.A.; Perdrial, N.; Maier, R.M.; Chorover, J. Surficial weathering of iron sulfide mine tailings under semi-arid climate. Geochim. Cosmochim. Acta 2014, 141, 240–257. [Google Scholar] [CrossRef] [PubMed]
  5. Wilkinson, B.H.; McElroy, B.J. The impact of humans on continental erosion and sedimentation. Geol. Soc. Am. Bull. 2007, 119, 140–156. [Google Scholar] [CrossRef]
  6. Bardossy, G.; Aleva, G.J.J. Lateritic Bauxites; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
  7. Power, G.; Grafe, M.; Klauber, C. Bauxite residue issues: I. Current management, disposal and storage practices. Hydrometallurgy 2011, 108, 33–45. [Google Scholar] [CrossRef]
  8. Santini, T.C.; Fey, M.V. Fly ash as a permeable cap for tailings management: Pedogenesis in bauxite residue tailings. J. Soils Sediments 2015, 15, 552–564. [Google Scholar] [CrossRef]
  9. Santini, T.C.; Fey, M.V. Assessment of Technosol formation and in situ remediation in capped alkaline tailings. Catena 2015. in review. [Google Scholar]
  10. Henin, S.; Pedro, G. The laboratory weathering of rocks. In Experimental Pedology; Hallsworth, E.G., Crawford, D.V., Eds.; Butterworths: London, UK, 1965; pp. 15–22. [Google Scholar]
  11. Williams, C.; Yaalon, D.H. An experimental investigation of reddening in dune sand. Geoderma 1977, 17, 181–191. [Google Scholar] [CrossRef]
  12. Singleton, G.A.; Lavkulich, L.M. Adaptation of the Soxhlet extractor for pedologic studies. Soil Sci. Soc. Am. J. 1978, 42, 984–986. [Google Scholar] [CrossRef]
  13. Sullivan, P.J.; Sobek, A.A. Laboratory weathering studies of coal refuse. Environ. Geochem. Health 1982, 4, 9–16. [Google Scholar] [CrossRef]
  14. Hodson, M.E. Experimental evidence for mobility of Zr and other trace elements in soils. Geochim. Cosmochim. Acta 2002, 66, 819–828. [Google Scholar] [CrossRef]
  15. Taylor, S.; Pearson, N. Properties of Bayer Process Solids from Alcoa WA Refineries and Their Component Minerals; Alcoa of Australia Ltd.: Perth, Australia, 2001; p. 86. [Google Scholar]
  16. Hurst, V.J.; Kunkle, A.C. Dehydroxlyation, rehydroxylation, and stability of kaolinite. Clays Clay Miner. 1985, 33, 1–14. [Google Scholar] [CrossRef]
  17. Imasuen, O.I.; Tazaki, K.; Fyfe, W.S.; Kohyama, N. Experimental transformation of kaolinite to smectite. Appl. Clay Sci. 1989, 4, 27–41. [Google Scholar] [CrossRef]
  18. Mosser-Ruck, R.; Cathelineau, M. Experimental transformation of Na, Ca smectite under basic conditions at 150 °C. Appl. Clay Sci. 2004, 26, 259–273. [Google Scholar] [CrossRef]
  19. Su, C.; Harsh, J.B. Dissolution of allophane as a thermodynamically unstable solid in the presence of boehmite at elevated temperatures and equilibrium vapor pressures. Soil Sci. 1998, 163, 299–312. [Google Scholar] [CrossRef]
  20. Nikraz, H.R.; Bodley, A.J.; Cooling, D.J.; Kong, P.Y.L.; Soomro, M. Comparison of physical properties between treated and untreated bauxite residue mud. J. Mater. Civ. Eng. 2007, 19, 2–9. [Google Scholar] [CrossRef]
  21. Wefers, K.; Misra, C. Oxides and Hydroxides of Aluminium; Alcoa Technical Paper No. 19 (revised); Aluminium Company of America: Pittsburgh, PA, USA, 1987; p. 92. [Google Scholar]
  22. Murray, J.; Kirwan, L.; Loan, M.; Hodnett, B.K. In situ synchrotron diffraction study of the hydrothermal transformation of goethite to hematite in sodium aluminate solutions. Hydrometallurgy 2009, 95, 239–246. [Google Scholar] [CrossRef]
  23. Whittington, B.I. The chemistry of CaO and Ca(OH)2 relating to the Bayer process. Hydrometallurgy 1996, 43, 13–35. [Google Scholar] [CrossRef]
  24. Smith, P. The processing of high silica bauxites—Review of existing and potential processes. Hydrometallurgy 2009, 98, 162–176. [Google Scholar] [CrossRef]
  25. Thompson, T.L.; Hossner, L.R.; Wilding, L.P. Micromorphology of calcium carbonate in bauxite processing waste. Geoderma 1991, 48, 31–42. [Google Scholar] [CrossRef]
  26. Menzies, N.W.; Fulton, I.M.; Kopittke, R.A.; Kopittke, P.M. Fresh water leaching of alkaline bauxite residue after sea water neutralization. J. Environ. Qual. 2009, 38, 2050–2057. [Google Scholar] [CrossRef] [PubMed]
  27. Hawkins, D.B.; Roy, R. Experimental hydrothermal studies on rock alteration and clay mineral formation. Geochim. Cosmochim. Acta 1963, 27, 1047–1054. [Google Scholar] [CrossRef]
  28. Knauss, K.G.; Wolery, T.J. Muscovite dissolution kinetics as a function of pH and time at 70 °C. Geochim. Cosmochim. Acta 1989, 53, 1493–1501. [Google Scholar] [CrossRef]
  29. Huang, W.L. Stability and kinetics of kaolinite to boehmite conversion under hydrothermal conditions. Chem. Geol. 1993, 105, 197–214. [Google Scholar] [CrossRef]
  30. Frogner, P.; Schweda, P. Hornblende dissolution kinetics at 25 °C. Chem. Geol. 1998, 151, 169–179. [Google Scholar] [CrossRef]
  31. Kuwahara, Y. In situ observations of muscovite dissolution under alkaline conditions at 25–50 °C by AFM with an air/fluid heater system. Am. Mineral. 2008, 93, 1028–1033. [Google Scholar] [CrossRef]
  32. Oelkers, E.H.; Schott, J.; Gauthier, J.M.; Herrero-Roncal, T. An experimental study of the dissolution mechanism and rates of muscovite. Geochim. Cosmochim. Acta 2008, 72, 4948–4961. [Google Scholar] [CrossRef]
  33. Gudbrandsson, S.; Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H. An experimental study of crystalline basalt dissolution from 2 ≤ pH ≤ 11 and temperatures from 5 to 75 °C. Geochim. Cosmochim. Acta 2011, 75, 5496–5509. [Google Scholar] [CrossRef]
  34. Saldi, G.D.; Schott, J.; Pokrovsky, O.S.; Gautier, Q.; Oelkers, E.H. An experimental study of magnesite precipitation rates at neutral to alkaline conditions and 100–200 °C as a function of pH, aqueous solution composition and chemical affinity. Geochim. Cosmochim. Acta 2012, 83, 93–109. [Google Scholar] [CrossRef]
  35. Heimann, R.B.; Vandergraaf, T.T. Cubic zirconia as a candidate waste form for actinides: Dissolution studies. J. Mater. Sci. Lett. 1988, 7, 583–586. [Google Scholar] [CrossRef]
  36. Coelho, A. TOPAS-Academic v 4.1, Coelho Software: Brisbane, Australia, 2007.
  37. Vogel, A.I. A Textbook of Quantitative Inorganic Analysis; Longman Group: New York, NY, USA, 1978; p. 925. [Google Scholar]
  38. GBC Scientific Equipment Pty. Ltd. Traces: X-ray Diffraction Screen Processing Software and Accessories, v 6.7.20, GBC Scientific Equipment: Hampshire, NH, USA, 2006.
  39. Chester, R.; Jones, F.; Loan, M.; Oliviera, A.; Richmond, W.R. The dissolution behaviour of titanium oxide phases in synthetic Bayer liquors at 90 °C. Hydrometallurgy 2009, 96, 215–222. [Google Scholar] [CrossRef]
  40. Norby, P. Hydrothermal conversion of zeolites: An in situ synchrotron X-ray powder diffraction study. J. Am. Chem. Soc. 1997, 119, 5215–5221. [Google Scholar] [CrossRef]
  41. Sharp, J.H.; Hancock, J.D. Method of comparing solid state kinetic data and its application to the decomposition of kaolinite, brucite, and BaCO3. J. Am. Ceram. Soc. 1972, 55, 74–77. [Google Scholar]
  42. Avrami, M. Kinetics of phase change. I. General theory. J. Chem. Phys. 1939, 7, 1103–1113. [Google Scholar] [CrossRef]
  43. Avrami, M. Kinetics of phase change. II. Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–225. [Google Scholar] [CrossRef]
  44. Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. III. J. Chem. Phys. 1941, 9, 177–185. [Google Scholar] [CrossRef]
  45. Erofe’ev, B.V. Generalised equation of chemical kinetics and its application in reactions involving solids. C. R. (Dokl.) Acad. Sci. URSS 1946, 52, 511–514. [Google Scholar]
  46. Tsuchida, T. Hydrothermal synthesis of submicrometer crystals of boehmite. J. Eur. Ceram. Soc. 2000, 20, 1759–1764. [Google Scholar] [CrossRef]
  47. Gong, X.; Nie, Z.; Qian, M.; Liu, J.; Pederson, L.A.; Hobbs, D.T.; McDuffle, N.G. Gibbsite to boehmite transformation in strongly caustic and nitrate environments. Ind. Eng. Chem. Res. 2003, 42, 2163–2170. [Google Scholar] [CrossRef]
  48. Mehta, S.K.; Kalsotra, A. Kinetics and hydrothermal transformation of gibbsite. J. Ther. Anal. Calorim. 1991, 367, 267–275. [Google Scholar] [CrossRef]
  49. Dash, B.; Tripathy, B.C.; Bhattacharya, I.N.; Das, S.C.; Mishra, C.R.; Pani, B.S. Effect of temperature and alumina/caustic ratio on precipitation of boehmite in synthetic sodium aluminate liquor. Hydrometallurgy 2007, 88, 121–126. [Google Scholar] [CrossRef]
  50. Dash, B.; Tripathy, B.C.; Bhattacharya, I.N.; Das, S.C.; Mishra, C.R.; Mishra, B.K. Precipitation of boehmite in sodium aluminate liquor. Hydrometallurgy 2009, 95, 297–301. [Google Scholar] [CrossRef]
  51. Grenman, H.; Salmi, T.; Murzin, D.Y.; Addai-Mensah, J. The dissolution kinetics of gibbsite in sodium hydroxide at ambient pressure. Ind. Eng. Chem. Res. 2010, 49, 2600–2607. [Google Scholar] [CrossRef]
  52. Adamson, A.N.; Bloore, E.J.; Carr, A.R. Extractive Metallurgy of Aluminium—Volume 1; Interscience: New York, NY, USA, 1963; pp. 23–58. [Google Scholar]
  53. Cresswell, P.J. Factors affecting desilication of Bayer process liquors. In Proceedings of the Chemeca 84: The 12th Australian Chemical Engineering Conference, Melbourne, Australia, 26–29 August 1984.
  54. Barnes, M.C.; Addai-Mensah, J.; Gerson, A. A methodology for quantifying sodalite and cancrinite phase mixtures and the kinetics of the sodalite to cancrinite phase transformation. Microporous Mesoporous Mater. 1999, 31, 303–319. [Google Scholar] [CrossRef]
  55. Francis, R.J.; O’Brien, S.; Fogg, A.M.; Halasyamani, P.S.; O’Hare, D.; Loiseau, T.; Ferey, G. Time-resolved in situ energy and angular dispersive X-ray diffraction studies of the formation of the microporous gallophosphate ULM-5 under hydrothermal conditions. J. Am. Chem. Soc. 1999, 121, 1002–1015. [Google Scholar] [CrossRef]
  56. Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
  57. IUSS Working Group WRB. World Reference Base for Soil Resources 2014; World Soil Resources Reports No. 106; Food and Agriculture Organisation of the United Nations: Rome, Italy, 2014. [Google Scholar]

Share and Cite

MDPI and ACS Style

Santini, T.C.; Fey, M.V.; Gilkes, R.J. Experimental Simulation of Long Term Weathering in Alkaline Bauxite Residue Tailings. Metals 2015, 5, 1241-1261. https://doi.org/10.3390/met5031241

AMA Style

Santini TC, Fey MV, Gilkes RJ. Experimental Simulation of Long Term Weathering in Alkaline Bauxite Residue Tailings. Metals. 2015; 5(3):1241-1261. https://doi.org/10.3390/met5031241

Chicago/Turabian Style

Santini, Talitha C., Martin V. Fey, and Robert J. Gilkes. 2015. "Experimental Simulation of Long Term Weathering in Alkaline Bauxite Residue Tailings" Metals 5, no. 3: 1241-1261. https://doi.org/10.3390/met5031241

Article Metrics

Back to TopTop