Exploring Lattice Rotations Induced by Kinematic Constraints in Deep Drawing from Crystal Plasticity Approach

Abstract

The anisotropic nature of cup ears formed during the deep drawing of sheet metals is governed by the distribution of crystallographic orientation in interaction between earing. In this study, we examined the orientation development of a cube-oriented aluminum single crystal to couple the deep drawing kinematics with the formation of anisotropic orientations. A quarter model of a circular deep-drawn blank was simulated in the finite element software using a user-defined material subroutine. A cube-oriented aluminum single crystal was designed to serve as a reference and trace the orientation evolution in the deep drawing process. After the deep drawing, the bottom, wall, and flange of the drawn cup were investigated at azimuthal angles ($\alpha$ ) of 0° and 45° with respect to the radial direction (RD) in terms of the orientation. Our findings show that the change in the lattice orientation could be attributed to the rotation induced by drawing and bending processes under kinematic constraints. Thus, the initial cube orientation developed into different orientations during the deep drawing. The type-A slip system mainly contributed to the radial strain at α = 0°, and type-B and C slip systems accounted for the longitudinal and circumferential strains at α = 45°.

1. Introduction

The deep drawing process is widely applied to the aerospace, automobile, and packaging industries, particularly in manufacturing axisymmetric components. This process is generally based on a complex deformation mechanism involving bending, sliding, stretching, friction, and compression. However, defects in the drawn parts, such as earing, wrinkling, spring back, surface roughness, and sheet thickness variation, negatively affect the product quality [1]. The change in the shape of the sheet metal will provide major benefits, such as reducing tool wear rate owing to reducing scrap or reducing thickness [2]. In the deep drawing of cylindrical cups at the macroscale, the maximum and minimum sheet thicknesses are, respectively, observed in the flange and cup wall, in comparison with the initial blank thickness, while the bottom of the drawn part generally retains its original thickness due to the absence of deformation [3]. The stress state in the flange area can be characterized by a tensile load in the radial direction (RD) and a compressive load in the tangential direction (TD). The cup wall and bottom are subjected to biaxial stress [4]. Therefore, sheet thickness variation must be avoided, and a uniform sheet thickness should be maintained to improve product quality [5]. Among the various defects found in deep-drawn parts, the earing phenomenon, which can be characterized by a wavy edge at the top, has been a major subject in the deep drawing process due to the plastic anisotropy of sheet metals. Recently, Zhang et al. [6] analyzed the influence of initial surface roughness on the evolution of the surface of metallic materials constrained by the mold with mandrel and found that an increase in the initial surface roughness reduces the change rate of surface roughness. In addition, copper single crystal, with its low resistance and good ductility, has been applied in special mechanical manufacturing of deep-drawn cup-like parts [7].

Ears are wavy projections or unevenness formed along the edge of the flange or end of the wall of the cup during the deep drawing process, resulting in anisotropic thickness. It is a characteristic phenomenon associated with the anisotropic yield surface function and the crystallographic texture of the material. The flange earing can be modeled using anisotropic yield surface functions under loading conditions at the macroscopic scale. Hill [8] established a quadratic yield function for the plane and full stress state, which has six material parameters. Barlat and co-workers developed anisotropic yield functions to improve the formulations of Hill. Barlat and Lian [9] presented an anisotropic yield function under a full plane stress state, including four independent material parameters referred to as Yld89. Then, Barlat et al. introduced anisotropic yield functions of Yld91 [10], Yld94 [11], Yld96 [12], Yld2000–2d [13], Yld2004–18p [14], and Yld2004–27p [15]. Furthermore, Aretz and Barlat [16] introduced two anisotropic yield functions of Yld2011–18p and Yld2011–27p, containing 18 and 27 parameters, respectively. Lou et al. [17] presented a modified version of the Yld2004–18p yield function with twelve material parameters. For advanced yield criteria, Aretz and Barlat [16] proposed to use numerical approximations of the yield function gradients to avoid the singularities in the analytical counterparts. Choi and Yoon [18] modified the stress integration algorithm developed by Aretz and Barlat [16] to implement in ABAQUS/Standard various anisotropic constitutive models with distortional hardening.

Variational finite element (FE) methods explicitly consider the mechanical interactions between crystals in a polycrystal and the complex internal or external boundary conditions [17,19]. For metal forming applications, the crystal plasticity finite-element model (CPFEM) [20,21,22] is based on the variational solution of the equilibrium of forces and the compatibility of the displacements using a weak form of the principle of virtual work [23,24]. Shi et al. [25] observed that the initial texture and its grain spatial distribution influence the earing phenomenon in AA4104-H19 sheets, where a finite element-based crystal plasticity model for four, six, and eight ears was used. Through a simulation of deep drawing using multiscale finite elements for AA6K21, Wang et al. [26] discovered that {011}<211> brass and {123}<634> S orientations had six ears at azimuthal angles of 0° and 55°, and the {112}<111> copper orientation had eight ears at angles of 40° and 70°. Moreover, the earing profile was symmetrical at approximately 45° for the {001}<100> cube orientation. Pei et al. [27] predicted the microstructure evolution of the hydro-bulging process of 2219 aluminum alloy sheets using CPFEM. It is pointed out that an increase in the strain ratio increases the {011}<566> P texture component at the expense of the initial rotated copper texture component and γ-Fiber texture component. The rotated cube component is inclined to rotate towards the cube component.

In addition to CPFEMs, crystallographic texture-based crystal plasticity modeling involves directly incorporating crystal plasticity (deformation physics) [28,29,30] into the computational tools (continuum mechanics) [31] via the initial grain orientation obtained from scanning electron microscopy–electron backscatter diffraction. Thus, crystallographic texture-based CPFEMs consider crystallographic texture and deformation anisotropy when applied to predict earing behavior in deep drawing.

As mentioned, early studies focused on finding the relationship between ears and textures. However, the relationship between the crystal rotation kinematics of deep drawing and earing behavior remains unclear. The novelty of this study is to unveil the anisotropic lattice rotation of a well-defined aluminum single crystal by virtual testing of deep drawing through a CPFEM. As previously discussed, the anisotropic phenomenon of ears can be predicted using Taylor–Bishop–Hill (TBH) models, self-consistent models, FE methods, CPFEMs, and crystallographic texture-based crystal models. The CPFEM has become a widely accepted method for virtual deep drawing to predict the anisotropic phenomenon of ears. The deformation kinematics of the crystal plasticity formulation reveals the tensorial crystallographic nature of dislocations and leads to changes in the shape and orientation. Hence, the texture can be used to describe the integral anisotropy of polycrystals and index the deformed states besides stress and strain, which can be extracted from the calculation of CPFEM.

The purpose of this study is to bridge the connection between the body rigid rotation at the macroscale and the lattice rotation at the mesoscale during deep drawing. Here, the cube orientation of an aluminum single crystal, which provides the clear and simple physics of crystal plasticity, was selected as the reference orientation. In addition, the CPFEM, which represents a direct and effective approach by considering crystal plasticity and orientation, was used for virtual testing of deep drawing to determine the crystal rotation kinematics and earing behavior.

2. Numerical Simulation and Modeling

2.1. Crystal Plasticity Model

The constitutive framework adopted in this study is briefly summarized. Considering the rate-dependent crystal plasticity model, the deformation gradient $\mathit{F}$ for each grain can be decomposed into two components:

$$\mathit{F}={\mathit{F}}_e{\mathit{F}}_p$$

(1)

where ${\mathit{F}}_e$ and ${\mathit{F}}_p$ denote the elastic and plastic deformation gradients, respectively. In addition, the spatial gradient of the total velocity L is defined as follows:

$$\mathit{L}=\dot{\mathit{F}}{\mathit{F}}^{-1}={\mathit{L}}_e+{\mathit{F}}_e{\mathit{L}}_P{\mathit{F}}_e^{-1}$$

(2)

where ${\mathit{L}}_e$ and ${\mathit{L}}_p$ indicate the elastic and plastic velocity gradients, respectively.

The unit vectors of ${\mathit{m}}_0^s$ and ${\mathit{n}}_0^s$ show the slip direction and normal to slip plane of the {111}<110> slip systems for fcc in the undeformed configuration. After deformation, the crystal lattices are distorted and rotated, and both vectors of ${\mathit{b}}^{s\ast }$ and ${\mathit{n}}^{s\ast }$ are expressed by:

$${\mathit{b}}^{s\ast }={\mathit{F}}_e·{\mathit{b}}^s$$

(3)

$${\mathit{n}}^{s\ast }={\mathit{n}}^s·{\mathit{F}}_e^{-1}$$

(4)

The plastic velocity gradient ${\mathit{L}}_p$ can be considered the sum of the shear rates on all slip systems obtained using first-order terms only:

$${\mathit{L}}_P={\dot{\mathit{F}}}_p{\mathit{F}}_p^{-1}=\sum _{s=1}^n{\dot{\gamma }}^s{\mathit{b}}^s ⨂ {\mathit{n}}^s$$

(5)

where ${\dot{\gamma }}^s$ is the shear rate on the slip system $s$, and n denotes the number of the slip system. The shear rate ${\dot{\gamma }}^s$ is formulated as a function of the resolved shear stress ${\tau }^s$ obtained using the kinetic law:

$${\dot{\gamma }}^s={\dot{\gamma }}_0 {\left|{\displaystyle \frac{{\tau }^s}{{\tau }_c^s}}\right|}^{{\displaystyle \frac{1}{m}}}\mathit{sign}({\tau }^s)$$

(6)

where ${\dot{\gamma }}_0$ refers to the reference shear strain rate, m denotes the strain rate sensitivity, ${\tau }^s=({\mathit{b}}^s ⨂ {\mathit{n}}^s)·\mathit{\sigma }$ indicates the resolved shear stress, and ${\tau }_c^s$ is the critical resolved shear stress. The hardening evolution of a fixed slip system $\alpha$ with another slip system $\beta$ can be formulated as follows:

$${\dot{\tau }}_c^{\alpha }=\sum _{\beta =1}^n{h}^{\alpha \beta }\left|{\dot{\gamma }}^{\beta }\right|$$

(7)

where ${\dot{\gamma }}^{\beta }$ is the shear rate of the slip system $\beta$, and $h^{\alpha \beta }$ is the hardening matrix, computed as follows:

$$h^{\alpha \beta }=[q^{\alpha \beta }+\left(1-q^{\alpha \beta }\right){\delta }^{\alpha \beta }]h^{\beta }$$

(8)

where $q^{\alpha \beta }$ refers to a latent hardening parameter. For a coplanar slip system, $q^{\alpha \beta }$ = ${\delta }^{\alpha \beta }$ = 1, and for a noncoplanar slip system, $q^{\alpha \beta }=1.4$ and ${\delta }^{\alpha \beta }=0$. $h^{\beta }$ is the self-hardening rate computed through the following:

$$h^{\beta }=h_0{(1-{\displaystyle \frac{{\tau }_c^{\beta }}{{\tau }_s}})}^a$$

(9)

where $h_0$ denotes the initial hardening rate, ${\tau }_s$ refers to the saturation value of ${\tau }_c^{\beta }$, and $a$ is the hardening exponent. ${\tau }_s$ is assumed to be the same for all slip systems.

2.2. Numerical Simulation Model of Deep Drawing

We considered a circular blank sheet with an initial thickness and a radius, subjected to deep drawing to produce a cup (Figure 1). In the sheet, the X-direction is aligned along the RD, the Y-direction is along the TD, and the Z-direction is along the normal direction (ND) (Figure 1). We assumed the application of a single element through the sheet thickness and mapped the mesh to the sheet at the RD–TD section. Simulations were performed using a user-defined material subroutine [32] and only a quarter of the blank was modeled, owing to sample symmetry during deep drawing, in the ABAQUS 6.13 finite element software using an implicit solver. Figure 2 shows the simulation setup for modeling the cup drawing process, comprising a blank, blank holder, die, and punch.

Table 1. Parameters of tool systems (unit in mm).

Radius of Blank ($R_b$)	39.50
Thickness of blank ($t$)	0.81
Radius of punch ($R_p$)	20.64
Radius of punch profile ($r_p$)	4.57
Radius of die ($R_d$)	22.03
Radius of die profile ($r_d$)	5.08

presents the dimensions of the simulation setup.

The cylindrical blank used had a diameter of 79 mm and a thickness of 0.81 mm, and the punch diameter was 41 mm with a punch radius of 4.57 mm. The die was 22.03 mm long with a die radius of 5.08 mm. The blank holder, die, and punch were modeled as analytically rigid surfaces, and the blank was modeled using two types of elements (C3D6 and C3D8;

Table 2. Details of mesh discretization.

Parts	Element Type	Total Number of Elements
Blank	C3D6 and C3D8	$\approx$800
Punch	R3D3 and R3D4	$\approx$60
Holder	R3D4	$\approx$70
Die	R3D4	$\approx$110

). Coulomb friction was assumed between the blank and the blank holder, and the friction coefficient was set to μ = 0.05. In addition, a state-based contact tracking algorithm was used to enforce the hard contact between the blank and the holder.

3. Results and Discussion

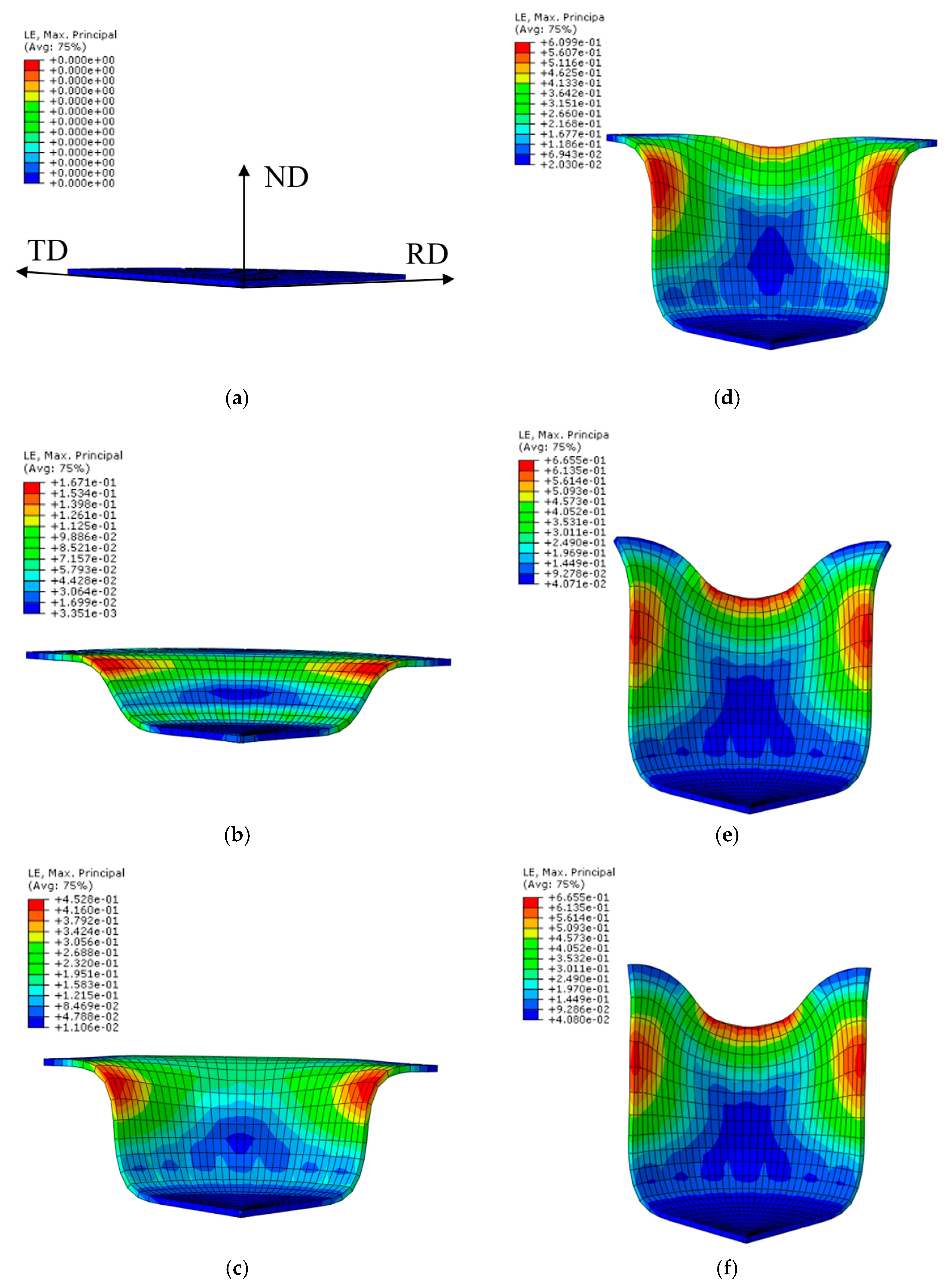
3.1. Anisotropic Earing and Deformation Heterogeneity in Deep Drawing

To comprehend the relationship between the crystal rotation kinematics of deep drawing and earing behavior, we adapted a CPFEM and compared the simulated results with the experimental findings on aluminum single crystals obtained from the study conducted by Tucker [33]. Subsequently, we focused on the development of crystal rotation induced by deep drawing kinematics for cube orientation. The development of earing behavior resulting from crystal rotation will be discussed for cube orientation in the following sections. In this study, the RD, TD, and ND of the sample coordinates are the X, Y, and Z axes, respectively (Figure 1). The position of a pole figure can be described using the azimuthal angle $\alpha$, and the radial angle $\beta$ is illustrated in a pole figure shown in Figure 1b.

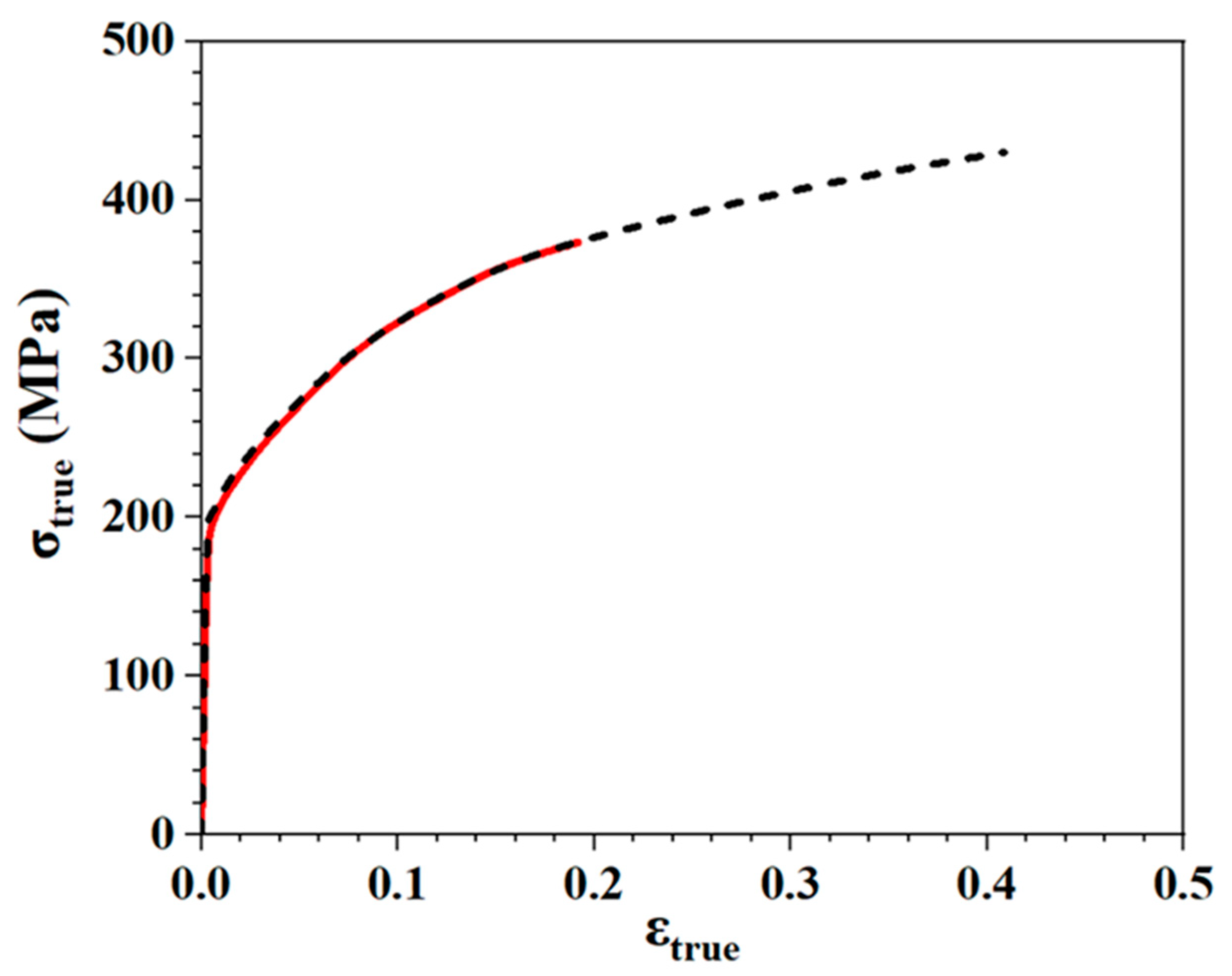
The values of the work-hardening parameters listed in

Table 3. Crystal elastic constants and hardening parameters for the crystal plasticity model of aluminum.

Crystal Elastic Constants			Hardening Parameters
$C_{11}$ (GPa)	$C_{12}$ (GPa)	$C_{44}$ (GPa)	${\dot{\gamma }}_0$ (s−1)	m	$h_0$ (Mpa)	${\tau }_s$ (Mpa)	a	$q^{\alpha \beta }$
107	61	28.3	0.001	0.1	60	61	2	1.2

were used to plot the stress–strain curve under uniaxial tension through numerical simulations along the RD, as shown in Figure 3, where the numerical model has one element with a thickness of 3.2 mm. The predicted stress–strain curve corresponded to the experimental data obtained in a previous study [34] (Figure 4). The material model could accurately capture the anisotropic yield and the differential work hardening observed experimentally. 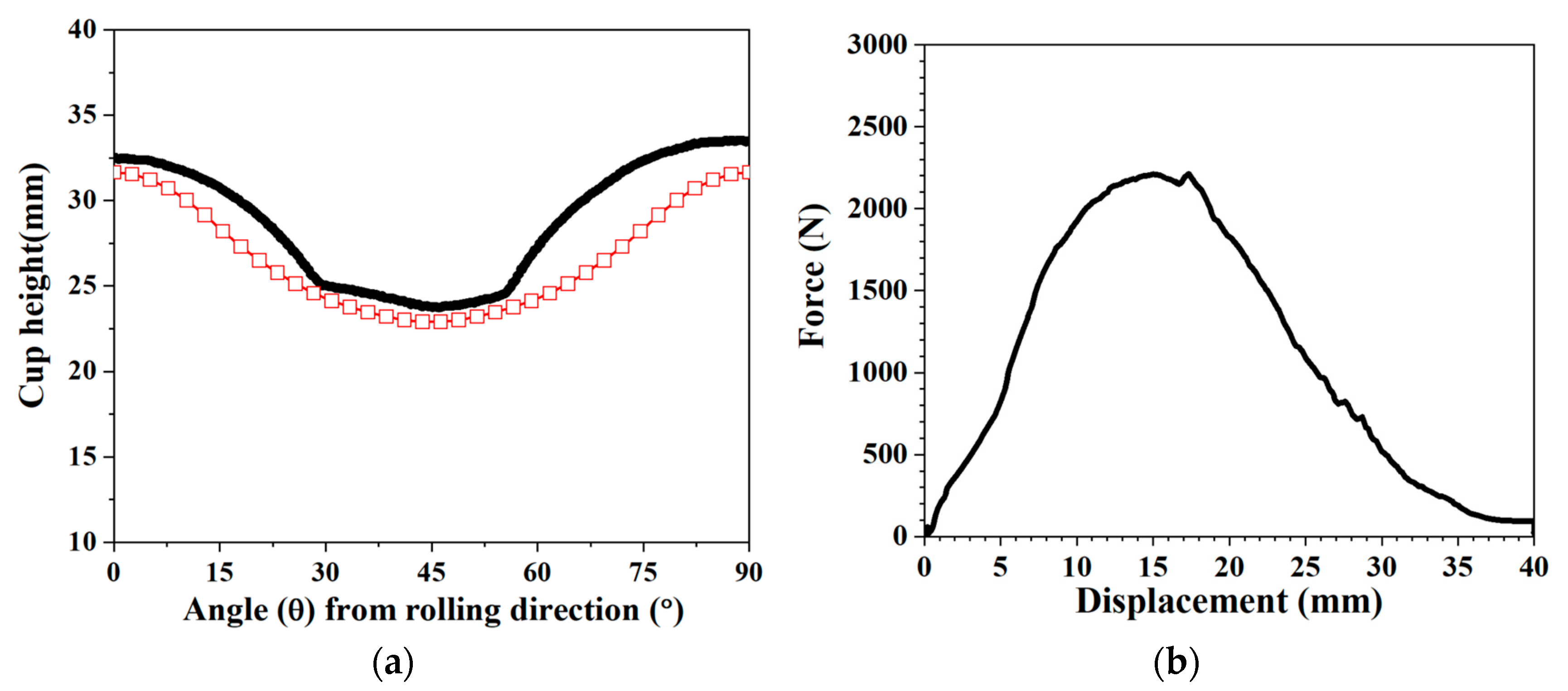The experimental data on the earing profile collected by Tucker [33] were employed in the comparison with the cup height predicted using the CPFEM (Figure 5a). For the cube orientation {001}<100>, two ears were formed in the simulation and experiment at azimuthal angles ($\alpha$) of 0° and 90° with respect to the RD in the range of 0–90°, that is, four ears at $\alpha$ = 0°, 90°, 180°, and 360°, owing to sample symmetry. Figure 5a shows the cup height plotted with respect to $\alpha$. The simulation and experimental results show two ears at $\alpha$ = 0° and 90°. The agreements were reasonable in terms of the cup height prediction, although the absolute cup height could not be determined due to the lubrication condition during deep drawing. In addition, the CPFEM results were used to plot the punch force–displacement curve of the deep drawing process (Figure 5b).

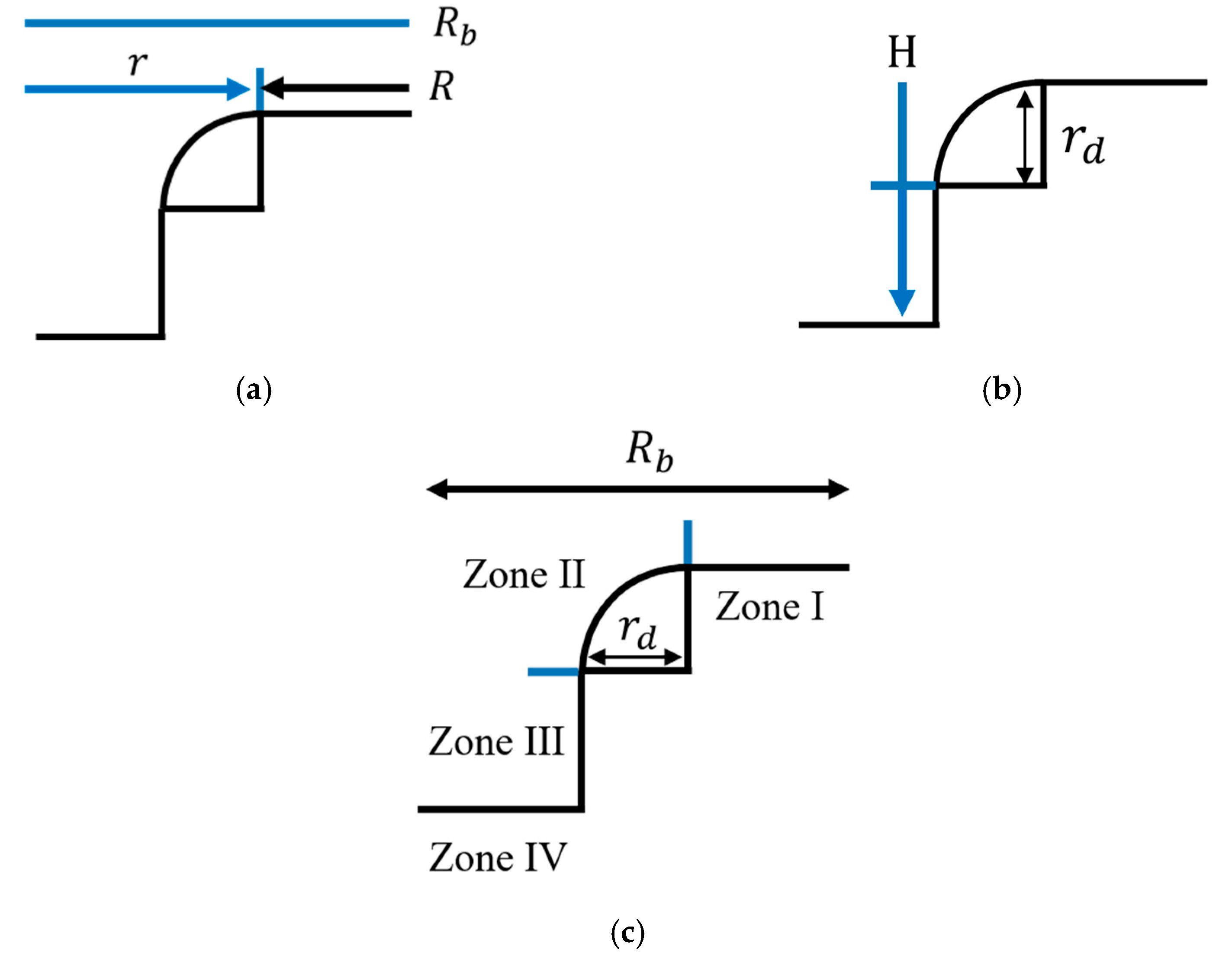
The specified position A of the cup shape during deep drawing can be described by the $Z$ position along the ND, as shown in Figure 6b, and by the radial position $r$ and circumferential position $\alpha$ along the $\overrightarrow{r}$ and $\overrightarrow{\alpha }$ directions in the coordinates of the RD and TD planes, where the drawing depth $H$ is used for position Z of the cup. The radial positions of $r$ and $R$ = $R_b$ − $r$ imply the distance measured from the center and that measured from the rim of the circle, respectively (Figure 7a). In addition, the drawing depth $H$ and radial distance $R$ are expressed in terms of the die radius $r_d$ as $H/r_d$ and $R/r_d$, respectively. With this, the current position of a given node during deep drawing can be specified. 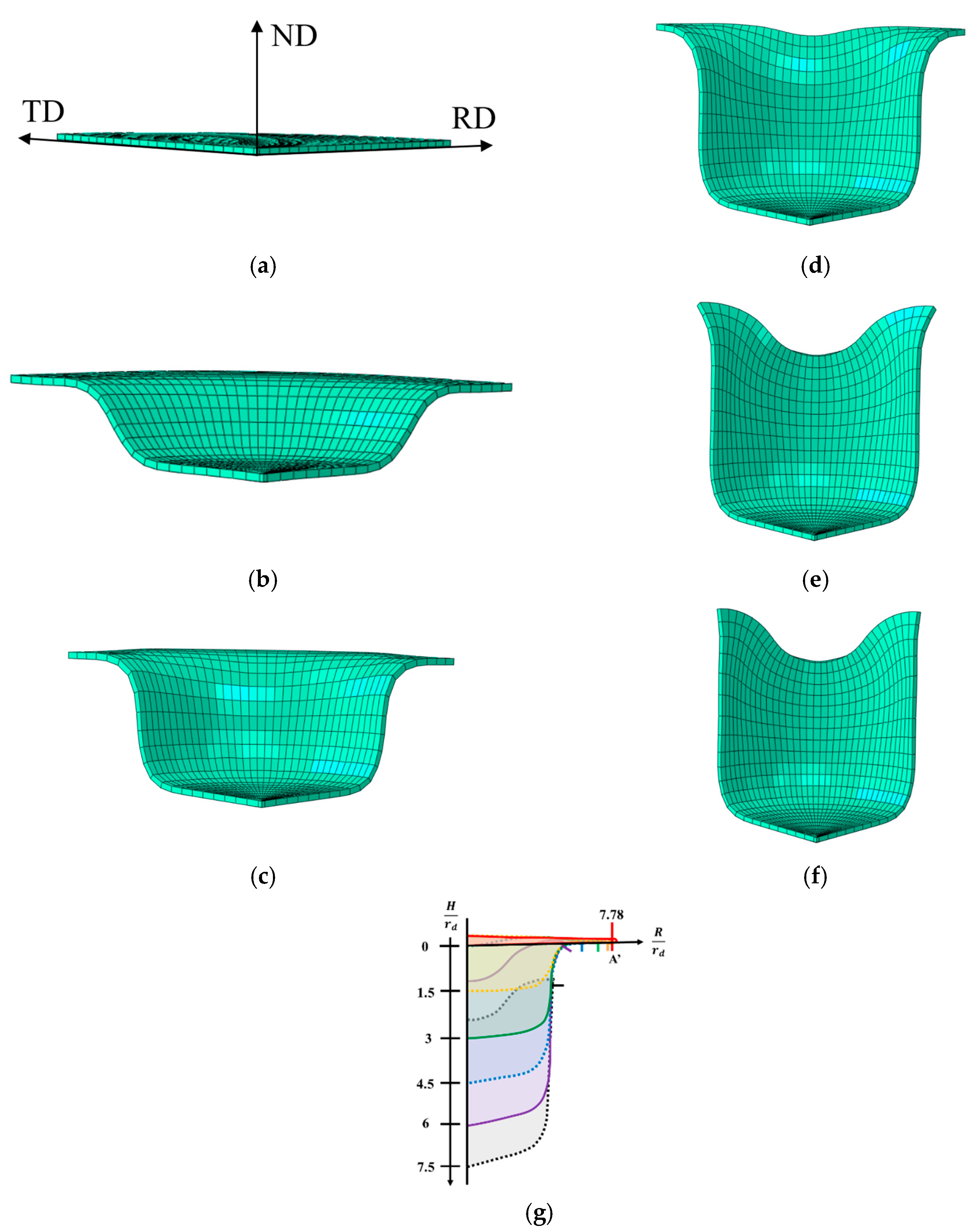Figure 8 and Figure 9 show the cup shape and strain field contour in the drawn cups as a function of the drawing depth using the $H/r_d$ ratio, respectively. In terms of the cup shape, the drawn cup can be split into three zones: a cup flange (Zone I), the transition region between the flange and the wall (Zone II), and the cup wall (Zone III) and cup bottom (IV) (Figure 7c). The stresses at the various regions of the cup, i.e., bottom, wall, and flange, are different, and the normal stress component is neglected. The cup flange (Zone I) is under tensile stress along the RD and compressive stress along the circumferential direction. The cup wall (Zone III) and cup bottom (Zone IV) are in a biaxial tensile stress state. During material flow from the flange into the die, the bending of the sheet metal (Zone II) induces tensile and compressive bending stresses in the outermost and innermost layers, respectively.

The principal strains at an angle of α = 0° completely differed from those at α = 45° (Figure 9d–f)). The cup shapes and principal strain contours revealed a complex local deformation depending on the position at angle $\alpha$ with respect to the RD. Herein, we traced the initial positions A–F at $\alpha =$ 0°, 45°, which corresponded to the final positions A’–F’ at the cup bottom, wall, and flange (Figure 6).

3.2. Effect of Drawing Process on the Lattice Rotation

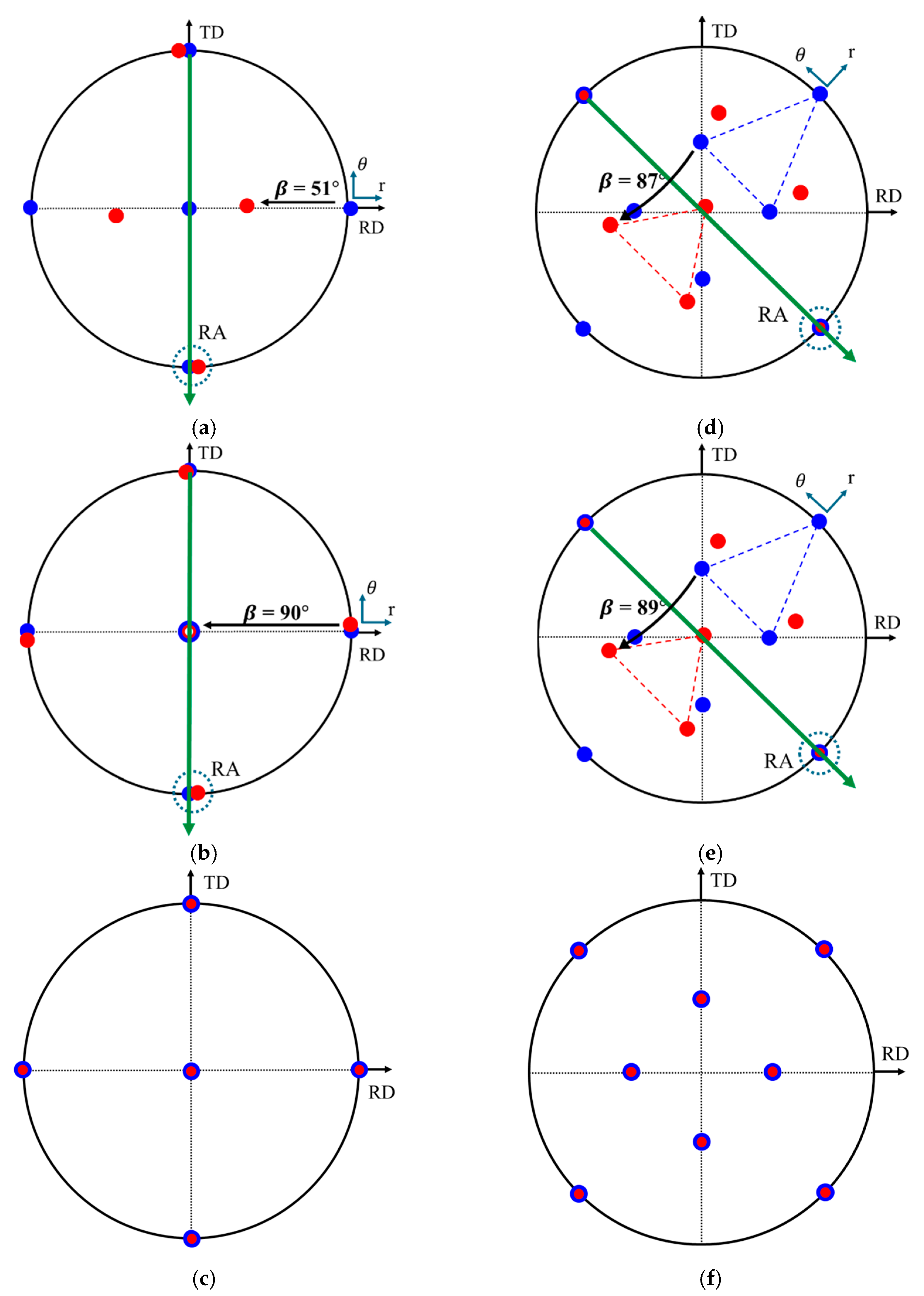
To determine the lattice rotation, the orientation evolution at the given positions A–F in Figure 9 during deep drawing must be identified. In this study, we expressed the crystal orientation $g$ of a single crystal with respect to the sample coordinates in the RD, TD, and ND directions (Figure 1). For a CPFEM simulation, cube orientation refers to the initial orientation of aluminum single crystals and serves as the reference orientation. Considering that position A has a given orientation $g_0$ of the cube marked in blue, the {100} pole figure with all {100} poles can be visualized as the NDs of the {100} planes with respect to the RD and TD (Figure 10a).

After deep drawing, position A changed its orientation to the orientation $g_1$ of position A’ with Euler angles of 274°, 51°, and 90° marked in red. The rotation from orientation A marked in blue is expressed by the rotation angle $\beta$ = 51°, which is counterclockwise to the rotation axis ($\overrightarrow{RA}$) of $\left[0\overline{1}0\right]$ with respect to the A’ orientation marked in red. A comparison of the {010} pole figures of A and A’ revealed that these poles were largely at the same position RA in Figure 10a. Such an outcome was observed because the RA remained unchanged, whereas the other poles changed their positions through the rotation of angle $\beta$ = 51°. The vector of $\overrightarrow{RA}$ = $\left[0\overline{1}0\right]$ was directed from the center to the $\left(0\overline{1}0\right)$ pole parallel to the negative TD. The lattice rotation can be expressed using the rotation axis $\beta /\overrightarrow{RA}$ = ${51}^o/\left[0\overline{1}0\right]$ between the initial orientation $g_0$ and orientation $g_1$ at A and A’ positions after drawing.

Considering the different positions at $\alpha =0^o$ after deep drawing with $H/r_d$ = 6, we determined the {100} poles of positions A’, B’, and C’ at the cup flange (Zone I), cup wall (Zone III), and cup bottom (Zone IV) after the deep drawing (Figure 10a–c). Biaxial tension occurred in Zone IV, with σ₁ = σ_r = σ₂ = σ_θ > 0 and σ₃ = σ_t = 0, which led to ${∆\epsilon }_1^p={∆\epsilon }_r^p={∆\epsilon }_2^p={∆\epsilon }_{\theta }^p>0$ and ${∆\epsilon }_3^p={∆\epsilon }_t^p<0$. Although the blank thickness decreased in this region of Zone IV, according to the predictions made by applying the von Mises yield criterion and associated flow rule, plastic deformation barely occurred owing to the high flow stress [35]. The {100} poles of the C’ position in Zone IV with Euler angles of 270°, 0°, and 90° at the cup bottom remained at the same position without any rotation, as shown in Figure 10c. Thus, lattice rotation did not occur here. In Zones I and II, the plane stress states were the maximum principal stress σ₁ = σ_r > 0, the medium one σ₂ = σ_t = 0 (near zero), and the minimum one σ₃ = σ_θ < 0, resulting in incremental principal plastic strains: ${∆\epsilon }_1^p={∆\epsilon }_r^p>0$, ${∆\epsilon }_2^p={∆\epsilon }_t^p>0$, and ${∆\epsilon }_3^p={∆\epsilon }_{\theta }^p<0$. Detailed discussions on the relationship between the stress and plastic strain components can be found in a previous work [35]. Thus, the blank thickness in this region increased. Position A’ in Zone I with Euler angles of 274°, 51°, and 90° at the cup flange showed a lattice rotation by $\beta /\overrightarrow{RA}$ = ${51}^o/\left[0\overline{1}0\right]$ (Figure 10a). In Zone III, plane strain occurred, and the stress states can be expressed as σ₁ = σ_r > 0 and σ₂ = σ_θ = 1/2σ_r > 0 due to the von Mises yield criterion and σ₃ = σ_t = 0. Therefore, ${∆\epsilon }_1^p={∆\epsilon }_r^p>0$, ${∆\epsilon }_2^p={∆\epsilon }_{\theta }^p=0$, and ${∆\epsilon }_3^p={∆\epsilon }_t^p<0$, that is, the blank thickness also decreased. Position B’ in Zone III with Euler angles of 273°, 90°, and 90° at the cup wall rotated the angle $\beta$ of 90° at the rotation axis $\left[0\overline{1}0\right]$ by $\beta /\overrightarrow{RA}$ = ${90}^o/\left[0\overline{1}0\right]$, as shown in Figure 10b. Therefore, for the positions at an inclination of $\alpha =0^o$ to the RD, the positions of A and B indicate the rotation axis of $\left[0\overline{1}0\right]$.

For α = 45°, after deep drawing with $H/r_d$ = 6, we determined the {110} pole figures of the D’, E’, and F’ positions at the cup flange (Zone I), cup wall (Zone III), and cup bottom (Zone IV) (Figure 10d–f). The {110} poles of the F’ orientation with Euler angles of 135°, 0°, and 225° in Zone IV at the cup bottom remained at the same position without rotation, as shown in Figure 10f, that is, lattice rotation did not occur. Position D’ with Euler angles of 315°, 87°, and 45° in Zone I at the cup flange presented lattice rotation by $\beta /\overrightarrow{R}$ = ${87}^o/\left[1 \overline{1} 0\right]$ (Figure 10d). Position E’ with Euler angles of 315°, 89°, and 45° in Zone III at the cup wall rotated the angle $\beta$ = 90° at the rotation axis $\left[1 \overline{1} 0\right]$ by $\beta /\overrightarrow{RA}$ = ${90}^o/\left[1 \overline{1} 0\right]$ (Figure 10e).

From the results on the rotation axis at positions A–F for α = 0° and 45°, positions A–C at $\alpha =0^o$ had the rotation axis of $\left[0\overline{1}0\right]$ and positions D–F at α = 45° exhibited a rotation axis of $\left[1 \overline{1} 0\right]$. These observations suggest a direct dependence of the rotation axis on angle $\alpha$. For $\alpha =0^o$, the $\overrightarrow{RA}$ = $\left[0 \overline{1} 0\right]$ was parallel to the negative TD, which could be derived by determining the tangent to the circle at α = 0°, as shown in Figure 10a,b. In addition, the tangent direction is defined using the circumferential direction $\overrightarrow{\theta }$ and corresponds to the rotation axis. Given the polar coordinates, the local coordinates of a specified position are given by the RD $\overrightarrow{r}$ and circumferential direction $\overrightarrow{\theta }$, as shown in Figure 10a,d, respectively. Therefore, the circumferential direction $\overrightarrow{\theta }$ can be defined as the rotation axis.

During deep drawing, the drawing trajectory, called the drawing path, which is constrained by the circular shape of the die, must be specified in the RD. In addition, the rotation axis, which lies along the circumferential direction, is perpendicular to the RD (Figure 10a,d). Thus, we can propose an $\alpha$-angle dependence relationship of $\overrightarrow{RA}\left(\alpha \right)$, which can be formulated with the angular position $\alpha$ measured from the RD in a counterclockwise manner as follows:

$$\overrightarrow{RA}(\alpha )=\left(\begin{array}{c}{r\prime }_1\\ {r\prime }_2\\ {r\prime }_3\end{array}\right)=\left[\begin{array}{ccc}\mathit{cos}\alpha & \mathit{sin}\alpha & 0\\ -\mathit{sin}\alpha & \mathit{cos}\alpha & 0\\ 0& 0& 1\end{array}\right]\left(\begin{array}{c}{r}_{1 }\\ r_{2 }\\ r_{3 }\end{array}\right)=\left(\begin{array}{c}\mathit{sin}\alpha \\ -\mathit{cos}\alpha \\ 0\end{array}\right)$$

(10)

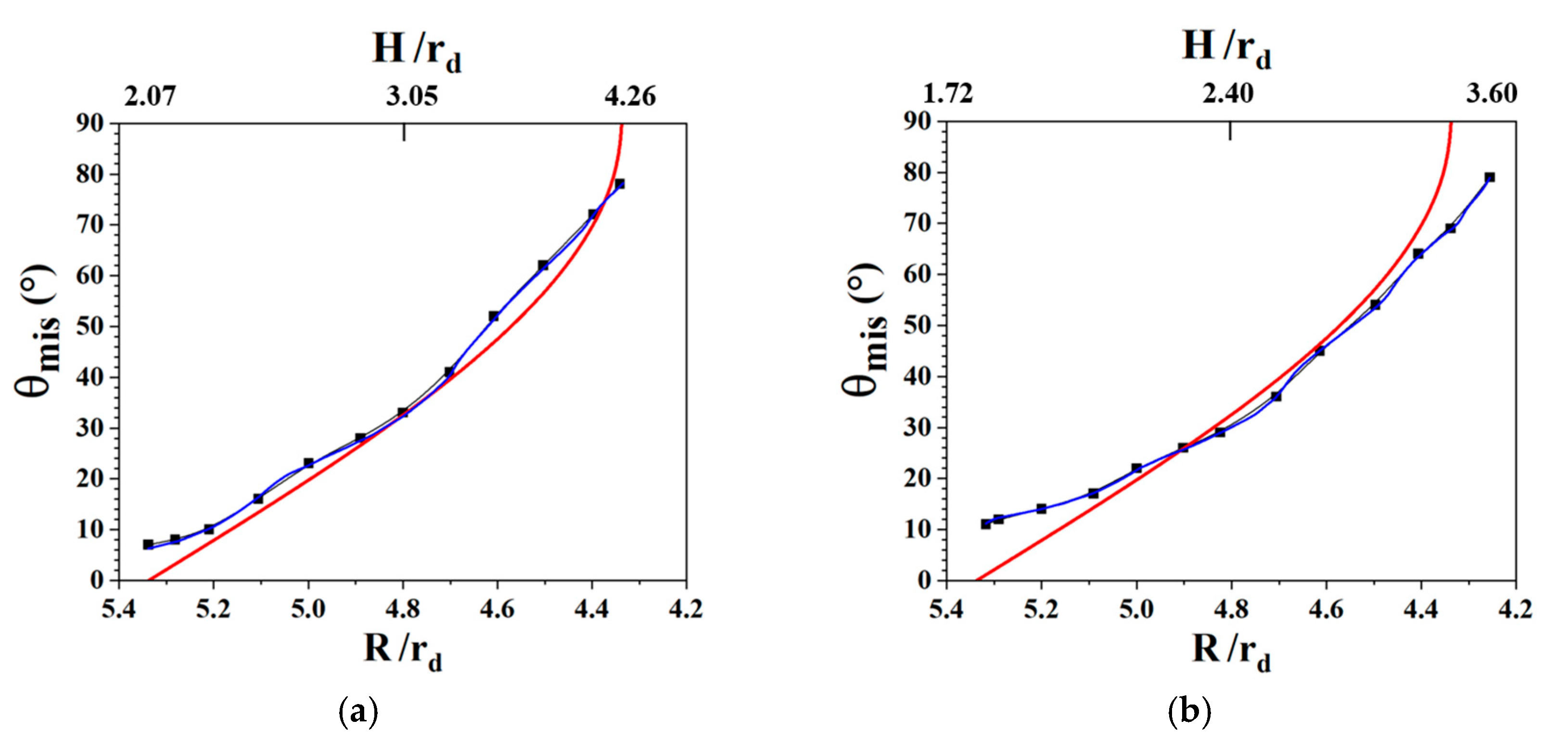
For the verification of this equation at α = 22°, we considered the cup flange and cup wall, denoted by G and H, respectively, at α = 22° with respect to the RD and with the same radius as the positions of A and B. After deep drawing, the new orientations of G’ and H’ predicted through the CPFEM simulation rotated to Euler angles of 298°, 82°, and 98° and 283°, 90°, and 331°, with Bunge’s definition expressed by rotation angle/axis $\beta /\overrightarrow{RA}=$ 84° $\left[2 \overline{6} 1\right]$, 91° $\left[2 \overline{5} 1\right]$. Applying Equation (10), we found that the theoretical $\overrightarrow{RA}$ of $\left[2 \overline{5} 0\right]$ was close to the simulated RA of $\left[2 \overline{5} 1\right]$. Only a slight difference between the theoretical and simulated angles was observed owing to the minimal distortion during deep drawing.

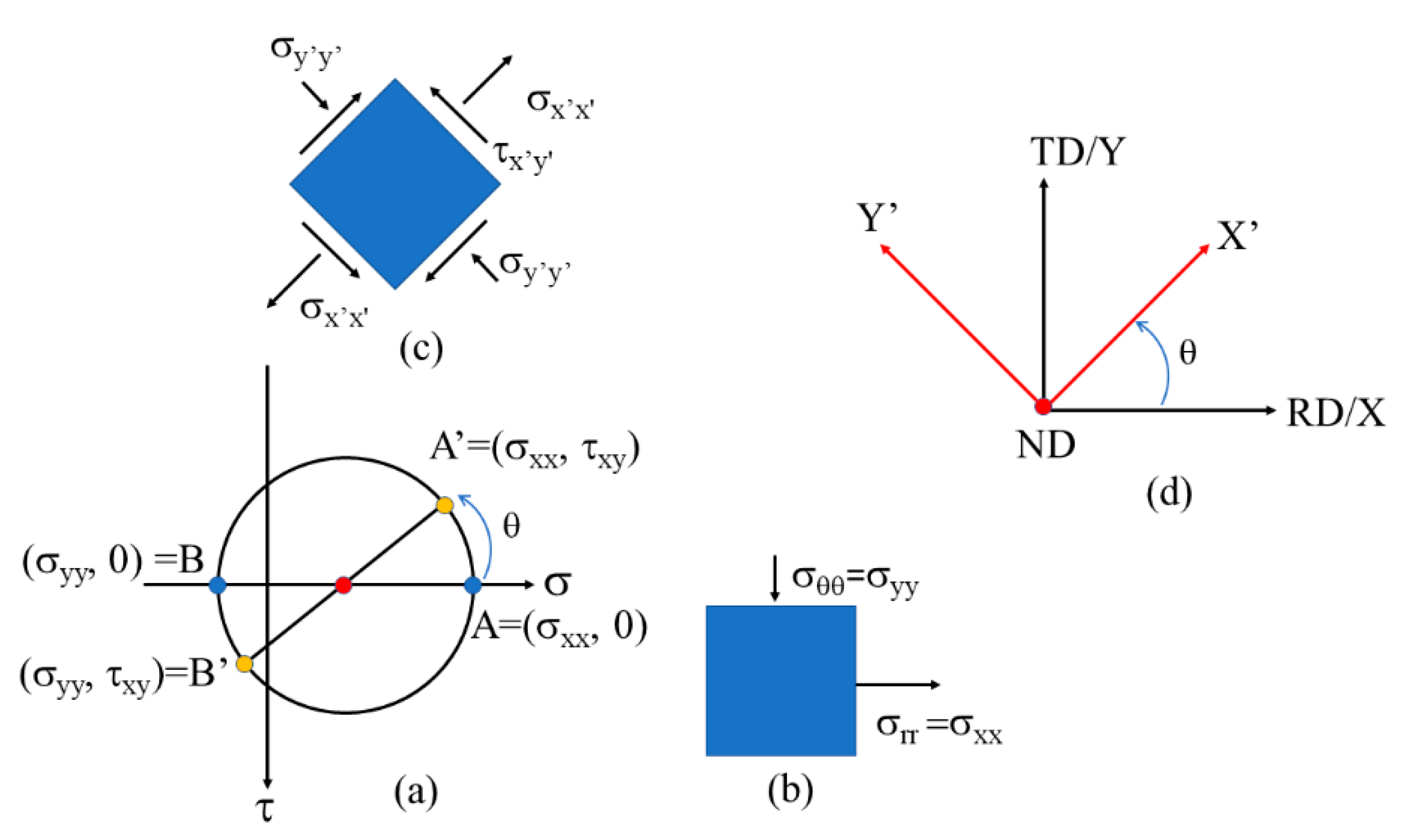
Figure 6a shows the local coordinates of a specified position given by the polar coordinate of the radial direction $\overrightarrow{r}$, the circumferential direction $\overrightarrow{\theta }$, and the thickness direction $\overrightarrow{t}$. The radial and thickness directions of the local coordinates at a given position can be expressed using the rotation angle $\alpha$ measured from the RD about the ND. The orientation $g_0$ of the position at $\alpha$ = 0° with Euler angles of $\left({\phi }_1, \varnothing , {\phi }_2\right)$ can be used to describe the relationship between the sample and local coordinates:

$$\overrightarrow{r}=\left(\begin{array}{c}\mathit{cos}{\phi }_1\mathit{cos}{\phi }_2-\mathit{sin}{\phi }_1\mathit{sin}{\phi }_2\mathit{cos}\varnothing \\ -\mathit{cos}{\phi }_1\mathit{sin}{\phi }_2-\mathit{sin}{\phi }_1\mathit{cos}{\phi }_2\mathit{cos}\varnothing \\ \mathit{sin}{\phi }_1\mathit{sin}\varnothing \end{array}\right)$$

(11)

$$\overrightarrow{t}=\left(\begin{array}{c}\mathit{sin}{\phi }_1\mathit{cos}{\phi }_2+\mathit{cos}{\phi }_1\mathit{sin}{\phi }_2\mathit{cos}\varnothing \\ -\mathit{sin}{\phi }_1\mathit{sin}{\phi }_2+\mathit{cos}{\phi }_1\mathit{cos}{\phi }_2\mathit{cos}\varnothing \\ -\mathit{cos}{\phi }_1\mathit{sin}\varnothing \end{array}\right)$$

(12)

In addition, the radial $\overrightarrow{r}(\alpha )$ and thickness $\overrightarrow{t}(\alpha )$ directions of the position at $\alpha$ can be calculated as follows:

$$\overrightarrow{r}(\theta )=\left(\begin{array}{c}\mathit{cos}{\phi }_1\mathit{cos}({\phi }_2+\alpha )-\mathit{sin}{\phi }_1\mathit{sin}({\phi }_2+\alpha )\mathit{cos}\varnothing \\ -\mathit{cos}{\phi }_1\mathit{sin}({\phi }_2+\alpha )-\mathit{sin}{\phi }_1\mathit{cos}({\phi }_2+\alpha )\mathit{cos}\varnothing \\ \mathit{sin}{\phi }_1\mathit{sin}\varnothing \end{array}\right)$$

(13)

$$\overrightarrow{t}(\theta )=\left(\begin{array}{c}\mathit{sin}{\phi }_1\mathit{cos}({\phi }_2+\alpha )+\mathit{cos}{\phi }_1\mathit{sin}({\phi }_2+\alpha )\mathit{cos}\varnothing \\ -\mathit{sin}{\phi }_1\mathit{sin}({\phi }_2+\alpha )+\mathit{cos}{\phi }_1\mathit{cos}({\phi }_2+\alpha )\mathit{cos}\varnothing \\ -\mathit{cos}{\phi }_1\mathit{sin}\varnothing \end{array}\right)$$

(14)

The relationship between the initial orientation $g_0$ and orientation $g\left(\alpha \right)$ in the RD at $\alpha$ with respect to the RD can be expressed as follows:

$$g\left(\alpha \right)=R\left(\alpha \right)g_0$$

(15)

where $R\left(\alpha \right)$ denotes the rotation matrix corresponding to the rotation of angle $\alpha$ at approximately the ND. This $\alpha$-dependent orientation function was applied to predict the earing of single crystals according to [33,34,35,36,37]. Thus, the orientation of the rim in a circular single-crystal blank is a function of the $\alpha$ angle measured from the RD using Equation (15).

Finally, it comes to the question of the ND rotation during drawing. In the process of deep drawing, the punch force loading on the circular blank causes the blank edge to wrap over the punch surface. This force at the cup bottom transfers to the cup wall, and the edge of the circular blank is radially pulled toward the die cavity. Thus, the cylindrical elements in the edge of the ring blank are subjected to the same radial tension of ${\sigma }_{xx}{= \sigma }_{rr}$ and circumferential compression of ${\sigma }_{yy}={ \sigma }_{\theta \theta }$ because the black edge is constrained by the blank holder. It is observed under the same sample coordinates of RD, TD and ND directions that the stresses after θ rotation show ${\sigma }_{x\prime x\prime }$, ${\sigma }_{y\prime y\prime }$ and ${\tau }_{x\prime y\prime }$ using Mohr’s circle analysis in Figure 11a. It is impossible to meet the constraint conditions of ${\sigma }_{x\prime x\prime }{= \sigma }_{rr}$ and ${\sigma }_{y\prime y\prime }={ \sigma }_{\theta \theta }$ because the stress of ${\tau }_{x\prime y\prime }$ is not equal to zero in Figure 11c.

Consequently, the body rigid rotation along the ND direction shown in Figure 11d is required in order to satisfy the conditions of the same ${\sigma }_{rr}$ and ${\sigma }_{\theta \theta }$ for the cylindrical elements. This relationship between the initial $g_0$ orientation and $g\left(\mathsf{\theta }\right)$ orientation of the cylindrical element at $\mathsf{\theta }$ with respect to the RD is expressed in Equation (15). With the help of the body rigid rotation along the ND, the stresses are ${\sigma }_{x\prime x\prime }{= \sigma }_{rr}$ and ${\sigma }_{y\prime y\prime }={ \sigma }_{\theta \theta }$, and the body rigid rotation around the ND direction is found by comparing the pole positions between the {100} and {110} pole figures in Figure 10c,f.

3.3. Effect of Bending Process on Lattice Rotation

To gain insights into the lattice rotation in the drawing path, we plotted a misorientation called the rotation angle $\beta$ as a function of the deep depth ratio $H/r_d$ for positions A and B (Figure 12a,b, respectively) because no rotation was observed in Zone IV. Position A was subjected to bending in Zone II at $H/r_d$ = 5.0, with the rotation angle $\beta$ ranging from 20° to 75°. For the B position, the starting point in Zone II was at $H/r_d$ = 2.0, with the rotation angle $\beta$ between 10° and 75°. These results imply considerable rotation in Zone II for Positions A and B under bending deformation, whereas a slight lattice rotation occurred in Zones I and III at the cup flange and wall.

After discussions on the angle dependence of the rotation axis, we focused on the lattice rotation behaviors during deep drawing. The lattice rotation between the deformed and initial orientations can be expressed using the RA and rotation angle called misorientation. First, considering the case of $\alpha =0^o$, we plotted the misorientation as a function of the deep depth ratio $H/r_d$ for positions A and B at the cup flange and wall (Figure 12a,b), where the deep depth ratio is described in Section 3.1. The cup bottom in Zone IV did not present any misorientation because no rotation was observed in this region. The drawing path of any specific node is expressed in terms of the time and positions of Z and RD. Thus, the deep depth ratio $H/r_d$ can be considered the drawing path of the node, and the transition point between Zones I and II represents the beginning of bending in Zone II at $H/r_d$ = 5.0 for position A. The deep depth ratio in Zone II ranged from 5 to 7, corresponding to the rotation angle $\beta$ ranging from 20° to 75°. In case position B, the starting point in Zone II was at $H/r_d$ = 2.0, with the rotation angle $\beta$ ranging from 10 to 75°. For positions A and B, a notable rotation occurred in Zone II in the transition region during the bending process, and a slight lattice rotation transpired in Zones I and III at the cup flange and wall.

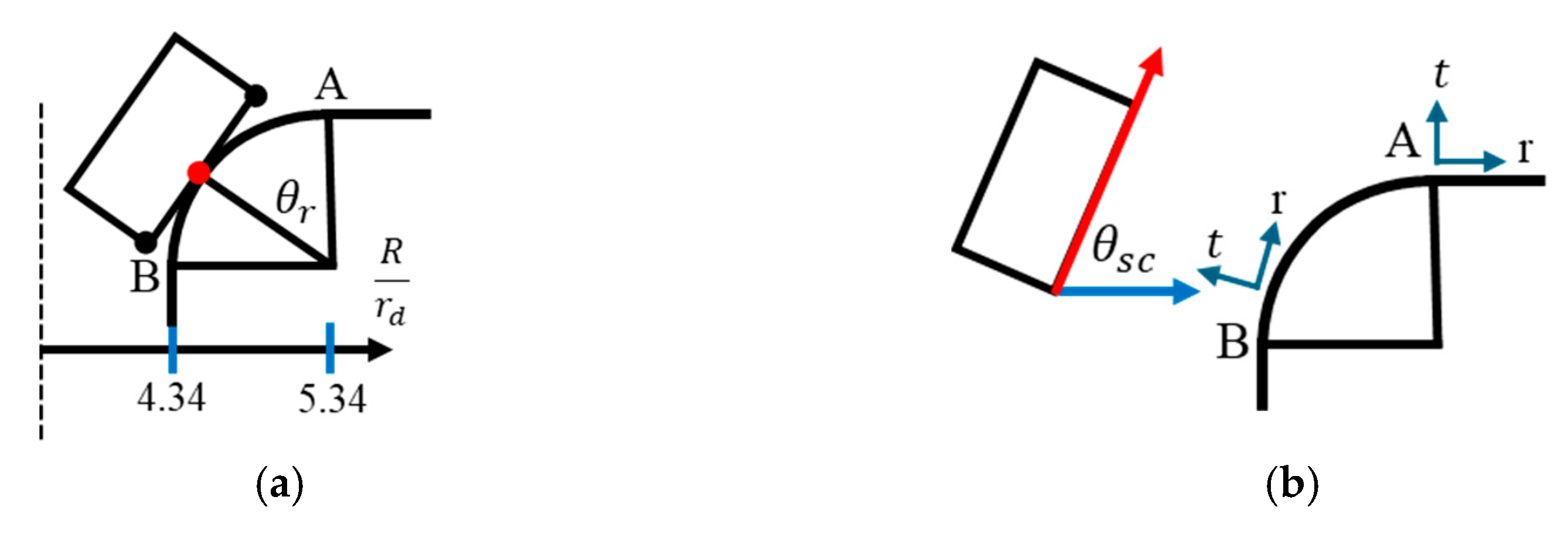
The rotation angle can be described using two methods: radial angle ${\theta }_r$ and tangential angle ${\theta }_{sc}$ (Figure 13). The radial angle ${\theta }_r$ was measured using the circular motion of a given position along the circumference of a quarter circle from the vertical position A to a specific position shown in Figure 13a. The value was ${\theta }_r$ = 0° at position A and 90° at position B. The tangential angle ${\theta }_{sc}$ was calculated using the slope of a node at a specific position shown in Figure 13b, and its value was 0° at position A and 90° at position B. Figure 14 shows the rotation angle $\beta$ predicted using the calculation method of the ${\theta }_{sc}$ angle compared with the theoretical angles of ${\theta }_r$ and ${\theta }_{sc}$. The misorientations were consistent with ${\theta }_r$ and ${\theta }_{sc}$.

According to the kinematic considerations of bending based on the stationary axis of rotation and bending radius r, the effective arc length s of the specimen can be calculated as a function of the rotation angle $\beta$ under pure bending:

$$\mathrm{s}=r\beta$$

(16)

Thus, Zone II can be considered the sum of an infinite decrement arc length ∆s, that is, the sum of infinite decrements of the rotation angle $∆\beta$. The rotation angle increases with the increase in the arc length. During deep drawing, the drawing trajectory is constrained along the circumference of the quarter circle of a die subjected to the bending process. Therefore, such bending kinematics of deep drawing can lead to lattice rotation, and the rotation angle increases with an increase in the depth of deep drawing. This finding is supported by the agreement of the misorientations with ${\theta }_{sc}$, that is, the lattice rotation around the circumferential direction induced by the kinematic bending process. We calculated the deformed orientation from the initial orientation by the rotation around the circumferential direction with the rotation angle $\beta$:

$$g^{\prime }\left(\alpha \right)=R\left(\beta \right)g\left(\alpha \right)=R\left(\beta \right)R\left(\alpha \right)g_0$$

(17)

where $g\left(\alpha \right)$ and $g\prime \left(\alpha \right)$ denote the orientations in the $\alpha$ direction before and after the bending process, respectively, $g_0$ represents the initial orientation, and $R\left(\beta \right)$ indicates the rotation at $\overrightarrow{RA}$ in terms of the matrix.

3.4. Earing Formation Induced by Crystal Plasticity

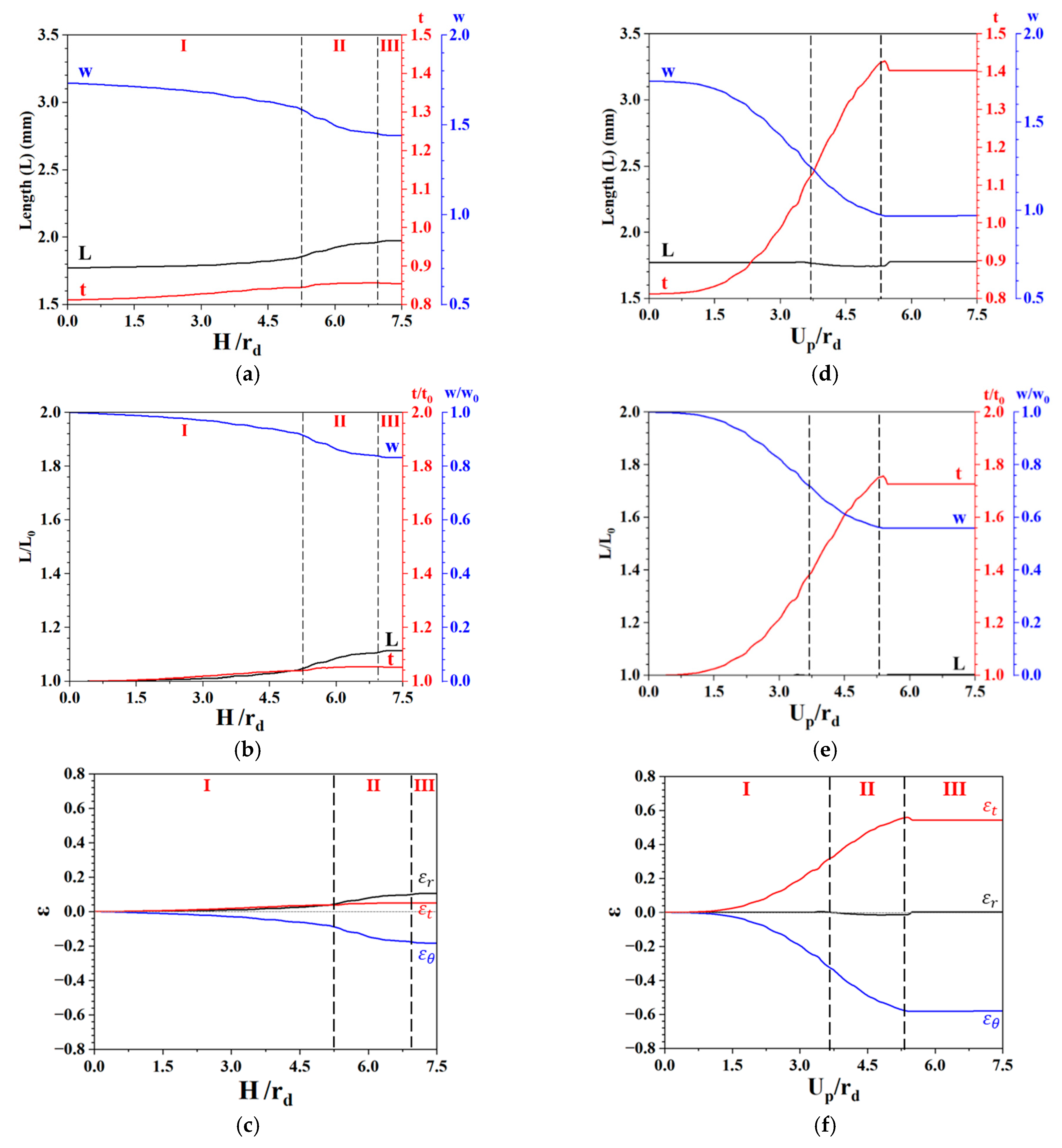
After comprehending the angle dependence relationship and orientation change, we combined the concepts of crystal plasticity and orientation to calculate the cup height to gain insights into the formation mechanism of ears during deep drawing. Following the drawing path of position A at $\alpha$ = 0°, the evolutions of the length, width, and height were determined (Figure 15a). Figure 15b shows the normalized length, width, and height obtained from the simulation results of the CPFEM. Figure 15c shows the strains of ${\epsilon }_r$, ${\epsilon }_{\theta }$, and ${\epsilon }_t$, which were used to trace the values along the drawing path for position A. The absolute value of ${\epsilon }_{\theta }$ was greater than that of ${\epsilon }_r$, and the ${\epsilon }_t$ strain was lower than the others. Furthermore, the radial strain ${\epsilon }_r$ in Zone III was greater than that in Zone II and close to zero in Zone I. This finding suggests the occurrence of radial strain in Zone III at the cup flange.

After discussing the angle-dependent orientation relationship, we now comprehend earing formation in the deep drawing of a circular blank. The formation of the earing can be attributed to the inhomogeneity of the radial strain along the circumferential direction in the flange of a circular blank. The strain ${\mathit{\epsilon }}_{\mathit{r}}$ along the RD can be expressed in terms of the shear ${\mathit{\gamma }}^{\mathit{s}}$ for activated slip systems s:

$${\epsilon }_r=\sum _s\left(m_{ij}^s+m_{ji}^s\right){\displaystyle \frac{{\gamma }^s}{2}}$$

(18)

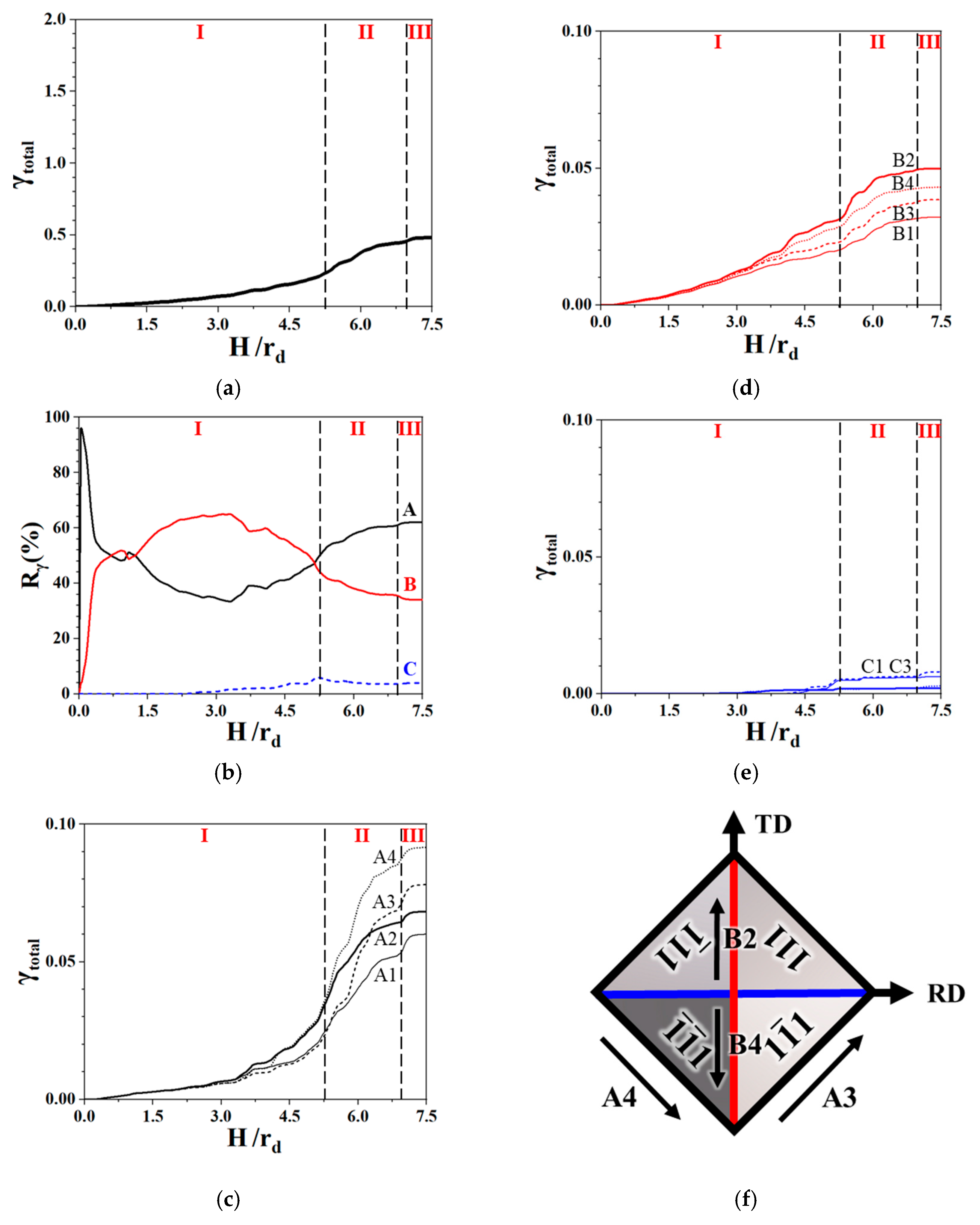
where the Schmid tensor $m_{ij}^s=b_i^s⨂n_j^s$ is defined using the component of the unit vector $n_j^s$, which is normal to the slip plane, and unit vector $b_i^s$, which is parallel to the slip direction of the slip system s. The slip systems, as shown in

Table 4. The definition of the three groups of slip systems in the face-centered cubic.

Symbol	Slip Direction	Slip Plane
A1	$1\overline{1}0$	$111$
A2	$110$	$\overline{1}11$
A3	$110$	$1\overline{1}1$
A4	$1\overline{1}0$	$\overline{1}\overline{1}1$
B1	$01\overline{1}$	$111$
B2	$01\overline{1}$	$\overline{1}11$
B3	$011$	$1\overline{1}1$
B4	$0\overline{1}\overline{1}$	$\overline{1}\overline{1}1$
C1	$10\overline{1}$	$111$
C2	$101$	$\overline{1}11$
C3	$10\overline{1}$	$1\overline{1}1$
C4	$\overline{1}0\overline{1}$	$\overline{1}\overline{1}1$

, were divided into three types, namely, A, B, and C, based on the projection direction of the slip direction on the RD–TD plane (Figure 16), where A is 45° with respect to RD or TD, and B and C are parallel to the TD and RD, respectively. Figure 17a shows that the simulated total shear ($\gamma$) of 12 slip systems in Zone III is greater than that in Zone II and close to zero in Zone I. During the deep drawing process, the change in the orientation is first attributed to the $\alpha$-dependent rotation axis constrained by the die, as expressed in Equation (15), in Zone I and then to the bending rotation, as expressed in Equation (17), in Zone II. The radial strain considerably increased during the bending process in Zone II and reached the saturation value in Zone III (Figure 15c). This observation is in agreement with the results of the radial strain shown in Figure 15c. The total shear was mainly contributed by types A and B (Figure 17b). In addition, types A and B mainly contributed to A3, A4, B2, and B4 (Figure 17c,d). The shears of ${\gamma }^{A3}$ and ${\gamma }^{A4}$ resulted in the increased components of ${\epsilon }_r$ and ${\epsilon }_{\theta }$ along the RD and TD, and the shears of ${\gamma }^{B2}$ and ${\gamma }^{B4}$ led to the increased component of ${\epsilon }_{\theta }$ along the TD. This outcome explains why the absolute value of ${\epsilon }_{\theta }$ contributed by the four major shears (${\gamma }^{A3}$, ${\gamma }^{A4}$, ${\gamma }^{B2}$, and ${\gamma }^{B4}$) was greater than that of ${\epsilon }_r$ from two major shears (${\gamma }^{A3}$ and ${\gamma }^{A4}$) (Figure 17f).

For the drawing path of position D at $\alpha$ = 45°, Figure 15d shows the evolutions of the length, width, and height. Figure 15e shows the normalized length, width, and height. Figure 15f reveals the strains ${\epsilon }_r$, ${\epsilon }_{\theta }$, and ${\epsilon }_t$, which were used to trace the drawing path of position D. The absolute value of ${\epsilon }_{\theta }$ was greater than that of ${\epsilon }_t$, and that of the ${\epsilon }_r$ strain was close to zero. Furthermore, the strain ${\epsilon }_t$ substantially increased between Zones I and II for position D at $\alpha$ = 45°, and the strain ${\epsilon }_r$ increased from Zone II for position A at $\alpha$ = 0°. This finding supports the earing formation at $\alpha$ = 45° due to the radial strain. In addition, the difference in the boundary conditions depends on its orientation during the bending process.

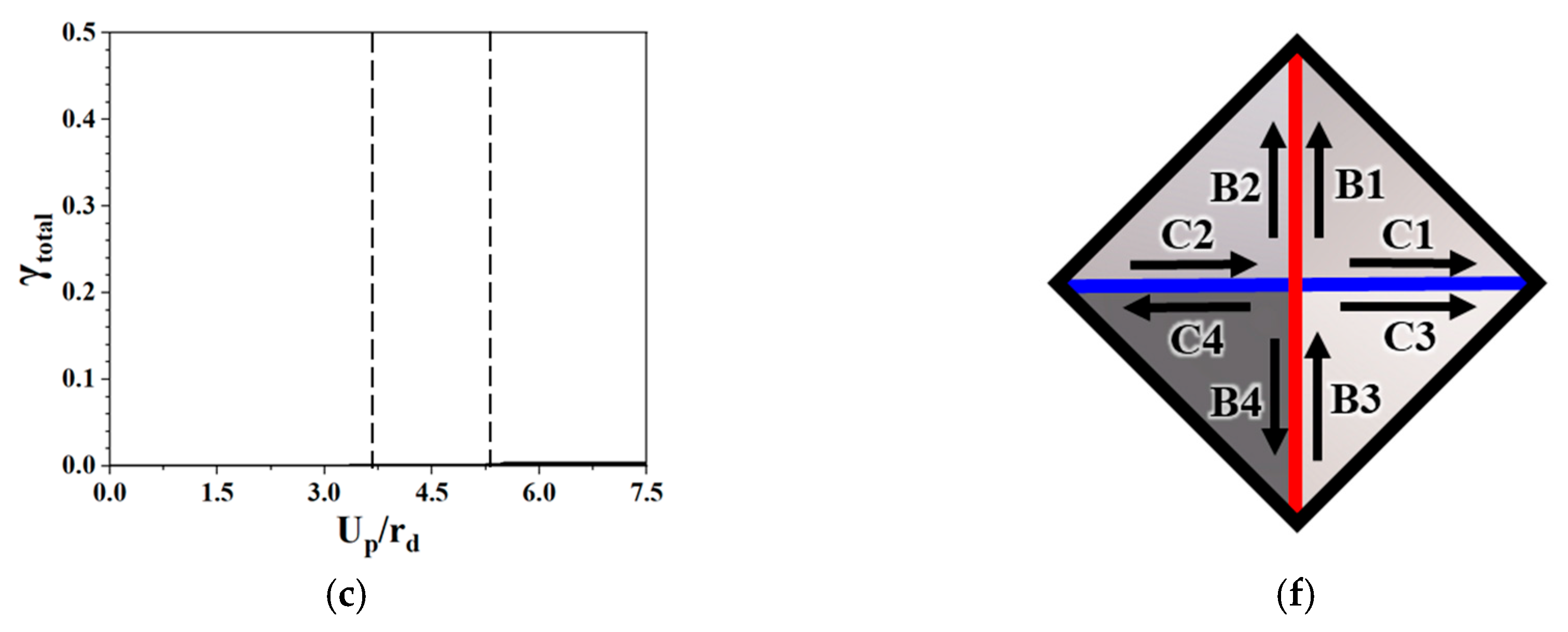
With regard to slip systems, the simulated total shear ($\gamma$) of the 12 slip systems in Zone III was greater than that in Zone II (Figure 18a). In addition, the radial strain substantially increased during the bending process in Zone II and reached the saturation value in Zone III (Figure 15f). This observation is in good agreement with the results of the radial strain shown in Figure 15f. In addition, the total shear in Figure 18b was mainly contributed by types A and B. Moreover, types B and C mainly contributed to B2, B3, C2, and C3 (Figure 18c,d). The shears of ${\gamma }^{B2}$ and ${\gamma }^{B3}$ resulted in an increase in the components of ${\epsilon }_t$ and ${\epsilon }_{\theta }$ along the ND and TD, and those of ${\gamma }^{C2}$ and ${\gamma }^{C3}$ led to an increase in the components of ${\epsilon }_t$ and ${\epsilon }_{\theta }$ along the ND and TD. This finding explains the greater absolute value of ${\epsilon }_{\theta }$ contributed by the four major shears ${\gamma }^{B2}$, ${\gamma }^{B3}$, ${\gamma }^{C2}$, and ${\gamma }^{C3}$ than that of ${\epsilon }_t$ from the four major shears ${\gamma }^{B2}$, ${\gamma }^{B3}$, ${\gamma }^{C2}$, and ${\gamma }^{C3}$ (Figure 18f). A comparison at $\alpha$ = 0° and $\alpha$ = 45° revealed that type A of the slip systems contributed to the radial strain ${\epsilon }_r$ at $\alpha$ = 0°, and types B and C of the slip systems accounted for strains ${\epsilon }_t$ and ${\epsilon }_{\theta }$ in the circumferential and thickness directions at $\alpha$ = 45°.

Preferred crystallographic orientation or texture induced during the deep drawing process gives rise to an anisotropic yield function. Thus, variational anisotropic yield functions have been employed to calculate the anisotropy of the Lankford coefficient, ignoring the sheet textures [14,38,39]. Apart from the anisotropic yield functions, CPFE methods explicitly consider variational crystal plasticity formulations in a polycrystal for direct, comprehensive visualization of the physics of deformation processes [19]. CPFE methods were recently applied to predict the earing phenomenon by combining different texture components [25]. These observations support a direct relationship between the earing phenomenon and texture components.

Tucker [33], Kanetake et al. [36], and Hsiao et al. [37] considered the $\alpha$-dependent function of resolved shear stresses on slip systems resulting in earing. Resolved shear stress is determined by the stress state applied at the rim in a circular blank, and the position of the rim depends on the $\alpha$ angle measured from the RD. Herein, the orientation of single crystals is fixed but the stress state is the $\alpha$-dependent function. In the present study, it was found that the α-angle dependence of the crystal rotation gives rise to variational orientations. This observation is consistent with the results reported by Tucker [33]. Hence, earing is a characteristic phenomenon associated with the crystallographic textures of the material.

4. Conclusions

The coupling mechanism between earing behavior and crystal rotation kinematics during deep drawing remains unclear. Our results show that during drawing lattice rotation at the mesoscale reveals a rigid body rotation at the macroscale under constraint by holding the blank edge. The rotation axis is specifically tangential to the circle, which reveals an $\alpha$-angle dependence of the bending axis $\overrightarrow{RA}(\alpha )$, with the $\alpha$ value measured from the RD. This simplified modeling supports the fact that different orientations located at $\alpha$ = 0° and $\alpha$ = 45° of the circular cup can be attributed to body rigid rotation about the ND direction under drawing and the lattice rotation around the circumferential direction by bending, with the $\beta$ value measured from the RD. Thus, both effects cause the change in the local orientations, and different slip systems are activated, such as type A for $\alpha$ = 0° and types B and C for $\alpha$ = 45°. This finding can help us understand the interaction between the earing physics of circular cup drawing and orientation development. In this study, the aluminum single crystal is limited in terms of cube orientation, and the employed CP model is a traditional one. In the future, we can extend to other orientations of aluminum single crystals.