Double-Flush Riveting for Hybrid Busbar Assembly
Abstract
1. Introduction
2. Materials and Methods
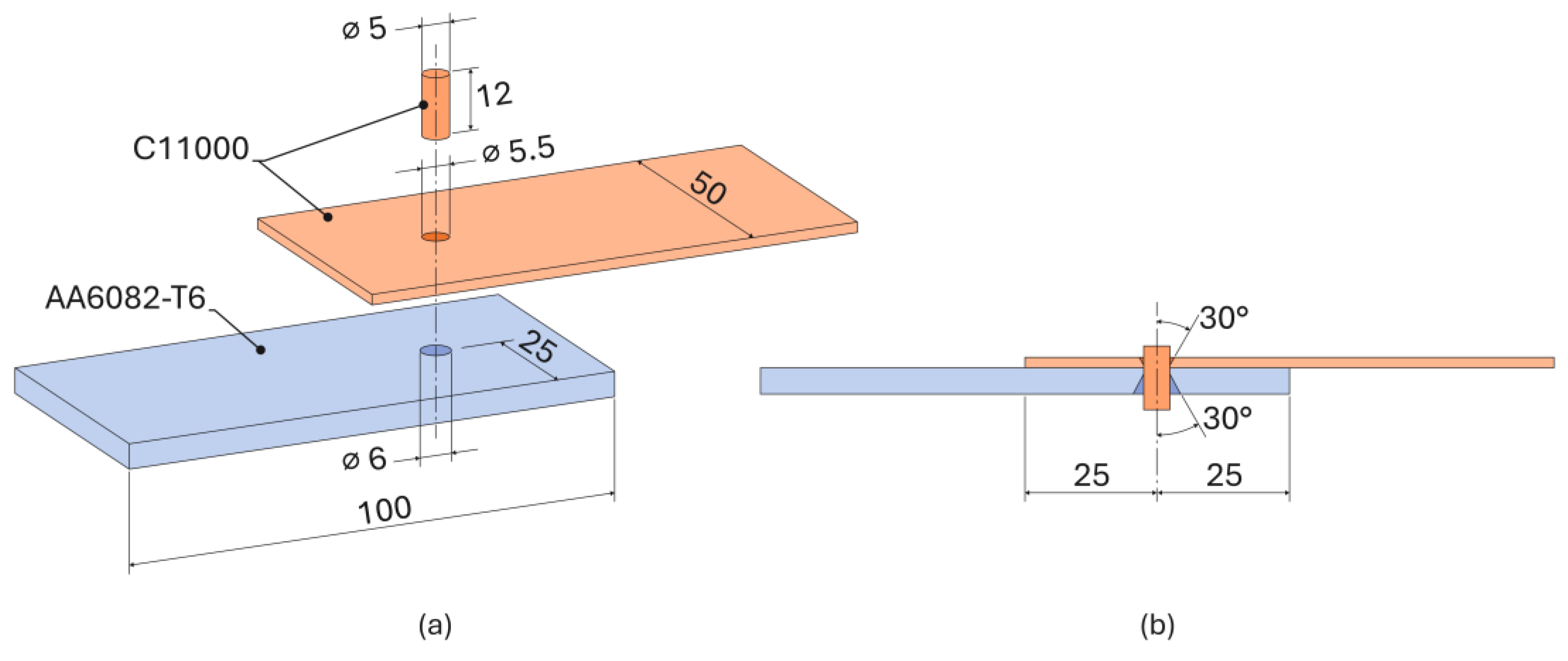
2.1. Materials, Flow Curves, and Electrical Resistivity
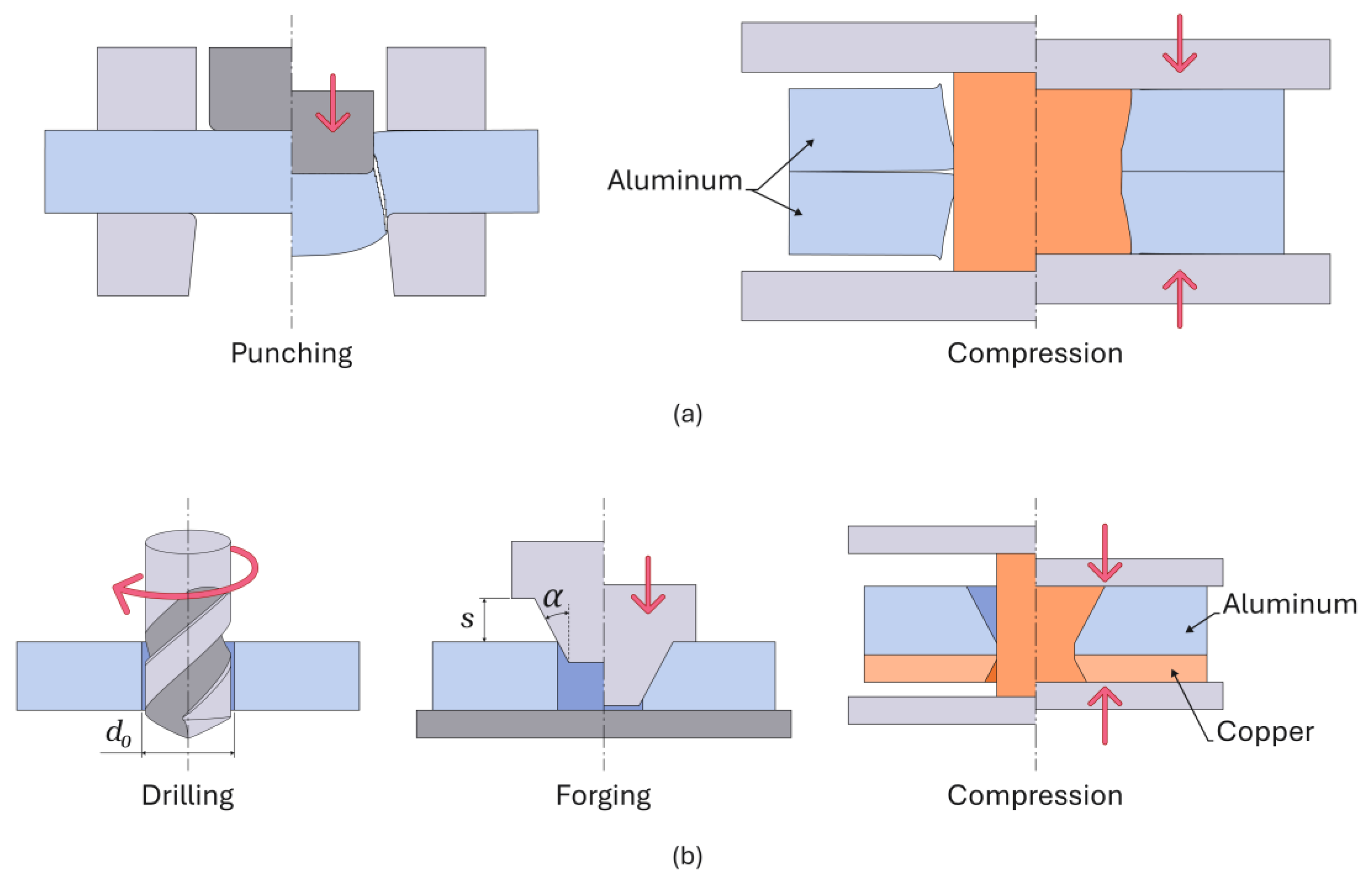
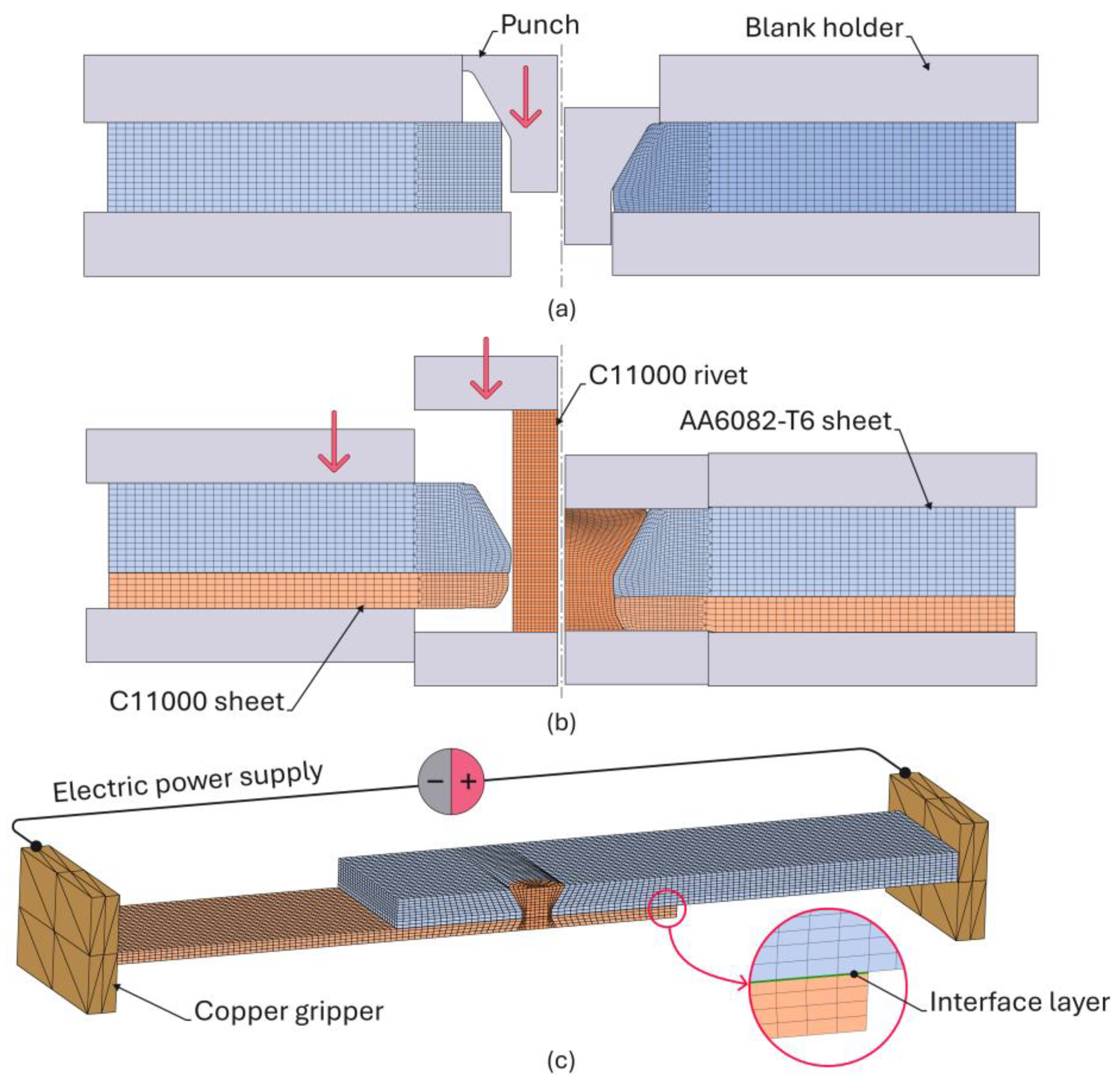
2.2. Double-Flush Riveting
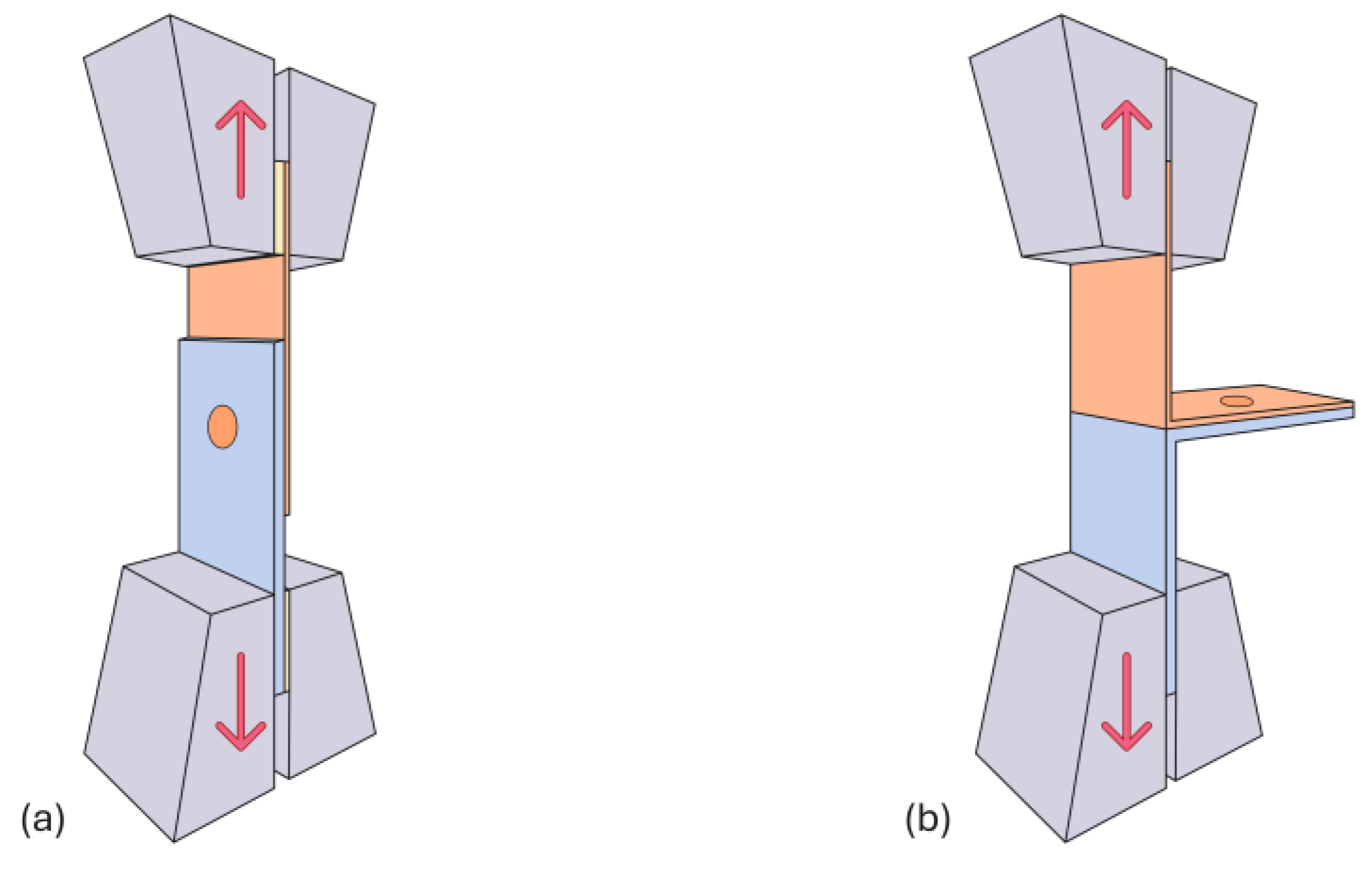
2.3. Electro-Mechanical Testing of the Double-Flush Riveted Joints
2.4. Finite Element Modeling
3. Results and Discussion
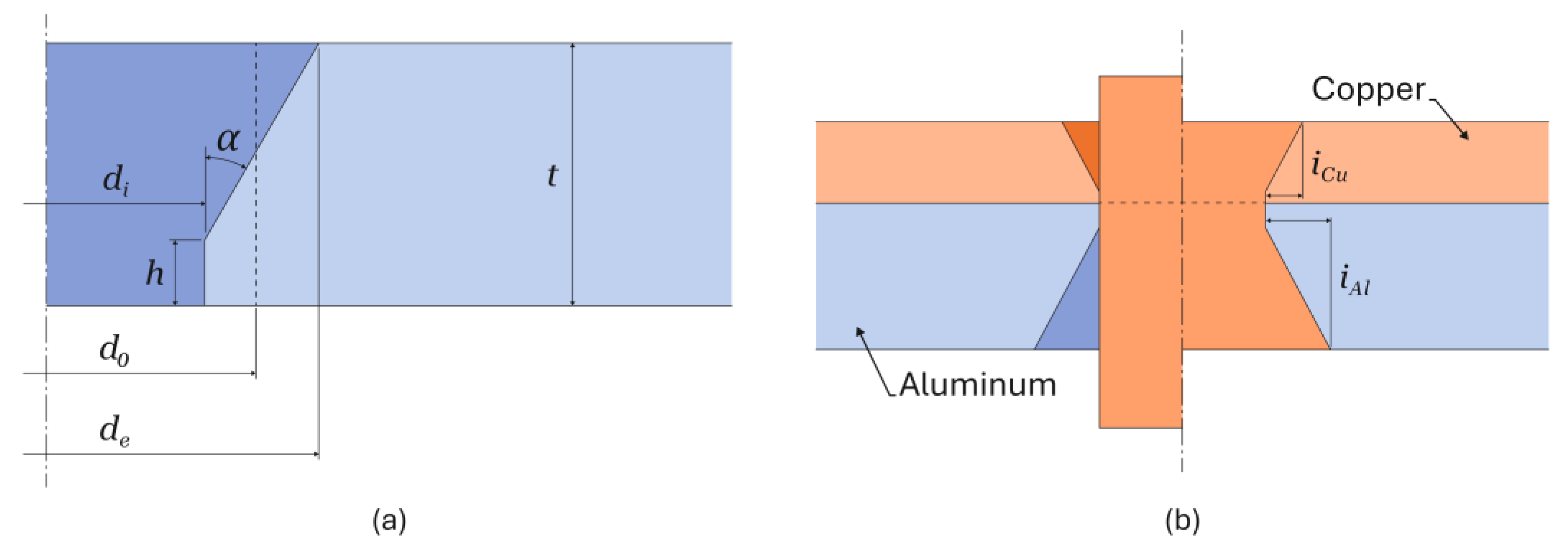
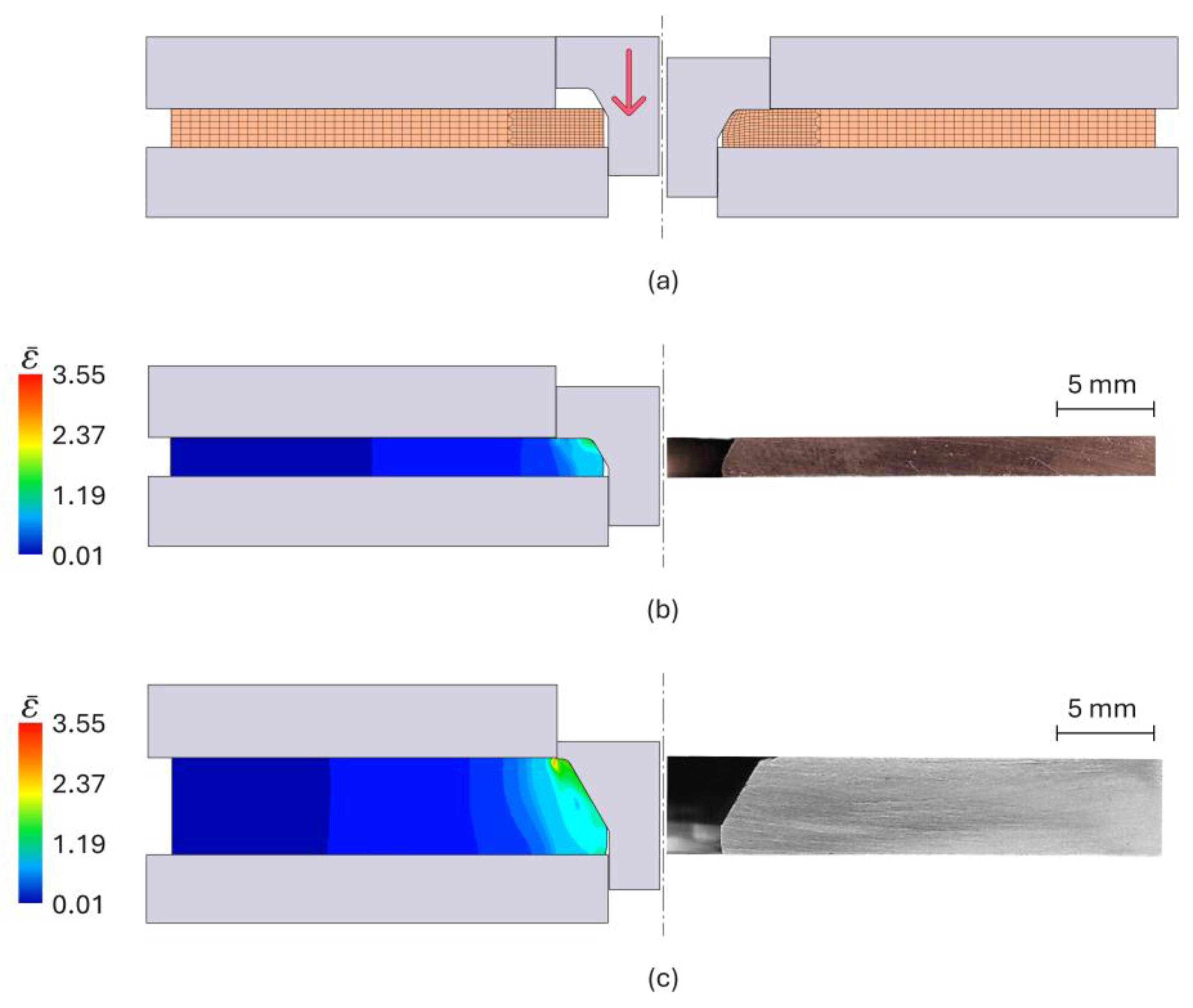
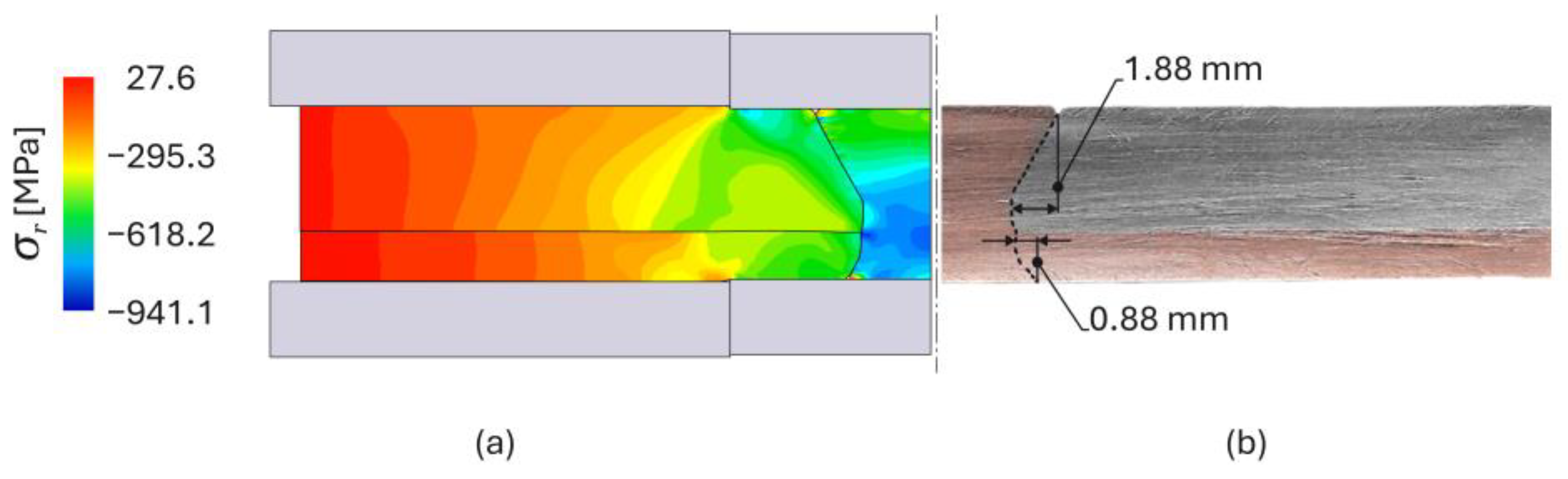
3.1. Mechanical Joining
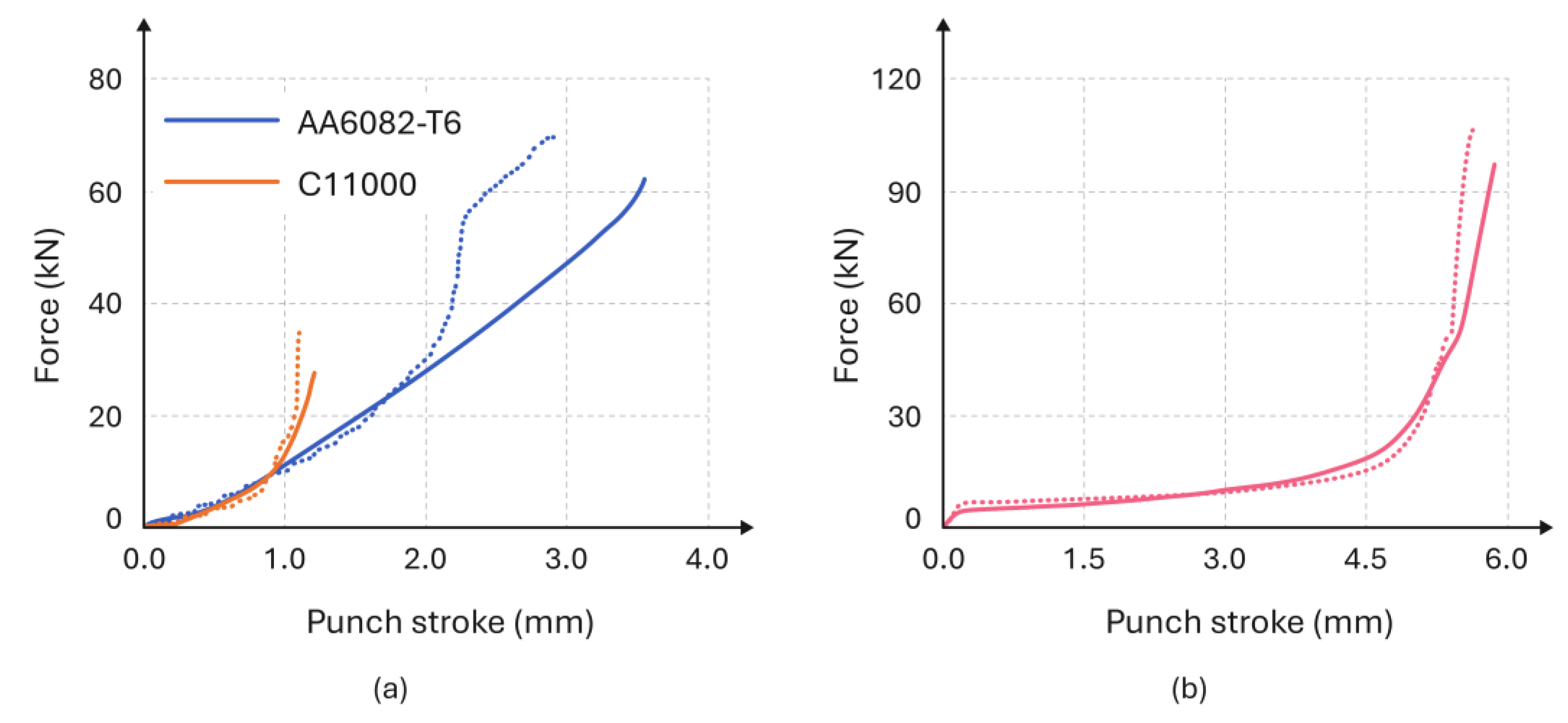
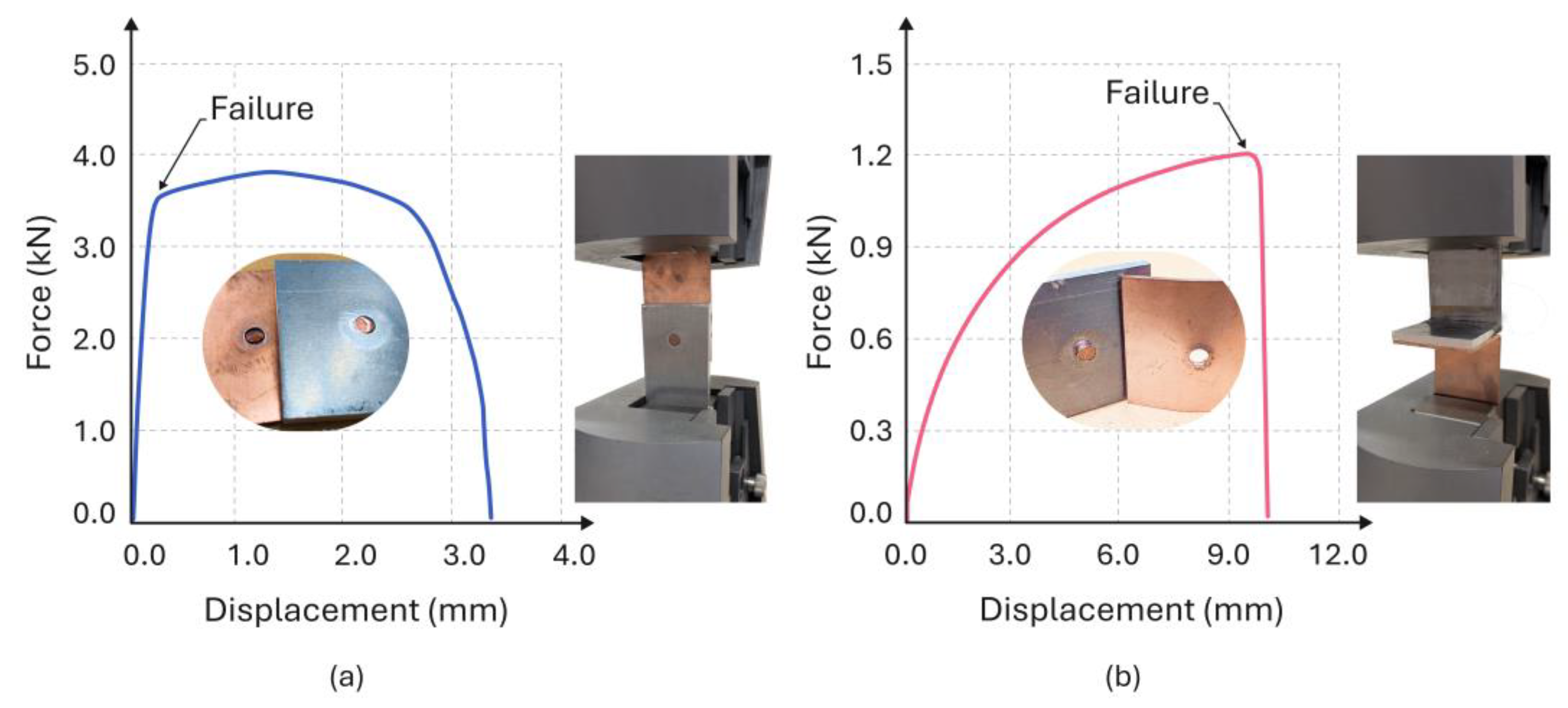
3.2. Mechanical Performance of the Joints
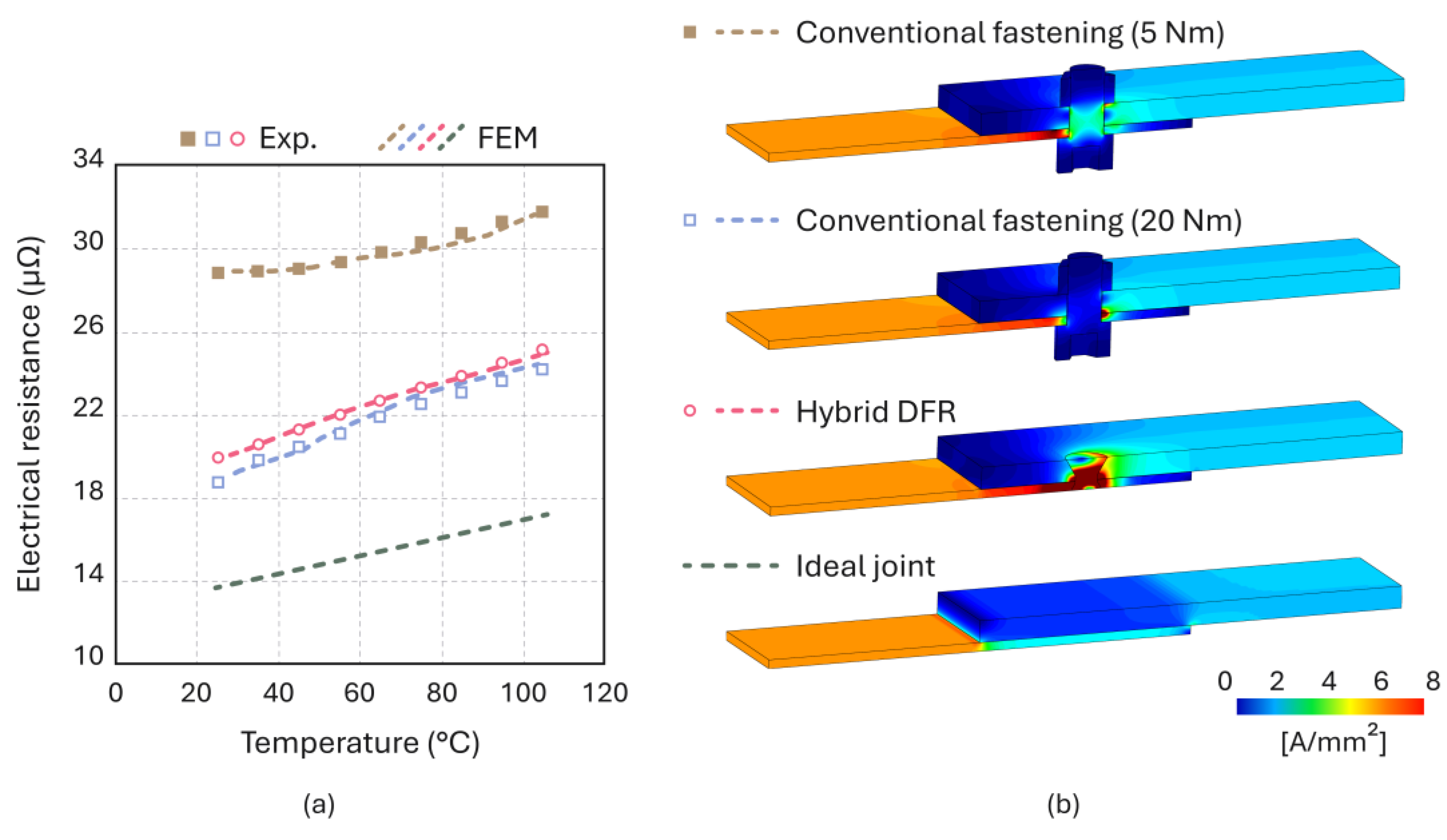
3.3. Thermo-Electrical Performance of the Joints
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chastel, Y.; Passemard, L. Joining Technologies for Future Automobile Multi-Material Modules. Procedia Eng. 2014, 81, 2104–2110. [Google Scholar] [CrossRef]
- Casalino, G. Advances in Welding Metal Alloys, Dissimilar Metals and Additively Manufactured Parts. Metals 2017, 7, 32. [Google Scholar] [CrossRef]
- Cavezza, F.; Boehm, M.; Terryn, H.; Hauffman, T. A Review on Adhesively Bonded Aluminium Joints in the Automotive Industry. Metals 2020, 10, 730. [Google Scholar] [CrossRef]
- Fernando, S. Mechanisms and prevention of vibration loosening in bolted joints. Aust. J. Mech. Eng. 2005, 2, 73–92. [Google Scholar] [CrossRef]
- Li, D.; Chrysanthou, A.; Patel, I.; Williams, G. Self-piercing riveting-a review. Int. J. Adv. Manuf. Technol. 2017, 92, 1777–1824. [Google Scholar] [CrossRef]
- He, X. Clinching for sheet materials. Sci. Technol. Adv. Mater. 2017, 18, 381–405. [Google Scholar] [CrossRef] [PubMed]
- Buffa, G.; Fratini, L.; La Commare, U.; Römisch, D.; Wiesenmayer, S.; Wituschek, S.; Merklein, M. Joining by forming technologies: Current solutions and future trends. Int. J. Mater. Form. 2022, 15, 27. [Google Scholar] [CrossRef]
- Wronicz, W.; Kaniowski, J.; Malicki, M.; Kucio, P.; Klewicki, R. Experimental and Numerical Study of NACA and Conventional Riveting Procedure. Fatigue Aircr. Struct. 2017, 2017, 157–170. [Google Scholar] [CrossRef]
- Melhem, G.N. Aerospace Fasteners: Use in Structural Applications. In Encyclopedia of Aluminum and Its Alloys; CRC Press: Boca Raton, FL, USA, 2019; ISBN 978-1-351-04563-6. [Google Scholar]
- Zeng, C.; Xue, J.T.; Liu, X.Y.; Tian, W. Design variables influencing the fatigue of Al 2024-T3 in riveted aircraft lap joints: Squeeze force and initial fit tolerance. Int. J. Fatigue 2020, 140, 105751. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, Z.; Guo, Y.; Cao, Y.; Zheng, G.; Huo, L. Stress, damage, and fatigue performance analysis of CFRP/Al double-sided countersunk riveted joints with variable rivet-hole clearance. Int. J. Fatigue 2024, 186, 108385. [Google Scholar] [CrossRef]
- Li, G.; Shi, G.; Bellinger, N.C. Studies of Residual Stress in Single-Row Countersunk Riveted Lap Joints. J. Aircr. 2012, 43, 592–599. [Google Scholar] [CrossRef]
- Qu, L.; Li, P.; Lv, G.; Li, J.; Luo, X. Rivet Structural Design and Process Optimization for the Double-Sided Countersunk Riveting of Composite Wedge Structures. Aerospace 2024, 11, 165. [Google Scholar] [CrossRef]
- Hasirci, Z.; Cavdar, I.H.; Ozturk, M. Modeling and Link Performance Analysis of Busbar Distribution Systems for Narrowband PLC. Radioengineering 2017, 26, 611–620. [Google Scholar] [CrossRef]
- Sampaio, R.F.V.; Larue, P.; Pragana, J.P.M.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Double-Flush Riveting by Punching and Compression. J. Adv. Join. Process. 2023, 8, 100155. [Google Scholar] [CrossRef]
- Da Silva, B.F.A.; Kasaei, M.M.; Akhavan-Safar, A.; Carbas, R.J.C.; Marques, E.A.S.; Da Silva, L.F.M. Failure Behavior of Hole Hemmed Joints with a Novel Configuration for Hybrid Busbars in Electric Vehicle Batteries. Eng. Fail. Anal. 2025, 167, 109019. [Google Scholar] [CrossRef]
- Sampaio, R.F.; Pragana, J.P.; Bragança, I.M.; Silva, C.M.; Martins, P.A. Thermo-Electrical Performance of Hybrid Busbars: An Experimental and Numerical Investigation. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 70–80. [Google Scholar] [CrossRef]
- Olafsson, D.; da Silva, P.S.V.; Vesanko, J. Characterization of FSW of Aluminium to Copper for Electrical Busbars. In Proceedings of the International Institute of Welding Annual Assembly and International Conference, Bali, Indonesia, 15–20 July 2018; p. III–1859-18. [Google Scholar]
- ASTM E8/E8M; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2024. [CrossRef]
- ASTM E9-89A; Standard Test Methods for Compression Testing of Metallic Materials at Room Temperature. ASTM International: West Conshohocken, PA, USA, 2010. [CrossRef]
- Kumar, N.; Masters, I.; Das, A. In-Depth Evaluation of Laser-Welded Similar and Dissimilar Material Tab-to-Busbar Electrical Interconnects for Electric Vehicle Battery Pack. J. Manuf. Process. 2021, 70, 78–96. [Google Scholar] [CrossRef]
- IEEE C37.20.2-2015; IEEE Standard for Metal-Clad Switchgear. IEEE: New York, NY, USA, 2015. [CrossRef]
- MatWeb Medium Carbon Steel of Class 8.8 Data Sheet. Available online: https://www.matweb.com/ (accessed on 4 January 2025).
- Silva, C.M.A.; Pragana, J.P.M.; Sampaio, R.F.V.; Bragança, I.M.F.; Martins, P.A.F. Advanced Double-Flush Riveting for Multistage Forming Tools. CIRP Ann. Manuf. Technol. 2025, in press. [Google Scholar] [CrossRef]
- ISO 14270:2016; Resistance Welding—Destructive Testing of Welds—Specimen Dimensions and Procedure for Mechanized Peel Testing Resistance Spot, Seam and Embossed Projection Welds. International Organization for Standardization: Geneva, Switzerland, 2021.
- Nielsen, C.V.; Martins, P.A.F. Finite Element Flow Formulation. In Metal Forming; Elsevier: Amsterdam, The Netherlands, 2021; pp. 181–249. ISBN 978-0-323-85255-5. [Google Scholar]
- Banabic, D. FE-Models of the Sheet Metal Forming Processes. In Sheet Metal Forming Processes; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–25. ISBN 978-3-540-88112-4. [Google Scholar]
- Studer, F.J. Contact Resistance in Spot Welding. Weld. J. 1939, 18, 374–380. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sampaio, R.F.V.; Pragana, J.P.M.; Figueiredo, M.P.; Bragança, I.M.F.; Silva, C.M.A.; Martins, P.A.F. Double-Flush Riveting for Hybrid Busbar Assembly. Metals 2025, 15, 521. https://doi.org/10.3390/met15050521
Sampaio RFV, Pragana JPM, Figueiredo MP, Bragança IMF, Silva CMA, Martins PAF. Double-Flush Riveting for Hybrid Busbar Assembly. Metals. 2025; 15(5):521. https://doi.org/10.3390/met15050521
Chicago/Turabian StyleSampaio, Rui F. V., João P. M. Pragana, Miguel P. Figueiredo, Ivo M. F. Bragança, Carlos M. A. Silva, and Paulo A. F. Martins. 2025. "Double-Flush Riveting for Hybrid Busbar Assembly" Metals 15, no. 5: 521. https://doi.org/10.3390/met15050521
APA StyleSampaio, R. F. V., Pragana, J. P. M., Figueiredo, M. P., Bragança, I. M. F., Silva, C. M. A., & Martins, P. A. F. (2025). Double-Flush Riveting for Hybrid Busbar Assembly. Metals, 15(5), 521. https://doi.org/10.3390/met15050521










