Distribution and Characteristics of Residual Stresses in Super Duplex Stainless Steel Pipe Weld
Abstract
1. Introduction
2. Experimental Observation
2.1. Tensile Test at Elevated Temperature
2.2. Metallographic Observation and Hardness Test
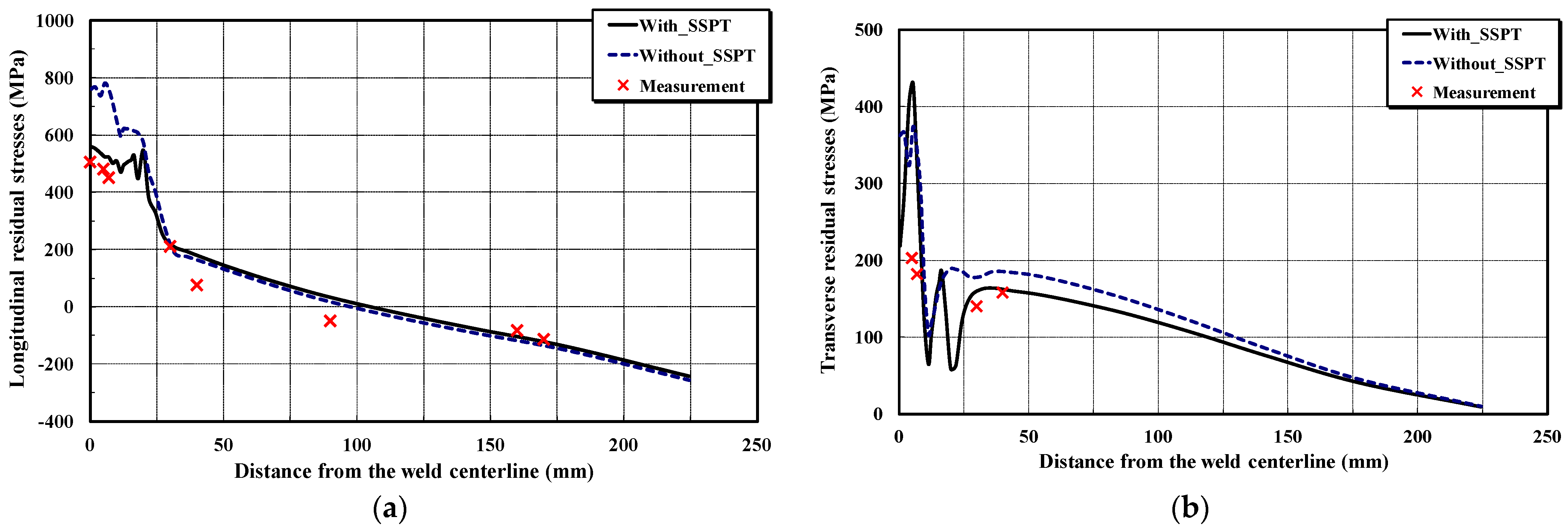
2.3. Residual Stress Measurement
3. FE Simulation
3.1. Model Geometry and Material Properties
3.2. FE Formulation
3.2.1. Heat Transfer Analysis
3.2.2. Mechanical (Structural) Analysis
- Equilibrium equation:
- Stress–strain constitutive equation:
3.2.3. Metallurgical Phase Transformation
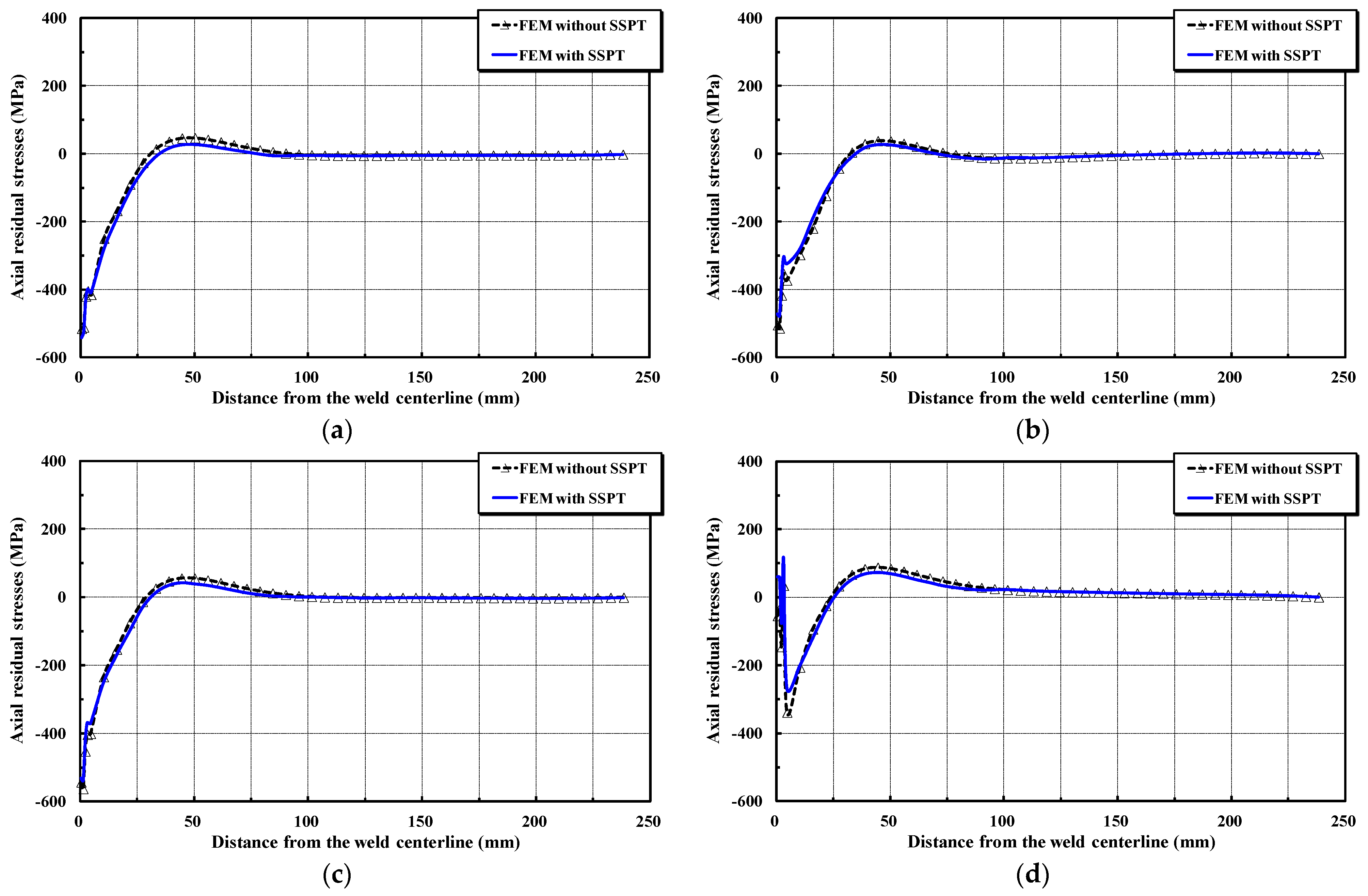
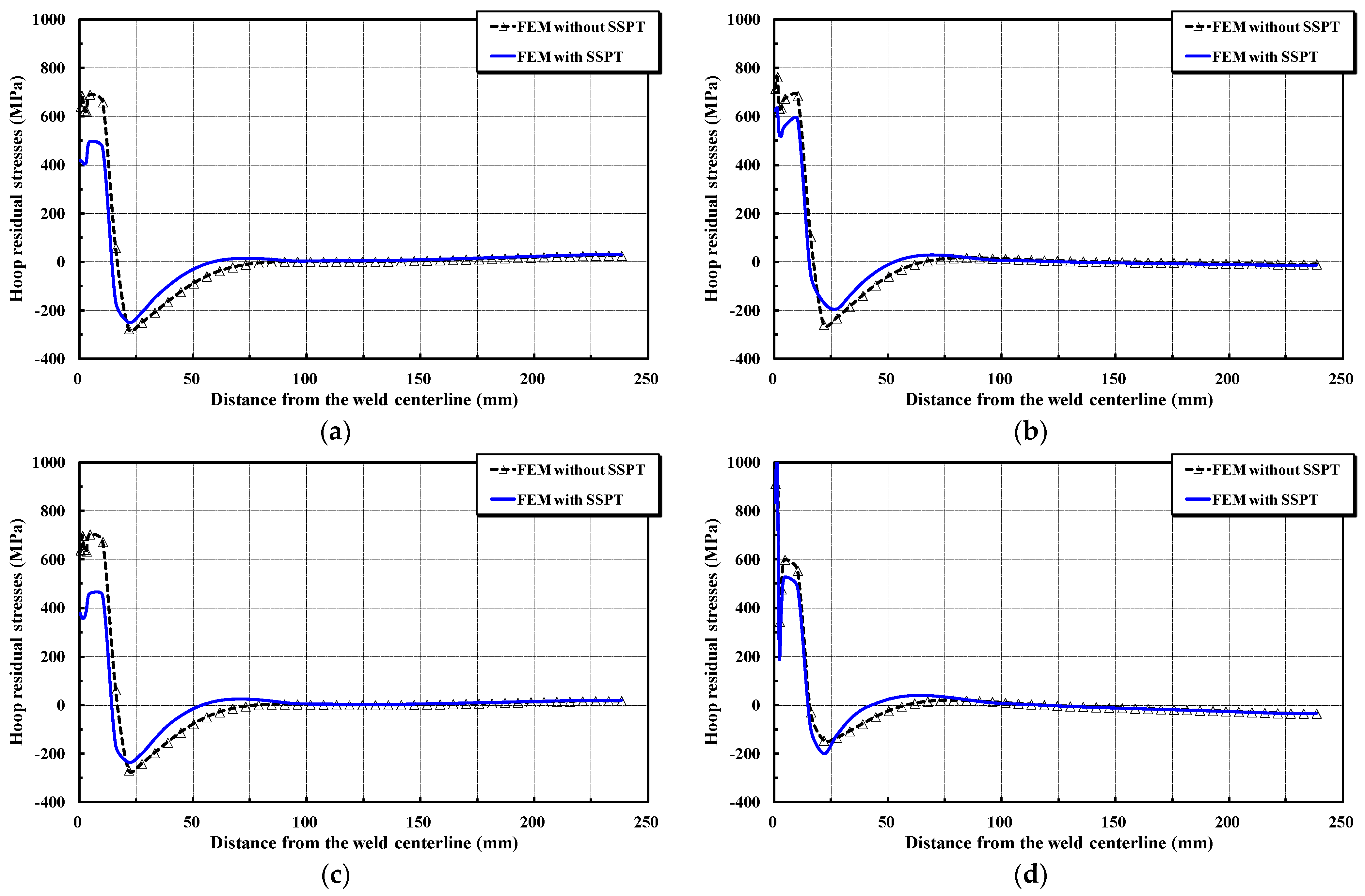
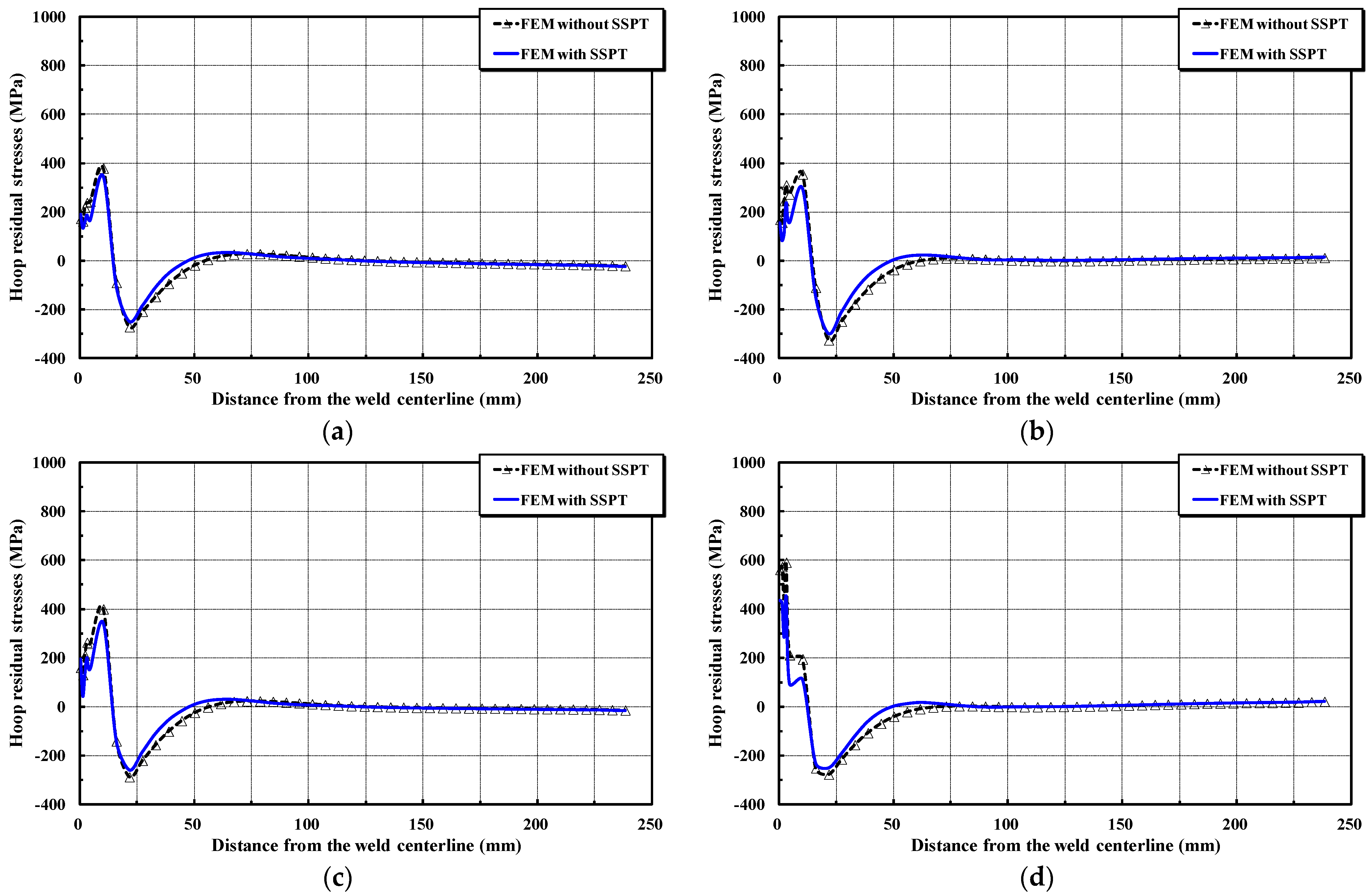
4. Results and Discussion
5. Conclusions
- (a)
- Super duplex stainless steel undergoes martensitic phase evolution in the HAZ and the weld metal in the process of cooling during welding.
- (b)
- The martensitic phase transformation has little impact on the evolution of axial residual stresses, i.e., the axial residual stresses are mainly formed by circumferential shrinkage during the cooling process. On the other hand, a considerable release of hoop residual stresses in the weld region and its vicinity takes place owing to the volume change in the process of phase transformation. Thus, the metallurgical phase transformation cannot be disregarded in numerical simulations of the girth-welding process to provide an accurate expression of the weld-induced residual stresses.
- (c)
- A 3D FE model should be utilized to accurately simulate the distribution of residual stresses and their characteristics along the circumference in girth-welded super duplex stainless steel pipes, since the residual stresses are by no means axisymmetric, and are caused by both the spatial deposition of the weld filler and the welding start/end effect.
- (d)
- Knowledge of the distribution and characteristics of the residual stresses found in this work can assist the production of an efficient and economic design of welded super duplex stainless steel structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iris, A.-A. Duplex stainless steels: Brief history and some recent alloys. Recent Pat. Mech. Eng. 2008, 1, 51–57. [Google Scholar]
- Li, L.; Du, Z.; Sheng, X.; Zhao, M.; Song, L.; Han, B.; Li, X. Comparative analysis of GTAW+SMAW and GTAW welded joints of duplex stainless steel 2205 pipe. Int. J. Press. Vessel. Pip. 2022, 199, 104748. [Google Scholar] [CrossRef]
- Sharma, L.; Sharma, K. Dissimilar welding of super duplex stainless steel (SDSS) and pipeline steel—A brief overview. Mater. Today Proc. 2022, in press. [CrossRef]
- Rezanov, V.A.; Martyushev, N.V.; Kukartsev, V.V.; Tynchenko, V.S.; Kukartsev, V.A.; Grinek, A.V.; Skeeba, V.Y.; Lyosin, A.V.; Karlina, A.I. Study of melting methods by electric resistance welding of Rails. Metals 2022, 12, 2135. [Google Scholar] [CrossRef]
- Gonçalves e Silva, R.H.; Barancelli Schwedersky, M.; Fernandes da Rosa, Á. Evaluation of toptig technology applied to robotic orbital welding of 304L pipes. Int. J. Press. Vessel. Pip. 2020, 188, 104229. [Google Scholar] [CrossRef]
- Withers, P.J. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 2211–2264. [Google Scholar] [CrossRef]
- Wan, Y.; Jiang, W.; Song, M.; Huang, Y.; Li, J.; Sun, G.; Shi, Y.; Zhai, X.; Zhao, X.; Ren, L. Distribution and formation mechanism of residual stress in duplex stainless steel weld joint by neutron diffraction and electron backscatter diffraction. Mater. Des. 2019, 181, 108086. [Google Scholar] [CrossRef]
- Jiang, W.; Wan, Y.; Tu, S.-T.; Wang, H.; Huang, Y.; Xie, X.; Li, J.; Sun, G.; Woo, W. Determination of the through-thickness residual stress in thick duplex stainless steel welded plate by wavelength-dependent neutron diffraction method. Int. J. Press. Vessel. Pip. 2020, 196, 104603. [Google Scholar] [CrossRef]
- Li, D.; Paradowska, A.; Uy, B.; Wang, J.; Proust, G.; Azad, S.K.; Huang, Y. Residual stress measurements of lean duplex stainless steel welded sections. J. Constr. Steel Res. 2021, 186, 106883. [Google Scholar] [CrossRef]
- Brickstad, B.; Josefson, B.L. A parametric study of residual stresses in multi-pass butt-welded stainless steel pipes. Int. J. Press. Vessel. Pip. 1998, 75, 11–25. [Google Scholar] [CrossRef]
- Duranton, P.; Devaux, J.; Robin, V.; Gilles, P.; Bergheau, J.M. 3D modeling of multipass welding of a 316L stainless steel pipe. J. Mater. Process. Technol. 2004, 153–154, 457–463. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Yaghi, A.; Hyde, T.H.; Becker, A.A.; Sun, W.; Williams, J.A. Residual stress simulation in thin and thick–walled stainless steel pipe welds including pipe diameter effects. Int. J. Press. Vessel. Pip. 2006, 83, 864–874. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H.; Liang, W. Numerical and experimental investigations on welding residual stress in multi-pass butt-welded austenitic stainless steel pipe. Comput. Mater. Sci. 2008, 42, 234–244. [Google Scholar] [CrossRef]
- Sattari-Far, I.; Farahani, M.R. Effect of the weld groove shape and pass number on residual stresses in butt-welded pipes. Int. J. Press. Vessel. Pip. 2009, 86, 723–731. [Google Scholar] [CrossRef]
- Deng, D.; Kiyoshima, S. FEM prediction of welding residual stresses in a SUS304 girth-welded pipe with emphasis on stress distribution near weld start/end location. Comput. Mater. Sci. 2010, 50, 612–621. [Google Scholar] [CrossRef]
- Jin, X.; Huo, L.; Yu, H.; Bai, B.; Li, X.; Cao, J. Numerical simulation of parameter of residual stresses on butt-welded duplex stainless steel pipes. J. Tianjin Univ. 2004, 37, 116–125. [Google Scholar]
- Lee, C.H.; Chang, K.H. Comparative study on girth weld-induced residual stresses between austenitic and duplex stainless steel pipe welds. Appl. Therm. Eng. 2014, 63, 140–150. [Google Scholar] [CrossRef]
- KS D 0026 (ISO 783); Method of Elevated Temperature Tensile Test for Steels and Heat-Resisting Alloys. Korean Standards: Seoul, Republic of Korea, 2002.
- Lee, C.H. Computational modelling of the residual stress evolution due to solid-state phase transformation during welding. Model. Simul. Mater. Sci. Eng. 2008, 16, 075003. [Google Scholar] [CrossRef]
- Arun, D.; Devendranath Ramkumara, K.; Vimala, R. Multi-pass arc welding techniques of 12 mm thick super-duplex stainless steel. J. Mater. Process. Technol. 2019, 271, 126–143. [Google Scholar] [CrossRef]
- Chandra Sekhara Rao, P.V.; Manoj, A.; Renuka Swathi, B. Residual stress measurement of Inconel 600 on different welding techniques by using conventional and XRD method. Mater. Today Proc. 2021, 41, 1160–1163. [Google Scholar] [CrossRef]
- Sattari-Far, I.; Javadi, Y. Influence of welding sequence on welding distortions in pipes. Int. J. Press. Vessel. Pip. 2008, 85, 265–274. [Google Scholar] [CrossRef]
- Del Coz Díaz, J.J.; Menéndez Rodríguez, P.; García Nieto, P.J.; Castro-Fresno, D. Comparative analysis of TIG welding distortions between austenitic and duplex stainless steels by FEM. Appl. Therm. Eng. 2010, 30, 2448–2459. [Google Scholar] [CrossRef]
- Haz Metal. Stainless Steels and Their Properties. 2013. Available online: http://www.hazmetal.com/f/kutu/1236776229.pdf (accessed on 10 January 2024).
- Barsoum, Z. Residual stress analysis and fatigue of multi-pass welded tubular structures. Eng. Fail. Anal. 2008, 15, 863–874. [Google Scholar] [CrossRef]
- Teng, T.L.; Chang, P.H.; Tseng, W.C. Effect of welding sequence on residual stresses. Comput. Struct. 2003, 81, 273–286. [Google Scholar] [CrossRef]
- Taljat, B.; Radhakrishnan, B.; Zacharia, T. Numerical analysis of GTA welding process with emphasis on post -solidification phase transformation effects on the residual stresses. Mater. Sci. Eng. A 1998, 246, 45–54. [Google Scholar] [CrossRef]
- Lee, C.H. A Study on the Mechanical Characteristics of High Strength Steel for the Application to the Steel Bridge. Ph.D. Thesis, Chung-Ang University, Seoul, Republic of Korea, 2005. [Google Scholar]
- Pardo, E.; Weckman, D.C. Prediction of weld pool and reinforcement dimensions of GMA welds using a finite element model. Metall. Mater. Trans. 1989, 20B, 937–947. [Google Scholar] [CrossRef]
- Lindgren, L.-E. Finite element modelling and simulation of welding, Part 2 Improved material modeling. J. Therm. Stress. 2001, 24, 195–231. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Saddle River, NJ, USA, 1996. [Google Scholar]
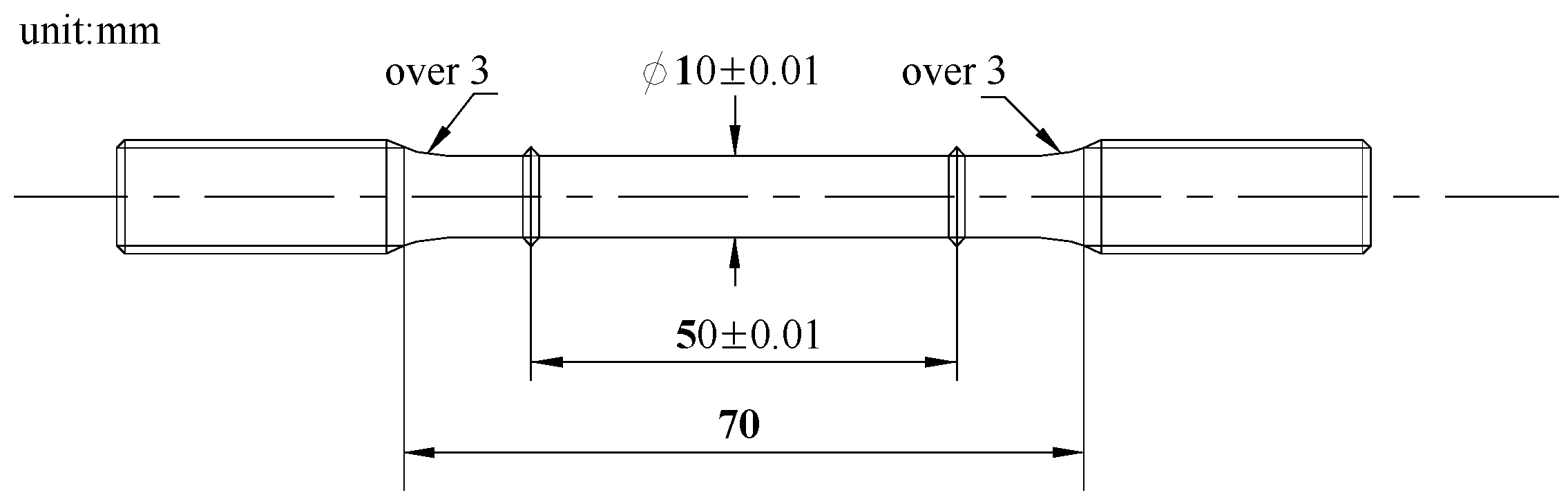




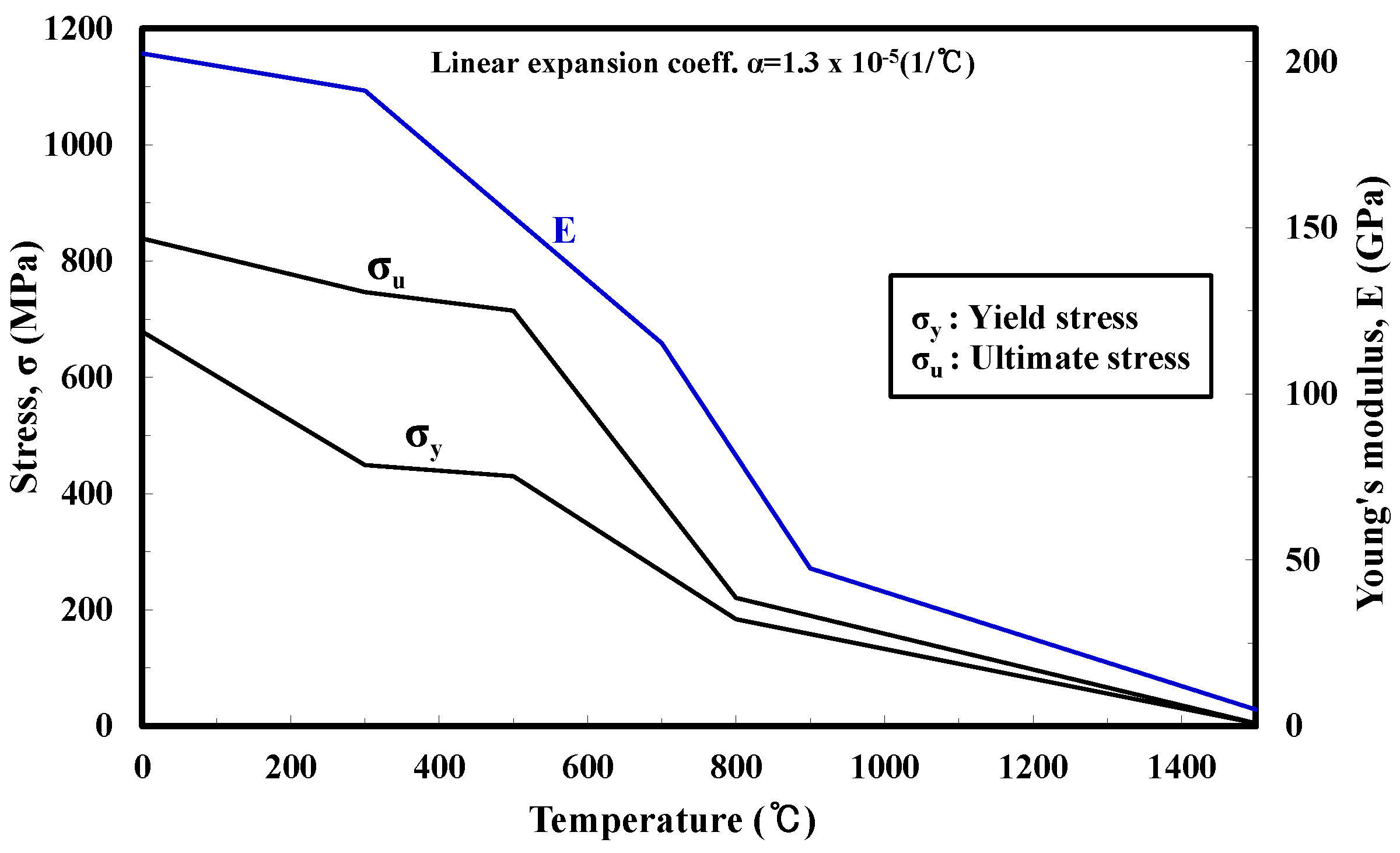


| Chemical Composition (mass, %) | ||||||||
|---|---|---|---|---|---|---|---|---|
| C | Mn | P | S | Si | Ni | Cr | Mo | N |
| 0.019 | 1.848 | 0.028 | 0.0004 | 0.468 | 5.065 | 22.255 | 2.535 | 0.1535 |
| Mechanical Properties | ||||||||
| Yield stress (MPa) | Ultimate strength (MPa) | Elongation (%) | ||||||
| 678 | 839 | 35 | ||||||
| PASS | Current (A) | Voltage (V) | Velocity (mm/s) |
|---|---|---|---|
| 1 | 140 | 12 | 0.9 |
| 2 | 160 | 12 | 1.9 |
| 3 | 170 | 12 | 1.7 |
| 4 | 170 | 12 | 1.2 |
| 5 | 170 | 12 | 1.3 |
| 6 | 160 | 12 | 1.0 |
| Base Metal | HAZ | Weld Metal | HAZ | Base Metal | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Point number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Averaged value | 235 | 236 | 235 | 252 | 252 | 253 | 251 | 254 | 255 | 253 | 255 | 254 | 235 | 235 | 235 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, C.B.; Lee, J.-H.; Lee, C.-H. Distribution and Characteristics of Residual Stresses in Super Duplex Stainless Steel Pipe Weld. Metals 2024, 14, 136. https://doi.org/10.3390/met14020136
Cho CB, Lee J-H, Lee C-H. Distribution and Characteristics of Residual Stresses in Super Duplex Stainless Steel Pipe Weld. Metals. 2024; 14(2):136. https://doi.org/10.3390/met14020136
Chicago/Turabian StyleCho, Chang Beck, Joo-Ho Lee, and Chin-Hyung Lee. 2024. "Distribution and Characteristics of Residual Stresses in Super Duplex Stainless Steel Pipe Weld" Metals 14, no. 2: 136. https://doi.org/10.3390/met14020136
APA StyleCho, C. B., Lee, J.-H., & Lee, C.-H. (2024). Distribution and Characteristics of Residual Stresses in Super Duplex Stainless Steel Pipe Weld. Metals, 14(2), 136. https://doi.org/10.3390/met14020136






