Structural Transformations in Duplex Stainless Steel CF8 Under Intensive Cold Plastic Deformation
Abstract
:1. Introduction
2. Materials and Methods
3. Results
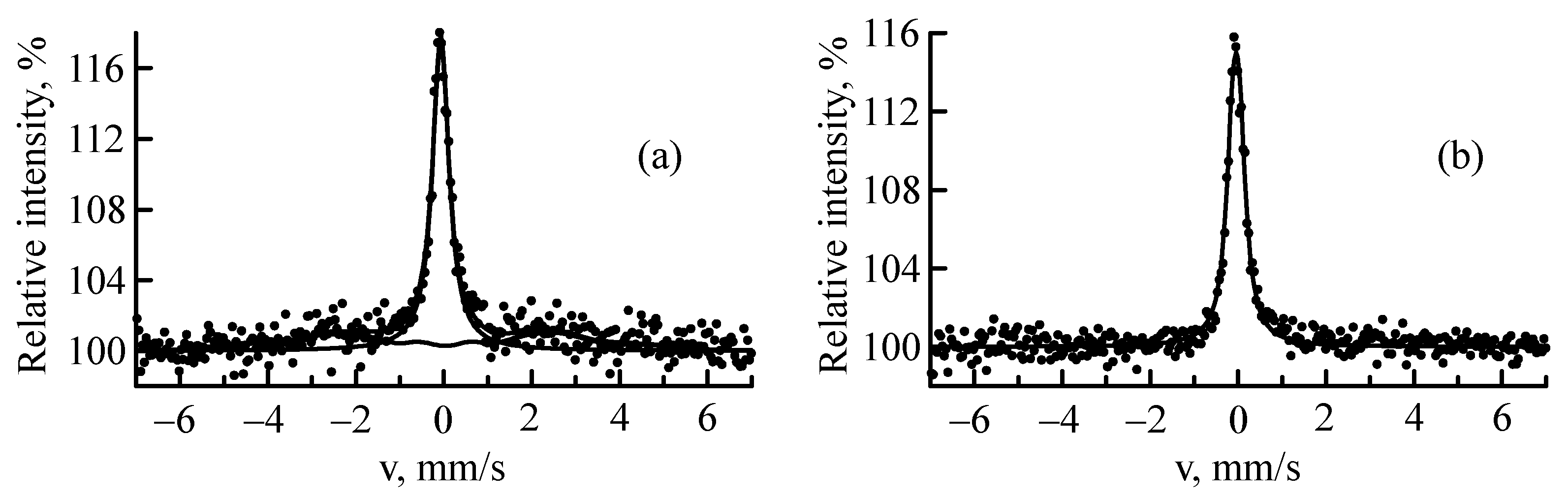
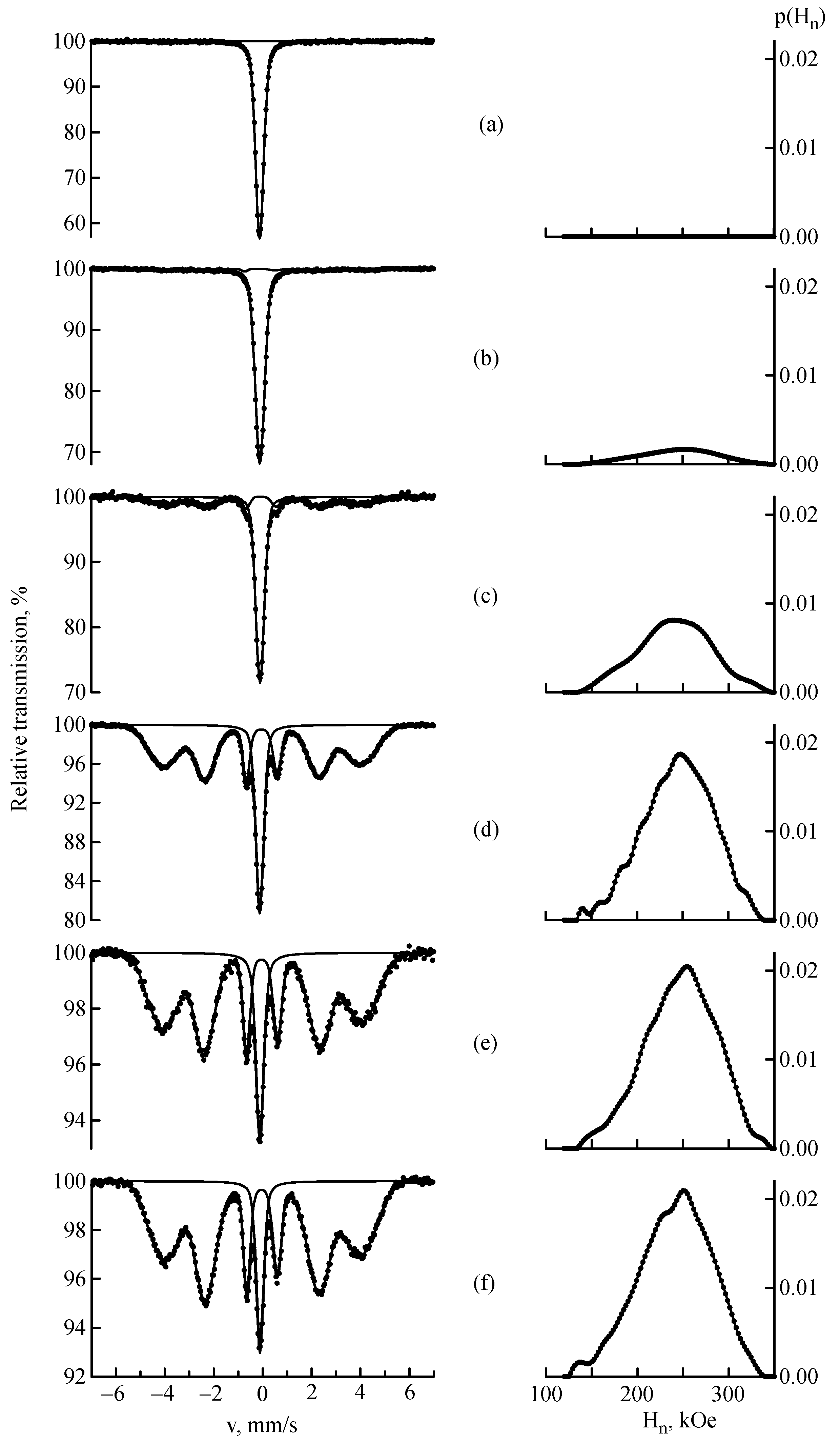
3.1. Mössbauer Spectroscopy
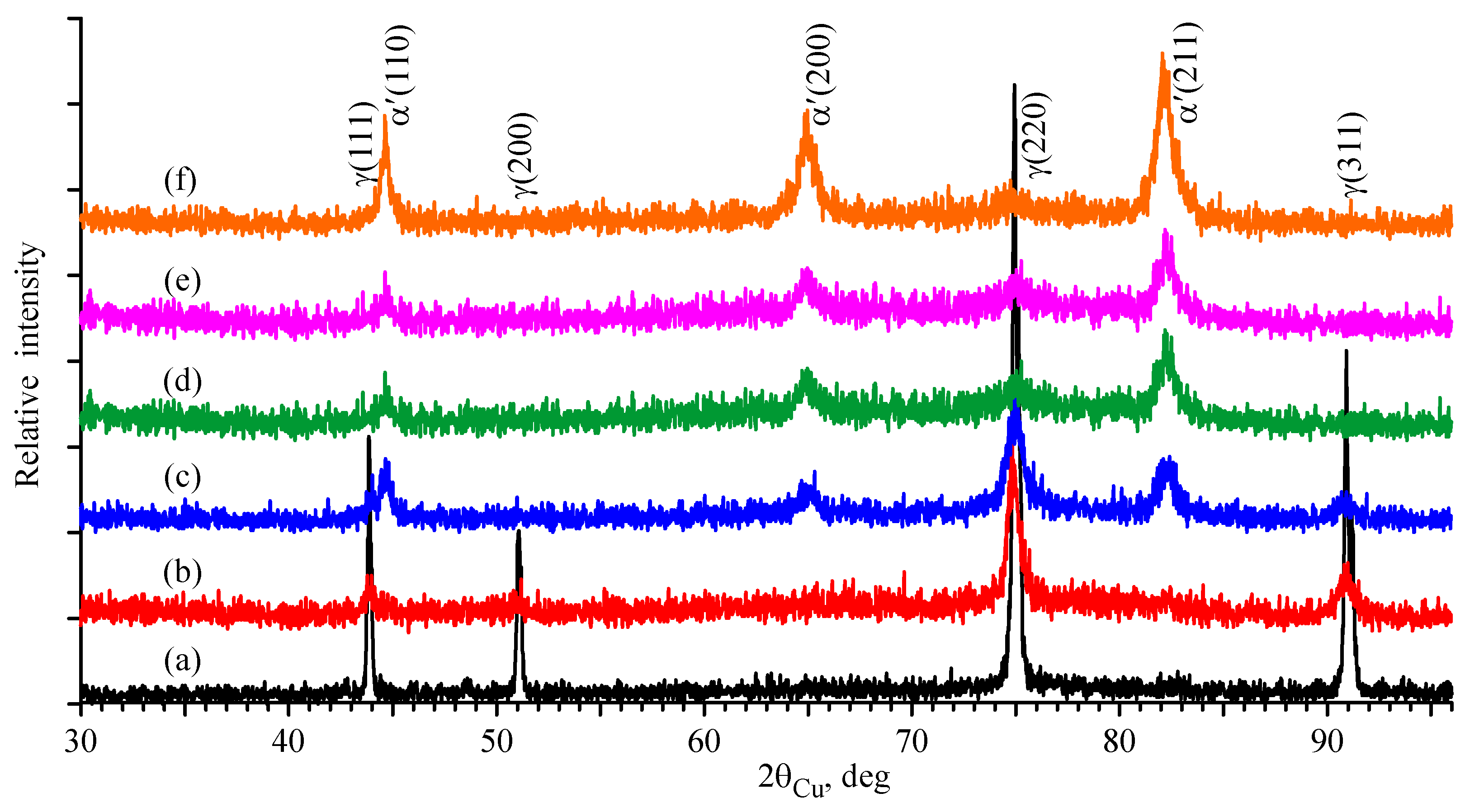
3.2. X-Ray Diffraction
3.3. Olson–Cohen Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meric de Bellefon, G.; van Duysen, J.C. Tailoring plasticity of austenitic stainless steels for nuclear applications: Review of mechanisms controlling plasticity of austenitic steels below 400 °C. J. Nucl. Mater. 2016, 475, 168–191. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Wang, H.; Xin, C.; Wang, X. Effects of long-term thermal aging on the stress corrosion cracking behavior of cast austenitic stainless steels in simulated PWR primary water. J. Nucl. Mater. 2016, 469, 262–268. [Google Scholar] [CrossRef]
- Collins, D.A.; Barkley, E.L.; Lach, T.G.; Thak, S.B. Effects of thermal aging on the fracture toughness of cast stainless steel CF8. Int. J. Press. Vessels Pip. 2019, 173, 45–54. [Google Scholar] [CrossRef]
- Saillet, S.; Le Delliou, P. Prediction of J-R curves and thermoelectric power evolution of cast austenitic stainless steels after very long-term aging (200,000 h) at temperatures below 350 °C. J. Nucl. Mater. 2020, 540, 152328. [Google Scholar] [CrossRef]
- Lu, W.-F.; Huang, J.-Y.; Yung, T.-Y.; Chen, T.-C.; Tsai, K.-C. Effects of thermal aging on the stress corrosion cracking behavior of cast stainless steel with different δ-ferrite levels in high temperature water environment. J. Nucl. Mater. 2022, 568, 153900. [Google Scholar] [CrossRef]
- Chen, Y.; Alexandreanu, B.; Natesan, K.; Rao, A.S. Cracking of irradiated cast stainless steels in low corrosion potential environments. In Proceedings of the The 16th International Conference on Environmental Degradation of Materials in Nuclear Power Systems-Water Reactors, Asheville, NC, USA, 11–15 August 2013; NACE International: Houston, TX, USA, 2013. [Google Scholar]
- Lo, K.H.; Shek, C.H.; Lai, J.K.L. Recent developments in stainless steels. Mater. Sci. Eng. R Rep. 2009, 65, 39–104. [Google Scholar] [CrossRef]
- Li, M.; Miller, M.K.; Chen, W.-Y. Phase stability in thermally-aged CASS CF8 under heavy ion irradiation. J. Nucl. Mater. 2015, 462, 214–220. [Google Scholar] [CrossRef]
- Kwon, J.-D.; Park, J.-C.; Lee, Y.-S.; Lee, W.-H.; Park, Y.-W. An investigation of the degradation characteristics for casting stainless steel, CF8M, under high temperatures. Nucl. Eng. Des. 2000, 198, 227–240. [Google Scholar] [CrossRef]
- Zheng, C.; Liu, C.; Ren, M.; Jiang, H.; Li, L. Microstructure and mechanical behavior of an AISI 304 austenitic stainless steel prepared by cold- or cryogenic-rolling and annealing. Mater. Sci. Eng. A 2018, 724, 260–268. [Google Scholar] [CrossRef]
- Lia, J.; Wang, Y.; Chen, X.; Yan, X.; Xiang, L. Microstructure evolution in stress relaxation behavior of austenite AISI 304 stainless steel spring. Mater. Charact. 2019, 148, 266–271. [Google Scholar] [CrossRef]
- Eid, E.A.; Sadawy, M.M. Role of effective strain during cold rolling deformation on mechanical characteristics of AISI 304 steel. Met. Mater. Int. 2021, 27, 4536–4549. [Google Scholar] [CrossRef]
- Mijovilovich, A.; Goncalves Viera, A.; Paniago, R.; Pfannes, H.-D.; Mendonca Gonzales, B. Mössbauer study of the retained austenitic phase in multiple steels. Mater. Sci. Eng. A 2000, 283, 65–69. [Google Scholar] [CrossRef]
- Oliveira, D.A.; Brito, P.P.; Magalhaes, F.C.; Azzi, P.C.; Ardisson, J.D.; Abrao, A.M. Influence of low plasticity burnishing on the formation of strain induced martensite in the surface layer. J. Mater. Res. Technol. 2023, 27, 4573–4594. [Google Scholar] [CrossRef]
- Cabanillas, E.D.; Terminiello, L.; Cantalejos, N.A.; Versaci, R.; Mercader, R.C. Mössbauer studies of strain-induced transformation of retained austenite in dual-phase steels. Mater. Sci. Eng. A 1992, 150, 113–116. [Google Scholar] [CrossRef]
- Pechousek, J.; Kouril, L.; Novak, P.; Kaslik, J.; Navarik, J. Austenitemeter—Mössbauer spectrometer for rapid determination of residual austenite in steels. Measurement 2019, 131, 671–676. [Google Scholar] [CrossRef]
- Goldanskii, V.; Herber, R. Chemical Applications of Mössbauer Spectroscopy; Academic: New York, NY, USA, 1968; 701p. [Google Scholar]
- Kozlov, K.; Shabashov, V.; Kozlov, A.; Sagaradze, V.; Semyonkin, V.; Panchenko, V.; Zamatovskii, A.; Kataeva, N.; Nikitina, A. Mössbauer spectroscopy investigation of the effect of a high-dose neutron irradiation on the atomic redistribution in the industrial steel EP823. J. Nucl. Mater. 2022, 558, 153384. [Google Scholar] [CrossRef]
- Dubiel, S.M.; Cies´lak, J.; Zukrowski, J. Distribution of Cr atoms in the surface zone of Fe-rich Fe–Cr alloys quenched into various media: Mössbauer spectroscopic study. Appl. Surf. Sci. 2015, 359, 526–532. [Google Scholar] [CrossRef]
- Waanders, F.; Vorster, S.; Engelbrecht, A. Mössbauer and SEM characterisation of the scale on type 304 stainless steel. Scr. Mater. 2000, 42, 997–1000. [Google Scholar] [CrossRef]
- Andrianov, V.A.; Bedelbekova, K.A.; Ozernoy, A.N.; Vereshchak, M.F.; Manakova, I.A. Mössbauer studies of 57Fe implantation in metal Ta and Mo. Nucl. Instrum. Methods Phys. Res. Sect. B 2020, 475, 71–76. [Google Scholar] [CrossRef]
- Vereshchak, M.; Manakova, I.; Shokanov, A. Mössbauer and X-ray Studies of Radiation-Induced Processes in Nb–Zr Alloys Implanted with 57Fe Ions. Materials 2023, 16, 3813. [Google Scholar] [CrossRef]
- Kislitsin, S.B.; Vereschak, M.F.; Manakova, I.A.; Ozernoi, A.N.; Satpaev, D.A.; Tuleushev, Y.Z. Blistering and α ⇆ γ phase transitions at annealing of stainless steel C12Cr18Ni10Ti irradiated by low energy alpha-particles. Probl. At. Sci. Tech. 2013, 2, 17–22. [Google Scholar]
- Deryagin, A.I.; Zavalishin, V.A.; Sagaradze, V.V. Atomic redistribution of alloying elements in nanocrystalline austenitic chromium-nickel steels obtained by strong plastic deformation. Nanostructured Mater. 1998, 10, 411–418. [Google Scholar] [CrossRef]
- Shabashov, V.; Sagaradze, V.; Zamatovskii, A.; Kozlov, K.; Kataeva, N.; Danilov, S. Regulation of the concentration heterogeneity and thermal expansion coefficient in the metastable invar FeNi31.1 alloy. Materials 2022, 15, 8627. [Google Scholar] [CrossRef]
- Shabashov, V.; Sagaradze, V.; Kozlov, K.; Ustyugov, Y. Atomic order and submicrostructure in iron alloys at megaplastic deformation. Metals 2018, 8, 995. [Google Scholar] [CrossRef]
- Shabashov, V.; Kozlov, K.; Ustyugov, Y.; Zamatovskii, A.; Tolmachev, T.; Novikov, E. Mössbauer analysis of deformation–induced acceleration of short-range concentration separation in Fe-Cr alloys—Effect of the substitution impurity: Sb and Au. Metals 2020, 10, 725. [Google Scholar] [CrossRef]
- Kozlov, K.; Shabashov, V.; Zamatovskii, A.; Novikov, E.; Ustyugov, Y. Inversion of the sign of the short-range order as a function of the composition of Fe–Cr alloys at warm severe plastic deformation and electron irradiation. Metals 2020, 10, 659. [Google Scholar] [CrossRef]
- Eymerya, J.-P.; Merakebb, N.; Goudeaua, P.; Fnidikic, A.; Bouzabatab, B. A Mossbauer comparative study of the local environment in metastable 304 stainless steel films depending on the preparation mode. J. Magn. Magn. Mater. 2003, 256, 227–236. [Google Scholar] [CrossRef]
- Principi, G. The Mössbauer effect: A romantic scientific page. Metals 2020, 10, 992. [Google Scholar] [CrossRef]
- Linderhof, F.; Mashlan, M.; Doláková, H.; Ingr, T.; Ivanova, T. Surface micromorphology and structure of stainless and maraging steel obtained via selective laser melting: A Mössbauer spectroscopy study. Metals 2021, 11, 1028. [Google Scholar] [CrossRef]
- Matsnev, M.E.; Rusakov, V.S. SpectrRelax: An application for Mössbauer spectra modeling and fitting. AIP Conf. Proc. 2012, 1489, 178–185. [Google Scholar]
- Cook, D.C. Strain induced martensite formation in stainless steel. Met. Mater. Trans. A 1987, 18, 201–210. [Google Scholar] [CrossRef]
- Gavrilyuk, V.G.; Nadutov, V.M.; Gladun, O.V. Distribution of nitrogen in Fe-N austenite. Phys. Met. Metallogr. 1990, 69, 129–135. [Google Scholar]
- Etienne, A.; Radiguet, B.; Genevois, C.; Le Breton, J.-M.; Valiev, R.Z.; Pareige, P. Thermal stability of ultrafine-grained austenitic stainless steels. Mater. Sci. Eng. A 2010, 527, 5805–5810. [Google Scholar] [CrossRef]
- Hedayati, A.; Najafizadeh, A.; Kermanpur, A.; Forouzan, F. The effect of cold rolling regime on microstructure and mechanical properties of AISI 304L stainless steel. J. Mater. Process. Technol. 2010, 210, 1017–1022. [Google Scholar] [CrossRef]
- Talonen, J.; Hänninen, H.; Nenonen, P.; Pape, G. Effect of strain rate on the strain-induced γ– α′martensite transformation and mechanical properties of austenitic stainless steels. Metall. Mater. Trans. A 2005, 36, 421–432. [Google Scholar] [CrossRef]
- Fultz, B.; Howe, J.M. Transmission Electron Microscopy and Diffractometry of Materials, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002; 748p. [Google Scholar]
- Olson, G.B.; Cohen, M. Kinetics of strain-induced martensitic nucleation. Metall. Trans. A 1975, 6, 791–795. [Google Scholar] [CrossRef]
- Soleimani, M.; Kalhor, A.; Mirzadeh, H. Transformation-induced plasticity (TRIP) in advanced steels: A review. Mater. Sci. Eng. A 2020, 795, 140023. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Mirzadeh, H. Modeling the kinetics of deformation-induced martensitic transformation in AISI 316 metastable austenitic stainless steel. Vacuum 2018, 157, 243–248. [Google Scholar] [CrossRef]
- Zheng, C.; Jiang, H.; Hao, X.; Ye, J.; Li, L.; Li, D. Tailoring mechanical behavior of a fine-grained metastable austenitic stainless steel by pre-straining. Mater. Sci. Eng. A 2019, 746, 332–340. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Mirzadeh, H. Processing of fine grained AISI 304L austenitic stainless steel by cold rolling and high-temperature short-term annealing. Mater. Res. Express 2018, 5, 056529. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. ANN modeling of strain-induced martensite and its applications in metastable austenitic stainless steels. J. Alloys Compd. 2009, 476, 352–355. [Google Scholar] [CrossRef]
- Ahmedabadi, P.M.; Kain, V.; Agrawal, A. Modelling kinetics of strain-induced martensite transformation during plastic deformation of austenitic stainless steel. Mater. Des. 2016, 109, 466–475. [Google Scholar] [CrossRef]


| Degree of Deformation, % | Thickness, µm |
| 0 | 50 |
| 10 | 45 |
| 20 | 40 |
| 40 | 30 |
| 50 | 50 |
| 60 | 40 |
| 70 | 30 |
| 80 | 20 |
| 92 | 50 |
| 95 | 30 |
| Elements | ASTM A743 | Measured Value | Absolute Error |
|---|---|---|---|
| C | <0.08 | 0.07 | 0.01 |
| Si | <2 | 1.6 | 0.1 |
| Mn | <1.5 | 1.0 | 0.1 |
| P | <0.04 | - | - |
| S | <0.04 | - | - |
| Cr | 18.0–21.0 | 19.4 | 0.6 |
| Ni | 8.0–11.0 | 8.6 | 0.4 |
| Fe | balance | 69.3 | 2.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vereshchak, M.; Manakova, I.; Yeshmanova, G.; Tleubergenov, Z. Structural Transformations in Duplex Stainless Steel CF8 Under Intensive Cold Plastic Deformation. Metals 2024, 14, 1449. https://doi.org/10.3390/met14121449
Vereshchak M, Manakova I, Yeshmanova G, Tleubergenov Z. Structural Transformations in Duplex Stainless Steel CF8 Under Intensive Cold Plastic Deformation. Metals. 2024; 14(12):1449. https://doi.org/10.3390/met14121449
Chicago/Turabian StyleVereshchak, Mikhail, Irina Manakova, Gaukhar Yeshmanova, and Zhandos Tleubergenov. 2024. "Structural Transformations in Duplex Stainless Steel CF8 Under Intensive Cold Plastic Deformation" Metals 14, no. 12: 1449. https://doi.org/10.3390/met14121449
APA StyleVereshchak, M., Manakova, I., Yeshmanova, G., & Tleubergenov, Z. (2024). Structural Transformations in Duplex Stainless Steel CF8 Under Intensive Cold Plastic Deformation. Metals, 14(12), 1449. https://doi.org/10.3390/met14121449





