A Rapid, Open-Source CCT Predictor for Low-Alloy Steels, and Its Application to Compositionally Heterogeneous Material

Abstract

The ability to predict transformation behaviour during steel processing, such as primary heat treatments or welding, is extremely beneficial for tailoring microstructures and properties to a desired application. In this work, a model for predicting the continuous cooling transformation (CCT) behaviour of low-alloy steels is developed, using semi-empirical expressions for isothermal transformation behaviour. Coupling these expressions with Scheil’s additivity rule for converting isothermal to non-isothermal behaviour, continuous cooling behaviour can be predicted. The proposed model adds novel modifications to the Li model in order to improve CCT predictions through the addition of a carbon-partitioning model, thermodynamic boundary conditions, and a Koistinen–Marburger expression for martensitic behaviour. These modifications expanded predictions to include characteristic CCT behaviour, such as transformation suppression, and an estimation of the final constituent fractions. The proposed model has been shown to improve CCT predictions for EN3B, EN8, and SA-540 B24 steels by better reflecting experimental measurements. The proposed model was also adapted into a more complex simulation that considers the chemical heterogeneity of the examined SA-540 material, showing a further improvement to CCT predictions and demonstrating the versatility of the model. The model is rapid and open source.

1. Introduction

It is well understood that alloy processing has a direct impact on steel performance. Through understanding the transformation kinetics, alloy-processing routes and/or compositions can be modified to produce unique properties unlike those predicted under equilibrium. It is this relationship that grants the ability, and the desire, to model steel behaviour and predict the performance of post-processed components. There are multiple databases that have measured and collected time temperature transformation (TTT) and continuous cooling transformation (CCT) data [1,2,3]; however, matching diagrams to a specific alloy, with specific test conditions, can prove to be somewhat tricky. This is especially true for CCT diagrams, which are dependent on the alloy composition, austenitisation temperature and time, cooling regime and prior plastic deformation. The ability to predict CCT behaviour is therefore extremely beneficial, reducing laborious experimental work and providing a more convenient platform with which to view cooling behaviour.

There has been a significant amount of research dedicated to the prediction of steel transformation behaviour, primarily for isothermal transformations, as many of the classical first-theory principles are based around such conditions. Some attention, however, has been given to non-isothermal predictions, especially through the incorporation of Scheil’s additivity rule, which converts TTT to CCT behaviour [4]. Most of this attention has been focused on modelling two important features: start and finish transformation times ($T_{\mathrm{s}}$/$T_{\mathrm{f}}$), and final product fractions (X). There are three types of modelling approach that can be distinguished: empirical regression modelling, semi-empirical physical modelling, and fundamental thermodynamic modelling. The latter focuses on fundamental thermodynamic theory, usually requiring complex modelling and large processing power [5,6]. In contrast, simplified empirical models have been successful in predicting steel CCT behaviour quickly and accurately [7,8]. These models, though favourable, are limited to their regression data ranges and, if extrapolated outside of them, can become unreliable. More recently, the use of machining learning and deep learning artificial neural networks (ANNs) have improved the accuracy of empirical CCT predictions and expanded the predictive capabilities of CCT models by allowing larger composition ranges to be considered within one model [9,10,11,12]. Nevertheless, machining learning regression models are still limited to the size of their data ranges, as well as the accuracy and extensiveness of the datasets used. Many models are thereby restricted to the prediction of constituent $T_{\mathrm{s}}$ and $T_{\mathrm{f}}$, as this is all that is generally provided in most CCT datasets. Empirical models therefore do not consider the intricacies of steel behaviour, such as nucleation and growth, and are thereby limited to trend-based predictions. Semi-empirical models combine the usability of empirical models, with the extrapolation potential of fundamental thermodynamic modelling [13,14]. Because of this, semi-empirical models are quick and easy to use but, by considering thermodynamic and kinetic behaviours, are more versatile than simple empirical assessments.

Most software packages that predict TTT and CCT behaviour typically establish their predictions around fundamental thermodynamics or semi-empirical modelling. Some of the more popular software packages include JMatPro [15], Thermo-Calc [16] and MuCG83 [17]. Many of these packages do not specify how exactly they predict steel behaviour and end up restricting model adaptation and modification. Furthermore, the majority of these packages are not open source, thereby limiting their accessibility. The CCT predictions made by Thermo-Calc are built on computational thermodynamics and diffusion kinetics by adopting models developed by Lange et al. [18] for ferrite, Yan et al. [19] for pearlite, Leach et al. [20] and Leach et al. [21] for bainite and Widmanstätten ferrite, and Stormvinter et al. [22], Hanumantharaju [23] and Huyan et al. [24] for martensite. Most of these models were calibrated using either binary or binary and ternary alloys. This then questions whether predictions can be accurately extrapolated past these systems to alloys with more than three components. Some of the more recent of these models [19,21] predicted the behaviour of quaternary alloys reasonably well; however, the accuracy of these predictions showed a notable decrease. Thermo-Calc predictions are also very slow, when compared to the rapidness of empirical and semi-empirical models, making the software undesirable when a large number of CCT predictions are required. JMatPro appears to adopt a more semi-empirical approach [25] by modifying expressions originally published by Kirkaldy and Venugopalan [13] in 1984. This approach greatly expands the range of alloys that can be modelled, as well as the complexity of these alloy compositions, and provides predictions that are both quick and reliable. Recent studies have had good success with using JMatPro to predict the CCT behaviour of steels [26,27]; however, direct comparisons with experimental CCTs showed some discrepancies in the study by Krbat’a et al. [27], with small deviations observed between $T_{\mathrm{s}}$ and $T_{\mathrm{f}}$ values and critical cooling rates. These differences were concluded to be a result of variations in chemical composition, which is a reasonable assumption. Although versatile, semi-empirical models can become limited by their empiricisms. The original expressions by Kirkaldy [13], on which JMatPro is based, predict constituent behaviour using empirical fits on nucleation and growth theories [28,29,30,31]. However, these predictions for each constituent are made independently from one another. This means the impact of prior, high-temperature transformations on the behaviour of succeeding transformations is not explicitly considered. This disconnect between forming constituents, which would ordinarily interact and impact one another, can limit the accuracy of CCT predictions, especially for multi-constituent alloys. It is suggested, in a paper by Guo et al. [32], that JMatPro considers this behaviour on cooling transformations; however, there is no evidence from CCT predictions that this behaviour has been adequately incorporated into the software (e.g., the absence of transformation suppressions in the paper by Krbat’a et al. [27]).

This paper proposes a novel model for predicting the CCT behaviour of low-alloy steels. The model improves an existing semi-empirical model for isothermal transformation behaviour by incorporating the effects of carbon partitioning during austenite decomposition in order to create an explicit coupling effect between individual constituent predictions, whilst also applying the updated boundary conditions for constituent transformations. To convert between isothermal to non-isothermal behaviour, the Scheil additivity rule is adopted [4]. These modifications are made in order to improve the accuracy of CCT predictions while also enhancing model accessibility. Hence, the key novelty of this model lies in its inclusion of carbon partitioning and the characteristic steel behaviours, such as transformation suppression, that are predicted as a result. It should be noted that the purpose of this work is not to advance our knowledge of the transformation mechanisms in steel, but rather incorporate known mechanisms into a rapid CCT predictor. The model is built using Python programming language in order to promote usability and readability. Consequentially, this also allows for fast runtimes, often taking under 10 s to output a single CCT prediction containing 10 cooling rates (tested using computer specifications: Intel(R) Xeon(R) W-2104 CPU @ 3.20 GHz processor and 32.0 GB of RAM). Writing the model in Python also encourages users to both modify and adapt the model into their own predictions. The proposed model is free, open-source and the code is published online [33].

The aim of this study was to develop a rapid, open-source model for predicting the CCT behaviour of low-alloy steels that improves upon the limitations of current models. In its basic form, the model can be quickly used to obtain microstructural predictions for continuous cooling treatments, or it can be easily incorporated into more complex models requiring multiple predictions for steel reaction kinetics, e.g., for models considering weld residual stresses. The predictive capabilities of both Thermo-Calc (Version 2022.1.93985-389, Thermo-Calc Software, Stockholm, Sweden) and JMatPro (Version 13.1, Sente Software, Guildford, UK) will also be briefly considered within this work as comparative examples of existing modelling software.

2. Model Formulation

2.1. Modelling Reaction Kinetics

The proposed model bases itself around a group of semi-empirical equations for isothermal transformation behaviour. Like JMatPro, these expressions were originally developed by Kirkaldy and Venugopalan [13] in 1984 but, instead, were modified by Li et al. [14] in 1998. The model combines local Zener–Hillert [28,29] kinetic growth models with a global Johnson–Mehl–Cahn [30,31] site saturation model to predict isothermal kinetic behaviour. The main benefit of Kirkaldy’s model is its practicability. By developing a semi-empirical approach that incorporates the well-regarded kinetic theories with simplified empirical assessments, the model provides both a reliable and convenient process for predicting transformation behaviour. The modifications made by Li et al. work to correct the limitations of the Kirkaldy model, primarily by extending predictions to higher alloying concentrations and increased carbon contents. The first primary change occurs in the model’s approach to the effects of alloying elements on steel hardenability. The Kirkaldy model assumes these effects are additive, whereas the Li model adjusts this approach to be multiplicative, better reflecting the experimental observations. Secondly, the Li model more explicitly considers the impact of the carbon content on reaction kinetics (something that was neglected in the Kirkaldy model). The prediction for the reaction rate was also adjusted by Li et al. to better reflect the original empirical observations made by Kirkaldy and Venugopalan [13,14]. Previous research used, and adapted, the Li model for predicting the CCT behaviour of steels with good success [34,35].

The general expression for the modified Kirkaldy model is as follows:

$$\tau (X,T)=\frac{F(\mathrm{C},\mathrm{Mn},\mathrm{Si},\mathrm{Ni},\mathrm{Cr},\mathrm{Mo},G)}{\Delta T^{n}exp(-Q/\mathrm{R}T)}S\left(X\right)$$

(1)

where $\tau$ is the isothermal incubation time for the transformation of a fraction X of either ferrite, pearlite or bainite, at a temperature T. F is a function of steel composition (C, Mn, Si, Ni, Cr, Mo in wt.%) and the ASTM prior austenite grain size G, $\Delta T$ is the undercooling from the maximum transformation start temperature, n is an exponent dependent on the diffusion mechanism, Q is the activation energy for nucleation, and R is the gas constant. $S\left(X\right)$ is an empirical reaction rate term approximating the sigmoidal effect of phase transformations and is expressed as

$$S\left(X\right)={\int }_0^X\frac{\mathrm{d}X}{X^{0.4(1-X)}{(1-X)}^{0.4X}}$$

(2)

The prior austenite grain size G can be calculated from experimental measurements using the methods described in ASTM Standards E112 [36], where G can be calculated from the mean linear intercept $\overline{\mathsf{\ell }}$:

$$G=-3.2877-6.6439{log}_{10}\overline{\mathsf{\ell }}$$

(3)

and the mean planar grain diameter $\overline{d}$:

$$\overline{\mathsf{\ell }}=\sqrt{\frac{\pi }{4}}\overline{d}$$

(4)

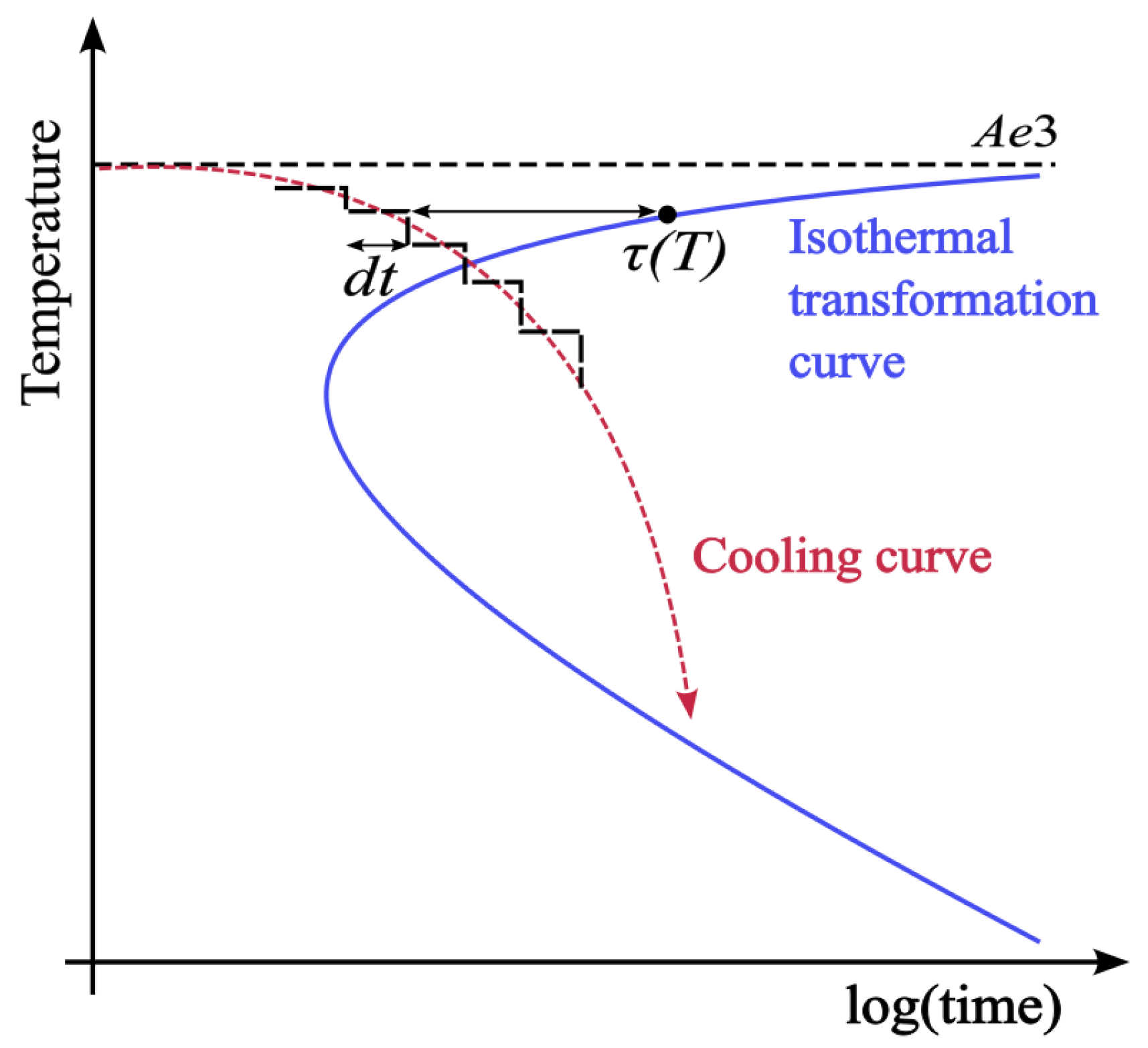
2.2. Converting to Non-Isothermal Behaviour

To convert between isothermal to non-isothermal behaviour, a Scheil additivity rule is adopted [4]. This method works by breaking non-isothermal reactions into individual isothermal steps—as demonstrated in Figure 1. At each step, a fraction of the total nucleation time is calculated by dividing the time spent at each temperature step dt (i.e., the time step), by the incubation time at the same temperature $\tau \left(T\right)$. The time at which the sum of these individual fractions reaches unity is the time at which the non-isothermal transformation begins as is represented by the equation

$$\sum \frac{\mathrm{d}t}{\tau \left(T\right)}=1$$

(5)

The additivity rule is only truly valid when transformations are additive. Avrami [37] described an additive reaction as one in which the nucleation and growth rates are proportional to one another. As such, the processes would have the same temperature dependence. This would ensure that, whatever the path taken to a fraction of phase X, the microstructures will be the same. Avrami dubbed these types of reactions as “isokinetic”, with an isokinetic range defined as the range of temperatures and concentrations in which the kinetics of a phase change remain constant. Cahn [38] argued that a second condition could also be described, in which a reaction would be additive. Cahn proposed that if all nucleation sites saturate early in a reaction, and the growth rate is a function of the instantaneous temperature only, then the reaction would also be additive. A third condition was briefly discussed by Umemoto et al. [39], who stated that an additive reaction could also be achieved when rapid grain growth is suddenly limited, resulting in a nucleation controlled transformation. Difficulty lies in determining whether a transformation is additive or not. This is especially true when predicting non-isothermal transformation behaviour, as an assumption must eventually be made. Previous studies showed good agreement between the experimental and predicted non-isothermal behaviour, even in cases where reactions did not completely satisfy the additive conditions [8,39,40].

Further complications arise when considering the accuracy of empirical TTT data. Experimentally determined TTT curves typically contain an initial temperature transient that originates from quenching the isothermal hold temperature. This transient typically occurs within the austenite decomposition range and, as such, can produce a shift in the measured TTT curves. Thus, the measured TTT is only representative of the exact experimental conditions used. Wierszyłłowski first proposed in 1991 [41] that a ‘true’ TTT could only be achieved if an infinitely fast quench is used to reach the isothermal hold temperature—an unattainable solution. Instead, Wierszyłłowski derived an equation for converting from experimental to ‘true’ TTTs using the inverse additivity rule. Lee et al. [8] were able to demonstrate good success in using this technique to predict both TTT and CCT diagrams from ideal TTTs. A mixture of both isothermal and non-isothermal transformation diagrams were used to calibrate the model developed by Li et al. [14]. As such, the prediction of both TTT and CCT behaviour is not solely reliant on isothermal experimental data, and thus a conversion to ‘true’ behaviour would be inappropriate. Nevertheless, the impact of this consumed incubation time during the quench to the isothermal hold temperature is likely to impact CCT predictions. Lee et al. [8] found that the accuracy of both CCT and TTT predictions was greatly dependent on the cooling method used prior to the isothermal measurements. Inconsistencies in these cooling methods between empirical datasets are therefore likely to cause disruptions in the accuracy of the additivity method.

2.3. Predicting Constituent Behaviour

Using the additivity rule, Li et al. [14] calibrated the general expression in Equation (1) against both TTT and CCT diagrams within the literature to develop individual kinetic equations for ferrite (${\tau }_{\mathrm{f}}$), pearlite (${\tau }_{\mathrm{p}}$), and bainite (${\tau }_{\mathrm{b}}$). These are expressed below.

2.3.1. Predicting Ferrite

Li et al. expressed the isothermal behaviour of ferrite using the equation

$${\tau }_{\mathrm{f}}=\frac{\mathrm{FC}}{2^{0.41G}{(A{e}_3-T)}^{3}exp(-\mathrm{115,060}/\mathrm{R}T)}S\left(X\right)$$

(6)

where the universal gas constant R is given in J mol${}^{-1}{\mathrm{K}}^{-1}$ and FC describes the effects of alloying elements (C, Mn, Si, Ni, Cr, and Mo) in wt.% on the ferrite kinetics and can be described by

$$\begin{array}{c}\hfill \mathrm{FC}=exp(1.00+6.31\mathrm{C}+1.78\mathrm{Mn}+0.31\mathrm{Si}\\ \hfill +1.12\mathrm{Ni}+2.70\mathrm{Cr}+4.06\mathrm{Mo})\end{array}$$

(7)

Ferrite undercooling is calculated using the $A{e}_3$ temperature, where the $A{e}_3$ is denoted as the temperature at which austenite begins to decompose into a mixture of both ferrite and austenite ($\gamma \rightleftharpoons \alpha +\gamma$) under equilibrium conditions. An empirical prediction for this value can be calculated using an expression derived by Grange [42]—shown in Equation (8). This calculation was deemed most suitable for calculating the $A{e}_3$ temperature due to its convenience and applicability within the model. An equivalent equation by Andrews [43] was also considered for the model; however, due to the technique in which the C and Ni expressions are derived, the authors elected to disregard the prediction.

The Grange equation for the $A{e}_3$ temperature is expressed as follows:

$$A{e}_3(°\mathrm{C})=(1570-323\mathrm{C}-25\mathrm{Mn}+80\mathrm{Si}-32\mathrm{Ni}-3\mathrm{Cr}-32)(5/9)$$

(8)

where elemental composition is in wt.% and $A{e}_3$ is calculated in °C.

2.3.2. Predicting Pearlite

The isothermal behaviour of pearlite is represented by the equation

$${\tau }_{\mathrm{p}}=\frac{\mathrm{PC}}{2^{0.32G}{(A{e}_1-T)}^{3}exp(-\mathrm{115,060}/\mathrm{R}T)}S\left(X\right)$$

(9)

where the universal gas constant, R, is given in J mol${}^{-1}{\mathrm{K}}^{-1}$ and PC describes the effects of alloying elements (C, Mn, Si, Ni, Cr, and Mo) in wt.% on the pearlite kinetics and is expressed as

$$\begin{array}{c}\hfill \mathrm{PC}=exp(-4.25+4.12\mathrm{C}+4.36\mathrm{Mn}+0.44\mathrm{Si}\\ \hfill +1.71\mathrm{Ni}+3.33\mathrm{Cr}+5.19\sqrt{\mathrm{Mo}})\end{array}$$

(10)

The $A{e}_1$ temperature can be defined as the intersection point between the $A{e}_3$ ($\gamma \rightleftharpoons \alpha +\gamma$) and $A{e}_{\mathrm{cm}}$ ($\gamma \rightleftharpoons {\mathrm{Fe}}_3\mathrm{C}+\gamma$) transitions—the eutectoid temperature—below which pearlite is expected to form. Another expression by Grange [42] is selected for calculating $A{e}_1$ and is expressed as follows:

$$A{e}_1(°\mathrm{C})=(1333-25\mathrm{Mn}+40\mathrm{Si}-26\mathrm{Ni}+42\mathrm{Cr}-32)(5/9)$$

(11)

where elemental composition is in wt.%, and $A{e}_1$ is calculated in °C.

2.3.3. Predicting Bainite

The isothermal behaviour of bainite is represented by the equation

$${\tau }_{\mathrm{b}}=\frac{\mathrm{BC}}{2^{0.29G}{(B_{\mathrm{s}}-T)}^{2}exp(-\mathrm{115,060}/\mathrm{R}T)}S\left(X\right)$$

(12)

where the universal gas constant, R, is given in J mol${}^{-1}{\mathrm{K}}^{-1}$ and BC describes the effects of alloying elements (C, Mn, Ni, Cr, and Mo) in wt.% on the bainite kinetics and is expressed as

$$\begin{array}{c}\hfill \mathrm{BC}=exp(-10.23+10.18\mathrm{C}+0.85\mathrm{Mn}+0.55\mathrm{Ni}\\ \hfill +0.90\mathrm{Cr}+0.36\mathrm{Mo})\end{array}$$

(13)

In their work, Li et al. [14] also developed an equation for the bainite start temperature, $B_{\mathrm{s}}$ based on a similar equation by Kirkaldy [13]. The modified equation adjusts for the effect of Si, which is assumed to be negligible on $B_{\mathrm{s}}$ and can be expressed by

$$B_{\mathrm{s}}(°\mathrm{C})=637-58\mathrm{C}-35\mathrm{Mn}-15\mathrm{Ni}-34\mathrm{Cr}-41\mathrm{Mo}$$

(14)

where elemental composition is in wt.% and $B_{\mathrm{s}}$ is calculated in °C.

2.4. Model Modifications

The following section details the novel additions made in this work. These include implementing carbon partitioning during the transformation of ferrite and bainite, adjusting the model boundary conditions to account for this partitioning of carbon to austenite during these transformations, and including a Koistinen–Marburger prediction for martensite transformation behaviour.

2.4.1. Modelling Carbon Partitioning

The previous semi-empirical CCT models predict individual transformation curves that are independent of other forming constituents [13,14]. As a consequence, a transformation to ferrite, whether it be 10%, 50% or 95%, would not alter the subsequent transformations to pearlite, bainite or martensite. This is a significant oversight within these models, as it results in the overestimation of transformation start temperatures and an inaccurate prediction of the final microconstituent fractions. Instead, this can be adjusted by implementing the effects of carbon partitioning during austenite decomposition. As ferrite forms, carbon is rejected from the transforming phase and partitions into the remaining untransformed austenite. As a result, the carbon content in the austenite increases, and its stability is altered. The exception, of course, is pearlite, where the carbon-enriched austenite decomposes into cementite simultaneously with ferrite. Carbon partitioning predominantly occurs during transformations to ferrite and bainite as was previously observed [44]. Of course, due to the empirical nature of the model, a fraction of this behaviour may be inadvertently considered within the predictions. This is likely true for the reaction rate term, which was empirically determined from ferrite isothermal behaviour. It is for this reason that the proposed model will only consider the effects of carbon enrichment on subsequent microconstituent transitions and not on the current transformation.

Carbon partitioning is modelled using an equation by Bhadeshia and Edmonds [45], for the enrichment of carbon in austenite, $x_{\gamma }$ with increasing ferrite fraction, X:

$$x_{\gamma }=\overline{x}+\frac{X(\overline{x}-s)}{(1-X)}$$

(15)

where $\overline{x}$ is the average carbon content of the alloy and s the amount of carbon retained within the ferrite/bainitic ferrite—either in solid solution (s = 0.03 wt.% C) or in the form of intralath carbides (s = 0.27 wt.% C) [46,47]. This prediction assumes that all partitioned carbon is supersaturated within the untransformed austenite and none is lost to interlath carbide precipitation. The impact of carbon partitioning on cooling behaviour can be implemented into the model by updating the average austenite composition with each fraction transformed. As austenite decomposes into ferrite (s = 0.03 wt.% C), upper bainite (s = 0.03 wt.% C) and lower bainite (s = 0.27 wt.% C), the amount of carbon retained in the austenite increases. This will result in the start temperatures of transformations successive to these transformations being suppressed.

2.4.2. Adjusting Boundary Conditions

As previously discussed, the model assumes that any ongoing transformations are not slowed by their own carbon partitioning—regardless of the amount of carbon rejected—as it is expected that this is considered within the empirical assessment of the reaction rate. Nevertheless, suitable boundary conditions must be implemented in order to control the extent of transformation at each temperature. For ferrite, this is defined by the ferrite–austenite ($\alpha -\gamma$) equilibrium as dictated by the $A{e}_2$, $A{e}_3$ and $A{e}_{\mathrm{cm}}$ equilibria. For simplicity, the proposed model assumes that the carbon content in ferrite remains at 0.03 wt.% C for all temperatures. Combining this with the lever rule, a maximum ferrite fraction is obtainable.

For bainite, $T_0^{{}^{\prime }}$ equilibria are used. The bainite transformation is experimentally shown to halt prematurely due to a mechanism dubbed the “incomplete reaction phenomenon” [46,48]. One theory for this mechanism relies on the belief that bainite initially transforms displacively—much like martensite. Carbon is then partitioned into the untransformed austenite following the transformation. As the carbon content in the austenite increases, the free energy change between ferrite and austenite tends towards zero ($\Delta G^{\gamma \to \alpha }\to 0$). In the case of a diffusive transformation, carbon redistribution would lower the overall free energy of the system and allow further ferrite to transform. Instead, regarding bainite as displacive, carbon cannot redistribute, and thereby the transformation is interrupted. The point at which the free energy change between ferrite and austenite reaches zero is known as the $T_0$ point. Accounting for the stored energy of ferrite during the displacive transformation (400 J mol${}^{-1}$) results in a $T_0^{{}^{\prime }}$ curve [49]. The authors acknowledge that there is still much debate regarding the mechanism behind the bainite reaction and whether the transformation is diffusion driven or diffusionless. Many of the expressions incorporated into the proposed model consider the theory that bainite is initially displacive. These expressions were chosen primarily for their simplicity and easy adoption into the model. For example, by assuming a displacive–controlled reaction, the $T_0^{{}^{\prime }}$ equilibria can be quickly implemented within the model to simulate the effects of the incomplete reaction. Diffusion-based predictions for the incomplete reaction, such as those for the coupled solute drag effect [50], typically consider more complex behaviours, such as solute–solute interactions, that would require more computationally extensive modelling and, as such, are not considered here.

$T_0$ has been historically calculated using predictions for the free energy change accompanying the austenite-to-ferrite transformation ($\Delta G^{\gamma \to \alpha }$). There are multiple published methods for calculating $\Delta G^{\gamma \to \alpha }$—and thus $T_0$/$T_0^{{}^{\prime }}$—for multicomponent steels [51,52]. For this model, a simplified method by Bhadeshia and Honeycombe, published in ‘Steels: Microstructure and Properties’ [53], was selected. The general expression for this model is as follows:

$$T_0^{{}^{\prime }}\left(\mathrm{K}\right)\simeq 970-80x_{\mathrm{C}}-\Delta T_0$$

(16)

where $x_{\mathrm{C}}$ is the composition of carbon in at.%, and $\Delta T_0$ is the effect of alloying elements on the $T_0^{{}^{\prime }}$ curve. Further description can be found in Appendix A. Incorporating the incomplete reaction phenomenon via the $T_0^{{}^{\prime }}$ prediction should stop the model from over-predicting the extent of bainite transformation.

Previous work by Reynolds [54] observed that, during an isothermal hold, reaching $T_0^{{}^{\prime }}$ does not stop the transformation of bainite completely. Instead, Reynolds found that the bainitic reaction reaches a transformation stasis, where, if held isothermally, the reaction will eventually continue to completion. It was concluded that this continuation of the bainite reaction was caused by the eventual precipitation of interlath carbides, lowering the carbon concentration in the austenite and re-establishing bainite transformation kinetics. Early observations of the incomplete reaction, such as those conducted by Bhadeshia [46], were made using high Si steels. The reason for this was to stop carbide precipitation to better observe ferrite–austenite reaction mechanisms. These studies never observed this continuation of the bainite reaction, and thus they were always deemed to remain incomplete. It is difficult to predict whether this behaviour observed by Reynolds would also happen for other low alloy steels and whether it would happen during non-isothermal conditions. Nevertheless, it can be assumed that, during a continuous cool, the temperature would drop to a level where the thermodynamic driving forces are once again shifted in favour of the bainite transformation before the precipitation of interlath carbides can influence the bainite kinetics, thereby bypassing this effect completely. It is for this reason that the proposed model will disregard the effects of interlath carbide precipitation on the bainite reaction until a more thorough understanding of this mechanism is known.

The partitioning of carbon into the untransformed austenite alters the stability of the austenitic phase and produces a shift in the constituent transformation behaviour. This is incorporated into the model by adjusting the kinetic expressions for isothermal transformation behaviour through the F function and the undercooling ($\Delta T$) term in Equation (1). For pearlite, the Li model uses the $A{e}_1$ temperature in the $\Delta T$ term as the maximum temperature at which pearlite can transform. Pearlite can only transform at this temperature if the carbon content of the austenite reaches the eutectoid composition $C_{\mathrm{eu}}$. This is the point at which the $A{e}_3$ and $A{e}_{\mathrm{cm}}$ curves intersect on the iron–carbon phase diagram. Thereby, this assumes that the carbon composition within the austenite has reached $C_{\mathrm{eu}}$. This is more difficult to achieve under non-equilibrium conditions where ferrite transformation, and thus carbon enrichment of the austenite, is limited. If the austenite carbon concentration is lower than $C_{\mathrm{eu}}$, then the pearlite start temperature becomes suppressed. Pearlite can only start to transform once the temperature drops below both the $A{e}_3$ and $A{e}_{\mathrm{cm}}$ equilibriums. This is not explicitly considered within the Li model and is not likely accounted for in many other empirical models. Equation (9) calculates the impact of undercooling on pearlite transformation kinetics using the $A{e}_1$ temperature. The extent of this impact is determined empirically and as such is not adjusted in this proposed model. Instead, the proposed model accounts for this non-equilibrium behaviour by delaying the pearlite transformation until the equilibrium is satisfied (i.e., the temperature is at or below both the $A{e}_3$ and the $A{e}_{\mathrm{cm}}$ temperatures). The $A{e}_{\mathrm{cm}}$ temperature can be predicted using an equation by Lee and Lee [55] as follows:

$$\begin{array}{c}\hfill A{e}_{\mathrm{cm}}(°\mathrm{C})=224.4+992.4\mathrm{C}-465.1{\mathrm{C}}^2+46.7\mathrm{Cr}+19.0\mathrm{C}\mathrm{Cr}\\ \hfill -6.1{\mathrm{Cr}}^2+7.6\mathrm{Mn}+10.0\mathrm{Mo}-6.8\mathrm{Cr}\mathrm{Mo}-6.9\mathrm{Ni}\\ \hfill +3.7\mathrm{C}\mathrm{Ni}-2.7\mathrm{Cr}\mathrm{Ni}+0.8{\mathrm{Ni}}^2+16.7\mathrm{Si}\end{array}$$

(17)

where elemental composition is in wt.% and $A{e}_{\mathrm{cm}}$ is calculated in °C.

2.4.3. The Upper-to-Lower Bainite Transition

Bainite is routinely classified into two subcategories: upper and lower bainite. Both tend to form as aggregates of subunits of ferrite, in the form of small platelets or laths. Upper bainite is characterised as being free from carbide precipitation within its ferrite subunits. Instead, interlath carbides typically precipitate from carbon-rich austenite between ferrite subunits. As well as these interlath carbides, lower bainite also contains a fine dispersion of plate-like carbides (usually $ϵ$ carbide or cementite) within the ferrite subunits (intralath) [49]. Upper bainite typically transforms at higher temperatures, but both have been observed transforming at the same temperature [46].

Understanding the transition temperature between upper and lower bainite is crucial for this model, as the extent of carbon partitioning differs between each. It is commonly stated that the transition between upper and lower bainite occurs around 350 °C. This was initially observed by Matas and Hehemann [56] in 1961, who demonstrated this transition was consistent for a range of steel compositions. Further exploration by Pickering [57] found this was true but only for higher carbon steels. Pickering found that, at low carbon levels, increasing carbon content resulted in a subsequent increase in the upper-to-lower bainite transition. This continued until a maximum was reached, from which a sudden drop to a 350 °C plateau was observed. Takahashi and Bhadeshia [58] later argued that the maxima occurred because of an interception with the $B_{\mathrm{s}}$ curve and that the 350 °C plateau was more of a misinterpretation of the results. Instead, it was argued that the upper-to-lower bainite transition should initially increase with carbon, as observed by Pickering, but will begin to decrease once the $B_{\mathrm{s}}$ is reached, at which the transition temperature will follow $B_{\mathrm{s}}$. In their work [58], Takahashi and Bhadeshia developed a model for the upper-to-lower bainite transition based on the idea that lower bainite is only achieved when the time required for cementite transformation is shorter than the time for carbon diffusion out of the supersaturated ferrite. The authors argued that there is no fundamental difference between the mechanism of upper and lower bainite but rather that both initially form in the same manner. The difference lies in the rate at which carbon can partition out of the ferrite sub-units. This would explain why the upper-to-lower bainite transition (referred to as $L_{\mathrm{s}}$) initially increases with carbon. The calculations made by Takahashi and Bhadeshia’s model are unfortunately limited to the Fe-C system and therefore its accuracy, when extrapolated to a multi-component system, is unclear. Guo et al. [59] published an updated model for multi-component steels; however, it relies on an external software package to calculate the kinetics of the cementite precipitation. Correspondingly, neither the original model nor Guo’s models consider the kinetics of other carbides besides cementite. Additional complex theory would be required to consider these effects and as such would be difficult to implement. This is unfortunate, as neglecting these effects would likely have an impact on the multi-component model accuracy. Nevertheless, the model appears to corroborate well with the experimental data and seems to be a reasonable empirical assessment of the upper-to-lower bainite transition.

Predicting Ferrite Decarburisation

Takahashi and Bhadeshia’s model [58] works by predicting the rate of decarburisation of a supersaturated ferrite plate ($t_{\mathrm{d}}$) and the rate of cementite transformation ($t_{\theta }$). They hypothesise that if $t_{\mathrm{d}}$ is smaller than $t_{\theta }$, then upper bainite will likely transform, and vice versa. Assuming that the diffusivity of carbon in ferrite is very high, compared to that in austenite, and that a local paraequilibrium between the austenite and ferrite is achieved during carbon partitioning, the time required to decarburise a supersaturated bainitic ferrite plate can be calculated by

$$t_{\mathrm{d}}=\frac{w^2\pi {(\overline{x}-x^{\alpha \gamma })}^2}{16\underline{D}{(x^{\gamma \alpha }-\overline{x})}^2}$$

(18)

where $\overline{x}$ is the average molar carbon concentration in steel, $x^{\alpha \gamma }$ is the mole fraction of carbon in ferrite and $x^{\gamma \alpha }$ is the mole fraction of carbon in austenite at the local paraequilibrium. It should be noted that there is an error in the original published paper [58] and the power of 2 in the denominator $(x^{\gamma \alpha }-\overline{x})$ is accidentally omitted. w is the thickness of the ferrite plate and is assumed to be 0.2 $\mathsf{\mu }$m for this work. $\underline{D}$ is described as the weighted average diffusivity of carbon. Further description into the calculation of $\underline{D}$ can be found in Appendix B. A weighted average diffusivity was chosen to more accurately capture the sensitivity of carbon diffusion in austenite, especially when considering carbon enrichment. The value for $x^{\gamma \alpha }$ can be calculated using the extrapolated $A{e}_3$ line (see Equation (8)) and $x^{\alpha \gamma }$ is the amount of carbon retained in the bainitic ferrite as a solid solution (0.03 wt.% C).

Predicting Cementite Formation Kinetics

Takahashi and Bhadeshia [58] derived a model for the rate of cementite transformation using empirical data from the isothermal tempering of martensite collected by Speich [60]. During the tempering of supersaturated martensite, carbon will precipitate into carbides in a manner not unlike that seen in lower bainite. It is acknowledged that Speich’s work is not the most comparable data to build a model from; however, data for the kinetics of cementite precipitation were not available at the time. Nevertheless, alternative models can be viewed in the Appendix of Takahashi and Bhadeshia’s work [58]. Empirical hardness measurements were used to develop an Avrami-type equation for the prediction of cementite fraction. Parameters for the Avrami equation were obtained by fitting to measured hardness data, resulting in the following expression:

$$\xi \left(t\right)=1-exp\left(k{t}^{0.62}\right)$$

(19)

where $\xi \left(t\right)$ is the volume fraction of cementite normalised by its equilibrium volume fraction, t is time in seconds, and k is described by

$$k=-4.07\times {10}^4{\overline{x}}^{0.635}exp\left(-\frac{\mathrm{33,598}}{\mathrm{R}T}\right)$$

(20)

where $\overline{x}$ is the mole fraction of carbon in the alloy, R is the universal gas constant in J mol${}^{-1}{\mathrm{K}}^{-1}$, and T is the temperature in K. Equation (19) can then be rearranged to give an expression for the time required to precipitate cementite, $t_{\mathsf{\theta }}$. Takahashi and Bhadeshia concluded that 0.01 was a reasonable value for $\xi \left(t\right)$, as this gave a “detectable” volume fraction of cementite. It should be noted that the exponential in Equation (20) ($exp\left(-\frac{\mathrm{33,598}}{\mathrm{R}T}\right)$) was not included in the original derivation [58]. This was deemed an error and is included here.

Estimating $L_{\mathrm{s}}$

Equations (18) and (19) can then be used to calculate $t_{\mathrm{d}}$ and $t_{\mathsf{\theta }}$, respectively, and $L_{\mathrm{s}}$ can be determined—where $L_{\mathrm{s}}$ is the temperature at the interception between the $t_{\mathrm{d}}$ and $t_{\mathsf{\theta }}$ curves.

2.4.4. Predicting Martensite

The Li model does not distinctly consider the transformation behaviour of martensite, focusing only on predicting the martensite start temperature, $M_{\mathrm{s}}$. Martensite is generally said to transform athermally, which means its fraction transformed is dependent on temperature only, and not time. This makes modelling its behaviour a little more straightforward. $M_{\mathrm{s}}$ can be calculated using a modified Steven and Haynes equation [61] by Kung and Rayment [62]. The equation incorporates two more additional terms for Co and Si into the original Steven and Haynes prediction, and is expressed as

$$M_{\mathrm{s}}(°\mathrm{C})=561-474\mathrm{C}-33\mathrm{Mn}-17\mathrm{Cr}-17\mathrm{Ni}-21\mathrm{Mo}+10\mathrm{Co}-7.5\mathrm{Si}$$

(21)

where elemental composition is in wt.% and $M_{\mathrm{s}}$ is calculated in °C. Steven and Haynes determined that the martensite finish temperature, $M_{\mathrm{f}}$, generally occurred around 215 °C below the $M_{\mathrm{s}}$ [61]. Using this temperature range, the Koistinen–Marburger (K-M) equation can be used to describe the change in martensite volume fraction at each temperature [63]. Extrapolating the original equation to include an input for the martensite transformation range ($M_{\mathrm{s}}-M_{\mathrm{f}}$), the K-M equation can be expressed as

$$X_{\mathrm{M}}=X_{\mathrm{A}}^0(1-exp(-k({\mathrm{M}}_s-T)))$$

(22)

where $X_{\mathrm{A}}^0$ is the austenite volume fraction at the start of the martensite transformation and k is a material property which can be calculated using the martensite start, $M_{\mathrm{s}}$, and finish, $M_{\mathrm{f}}$, temperatures:

$$k=\frac{-ln\left(0.01\right)}{M_{\mathrm{s}}-M_{\mathrm{f}}}$$

(23)

2.5. Model Layout

The following section describes the layout of the CCT model, its implementation and the primary assumptions made.

2.5.1. Model Implementation

The basis of the model works by looping through austenite fractions, $X\mathrm{a}$, and determining what each fraction of austenite will transform into, whether that be ferrite—f, pearlite—p, bainite—b, or martensite—m. For each fraction of austenite, a temperature profile is looped through. At each temperature, isothermal incubation times are calculated (${\tau }_{\mathrm{f}}$, ${\tau }_{\mathrm{p}}$, ${\tau }_{\mathrm{b}}$) and the additivity rule is tested. Once the additivity rule reaches unity for a specific constituent, a percentage of that constituent is deemed to be formed, and the temperature loop restarts with updated parameters. The carbon content in the untransformed austenite is adjusted as per the carbon partitioning model and the kinetic driving forces of the system are redefined. If the additivity rule is never satisfied, and the temperature reaches the martensite regime, the model deems there to be a martensitic transformation with any subsequent martensitic transformations occurring as per the Koistinen–Marburger relation. This continues until either all available austenite has been used up (i.e., $X\mathrm{a}$ = 0) or the temperature reaches 25 °C (i.e., ambient room temperature). The model repeats for each cooling rate until all rates have been tested. The raw data that are outputted exist in the form of transformation temperatures ($T_{X\%}$) for each percentage of constituent (X%) formed, over each cooling rate tested. From this, CCT data can be plotted and the final constituent fractions gathered. A flowchart depicting the layout of the model is presented in Figure 2.

2.5.2. Model Assumptions

The primary assumptions made by the model are as follows, many of which were discussed previously within the text but are revisited here:

• Simple, homogeneous austenite grains—the basis of the model predicts steel cooling transformation behaviour within a single, homogeneous austenite grain of a set size. The rest of the material is assumed to comprise solely these homogeneous grains. As a consequence, constraints to constituent nucleation and growth due to the size and shape of the austenite grain, neighbouring grains and ongoing transformations within the grain are not explicitly considered, and any effect on transformation behaviour is assumed to be accounted for empirically. This also includes the impact of residual plastic strain as a result of specimen deformation. The partitioning of carbon is also assumed to occur homogeneously, and the remaining untransformed austenite is enriched equally.
• Additivity is satisfied—all transformations are assumed to be additive and a conversion to a ‘true’ TTT (before conversion to non-isothermal conditions) is deemed unnecessary.
• Consistent reaction rate—the time-dependent reaction rate of austenite decomposition is assumed to be consistent between each constituent, aside from martensite. This follows the original assumptions made in the Li model.
• Simplified transformations—austenite is assumed to only decompose into either ferrite ($\mathsf{\alpha }$), pearlite ($\mathsf{\alpha }$ + $\mathsf{\theta }$), upper bainite ($\mathsf{\alpha }$), lower bainite ($\mathsf{\alpha }$ + intralath $\mathsf{\theta }$) and martensite ($\mathsf{\alpha }$’). Other transformations, such as second-phase particles or interlath carbides, are not currently considered. It is assumed that no constituent can transform simultaneously with another and transformations obey an order. Predictions for ferritic transformation behaviour are assumed to encompass the formation of all ferrite morphologies (allotriomorphic, Widmanstätten, and idiomorphic), as the predictions made by both Kirkaldy and Li do not distinguish between them. There is debate as to whether some of these morphologies should be considered ferritic; however, the determination of this lies outside the scope of this study.
• Diffusionless bainite transformation—there is much debate regarding the mechanism of the bainitic transformation and whether it is diffusion- or displacive controlled. For this model, for simplicity, it is assumed that bainite initially transforms displacively in the form of supersaturated laths of ferrite with carbon diffusion occurring after transformation.

3. Validation of Model

The developed CCT model is validated against experimentally determined CCT data and microhardness analysis. Three low alloy steels with varying chemistry were selected for empirical measurement: EN3B, EN8, and SA-540 B24 (compositionally similar to EN24). The compositions of these alloys are displayed in

Table 1. Chemical compositions (wt.%) of alloys examined.

Alloy	C	Si	Mn	Ni	Cr	Mo	S	Al	Cu	Fe
EN3B	0.18	0.16	0.73	0.04	0.06	0.01	0.008	0.000	0.11	Bal.
EN8	0.44	0.20	0.77	0.07	0.14	0.02	0.029	0.028	0.15	Bal.
SA-540	0.40	0.26	0.75	1.81	0.86	0.32	0.008	0.031	0.08	Bal.

.

3.1. Experimental Measurements

A TA DIL-805 dilatometer (TA Instruments, New Castle, DE, USA) was used to simulate conventional austenitisation treatments for all three steels. Cylindrical specimens of 4 mm diameter and 10 mm length were heat treated to hold temperature T${}_{\mathrm{A}}$ above their austenitisation temperature ($A{e}_3$) and held for a time sufficient for full austenitisation to occur. Specimens were continuously cooled over a range of cooling rates (0.1–50 °C s${}^{-1}$) to room temperature. The heat treatment setups used are presented in

Table 2. Dilatometer heat treatments used for each alloy examined.

Alloy	T${}_{\mathbf{A}}$ (°C)	Step 1	Step 2	Step 3
EN3B	900	Heat to T${}_{\mathrm{A}}$ at 10 °C s${}^{-1}$.	Hold at T${}_{\mathrm{A}}$ for 10 min.	Cool at 0.1, 0.2, 0.5, 1, 2, 5, 10, 20 or 50 °C s${}^{-1}$.
EN8	900	Heat to T${}_{\mathrm{A}}$ at 10 °C s${}^{-1}$.	Hold at T${}_{\mathrm{A}}$ for 10 min.	Cool at 0.1, 0.2, 0.5, 1, 2, 5, 10, 20 or 50 °C s${}^{-1}$.
SA-540	870	Heat to T${}_{\mathrm{A}}$ at 10 °C s${}^{-1}$.	Hold at T${}_{\mathrm{A}}$ for 2 h.	Cool at 0.1, 0.2, 0.5, 1, 2, 5, 10, 20 or 50 °C s${}^{-1}$.

. A set of silica pushrods was used to measure sample dilation during treatment. Phase transformations from face centred cubic (FCC) crystal structures to body centred cubic (BCC), and vice versa, induced sudden volume changes within the specimens. The transformation start temperatures $T_{\mathrm{s}}$ could then be measured using an offset method as described by Yang and Bhadeshia [64]. By estimating the strain induced by the formation of 1% of new constituent in 100% of austenite, $T_{\mathrm{s}}$ can be measured. A modified version of this method that considers the effect of temperature and constituent composition on this transformation strain was used for this study. For transformations occurring directly after higher temperature transformations, where the implementation of the offset method would be difficult, a measurement of the temperature at the inflection point (i.e., when $d^2\epsilon /d{T}^2=0$) between the transitions was used. Both techniques were automated using Python programming language and published online [65]. Dilatometry specimens were heated using an induction coil, under vacuum, and cooled by either helium or argon gas. Samples were cooled under partial pressure during medium to fast cooling rates. The 0.1 and 0.2 °C s${}^{-1}$ cooling rates were slow enough to not require cooling gas and, as such, these samples were cooled under vacuum only. Temperature measurements were recorded using an S-type thermocouple spot welded onto the specimen surface. Dilatometry specimens were extracted from the as-received material, using electric discharge machining, with their lengths parallel to the material forging direction. The measured dilatometry curves for each alloy can be viewed in Supplementary Figures S1–S3. An example of how $T_{\mathrm{s}}$ values were measured using the modified offset and second derivative methods is shown in Supplementary Figure S4.

A BH2 series Olympus optical microscope (Evident Corporation, Tokyo, Japan) was used to examine the post-treated microstructure of dilatometry samples and support dilatometry conclusions. Sample cross sections were polished to a 0.25 $\mathsf{\mu }$m finish and etched using 2% Nital etchant. Microhardness analysis was conducted on post-treated dilatometry samples. A Matsuzawa MMT-X7A microhardness indenter (Matsuzawa Co., Ltd., Akita, Japan) was used to collect a total of 16 hardness measurements per specimen using a 1 kg force, over a dwell of 10 s. Hardness readings were measured across the cross-sectional surface of the cylindrical dilatometry specimens. Care was taken to ensure measurements were taken at least 500 $\mathsf{\mu }$m apart to minimise any potential effects of deformation on subsequent readings.

Prior austenite grain (PAG) size measurements were obtained for SA-540 using EBSD (electron backscatter diffraction) parent grain reconstruction, from which a weighted-average, equivalent circular diameter was calculated. EBSD data was collected using a Thermo Scientific Apreo 2 scanning electron microscope (SEM) (Thermo Fisher Scientific Inc., Waltham, MA, USA) fit with an Oxford Instruments Symmetry EBSD detector (Oxford Instruments, Abingdon, UK). EBSD analysis and parent grain reconstruction was conducted using Aztec Crystal software (Version 2.1.259, Oxford Instruments, Abingdon, UK) [66]. EN3B and EN8 PAG sizes were estimated from microstructural images captured using optical microscopy via a linear intercept method. EN3B and EN8 PAG boundaries were determined using the nucleation of small fractions of allotriomorphic ferrite in rapidly cooled specimens. It is acknowledged that PAG measurements taken from optical microscopy will be less accurate than those determined from EBSD reconstruction; however, due to the nature of the EN3B and EN8 microstructures, consistent techniques could not be used. The EN3B and EN8 micrographs and SA-540 EBSD maps used to determine PAG sizes can be viewed in Supplementary Figures S5 and S6.

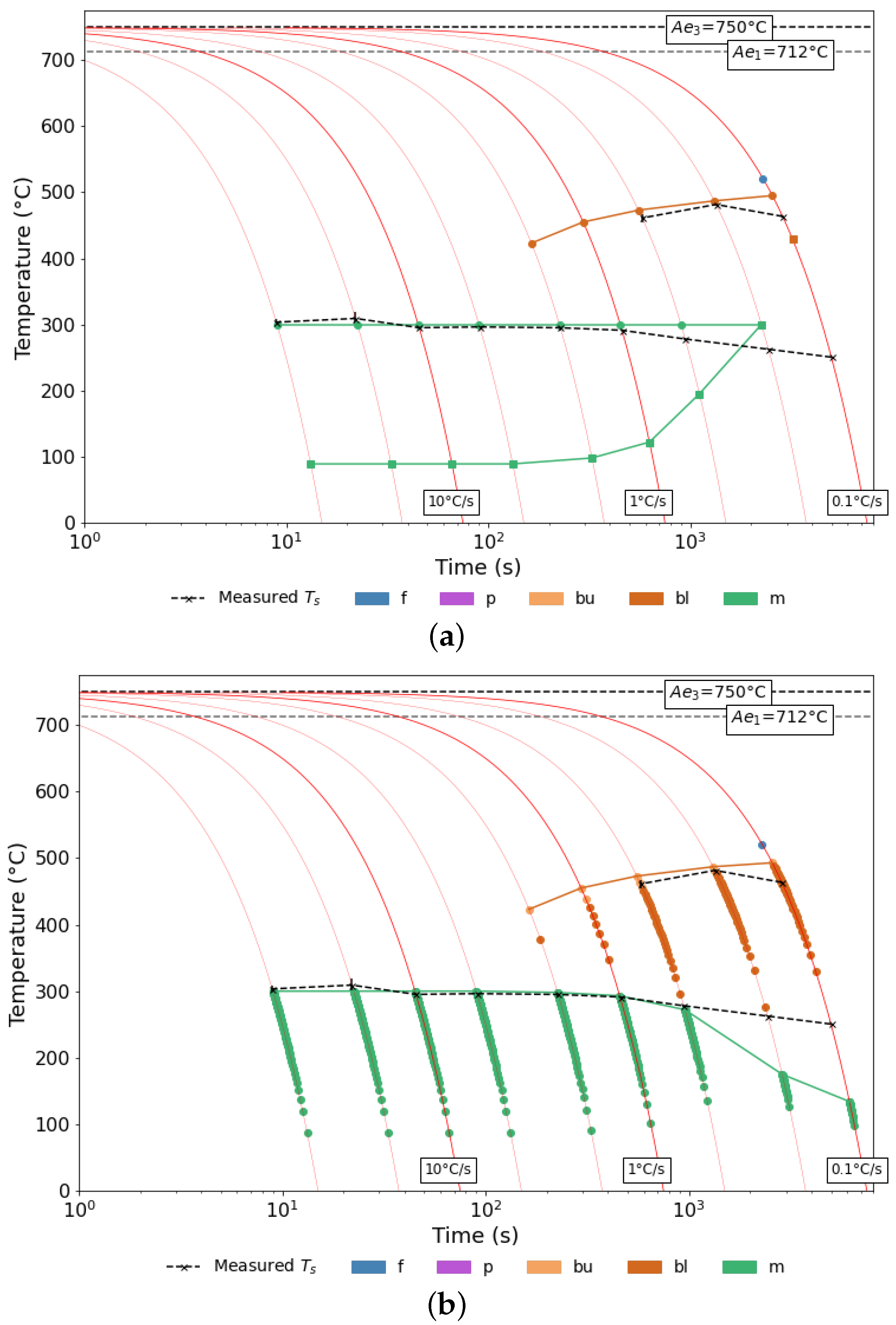
3.2. Evaluating Modelled CCTs

Experimental results from quenching dilatometry, optical microscopy and microhardness analysis are presented in Figure 3, Figure 4 and Figure 5 for EN3B, Figure 6, Figure 7 and Figure 8 for EN8 and Figure 9, Figure 10 and Figure 11 for SA-540 B24. The experimentally measured $T_{\mathrm{s}}$ curves in Figure 3, Figure 6 and Figure 9 are plotted alongside predicted CCTs. Each figure is separated into two CCT plots: one showing the basic Li model prediction (without any modifications), and the other showing the prediction of the model described in this study (referred to as the ‘proposed model’). Experimentally determined $T_{\mathrm{s}}$ values are superimposed on top of both plots for evaluation. Cooling transformation predictions made using the Li model are plotted as dots, representing the $T_{\mathrm{s}}$ for each constituent, and squares, representing the point of complete austenite decomposition. As the Li model does not predict $M_{\mathrm{f}}$, an assumption was made, where appropriate, using the original observations made by Steven and Haynes [61]. Predictions made using the proposed model are plotted as individual dots representing a single percentage (1%) of phase/constituent transformed. Constituent nomenclature used within these figures includes f—ferrite, p—pearlite, b—bainite, bu—upper bainite, bl—lower bainite, and m—martensite.

Optical micrographs of the as-cooled alloy microstructures were collected for each cooling rate tested. The micrographs of the most notable cooling rates for each alloy are presented in Figure 4 for EN3B, Figure 7 for EN8 and Figure 10 for SA-540. A full collection of micrographs can be viewed in the Supplementary Material published alongside this study. Hardness predictions for each modelled CCT were also calculated and plotted alongside microhardness measurements. Hardness values were calculated from the final constituent fractions obtained from the proposed CCT model. From these fraction values, alloy hardness can be predicted using equations by Blondeau et al. [67], which can be viewed in Appendix C. Final constituent fractions for each cooling rate are plotted alongside the hardness plots and both are shown in Figure 5 for EN3B, Figure 8 for EN8 and Figure 11 for SA-540.

3.2.1. EN3B

Analysis of the EN3B dilatometry curves (see Supplementary Figure S1) suggests that a primarily ferritic microstructure is achieved for the majority of cooling rates tested. The measured $T_{\mathrm{s}}$ values are plotted alongside the modelled results in Figure 3. The EN3B dilatometry curves suggest that only a single, high-temperature transformation is measured for cooling rates less than 20 °C s${}^{-1}$. It is likely that a secondary, pearlitic transformation does also occur at these cooling rates. The transition between ferrite and pearlite is likely to be blurred by dilatometry, with the latter continuing on from the former somewhat smoothly. At cooling rates of 20 and 50 °C s${}^{-1}$ a second transformation is measured. The temperature at which these transformations occur suggests that the transitions are either pearlitic or bainitic. The 50 °C s${}^{-1}$ cooling rate also contains a third transformation at around 450 °C, which is likely to be martensitic.

Both the Li model and the proposed model predict the shape of the ferrite start curve for EN3B well (see Figure 3), although there appears to be a shift in the temperature values of this curve, with both models predicting consistently higher start values than measured. For cooling rates less than 5 °C s${}^{-1}$, the Li model predicts a fully ferritic microstructure, whereas the proposed model predicts the transformation of pearlite immediately following the ferrite. It is not until a 5 °C s${}^{-1}$ cooling rate that the Li model predicts the transformation of pearlite. At a 50 °C s${}^{-1}$ cool, both models predict a highly mixed microstructure. The Li model predicts a mixture of ferrite, pearlite and bainite, whereas the proposed model predicts the presence of ferrite, bainite (upper and lower) and martensite. The proposed model appears to be more accurate here, as it encompasses the low temperature transformation measured experimentally—although the start values do differ significantly.

Micrographs of the most notable cooling rates for EN3B are presented in Figure 4. Inspection of the EN3B microstructure reveals that the steel is ferritic–pearlitic at most cooling rates, better supporting the predictions made by the proposed model. At the slowest cooling rates, the ferrite morphology is predominately that of allotriomorphic ferrite as indicated by the lighter etched regions. The darker etched microstructure is indicative of pearlite. As cooling rates increase, a mixture of allotriomorphic and Widmanstätten ferrite is observed. Simultaneously, the fraction of pearlite appears to increase. This continues until a 50 °C s${}^{-1}$ cooling rate, where the microstructure changes drastically. An accurate identification of this microstructure is unable to be made using these micrographs alone; however, it appears to be a mixture of allotriomorphic ferrite, Widmanstätten ferrite, pearlite, upper (coarse) bainite and lower (fine) bainite. These observations better support the Li model predictions for the 50 °C s${}^{-1}$ cooling rate; however, the presence of martensite cannot be ruled out as indicated by the low temperature transformation measured on the dilation curve.

The sudden change from a ferritic–pearlitic microstructure to one that is highly mixed at 50 °C s${}^{-1}$ is illustrated by the hardness predictions in Figure 5a. While EN3B is predicted to be ferritic–pearlitic, between 0.1 and 20 °C s${}^{-1}$, the predicted hardness gradually increases linearly with the cooling rate. At 50 °C s${}^{-1}$, when the EN3B microstructure is predicted to change drastically (see Figure 5b), the predicted hardness spikes in response. In contrast, the measured EN3B hardness suggests that this transition is more gradual. Instead of a step-wise trend in hardness, the experimental measurements show a continuous increase with cooling rate. It is likely that the transition from a ferritic–pearlitic microstructure occurs less aggressively and initiates at a cooling rate slower than 50 °C s${}^{-1}$. The EN3B microstructures for the 10 and 20 °C s${}^{-1}$ cools, in Figure 4, show signs of varying levels of etching within the darker etched regions. This could indicate the transformation of a different constituent other than pearlite and would explain the gradual trend in hardness measured experimentally. Equally, the optical micrograph for the 50 °C s${}^{-1}$ cool shows the presence of pearlite, which is not predicted by the proposed model. This likely causes an overprediction of bainite and, thus, an exaggeration of the predicted hardness. It should also be noted that because the ferrite and pearlite hardness predictions by Blondeau et al. [67] are combined into one expression, the accuracy of these predictions will be limited. The Blondeau equations do not consider the impact of individual ferrite or pearlite fractions, or the effect of different constituent morphologies, such as allotriomorphic versus Widmanstätten ferrite or fine versus coarse pearlite. It is therefore also likely that this gradual increase in measured hardness occurs because of an increase in harder ferritic and pearlitic morphologies. In fact, this is seen in the optical micrographs, where more non-equilibrium ferritic structures are observed with the increasing cooling rate. It is therefore also not unreasonable to assume that pearlite behaves in a similar manner, likely forming harder, fine lamella structures as cooling rates increase. Nevertheless, the proposed model predicts the EN3B hardness well, and the step-wise progression of these predicted hardness results is likely to be indicative of the empirical nature of, and simplified assumptions made by, the model. Experimental analysis suggests that the proposed model gives a successful prediction of the EN3B cooling behaviour, and one that is more accurate than that of the Li model.

3.2.2. EN8

The measured dilatometry curves for EN8 (see Supplementary Figure S2) show a mixed ferrite–pearlite microstructure at the majority of cooling rates tested. A high temperature ferritic curve is initially measured, followed closely by a second pearlite transition. This continues up to the 50 °C s${}^{-1}$ cooling rate, where a third low temperature transformation is measured, which is likely to be martensitic. It should be noted that dilatometry curves were distorted by sudden increases in latent heat during treatments that involved medium-to-fast cooling rates (i.e., greater than 2 °C s${}^{-1}$). This behaviour impacted how linear the cooling was and made the pearlite start temperatures more difficult to measure. As such, the pearlite start temperature appears to increase at these cooling rates; however, this is likely an artefact caused by this influx of latent heat. In this work, pearlite is assumed to form at temperatures lower than measured at these cooling rates.

Analysed $T_{\mathrm{s}}$ values from EN8 dilatometry curves are plotted alongside modelled CCTs in Figure 6. Both the Li model and the proposed model predict a primarily ferritic–pearlitic microstructure for EN8. The proposed model does this consistently for cooling rates less than 50 °C s${}^{-1}$. The Li model only starts predicting a mixed ferrite–pearlite microstructure between 0.5 and 20 °C s${}^{-1}$ cooling rates. Below 0.5 °C s${}^{-1}$, a fully ferritic microstructure is predicted. The measured $T_{\mathrm{s}}$ curves suggest that the pearlite start is suppressed as the cooling rates increase. This is measured at a 2 °C s${}^{-1}$ cooling rate, before the artefacts produced by latent heat are observed. Although this is not predicted by the Li model, it is predicted by the proposed model. As the cooling rates increase, and the proportion of ferrite transformed is lessened, the quantity of carbon enrichment within the untransformed austenite is reduced. This results in a reduced driving force for the pearlite reaction and, consequently, a suppressed $T_{\mathrm{s}}$. It can therefore be concluded that under-transformed ferrite is the likely cause of this observed suppression in the measured $T_{\mathrm{s}}$, due to the non-isothermal conditions and the limited austenite–ferrite regime. At a 20 °C s${}^{-1}$ cooling rate, the Li model stops predicting ferrite and suggests that the microstructure is primarily pearlitic with a small amount of bainite. The proposed model, on the other hand, continues to predict both ferrite and pearlite. The modifications made within the proposed model appear to suppress the pearlite start temperature enough to allow ferrite to still transform at this cooling rate, which is more consistent with what is observed experimentally. At a 50 °C s${}^{-1}$ cooling rate, both models predict a pearlitic–bainitic–martensitic microstructure, with the proposed model predicting a very small fraction of ferrite alongside. The proposed model predicts a more suppressed pearlite start temperature in response to this reduction in ferrite, which agrees better with the experimental measurements, although there is some discrepancy between the measured and predicted ferrite starts. In addition to this, the proposed model predicts a transformation of bainite comprised solely of upper bainite. Both models predict a martensitic transformation at around 300 °C, which coincides well with the measured low temperature transition; however, the extent of this transformation is far greater than that measured experimentally.

The optical micrographs in Figure 7 show that EN8 has a predominately ferritic–pearlitic microstructure between 0.1 and 20 °C s${}^{-1}$, supporting the predictions from the proposed CCT model. The morphology of the ferrite (i.e., the light etched regions) appears to stay consistently allotriomorphic at all cooling rates, likely the result of the small PAG size in EN8. As cooling rates rise, the proportion of ferrite appears to decline, with the fraction of pearlite (i.e., the darker etched regions) increasing. At a 50 °C s${}^{-1}$ cooling rate, the fraction of ferrite is very small, but not insignificant. The microstructure at this cooling rate appears to include a wider variety of constituents. Allotriomorphic ferrite and pearlite still appear to be present, but bainite, and even martensite, could also reside within the microstructure. Non-equilibrium constituents could also be present in the 10 and 20 °C s${}^{-1}$ cooled specimens, although it is difficult to determine from these micrographs alone.

The experimental and predicted hardness for EN8 are plotted in Figure 8a. As cooling rates increase to 20 °C s${}^{-1}$, EN8 is predicted to be ferritic–pearlitic (see Figure 8b) and, as such, the modelled hardness linearly increases. The measured hardness appears to follow a similar trend; however, a slight step in hardness is observed between the 1 and 2 °C s${}^{-1}$ cooling rates. It is likely that this slight jump in hardness is a result of the decreasing ferrite fraction with the increasing cooling rate. This behaviour coincides well with the measured drop in pearlite start temperature in Figure 6 and suggests an increase in pearlite hardness as a result of the lower transformation temperatures. This behaviour is also captured by the proposed CCT model but is not considered in the Blondeau et al. [67] hardness predictions. At 50 °C s${}^{-1}$, both the measured and predicted hardness sharply increase in response to the sudden change in microstructure. Although both bainite and martensite are assumed to transform at this cooling rate, the proposed model appears to overestimate the fraction of martensite, predicting a far greater hardness than what is measured experimentally. Aside from this cooling rate, the proposed model predicts the continuous cooling behaviour of EN8 with good accuracy.

3.2.3. SA-540 B24

At fast cooling rates, the dilatometry curves (see Supplementary Figure S3) suggest that SA-540 is predominately martensitic, with an $M_{\mathrm{s}}$ measured around 300 °C. At cooling rates less than 1 °C s${}^{-1}$, both bainitic and martensitic transformations are observed. During these cooling rates, the martensitic transformation is slightly suppressed, likely due to carbon partitioning during the transformation of bainite.

The measured $T_{\mathrm{s}}$ curves are plotted in Figure 9 alongside modelled CCTs. For the majority of cooling rates, the Li model predicts SA-540 cooling behaviour well. For 0.1 and 0.2 °C s${}^{-1}$ cooling rates, however, the Li model appears to over-predict the amount of bainite transformed, thereby under-predicting the amount of martensite. The proposed model, on the other hand, limits the reaction of bainite by considering the impact of carbon enrichment on the $T_0^{{}^{\prime }}$ equilibria. This then allows martensite to transform after bainite but at a suppressed temperature. Interestingly, the extent of this suppression is far greater than that measured experimentally. Both models predict a transition between a fully martensitic and a mixed microstructure at between 2 to 5 °C s${}^{-1}$. This is not observed in the experimental dilation curves, which suggest a lower rate of transition.

As cooling rates increase, the SA-540 micrographs (Figure 10) show a transition from a predominately bainitic microstructure to one that is fully martensitic. This transition between microstructures (i.e., the critical cooling rate) appears to occur between 2 and 5 °C s${}^{-1}$, where only a small fraction of bainite is present in the 2 °C s${}^{-1}$ cooled sample. This supports the predictions of the proposed model in Figure 9b and suggests that some bainite transformations were not measured using dilatometry. This is known to happen if the transformation is too small and/or if the reaction rate is distinctly slow enough to not produce significant volume changes. As the cooling rate decreases from the critical cooling rate, the proportion of bainite increases. This can be observed by the dark-etched regions of the microstructure in Figure 10a–e. In response to this, the fraction of martensite (the lighter etched regions) decreases. The bainitic microstructure across this range appears to comprise two distinct morphologies; a coarse structure of ferrite and carbide, analogous to an upper bainite, and a finer structure, akin to a lower bainite. Small fractions of upper bainite are also predicted to transform by the proposed model, although to a lesser extent to what is observed in the micrographs. At both 0.1 and 0.2 °C s${}^{-1}$ cooling rates, significant fractions of martensite (light etched regions) are observed within the microstructure, further supporting the predictions made by the proposed model. At cooling rates 5 °C s${}^{-1}$ and higher, the SA-540 microstructure appears to be fully martensitic, with darker etched regions likely to be autotempered structures.

Figure 11a compares the measured hardness results for SA-540 against the hardness predictions made using the proposed model. The predicted trend in hardness fits the experimental results very closely. At the cooling rates above 2 °C s${}^{-1}$, where SA-540 is fully martensitic, the hardness increases linearly with cooling rate. There does appear to be a small systematic error between the measured and predicted hardness values at these cooling rates. As the Blondeau expressions [67] for predicting steel hardness do not consider the impact of microstructural morphology, it is assumed that this discrepancy is likely a consequence of increased martensite lath size strengthening—which, in turn, is influenced by the PAG size. For cooling rates at and below 2 °C s${}^{-1}$, the hardness begins to decrease more harshly. This can be explained by the transition to a mixed martensite–bainite microstructure at the 2 °C s${}^{-1}$ cooling rate. As cooling rates decrease, and more bainite is observed in the microstructure, the hardness decreases further. This measured behaviour is reflected in the proposed model and is visualised well in Figure 11b. As cooling rates drop to 0.1 °C s${}^{-1}$, both the measured and predicted hardness trends appear to level out. A significant fraction of martensite is still observed in the SA-540 microstructure at 0.1 °C s${}^{-1}$, and this is also reflected in the proposed model. This close correlation of the hardness curves across all cooling rates suggests that the proposed model accurately predicts the final constituent fractions of SA-540. The Li model, on the other hand, under-predicts martensite at the slowest cooling rates, thereby limiting its accuracy.

Thermo-Calc (Version 2022.1.93985-389, Thermo-Calc Software, Stockholm, Sweden) and JMatPro (Version 13.1, Sente Software, Guildford, UK) were used to predict the CCT curves for SA-540 and were compared against experimental measurements. The predictions can be viewed in Supplementary Figure S7. The same parameters used in the proposed model (i.e., the SA-540 composition displayed in Table 1, an ASTM PAG size of 6.7 and cooling rates between 0.1 and 50 °C s${}^{-1}$) were used. The CCT prediction for Thermo-Calc took 1.5 h to run using the “Quick” setting and JMatPro took approximately 2 min (software ran using computer specifications: Intel(R) Xeon(R) CPU E5645 @ 2.40 GHz processor and 12.0 GB of RAM). Overall, JMatPro was much better at predicting the CCT behaviour of SA-540 than Thermo-Calc. Thermo-Calc predicted a far less hardenable alloy, with a critical cooling rate higher than what was measured experimentally. The Thermo-Calc prediction showed no martensite transformation until above a 1 °C s${}^{-1}$ cooling rate, below which a predominately bainitic microstructure was predicted. These huge discrepancies between the predicted and experimental behaviour may be a consequence of Thermo-Calc’s extrapolation potential when extended to alloys with high numbers of components. JMatPro predicts the bainite and martensite start temperatures well, and similarly to the proposed model. However, a fully bainitic microstructure is predicted at 0.1 °C s${}^{-1}$. Additionally, JMatPro does not predict the suppression of $M_{\mathrm{s}}$, which was observed experimentally at cooling rates below 1 °C s${}^{-1}$. These results suggest that JMatPro does not adequately consider the impact of higher-temperature transformations on subsequent transformation behaviour.

4. Discussion

4.1. Model Advantages

After comparison with the predictions made by the Li model, the primary advantages of the proposed model are (i) improved CCT predictions, (ii) expanded predictive capabilities, and (iii) enhanced usability and accessibility. These advantages are discussed below.

4.1.1. Improved CCT Predictions

The modifications made to the Li model demonstrate improved CCT prediction, primarily by better regulating the transformation behaviour. The two major modifications made to the Li model are the inclusion of carbon partitioning during austenite decomposition, and the adjustment of thermodynamic boundary conditions to better facilitate cooling behaviour. Li model predictions have been shown to be reasonably reliable for low alloy steels [34,35], but are shown in this work to struggle during periods of microstructural transition (e.g., when transitioning from a bainitic to a martensitic microstructure). As a result, the accuracy of the Li model is routinely limited by the over-prediction of the transformation extent. This limitation is likely a result of the semi-empirical nature of the model. Each prediction for constituent transformation behaviour is made independently of other transformations. Furthermore, empirical fits were likely conducted around datasets that focused primarily on the target constituent, where interactions with other constituents were less common. For example, the bainite start curve prediction was likely fit around bainitic data that were not influenced by previous ferritic or pearlitic transformations. Thus, constituent–constituent interactions will not be explicitly accounted for empirically. The exception is the pearlite interaction with ferrite, as there are few alloys where pearlite will consistently transition without first transforming ferrite. It is for this reason that the pearlite prediction is modified slightly differently in the proposed model as discussed in Section 2.4.2.

The modifications made in this work aimed to incorporate dependencies between the constituent predictions that are not already empirically considered. The success of these modifications can be seen across all alloys tested. For EN3B, a ferritic–pearlitic microstructure is predicted, where the Li model restricts itself to exclusively ferrite (see Figure 3). This is also observed when comparing the EN8 predictions (Figure 6). Dilatometry analysis of EN3B also indicates the presence of a martensitic transformation at a 50 °C s${}^{-1}$ cooling rate. This is captured by the proposed model, which predicts a ferritic–bainitic–martensitic microstructure, but is overlooked by the Li model. These modifications made to the proposed model also allow for the prediction of transformation suppressions. This can be seen in the EN8 prediction, where the pearlite start temperature is suppressed by a reduced ferrite transformation. Although, most notably, this effect can be seen in the martensitic suppression, predicted for SA-540 in Figure 9. The proposed model provides a far improved prediction for SA-540 behaviour at the slower cooling rates where a mixed bainitic–martensitic microstructure is observed. The Li model overestimates the fraction of bainite at these cooling rates, consequently underestimating martensite fraction. The proposed model fixes this issue by restricting the bainite transformation and allowing martensite to transition.

4.1.2. Expanded Predictive Capabilities

In addition to its improved predictive capabilities, the proposed model also expanded these capabilities to include the estimation of final constituent fractions. This ability is something not typically available with other CCT models and was shown to produce results with reasonable accuracy. Hardness predictions using these fraction estimations were shown to agree well with the experimental measurements for all alloys examined. An estimation of constituent fraction is highly beneficial for both alloy design and further modelling.

4.1.3. Enhanced Usability and Accessibility

The proposed model was written and built using Python programming language. Not only does this make the model more accessible to users, but it also encourages future modifications and/or adaptations into more sophisticated models. Building within the Python programming language also allows the model to run efficiently, providing users with rapid CCT predictions and final constituent estimations—often taking under 10 s (tested using computer specifications: Intel(R) Xeon(R) W-2104 CPU @ 3.20 GHz processor and 32.0 GB of RAM). Users additionally only require three primary inputs for the model—alloy composition, PAG size and the desired cooling rates to be tested—making the requirements simple and easy to obtain. The proposed model is free to use and published online [33].

4.2. Model Limitations

Although the proposed model was shown to improve the original Li model predictions, its accuracy is still limited by a number of factors. These include (i) inherent limitations within the Li model, (ii) the over partitioning of carbon, and (iii) problems caused by material heterogenity. These issues are discussed below.

4.2.1. Inherent Limitations

The main limiting factor of the proposed model, and the one that is most clear from the results, is the accuracy of the original Li predictions. These predictions provide the basis on which the proposed model operates, so any inaccuracies in these estimations inevitably impact the results generated by the proposed model. An example of this is illustrated well in the EN8 prediction in Figure 6. Both models appear to over-predict the amount of martensitic transformation during the 50 °C s${}^{-1}$ cooling rate, which likely occurs due to an under-prediction of the bainite transformation extent. This suggests that the issue lies within the Li model’s empirical prediction of bainite kinetics. The empirical nature of the Li model does eventually restrict the accuracy of predictions, especially as transformations become more complex through increased alloying and consecutive constituent transitions. Furthermore, the fixed reaction rate term $S\left(X\right)$ in the Li model is likely to lead to inaccurate predictions of transformation behaviour. $S\left(X\right)$ was determined through empirical ferrite data; however, approximating this same reaction term for both pearlite and bainite is somewhat imprecise and likely leads to inaccurate predictions of their transformation behaviours.

A fundamental issue with the Li model could originate from the empirical source data used to calibrate their predictions. Li et al. [14] reference a few data sources for calibrating their CCT predictions, one of which is the Atlas of Continuous Cooling Transformation Diagrams for Engineering Steels by M. Atkins [2]. The CCT diagrams published in this atlas were obtained through a similar dilatometry technique used in this work; however, the specific parameters used for the collection of this data are unclear. Furthermore, cools were simulated using a variety of quenching mediums and specimen thicknesses, rather than through carefully controlled cooling rates, leading to non-linear cools. Temperature fluctuations as a result of transformation latent heat were also not controlled during cooling. The extent of chemical heterogeneity within the alloys examined was additionally not disclosed. Chemical impurities and heterogeneities would have impacted the alloy transformation behaviour. The applicability of the data collected is therefore questionable. Finally, the compositional ranges tested by Li et al. when developing their expressions were not discussed in their work. Empirical equations, such as the $A{e}_3$ and $A{e}_1$ predictions by Grange [42], and the $M_{\mathrm{s}}$ prediction by Steven and Haynes [61], defined the compositional ranges of validity in which they were tested. These ranges can be viewed in Appendix D. No such ranges are discussed by Li et al. [14], making it difficult to determine what levels and combinations of alloying are valid.

4.2.2. Over Partitioning

Another limitation within the proposed model lies in the estimation of carbon partitioning. This is best shown in the prediction for the SA-540 cooling behaviour in Figure 9b. The temperature at which the $M_{\mathrm{s}}$ is predicted is significantly lower than what is measured experimentally. In reality, this transformation likely occurs slightly lower than measured. The martensitic transformations at 0.1 and 0.2 °C s${}^{-1}$ cooling rates occur directly after substantial bainitic transformations, making it more difficult to accurately determine the start temperatures using the offset method described in Yang and Bhadeshia’s work [64]. Because of this, $M_{\mathrm{s}}$ was measured by finding the point of inflection on the dilatometry curve by calculating the second derivative. As a consequence, this method will tend to overestimate $T_{\mathrm{s}}$, as it does not measure the temperature at which 1% of the constituent has formed but rather the temperature at which the transformation initiates. Thus, there will likely be some error regarding the exact $M_{\mathrm{s}}$ at these cooling rates. Nevertheless, the extent of suppression is far larger than expected, suggesting that the proposed model over-predicts the amount of carbon partitioning during transformation. This is not surprising, as the initial empirical observations of carbon partitioning by Bhadeshia and Edmonds [46] were measured in high-Si steels. The high Si content in these steels impedes the transformation of cementite within the austenite and, as such, the amount of carbon within the austenite is measured at its maximum. This results in the proposed model assuming that all partitioned carbon exists within the supersaturated austenite and not in any interlath carbides. Unfortunately, the model does not yet have the capacity to predict these carbide kinetics during continuous cooling, and therefore is limited in this regard. Nonetheless, the incorporation of carbon partitioning within the proposed model results in an improved CCT prediction but further investigation is required in order to perfect its integration.

4.2.3. Material Heterogeneity

A primary assumption of the model is that the austenite is completely homogeneous throughout the cooling. This extends into the assumption that the microstructure comprises equally sized, homogenous, independent austenite grains. Achieving homogeneity this ideal is unlikely in practice, as steels typically contain some level of chemical segregation—with areas that are enriched and depleted in solute. This segregation leads to varying austenite composition and grain size, ultimately impacting overall alloy behaviour. Chemical heterogeneity can drastically change both isothermal and non-isothermal transformation behaviour, altering transformation start temperatures and critical cooling rates [68,69]. It is, therefore, not unreasonable to assume that heterogeneity could be impacting the measured CCT behaviour of the alloys tested in this study. In fact, all of the steels examined show the presence of microstructural heterogeneity when studying their microstructures optically. Both the EN3B and EN8 microstructures show a classical banded structure, when imaged parallel to their forging directions, with bands of alternating ferrite and pearlite. Micrographs showing these structures can be viewed in Supplementary Figure S8. This chemical heterogeneity could be creating disparities between measured and modelled CCT curves, for example, the absence of pearlite predicted in EN3B or of ferrite predicted in EN8 at the 50 °C s${}^{-1}$ cooling rate. In saying this, there will always be some level of empirical consideration of microstructural heterogeneity within the model; however, levels of heterogeneity can vary significantly between material. SA-540 displays a microsegregation that is more dendritic-like when viewed perpendicular to its forging direction, with depleted regions that are bainitic and enriched zones that are martensitic. These structures can be observed in the 0.5 °C s${}^{-1}$ cooled sample in Figure 10c. These microstructures are remnant to the dendritic segregation initially established during casting. Significant variations in PAG size have also been witnessed in the SA-540 microstructure using EBSD reconstruction analysis. PAGs are measured to vary between 3 and 100 $\mathsf{\mu }$m. A weighted average PAG size is used within the model, but the impact of this extreme level of variation should not be overlooked and is likely to adjust the measured transformation behaviour.

4.3. Considering Chemical Heterogeneity

To examine the possible effects of chemical heterogeneity on CCT predictions, quantitative analysis into the level of element heterogeneity in the examined SA-540 was conducted using an electron probe micro-analyser (EPMA). A map area of approximately 4 × 4 mm${}^2$ was analysed on a polished sample surface perpendicular to its forging direction using a JEOL 8530F FEG-EPMA (JEOL Ltd., Tokyo, Japan). The EPMA maps measured for Al, C, Cr, Mn, Mo, Ni, Si, and V can be viewed in Supplementary Figure S9. A detailed description of the parameters and setup used for collecting these maps can be found in Appendix E.

The collected EPMA maps indicated that the composition of the SA-540 material was significantly heterogeneous. Together with observations of the SA-540 microstructure, it can be concluded that this level of heterogeneity is substantial enough to induce a significant change in the phase behaviour. In review of this, the relevance of the experimental SA-540 results is questioned, as they cannot be directly compared to a prediction of homogenous behaviour. Instead, we propose that the developed model can be adapted to predict chemically heterogeneous behaviour. Each position of the EPMA maps is related to a measured composition. By modelling the CCT behaviour for each of these compositions, a range of SA-540 behaviours can be predicted. For this to work, each spatial composition on the EPMA map (i.e., each pixel) was modelled as a single, homogenous PAG, and the CCT behaviour was predicted. A 1 × 1 mm${}^2$ area of the EPMA measurements was selected for this prediction. By combining the predictions for each measured composition across the EPMA map, a map of predicted constituent positions was determined for each cooling rate. The predicted constituent map for a 0.5 °C s${}^{-1}$ cool is presented in Figure 12 alongside a map of the Ni EPMA data used. Predicted constituent maps for the other examined cooling rates can be viewed in Supplementary Figure S10. At this cooling rate, a mixed bainitic–martensitic microstructure is predicted with chemically depleted regions being predominately bainitic, with small fractions of martensite, and enriched regions being primarily martensitic. This prediction is comparable to the imaged SA-540 microstructure in Figure 10c, which shows a striking resemblance to the predicted map, even when assuming a consistent PAG size. The results of this heterogeneous modelling can also be presented in the form of a CCT (Figure 12c). By incorporating the effects of chemical inhomogeneities, this CCT appears to better simulate the martensite start curve by showing a reduction in suppression and an $M_{\mathrm{s}}$ closer to that seen experimentally. This is most notable for the 0.1 and 0.2 °C s${}^{-1}$ cooling rates, where the predicted CCT in Figure 9b, which assumes a chemically homogenous microstructure, predicts a far greater suppression of $M_{\mathrm{s}}$. A slight increase in start temperature is also seen in the predicted bainite curve but is not inconsistent with the experimental measurements. It is possible that this discrepancy could be a result of varying PAG size, which is not considered in this work. Nevertheless, these increases in start temperatures are clearly impacted by the consideration of solute variation. Depleted compositions are likely to transform bainite earlier, resulting in an increased $B_{\mathrm{s}}$, whereas enriched compositions are likely to reduce $B_{\mathrm{s}}$, therefore decreasing the amount of carbon partitioning and resulting in earlier martensitic transformations. Overall, the CCT prediction for SA-540 that considers the effects of chemical heterogeneity is more comparable to the experimental findings. This suggests improved prediction and the capacity for the model to accurately adapt to heterogeneous compositions if it is applied in such a way that accounts for chemical heterogeneity. Fortunately, the versatility of the proposed model is ideally suited to be implemented as such, and thus this provides a fitting example of how this CCT model can be easily adapted into more complex predictions.

5. Conclusions

A rapid and effective CCT predictor is proposed that modifies previously defined semi-empirical predictions by Li et al. [14] to produce more accurate assessments of low-alloy steel behaviour. The primary modifications made include a model for carbon partitioning during austenite decomposition, updated thermodynamic boundary conditions to better regulate transformation behaviour, and a Koistinen–Marburger expression for the martensitic reaction. A total of three low alloy steels are used to validate the improvements of the proposed model: EN3B, EN8 and SA-540 B24 steels. The proposed model is written in Python programming language and is free to access online [33]. If you use this CCT model in your research, then please cite this paper and the published code.

The conclusions of this work are as follows:

• Li model predictions of continuous cooling behaviour were improved by the modifications outlined in this study. More accurate predictions were observed for all steels examined; however, this was best demonstrated in the SA-540 prediction, where the Li model underestimated the martensitic behaviour succeeding a higher-temperature bainitic transformation.
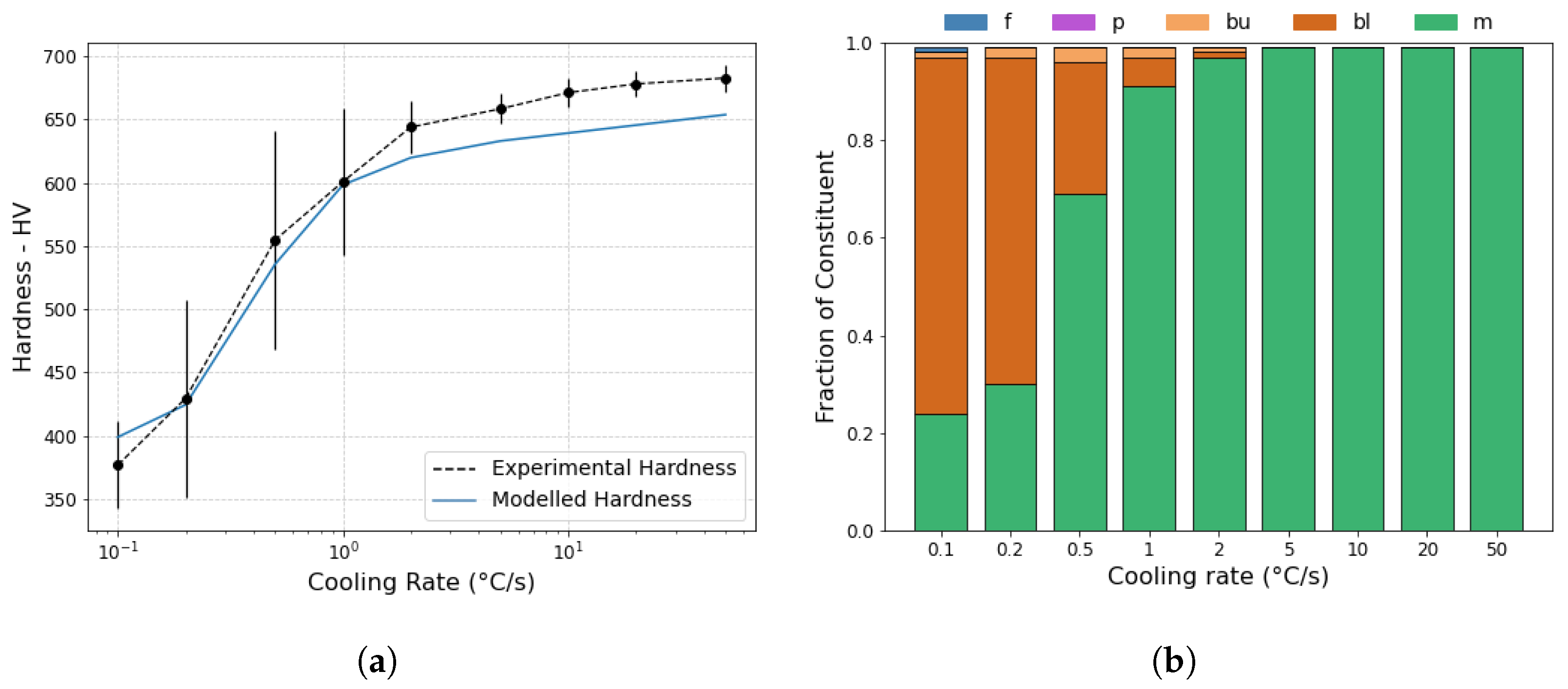
• The predictive capabilities of the model were expanded to include a prediction of final constituent fraction. The accuracy of these estimations were determined using hardness predictions, which agreed well with the experimental measurements.
• Although improvements were made to the CCT predictions, the accuracy of the proposed model is restricted by the inherent, empirical limitations of the original semi-empirical expressions. Correcting these limitations would require developing new sets of constituent transformation expressions around reliable and carefully controlled TTT and CCT datasets.
• The extent of carbon partitioning during austenite decomposition appears to be over-predicted, likely due to the technique used when measuring the empirical data, resulting in larger suppressions of $T_{\mathrm{s}}$. Nevertheless, the inclusion of this model incorporates a more realistic CCT prediction, but a more accurate measurement of partitioning would be required if this model was to be improved.
• Many disparities between the measured and predicted CCT behaviour were considered to be a result of microstructural heterogeneity within the examined material. The proposed model was implemented into a more sophisticated model that considered the measured chemical segregation in SA-540. Results from this adapted model showed an improved prediction of the SA-540 cooling behaviour.