Next Article in Journal
Microstructure and Mechanical Properties of Friction Stir Lap Welding Joint of Al/CU Dissimilar Metals
Previous Article in Journal
Microstructural Characterization of In Situ Aluminum Matrix Composites with Interconnected Aluminum Nitride Produced by Arc Plasma-Induced Accelerated Volume Nitridation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 13
Issue 12
10.3390/met13121968
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Computational and Experimental Study on Failure Mechanism of a GTD-111 First-Stage Blade of an Industrial Gas Turbine

by
Roberto Guillermo Bayro-Lazcano
1,
Saúl Piedra-Gonzalez
2,3,
Angel-Iván García-Moreno
2,3,
Diego German Espinosa-Arbelaez
3 and
Jhon Alexander Villada-Villalobos
2,3,*
1
Posgrado Interinstitucional en Ciencia y Tecnología PICYT, CIDESI, Queretaro 76125, Mexico
2
Consejo Nacional de Humanidades, Ciencia y Tecnología (CONAHCYT), Av. Insurgentes Sur 1582, Col. Crédito Constructor, Demarcación Territorial Benito Juárez, Mexico City 03940, Mexico
3
Center for Engineering and Industrial Development, CIDESI, Av. Pie de la Cuesta 702, Queretaro 76125, Mexico
*
Author to whom correspondence should be addressed.
Metals 2023, 13(12), 1968; https://doi.org/10.3390/met13121968
Submission received: 27 October 2023 / Revised: 25 November 2023 / Accepted: 26 November 2023 / Published: 1 December 2023
(This article belongs to the Section Computation and Simulation on Metals)
Browse Figures
Versions Notes

Abstract

:
This paper investigates the root cause of a recurring failure observed in the first-stage blades of an industrial gas turbine. The failure involves the loss of the trailing edge tip of the blades. The study employs a combination of metallographic analysis and computational simulations utilizing the finite element method and computational fluid dynamics. The metallographic analysis reveals significant degradation in the GTD-111 nickel-based superalloy within the region where the failure occurs. This degradation is characterized by the coarsening and coalescence of the gamma prime phase, which can be attributed to localized overheating. Additionally, the computational study enables the calculation of the trajectory, pressure, and temperature profiles of the hot gases, as well as the distribution of temperatures within the blade. These findings demonstrate that the cooling airflow is influenced by the hot gas flow, particularly in the vicinity of the fault location, owing to the orientation of the cooling ducts, which results in overheating in this area. Ultimately, the temperatures derived from the microstructural analysis using the Ostwald-ripening theory align remarkably well with the results obtained from the simulation, validating the accuracy of the computational model. By combining metallographic analysis and computational simulations, this study provides crucial insights into the failure mechanism of the first-stage blades.

1. Introduction

Gas turbines (GTs) are pivotal in various industrial applications, providing efficient power generation and propulsion capabilities. According to the Brayton cycle, their efficiency rises as the combustion temperature increases [1,2]. For this reason, the components are designed to withstand temperatures as high as possible. However, the reliable operation of a GT relies heavily on the integrity and performance of its critical components, such as the turbine blades. In particular, the first-stage blades (FSBs) in industrial GTs are subjected to extreme conditions, including high temperatures, pressures, and mechanical stresses [3]. Any failures or degradations in these blades can significantly impact the overall turbine performance and result in costly downtime for maintenance and repairs [4].
Due to the high operating temperature, the common failures in GT blades are related to thermal stress, fatigue, creep, coating degradation, corrosion, and erosion [5,6]. Hence, the highest operating temperature is limited by the thermal properties of the materials in the hot gas path (HGP).
Among the failure modes observed in gas turbine blades, the recurring loss of the trailing edge tip in the first-stage blades of industrial GTs has been a persistent concern [7,8]. Investigating the root cause of this recurring failure is paramount to ensure the continuous operation and optimal performance of gas turbines in industrial settings.
The turbine manufacturers have developed complex cooling cavities, advanced materials, and improved coatings to cope with the extreme operating conditions of the FSBs. The geometrical design, material selection, and life cycle estimation of turbine blades are based on the expectation of in-service temperature. However, the aggressive environment in the hot gas path prevents a reliable measurement of the temperature distribution despite several devices that have been used, such as pyrometers, thin film thermocouples, and thermal index paint [9,10]. As a consequence, the FSB requires special attention to prevent failures.
Another alternative approach to evaluating the in-service temperature is assessing the γ’-phase (Ni3Ti) evolution [11,12,13,14,15]. It is well known that nickel-based superalloys undergo microstructural degradation during their lifetime caused by γ’-phase coarsening and coalescence [14]. The Ostwald-ripening theory [16] allows for obtaining the in-service temperature from a microstructural analysis.
Finally, computational simulations provide a feasible alternative approach to better understand the gas flow and heat transfer phenomena inside turbomachinery components. However, many GT models still in operation were designed during the last century when computational resources and methods were not developed enough, and repetitive failures have been detected [4]. In those cases, a reliable temperature estimation could be obtained by computational simulations as long as the geometry of the GT components can be representative of the actual components. The results from the simulations contribute to understanding the failure mechanisms that occur throughout the GT life cycle. In this sense, Computational Fluid Dynamics (CFD) and heat transfer models have been widely developed and implemented to analyze and predict the combustion gas flow and blade bulk temperature [13,17]. The results obtained from these simulations were applied to improve blade cooling using external film cooling and thermal barrier coatings (TBC) [18,19,20]. The combined effect of the film cooling, the TBC system, and the cooling cavities keep the blade below the critical temperature, avoiding component damage [21,22].
The Conjugate Heat Transfer (CHT) approach is the most utilized technique since it allows the coupled calculation of all external hot gases, cooling air, and heat conduction in the blade bulk. Moritz et al. developed the CHTflow code to solve the CHT approach and predict the temperature distribution in a turbine blade at service conditions [23]. The CHTflow solves the compressible Reynolds-averaged Navier–Stokes (RANS) equations with a Baldwin–Lomax turbulence model to predict the heat transfer and fluid flow at the leading edge region of the first-stage turbine blade of an industrial GT. Mensch et al. performed a conjugate heat transfer approach to examine the effect of the internal impingement channel geometry on the heat transfer in the blade end-wall, using a steady-state CFD model (implemented in ANSYS FLUENT), which is based on solving the RANS equations through the k-ω turbulence model [24].
Although several simulation studies have considered cooling cavities, their geometries have been simplified to facilitate simulations and reduce computational and modeling costs, decreasing their reliability [20,25,26]. In this regard, reports have pointed out the relevance of including a complete and precise geometrical description of cooling cavities to improve the reliability of the analysis in the blade [27]. The applicability of the Conjugate Calculation Technique on a realistic gas turbine blade under hot gas operations was analyzed by Kusterer et al. [28]. Due to the complexity of the external and internal blade geometries, the authors established a methodology in which the conjugate calculation was divided into two tasks. The first one dealt with the leading-edge cooling simulation, and the second task neglected the leading-edge ejection and supply channel. Kusterer et al. stated that for future blade calculations, the models should contain complex internal geometry from turbulators to pin-fins and all cooling holes to obtain more reliable results that can be compared quantitatively with experimental results.
This work used a computational and experimental approach to investigate the root cause of a recurring failure observed in the first-stage blades from a 7FA industrial GT by General Electric and its relation with the in-service temperature distribution. The simulations were implemented in SolidWorks Flow Simulation software (https://www.solidworks.com/product/solidworks-flow-simulation, Dassault Systèmes SolidWorks Corporation, Waltham, MA, USA) [29,30,31], using a detailed geometry for the cooling cavities obtained from a Coordinate Measuring Machine (CMM) for the external surface and Computed Tomography (CT-SCAN) for the cooling cavities.
The computational results exhibit temperatures ranging from 400 to 1400 K in the bulk of the blade, showing a good agreement between calculated and predicted temperatures based on the post-mortem microstructural analysis applying the Ostwald-ripening theory. These findings demonstrate that the cooling airflow is influenced by the hot gas flow, particularly in the vicinity of the fault location, owing to the orientation of the cooling ducts, which results in overheating in this area.

2. Materials and Methods

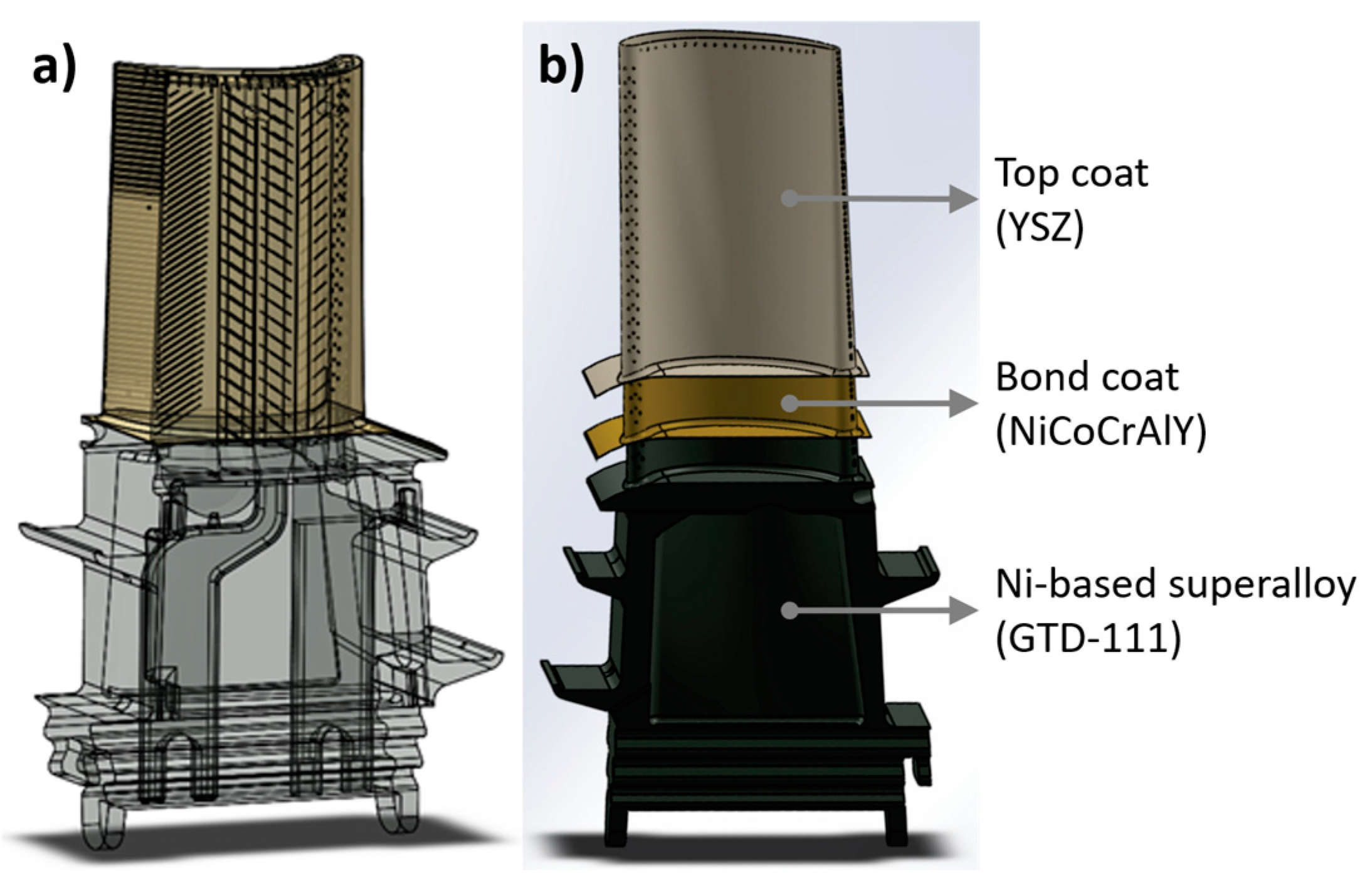
2.1. First-Stage Turbine Blade

This work was carried out on a first-stage blade (7FA General Electric GT, model PG7241FA) of nickel-based superalloy GTD-111 thermal isolated with a TBC system composed of a bond coat (NiCoCrAlY) and a top-coat (YSZ, yttria-stabilized Zirconia). This blade exhibits a failure in the trailing edge tip after 16,000 h in service, as shown in Figure 1.
To study the origin of the failure, a microstructural analysis was made in five different locations of the trailing edge. Samples from these locations were obtained using an electro-discharge machine to minimize the impact of the cutting process on the sample microstructure. The samples’ description is shown in Table 1, and their locations are indicated in Figure 1. A reference sample was obtained from the blade dovetail tip since there is a general agreement in the literature stating that this zone suffers a minimum effect during service and, therefore, a minimal microstructural degradation [25,32].
The samples were hot mounted in epoxy resin, ground, and polished to mirror surface, followed by an etching step using Marble’s reagent by 10 s immersion and rinsing with ethanol and deionized water. Microstructural analysis was carried out by Field Emission Scanning Electron Microscopy (FESEM, JEOL microscope, JEOL, Tokyo, Japan) to measure the size of the γ’ precipitates. Ten micrographs were analyzed for each sample to have a representative statistical study. Micrographs were taken from locations away from the blade surface (i.e., >2 mm) to avoid any influence of the chemical inter-diffusion between the superalloy and bond coat during service.
It is well known that GTD-111 undergoes a microstructural degradation caused mainly by γ’-phase coarsening and coalescence. Several authors have found a gradual increase in γ’ particle size, depending on the temperature and thermal exposure time [15,33,34]. Therefore, the size of γ’ particles can be used to evaluate the in-service temperature at different blade locations. γ’ precipitate sizes (Feret’s diameter) were obtained from the FESEM images using FIJI software (https://fiji.sc/, Open source, Madison, WI, USA) [35]. Based on the Ostwald-ripening theory [11,12,36,37,38,39], γ’ phase coarsening was used to calculate the in-service temperature in the five samples under study.

2.2. Computational Methods

A comprehensive computational aero-thermal analysis was conducted to obtain the in-service temperature distribution and its relation with the observed failure. This analysis was divided into two domains (hereinafter named main- and sub-domain), following the same strategy of prior publications [40,41]. However, our approach diverges from the works cited as we employed a three-dimensional CFD model, which includes the turbine components before and after the first blade stage. Figure 2 shows a graphical description of the main- and sub-domain. The CFD simulations were implemented using SolidWorks® Flow Simulation software (https://www.solidworks.com/product/solidworks-flow-simulation, Dassault Systèmes SolidWorks Corporation, Waltham, MA, USA).

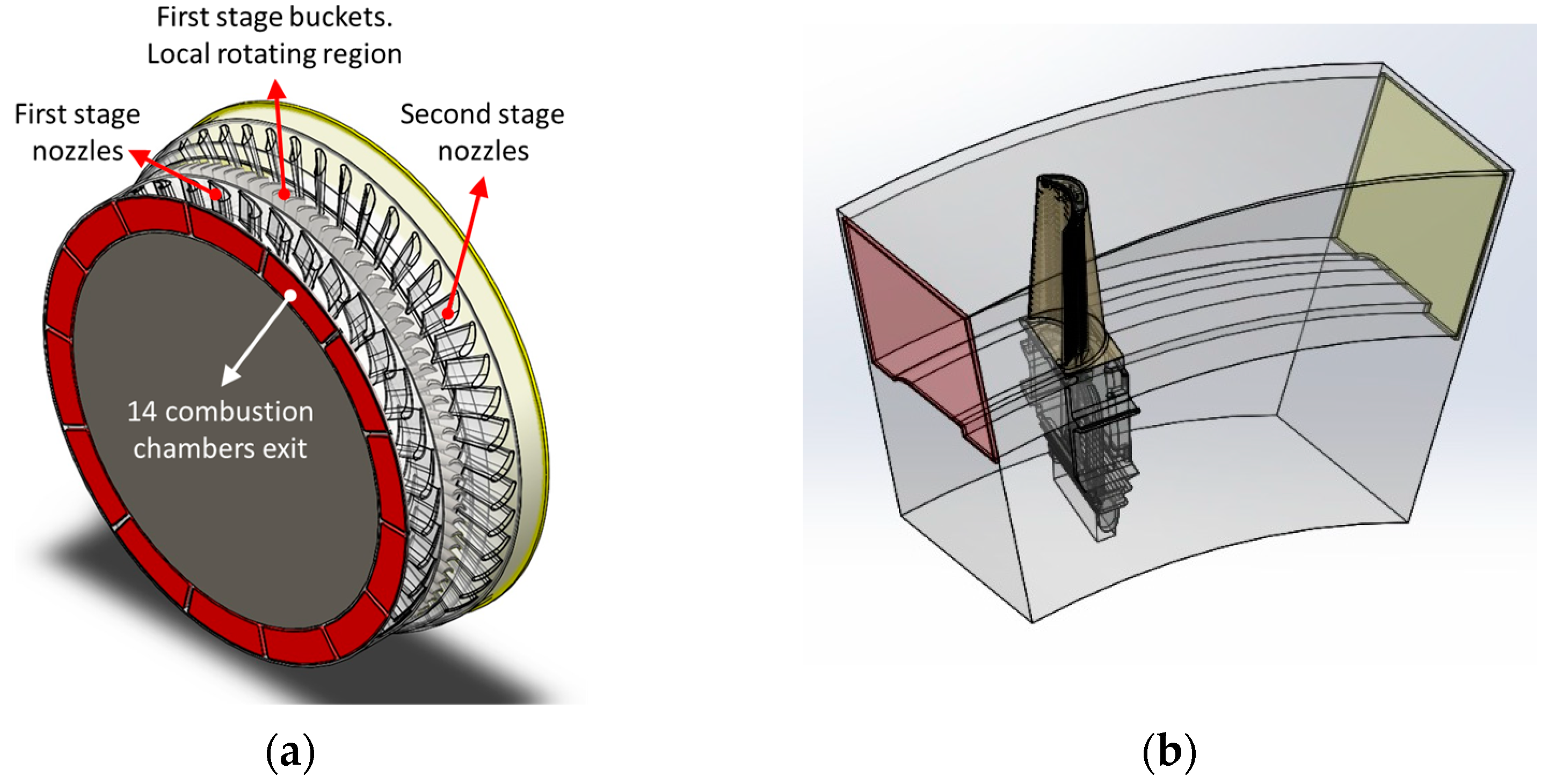
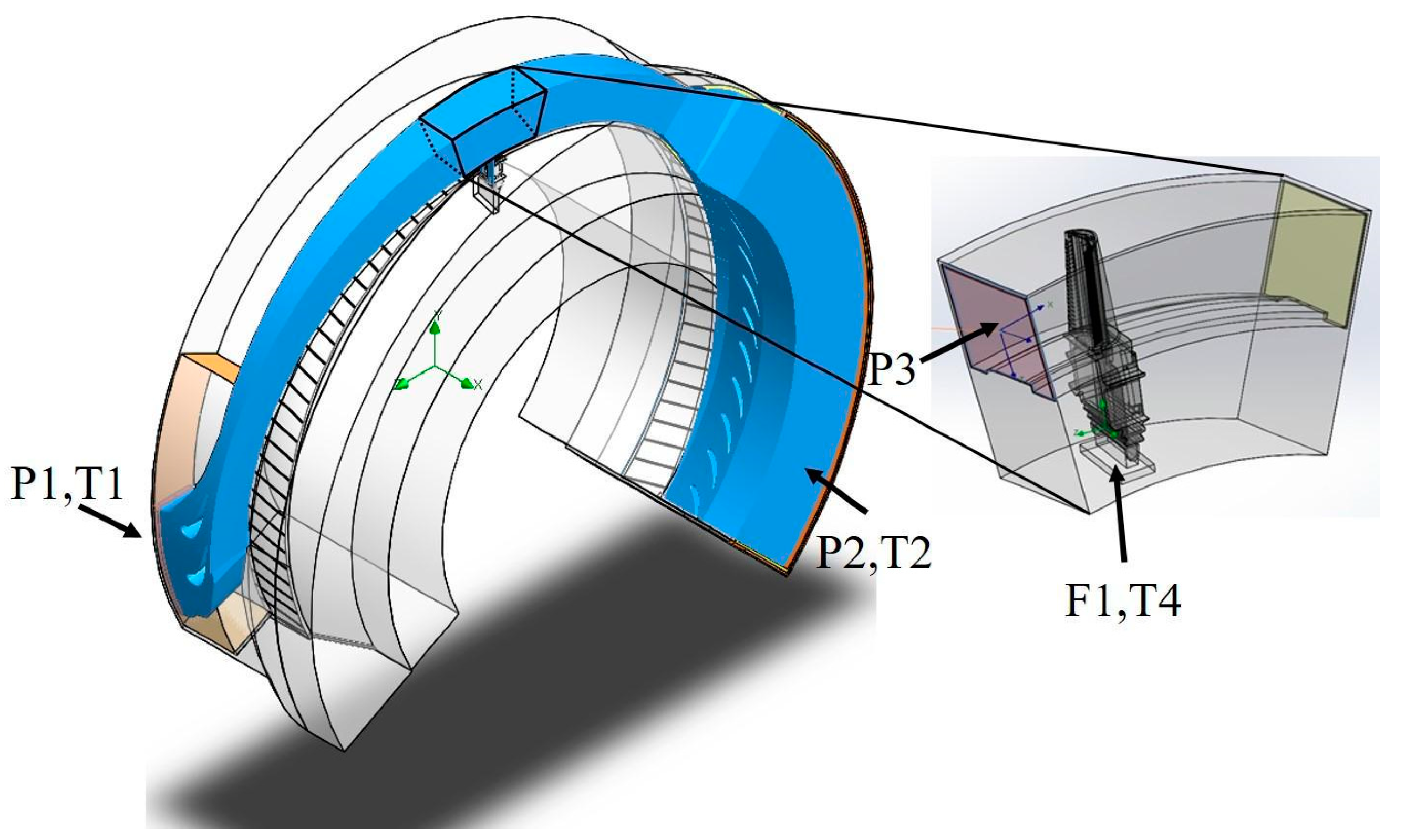
2.2.1. Main Domain

The first challenge in the proposed methodology is establishing the path of the combustion gases through the entire running turbine. This information is essential to define the direction in which the hot gases impact the blades (i.e., gas inlet angle). In addition, the temperature, velocity, and pressure of the hot gases are also critical. For this reason, the main domain was focused on analyzing the behavior of the external gas flow in a broad region, from the combustor’s exit to the second stage of nozzles (Figure 2a). The outer shell was also included. For that purpose, a computer model (computer-aided design, CAD) of each component was obtained using a Coordinate Measuring Machine (CMM) and a 3D scanner (Artec 3D, Spider model). For the main domain, the CAD models include only the external geometry of each component. Then, the 92 blades, first-stage nozzles, and second-stage nozzles were assembled. The assembly of the first-stage blades was treated as a local rotating region in the implemented model (see Figure 2a), considering the GT’s rotational operating conditions (Table 2).
As a result of the analysis, the trajectory (i.e., gas inlet angle), velocity, pressure, and temperature of the combustion gas flow by CFD were obtained using the typical operation parameters of a 7FA General Electric GT model PG7241FA (Table 2) [2,42].
The material and properties of each assembly part were assigned according to Table 3 [43]. GTD-111 properties were obtained from [44].

2.2.2. Sub-Domain

To analyze the flow and heat transfer for a single blade in detail, improving the accuracy of the calculations without additional computational cost, the computational analysis was reduced to the volume of a single blade named the sub-domain, which considered parameters found in the main domain such as the trajectory, velocity, pressure, and temperature of the combustion gas flow. The detailed internal geometry of the blade (cooling cavities), obtained by a computer tomography scan system (CT-SCAN, 300 kV/500 W GE Phoenix v|tome|xm), and the TBC were considered. The heat transfer due to the internal cooling flow was also calculated using CFD modeling into the sub-domain.
The results obtained from the main domain were employed as input parameters for the computational sub-domain. The total pressure (P3 = 7 atm), obtained by the CFD model at the main domain, was used at the inlet parameter of the sub-domain. An average static pressure of the combustion gasses was imposed at the outlet parameter as a boundary condition [26,27]. The flow’s angle (α) at the inlet was obtained from the absolute velocity of the flow (V1), also calculated in the main domain simulation at the inlet position of the selected sub-domain.
A particular mesh strategy (mesh refinement) was applied in zones close to the blade’s cooling cavities. N2 and air fluids were used for this case: N2 as the main combustion product, and air as cooling gas injected in the internal cavities. As a result, the blade’s external and internal surface temperatures were calculated.
The bulk temperature distribution of the blade was calculated by a heat conduction Finite Element Model. The external and internal surface temperature distribution were used as boundary conditions.
Figure 3 shows the CAD model obtained using the external and internal geometry information from CMM and CT-SCAN measurements. The CT-SCAN technique allowed the reconstruction of the internal cavities with high precision (<1 μm), obtaining detailed information about the cooling cavities in the blade, which is critical to predicting the flow and heat transfer around and inside of the component in-service. Figure 3a reveals the complex geometry and the particular high-relief pattern on the internal surface of the cooling cavities. The TBC system consisting of a YSZ top-coat (300 μm) and NiCoCrAlY bond coat (300 μm) was also included in the model and is shown in Figure 3b. Dimensions and geometry of the CAD model (Figure 3) were validated in the assembly by verifying a perfect match and no overlap between adjacent blades.
Once the CAD model was reconstructed, computational CFD and FEM simulations were implemented to solve the flow and heat transfer around and inside the blade.
The subdomain was defined considering the air flowing in the cooling ducts of the blade. In this kind of turbine, the cooling air is taken from the last stage of the compressor; therefore, the pressure of the cooling air (P1) was considered at 14.8 atm. For the heat transfer model, the ignition temperature reported in Table 1 was kept constant at the inlet of the combustion gases. The temperature profile at the gas inlet from the combustors was considered uniform (i.e., 1600 K) in the radial and circumferential direction. Finally, at the cooling air inlet, the temperature was maintained constant at 569 K.
After the material properties and turbine parameters were set, the turbulent flow and heat transfer were computed for a single blade by solving the compressible Favre-averaged Navier–Stokes equations. The transient effects can be neglected, considering the long operational time of GTs. For this reason, steady-state simulations for the two domains (main- and sub-domain) of the CFD models described above were implemented. The simulations used a modified k-ε model with the Lam and Bremhorst damping functions [45]. The two-scale wall function proposed by Balakin et al. [46] and implemented in SolidWorks® Flow Simulation was used to capture the boundary layer effects. This approach combines two methods to couple the boundary layer solution with the bulk flow. The first method, called the thin boundary layer, is used when the number of cells across the boundary layer is insufficient to determine the flow directly. In this case, the Prandtl equations are integrated from the solid region into the boundary layer thickness. In the second method, called the thick boundary layer, enough cells across the boundary layer are required to use the wall function proposed by Van Driest [47].
The computational mesh was based on the immersed-body mesh approach [48,49]. The mesh construction starts independently from the body’s geometry, and the control volumes can intersect the boundary between solid and fluid. For the CFD blade simulation, the mesh considers the airfoil (external) surface and the cooling cavity (internal) shapes of the blade to solve the external and internal flows, respectively. The mesh refinement at the outer surface of the blade was implemented such that the thin boundary approach was valid. For the inner flow case, a mesh refinement for the cooling cavities was performed such that the Cartesian Mesh appropriately represented the smallest passages.
The heat transfer model for the internal structure of the blade was solved using the FEM methodology after the temperature distribution on the blade surface was calculated using CFDs. The temperature distributions at the airfoil (external) and cooling cavity (internal) surfaces were taken as boundary conditions for the FEM model. The steady-state heat transfer equation was solved in an unstructured tetrahedral grid. The main features of the constructed mesh can be observed in Figure 4. As it is shown, the mesh was refined in the zones close to the cooling cavities (0.024 mm < mesh size < 1.209 mm), considering at least seven elements enclosed into a circle perimeter of one cooling cavity. The total element number was 128,631.

3. Results and Discussion

3.1. Microstructural Analysis

According to the Ostwald-ripening theory [21,22,43,44], the size of the γ’ phase is related to time by
d 3 − d 0 3 = K t
where d is the average size (in μm) of the particles at a time t (16,000 h for the studied blade) and d0 is the initial average size. K is called the coarsening rate constant and depends upon the temperature and several parameters of the material, as shown in Equation (2) [38,39,50,51]:
K = a T e x p ( − Q R T )
where
a = 64 C e γ s V m 2 D 0 9 R
Ce is the equilibrium concentration γ’, γs is the interfacial free energy, Vm is the molar volume, D0 is the initial diffusion coefficient, R is the gas constant, Q is the activation energy for diffusion, and T is the absolute temperature.
Ten micrographs were taken per sample to estimate the temperature from the γ’ phase size. Figure 5 shows a typical SEM image from the reference sample where the dark squares represent the γ’ phase. The FIJI software was used to obtain the d0 value (0.583 µm) from the reference sample.
Similar images were obtained for each sample (S1–S5). Figure 6 shows SEM images from different heights along the trailing edge of the blade. From these images, it is possible to observe that the γ’ phase size at the trailing edge tip (h = 330 mm, S5) is the most significant (2.1 μm), evidencing the coarsening effect. The coarsening and coalescence of the γ’ phase at the trailing edge tip could be associated with a high temperature in this zone.
In contrast, for the reference sample (h = 10 mm), the size (0.583 µm) and shape (squares) of the γ’ phase are closer to the original characteristics of this phase in GTD-111 superalloy. An evident variation in size and morphology of the γ’ phase from the dovetail to the blade tip is observed. The γ’ size and shape evolution directly relate to the temperature differences during the turbine service.
The average γ’ size (d) and standard deviation (σ) for each sample were obtained from the SEM images using FIJI software. The d values are shown in Table 4. The K values for each sample were calculated from Equation (1), and the results are also reported in Table 4.
Experiments under laboratory conditions conducted on the GTD-111 superalloy provide information about the evolution of the γ’ phase as a function of the temperature in [34]. These results were used to obtain Q (255.96 KJ/mol) and a (5,983,840,378.22 µm3 K/h) by linear fitting of the Log(KT) versus the 1/T plot. Based on this, it is possible to transform Equation (2) into a linear one given by:
L n ( K T ) = 22.51233 − 30 , 786.6250 ( 1 T )
This transcendental equation can be solved using the graphical method to obtain the temperature for each sample as a function of the K value. We use the online version of the software WolframAlpha (https://www.wolframalpha.com/calculators/equation-solver-calculator, Wolfram Research, Champaign, IL, USA). [52].
Significantly elevated temperature values were obtained in samples S4 and S5, surpassing the known temperature thresholds for GTD-111 superalloy [53,54]. Consequently, the mechanical behavior of this material is subjected to various concurrent phenomena, including oxidation, which reduces yield strength and fracture toughness. These phenomena represent plausible contributors to the trailing edge tip failure observed in the blade. Additionally, it is important to note that the size of the γ’ phase directly influences the material’s mechanical properties.

3.2. Simulation Approach

While the microstructural analysis presented in the preceding section provides insights into localized temperature conditions and their correlation with the trailing edge tip failure, it is essential to obtain a comprehensive understanding of the in-service temperature distribution across the entire turbine blade. A simulation approach was employed, initially focusing on the studied section of the turbine, encompassing the first and second stages of vanes and the first stage of blades (main domain). Subsequently, a detailed simulation was explicitly conducted for the first stage blade (sub-domain), considering the results from the main domain simulation. The sub-domain simulation enhances our grasp of temperature distribution and gives information about potential factors contributing to the observed failure.

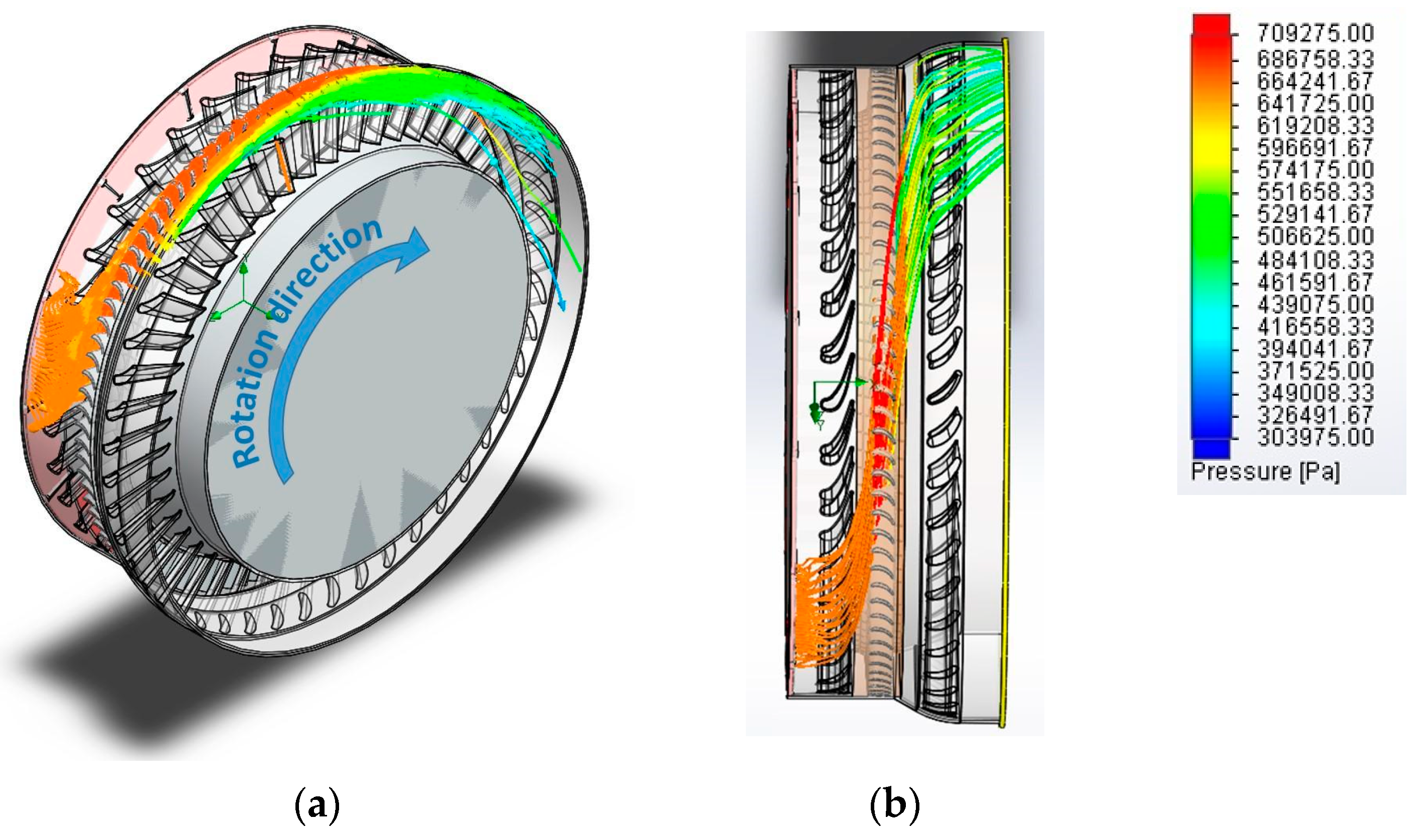
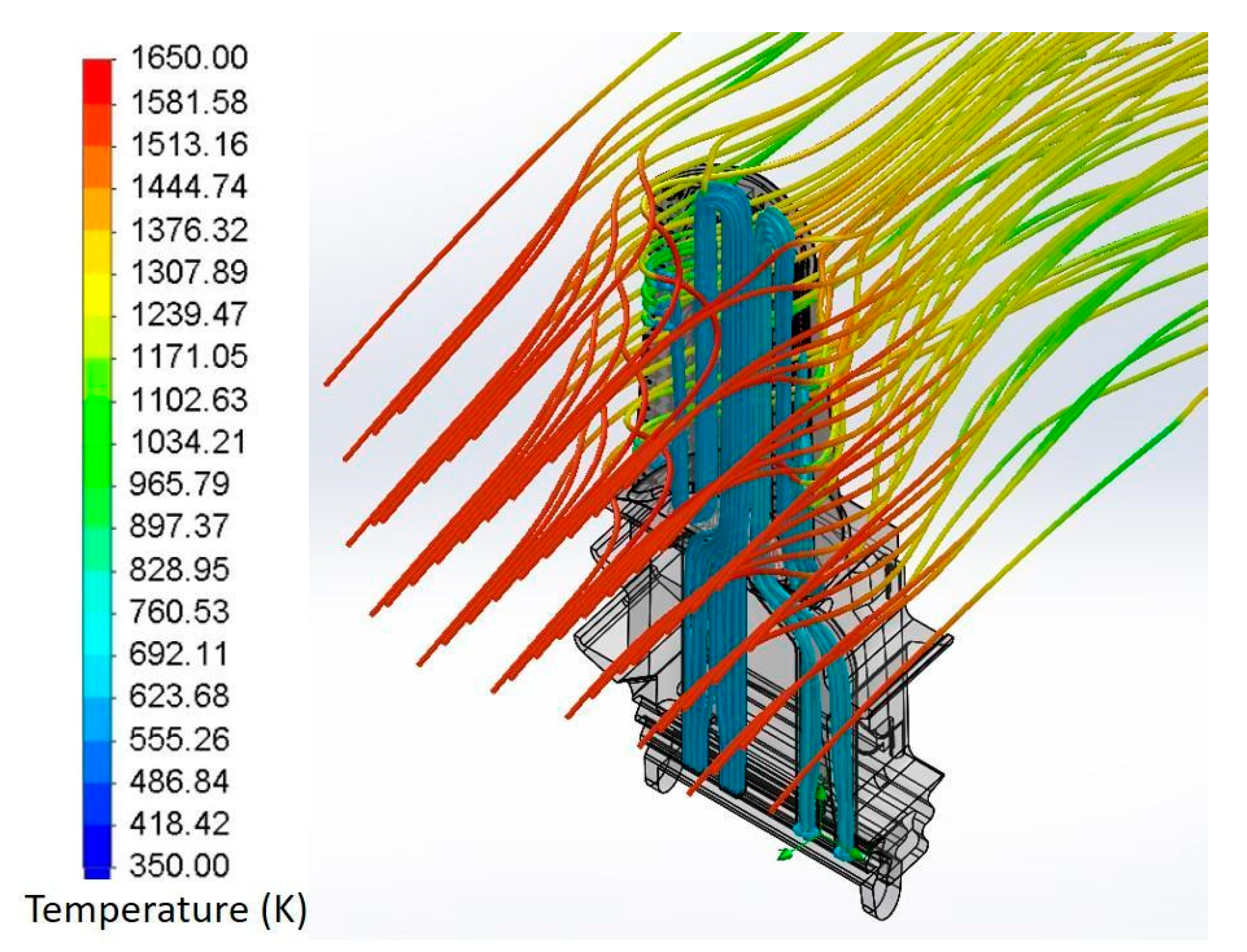
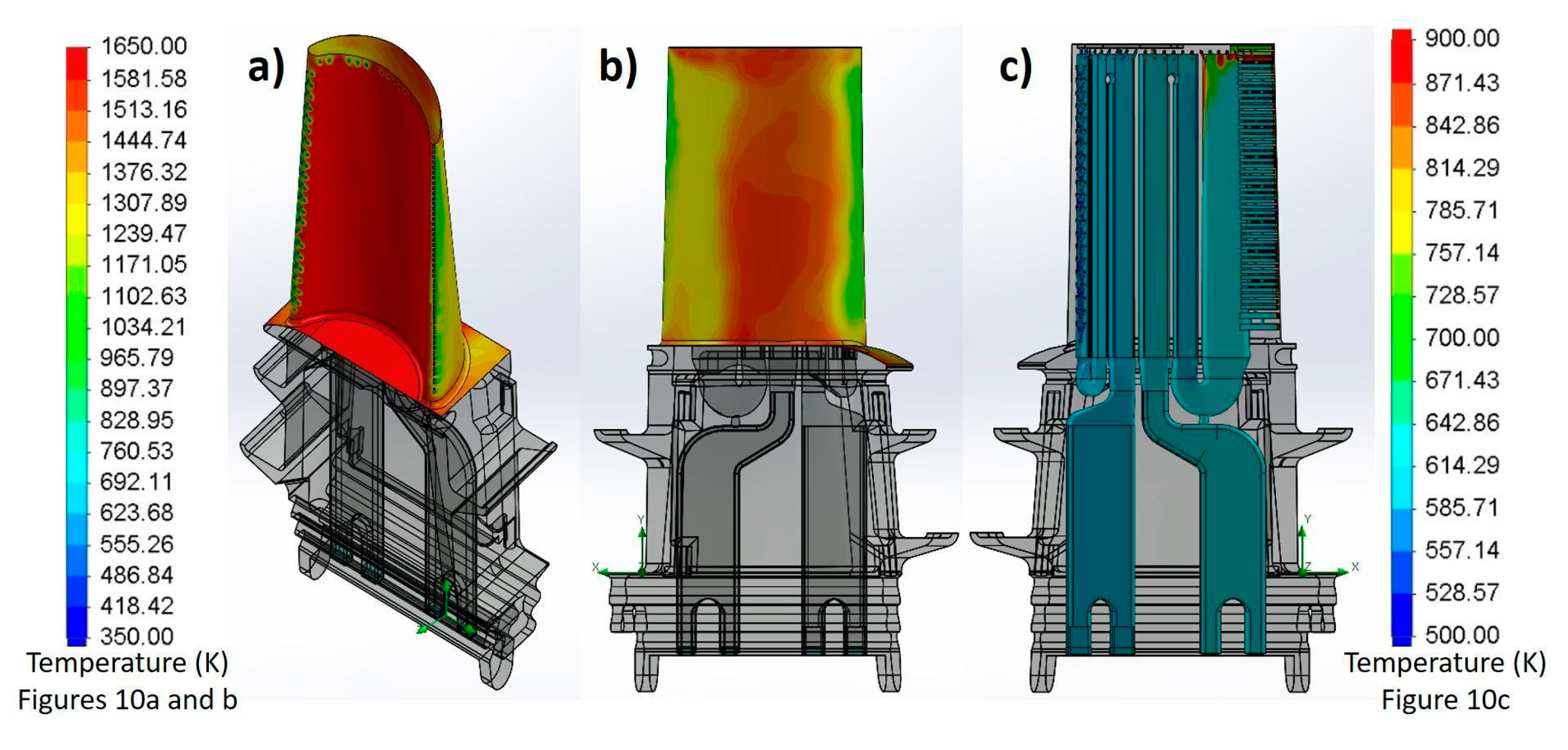
3.2.1. Main Domain Simulation

After the combustion chambers, the hot gases expand and move to the first stage nozzles. These nozzles convert the energy of the hot gases leaving the combustion system in a kinetic form and direct them at the proper angle to rotate the moving blades, producing mechanical rotational energy. Then, the hot gases are expanded again, leading to the second-stage rotating blades by the second-stage nozzles set. The simulations of the path flow of the combustion gases through the turbine allow us to know the gas inlet angle.
Figure 7a,b shows the trajectory of the hot gases from one of the fourteen combustors obtained from the first CFD simulation using the operation parameters (see Table 1). Similar results were found from each combustor. According to this simulation, the nozzle accelerates the fluid while the static pressure decreases and the hot gas velocity increases in the rotation direction. From this simulation, the velocity, pressure, and temperature of the hot gas were obtained.
Another important observation is that the gas flow path impacts the pressure side of the blade at a very high gas inlet angle (i.e., about 80°). This result contrasts with other works where the entry angle had significantly lower values. [23,24,40].

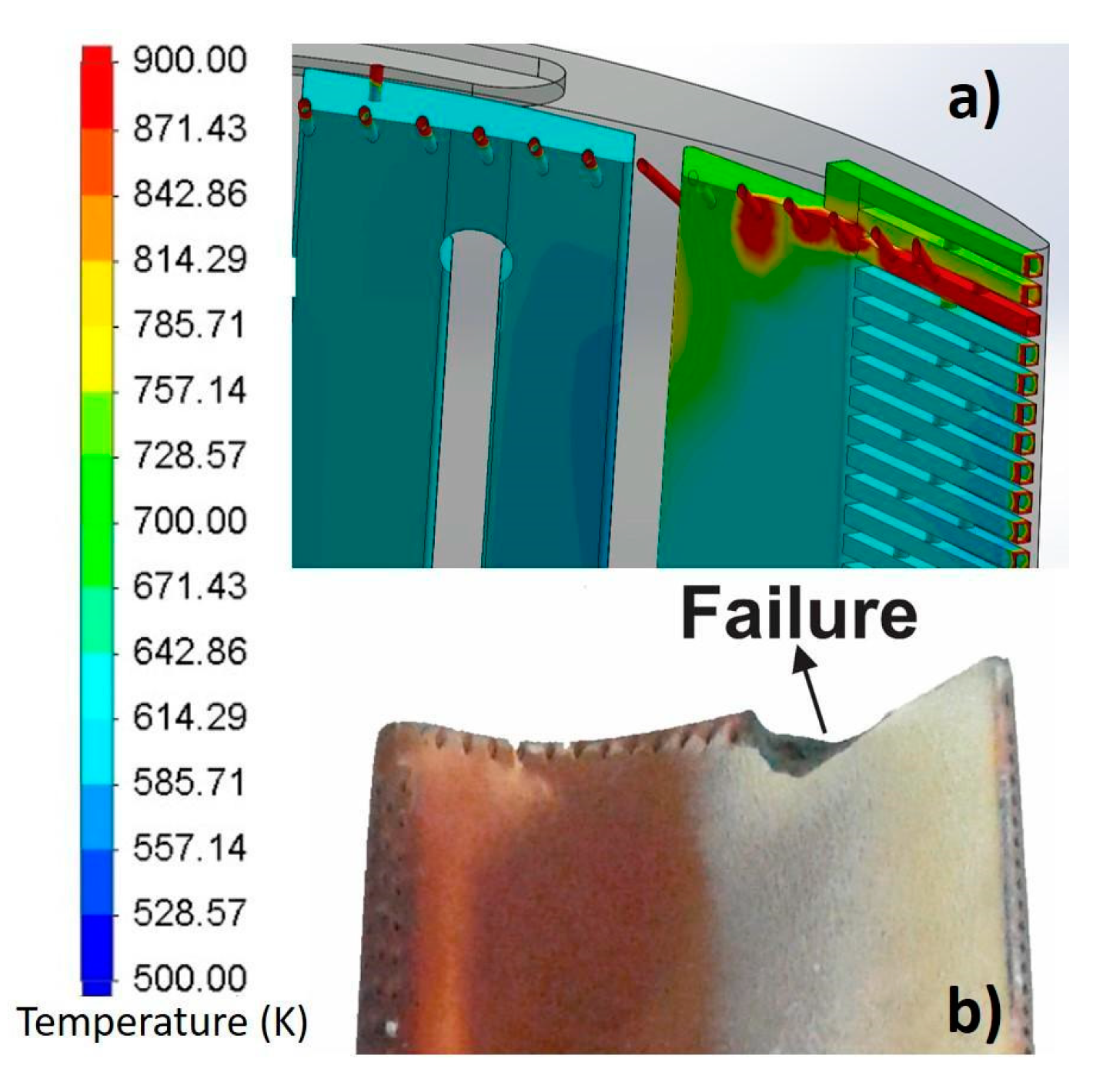
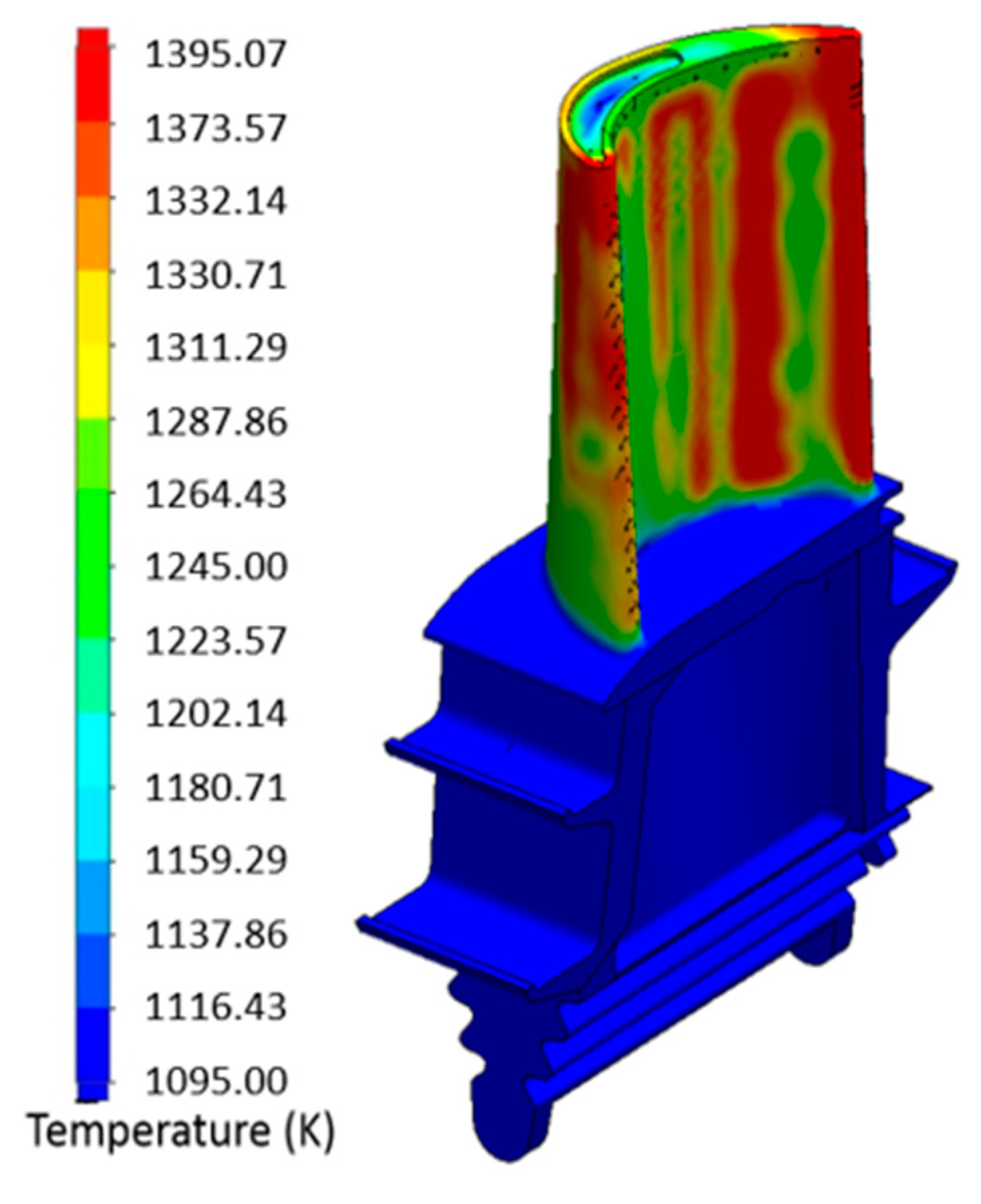
3.2.2. Sub-Domain Simulation

Once the combustion gas path flow was defined, a second computational domain (sub-domain) was generated. The refined computational sub-domain shown in Figure 8 was created following the trajectory of the combustion gases from a single combustor. This computational sub-domain was used to solve the fluid flow and heat transfer for a single blade and allows for improving the accuracy of the calculations without additional computational cost.
A detailed geometry of the FSB was used, including the internal cooling cavities. The turbine operation parameters (Table 1) were also included in this CFD model, as shown in Figure 8.
The pressure value P3 (7 atm) at the inlet of the computational sub-domain was obtained from the main domain simulation. This value agrees with the reported pressure variation chart through a GE turbine [55]. The boundary conditions (P3, F1, T4) used in the sub-domain for the second CFD simulation are shown in the inset of Figure 8. The V1 direction gave the inlet angle (α).
The streamlines of the flow around and inside the blade obtained from the sub-domain CFD simulation are presented in Figure 9. The color of the streamlines in this figure represents the temperature of the fluid. As observed, the temperature close to the blade decreases quickly due to the film cooling formed around the blade. As a result of this simulation, the temperature in the boundary layer between the fluid and the solid is obtained.
In Figure 10, the temperature distribution on the surface of the blade is shown. The maximum temperature appears at the pressure side (Figure 10a) since the hot gases directly impact this blade side.
On the other hand, on the suction side, the temperature is lower due to the film cooling, and the flow acceleration in this area is promoted by the sudden decrease in pressure at this side of the blade (see Figure 10b). It must be noted that the temperature gradient between the pressure and suction surfaces is quite large, close to the leading and trailing edges of the blade. Due to the small thickness of the trailing edge, the cooling airflow is reduced, and the temperature gradient increases. Consequently, the heat transfer from the main flow to the internal structure of the blade increases compared with other zones. Figure 10c shows the temperature distribution at the surface of the cooling cavities. The temperature in most of the internal ducts remains constant due to the high velocity of the airflow. However, overheating at the upper zone of the trailing edge is observed. This behavior confirms the increment in the heat transfer in this zone due to the large temperature gradient and the cooling flow reduction. The location of the overheating is associated with the typical failure observed in this blade.
In Figure 11a, the temperature contour map is shown at the surface of the cooling cavities, close to the overheating zone described previously. As observed, the overheated zone is localized at the ducts on the pressure side of the blade. These ducts are in direct contact with the hot gases coming from the combustors, and the airflow rate coming out from these ducts could be reduced by the hot gas flow due to the high inlet angle. Also, the lateral duct connected by the pressure surface ducts is overheated compared to the other lateral ducts in the trailing edge of the blade.
From this result, it is possible to infer that thermomechanical stresses promote the excessive wear of the blade in this zone (Figure 11b) due to high-temperature gradients generated by the combination of cooling air and hot gases flowing around and throughout the blade. According to the results, two mechanisms could explain the failure in this zone: The first one is the degradation of the top-coat and bond coat during service. The second one is the degradation of the mechanical properties of the GTD-111 superalloy due to overheated zones in the cooling cavities.
Once the temperature distribution on the blade’s surface was computed from the CFD simulations performed in Flow Simulation software, a steady-state heat transfer simulation was carried out to compute the temperature field in the blade’s internal structure. Figure 12 shows the temperature distribution under the top-coat and bond coat of the blade (surface of the GTD-111). It can be observed that the overheated zone at the trailing edge of the blade is around 1400 K. It is essential to highlight that the internal airflow cavities can chill the surface of the blade. However, some zones remain at a temperature high enough to exceed the safe working temperature of the GTD-111, approx. 1200 K.
In order to quantitatively compare the temperature obtained by microstructural analysis with the simulation results, different slices of the internal temperature distribution were selected at the same height as the corresponding samples used for microstructural analysis. Since it is possible to choose any arbitrary point to better match the experimental result, an attempt was made to select the points as close as possible to the corresponding position of the microstructural study. Figure 13 compares the temperatures obtained from microstructural analysis and CFD simulations as a function of the height, including negative and positive errors. According to this figure, the temperature values from simulation and microstructural analysis are in good agreement.
From this comparison, the computational simulation methodology proposed in this work seems a promising alternative to evaluating the temperature distribution into a GT’s hot gas path flow components.

4. Conclusions

This comprehensive investigation, combining computational and experimental approaches, has successfully unveiled the root cause of recurrent failure observed in a GTD-111 first-stage blade from a General Electric 7FA industrial gas turbine following 16,000 h of service.
The microstructural analysis reveals the coarsening and coalescence of the reinforcing phase γ’ near the failure zone. Using the Ostwald-ripening theory, temperatures at five distinct locations along the trailing edge of a failed blade were computed. The findings revealed significantly elevated temperature values in the failure region, surpassing established thresholds for GTD-111 superalloy. These phenomena present evidence as potential contributors to the observed trailing edge tip failures in the blade.
The simulation approach hinged on utilizing a detailed and true-to-life CAD model of the blade. The blade’s geometry was captured employing technologies such as CT scanning and CMM reconstruction, even encompassing the intricacies of cooling cavities. This level of geometric fidelity enabled approximation of the in-service temperature distribution in the first-stage blade, containing both the surface and bulk.
The computational simulations were partitioned into two domains. The first domain (main domain) focused on calculating the trajectory of hot gases emerging from the combustors. The results from this initial CFD model not only defined the computational domain needed for studying an individual blade but also facilitated the estimation of a gas inlet angle of approximately 80°, subsequently applied as a boundary condition in the second CFD model.
In the second domain (sub-domain), we conducted examinations of flow and heat transfer for a single blade. This approach yielded the temperature distribution within the blade’s bulk. By adopting this procedure, we achieved increased result accuracy without incurring additional computational costs.
The temperature distribution observed across the airfoil ranged from approximately 1100 to 1400 K, spanning from the root-airfoil interface to the trailing edge tip. Our results revealed an overheating zone near the trailing edge tip, primarily attributed to the high gas inlet angle at which combustion gases impinge upon the blade. This overheating zone closely aligns with the typical wear observed on these blades, suggesting a connection between elevated temperatures and blade failures.
The computational simulation results were subjected to comparison with microstructural analysis. The outcomes from simulations and the microstructural examination demonstrated quantitative agreement, affirming the reliability of our methodology.
The methodology employed in this investigation holds the potential for extension to various components within the hot gas path of a gas turbine, presenting a framework for future explorations and analyses.

Author Contributions

Conceptualization, J.A.V.-V. and D.G.E.-A.; methodology, J.A.V.-V.; software, S.P.-G. and A.-I.G.-M.; validation, J.A.V.-V., S.P.-G. and D.G.E.-A.; formal analysis, R.G.B.-L.; investigation, R.G.B.-L.; data curation, R.G.B.-L.; writing—original draft preparation, R.G.B.-L.; writing—review and editing, J.A.V.-V., S.P.-G. and D.G.E.-A.; visualization, R.G.B.-L.; supervision, J.A.V.-V.; project administration, J.A.V.-V.; funding acquisition, J.A.V.-V. and D.G.E.-A. All authors have read and agreed to the published version of the manuscript.

Funding

This research and the APC were funded by CONAHCYT, Mexico. Grant number 000000000319522.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The authors wish to acknowledge support to the “Investigadoras e Investigadores por México” program by CONAHCYT by providing research opportunities through projects 730 and 57. The authors also thank Hans van Esch from TEServices Company for providing the blade for this study. J.A. Villada-Villalobos thanks CONAHCYT for the financial support through the Call for Basic Science and/or Frontier Science. Modality: Paradigms and Controversies of Science 2022. R.G. Bayro-Lazcano would also like to personally thank CONAHCYT for the financial support for his Ph.D. studies.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Chen, L.; Shen, J.; Ge, Y.; Wu, Z.; Wang, W.; Zhu, F.; Feng, H. Power and efficiency optimization of open Maisotsenko-Brayton cycle and performance comparison with traditional open regenerated Brayton cycle. Energy Convers. Manag. 2020, 217, 113001. [Google Scholar] [CrossRef]
  2. Oliveira, M.C.; Iten, M.; Cruz, P.L.; Monteiro, H. Review on energy efficiency progresses, technologies and strategies in the ceramic sector focusing on waste heat recovery. Energies 2020, 13, 6096. [Google Scholar] [CrossRef]
  3. Salwan, G.K.; Subbarao, R.; Mondal, S. Comparison and selection of suitable materials applicable for gas turbine blades. Mater. Today Proc. 2021, 46, 8864–8870. [Google Scholar] [CrossRef]
  4. Puspitasari, P.; Andoko, A.; Kurniawan, P. Failure analysis of a gas turbine blade: A review. IOP Conf. Series: Mater. Sci. Eng. 2021, 1034, 012156. [Google Scholar] [CrossRef]
  5. Chowdhury, T.S.; Mohsin, F.T.; Tonni, M.M.; Mita, M.N.H.; Ehsan, M.M. A critical review on gas turbine cooling performance and failure analysis of turbine blades. Int. J. ThermoFluids 2023, 18, 100329. [Google Scholar] [CrossRef]
  6. Pauzi, A.A.; Ghazali, M.J.; Zamri, W.F.H.W.; Rajabi, A. Wear Characteristics of Superalloy and Hardface Coatings in Gas Turbine Applications–A Review. Metals 2020, 10, 1171. [Google Scholar] [CrossRef]
  7. Swain, B.; Mallick, P.; Patel, S.; Roshan, R.; Mohapatra, S.S.; Bhuyan, S.; Priyadarshini, M.; Behera, B.; Samal, S.; Behera, A. Failure analysis and materials development of gas turbine blades. Mater. Today: Proc. 2020, 33, 5143–5146. [Google Scholar] [CrossRef]
  8. Du, W.; Luo, L.; Jiao, Y.; Wang, S.; Li, X.; Sunden, B. Heat transfer in the trailing region of gas turbines—A state-of-the-art review. Appl. Therm. Eng. 2021, 199, 117614. [Google Scholar] [CrossRef]
  9. Taniguchi, T.; Sanbonsugi, K.; Ozaki, Y.; Norimoto, A. Temperature measurement of high speed rotating turbine blades using a pyrometer. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 521–529. [Google Scholar]
  10. Gao, S.; Zhang, X.; Chen, L.; Cui, Y.; Jiang, J.; Zhang, Z.; Yu, P.; Wang, C. Radiation temperature measurement methods for engine turbine blades and environment influence. Infrared Phys. Technol. 2022, 123, 104204. [Google Scholar] [CrossRef]
  11. Ghorbani, H.; Farhangi, H.; Malekan, M. Microstructural investigation and creep behavior of long-term exposed directionally solidified GTD-111 nickel based superalloy. Mater. Sci. Eng. A 2023, 145811. [Google Scholar] [CrossRef]
  12. Ghorbani, H.; Farhangi, H.; Malekan, M. Material characterization of long-term service-exposed GTD-111 nickel based superalloy. Eng. Fail. Anal. 2023, 148, 107061. [Google Scholar] [CrossRef]
  13. Ellison, K.A.; Daleo, J.A.; Hussain, K. A new method of metal temperature estimation for service-run blades and vanes. In Proceedings of the 10th International Symposium on Superalloys 2000, Champion, IL, USA, 17 September 2000; pp. 759–768. [Google Scholar] [CrossRef]
  14. Zhang, P.; Zhou, X.; Wang, X.; Lu, Y.; Cheng, X.; Zhang, W. Study on the microstructural degradation and rejuvenation heat treatment of directionally solidified turbine blades. J. Alloys Compd. 2020, 829, 154474. [Google Scholar] [CrossRef]
  15. Villada, J.A.; Bayro-Lazcano, R.G.; Martinez-Franco, E.; Espinosa-Arbelaez, D.G.; Gonzalez-Hernandez, J.; Alvarado-Orozco, J.M. Relationship Between γ′ Phase Degradation and In-Service GTD-111 First-Stage Blade Local Temperature. J. Mater. Eng. Perform. 2019, 28, 1950–1957. [Google Scholar] [CrossRef]
  16. Voorhees, P.W. The theory of Ostwald ripening. J. Stat. Phys. 1985, 38, 231–252. [Google Scholar] [CrossRef]
  17. Pinto, R.N.; Afzal, A.; D’souza, L.V.; Ansari, Z.; Samee, A.D.M. Computational fluid dynamics in turbomachinery: A review of state of the art. Arch. Comput. Methods Eng. 2016, 24, 467–479. [Google Scholar] [CrossRef]
  18. Wee, S.; Do, J.; Kim, K.; Lee, C.; Seok, C.; Choi, B.-G.; Choi, Y.; Kim, W. Review on mechanical thermal properties of superalloys and thermal barrier coating used in gas turbines. Appl. Sci. 2020, 10, 5476. [Google Scholar] [CrossRef]
  19. Masci, R.; Sciubba, E. A lumped thermodynamic model of gas turbine blade cooling: Prediction of first-stage blades temperature and cooling flow rates. J. Energy Resour. Technol. 2017, 140, 020901. [Google Scholar] [CrossRef]
  20. Zeng, L.; Chen, P.; Li, X.; Ren, J.; Jiang, H. Influence of simplifications of blade in gas turbine on film cooling performance. Appl. Therm. Eng. 2018, 128, 877–886. [Google Scholar] [CrossRef]
  21. He, W.; Deng, Q.; Zhou, W.; Gao, T.; Feng, Z. Film cooling and aerodynamic performances of a turbine nozzle guide vane with trenched cooling holes. Appl. Therm. Eng. 2019, 150, 150–163. [Google Scholar] [CrossRef]
  22. He, K. Investigations of film cooling and heat transfer on a turbine blade squealer tip. Appl. Therm. Eng. 2016, 110, 630–647. [Google Scholar] [CrossRef]
  23. Moritz, N.; Kusterer, K.; Bohn, D.; Sugimoto, T.; Tanaka, R.; Taniguchi, T. Conjugate calculation of a film-cooled blade for improvement of the leading edge cooling configuration. Propuls. Power Res. 2013, 2, 1–9. [Google Scholar] [CrossRef]
  24. Mensch, A.; Thole, K.A. Conjugate heat transfer analysis of the effects of impingement channel height for a turbine blade endwall. Int. J. Heat Mass Transf. 2015, 82, 66–77. [Google Scholar] [CrossRef]
  25. Reyhani, M.R.; Alizadeh, M.; Fathi, A.; Khaledi, H. Turbine blade temperature calculation and life estimation—A sensitivity analysis. Propuls. Power Res. 2013, 2, 148–161. [Google Scholar] [CrossRef]
  26. Mazaheri, K.; Zeinalpour, M.; Bokaei, H.R. Turbine blade cooling passages optimization using reduced conjugate heat transfer methodology. Appl. Therm. Eng. 2016, 103, 1228–1236. [Google Scholar] [CrossRef]
  27. Zhang, G.; Zhu, R.; Xie, G.; Li, S.; Sundén, B. Optimization of cooling structures in gas turbines: A review. Chin. J. Aeronaut. 2022, 35, 18–46. [Google Scholar] [CrossRef]
  28. Kusterer, K.; Bohn, D.; Sugimoto, T.; Tanaka, R. Conjugate calculations for a film-cooled blade under different operating conditions. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; pp. 675–684. [Google Scholar]
  29. Darsono, F.B.; Widodo, R.D.; Rusiyanto; Nurdin, A. Analysis of the Effect of Flow Rate and Speed on Four Blade Tubular Water Bulb-Turbine Efficiency Using Numerical Flow Simulation. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 90, 1–8. [Google Scholar] [CrossRef]
  30. Matsson, J. An Introduction to SOLIDWORKS Flow Simulation 2023; SDC Publications: Mission, KS, USA, 2023. [Google Scholar]
  31. Arteaga-López, E.; Ángeles-Camacho, C.; Bañuelos-Ruedas, F. Advanced methodology for feasibility studies on building-mounted wind turbines installation in urban environment: Applying CFD analysis. Energy 2018, 167, 181–188. [Google Scholar] [CrossRef]
  32. Sun, Z.; Jiang, X.; Qiu, C.; Cheng, S.; Liu, X.; Li, H.; Liu, X.; Wang, Y.; Dong, J.; Lou, L. The investigations of rejuvenation heat treatment on the microstructure and mechanical properties of a serviced gas turbine blade. J. Alloys Compd. 2023, 948, 169759. [Google Scholar] [CrossRef]
  33. Sabri, K.; Gaceb, M.; Si-Chaib, M.O. Analysis of a directionally solidified (DS) GTD-111 turbine blade failure. J. Fail. Anal. Prev. 2020, 20, 1162–1174. [Google Scholar] [CrossRef]
  34. Choi, B.G.; Kim, I.S.; Kim, D.H.; Jo, C.Y. Temperature dependence of MC decomposition behavior in Ni-base superalloy GTD 111. Mater. Sci. Eng. A 2008, 478, 329–335. [Google Scholar] [CrossRef]
  35. Schroeder, A.B.; Dobson, E.T.A.; Rueden, C.T.; Tomancak, P.; Jug, F.; Eliceiri, K.W. The ImageJ ecosystem: Open-source software for image visualization, processing, and analysis. Protein Sci. 2020, 30, 234–249. [Google Scholar] [CrossRef] [PubMed]
  36. Baldan, A. Review Progress in Ostwald ripening theories and their applications to nickel-base superalloys Part I: Ostwald ripening theories. J. Mater. Sci. 2002, 37, 2171–2202. [Google Scholar] [CrossRef]
  37. Ratke, L.; Voorhees, P.W. Growth and Coarsening: Ostwald Ripening in Material Processing; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-07644-2. [Google Scholar]
  38. Lifshitz, I.; Slyozov, V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
  39. Wagner, C. Theorie der alterung von niederschlägen durch umlösen (Ostwald reifung). Phys. Chem. Chem. Phys. 2010, 65, 581–591. [Google Scholar] [CrossRef]
  40. Wan, E.S.; Crimi, P.; Scheibel, J.; Viswanathan, R. Combustion turbine F-class life management of 1st stage turbine blades. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; pp. 683–690. [Google Scholar]
  41. Wan, E.; Hong, C.; Dewey, R.; Bernstein, H.; Norsworthy, D. Life Management System for Advanced F Class Gas Turbine; EPRI Report No. 1008319; EPRI: Palo Alto, CA, USA, 2005. [Google Scholar]
  42. Ginter, T.; Bouvay, T. “Uprate Options for the MS7001 Heavy Duty Gas Turbine,” General Electric Reference Document GER-3808C. 2006. Available online: https://www.ge.com/content/dam/gepower-pgdp/global/en_US/documents/technical/ger/ger-3808c-uprate-options-ms7001-heavy-duty-gas-turbine.pdf (accessed on 5 May 2023).
  43. Material Property Data. Available online: http://www.matweb.com (accessed on 11 September 2022).
  44. Liu, Z.; Qi, H. Numerical simulation of transport phenomena for a double-layer laser powder deposition of single-crystal superalloy. Met. Mater. Trans. A 2014, 45, 1903–1915. [Google Scholar] [CrossRef]
  45. Lam, C.K.G.; Bremhorst, K. A modified form of the k-ε model for predicting wall turbulence. J. Fluids Eng. 1981, 103, 456–460. [Google Scholar] [CrossRef]
  46. Balakin, V.; Churbanov, A.G.; Gavriliouk, V.; Makarov, M.; Pavlov, A. Verification and Validation of EFD.Lab code for predicting heat and fluid flow. In Proceedings of the International Symposium on Advances in Computational Heat Transfer, Norway, 19–24 April 2004; Available online: http://cadflo.ru/fileadmin/user_upload/FOR_PREDICTING_HEAT_AND_FLUID_FLOW.pdf (accessed on 7 August 2023).
  47. Van Driest, E.R. On turbulent flow near a wall. J. Aeronaut. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
  48. Sobachkin, A.; Dummov, G. Numerical Basis of CAD-Embedded CFD. In Proceedings of the NAFEMS World Congress 2013, Salzburg, Austria, 9–12 June 2013; Available online: https://pdfs.semanticscholar.org/56f5/4b31c528c588cfb465d953c2b0f24ea9e297.pdf (accessed on 5 February 2023).
  49. Hasbestan, J.J.; Senocak, I. Binarized-octree generation for Cartesian adaptive mesh refinement around immersed geometries. J. Comput. Phys. 2018, 368, 179–195. [Google Scholar] [CrossRef]
  50. Anderson, M.J.; Liao, L.; Basoalto, H.C. An assessment of statistical models of competitive growth during transient Ostwald ripening in turbine disc nickel-based superalloys. Model. Simul. Mater. Sci. Eng. 2022, 30, 075005. [Google Scholar] [CrossRef]
  51. Oriani, R.A. Ostwald ripening of precipitates in solid matrices. Acta Metallurgica 1964, 12, 1399–1409. [Google Scholar] [CrossRef]
  52. WolframAlpha. Available online: https://www.wolframalpha.com/calculators/equation-solver-calculator (accessed on 3 May 2023).
  53. Geranmayeh, A.; Malekan, M.; Forghani, F.; Ghorbani, H. Microstructural and mechanical investigations on the heat treatment rejuvenation of a long-term service-exposed GTD-111 Ni-based superalloy. Mater. Sci. Eng. A 2023, 862, 144381. [Google Scholar] [CrossRef]
  54. Taheri, M.; Jam, J.E.; Beni, M.H.; Khorram, A.; Kashani-Bozorg, S.F.; Torkamany, M.J. The effect of service temperature on the impact strength and fracture toughness of GTD-111 superalloy. Eng. Fail. Anal. 2021, 127, 105507. [Google Scholar] [CrossRef]
  55. Mattingly, J.D. Elements of Gas Turbine Propulsion; McGraw-Hill Science, Engineering & Mathematics: New Delhi, India, 1996; Volume 1. [Google Scholar]
Metals 13 01968 g001
Figure 1. First stage blade from a 7FA General Electric GT. S1–S5 are the samples extracted for microstructural analysis.
Figure 1. First stage blade from a 7FA General Electric GT. S1–S5 are the samples extracted for microstructural analysis.
Metals 13 01968 g001
Metals 13 01968 g002
Figure 2. (a) Main domain that includes first and second-stage nozzles and first-stage blades, (b) sub-domain constituted by one blade including its cooling cavities and thermal barrier coating.
Figure 2. (a) Main domain that includes first and second-stage nozzles and first-stage blades, (b) sub-domain constituted by one blade including its cooling cavities and thermal barrier coating.
Metals 13 01968 g002
Metals 13 01968 g003
Figure 3. 3D CAD model of blade’s internal geometry employed to solve the CFD and FEM calculation. (a) Transparency view of the blade, including the cooling cavities. (b) Exploded view of the blade’s TBC system.
Figure 3. 3D CAD model of blade’s internal geometry employed to solve the CFD and FEM calculation. (a) Transparency view of the blade, including the cooling cavities. (b) Exploded view of the blade’s TBC system.
Metals 13 01968 g003
Metals 13 01968 g004
Figure 4. Tetrahedral mesh generated for the heat transfer analysis.
Figure 4. Tetrahedral mesh generated for the heat transfer analysis.
Metals 13 01968 g004
Metals 13 01968 g005
Figure 5. SEM image of the γ’ phase into the γ matrix for the reference sample.
Figure 5. SEM image of the γ’ phase into the γ matrix for the reference sample.
Metals 13 01968 g005
Metals 13 01968 g006
Figure 6. SEM images of the γ’ phase from different locations along the trailing edge of the blade.
Figure 6. SEM images of the γ’ phase from different locations along the trailing edge of the blade.
Metals 13 01968 g006
Metals 13 01968 g007
Figure 7. (a) Streamlines along the path followed by the hot gases through the first stage of the 7FA General Electric gas turbine. (b) Top view of the flow streamlines.
Figure 7. (a) Streamlines along the path followed by the hot gases through the first stage of the 7FA General Electric gas turbine. (b) Top view of the flow streamlines.
Metals 13 01968 g007
Metals 13 01968 g008
Figure 8. Selection of the sub-domain for the CFD simulation around one blade. Values of the boundary parameters indicated in this figure are listed in Table 2. Pressure P3 was obtained from the main domain simulation.
Figure 8. Selection of the sub-domain for the CFD simulation around one blade. Values of the boundary parameters indicated in this figure are listed in Table 2. Pressure P3 was obtained from the main domain simulation.
Metals 13 01968 g008
Metals 13 01968 g009
Figure 9. Streamlines and temperature of the flow around and inside the blade obtained from the sub-domain CFD simulation.
Figure 9. Streamlines and temperature of the flow around and inside the blade obtained from the sub-domain CFD simulation.
Metals 13 01968 g009
Metals 13 01968 g010
Figure 10. Temperature distribution on the pressure side (a), suction side (b), and cooling cavity surfaces (c) of the blade.
Figure 10. Temperature distribution on the pressure side (a), suction side (b), and cooling cavity surfaces (c) of the blade.
Metals 13 01968 g010
Metals 13 01968 g011
Figure 11. (a) Temperature distribution at the surface of the cooling cavities of the blade near the trailing edge tip, (b) failure at the same zone of the blade.
Figure 11. (a) Temperature distribution at the surface of the cooling cavities of the blade near the trailing edge tip, (b) failure at the same zone of the blade.
Metals 13 01968 g011
Metals 13 01968 g012
Figure 12. Temperature distribution at the superalloy surface of the blade (under the top and bond coats).
Figure 12. Temperature distribution at the superalloy surface of the blade (under the top and bond coats).
Metals 13 01968 g012
Metals 13 01968 g013
Figure 13. Comparison of the estimated and simulated in-service temperature along the trailing edge as a function of the height of the blade.
Figure 13. Comparison of the estimated and simulated in-service temperature along the trailing edge as a function of the height of the blade.
Metals 13 01968 g013
Table 1. Description of the samples extracted from the blade.
Table 1. Description of the samples extracted from the blade.
Sample IDHeightDescription
Reference10From the dovetail tip
S1180From the airfoil-root interface
S2220From ¼ of the airfoil height
S3250From ½ of the airfoil height
S4290From ¾ of the airfoil height
A5330From the trailing edge tip
Table 2. Turbine operating parameters.
Table 2. Turbine operating parameters.
LabelParameterValue
P1Pressure ratio14.8
P2Pressure at the end of the 2nd nozzles stage5 atm.
T1Firing Temp.1600 K
T2Gas temp. at the end of the 2nd nozzles stage1000 K
T3Exhaust gas temp.874 K
T4Cooling Air Temp.569 K
F1Airflow432 Kg/s
S1Gas Turbine Speed (rpm)3600 RPM
Table 3. Materials and properties used in the simulation.
Table 3. Materials and properties used in the simulation.
ParameterGTD-111NiCoCrAlYYSZGTD-222FSX-4142 1/2-CrMo
First-Stage BladeBond-CoatTop-CoatSecond-Stage NozzlesFirst-Stage NozzlesShell
Density
(kg/m3)		817084206100790083007850
Thermal Conductivity
(W/(m·K))		Temp.
function [44].
(11 + 0.0125 T)		182.52001644.5
Specific Heat Capacity (J/(kg·K))Temp.
function [44].
(370 + 0.250 T)		430550149500475
Melting Point
(K)		152315932698140216731690
Table 4. γ’ phase size and K values obtained from the microstructural analysis at different blade heights. Values in parentheses correspond to the standard deviation calculated.
Table 4. γ’ phase size and K values obtained from the microstructural analysis at different blade heights. Values in parentheses correspond to the standard deviation calculated.
SampleHeight
(mm)		d
(µm)		K
(µm3/h × 10−5)		T
(K)
S11801.49 (0.11)19.569 (1.815)1288.69
S22201.54 (0.11)21.491 (2.020)1293.98
S32501.89 (0.16)40.903 (6.225)1331.61
S42902.01 (0.14)49.758 (7.484)1343.51
S53302.21 (0.24)66.416 (19.722)1361.46
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bayro-Lazcano, R.G.; Piedra-Gonzalez, S.; García-Moreno, A.-I.; Espinosa-Arbelaez, D.G.; Villada-Villalobos, J.A. Computational and Experimental Study on Failure Mechanism of a GTD-111 First-Stage Blade of an Industrial Gas Turbine. Metals 2023, 13, 1968. https://doi.org/10.3390/met13121968

AMA Style

Bayro-Lazcano RG, Piedra-Gonzalez S, García-Moreno A-I, Espinosa-Arbelaez DG, Villada-Villalobos JA. Computational and Experimental Study on Failure Mechanism of a GTD-111 First-Stage Blade of an Industrial Gas Turbine. Metals. 2023; 13(12):1968. https://doi.org/10.3390/met13121968

Chicago/Turabian Style

Bayro-Lazcano, Roberto Guillermo, Saúl Piedra-Gonzalez, Angel-Iván García-Moreno, Diego German Espinosa-Arbelaez, and Jhon Alexander Villada-Villalobos. 2023. "Computational and Experimental Study on Failure Mechanism of a GTD-111 First-Stage Blade of an Industrial Gas Turbine" Metals 13, no. 12: 1968. https://doi.org/10.3390/met13121968

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop