Abstract
The study of grain and defect structure evolution in materials subjected to thermomechanical processing is still an urgent problem because the state of a structure substantially determines the physical and mechanical macro properties of polycrystals and polycrystalline products. Significant changes in the structure of polycrystalline materials are associated with the process of dynamic recrystallization (DRX). To investigate DRX, an extended statistical model of inelastic deformation with internal variables is proposed, which takes into consideration contact interactions between neighboring grains. We constructed a geometric image of the grain structure by applying a Laguerre polyhedron in order to describe such interactions in the statistical framework. During the recrystallization simulation, this image is being reconstructed as new recrystallized grains emerge. This leads to the problem of establishing correspondence between an initial grain structure and a reconstructed structure with the required statistical consistency. To provide such consistency, an optimization problem is formulated to preserve the stress and strain parameters and the recrystallization driving force from changes in a statistical sense. This problem is posed with respect to the distributions of differences in defect-stored energy, mutual misorientation angles between grains and sizes of these grains. A genetic algorithm is applied for resolution. By the example of simulating inelastic deformation of a representative volume element (a macrosample analogue) of polycrystalline copper, the influence of the mentioned distributions on the material response upon structure reconstruction is shown. Reasonable values for the objective weights and the genetic algorithm parameters were obtained. This paper presents a detailed description of the grain structure correspondence establishment method, the formulation of the optimization problem and the algorithm to resolve it.
1. Introduction
Thermomechanical processing of metals and alloys significantly changes the properties of materials. For instance, the application of severe plastic deformation provides an opportunity for refining the grain structure and producing polycrystals with a characteristic grain size at the scale of hundreds or tens of nanometers (nanostructural materials). The properties of such materials are of particular interest because they have high plasticity, strength, and hardness [1,2,3]. The dependence of the physical and mechanical properties of polycrystals on the meso- and microstructure was confirmed by experimental data [1,4,5]. During inelastic deformation at elevated temperatures, the grain structure refinement and subsequent formation of equiaxed grains are realized mainly due to dynamic recrystallization (DRX) [5,6,7,8]. The small sizes of equiaxed grains contribute to the transition to structural superplasticity and activate the grain boundary slip mechanism in a material subject to certain thermo-mechanical treatments [9,10]. Such a regime is of great practical importance to the development of molding technology for critical large-sized products made of metals and alloys. To perform such a process, it is often necessary to homogenize a mixed (i.e., not totally recrystallized) grain structure. Microstructure control is realized as a result of thermo-mechanical treatments, usually by virtue of DRX [11,12,13] Homogeneity in grain structure contributes to a decrease in deformation inconsistency between coarse non-recrystallized grains and fine recrystallized grains, and thus leading to improvements in operational characteristics of the polycrystal, including its strength properties [11]. Additional influence on inelastic behavior and DRX is caused by impurity atoms and particles of secondary phases [5,8,14].
Thus, the theoretical and experimental study of the structure evolution in polycrystalline materials subjected to thermomechanical processing continues to be an issue of great current interest [1,5,6,7,10,15,16,17,18]. In [6], a contemporaneous theoretical basis of the DRX phenomenon is presented. Issues regarding the description for physical mechanisms of nucleation and evolution of recrystallized grains, the effect of material parameters and influences on such processes are stated. A more up-to-date review on the mentioned DRX aspects and the concomitant phenomena of structural-scale reconstructions in materials during thermo-mechanical processing is given in [5,7]. In [15,17,18], the concept of a polycrystalline material as a multilevel system is proposed. Primary emphasis is placed on importance of theoretical research on crystalline solids from the viewpoint of analyzing deformation and fracture mechanisms at different scales. A methodology of constructing and implementing multilevel models with internal variables for simulating deformation of mono- and polycrystalline metals and alloys is presented in [16]. It is shown that the development of the interdisciplinary approach together with an appropriate mathematical framework at the intersection of solid mechanics and physics is relevant for investigating thermo-mechanical processes of deforming metals.
The experimental methods of studying severe plastic deformation, nano-structures being formed under such deformations and properties of nano-structured materials are described in [19]. Experimental research methods are labor- and resource-intensive; therefore, theoretical methods are at the forefront of the latest achievements in mechanics of materials. The study tool that includes elaboration and application of physically based mathematical models in terms of a multilevel approach with internal variables was established as the most suitable for solving the problem under consideration [16,20,21,22]. The internal variables of the model are the carriers of information about the continuously evolving meso- and microstructure of materials during thermomechanical processing. The involvement of various structural-scale levels in the consideration provides a reliable description of the physical mechanisms of inelastic deformation and processes accompanying this deformation. Multilevel models permit studying the technological processes of thermomechanical treatment of metals and producing constructions and products with the required operational properties [23,24,25,26,27,28,29,30]. Fundamental problems of solid mechanics related to developing science-intensive technologies are stated in [29]. As indicated, there are demands for analyzing in detail material structures and creating treatment operations for controlling mechanical properties. General principles, approaches and ideas of material design with structure evolution taken into consideration can be found in [27]. In [23], mechanical design of samples with desired characteristics is modeled in the example of a beam subjected to bending. The so-called microstructure-sensitive design (MSD) is used as a framework. This approach is implemented using a multilevel constitutive model, which makes it possible to realize the sequence “processing—microstructure—properties—design”. In [24,25], the MSD of a thin orthotropic plate with a circular hole subjected to a tensile load (in the plane of the plate) is considered. A description of a finite element method-based software product for solving such a problem is provided. A macroscopic stress averaging principle for estimating sensitivities of a deformation process with perturbed parameters within the MSD framework is developed in [26]. In [28], a simulation of an asymmetric rolling process is performed and applied to manufacturing aluminum alloy sheets with a control for the microcrystalline structure in order to improve their formability and strength. In [30], the multilevel modeling framework is used to analyze the process of drawing a cylindrical polycrystalline copper sample from the viewpoint of changes in its properties, and particularly the crystallographic texture.
Thermomechanical processing of polycrystalline materials gives rise to a number of thermally activated processes responsible for changes in the defect, subgrain and grain structure of materials [5,7,8]. From the point of view of the evolution of material macroproperties, recrystallization was recognized to be the most significant process [5,7,8]. Recrystallization is a complex multi-scale and multi-stage process to change the material structure with the formation of new, less defective grains [6]. A special role in this process belongs to the high-angle grain boundaries that migrate deep into more defective grains. The main driving force of primary recrystallization is a difference in the internal energy stored on the defects formed in the adjacent grains and subgrains during inelastic deformation [6,31]. Depending on the stacking-fault energy, recrystallization is realized continuously (CDRX), discontinuously (DDRX) or in a combined way. Specifically in the last case, DDRX appears to be a leading process while CDRX plays an accommodating role [13]. Recrystallization is widely used in practice to produce materials with the desired plastic and strength properties through the creation of structures with required grain sizes and grain boundaries [5,7,13]. Some other processes which change material structures (for example, phase transitions in alloys [5,32]) are also of interest for consideration but are beyond the scope of this study.
There are two types of physical models that are based on a multilevel approach: direct and statistical [16,33,34]. In the direct models, the boundary value problem is solved to determine the field variables (stresses, strains, and internal variables) of each crystallite (grain, subgrain, and fragment) within a representative volume of the macroelement being considered. In the statistical models, a representative volume microelement of a material (“macropoint”—a macrosample analogue) is considered as a set of individual grains combined into a polycrystalline aggregate under the hypothesis of Voigt, Reiss, Kroener, etc. The solutions obtained with direct models are more accurate than those determined with statistical models. Although the direct models have some undoubted advantages, they still remain the most resource-intensive models.
In recent decades, much attention was given to the modeling of recrystallization. A wide variety of approaches and methods for describing recrystallization were developed. Detailed information about the process of recrystallization and accompanying phenomena can be found in reviews [6,8]. Examples of physically-reasonable models applicable for investigating recrystallization can also be found, e.g., [35,36,37,38]. The main theoretical difficulty encountered in describing recrystallization is the necessity to consider the formation of new, less defective grains. The simplest models providing an empirical or semi-empirical description of the recrystallized material fraction are the phenomenological models based on the Johnson–Mehl–Avrami–Kolmogorov (JMAK) kinetic relations [1,1]. The extension of the JMAK–approach are the models where such structural elements such as the size and shape of grains and the position of their boundaries are evaluated in advance [39,40]. The JMAK equations are often insufficient for studying the grain structure evolution, since they do not consider the heterogeneous nature of the formation and growth of recrystallization nuclei. Therefore, they are applicable only in a narrow range of variations of the initial structure, temperature, strain, and strain rate [37,41]. Thus, in view of and with the rapid development of computer technology, physical approaches that include an explicit consideration of the formation and development of the grain structure of a material have found wide application [5,16]. In the framework of this class of models, internal variables characterizing the meso- and microstructure of a material are introduced, and the evolution equations describing the formation of recrystallization nuclei and the migration of grain boundaries are formulated. When the process of recrystallization is described in terms of such models, the grain structure evolution is simulated by the following: (1) Monte-Carlo method [42], (2) cellular automaton method [43], (3) phase-field method [14,44], (4) level set method [45], (5) graph-theory methods [46], etc.
In this paper, we study the process of discontinuous dynamic recrystallization in the framework of the original statistical model describing inelastic deformation, which was modified considering the state and interaction of adjacent grains along their conjugate boundaries [38,47]. This makes it possible to correctly introduce into consideration the main driving force of primary recrystallization, viz., the difference in stored energy between neighboring grains. In order to simulate this interaction, a polyhedral grain structure, close to a real structure, was generated by using the Neper software package [48]. The parameters of the structure were transferred to the calculation modulus of the statistical model [49] to evaluate the structure evolution, including the formation of new recrystallized grains whereupon a need arose for multiple rearrangements of the grain structure. Thus, the present work addresses the problem of establishing a correspondence between the original and reconstructed grain structures to ensure the statistical consistency of these structures. Some restrictions are imposed so the parameters of the stress-strain state and the driving force of dynamic recrystallization remain unchanged during these rearrangements.
2. Establishment of the Correspondence of the Grain Structure Rearranged during the Process of Recrystallization
The statistical model of inelastic deformation which considers dynamic recrystallization was developed in [38]. A summary of the features of this model are presented below. There are the three structural-scale levels distinguished: macrolevel, mesolevel-I and mesolevel-II. At the macrolevel, a polycrystal with a statistically representative number of grains (i.e., a representative volume macroelement, a macrosample analogue) is considered. At mesolevel-I, a single grain consisting of mesolevel-II elements (homogeneous subgrains) is investigated. At each moment of the process, all variables and parameters characterizing the stress-strain state and the temperature of each element of the considered level are supposedly homogeneous. The grains are separated by high-angle boundaries whose misorientation is greater than 10–15 degrees [5,6]; the subgrain misorientation is several degrees and generally increases with increasing inelastic deformation [5,50,51].
Influences are transferred from the macrolevel to the underlying scale levels. For each instance of time , the kinematic and thermal effects are prescribed, i.e., the velocity gradient and the temperature are assumed to be known at the macrolevel. Thus, for every grain, the following equality (1) is true:
where is the Hamilton operator in the current Lagrangian coordinate system; is the velocity gradient of grain’s material particle; is the grain temperature; and and are the velocity vectors obtained at the macrolevel and mesolevel-I. The indexes denoting the grain (subgrain) number are omitted hereinafter, unless otherwise specified. At mesolevel-I, the problem of determining the stress-strain state of a grain and corresponding internal variables of the model is solved. The reader interested in the closed mathematical formulation of a the mesolevel-I model is referred to [38] for more details. At the macrolevel, the tensors of stresses , elastic properties and an inelastic part of the velocity gradient are evaluated by averaging over the representative volume microelement using the following Equation (2):
where is the macrovolume averaging operator, and , and are the tensors of stresses, elastic properties, and an inelastic component of the velocity gradient of a single grain (mesolevel-I element), respectively.
Mesolevel-II is an auxiliary level, which is introduced with the purpose of providing an accurate description of the recrystallization mechanism. The subgrains located at the high-angle boundary act as recrystallization nuclei and may grow into an adjacent grain [52]. According to the Bailey-Hirsch criterion (3), a decrease in the local volume energy of a crystallite at the expense of elimination of defects must be greater or equal to an increase in the grain boundary energy provoked by an increased boundary area observed during the formation of a recrystallized grain (subgrain) [52]:
where is the increase in the boundary area when a subgrain volume (recrystallization nucleus) changes by , is the difference between the specific (per unit volume) energies stored in the adjacent i-th and j-th subgrains, and is the specific (per area unit) energy stored on the boundary between the i-th and j-th subgrains.
In order to apply criterion (3) and calculate the values of , we introduce an additional mesolevel-II variable (a characteristic subgrain size) . It is assumed that the original shape of subgrains is spherical, the subgrain sizes are distributed with respect to the Rayleigh law [53], and their sizes and shapes remain unchanged at the initial stage of deformation. Recrystallization nuclei (subgrains) occur near the boundary, which is represented by a set of facets. A certain sample of subgrain (recrystallization nucleus) with size , and distributed according to the Rayleigh law is assigned to all facets of the considered grain. The validity of the recrystallization criterion (3) is verified for each subgrain separated by the high-angle boundary from the neighboring ones; upon the fulfillment of this criterion, every subgrain is treated as a new individual grain.
The subgrains of a single grain are separated by low-angle boundaries, and they are slightly misoriented relative to each other. Therefore, it is reasonable to believe that the stored energy, , is approximately the same in all subgrains within one grain (Equation (4)):
where is the stored energy of a separate grain determined at the mesolevel-I and calculated using the relation (5) given in [38]:
where are the total critical stresses in the considered grain at the current and initial instants of deformation, is the dimensionless (experimentally determined) correction factor which characterizes the energy part stored on dislocations, and is the shear modulus. The difference in stored energy between the subgrains , belonging to different grains but having a common high-angle boundary, may be significant. This difference leads to the migration of a section of the high-angle boundary towards a more defective grain and the appearance of a new recrystallized grain. During dynamic recrystallization, a continuous changes take place in both the shape and size of grains, and the number of these grains varies as well. In the advanced statistical model, the grain structure is determined by such internal variables as the grain volume , flat facets with normal and the area (where j indicates the number of a facet) and through assigning neighboring grains to the considered grain [38]. These data are obtained using the polyhedral structure constructed in the Neper software package [48]. In order to implement the polyhedra generation procedure in Neper, we apply the statistical distribution laws for the sphericity parameters (the ratio of the surface area of the sphere, whose volume is equal to the volume of a considered grain, to the grain surface area) and for the normalized grain size (, where is the grain size defined as the radius of a sphere of equivalent volume, and is the average grain size). The way of mapping the polyhedral structure data onto the statistical model is described in [49].
Introduction of the geometric characteristics of new recrystallized grains proceeds in two stages (Figure 1). A simplified mathematical description of the first stage is used. The subgrains in the vicinity of the intergrain boundary are the potential nuclei. When the recrystallization criterion (3) is fulfilled for these subgrains, they are considered to be independent grains and are added to a sample of the mesolevel-I statistical model. The volume fraction of the recrystallization nucleus is subtracted from the parent grain volume. It is assumed that these grains are spherical in shape and are immersed in the consumed grain (Figure 1). The new recrystallized grains are low-defective: therefore, all internal variables of a recrystallized grain are supposed to be compatible with the parameters in the reference configuration corresponding the annealed material with the exception of the grain topology redefined at the second stage and the orientation of the crystallographic coordinate system (CCS) relative to the laboratory coordinate system (LCS) determined by the tensor . We suppose that the grains which were recrystallized according to the Bailey-Hirsch criterion have the misorientation coherency with the parent grain [5,54]. The new grain is separated from the parent by the high-angle boundary and has the initial misorientation with respect to the parent grain within the range from 10° to 15° with a random axis of rotation [5,54]. The DRX grain orientation with respect to the neighboring (absorbed) grain is arbitrary. The index «+» in Figure 1 denotes the corresponding internal variables which describe the appearance of newly recrystallized grains.
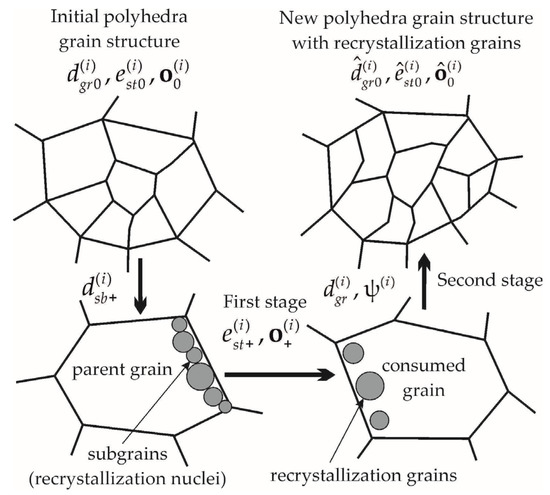
Figure 1.
The scheme of the grain structure rearrangement in the statistical model with new recrystallized grains introduced into consideration.
In the statistical model, the grain structure evolution is described via analyzing the two components’ deformation and migration of the recrystallized grain boundaries. The way to describe the grain structure evolution is presented in [38]. In the calculations with the statistical model, the grain size and sphericity distributions are determined the by chosen periods of time. These values are transferred to Neper to generate the rearranged polyhedral structure. When the qualitative fraction of recrystallized grains, , reaches a certain critical value, the second stage of the polyhedral structure rearrangement that involves the study of new grains is performed (Figure 1). To this end, Neper [48] was applied, where the polyhedral grain structure is generated taking into account the new grains and the distributions of and . With Neper, the optimization problem is solved until the maximally possible polyhedral grain structure correspondence determined (at the given instant of time) by the statistic distributions of and using the Praxis method is gained [55]. Next, to continue the calculation in the calculation module of the statistical model, it is necessary to determine a new grain structure, i.e., to establish the mutual relationship of grains and to set the values of , , and [49].
In view of the foregoing, the problem of primary concern is to establish (in the framework of the advanced statistical model) a correspondence between the grain structure observed at the first stage and that obtained after its rearrangement in Neper with the newly recrystallized grains at the second stage (Figure 1). Previously, the method of establishing this correspondence was proposed in [38]. In the method, the best fit of grain sizes was taken as the initial approximation, and a purposeful selection of the grains of the two structures was carried out by the optimization method. The search procedure was undertaken until a minimum in the average value of difference in stored energy between the neighboring grains of the original and new structures was reached. In solving this optimization problem, an attempt was made to carry out the statistical correspondence of the grain structure by providing the driving force of recrystallization is maintained. The conditions for ensuring correspondence with respect to the stress state (response) of a representative volume element of the material were dropped from consideration. In this work, we further investigate the issue regarding the grain structure correspondence, the definition of a mathematical criterion and the formulation of an optimization problem to ensure a smooth run of the considered physical process of inelastic deformation with a due account of recrystallization. The basic ideas of the proposed method for establishing a correspondence between grain structures are described below. A more detailed mathematical formulation of the problem is given in the next section.
A schematic illustration of the method of establishing the grain structure correspondence is shown in Figure 2. Each grain is characterized by the internal variables of the model. Most of these variables are “inherited” during the construction of a new grain structure pattern by means of the statistical model. Among the “inherited” variables, the most significant are the orientations of the CCS grains relative to the LCS , and the energy stored on defects [38]. The state of the grains determined by the internal variables can be assigned to different polyhedra of the new grain structure (Figure 2). In this case, both the geometric parameters of the considered grain (, , and ) and the grains adjacent to this grain may change. Consequently, changes may occur in some internal variables of the model that determine the inelastic behavior of the material, viz., the difference in the stored energy , and the mutual orientation of neighboring grains (i, j are the numbers of the current and adjacent crystallites).
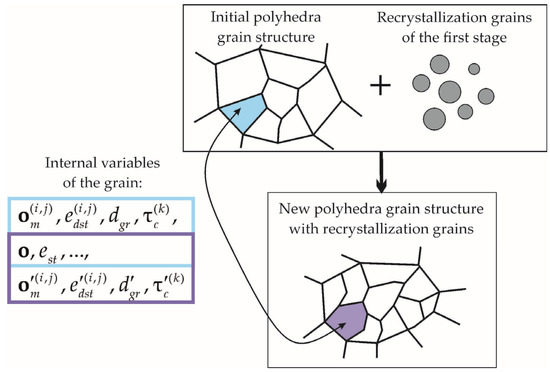
Figure 2.
The scheme of the method to establish correspondence between the initial grain structure and the rearranged structure, due to emergence of recrystallized grains.
We list the most important variables which determine inelastic deformation during dynamic recrystallization. The basic mechanism of inelastic deformation is the slip of edge dislocations, whose activity is defined by two main variables: (1) orientation of the CCS of the grain relative to the LCS (characteristic processing directions of the material) specified by the tensor ; and (2) slip system hardening. In the developed model, the strengthening of the material is assumed to be dependent on the drag of dislocations by random dislocation barriers (they are inherited together with the internal variables of the model and are assigned to the grain) and grain boundaries (this interaction depends on the grain size ). The main quantity which controls primary recrystallization is the difference in stored energy between neighboring grains, [5,8,52]. In the models of the statistical type, the difference in stored energy depends on the mutual disorientation of the CCS of neighboring grains [47]. The tensor of disorientation of the neighboring grains i and j is determined by the known tensors and , which combine the CCS orientation of the i-th and j-th grains with LCS (Equation (6)):
Using the known tensor , the mutual orientation angle between the adjacent i-th and j-the grains is obtained at each instant of deformation [56] by the following Equation (7):
where the value of the angle , determined according to (7), is used as a measure of mutual orientation of neighboring grains.
In order to ensure the statistical consistency of the material response, including dynamic recrystallization, during the establishment of grain structure correspondence, it is necessary to minimize the discrepancies in the distributions (via analyzing the histograms) of the following model variables: (1) the differences in stored energy , (2) angles of mutual misorientation of grains and (3) grain sizes . It should be noted that the material texture (provided that the grain volumes are not considered) remains fixed when the neighboring grains are changed. All the quantities mentioned above are deterministic—they are determined in the framework of a statistical model and represent a sample of relevant variables obtained step-by-step in the calculations with the multilevel model [38]. Since the present study addresses the problem of establishing a grain structure correspondence in a statistical sense, which is needed for a smooth run of the inelastic deformation process during recrystallization, the optimization problem is formulated by applying the distributions of considered variables and their statistical moments (e.g., mathematical expectation, dispersion, etc.).
For the representative volume element of a polycrystal, a sample of the variables , and is obtained. An example of this sample for the angles (the indexes of neighboring grains are omitted), which was found in our calculations, is shown in Figure 3. Next, the area below the curve is established, and the histogram of distribution of the angles is normalized to this area [57]. This yields the normalized histogram (Figure 3b). Similar manipulations were done with the distributions and . The objective function of the optimization problem includes the linear approximations of distribution functions , and grain sizes . It is worth noting that, for , there is no need to introduce distributions because is minimized in Neper. That is why the objective function of the optimization problem (formulation is given in Section 3) contains the sizes themselves. The formulated optimization problem is solved by applying a targeted selection technique which is needed to establish a correspondence between the polyhedral grain shape and the inherited internal variables of the model until the local minimum of the objective function is attained. The distributions of the normalized quantities and , calculated in terms of the statistical model with consideration of the grain sizes , are successively approximated to new distributions obtained via targeted selection (Figure 3c). The mathematical formulation of the optimization problem and the algorithm for solving this problem are given below. Due to the consistency of the material structure in terms of the listed variables, the deviation of the response (Cauchy stress tensor Σ) of the representative volume of the material is minimum, and the conditions for recrystallization are kept unchanged during subsequent deformation.
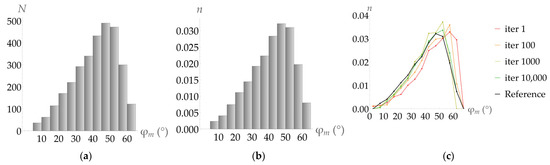
Figure 3.
(a) The histogram for the distribution of mutual misorientation angles in the in the copper polycrystal at temperature T = 773 and deformation . (b) The normalized histogram for the angles . (c) The evolution of the empirical () distribution function during the optimization procedure.
3. Selection and Justification of the Method for Finding a Solution to the Problem of Establishing Grain Structure Correspondence
Establishing a correspondence of grain structure, i.e., the correlation of the internal variables of grains when determining their location in the geometric structure of the polyhedra (Figure 2) is the problem of finding the optimal solution on a finite set. The elements of this set are the grains with the internal variables assigned to them. This is a kind of a discrete combinatorial optimization problem. It is important to note that, in this problem, we have a one-to-one correspondence, i.e., each grain in the statistical model corresponds to a single polyhedron of the rearranged polyhedral structure (Figure 2).
It is noteworthy that the identification of a material structure evolving during recrystallization by experimental methods is an extremely time-consuming problem; the authors were unable to find publications containing similar results. Therefore, the data calculated for the structure cannot be compared with the corresponding full-scale data at each instant of deformation; the latter is required for detailed model verification. However, there is a possibility in principle to experimentally obtain the model internal variables chosen for consideration—the difference in stored energies, , mutual misorientation angles and grain sizes . The stored energy can be estimated from analyzing the grain dislocation density data, while the angles of mutual misorientation and the grain sizes are calculated using the EBSD technique. For the above purpose, a comparison can be performed only between the calculated data. The above variables , and are compared between the first and second stages of grain structure rearrangement (Figure 1). This makes it possible to implicitly introduce a hypothesis that the grain structure of the material, considered at the first stage where recrystallized grains are introduced into the model in a simplified fashion (Figure 1), is a “reference” structure. As the plastic deformation continues, this grain structure ceases to be such. We suppose that the new grain completely immersed in the matrix of the neighboring grain is not fulfilled, since the recrystallized grains begin to contact each other. Thus, for verification purposes, we use the data showing how the considered parameters change within a short time interval of deformation; after the grain structure rearrangement, a small deformation of 3% is considered.
Some combinatorial problems apply optimization methods that provide an exact optimal solution. Among them, the following targeted selection techniques can be distinguished: branch and bound method [58], simplex method [59,60], dynamic programming methods [61], etc. Most of the existing optimization problems of practical importance, including the problem under consideration, cannot be classified as convex. They have no unique solution, and thus their solution is the smallest (largest) value of a local extremum [62]. The idea of these methods is to apply an iterative procedure for generating or improving the initial solution using nearest neighborhood; this yields a local extremum. To find the smallest extremum, it is necessary to study different local extrema, which in turn requires a wide variety of calculations with various initial approximations. These methods are characterized by an exponential increase in the time spent on finding the optimal solution with increasing problem dimensionality.
Another class of optimization methods are heuristic algorithms, which do not guarantee the best solution but can be used to find an acceptable result on the entire set of sought values and to avoid calculation stops at local extrema because at each iterative stage. Several options for a potential solution are considered [63]. Solutions include: simulated annealing [64,65,66], tabu search [67,68], swarm intelligence [69,70], migrating birds optimization [71], etc.
The heuristic methods are applicable to the high-dimensional computationally-expansive problems with some constraints. The most flexible and versatile of the heuristic methods is a genetic algorithm (GA) and its modifications. The efficiency of this method is supported by a wide range of applications in different fields of science [72]. GA is a technique that is based on the principles of genetics and natural selection [73]. For convenience, the biological terminology is applied to introduce basic mathematical concepts. The advantage of the GA over other heuristic algorithms is that, in order to find an extremum, the probabilistic rules for choosing solutions and the deterministic sequential comparison of these solutions are used simultaneously so that the most appropriate solutions can be obtained. At the same time, there is a possibility of restoring the “lost” solutions and obtaining the new solutions not previously considered due to the local change of the input parameters driven by the mutation and crossing procedures [74,75,76].
The main idea of GAs is the organization of “natural selection” among the trial solutions of the problem [76]. A set of optimization parameters is an individual and is represented as a vector: , where, for the problem under consideration, is the location (habitat) of the i-th grain in a new polyhedral structure (grain shape), and is a set of internal state variables of a grain. Each grain, including the new recrystallized grains, is assigned its location in the new polyhedral structure (Figure 2). Thus, an individual will be a trial version of the geometric structure with prescribed internal variables, and the evolution of an individual is a local change in the prescribed internal variables in the geometric structure. In this problem, all pairs and must be singular in the process of evolution of an individual. A set of individuals is called a population, where is the number of individuals in the population (size). On the one hand, if the number of options for establishing structure correspondence is small, then the search for a solution will be carried out mainly by changing these options and, to a lesser extent, by selecting the best individuals. On the other hand, if the number of individuals is too large, the solutions will be repeated, and this will lead to the degeneration of individuals at the selection stage and to the determination of a local extremum. The value of is determined empirically, based on computational complexity of the objective function, and is assumed to be constant during the evolution.
The following procedure was applied for establishing the correspondence of the grain structure during its rearrangement caused by the formation of new recrystallized grains. To determine the initial approximation, an auxiliary problem (8) of the grain structure correspondence in reference to the grain sizes is determined by the equivalent diameter of the sphere:
where is the characteristic size of the i-th grain obtained after rearranging in Neper at the second stage (Figure 1), and is the characteristic size of the i-th grain obtained in the statistical model calculations at the first stage (Figure 1). The solution of the auxiliary problem (8) converges rapidly because the use of Neper makes it possible to determine the correspondence of grain size distribution in reference to the prescribed distribution .
The objective function of the optimization problem includes the linear approximations of distribution functions , and the grain sizes normalized to the average value. The value of the objective function must be a real number characterizing the “quality” of the trial solution. As an objective function , we offer to use a weighted sum of three terms—the squared deviations of the key variables of the optimization problem (for comparing the structures) (9), which are often used as an objective function in many parameter identification problems [77,78,79]:
where , , and are the weight coefficients which are chosen empirically via analyzing the results of the computational experiments, is the number of grains in the representative volume of the polycrystal, are the numbers of intervals in the histogram of distribution of the normalized values of , , respectively, , are the normalized distribution of stored energy difference in the i-th intervals of the histogram implemented in Neper at the second stage and obtained in the statistical model calculations at the first stage, , are the normalized distribution of the stored energy difference in the i-th interval of the histogram obtained when rearranging in Neper at the second stage and in the statistical model calculations at the first stage, and , are the normalized characteristic size of the i-th grain obtained when rearranging in Neper at the second stage and in the statistical model calculations at the first stage. Thus, in order to solve the grain structure correspondence problem formulated in this study, it is necessary to find the locations (which determine the grain geometry, including the value of ) of grains and the corresponding distributions of and , which deliver a minimum to the objective function (9).
The genetic algorithm is reduced to a step-by-step simulation of the evolution of a population of living organisms, where each step describes a change in the generation (Figure 4). When initializing the initial set of trial solutions, the internal variables of grains with a new location and geometry in the polyhedral structure are randomly prescribed. At the first step of the algorithm, the quality of the obtained trial solutions is determined—for each individual, the value of the objective function is calculated.
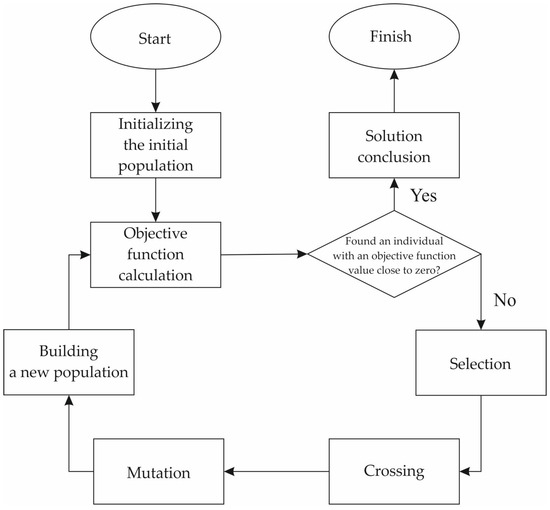
Figure 4.
The block scheme of the genetic algorithm.
The goal of the algorithm implementation steps (given below) is to generate a new, more perfect population. To eliminate hypothetically incorrect solutions, a selection procedure that consists in choosing the most promising candidates from all options is carried out. This provides an opportunity to get closer to the desired solution and to choose a more accurate structure correspondence. Therefore, it would be needed to use a variety of trial solutions, due to each individual having a certain choice to get into a new generation, depending on its value in the objective function . We have applied the tournament selection method, which has fast convergence and a lower relative error [74]. With this method, three individuals were randomly selected from the entire population, and an individual from this trio with the smallest value of the objective function going into the new generation. The tournament algorithm is repeated K times to maintain the number of individuals in the population. All individuals can participate in tournaments an unlimited number of times.
Upon the completion of the selection procedure, the population improves on average through exchanging the areas of comparable structures between individuals. For this purpose, we apply a crossing procedure to find a solution in a shorter amount of time. Crossing accelerates the search at the expense of combining the most correct, in terms of obtaining the minimum value of the objective function, and segments of the compared structure in one individual. This step can lead to population degeneration, namely, to the case when all individuals are similar to each other, which corresponds to a local extremum finding. To perform the crossing, two individuals of the current generation are taken (Equations (10) and (11)):
The implementation of crossing depends on the crossing chance, . When this step is omitted, the individuals move into a new population without changes. The “cut point” of an individual is chosen randomly, and the structure area exchange happens relative to this point (Equations (12) and (13)):
After crossing with a certain probability (probability of mutation) , the individual undergoes a mutation procedure. A mutation is considered as a local permutation of two grains in a polyhedral structure. The grains needed for exchange are chosen randomly with the probability equal to [76]. This is the key step of the genetic algorithm, which is sufficient to find an extremum of the objective function ; however, in the absence of other steps, its efficiency is exceedingly small. For the individuals of a new population, the value of the objective function is again calculated, and all steps are repeated, until the condition that must be reached in order to stop the execution of the algorithm is met.
4. Modelling Results and Their Analysis
In this section, the inelastic deformation of a copper polycrystal sample is studied. A description of the multilevel model, identification procedures and model parameters is given in [38]. For each moment of time, the thermomechanical and mechanical effects are prescribed, and the temperature and velocity gradient are assumed to be known at the macrolevel. We consider plastic deformations that correspond to quasiuniaxial loading by following Equation (14):
where is the orthonormalized basis of the coordinate system, and is the prescribed deformation velocity.
At the first stage, the issue of choosing the objective function and parameters for the genetic algorithm method was investigated. With this purpose, inelastic deformation up to intensity followed by the above-described grain structure rearrangement procedure was simulated. Figure 5 shows the , , and normalized distribution histograms obtained in the framework of the statistical model during the first grain structure rearrangement at the deformation magnitude . This figure also gives the and distributions; the distribution is determined in Neper. Analysis of the histograms revealed a good correspondence between the prescribed distribution of the considered values and the distribution of the values obtained in solving the optimization problem. For the distribution the deviation discrepancy is 6%, for the deviation discrepancy is 5%, and for the deviation discrepancy is 10%. In the absence of the optimization problem solution, a deviation discrepancy for and varies from 15 to 20%, and the distributions of these values do not coincide with the initial distributions of and .
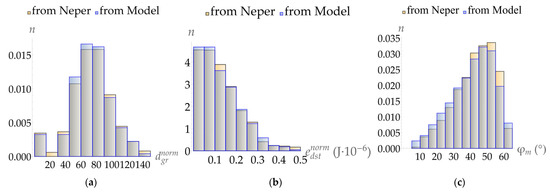
Figure 5.
The normalized histograms for the distributions of: (a) and , (b) and , and (c) and , obtained in the framework of the statistical model and by solving of the optimization problem for the grain structures being compared.
Table 1 lists the integral norms (introduced below) of the relative deviations of distributions and obtained in the framework of the statistical model from the prescribed values before the grain structure rearrangement and after the solution of the optimization problem for the deformation intensity interval at different values of the genetic algorithm parameters. The distributions and are calculated as follows (15):

Table 1.
The deviations of distributions and at different values of the genetic algorithm parameters.
In the above formula, and are understood as the physical time instants corresponding to the ends of the considered interval of deformation intensity . The values of and over the entire interval illustrate the case with the simplified introduction of recrystallized grains into the model (Figure 1). Analysis of the initial segment of deformation (the critical deformation is reached and new equiaxed grains are formed) makes it possible to consider this configuration (for establishing a correspondence) as a “reference” configuration. The conditions for mutual misorientations, the differences in stored energy and the differences in grain sizes are close to the desired values (the initial stage of plastic deformation). The grain structure rearrangement introduces additional “distortions” into the grain structure and changes in the material response. The value of the considered interval of change in the intensity of deformations was determined in the computational experiments and was equal to 3%. The preliminary calculations show that the value of the third term in the objective function, which is responsible for grain size comparisons, is much larger compared to other terms and has a negative effect on the significance of the first two terms of the objective function (9). The point is that the number of grains in the representative volume element of the polycrystal is much greater than the number of intervals in the distribution histograms . Bearing this in mind, the weight coefficients (9) are determined. The parameters and affect the rate of convergence of the optimization problem solution. At higher values of the crossing choice , the same individuals are more likely to participate in the exchange of parts of the structure, which leads to the degeneration of the population. At lower values of , the solution variants less often exchange parts of the compared structures, and the search for a solution is carried out at the expense of the mutation stage. In turn, an increase in the probability of mutation, , causes significant changes in individuals and is responsible for the loss of potentially optimal solutions to the problem.
The results given in Table 1 demonstrate the effect of the weight coefficients. The first row of the table contains results illustrating the effect of the weight coefficient α. At , the deviation is the least deviation, but the value of significantly worsens with an increasing α. The change in the parameter β causes the deviation to decrease and the deviation to slowly increase, which is why in further calculations . The third line contains the results of estimation of the weight coefficient γ. The sum in the third term is essentially higher than that in the first two terms. Therefore, γ is chosen considering the number of grains in the representative volume element (summands of the third sum) and the number of histogram intervals (summands of the first two sums of the objective function) so that the effect of all three sums of the objective function can be normalized.
The parameters and were chosen such that the mutations and crossing take place as often as possible to increase the convergence rate, while keeping the best solution options unchanged. The calculations performed indicate that, in order to solve the optimization problem using genetic algorithm, the rationally selected parameters summarized in Table 2 are applied.

Table 2.
The values of the genetic algorithm parameters used in the calculations.
Despite the stages of the algorithm that are aimed to approach an optimum, each stage taken separately is unable to achieve a satisfactory solution in a foreseeable number of steps, as confirmed by the results given in Figure 6. It demonstrates convergence of the genetic algorithm in the case when a new generation is formed during only some of the genetic algorithm stages.
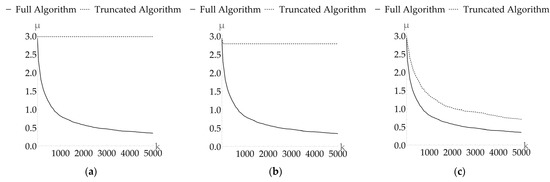
Figure 6.
Dependence of the objective function of the best data comparison option on the step number (generation) k when solving the optimization problem: (a) without mutation and crossing, (b) without mutation, and (c) without crossing.
It should be noted that an increase in the number of individuals in a population also make it possible to increase the rate of convergence, but it must be remembered that, for each trial solution, the value of the objective function is determined at each iteration. Therefore, the more individuals in a population, the more time is required to solve the optimization problem at a step. This also leads to frequent repetitions of the sections of the compared structures and to the possible degeneration of the population at subsequent algorithm steps.
Table 3 contains the values of relative deviations of stress intensities , stored energy differences , mutual disorientation angle for the deformation intensity interval and different definitions of the objective function obtained as a result of the grain structure rearrangement and the optimization problem solution. The objective function (9) was sequentially determined—one or two terms are removed alternatively and the distributions of the considered quantities are replaced by their mathematical expectation. is determined by the following relation (16):
where is the macrolevel stress intensity before and after the grain structure reconstruction in Neper.

Table 3.
The relative values of deviations of stress intensities , and for different definitions of the objective function .
The designations used in Table 3 are as follows: is the value of the objective function obtained in solving the optimization problem during grain structure reconstruction, the indexes , and denote the corresponding terms left in the objective function determined using (9), and the index indicates that, in the objective function (9), instead of the distributions of the considered values, their mathematical expectations are used. As one can see, the proposed objective function (9) (first line in Table 3) demonstrates the least deviation of the material response , which can be attributed to the fact that the elimination of one or more terms from (9) leads to violations in the conditions for plastic deformation and recrystallization (Section 2).
The structure obtained by solving the optimization problem is used in further calculation within the framework of the statistical model of inelastic deformation, with allowance for recrystallization. Figure 7 shows the loading diagram of the performed quasi-uniaxial tension; the area under study is shown as a separate graph to illustrate the case when the grain structure is reconstructed for deformations. The results obtained indicate that the formulated optimization problem brings the response of the material response closer to the solution of a multilevel model without reconstructing the grain structure, i.e., in the case when the new recrystallized grains are added in the simplified way (Figure 1). At the initial stage, after the addition of new recrystallized grains, these parts of the curves (black and blue) should be close. The subsequent inelastic deformation results in the non-physical representation of a simplified picture of recrystallized grains, where each new grain is immersed in the matrix of the neighboring grain, since the recrystallized grains begin to contact each other. While considering the recrystallization process, the parameters of the stress-strain state remain unchanged by virtue of proper selection of the physical-mechanical and geometric characteristics of grains in the structure generated at the second stage of the calculation. To do so, the genetic algorithm is used to solve the problem of minimizing the objective function (9), which provides the determination of a set of structural variables of the model needed to continue the numerical calculations of the problem of inelastic deformation.
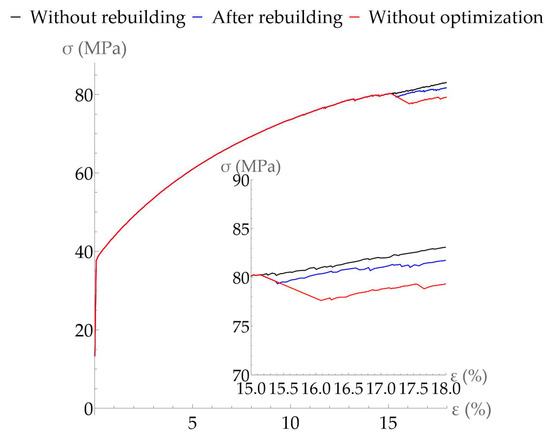
Figure 7.
Stress versus accumulated strain curves for the representative volume element of a polycrystal without grain structure rearrangement (black), with optimization (blue), and without optimization (red). The grain structure is reconstructed at the deformation instant of 15%.
5. Conclusions
In this work, a statistical model of inelastic deformation with allowance for DRX is described. We modified the model so that it can consider local interactions along the contact boundaries between neighboring grains. It is an alternative to the self-consistent modeling approach, which considers the grain immersed in an effective medium. Recrystallization is accompanied by the formation of new grains, leading to softening and a decrease in the yield strength. The new grain geometry should be explicitly introduced into consideration in the developed model. In this connection the problem of rearranging the grain structure with allowance for new grains was formulated and an appropriate resoling approach is proposed. The main results of the research are the following:
- We put forward a method for establishing statistical consistency of the grain structure during its rearrangement in order to keep the results of numerical simulation of the inelastic deformation process, with an account of unchanged recrystallization.
- We determined the main variables of the model; namely, the stored energy difference distribution, mutual misorientation angle distribution, and grain sizes.
- We posed the problem of minimizing the difference between these variables in a statistical sense during the grain structure rearrangement. To solve it, a genetic algorithm was applied.
- In preliminary calculations, the parameters of the weight coefficients included in the definition of the objective function and the parameters of the genetic algorithm were determined.
- It is shown that the agreement between the variables under consideration provides the smallest (among the considered variables) deviation of the material response during the grain structure rearrangement. If one or more of these parameters are removed from the optimization problem statement, the material behavior (response) may deviate significantly after the grain structure rearrangement.
Author Contributions
Conceptualization, P.T. and N.K.; methodology, P.T. and N.K.; software, A.P.; validation, A.P., N.K. and P.T.; formal analysis, N.K. and A.P.; investigation, N.K., P.T. and A.P.; data curation, N.K. and A.P.; writing—original draft preparation, N.K.; writing—review and editing, P.T., N.K. and A.P.; visualization, N.K. and A.P.; supervision, P.T.; funding acquisition, N.K. All authors have read and agreed to the published version of the manuscript.
Funding
The study was carried out with financial support from the Ministry of Education and Science of the Russian Federation as part of the implementation of the national project “Science and Universities” (the state task fulfillment in the laboratory of multilevel structural and functional materials modeling, project no. FSNM-2021-0012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Irani, M.; Joun, M. Determination of JMAK Dynamic Recrystallization Parameters through FEM Optimization Techniques. Comput. Mater. Sci. 2018, 142, 178–184. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Langdon, T.G. The Fundamentals of Nanostructured Materials Processed by Severe Plastic Deformation. JOM 2004, 56, 58–63. [Google Scholar] [CrossRef]
- Bagherpour, E.; Pardis, N.; Reihanian, M.; Ebrahimi, R. An Overview on Severe Plastic Deformation: Research Status, Techniques Classification, Microstructure Evolution, and Applications. Int. J. Adv. Manuf. Technol. 2019, 100, 1647–1694. [Google Scholar] [CrossRef]
- Glezer, A.M.; Kozlov, E.V.; Koneva, N.A.; Popova, N.A.; Kurzina, I.A. Plastic Deformation of Nanostructured Materials; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-11196-4. [Google Scholar]
- Rollet, A.; Rohrer, G.; Humphreys, J. Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Doherty, R.D.; Hughes, D.A.; Humphreys, F.J.; Jonas, J.J.; Jensen, D.J.; Kassner, M.E.; King, W.E.; McNelley, T.R.; McQueen, H.J.; Rollett, A.D. Current Issues in Recrystallization: A Review. Mater. Sci. Eng. A 1997, 238, 219–274. [Google Scholar] [CrossRef]
- Verlinden, B.; Driver, J.; Samajdar, I.; Doherty, R.D. Thermo-Mechanical Processing of Metallic Materials; Elsevier: Oxford, UK, 2007; ISBN 978-0-08-054448-9. [Google Scholar]
- Huang, K.; Logé, R.E. A Review of Dynamic Recrystallization Phenomena in Metallic Materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Shveykin, A.; Trusov, P.; Sharifullina, E. Statistical Crystal Plasticity Model Advanced for Grain Boundary Sliding Description. Crystals 2020, 10, 822. [Google Scholar] [CrossRef]
- Qiu, P.; Han, Y.; Le, J.; Huang, G.; Lei, L.; Xiao, L.; Lu, W. Particulate Induced Dynamic Globularization/Recrystallization and Unique Superplasticity in TiB/near-α Ti Matrix Composites. Mater. Charact. 2020, 167, 110458. [Google Scholar] [CrossRef]
- Li, Y.; Shen, P.; Zhang, H.; Dong, K.; Deng, Y.; Chen, X.; Cui, Z. Deformation Heterogeneity Induced Coarse Grain Refinement of the Mixed-Grain Structure of 316LN Steel through Limited Deformation Condition. Mater. Des. 2021, 210, 110057. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shang, X.; Liu, M.; Zhao, S.; Cui, Z. A Multiscale Investigation on the Preferential Deformation Mechanism of Coarse Grains in the Mixed-Grain Structure of 316LN Steel. Int. J. Plast. 2022, 152, 103244. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z.; Yu, H.; Ning, Y. Microstructural Origin and Control Mechanism of the Mixed Grain Structure in Ni-Based Superalloys. J. Alloy. Compd. 2022, 900, 163515. [Google Scholar] [CrossRef]
- Zhao, Y. Co-Precipitated Ni/Mn Shell Coated Nano Cu-Rich Core Structure: A Phase-Field Study. J. Mater. Res. Technol. 2022, 21, 546–560. [Google Scholar] [CrossRef]
- Panin, V.E. Overview on Mesomechanics of Plastic Deformation and Fracture of Solids. Theor. Appl. Fract. Mech. 1998, 30, 1–11. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel Models of Mono-and Polycrystalline Materials: Theory, Algorithms, Application Examples; SB RAS: Novosibirsk, Russia, 2019. (In Russian) [Google Scholar]
- Panin, V.E.; Yegorushkin, V.E.; Makarov, P.V.; Nemirovich-Danchenko, M.M.; Demidov, V.N.; Smolin, I.Y.; Cherepanov, O.I.; Psakhie, S.G.; Negreskul, S.I.; Zolnikov, K.P.; et al. Physical Mesomechanics and Computer Design of Materials; Novosibirsk Department of the publishing House “Science”: Novosibirsk, Russia, 1995; Volume 1, ISBN 5-02-030840-4. (In Russian) [Google Scholar]
- Panin, V.E.; Makarov, P.V.; Nemirovich-Danchenko, M.M.; Demidov, V.N.; Smolin, I.Y.; Cherepanov, O.I.; Psakhie, S.G.; Negreskul, S.I.; Zolnikov, K.P.; Korostelev, S.Y.; et al. Physical Mesomechanics and Computer Design of Materials; Novosibirsk Department of the Publishing House “Science”: Novosibirsk, Russia, 1995; Volume 2, ISBN 5-02-030841-2. (In Russian) [Google Scholar]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk Nanostructured Materials from Severe Plastic Deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Asaro, R.J. Crystal Plasticity. J. Appl. Mech. 1983, 50, 921–934. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in Crystal Plasticity Finite-Element Modeling: Theory, Experiments, Applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Niezgoda, S.R. Microstructural and Micromechanical Evolution during Dynamic Recrystallization. Int. J. Plast. 2018, 100, 52–68. [Google Scholar] [CrossRef]
- Adams, B.L.; Henrie, A.; Henrie, B.; Lyon, M.; Kalidindi, S.R.; Garmestani, H. Microstructure-Sensitive Design of a Compliant Beam. J. Mech. Phys. Solids 2001, 49, 1639–1663. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Houskamp, J.R.; Lyons, M.; Adams, B.L. Microstructure Sensitive Design of an Orthotropic Plate Subjected to Tensile Load. Int. J. Plast. 2004, 20, 1561–1575. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Houskamp, J.; Proust, G.; Duvvuru, H. Microstructure Sensitive Design with First Order Homogenization Theories and Finite Element Codes. Mater. Sci. Forum 2005, 495–497, 23–30. [Google Scholar] [CrossRef]
- Sundararaghavan, V.; Zabaras, N. Design of Microstructure-Sensitive Properties in Elasto-Viscoplastic Polycrystals Using Multi-Scale Homogenization. Int. J. Plast. 2006, 22, 1799–1824. [Google Scholar] [CrossRef]
- McDowell, D.L.; Olson, G.B. Concurrent Design of Hierarchical Materials and Structures. Sci. Model. Simul. 2008, 15, 34. [Google Scholar] [CrossRef]
- Nakamachi, E.; Kuramae, H.; Sakamoto, H.; Morimoto, H. Process Metallurgy Design of Aluminum Alloy Sheet Rolling by Using Two-Scale Finite Element Analysis and Optimization Algorithm. Int. J. Mech. Sci. 2010, 52, 146–157. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Morozov, N.F. Fundamental Problems of Solid Mechanics in High Technologies. Phys. Mesomech. 2012, 15, 5–13. [Google Scholar] [CrossRef]
- Ostapovich, K.V.; Trusov, P.V.; Yants, A.Y. Prediction of Crystallographic Texture Formation in Polycrystalline Samples under Severe Plastic Deformation Based on a Two-Level Statistical Elasto-Viscoplastic Model. Phys. Mesomech. 2021, 24, 225–236. [Google Scholar] [CrossRef]
- Doherty, R.D.; Cahn, R.W. Nucleation of New Grains in Recrystallization of Cold-Worked Metals. J. Less Common Met. 1972, 28, 279–296. [Google Scholar] [CrossRef]
- Xin, T.; Tang, S.; Ji, F.; Cui, L.; He, B.; Lin, X.; Tian, X.; Hou, H.; Zhao, Y.; Ferry, M. Phase Transformations in an Ultralight BCC Mg Alloy during Anisothermal Ageing. Acta Mater. 2022, 239, 118248. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel Crystal Plasticity Models of Single- and Polycrystals. Statistical Models. Phys. Mesomech. 2013, 16, 23–33. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel Crystal Plasticity Models of Single- and Polycrystals. Direct Models. Phys. Mesomech. 2013, 16, 99–124. [Google Scholar] [CrossRef]
- Puchi-Cabrera, E.S.; Guérin, J.D.; La Barbera-Sosa, J.G.; Dubar, M.; Dubar, L. Plausible Extension of Anand’s Model to Metals Exhibiting Dynamic Recrystallization and Its Experimental Validation. Int. J. Plast. 2018, 108, 70–87. [Google Scholar] [CrossRef]
- Zecevic, M.; Knezevic, M.; McWilliams, B.; Lebensohn, R.A. Modeling of the Thermo-Mechanical Response and Texture Evolution of WE43 Mg Alloy in the Dynamic Recrystallization Regime Using a Viscoplastic Self-Consistent Formulation. Int. J. Plast. 2020, 130, 102705. [Google Scholar] [CrossRef]
- Arun Babu, K.; Prithiv, T.S.; Gupta, A.; Mandal, S. Modeling and Simulation of Dynamic Recrystallization in Super Austenitic Stainless Steel Employing Combined Cellular Automaton, Artificial Neural Network and Finite Element Method. Comput. Mater. Sci. 2021, 195, 110482. [Google Scholar] [CrossRef]
- Trusov, P.; Kondratev, N.; Podsedertsev, A. Description of Dynamic Recrystallization by Means of An Advanced Statistical Multilevel Model: Grain Structure Evolution Analysis. Crystals 2022, 12, 653. [Google Scholar] [CrossRef]
- Vandermeer, R.A.; Rath, B.B. Microstructural Modeling of Recrystallization in Deformed Iron Single Crystals. Met. Mater. Trans. A 1989, 20, 1933–1942. [Google Scholar] [CrossRef]
- Lin, F.; Zhang, Y.; Tao, N.; Pantleon, W.; Juul Jensen, D. Effects of Heterogeneity on Recrystallization Kinetics of Nanocrystalline Copper Prepared by Dynamic Plastic Deformation. Acta Mater. 2014, 72, 252–261. [Google Scholar] [CrossRef]
- Matsumoto, H.; Velay, V. Mesoscale Modeling of Dynamic Recrystallization Behavior, Grain Size Evolution, Dislocation Density, Processing Map Characteristic, and Room Temperature Strength of Ti-6Al-4V Alloy Forged in the (A+β) Region. J. Alloy. Compd. 2017, 708, 404–413. [Google Scholar] [CrossRef]
- Yu, P.; Wu, C.; Shi, L. Analysis and Characterization of Dynamic Recrystallization and Grain Structure Evolution in Friction Stir Welding of Aluminum Plates. Acta Mater. 2021, 207, 116692. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, F.; Zhang, H.; Cui, Z. Review on Modeling and Simulation of Microstructure Evolution during Dynamic Recrystallization Using Cellular Automaton Method. Sci. China Technol. Sci. 2020, 63, 357–396. [Google Scholar] [CrossRef]
- Chang, K.; Chen, L.-Q.; Krill, C.E.; Moelans, N. Effect of Strong Nonuniformity in Grain Boundary Energy on 3-D Grain Growth Behavior: A Phase-Field Simulation Study. Comput. Mater. Sci. 2017, 127, 67–77. [Google Scholar] [CrossRef]
- Ruiz Sarrazola, D.A.; Pino Muñoz, D.; Bernacki, M. A New Numerical Framework for the Full Field Modeling of Dynamic Recrystallization in a CPFEM Context. Comput. Mater. Sci. 2020, 179, 109645. [Google Scholar] [CrossRef]
- Mellbin, Y.; Hallberg, H.; Ristinmaa, M. A Combined Crystal Plasticity and Graph-Based Vertex Model of Dynamic Recrystallization at Large Deformations. Model. Simul. Mater. Sci. Eng. 2015, 23, 045011. [Google Scholar] [CrossRef]
- Kondratev, N.S.; Trusov, P.V.; Podsedertsev, A.N. Multilevel model of polycrystals: Application to assessing the effect of texture and grains misorientation on the critical deformation of the dynamic recrystallization initiation. PNRPU Mech. Bull. 2021, 4, 83–97. [Google Scholar] [CrossRef]
- Quey, R.; Renversade, L. Optimal Polyhedral Description of 3D Polycrystals: Method and Application to Statistical and Synchrotron X-Ray Diffraction Data. Comput. Methods Appl. Mech. Eng. 2018, 330, 308–333. [Google Scholar] [CrossRef]
- Kondratev, N.; Podsedertsev, A.; Trusov, P. The Polycrystals Grain Structure Formation for Modified Two-Level Crystal Plasticity Statistical Models. Procedia Struct. Integr. 2022, 40, 239–244. [Google Scholar] [CrossRef]
- Hansen, N. Cold Deformation Microstructures. Mater. Sci. Technol. 1990, 6, 1039–1047. [Google Scholar] [CrossRef]
- Sandström, R. Formation of Cells and Subgrains and Its Influence on Properties. Metals 2022, 12, 497. [Google Scholar] [CrossRef]
- Bailey, J.E.; Hirsch, P.B. The Recrystallization Process in Some Polycrystalline Metals. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1962, 267, 11–30. [Google Scholar] [CrossRef]
- Cram, D.G.; Zurob, H.S.; Brechet, Y.J.M.; Hutchinson, C.R. Modelling Discontinuous Dynamic Recrystallization Using a Physically Based Model for Nucleation. Acta Mater. 2009, 57, 5218–5228. [Google Scholar] [CrossRef]
- Ponge, D.; Gottstein, G. Necklace Formation during Dynamic Recrystallization: Mechanisms and Impact on Flow Behavior. Acta Mater. 1998, 46, 69–80. [Google Scholar] [CrossRef]
- Brent, R.P. Algorithms for Minimization Without Derivatives; Courier Corporation: North Chelmsford, MA, USA, 2013; ISBN 978-0-486-14368-2. [Google Scholar]
- Knezevic, M.; Drach, B.; Ardeljan, M.; Beyerlein, I.J. Three Dimensional Predictions of Grain Scale Plasticity and Grain Boundaries Using Crystal Plasticity Finite Element Models. Comput. Methods Appl. Mech. Eng. 2014, 277, 239–259. [Google Scholar] [CrossRef]
- Kondratev, N.S.; Trusov, P.V. To Determination a Distribution Law of Subgrain Sizes Formed in the Cold Plastic Deformation Process. AIP Conf. Proc. 2020, 2216, 040010. [Google Scholar] [CrossRef]
- Jaber, A.; Lafon, P.; Younes, R. A Branch-and-Bound Algorithm Based on NSGAII for Multi-Objective Mixed Integer Nonlinear Optimization Problems. Eng. Optim. 2022, 54, 1004–1022. [Google Scholar] [CrossRef]
- Engels, J.K.; Vajragupta, N.; Hartmaier, A. Parameterization of a Non-Local Crystal Plasticity Model for Tempered Lath Martensite Using Nanoindentation and Inverse Method. Front. Mater. 2019, 6, 247. [Google Scholar] [CrossRef]
- Frydrych, K.; Papanikolaou, S. Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals 2022, 12, 1341. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, X.A. Stochastic Dual Dynamic Programming for Multistage Stochastic Mixed-Integer Nonlinear Optimization. Math. Program. 2022, 196, 935–985. [Google Scholar] [CrossRef]
- Ardia, D.; Boudt, K.; Carl, P.; Mullen, K.; Peterson, B.G. Differential Evolution with DEoptim: An Application to Non-Convex Portfolio Optimization. R J. 2011, 3, 27–34. [Google Scholar] [CrossRef]
- Pham, D.; Karaboga, D. Intelligent Optimisation Techniques: Genetic Algorithms, Tabu Search, Simulated Annealing and Neural Networks; Springer Science & Business Media: Berlin, Germany, 2012; ISBN 978-1-4471-0721-7. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Aydin, M.E.; Fogarty, T.C. A Distributed Evolutionary Simulated Annealing Algorithm for Combinatorial Optimisation Problems. J. Heuristics 2004, 10, 269–292. [Google Scholar] [CrossRef]
- Han, X.; Dong, Y.; Yue, L.; Xu, Q. State Transition Simulated Annealing Algorithm for Discrete-Continuous Optimization Problems. IEEE Access 2019, 7, 44391–44403. [Google Scholar] [CrossRef]
- Paul, G. Comparative Performance of Tabu Search and Simulated Annealing Heuristics for the Quadratic Assignment Problem. Oper. Res. Lett. 2010, 38, 577–581. [Google Scholar] [CrossRef]
- Hou, N.; He, F.; Zhou, Y.; Chen, Y. An Efficient GPU-Based Parallel Tabu Search Algorithm for Hardware/Software Co-Design. Front. Comput. Sci. 2020, 14, 145316. [Google Scholar] [CrossRef]
- Beni, G.; Wang, J. Swarm Intelligence in Cellular Robotic Systems. In Robots and Biological Systems: Towards a New Bionics? Dario, P., Sandini, G., Aebischer, P., Eds.; Springer: Berlin/Heidelberg, 1993; pp. 703–712. [Google Scholar]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Ulker, E.; Tongur, V. Migrating Birds Optimization (MBO) Algorithm to Solve Knapsack Problem. Procedia Comput. Sci. 2017, 111, 71–76. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Darwin, C. The Origin of Species by Means of Natural Selection; John Murray: London, UK, 1859. [Google Scholar]
- Jebari, K. Selection Methods for Genetic Algorithms. Int. J. Emerg. Sci. 2013, 3, 333–344. [Google Scholar]
- Das, A.K.; Pratihar, D.K. A Direction-Based Exponential Mutation Operator for Real-Coded Genetic Algorithm. In Proceedings of the 2018 Fifth International Conference on Emerging Applications of Information Technology (EAIT), Shibpur, India, 12–13 January 2018; pp. 1–4. [Google Scholar]
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning. Addion Wesley 1989, 1989, 36. [Google Scholar]
- Xie, C.L.; Ghosh, S.; Groeber, M. Modeling Cyclic Deformation of HSLA Steels Using Crystal Plasticity. J. Eng. Mater. Technol. 2004, 126, 339–352. [Google Scholar] [CrossRef]
- Skippon, T.; Mareau, C.; Daymond, M.R. On the Determination of Single-Crystal Plasticity Parameters by Diffraction: Optimization of a Polycrystalline Plasticity Model Using a Genetic Algorithm. J. Appl. Cryst. 2012, 45, 627–643. [Google Scholar] [CrossRef]
- Sedighiani, K.; Diehl, M.; Traka, K.; Roters, F.; Sietsma, J.; Raabe, D. An Efficient and Robust Approach to Determine Material Parameters of Crystal Plasticity Constitutive Laws from Macro-Scale Stress–Strain Curves. Int. J. Plast. 2020, 134, 102779. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
