Hot Deformation Behavior Coordination and Processing Maps of 40Cr/Q345B Bimetallic Blank by Centrifugal Casting
Abstract
1. Introduction
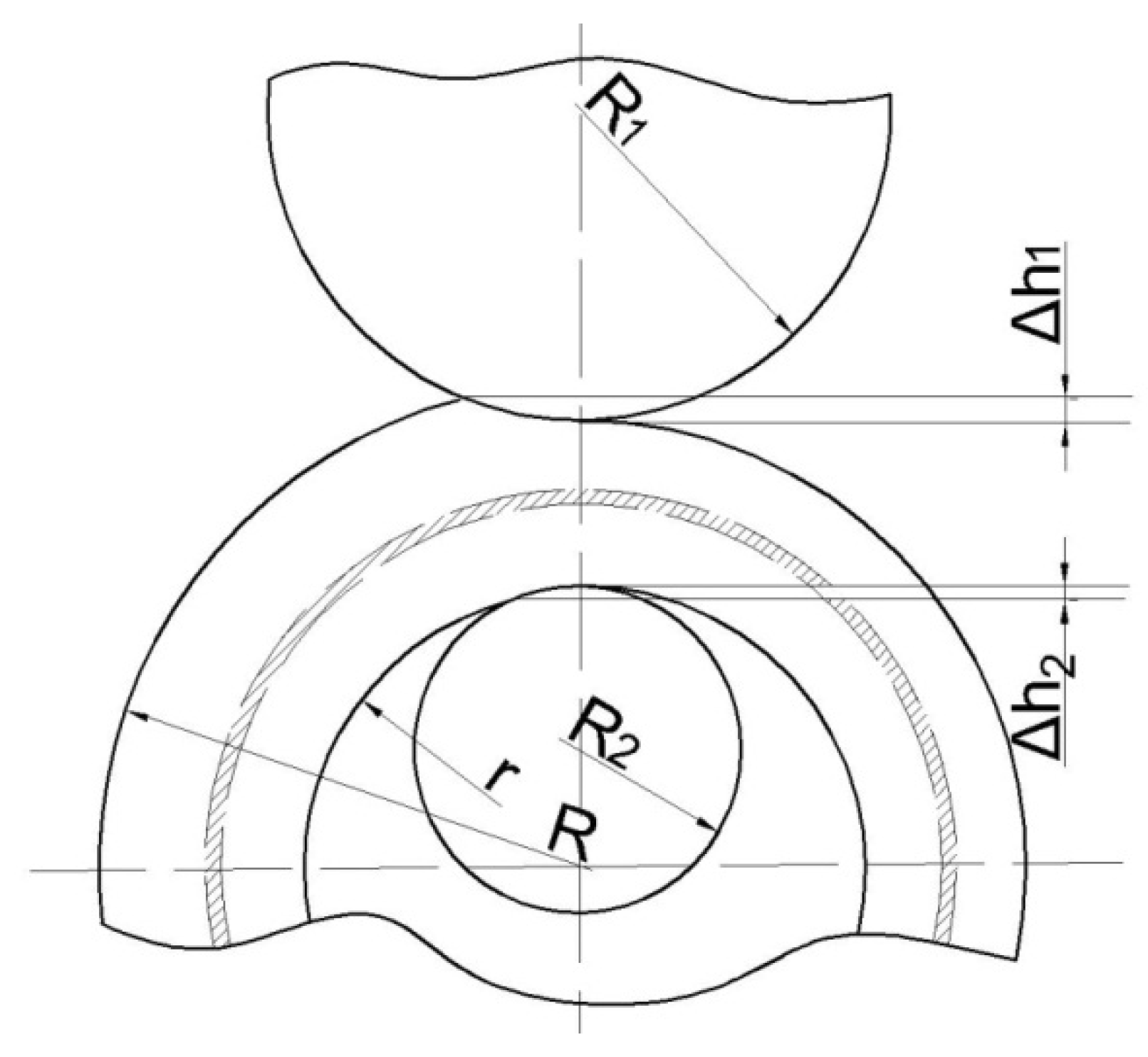
2. Materials and Methods
3. Results
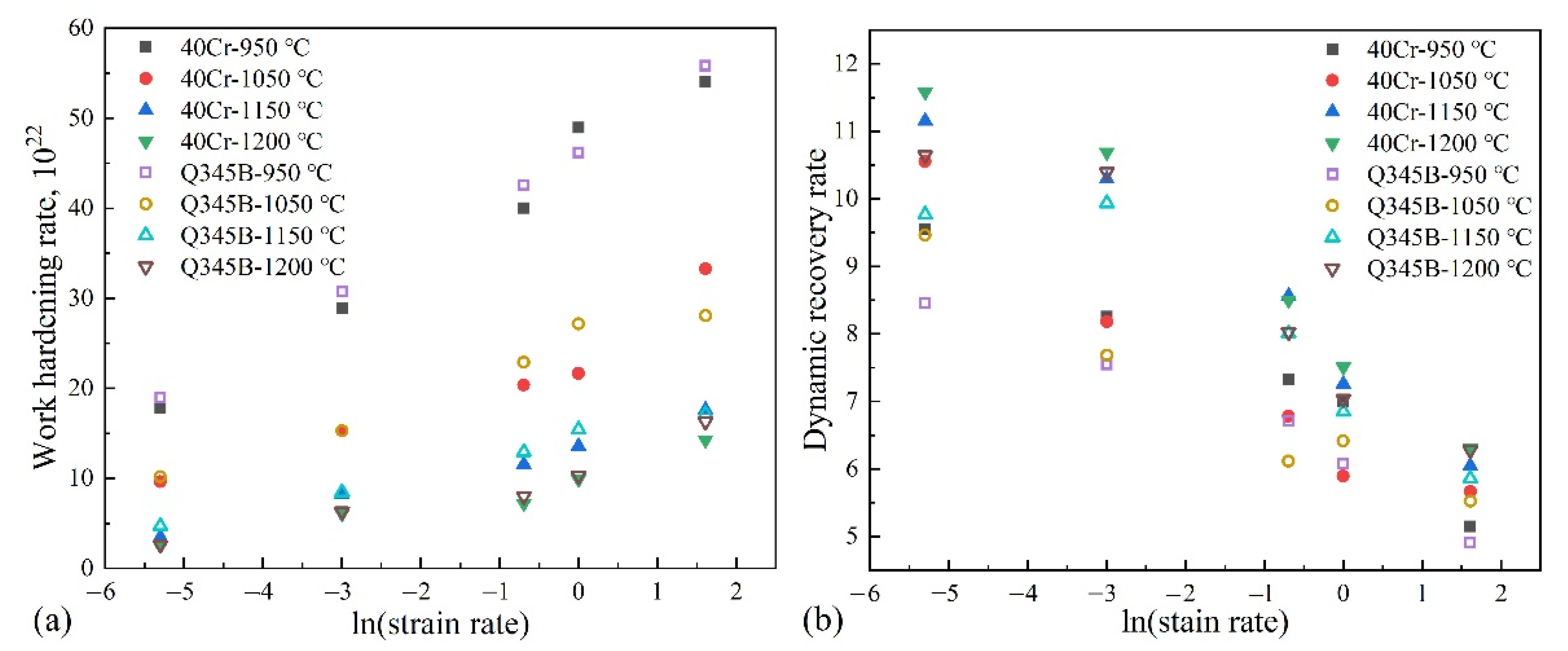
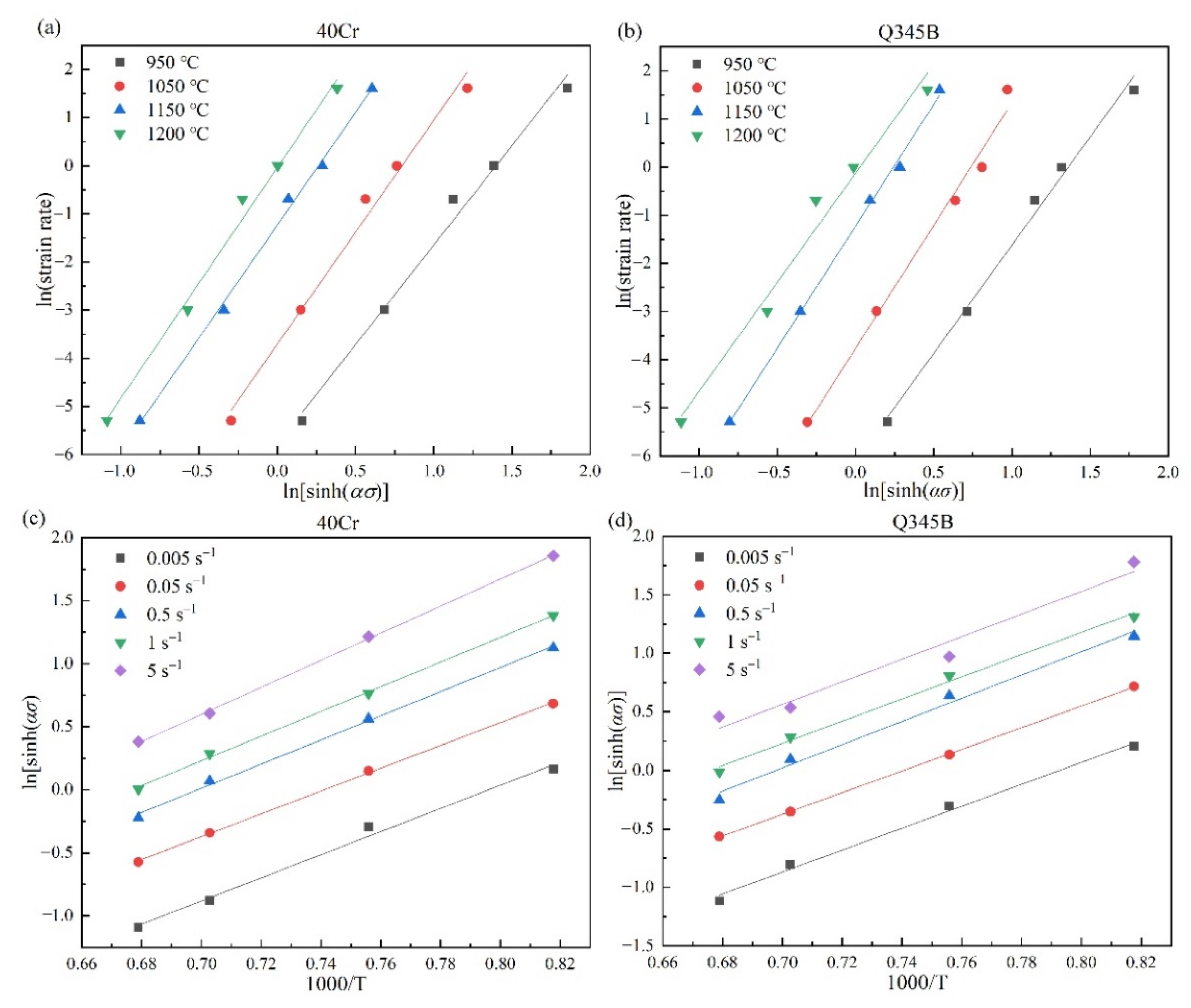
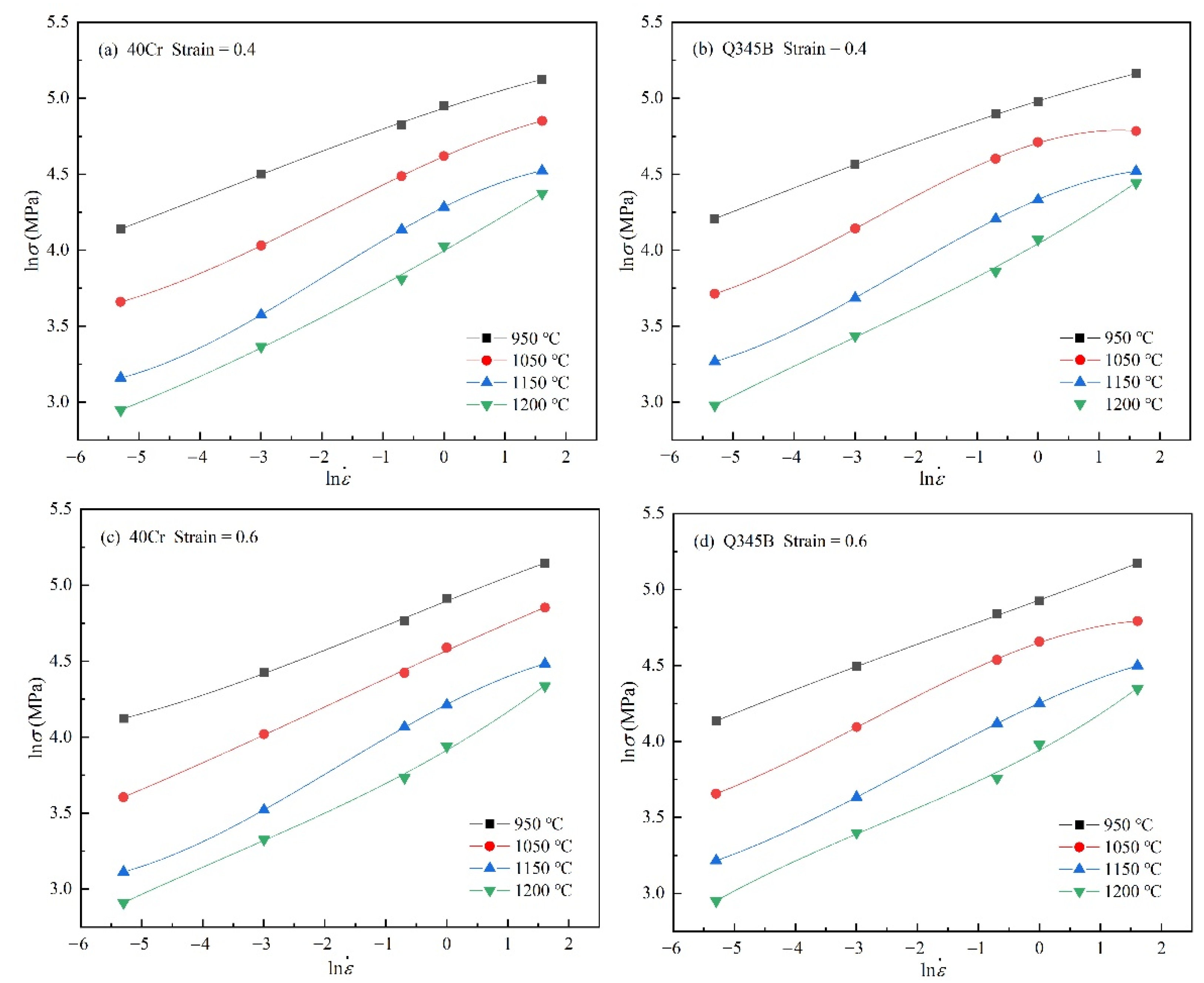
3.1. Flow Stress Behavior
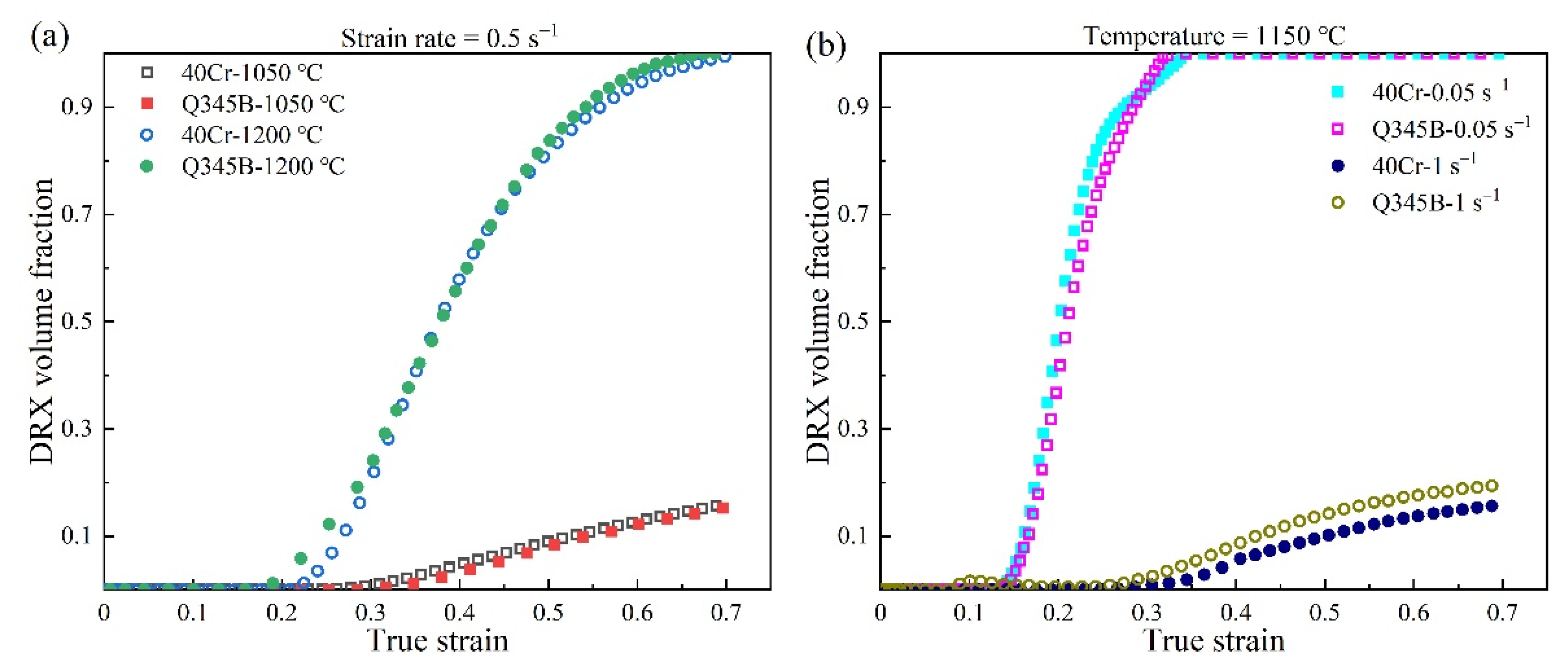
3.2. Coordinated Response to Hot Deformation of Bimetallic Ring Rolling
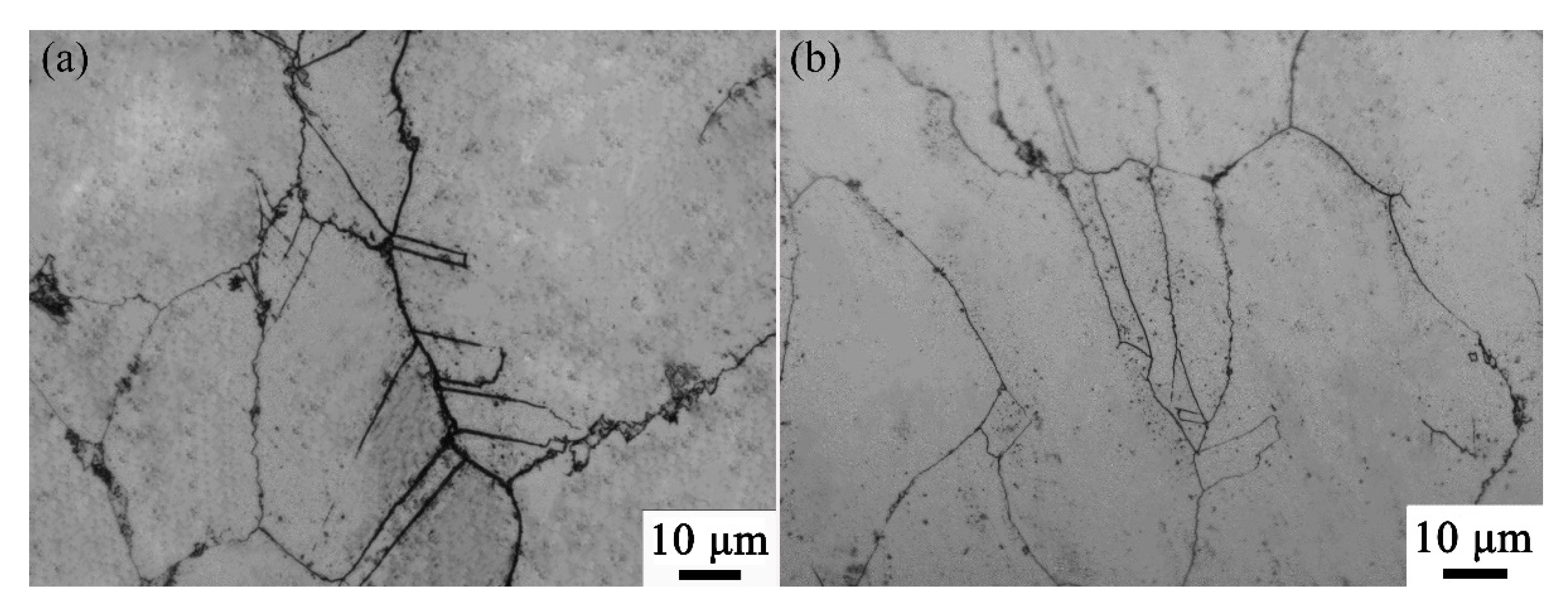
3.3. Rate-Controlling Mechanism
3.4. Processing Maps
4. Conclusions
- (1)
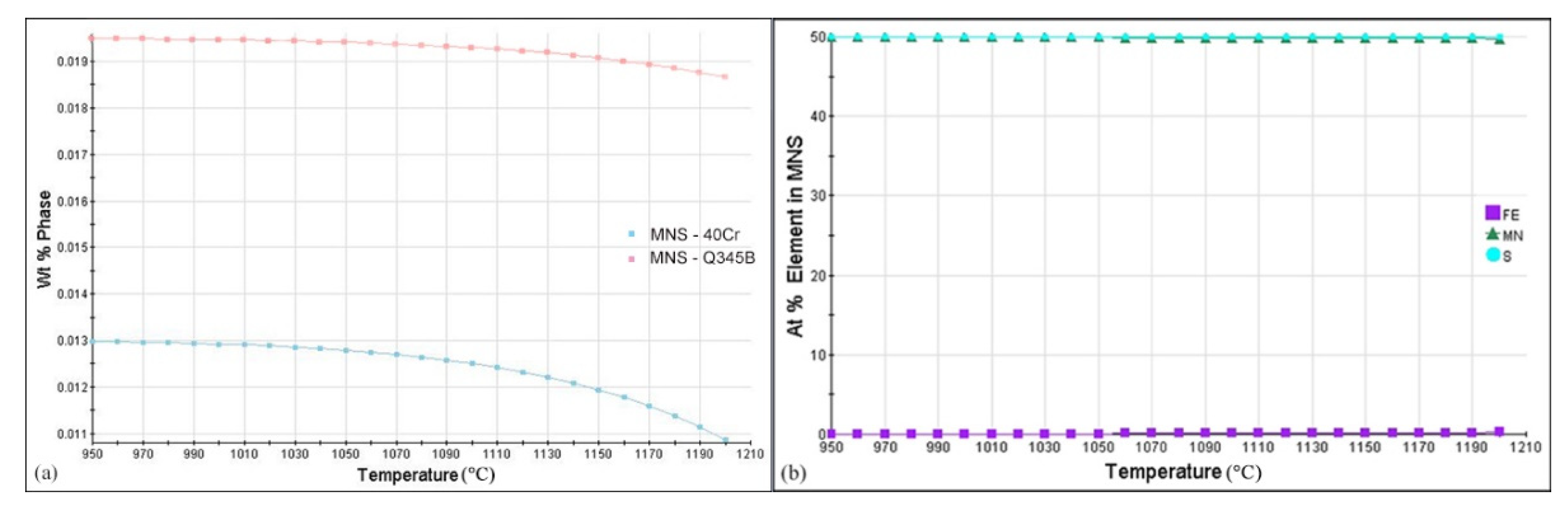
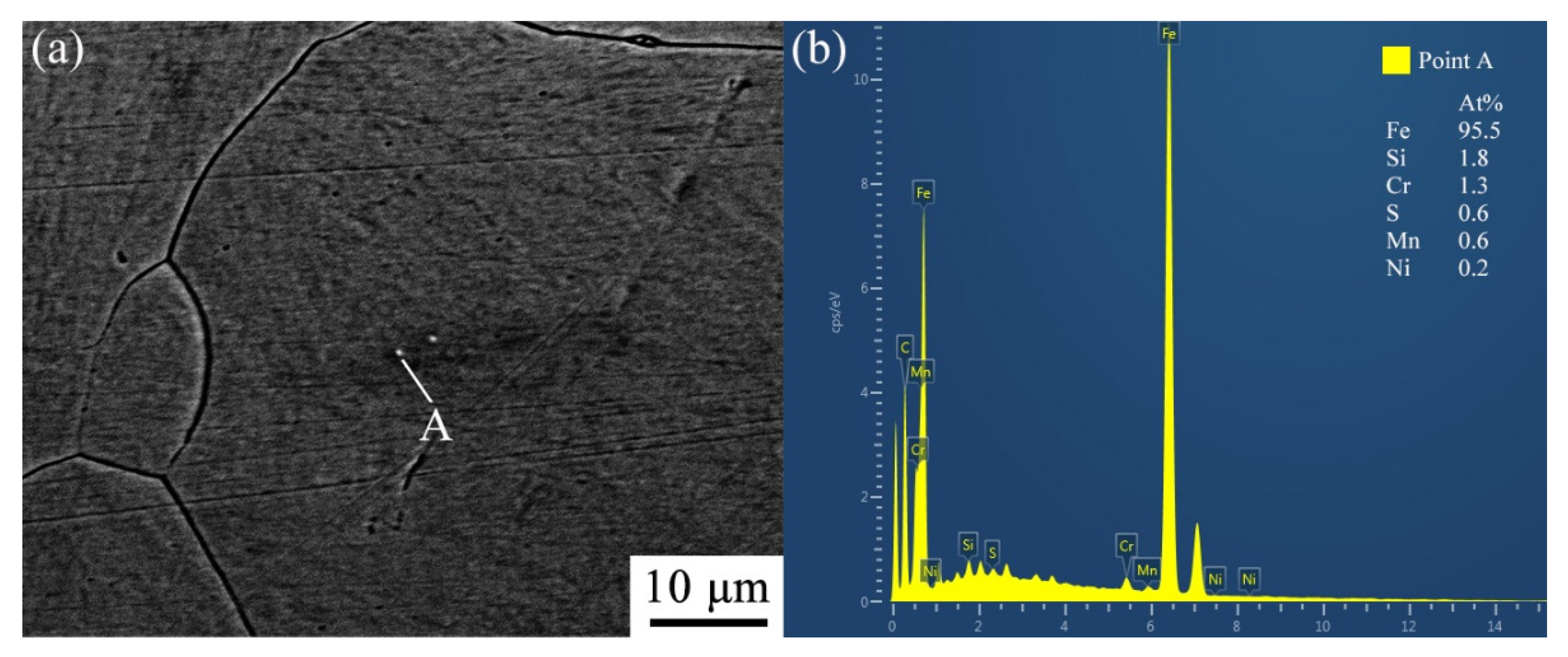
- Under the same deformation conditions, the flow stress curves of 40Cr and Q345B are consistent. 40Cr shows lower overall flow stress than Q345B due to softening of carbon and pinning of second phase particles (MnS). As the temperature increases, the flow stress difference between 40Cr and Q345B decreases.
- (2)
- Activation energy and activation volume of 40Cr and Q345B are not significantly different. Therefore, 40Cr and Q345B have the same rate-controlling mechanism, which is believed to be the motion of the creeping screw dislocation and the thermal fracture of the attracting junction.
- (3)
- In order to ensure that 40Cr and Q345B are in the optimum deformation region during the hot deformation, the optimal processing window for 40Cr/Q345B bimetallic blank at 1030–1100 °C and 0.5–1 s−1 with a strain of 0.6 are recommended. The bimetallic blanks exhibit good deformation coordination in the optimum processing window.
- (4)
- Easily deformable outer layer than inner layer and gradient transition of bonding layer facilitate the coordinated deformation of the bimetallic ring blank during rolling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qin, F.C.; Li, Y.T.; Qi, H.P. A Method of Casting-Rolling Forming of Q345B Inner-Layer and 40Cr Outer-Layer. CN Patent ZL201510610375.4, 22 May 2017. [Google Scholar]
- Qin, F.C.; Li, Y.T.; Qi, H.P. A Method of Hot Rolling of Centrifugal Casting Duplex-Metallic with an Irregular Profile. CN Patent ZL201710264730.6, 24 July 2018. [Google Scholar]
- Qin, F.C.; Qi, H.P.; Li, Y.T.; Wu, Y.H.; Qi, H.Q.; Liu, C.Y. Advances in Compact Cast-Rolling Forming Of Ring-Shape Parts. Mater. Rep. 2020, 34, 19152–19165. [Google Scholar]
- Wang, Y.; Qin, F.; Qi, H.; Qi, H.; Meng, Z. Interfacial Bonding Behavior and Mechanical Properties of a Bimetallic Ring Blank Subjected to Centrifugal Casting Process. J. Mater. Eng. Perform. 2021, 31, 3249–3261. [Google Scholar] [CrossRef]
- Qin, F.; Qi, H.; Kang, Y.; Liu, C. Study on Constitutive Characteristic of As-Cast AA6061 Alloy under Plane Strain Compression Based on Orthogonal Analysis. Adv. Mater. Sci. Eng. 2019, 2019, 9328630. [Google Scholar] [CrossRef]
- Zhu, F.-J.; Wu, H.-Y.; Lin, M.-C.; Lee, S.; Wang, W.-R. Hot Workability Analysis and Development of a Processing Map for Homogenized 6069 Al Alloy Cast Ingot. J. Mater. Eng. Perform. 2015, 24, 2051–2059. [Google Scholar] [CrossRef]
- Chen, X.-M.; Lin, Y.; Wen, D.-X.; Zhang, J.-L.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- He, A.; Chen, L.; Hu, S.; Wang, C.; Huangfu, L. Constitutive analysis to predict high temperature flow stress in 20CrMo continuous casting billet. Mater. Des. 2013, 46, 54–60. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K.; Ebrahimi, G. Modeling the initiation of dynamic recrystallization using a dynamic recovery model. J. Alloys Compd. 2011, 509, 9387–9393. [Google Scholar] [CrossRef]
- Shi, C.; Chen, X.-G. Effect of vanadium on hot deformation and microstructural evolution of 7150 aluminum alloy. Mater. Sci. Eng. A 2014, 613, 91–102. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, X.M.; Dong, C.Y.; Zhao, X.Y. Influence of Hot Deformation and Precipitates on the Recrystallization of Nb-V-Ti Free-Cutting Steel. Metals 2020, 10, 1587. [Google Scholar] [CrossRef]
- Momeni, A.; Abbasi, S. On the opposition of dynamic recrystallization and solute dragging in steels. J. Alloys Compd. 2015, 622, 318–326. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Met. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Guo, L.; Wang, F.; Zhen, P.; Li, X.; Zhan, M. A novel unified model predicting flow stress and grain size evolutions during hot working of non-uniform as-cast 42CrMo billets. Chin. J. Aeronaut. 2019, 32, 531–545. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, X.; Wang, K.; Miao, C. Physics-Based Constitutive Model to Predict Dynamic Recovery Behavior of BFe10-1-2 Cupronickel Alloy during Hot Working. High Temp. Mater. Process. 2016, 35, 1037–1045. [Google Scholar] [CrossRef]
- Haghdadi, N.; Martin, D.; Hodgson, P. Physically-based constitutive modelling of hot deformation behavior in a LDX 2101 duplex stainless steel. Mater. Des. 2016, 106, 420–427. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, É. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- McQueen, H.J.; Yue, S.; Ryan, N.D.; Fry, E. Modeling the flow behavior of a medium carbon microalloyed steel under hot working conditions. J. Mater Process. Tech. 1995, 53, 293–310. [Google Scholar] [CrossRef]
- Ma, J.; Liu, J.; Guo, Z. Establishment of a two-stage constitutive model based on dislocation density theory for as-forged SA508 Gr.3Cl.1. Mater. Res. Express 2020, 7, 026521. [Google Scholar] [CrossRef]
- Medina, S.; Hernandez, C. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, G.; Xu, L. Rate-controlling mechanisms of hot deformation in a medium carbon vanadium microalloy steel. Mater. Sci. Eng. A 2013, 559, 262–267. [Google Scholar] [CrossRef]
- Sarkar, A.; Chandanshive, S.A.; Thota, M.K.; Kapoor, R. High temperature deformation behavior of Zr-1Nb alloy. J. Alloys Compd. 2017, 703, 56–66. [Google Scholar] [CrossRef]
- Shah, N.S.; Chakravartty, J.K.; Sarkar, A. Comparative study on hot deformation behaviour of P91, RAFM-CLAM and Low C RAFM-CLAM steels by processing maps. Fusion Eng. Des. 2018, 138, 109–118. [Google Scholar] [CrossRef]
- Zhao, H.; Qi, J.; Liu, G.; Su, R.; Sun, Z. A comparative study on hot deformation behaviours of low-carbon and medium-carbon vanadium microalloyed steels. J. Mater. Res. Technol. 2020, 9, 11319–11331. [Google Scholar] [CrossRef]
- Xie, B.-S.; Cai, Q.-W.; Yu, W.; Xu, L.-X.; Ning, Z. Prediction for Flow Stress of 95CrMo Hollow Steel During Hot Compression. Acta Met. Sin. (Engl. Lett.) 2016, 30, 250–260. [Google Scholar] [CrossRef][Green Version]
- Mehrotra, B.N.; Tangri, K. High temperature (600 to 800 °C) thermally activated deformation behavior of α-Zircaloy-4-oxygen alloys. Acta Metall. 1980, 28, 1385–1394. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Sarkar, A.; Suwas, S. Investigation of stress-strain response, microstructure and texture of hot deformed pure molybdenum. Int. J. Refract. Met. Hard Mater. 2018, 73, 168–182. [Google Scholar] [CrossRef]
- Li, D.J.; Feng, Y.R.; Yin, Z.F.; Shangguan, F.S.; Wang, K.; Liu, Q.; Hu, F. Hot deformation behavior of an austenitic Fe-20Mn-3Si-3Al transformation induced plasticity steel. Mater Des. 2012, 34, 713–718. [Google Scholar] [CrossRef]
- Wang, B.; Liu, X.; Wang, G. Dynamic recrystallization behavior and microstructural evolution in a Mn–Cr gear steel. Mater. Sci. Eng. A 2005, 393, 102–108. [Google Scholar] [CrossRef]
- Cjba, B.; He, B.; Rp, A.; Is, C.; Jc, A.; Rn, A. The effect of microstructure and strain rate on the 25 °C and 700 °C compression deformation behavior of powder metallurgy processed Ti-45Al-2Nb-2Mn (at.%)-0.8 TiB 2 (vol%) alloy. Mater. Charact. 2021, 172, 110856. [Google Scholar]
- Prasad, Y.; Rao, K.P.; Sasidhara, S. Hot Working Guide: Compendium of Processing Maps, 2nd ed.; ASM international: Geauga, OH, USA, 2015. [Google Scholar]
- Wu, C.; Han, S. Hot Deformation Behavior and Dynamic Recrystallization Characteristics in a Low-Alloy High-Strength Ni–Cr–Mo–V Steel. Acta Met. Sin. (Engl. Lett.) 2018, 31, 963–974. [Google Scholar] [CrossRef]
- Zhao, H.; Qi, J.; Su, R.; Zhang, H.; Chen, H.; Bai, L.; Wang, C. Hot deformation behaviour of 40CrNi steel and evaluation of different processing map construction methods. J. Mater. Res. Technol. 2020, 9, 2856–2869. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, Z.; Volinsky, A.; Tian, B.; Sun, H.; Liu, P.; Liu, Y. Processing maps for the Cu-Cr-Zr-Y alloy hot deformation behavior. Mater. Sci. Eng. A 2016, 662, 320–329. [Google Scholar] [CrossRef]
- Momeni, A.; Dehghani, K. Characterization of hot deformation behavior of 410 martensitic stainless steel using constitutive equations and processing maps. Mater. Sci. Eng. A 2010, 527, 5467–5473. [Google Scholar] [CrossRef]
- Prasad, Y.; Seshacharyulu, T. Processing maps for hot working of titanium alloys. Mater. Sci. Eng. A 1998, 243, 82–88. [Google Scholar] [CrossRef]
- Zhai, R.; Wang, W.; Ma, R.; Zhang, S.; Ma, S.; Li, L.; Gong, S.; Zhang, H. Hot Deformation Behavior and Processing Map of As-Cast 40CrNiMo Alloy Steel. J. Mater. Eng. Perform. 2020, 29, 964–974. [Google Scholar] [CrossRef]
- Li, Z.; Xie, H.B.; Jia, F.H.; Lu, Y.; Yuan, X.Q.; Jiao, S.H.; Jiang, Z.Y. Study on Deformation Characteristics and Microstructure Evolution of 2205/AH36 Bimetal Composite in a Novel Hot Forming Process. Metals 2020, 10, 1375. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, J.; Jia, F.; Lu, Y.; Liang, X.; Yuan, X.; Jiao, S.; Zhou, C.; Jiang, Z. Hot deformation behaviour and interfacial characteristics of bimetal composite at elevated temperatures. Intermetallics 2020, 125, 106893. [Google Scholar] [CrossRef]
- Li, Z.; Lin, Y.; Zhang, L.; Jia, F.; Jiang, Z.; Jiao, S. Investigation of compact tensile and fracture mechanical properties of a duplex stainless steel bimetal composite with the interfacial zone. J. Mater. Res. Technol. 2022, 19, 809–820. [Google Scholar] [CrossRef]
- Xu, J.; Gao, X.; Jiang, Z.; Wei, D.; Jiao, S. Microstructure and hot deformation behaviour of high-carbon steel/low-carbon steel bimetal prepared by centrifugal composite casting. Int. J. Adv. Manuf. Technol. 2015, 86, 817–827. [Google Scholar] [CrossRef]
- Gao, X.; Jiang, Z.; Wei, D.; Li, H.; Jiao, S.; Xu, J.; Zhang, X.; Han, J.; Chen, D. Constitutive analysis for hot deformation behaviour of novel bimetal consisting of pearlitic steel and low carbon steel. Mater. Sci. Eng. A 2014, 595, 1–9. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U. Kinetics of flow and strain-hardening. Acta Met. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Wei, H.-L.; Liu, G.-Q.; Zhao, H.-T.; Zhang, M.-H. Effect of carbon content on hot deformation behaviors of vanadium microalloyed steels. Mater. Sci. Eng. A 2014, 596, 112–120. [Google Scholar] [CrossRef]
- Lesuer, D.R.; Syn, C.K.; Sherby, O.D.; Wadsworth, J.; Lewandowski, J.J.; Hunt, W.H. Mechanical behaviour of laminated metal composites. Metall. Rev. 1996, 41, 169–197. [Google Scholar] [CrossRef]
- Hua, L.; Huang, X.G.; Zhu, C.D. Theory and Technology of Ring Rolling, 1st ed.; Mechanical Industry Press: Beijing, China, 2001; pp. 54–58. [Google Scholar]
- Qian, D.; Pan, Y. 3D coupled macro–microscopic finite element modelling and simulation for combined blank-forging and rolling process of alloy steel large ring. Comput. Mater. Sci. 2013, 70, 24–36. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Sun, Y.; Wan, Z.P.; Hu, L.X.; Ren, J.S. Characterization of hot processing parameters of powder metallurgy TiAl-based alloy based on the activation energy map and processing map. Mater. Des. 2015, 86, 922–932. [Google Scholar] [CrossRef]
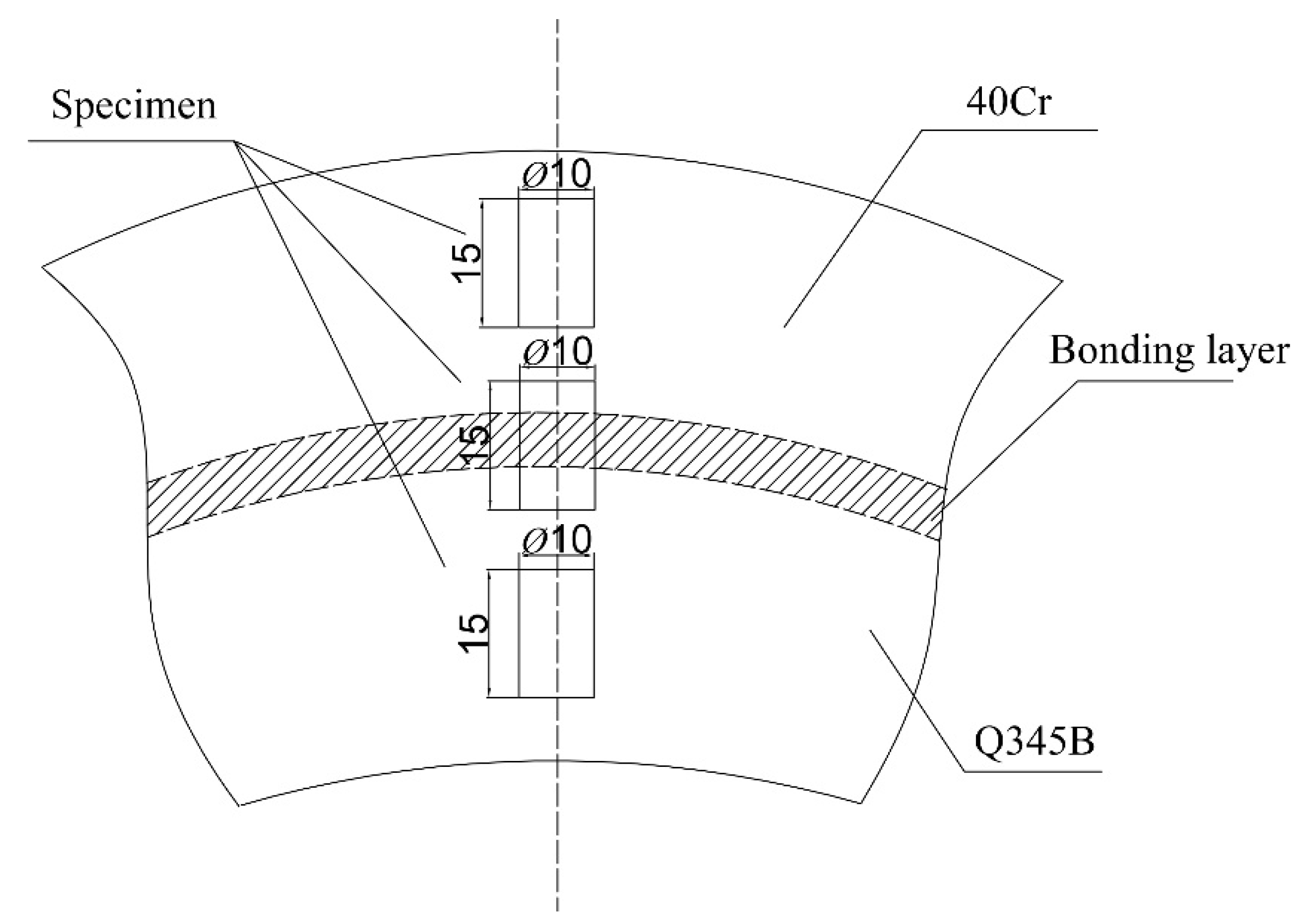






| Parameters | Values |
|---|---|
| Material thickness ratio | 1:1 |
| Pouring temperature of outer layer | 1560 °C |
| Pouring temperature of inner layer | 1580 °C |
| Pouring interval | 161 s |
| Mold release temperature | 850 °C |
| Materials | C | Cr | Mn | Si | P | S | Ni | Cu | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 40Cr | 0.445 | 1.091 | 0.591 | 0.301 | 0.010 | 0.005 | <0.3 | ≤0.030 | Bal. |
| Q345B | 0.168 | 0.299 | 1.609 | 0.461 | 0.013 | 0.007 | ≤0.5 | ≤0.030 | Bal. |
| Steel | A (s−1) | β | n1 | α (MPa−1) | n | Q (kJ/mol) |
|---|---|---|---|---|---|---|
| 40Cr | 8.73 × 1012 | 0.094 | 6.353 | 0.01480 | 4.547 | 366.901 |
| Q345 | 2.79 × 1013 | 0.092 | 6.629 | 0.01391 | 4.782 | 380.307 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Qi, H.; Pei, M.; Li, Z.; Qin, F.; Jia, L. Hot Deformation Behavior Coordination and Processing Maps of 40Cr/Q345B Bimetallic Blank by Centrifugal Casting. Metals 2022, 12, 1281. https://doi.org/10.3390/met12081281
Jia Y, Qi H, Pei M, Li Z, Qin F, Jia L. Hot Deformation Behavior Coordination and Processing Maps of 40Cr/Q345B Bimetallic Blank by Centrifugal Casting. Metals. 2022; 12(8):1281. https://doi.org/10.3390/met12081281
Chicago/Turabian StyleJia, Yanlong, Huiping Qi, Mengmeng Pei, Zhenjiang Li, Fangcheng Qin, and Lu Jia. 2022. "Hot Deformation Behavior Coordination and Processing Maps of 40Cr/Q345B Bimetallic Blank by Centrifugal Casting" Metals 12, no. 8: 1281. https://doi.org/10.3390/met12081281
APA StyleJia, Y., Qi, H., Pei, M., Li, Z., Qin, F., & Jia, L. (2022). Hot Deformation Behavior Coordination and Processing Maps of 40Cr/Q345B Bimetallic Blank by Centrifugal Casting. Metals, 12(8), 1281. https://doi.org/10.3390/met12081281






