A Comparison Study of Fatigue Behavior of S355J2+N, S690QL and X37CrMoV5-1 Steel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fatigue Behavior Assessment
2.2. Basic Properties of Studied Steels
2.3. Fatigue Analysis Using the Experimental Method
3. Results
4. Discussion
5. Conclusions
- The mild-strength S355J2+N steel was used as a reference point and was compared with S690QL and X37CrMoV5-1 steel.
- The fatigue behavior was investigated using uniaxial tension–compression stress-controlled experiments, with stress ratio R = −1, on smooth cylindrical specimens.
- Considering the high cycle fatigue regime and obtained S–N curves for all materials, the X37CrMoV5-1 steel grade showed superior fatigue behavior, and due to its yield strength, the X37CrMoV5-1 steel grade showed a higher endurance limit than the S355J2+N and S690QL steel grades at the same stress amplitudes.
- For the high cycle load, if we observe Basquin curves, the fatigue limit for the X37CrMoV5-1 steel grade tends to be similar to that of S690QL, even though these materials have very different stress–strain curves for the uniaxial tensile test.
- The X37CrMoV5-1 steel has a huge scattering of fatigue results, and it is very important to produce this steel under conditions as controlled as possible so that the structure is as uniform as possible.
- The utilization of high-strength steels increases the fatigue sensitivity of the construction components in comparison to components made of structural (mild-strength) steels because of the reduced cross-section and, consequently, increased stress.
- Therefore, such a new design would require verification using a numerical method, such as finite element analysis, and extensive experimental testing of the prototype [7], but the final product would have better quality and superior features.
- As a concluding remark, the design of construction components with high-strength steels (S690QL steel grade) should take advantage of the superior resistance of these steels to static and service (fatigue) loads.
- The S690QL steel grade has inferior fatigue properties to those of X37CrMoV5-1; however, it has much better weldability [12], and, therefore, it represents the optimum solution for designing lightweight, highly loaded constructions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stanford, N. Introducing Alloys: A Journal for Fundamental and Applied Research. Alloys 2022, 1, 1–2. [Google Scholar] [CrossRef]
- Esha, E.; Hausmann, J. Development of an Analytical Model to Predict Stress–Strain Curves of Short Fiber-Reinforced Polymers with Six Independent Parameters. J. Compos. Sci. 2022, 6, 140. [Google Scholar] [CrossRef]
- Tisza, M.; Czinege, I. Comparative Study of the Application of Steels and Aluminium in Lightweight Production of Automotive Parts. Int. J. Lightweight Mater. Manuf. 2018, 1, 229–238. [Google Scholar] [CrossRef]
- Moynihan, M.C.; Allwood, J.M. Utilization of Structural Steel in Buildings. Proc. R. Soc. A 2014, 470, 20140170. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L. Prediction Method of Fatigue Crack Growth Life of High-Strength Steel for Industry 4.0. IETE J. Res. 2022, 1–8. [Google Scholar] [CrossRef]
- Milovanović, V.; Zivković, M.; Jovičić, G.; Kozak, D. The Analysis of Choice Influence in Fatigue Failure Criteria on Integrity Assessment of Wagon Structure. Teh. Vjesn. 2016, 23, 701–705. [Google Scholar] [CrossRef] [Green Version]
- Correia, J.A.F.O.; da Silva, A.L.L.; Xin, H.; Lesiuk, G.; Zhu, S.-P.; de Jesus, A.M.P.; Fernandes, A.A. Fatigue Performance Prediction of S235 Base Steel Plates in the Riveted Connections. Structures 2021, 30, 745–755. [Google Scholar] [CrossRef]
- Ho, H.C.; Chung, K.F.; Xiao, T.Y.; Yam, M.C.H.; Nethercot, D.A. Non-Linear Necking Behaviour of S275 to S960 Structural Steels under Monotonic Tension. Eng. Struct. 2022, 261, 114263. [Google Scholar] [CrossRef]
- Guo, Y.B.; Ho, H.C.; Chung, K.F.; Elghazouli, A.Y. Cyclic Deformation Characteristics of S355 and S690 Steels under Different Loading Protocols. Eng. Struct. 2020, 221, 111093. [Google Scholar] [CrossRef]
- Anandavijayan, S.; Mehmanparast, A.; Braithwaite, J.; Brennan, F.; Chahardehi, A. Material Pre-Straining Effects on Fatigue Behaviour of S355 Structural Steel. J. Constr. Steel Res. 2021, 183, 106707. [Google Scholar] [CrossRef]
- Milovanović, V.; Dunić, V.; Rakić, D.; Živković, M. Identification Causes of Cracking on the Underframe of Wagon for Containers Transportation—Fatigue Strength Assessment of Wagon Welded Joints. Eng. Fail. Anal. 2013, 31, 118–131. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, C.; Xie, J.; Hong, Y. Effects of Loading Frequency and Loading Type on High-Cycle and Very-High-Cycle Fatigue of a High-Strength Steel. Materials 2018, 11, 1456. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- EN 1993-1-9:2005; Eurocode 3: Design of Steel Structures—Part 1-9: Fatigue. European Committee for Standardization: Brussels, Belgium, 2005.
- EN 13001-3-1:2012 + A2:2018; Cranes—General Design—Part 3-1: Limit States and Proof Competence of Steel Structure. European Committee for Standardization: Brussels, Belgium, 2018.
- Toasa Caiza, P.D.; Ummenhofer, T. A Probabilistic Stüssi Function for Modelling the S–N Curves and Its Application on Specimens Made of Steel S355J2+N. Int. J. Fatigue 2018, 117, 121–134. [Google Scholar] [CrossRef]
- Spriestersbach, D.; Brodyanski, A.; Lösch, J.; Kopnarski, M.; Kerscher, E. Very High Cycle Fatigue of High-Strength Steels: Crack Initiation by FGA Formation Investigated at Artificial Defects. Procedia Struct. Integr. 2016, 2, 1101–1108. [Google Scholar] [CrossRef] [Green Version]
- Glodež, S.; Knez, M.; Jezernik, N.; Kramberger, J. Fatigue and Fracture Behaviour of High Strength Steel S1100Q. Eng. Fail. Anal. 2009, 16, 2348–2356. [Google Scholar] [CrossRef]
- Pijpers, R.J.M.; Kolstein, M.H.; Romeijn, A.; Bijlaard, F.S.K. Fatigue experiments on very high strength steel base material and transverse but welds. Adv. Steel Constr. 2009, 5, 14–32. [Google Scholar] [CrossRef] [Green Version]
- Yin, G.-Q.; Kang, X.; Zhao, G.-P. Fatigue Properties of the Ultra-High Strength Steel TM210A. Materials 2017, 10, 1057. [Google Scholar] [CrossRef]
- Yang, S.; Sun, J. Multiaxial Fatigue Life Assessment of 304 Austenitic Stainless Steel with a Novel Energy-Based Criterion. Int. J. Fatigue 2022, 159, 106728. [Google Scholar] [CrossRef]
- Wei, H.; Liu, Y. An Energy-Based Model to Assess Multiaxial Fatigue Damage under Tension-Torsion and Tension-Tension Loadings. Int. J. Fatigue 2020, 141, 105858. [Google Scholar] [CrossRef]
- Benedetti, M.; Berto, F.; Le Bone, L.; Santus, C. A Novel Strain-Energy-Density Based Fatigue Criterion Accounting for Mean Stress and Plasticity Effects on the Medium-to-High-Cycle Uniaxial Fatigue Strength of Plain and Notched Components. Int. J. Fatigue 2020, 133, 105397. [Google Scholar] [CrossRef]
- Branco, R.; Prates, P.A.; Costa, J.D.; Berto, F.; Kotousov, A. New Methodology of Fatigue Life Evaluation for Multiaxially Loaded Notched Components Based on Two Uniaxial Strain-Controlled Tests. Int. J. Fatigue 2018, 111, 308–320. [Google Scholar] [CrossRef]
- Ulewicz, R.; Szataniak, P.; Novy, F.; Trsko, L.; Bokuvka, O. Fatigue Characteristics of Structural Steels in the Gigacycle Region of Loading. Mater. Today Proc. 2017, 4, 5979–5984. [Google Scholar] [CrossRef]
- Nový, F.; Petrů, M.; Trško, L.; Jambor, M.; Bokůvka, O.; Lago, J. Fatigue Properties of Welded Strenx 700 MC HSLA Steel after Ultrasonic Impact Treatment Application. Mater. Today Proc. 2020, 32, 174–178. [Google Scholar] [CrossRef]
- Riccardo, G.; Rivolta, B.; Gorla, C.; Concli, F. Cyclic Behavior and Fatigue Resistance of AISI H11 and AISI H13 Tool Steels. Eng. Fail. Anal. 2021, 121, 105096. [Google Scholar] [CrossRef]
- Dobrzański, L.A.; Polok, M.; Adamiak, M. Structure and Properties of Wear Resistance PVD Coatings Deposited onto X37CrMoV5-1 Type Hot Work Steel. J. Mater. Process. Technol. 2005, 164–165, 843–849. [Google Scholar] [CrossRef]
- Pralea, B.; Nagit, G. Study of the Milling Tools When Machining X37CrMoV5-1 after Heat Treatment. Procedia Manuf. 2019, 32, 877–882. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, C.L.; Zhao, Z.; Li, A.P.; Xu, X.L.; Shi, W.B. Low Cycle Fatigue Behaviour of a Cr–Mo–V Matrix-Type High-Speed Steel Used for Cold Forging. Mater. Des. 2013, 44, 612–621. [Google Scholar] [CrossRef]
- Basquin, O.H. The Exponential Law of Endurance Tests. Proc. ASTM 1910, 10, 625–630. [Google Scholar]
- Stephens, R.; Fatemi, A.; Stephens, R.; Fuchs, H. Metal Fatigue in Engineering; John Wiley & Sons Inc.: New York, NY, USA, 2001. [Google Scholar]
- Manson, S.S. Discussion: “Experimental Support for Generalized Equation Predicting Low Cycle Fatigue”. J. Basic Eng. 1962, 84, 537–541. [Google Scholar] [CrossRef]
- Morrow, J. Cyclic Plastic Strain Energy and Fatigue of Metals. In Internal Friction, Damping, and Cyclic Plasticity; Lazan, B., Ed.; ASTM International: Montgomery, PA, USA, 1965; pp. 43–45. ISBN 9780803161603. [Google Scholar]
- Mlikota, M.; Schmauder, S.; Božić, Ž. Calculation of the Wöhler (S–N) Curve Using a Two-Scale Model. Int. J. Fatigue 2018, 114, 289–297. [Google Scholar] [CrossRef]
- Živković, J.; Dunić, V.; Milovanović, V.; Pavlović, A.; Živković, M. A Modified Phase-Field Damage Model for Metal Plasticity at Finite Strains: Numerical Development and Experimental Validation. Metals 2021, 11, 47. [Google Scholar] [CrossRef]
- Lazić, V.; Aleksandrović, S.; Arsić, D.; Sedmak, A.; Ilić, A.; Đorđević, M.; Ivanović, L. The Influence of Temperature on Mechanical Properties of the Base Material and Welded Joint Made of Steel S690QL. Metal.-Metall. 2016, 55, 213–216. [Google Scholar]
- Arsić, D.; Djordjević, M.; Zivković, J.; Sedmak, A.; Aleksandrović, S.; Lazić, V.; Rakić, D. Experimental-Numerical Study of Tensile Strength of the High-Strength Steel S690QL at Elevated Temperatures. Strength Mater. 2016, 48, 687–695. [Google Scholar] [CrossRef]
- Arsić, D.; Lazić, V.; Sedmak, A.; Aleksandrović, S.; Živković, J.; Djordjević, M.; Mladenović, G. Effect of Elevated Temperatures on Mechanical Properties of Ultra High Strength Hot Work Tool Steel H11. Trans. Famena 2020, 44, 71–82. [Google Scholar] [CrossRef]
- EN ISO 6892-1:2011; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization: Geneva, Switzerland, 2011.
- ASTM: E8M-01; Standard Test. Method for Tension Testing of Metalic Material. ASTM International: West Conshohocken, PA, USA, 2002.
- ASTM: E646-07; Standard Test. Method for Tensile Strain-Hardening Exponents (n-Values) of Methalic Sheet Materials. ASTM International: West Conshohocken, PA, USA, 2007.
- ASTM: E468-90; Standard Practice for Presentation on Constant Amplitude Fatigue Test Results for Metalic Materials. ASTM International: West Conshohocken, PA, USA, 2004.
- ASTM: E739-91; Standard Practice for Statistical Analysis of Linear or Linearised Stress-Life (S–N) and Strain-Life (ε-N) Fatigue Data. ASTM International: West Conshohocken, PA, USA, 2004.
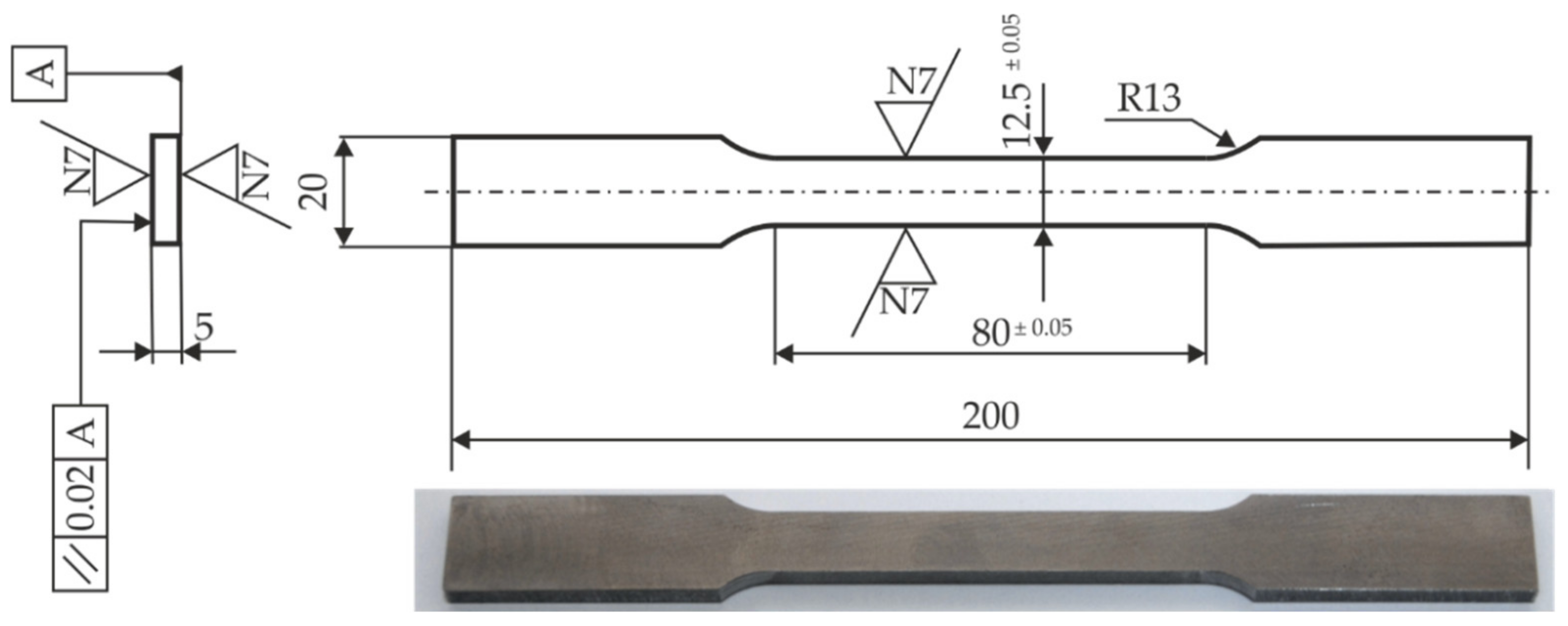






| Steel Grade | C | Si | Mn | P | S | Cr | Ni |
|---|---|---|---|---|---|---|---|
| S355J2+N | 0.161 | 0.046 | 1.488 | 0.0224 | 0.0086 | 0.040 | 0.014 |
| S690QL | 0.11 | 0.093 | 0.64 | 0.009 | 0.017 | - | - |
| X37CrMoV5-1 | 0.37 | 1.0 | 0.4 | <0.03 | <0.02 | 5.2 | - |
| Steel grade | Mo | Cu | N | Al | Nb | V | Ti |
| S355J2+N | 0.05 | 0.005 | 0.004 | 0.049 | - | - | - |
| S690QL | - | - | - | 0.017 | 0.088 | 0.19 | 0.14 |
| X37CrMoV5-1 | 1.2 | - | - | - | - | 0.4 | - |
| Steel Grade | Yield Strength (MPa) |
Tensile Strength (MPa) |
Young’s Modulus (GPa) |
Tensile Strain-Hardening Exponent (-) | Strength Coefficient (MPa) |
|---|---|---|---|---|---|
| S355J2+N | 401.24 | 539.36 | 206.26 | 0.2129 | 920.49 |
| S690QL | 767.97 | 818.08 | 228.89 | 0.0509 | 992.67 |
| X37CrMoV5-1 | 1499 | 1687 | 218 | 0.01667 | 1961.3 |
| Steel Grade | S355J2+N | ||
|---|---|---|---|
| Specimen Designation | Stress Amplitude σa (MPa) | Frequency (Hz) | Number of Cycles to Failure Nf |
| 1 | 350 | 10 | 12,843 |
| 2 | 350 | 10 | 14,564 |
| 3 | 350 | 10 | 18,394 |
| 4 | 310 | 10 | 25,817 |
| 5 | 310 | 10 | 40,336 |
| 6 | 310 | 10 | 53,241 |
| 7 | 280 | 10 | 62,710 |
| 8 | 280 | 10 | 93,607 |
| 9 | 280 | 10 | 112,985 |
| 10 | 250 | 15 | 130,770 |
| 11 | 250 | 15 | 1,097,720 |
| 12 | 225 | 15 | 352,961 |
| 13 | 225 | 15 | 371,019 |
| 14 | 200 | 15 | 1,562,024 |
| 15 | 200 | 15 | 2,000,000 |
| Steel Grade | S690QL | ||
| Specimen Designation | Stress Amplitude σa (MPa) | Frequency (Hz) | Number of Cycles to Failure Nf |
| 1 | 540 | 10 | 9857 |
| 2 | 540 | 10 | 11,227 |
| 3 | 540 | 10 | 8976 |
| 4 | 500 | 10 | 30,169 |
| 5 | 500 | 10 | 21,842 |
| 6 | 500 | 10 | 49,089 |
| 7 | 450 | 10 | 69,214 |
| 8 | 450 | 10 | 80,676 |
| 9 | 450 | 10 | 130,693 |
| 10 | 400 | 15 | 141,337 |
| 11 | 400 | 15 | 364,719 |
| 12 | 350 | 15 | 483,181 |
| 13 | 350 | 15 | 566,316 |
| 14 | 300 | 15 | 1,430,074 |
| 15 | 300 | 15 | 2,000,000 |
| Steel Grade | X37CrMoV5-1 | ||
| Specimen Designation | Stress Amplitude σa (MPa) | Frequency (Hz) | Number of Cycles to Failure Nf |
| 1 | 1000 | 10 | 10,613 |
| 2 | 1000 | 10 | 4025 |
| 3 | 1000 | 10 | 12,839 |
| 4 | 1000 | 10 | 12,280 |
| 5 | 800 | 10 | 87,089 |
| 6 | 800 | 10 | 12,554 |
| 7 | 800 | 10 | 95,546 |
| 8 | 600 | 15 | 38,035 |
| 9 | 600 | 15 | 58,871 |
| 10 | 600 | 15 | 25,192 |
| 11 | 600 | 15 | 70,825 |
| 12 | 600 | 15 | 51,055 |
| 13 | 500 | 15 | 164,237 |
| 14 | 500 | 15 | 2,110,777 |
| 15 | 500 | 15 | 2,583,827 |
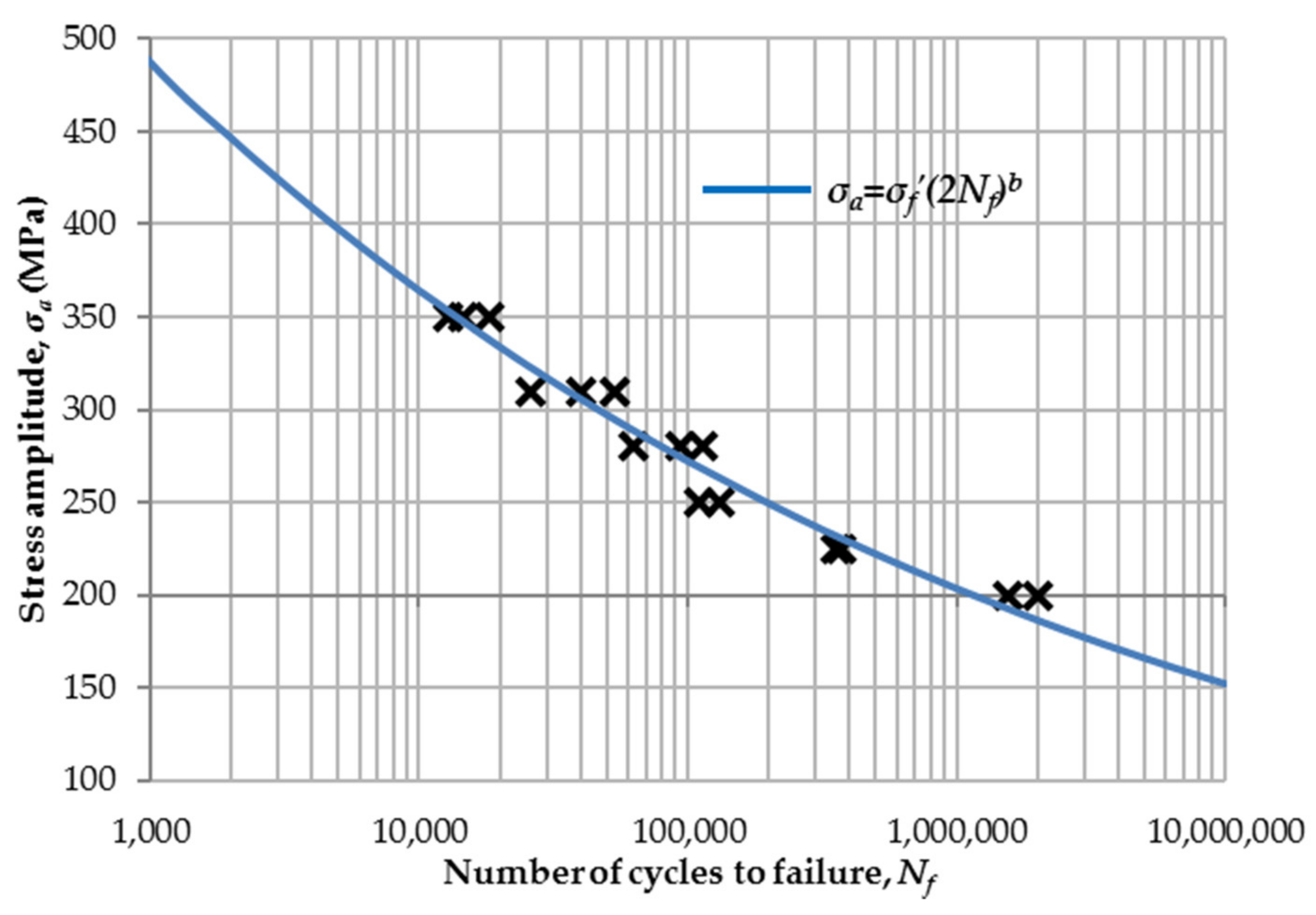
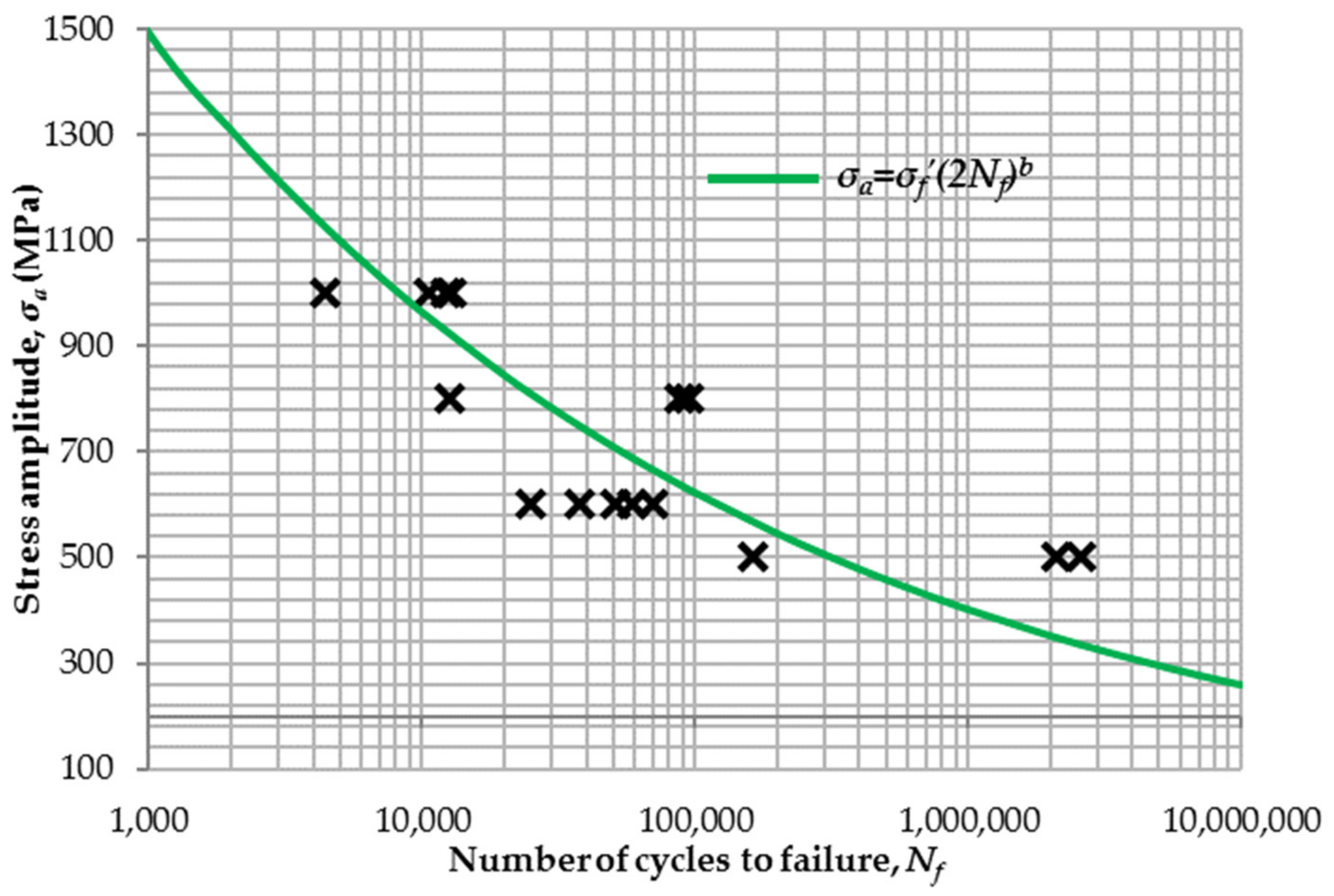
| Steel Grade | Fatigue Strength Coefficient (MPa) | Fatigue Strength Exponent (-) |
|---|---|---|
| S355J2+N | 1274.39 | −0.1264 |
| S690QL | 1814.61 | −0.1181 |
| X37CrMoV5-1 | 6321.03 | −0.1896 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milovanović, V.; Arsić, D.; Milutinović, M.; Živković, M.; Topalović, M. A Comparison Study of Fatigue Behavior of S355J2+N, S690QL and X37CrMoV5-1 Steel. Metals 2022, 12, 1199. https://doi.org/10.3390/met12071199
Milovanović V, Arsić D, Milutinović M, Živković M, Topalović M. A Comparison Study of Fatigue Behavior of S355J2+N, S690QL and X37CrMoV5-1 Steel. Metals. 2022; 12(7):1199. https://doi.org/10.3390/met12071199
Chicago/Turabian StyleMilovanović, Vladimir, Dušan Arsić, Miroslav Milutinović, Miroslav Živković, and Marko Topalović. 2022. "A Comparison Study of Fatigue Behavior of S355J2+N, S690QL and X37CrMoV5-1 Steel" Metals 12, no. 7: 1199. https://doi.org/10.3390/met12071199
APA StyleMilovanović, V., Arsić, D., Milutinović, M., Živković, M., & Topalović, M. (2022). A Comparison Study of Fatigue Behavior of S355J2+N, S690QL and X37CrMoV5-1 Steel. Metals, 12(7), 1199. https://doi.org/10.3390/met12071199








