Utilization of Bayesian Optimization and KWN Modeling for Increased Efficiency of Al-Sc Precipitation Strengthening
Abstract
:1. Introduction
2. Materials and Methods
- Precipitation and Strengthening Model—By simulating nucleation and growth of Al3Sc in Al-Sc binary alloys, this program predicts strengthening behavior with aging.
- Experimental Verification—Casting, aging, and hardness testing of Al-Sc binary alloys generated data for fitting and verification of the precipitation and strengthening model.
- Bayesian Optimization—Bayesian optimization (BO) was used to obtain the best fit between experimentally observed and simulated strengthening behavior. After the model was calibrated, BO was used again to suggest heat treatments for optimal strengthening.
2.1. Precipitation and Strengthening Model
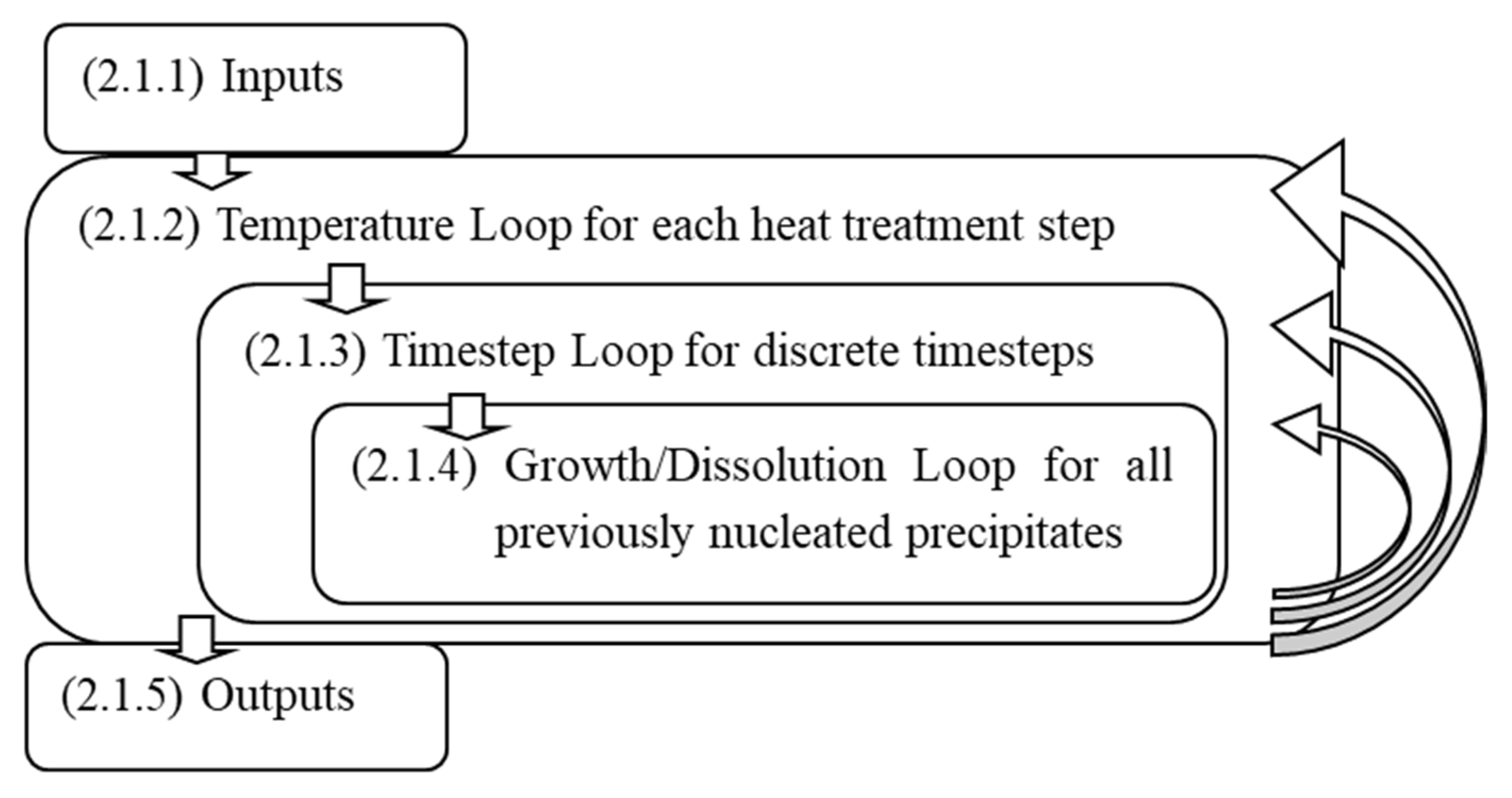
2.1.1. Model Inputs
2.1.2. Model Temperature Loop
2.1.3. Model Timestep Loop
2.1.4. Model Growth/Dissolution Loop
2.1.5. Model Outputs
2.1.6. Model Special Considerations
2.2. Experimental Verification Setup
2.3. Bayesian Optimization
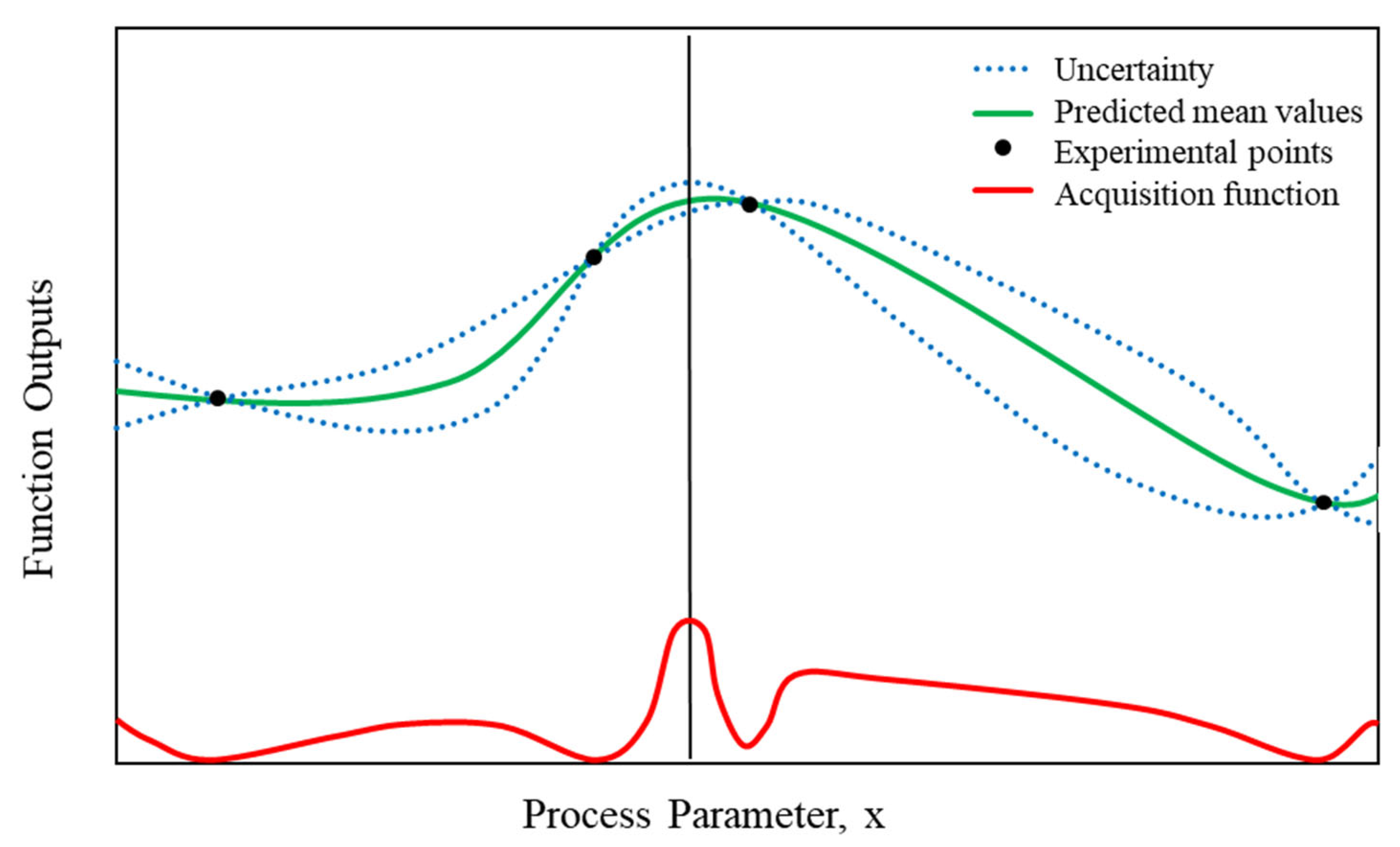
2.3.1. Gaussian Process
2.3.2. Acquisition Function
2.3.3. Illustration of Bayesian Optimization, Gaussian Process, and Acquisition Function
3. Results and Discussion
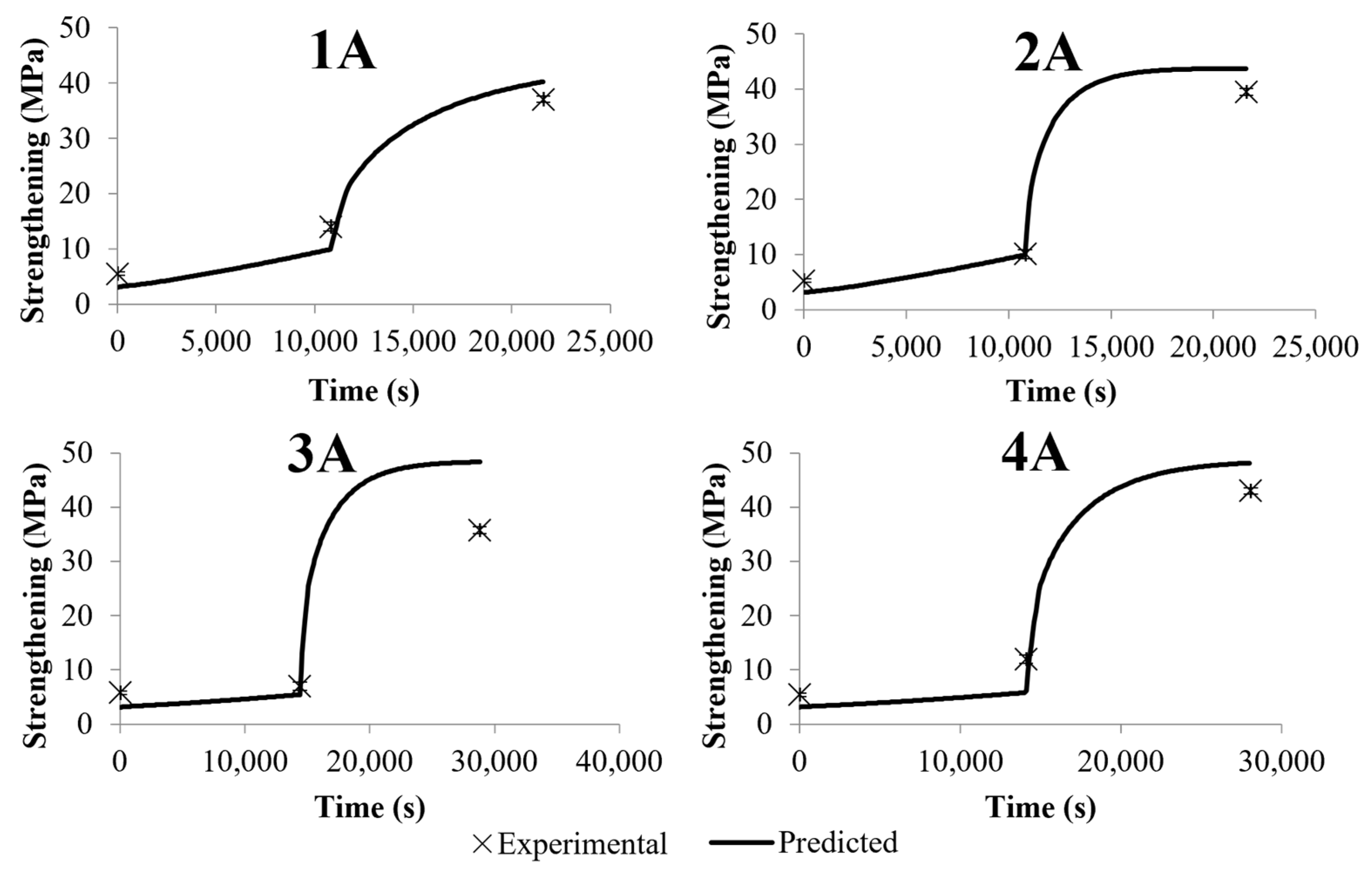
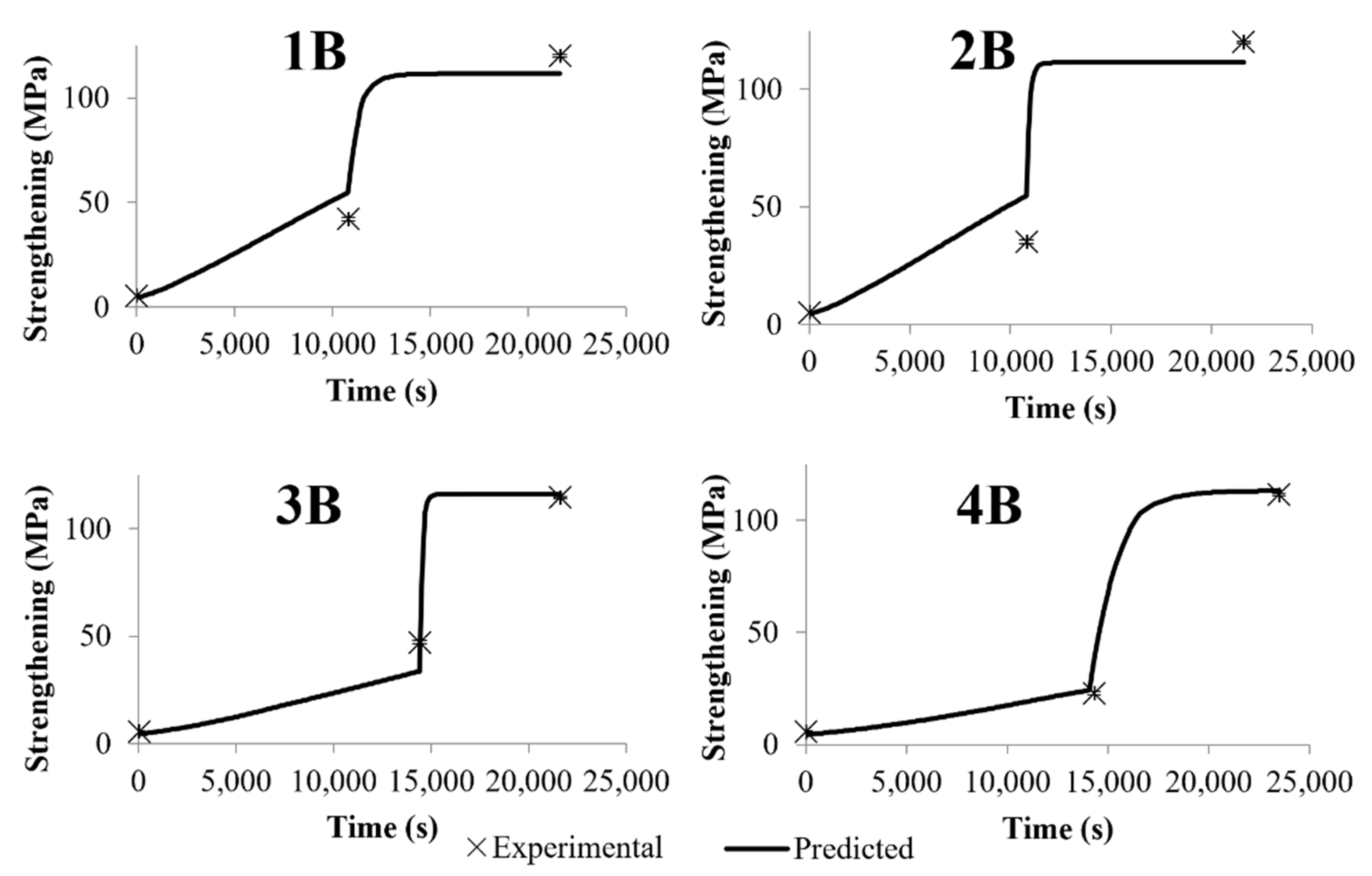
3.1. Bayesian Optimization of the Precipitation and Strengthening Model
3.2. Analysis of Simulation Trends
- During the first heat-treatment step (T1), the nucleation rate and precipitate growth rate maintained a relatively constant order of magnitude. The matrix concentration declined only slightly due to these effects, which were themselves due to the relatively slow rate of depletion corresponding with the precipitate formation of radii of 1 nm or less.
- At the onset of the second step (T2), the nucleation rate immediately dropped by several orders of magnitude, and the rate of precipitate growth increased significantly.
- As the pre-existing precipitates grew throughout the second step, the matrix became depleted at an accelerated rate and approached the equilibrium solubility at T2.
- As the matrix approached the equilibrium concentration, the nucleation rate and precipitate growth rate decreased until they were nearly negligible, as both were driven by matrix depletion.
- As the precipitates were no longer changing significantly in size or in number, all the predicted strengthening mechanisms plateaued.
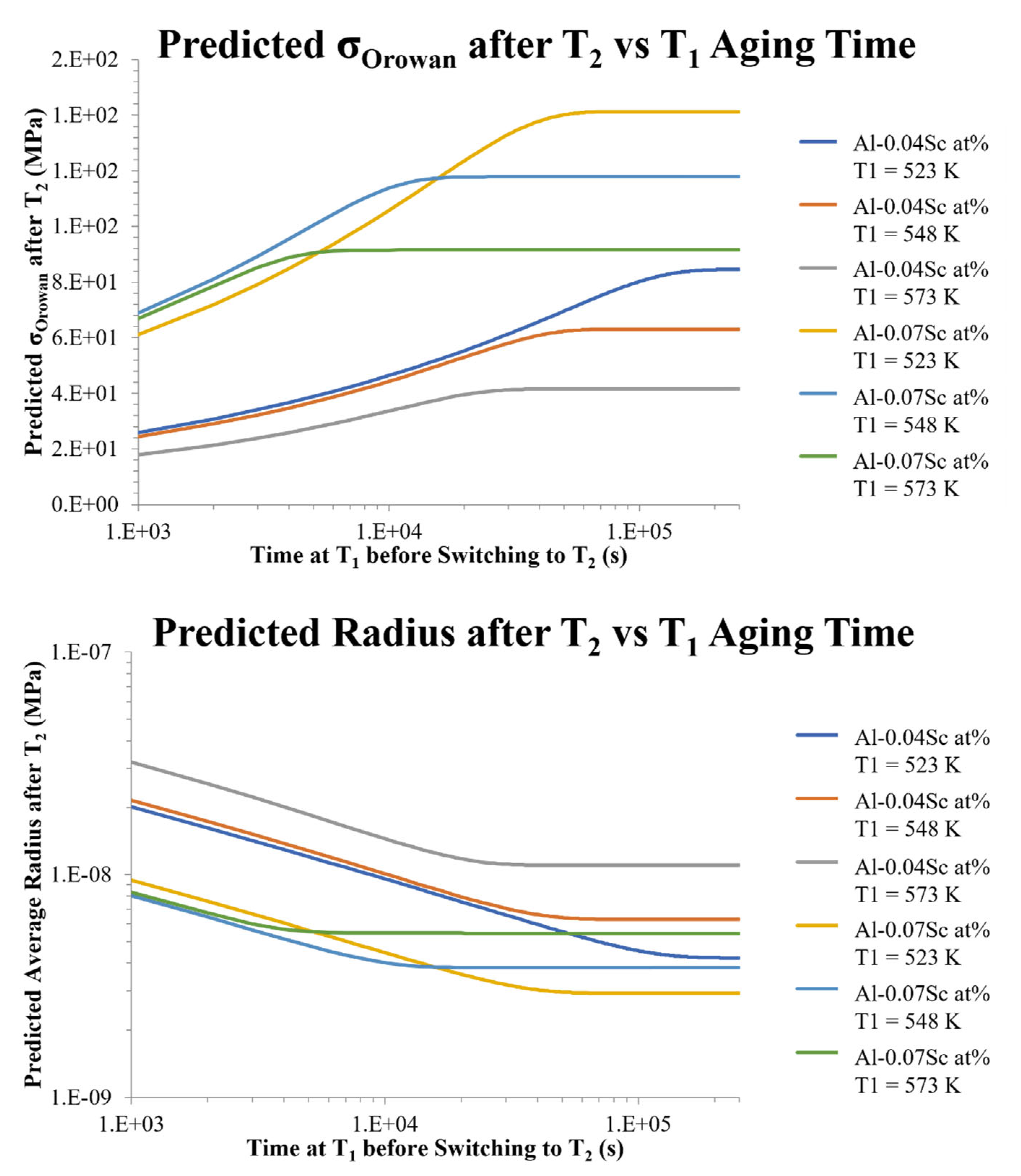
3.3. Optimized Heat Treatments with No Imposed Time Limit
- All long t1 heat treatments eventually reach an equilibrium, where nucleation effectively stops. At this point, no amount of additional heat treatment can continue to decrease the predicted final radius after T2, because the final average radius depends on the Sc atom-to-precipitate ratio. Ideal heat treatments should reach this equilibrium before moving to T2.
- When heat-treated at the same T1 until matrix depletion, Al-0.04Sc at% always results in larger average precipitates than Al-0.07Sc at%, as fewer precipitates can nucleate in alloys with lower concentration. Heat treatments of alloys with varying Sc content should take this into account.
- Heat treating at the lowest tested T1 of 523K (250 °C) requires more time than 548 or 573 K (275 or 300 °C), but it yields the highest strength. This is because, while the nucleation rates are similar between the three temperatures, considerably more precipitate growth occurs in the two higher temperatures. This results in larger precipitates at the end of t1 and in the more rapid depletion of the matrix. This rapid depletion accelerates the decline in the nucleation rate, limiting the final number of precipitates. Ideal heat treatments should be performed at low initial temperatures, such as 523 K (250 °C), for times that are sufficient to allow maximum strengthening.
- Between these two alloys, only Al-0.07Sc at% at 523 K (250 °C) achieved the target final average radius and, therefore, the maximum potential strengthening associated with the ordered strengthening mechanism. Ideal Al-Sc alloys for heat treatment should be of a concentration Al-0.07Sc at%, and, therefore, be able to achieve the maximum potential strengthening.
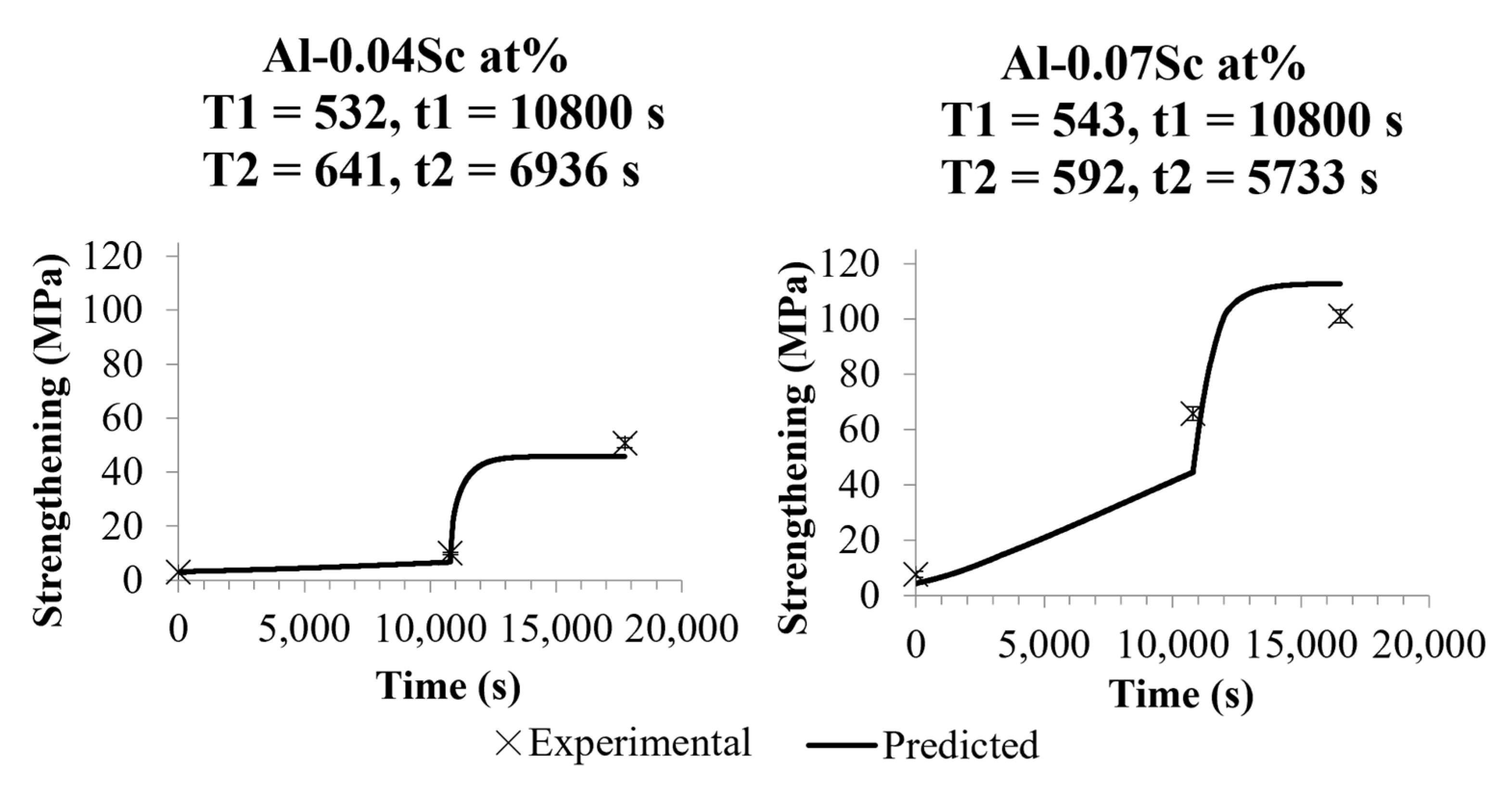
3.4. Optimized Heat Treatments with Imposed Time Limits
4. Conclusions
- In Al-Sc alloys that do not achieve order strengthening dominance, the greatest strength can be achieved by minimizing the final average radius. This can be achieved by initially holding at a heat treatment temperature with ample nucleation activity and minimal growth activity (e.g. 523 K) until the nucleation rate is negligible due to decreasing supersaturation. At this point, the maximum number of precipitates possible has been reached, and continuing heat treatment at this temperature, or at a reasonably high temperature (e.g. 573 K) results in a minimal average radius.
- Ideally, two heat-treatment steps should be used for Al-Sc alloys, as full the depletion of the matrix after the initial nucleation treatment at proper nucleation temperatures can be prohibitively time-consuming. Adding a short second step at a higher temperature can significantly decrease the total required time.
- Sc concentrations greater than Al-0.07Sc at% are suggested in order for the Sc additions to achieve their full potential. The simulations showed that increasing the solute concentration decreased the final achievable average sizes of the precipitates by allowing a greater comparative number density of the precipitates to be nucleated. An alloy with Al-0.04Sc at% is predicted to be unable to produce precipitates small enough to allow ordered strengthening dominance, while the Al-0.07Sc at% was predicted to be able to form small enough precipitates in only a minority of circumstances (e.g., T1 = 523 K, t1 = 10 h).
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knipling, K.E.; Dunand, D.C.; Seidman, D.N. Criteria for developing castable, creep-resistant aluminum-based alloys: A review. Z. Für Met. 2006, 97, 246–265. [Google Scholar] [CrossRef] [Green Version]
- Knipling, K.E.; Seidman, D.N.; Dunand, D.C. Ambient-and high-temperature mechanical properties of isochronally aged Al–0.06 Sc, Al–0.06 Zr and Al–0.06 Sc–0.06 Zr (at.%) alloys. Acta Mater. 2011, 59, 943–954. [Google Scholar] [CrossRef] [Green Version]
- Seidman, D.N.; Marquis, E.A.; Dunand, D.C. Precipitation strengthening at ambient and elevated temperatures of heat-treatable Al (Sc) alloys. Acta Mater. 2002, 50, 4021–4035. [Google Scholar] [CrossRef]
- Marquis, E.A.; Seidman, D.N. Nanoscale structural evolution of Al3Sc precipitates in Al (Sc) alloys. Acta Mater. 2001, 49, 1909–1919. [Google Scholar] [CrossRef] [Green Version]
- Knipling, K.E.; Karnesky, R.A.; Lee, C.P.; Dunand, D.C.; Seidman, D.N. Precipitation evolution in Al–0.1 Sc, Al–0.1 Zr and Al–0.1 Sc–0.1 Zr (at.%) alloys during isochronal aging. Acta Mater. 2010, 58, 5184–5195. [Google Scholar] [CrossRef]
- Wagner, R.; Kampmann, R.; Voorhees, P. Homogeneous Second-Phase Precipitation. In Phase Transformations in Materials; Kostorz, G., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2001; pp. 309–480. [Google Scholar]
- Robson, J.D. Modelling the overlap of nucleation, growth and coarsening during precipitation. Acta Mater. 2004, 52, 4669–4676. [Google Scholar] [CrossRef]
- Robson, J.D.; Jones, M.J.; Prangnell, P.B. Extension of the N-model to predict competing homogeneous and heterogeneous precipitation in Al-Sc alloys. Acta Mater. 2003, 51, 1453–1468. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the human out of the loop: A review of bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Dai Nguyen, T.; Gupta, S.; Rana, S.; Nguyen, V.; Venkatesh, S.; Deane, K.J.; Sanders, P.G. Cascade Bayesian Optimization. In Australasian Joint Conference on Artificial Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 268–280. [Google Scholar]
- Nguyen, V.; Rana, S.; Gupta, S.K.; Li, C.; Venkatesh, S. Budgeted batch Bayesian optimization. In Proceedings of the Data Mining (ICDM), 2016 IEEE 16th International Conference on IEEE, Barcelona, Spain, 12–15 December 2016; pp. 1107–1112. [Google Scholar]
- Murray, J.L. Al-Sc (aluminum-scandium) system. J. Phase Equilibria Diffus. 1998, 19, 380. [Google Scholar] [CrossRef]
- Booth-Morrison, C.; Mao, Z.; Diaz, M.; Dunand, D.C.; Wolverton, C.; Seidman, D.N. Role of silicon in accelerating the nucleation of Al3 (Sc, Zr) precipitates in dilute Al–Sc–Zr alloys. Acta Mater. 2012, 60, 4740–4752. [Google Scholar] [CrossRef]
- Manjeera, M. A First-Principles Methodology for Diffusion Coefficients in Metals and Dilute Alloys. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2008. [Google Scholar]
- Introduction of Thermodynamics of Materials-David R. Gaskell. Available online: https://www.scribd.com/doc/91993285/Introduction-of-Thermodynamics-of-Materials-David-R-Gaskell (accessed on 4 March 2016).
- Ardell, A.J. Precipitation hardening. Metall. Trans. 1985, 16, 2131–2165. [Google Scholar] [CrossRef]
- Courtney, T. Mechanical Behavior of Materials, 2nd ed.; Waveland Pr Inc.: Long Grove, IL, USA, 2005. [Google Scholar]
- Perez, M. Gibbs–Thomson effects in phase transformations. Scr. Mater. 2005, 52, 709–712. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Močkus, J. On Bayesian methods for seeking the extremum. In Optimization Techniques IFIP Technical Conference; Springer: Berlin/Heidelberg, Germany, 1975; pp. 400–404. [Google Scholar]
- Nguyen, V.; Gupta, S.; Rana, S.; Li, C.; Venkatesh, S. Regret for Expected Improvement over the Best-Observed Value and Stopping Condition. In Proceedings of the 9th Asian Conference on Machine Learning, Seoul, Korea, 15–17 November 2017. [Google Scholar]
- Hyland, R.W. Homogeneous nucleation kinetics of Al3Sc in a dilute Al-Sc alloy. Metall. Trans. 1992, 23, 1947–1955. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, W.; Seidman, D.N.; Wolverton, C. First-principles study of the nucleation and stability of ordered precipitates in ternary Al–Sc–Li alloys. Acta Mater. 2011, 59, 3012–3023. [Google Scholar] [CrossRef]
- Yang, Y.; Licavoli, J.J.; Sanders, P.G. Improved strengthening in supersaturated Al-Sc-Zr alloy via melt-spinning and extrusion. J. Alloys. Compd. 2020, 826, 154185. [Google Scholar] [CrossRef]




| Target Composition (at%) | ICP-OES Determined (at%) | |||
|---|---|---|---|---|
| Alloy (at%) | Sc | Si | Sc | Si |
| Al-0.04Sc | 0.04 | - | 0.041 | 0.005 |
| Al-0.07Sc | 0.07 | - | 0.068 | 0.007 |
| Heat-Treatment Step 1 (T1) | Heat-Treatment Step 2 (T2) | ||||
|---|---|---|---|---|---|
| Sample | Alloy (at%) | Temperature (K) | Time (s) | Temperature (K) | Time (s) |
| 1A | Al-0.04Sc | 548 | 10,800 | 598 | 10,800 |
| 2A | Al-0.04Sc | 548 | 10,800 | 623 | 10,800 |
| 3A | Al-0.04Sc | 518 | 14,400 | 608 | 14,400 |
| 4A | Al-0.04Sc | 521 | 14,091 | 603 | 13,971 |
| 1B | Al-0.07Sc | 548 | 10,800 | 598 | 10,800 |
| 2B | Al-0.07Sc | 548 | 10,800 | 623 | 10,800 |
| 3B | Al-0.07Sc | 531 | 14,400 | 623 | 7200 |
| 4B | Al-0.07Sc | 525 | 14,308 | 583 | 9171 |
| Reference | Surface Energy (J/m2) | Migration Energy (eV/atom) | Method | |
|---|---|---|---|---|
| Nucleation | Coarsening | |||
| Bayesian Optimized | 0.096 | 0.158 | 0.63 | BO |
| Hyland, 1992 [22] | 0.094 | - | - | Experimental |
| Mao, 2011 [23] | - | 0.165 | - | DFT |
| Booth-Morrison, 2012 [13] | - | - | 0.45–0.74 | DFT |
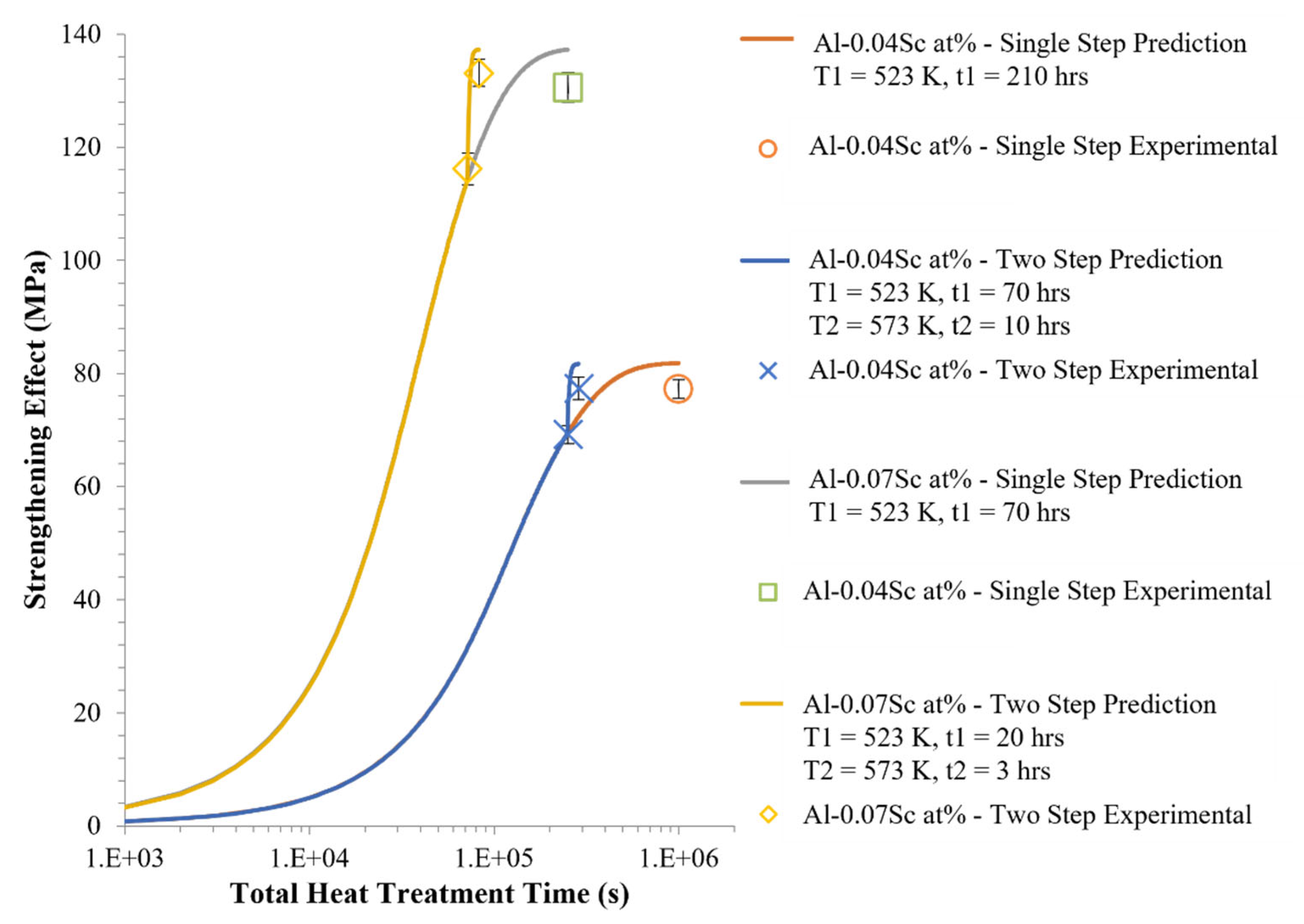
| 1st Step | 2nd Step | Final Strength (MPa) | |||||
|---|---|---|---|---|---|---|---|
| Description | T1 (K) | t1 (h) | T2 (K) | t2 (h) | Simulated | Observed | |
| Value | 2 Std Error | ||||||
| 0.04Sc at%, 1 Step | 523 | 210 | - | - | 82 | 77 | 2 |
| 0.04Sc at%, 2 Step | 523 | 70 | 573 | 10 | 82 | 77 | 2 |
| 0.07Sc at%, 1 Step | 523 | 70 | - | - | 137 | 131 | 3 |
| 0.07Sc at%, 2 Step | 523 | 20 | 573 | 3 | 137 | 133 | 2 |
| Experimental Strength | Predicted Strength | Accuracy | Ref | |
|---|---|---|---|---|
| Al-0.07Sc at% | 131 | 137 | 96% | Present |
| Al-0.18Sc at% | 140 | 160 | 87% | [3] |
| Al-0.4Sc-0.4Zr at% | 500 | 630 | 80% | [24] |
| Upper Time Limit (s) | Optimized Time (s) | Optimized Temp (K) | ||||
|---|---|---|---|---|---|---|
| Alloy (at%) | t1 | t2 | t1 | t2 | T1 | T2 |
| Al-0.04Sc | 10,800 | 14,400 | 10,800 | 6936 | 532 | 641 |
| Al-0.07Sc | 10,800 | 14,400 | 10,800 | 5733 | 543 | 592 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deane, K.; Yang, Y.; Licavoli, J.J.; Nguyen, V.; Rana, S.; Gupta, S.; Venkatesh, S.; Sanders, P.G. Utilization of Bayesian Optimization and KWN Modeling for Increased Efficiency of Al-Sc Precipitation Strengthening. Metals 2022, 12, 975. https://doi.org/10.3390/met12060975
Deane K, Yang Y, Licavoli JJ, Nguyen V, Rana S, Gupta S, Venkatesh S, Sanders PG. Utilization of Bayesian Optimization and KWN Modeling for Increased Efficiency of Al-Sc Precipitation Strengthening. Metals. 2022; 12(6):975. https://doi.org/10.3390/met12060975
Chicago/Turabian StyleDeane, Kyle, Yang Yang, Joseph J. Licavoli, Vu Nguyen, Santu Rana, Sunil Gupta, Svetha Venkatesh, and Paul G. Sanders. 2022. "Utilization of Bayesian Optimization and KWN Modeling for Increased Efficiency of Al-Sc Precipitation Strengthening" Metals 12, no. 6: 975. https://doi.org/10.3390/met12060975
APA StyleDeane, K., Yang, Y., Licavoli, J. J., Nguyen, V., Rana, S., Gupta, S., Venkatesh, S., & Sanders, P. G. (2022). Utilization of Bayesian Optimization and KWN Modeling for Increased Efficiency of Al-Sc Precipitation Strengthening. Metals, 12(6), 975. https://doi.org/10.3390/met12060975





