Microstructure Formation and Carbon Partitioning with Austenite Decomposition during Isothermal Heating Process in Fe-Si-Mn-C Steel Monitored by In Situ Time-of-Flight Neutron Diffraction
Abstract
1. Introduction
2. Materials and Methods
2.1. In Situ Neutron Diffraction
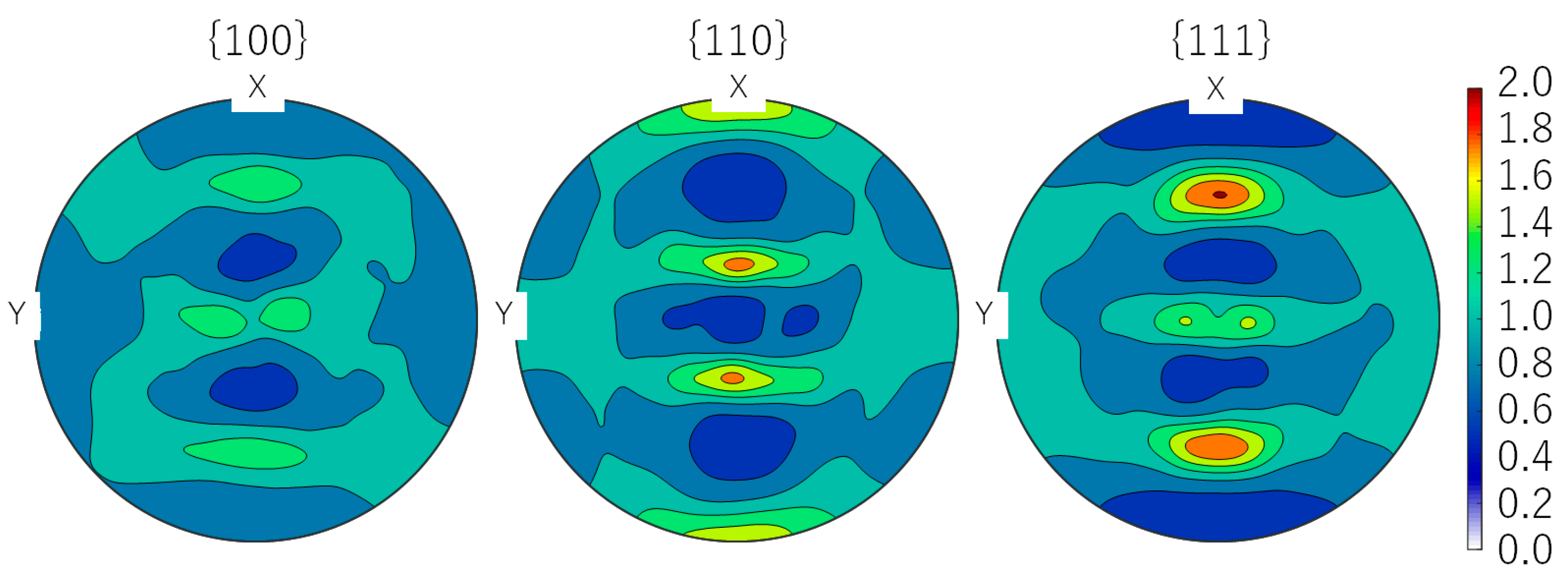
2.2. Analyses
2.3. Sample
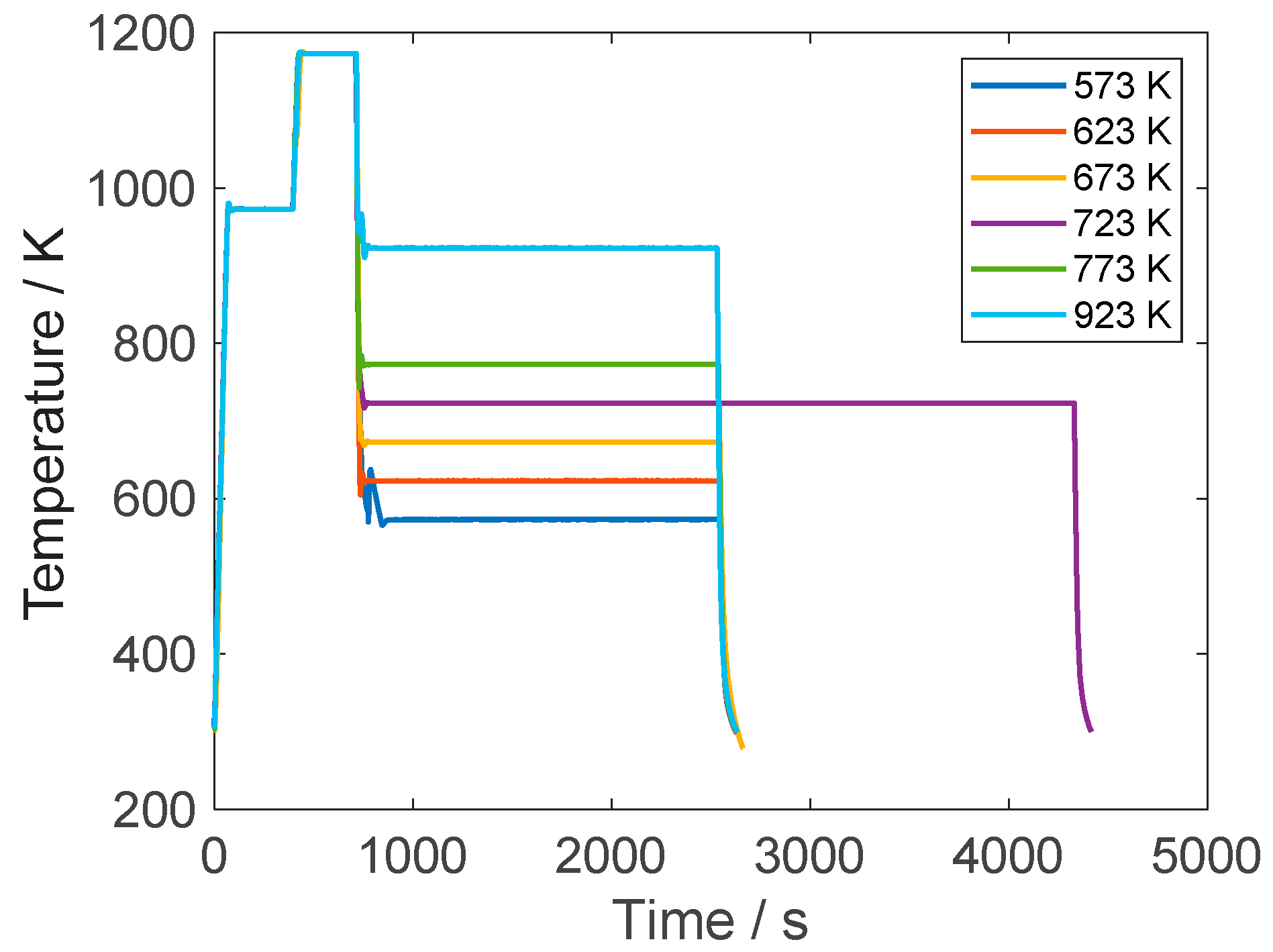
2.4. Heat Treatment Scheme
2.5. Microstructural Observation
3. Results
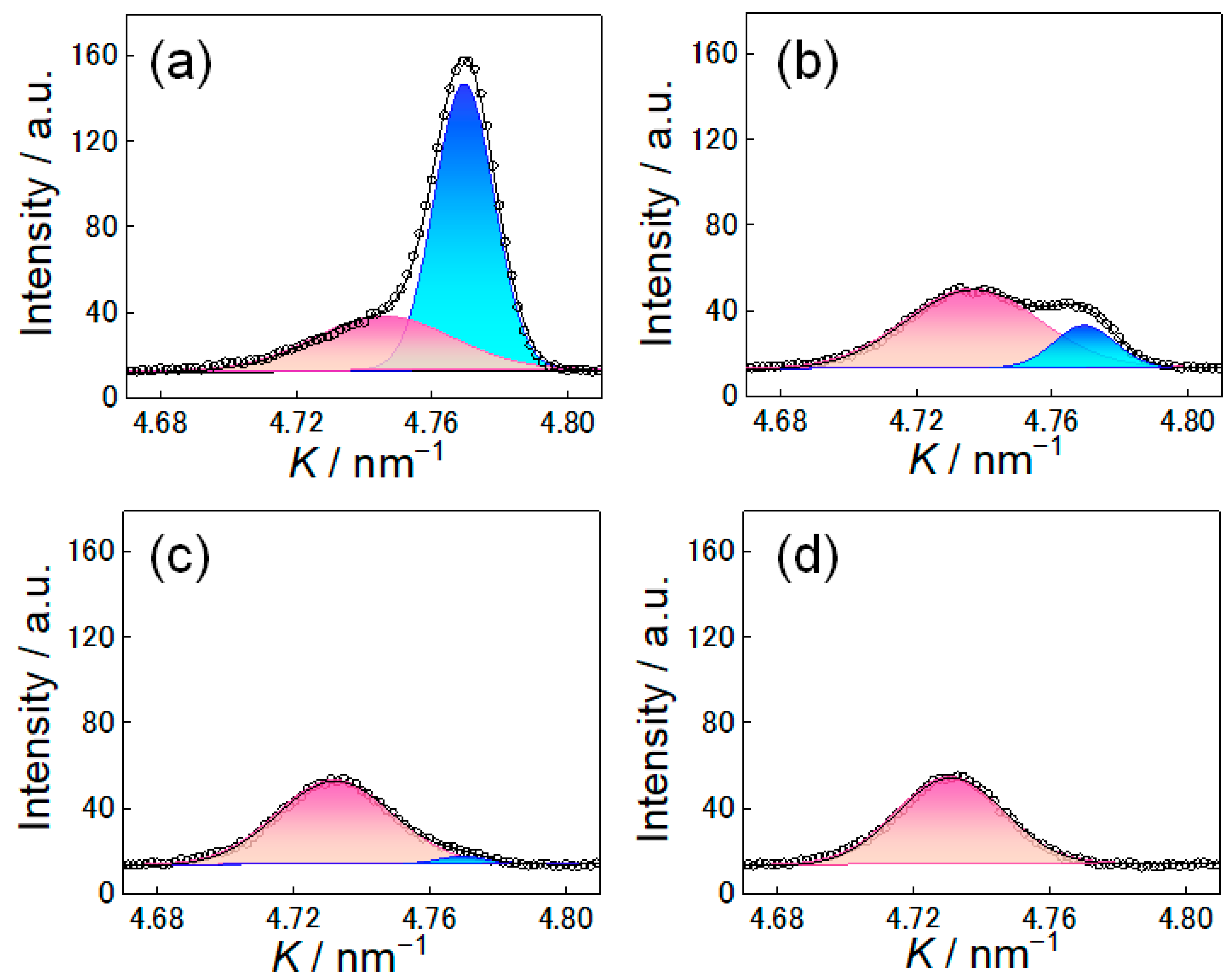
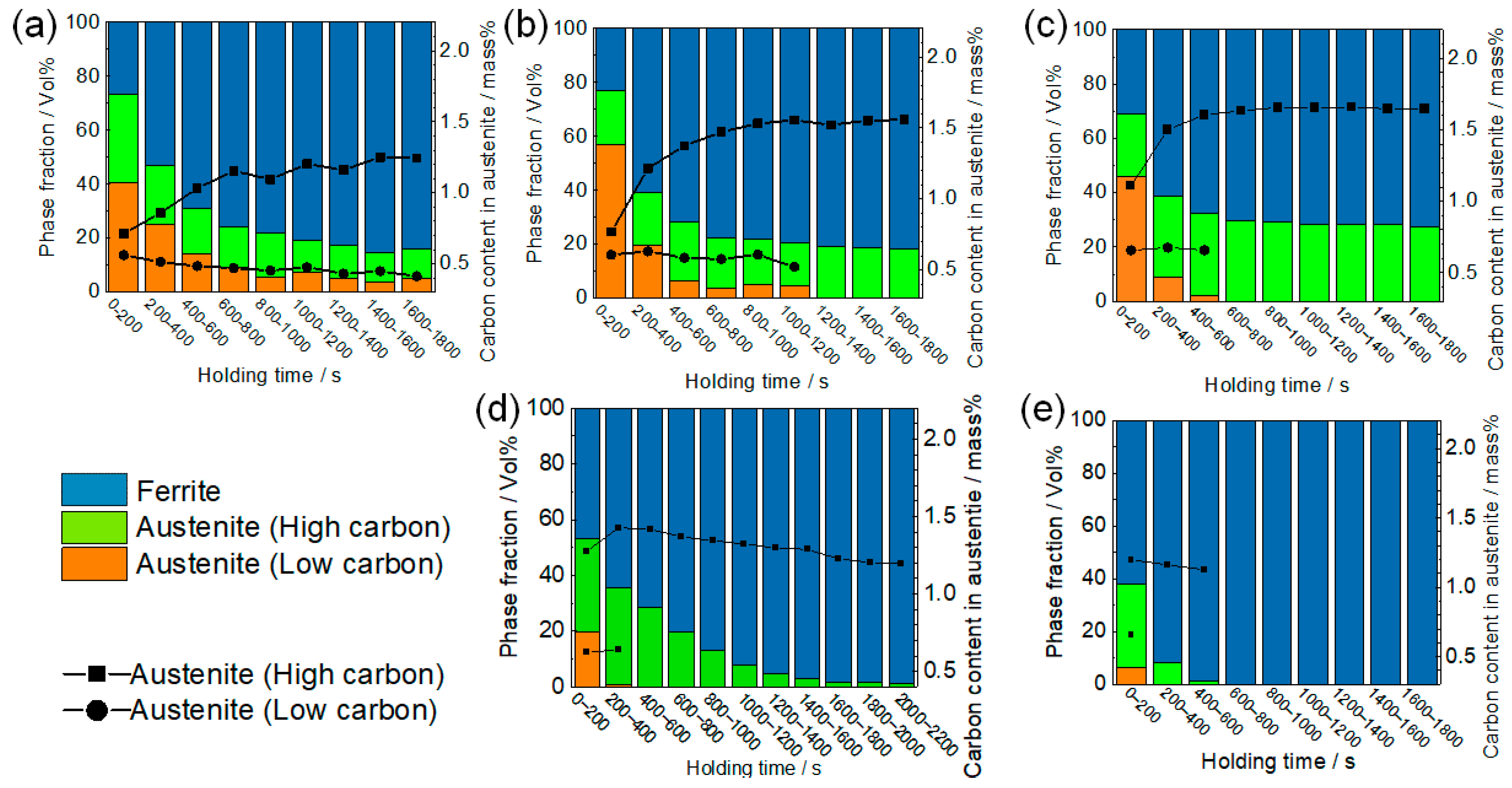
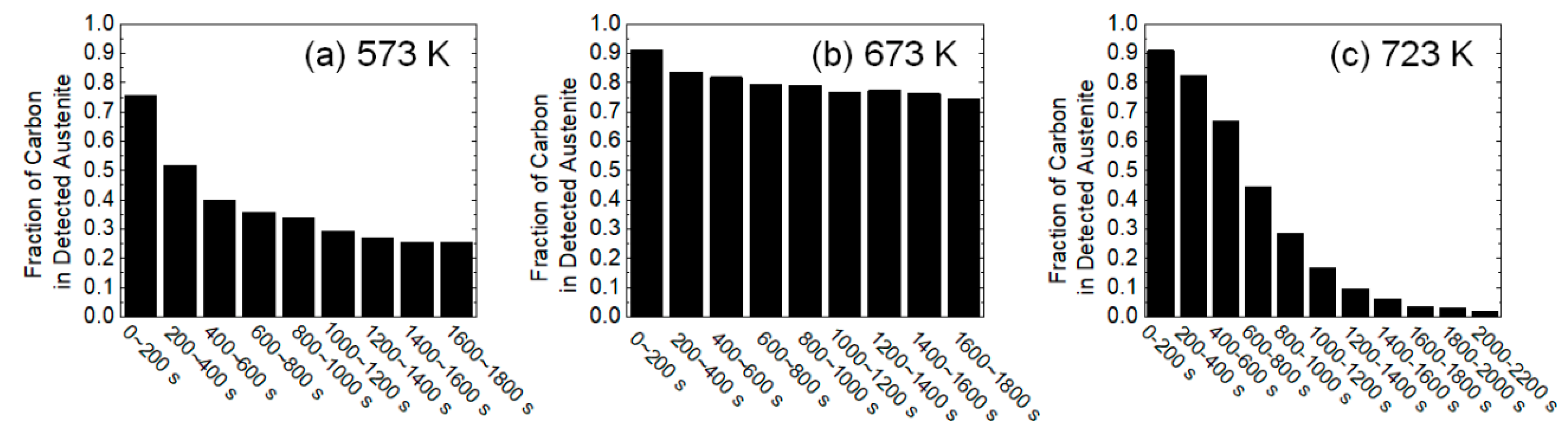
3.1. Dynamic Change in Phase Fractions and Carbon Distribution
3.2. Microstructural Features
4. Discussion
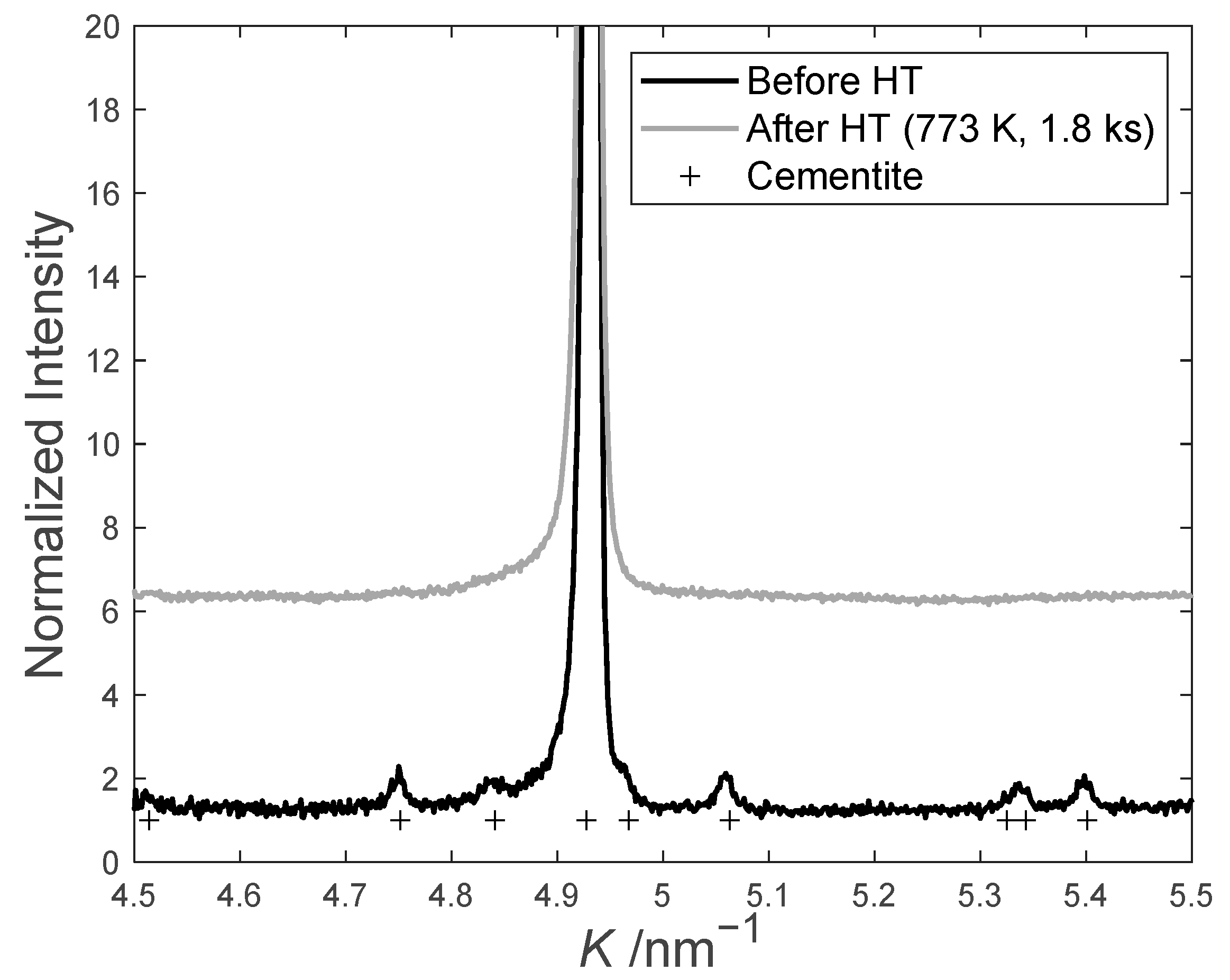
4.1. Carbide/Austenite Nano-Films
4.2. Carbon Migration Mechanisms
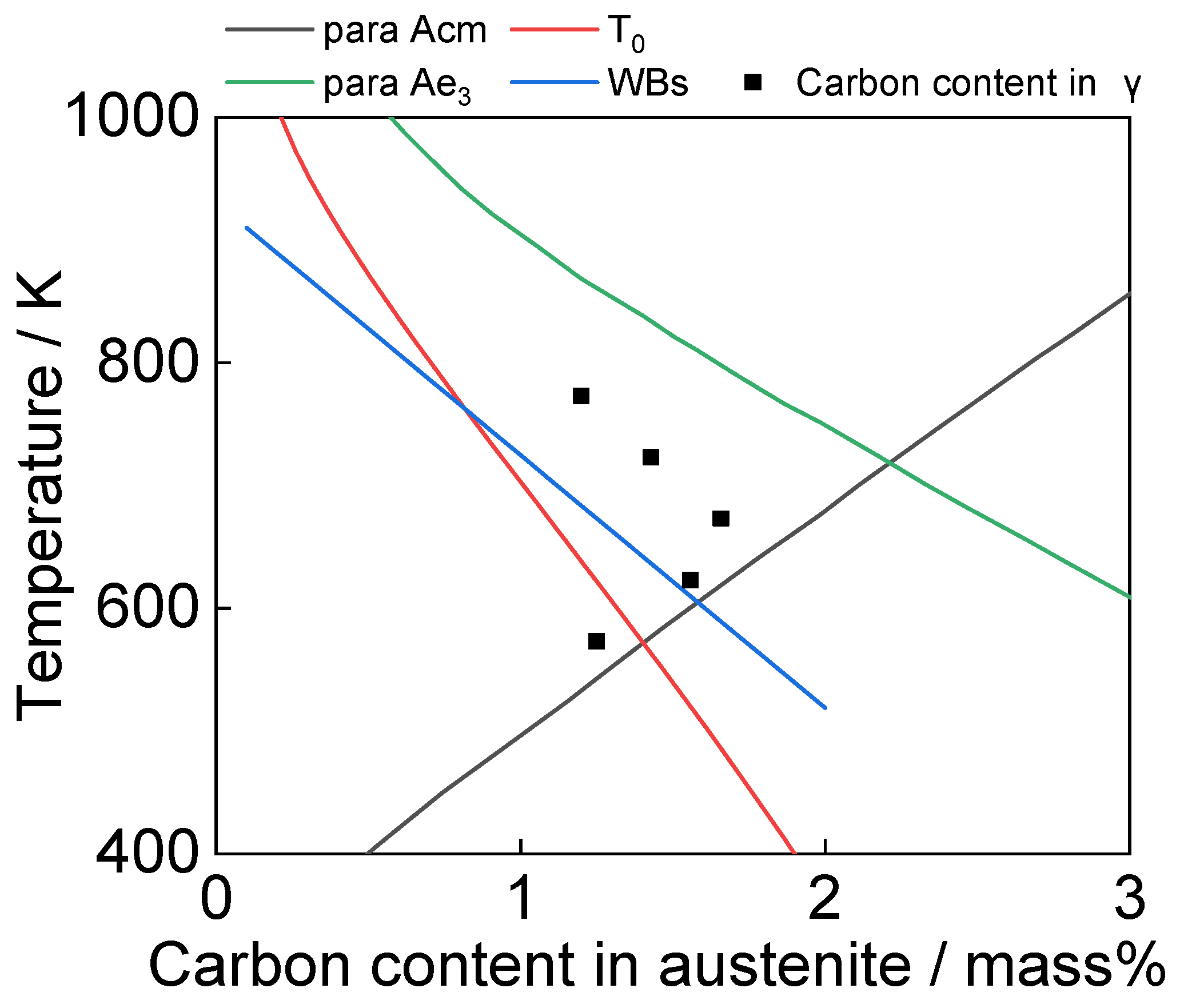
4.3. Formation of High Carbon Austenite at 673 K
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sugimoto, K.-I.; Kobayashi, M.; Hashimoto, S.-I. Ductility and strain-induced transformation in a high-strength transformation-induced plasticity-aided dual-phase steel. Metall. Trans. A 1992, 23, 3085–3091. [Google Scholar] [CrossRef]
- Tsuzaki, K.; Aki, K.; Maki, T. Formation Mechanism of Bainitic Ferrite in an Fe-2 Pct Si-0.6 Pct C Alloy. Metall. Mater. Trans. A 1994, 25, 2009–2017. [Google Scholar] [CrossRef]
- Guo, L.; Bhadeshia, H.K.D.H.; Roelofs, H.; Lembke, M.I. In situ synchrotron X-ray study of bainite transformation kinetics in a low-carbon Si-containing steel. Mater. Sci. Technol. 2017, 33, 2147–2156. [Google Scholar] [CrossRef]
- Onuki, Y.; Hirano, T.; Hoshikawa, A.; Sato, S.; Tomida, T. In Situ Observation of Bainite Transformation and Simultaneous Carbon Enrichment in Austenite in Low-Alloyed TRIP Steel Using Time-of-Flight Neutron Diffraction Techniques. Metall. Mater. Trans. A 2019, 50, 4977–4986. [Google Scholar] [CrossRef]
- Stone, H.; Peet, M.; Bhadeshia, H.; Withers, P.; Babu, S.S.; Specht, E.D. Synchrotron X-ray studies of austenite and bainitic ferrite. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 1009–1027. [Google Scholar] [CrossRef]
- Fielding, L.C.D. The Bainite Controversy. Mater. Sci. Technol. 2013, 29, 383–399. [Google Scholar] [CrossRef]
- Aaronson, H.I.; Reynolds, W.T.; Shiflet, G.J.; Spanos, G. Bainite viewed three different ways. Metall. Trans. A 1990, 21, 1343–1380. [Google Scholar] [CrossRef]
- Reynolds, W.T.; Liu, S.K.; Li, F.Z.; Hartfield, S.; Aaronson, H.I. An investigation of the generality of incomplete transformation to bainite in Fe-C-X alloys. Metall. Trans. A 1990, 21, 1479–1491. [Google Scholar] [CrossRef]
- Hillert, M. Diffusion in growth of bainite. Metall. Mater. Trans. A 1994, 25, 1957–1966. [Google Scholar] [CrossRef]
- Borgenstam, A.; Hillert, M.; Ågren, J. Metallographic evidence of carbon diffusion in the growth of bainite. Acta Mater. 2009, 57, 3242–3252. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Thermodynamic analysis of isothermal transformation diagrams. Met. Sci. 2013, 16, 159–166. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Bainite in Steels, 3rd ed.; Many Publishing: Leeds, UK, 2015; Volume 21. [Google Scholar]
- Caballero, F.G.; Bhadeshia, H.K.D.H.; Mawella, K.J.A.; Jones, D.G.; Brown, P. Very strong low temperature bainite. Mater. Sci. Technol. 2013, 18, 279–284. [Google Scholar] [CrossRef]
- Ohmori, Y.; Maki, T. Bainitic Transformation in View of Displacive Mechanism. Mater. Trans. JIM 1991, 32, 631–641. [Google Scholar] [CrossRef]
- Santofimia, M.J.; Caballero, F.G.; Capdevila, C.; García-Mateo, C.; de Andrés, C.G. New Model for the Overall Transformation Kinetics of Bainite. Part 1: The Model. Mater. Trans. 2006, 47, 2465–2472. [Google Scholar] [CrossRef]
- Timokhina, I.B.; Liss, K.D.; Raabe, D.; Rakha, K.; Beladi, H.; Xiong, X.Y.; Hodgson, P.D. Growth of bainitic ferrite and carbon partitioning during the early stages of bainite transformation in a 2 mass% silicon steel studied by in situ neutron diffraction, TEM and APT. J. Appl. Crystallogr. 2016, 49, 399–414. [Google Scholar] [CrossRef]
- Miyamoto, G.; Furuhara, T. Interaction of alloying elements with migrating ferrite/asutenite interface. ISIJ Int. 2020, 60, 2942–2953. [Google Scholar] [CrossRef]
- Hillert, M.; Höglund, L.; Ågren, J. Role of carbon and alloying elements in the formation of bainitic ferrite. Metall. Mater. Trans. A 2004, 35, 3693–3700. [Google Scholar] [CrossRef]
- Onuki, Y.; Hirano, T.; Umemura, K.; Sato, S.; Tomida, T. In Situ Neutron Diffraction Measurement during Bainite Transformation and Accompanying Carbon Enrichment in Austenite at iMATERIA, J-PARC MLF. In Proceedings of the International Conference on Processing and Manufacturing of Advanced Materials: Thermec 2021, Vienna, Austria, 1–5 June 2021; pp. 1079–1084. [Google Scholar]
- Ishigaki, T.; Hoshikawa, A.; Yonemura, M.; Morishima, T.; Kamiyama, T.; Oishi, R.; Aizawa, K.; Sakuma, T.; Tomota, Y.; Arai, M.; et al. IBARAKI materials design diffractometer (iMATERIA)—Versatile neutron diffractometer at J-PARC. Nucl. Instrum. Methods Phys. Res. Sect. A 2009, 600, 189–191. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lee, S.; De Cooman, B.C. Mn partitioning during the intercritical annealing of ultrafine-grained 6% Mn transformation-induced plasticity steel. Scr. Mater. 2011, 64, 649–652. [Google Scholar] [CrossRef]
- Onuki, Y.; Hoshikawa, A.; Sato, S.; Ishigaki, T.; Tomida, T. Quantitative phase fraction analysis of steel combined with texture analysis using time-of-flight neutron diffraction. J. Mater. Sci. 2017, 52, 11643–11658. [Google Scholar] [CrossRef]
- Lutterotti, L.; Matthies, S.; Wenk, H.R.; Schultz, A.S.; Richardson, J.W. Combined texture and structure analysis of deformed limestone from time-of-flight neutron diffraction spectra. J. Appl. Phys. 1997, 81, 594–600. [Google Scholar] [CrossRef]
- Wenk, H.R.; Lutterotti, L.; Vogel, S. Rietveld texture analysis from TOF neutron diffraction data. Powder Diffr. 2010, 25, 293–296. [Google Scholar] [CrossRef]
- Steinmetz, D.R.; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed–Akbari, A.; Hickel, T.; Roters, F.; Raabe, D. Revealing the strain-hardening behavior of twinning-induced plasticity steels: Theory, simulations, experiments. Acta Mater. 2013, 61, 494–510. [Google Scholar] [CrossRef]
- Suzuki, T.; Ono, Y.; Miyamoto, G.; Furuhara, T. Effects of Si and Cr on Bainite Microstructure of Medium Carbon Steels. Tetsu--Hagane 2010, 96, 392–399. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Ohnuki, T.; Tomota, Y.; Harjo, S.; Ohmura, T. Multi-scaled heterogeneous deformation behavior of pearlite steel studied by in situ neutron diffraction. Scr. Mater. 2017, 140, 45–49. [Google Scholar] [CrossRef]
- Burton, A.W.; Ong, K.; Rea, T.; Chan, I.Y. On the estimation of average crystallite size of zeolites from the Scherrer equation: A critical evaluation of its application to zeolites with one-dimensional pore systems. Microporous Mesoporous Mater. 2009, 117, 75–90. [Google Scholar] [CrossRef]
- Scherrer, P. Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen. Nachr. Ges. Wiss. Göttingen Math-Phys. Kl. 1918, 1918, 98–100. [Google Scholar]
- Chang, L.C. Microstructures and reaction kinetics of bainite transformation in Si-rich steels. Mater. Sci. Eng. A 2004, 368, 175–182. [Google Scholar] [CrossRef]
- Takahashi, M.; Bhadeshia, H.K.D.H. Model for transition from upper to lower bainite. Mater. Sci. Technol. 1990, 6, 592–603. [Google Scholar] [CrossRef]
- Leach, L.; Kolmskog, P.; Höglund, L.; Hillert, M.; Borgenstam, A. Critical Driving Forces for Formation of Bainite. Metall. Mater. Trans. A 2018, 49, 4509–4520. [Google Scholar] [CrossRef]
- Wu, H.-D.; Miyamoto, G.; Yang, Z.-G.; Zhang, C.; Chen, H.; Furuhara, T. Incomplete bainite transformation in Fe-Si-C alloys. Acta Mater. 2017, 133, 1–9. [Google Scholar] [CrossRef]




| C | Si | Mn | P | S | Al | N |
|---|---|---|---|---|---|---|
| 0.61 | 1.90 | 0.98 | 0.008 | 0.001 | 0.033 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onuki, Y.; Umemura, K.; Fujiwara, K.; Tanaka, Y.; Tomida, T.; Kawano, K.; Sato, S. Microstructure Formation and Carbon Partitioning with Austenite Decomposition during Isothermal Heating Process in Fe-Si-Mn-C Steel Monitored by In Situ Time-of-Flight Neutron Diffraction. Metals 2022, 12, 957. https://doi.org/10.3390/met12060957
Onuki Y, Umemura K, Fujiwara K, Tanaka Y, Tomida T, Kawano K, Sato S. Microstructure Formation and Carbon Partitioning with Austenite Decomposition during Isothermal Heating Process in Fe-Si-Mn-C Steel Monitored by In Situ Time-of-Flight Neutron Diffraction. Metals. 2022; 12(6):957. https://doi.org/10.3390/met12060957
Chicago/Turabian StyleOnuki, Yusuke, Kazuki Umemura, Kazuki Fujiwara, Yasuaki Tanaka, Toshiro Tomida, Kaori Kawano, and Shigeo Sato. 2022. "Microstructure Formation and Carbon Partitioning with Austenite Decomposition during Isothermal Heating Process in Fe-Si-Mn-C Steel Monitored by In Situ Time-of-Flight Neutron Diffraction" Metals 12, no. 6: 957. https://doi.org/10.3390/met12060957
APA StyleOnuki, Y., Umemura, K., Fujiwara, K., Tanaka, Y., Tomida, T., Kawano, K., & Sato, S. (2022). Microstructure Formation and Carbon Partitioning with Austenite Decomposition during Isothermal Heating Process in Fe-Si-Mn-C Steel Monitored by In Situ Time-of-Flight Neutron Diffraction. Metals, 12(6), 957. https://doi.org/10.3390/met12060957






