A Multiple Site Type Nucleation Model and Its Application to the Probabilistic Strength of Pd Nanowires
Abstract
:1. Introduction
2. Methods
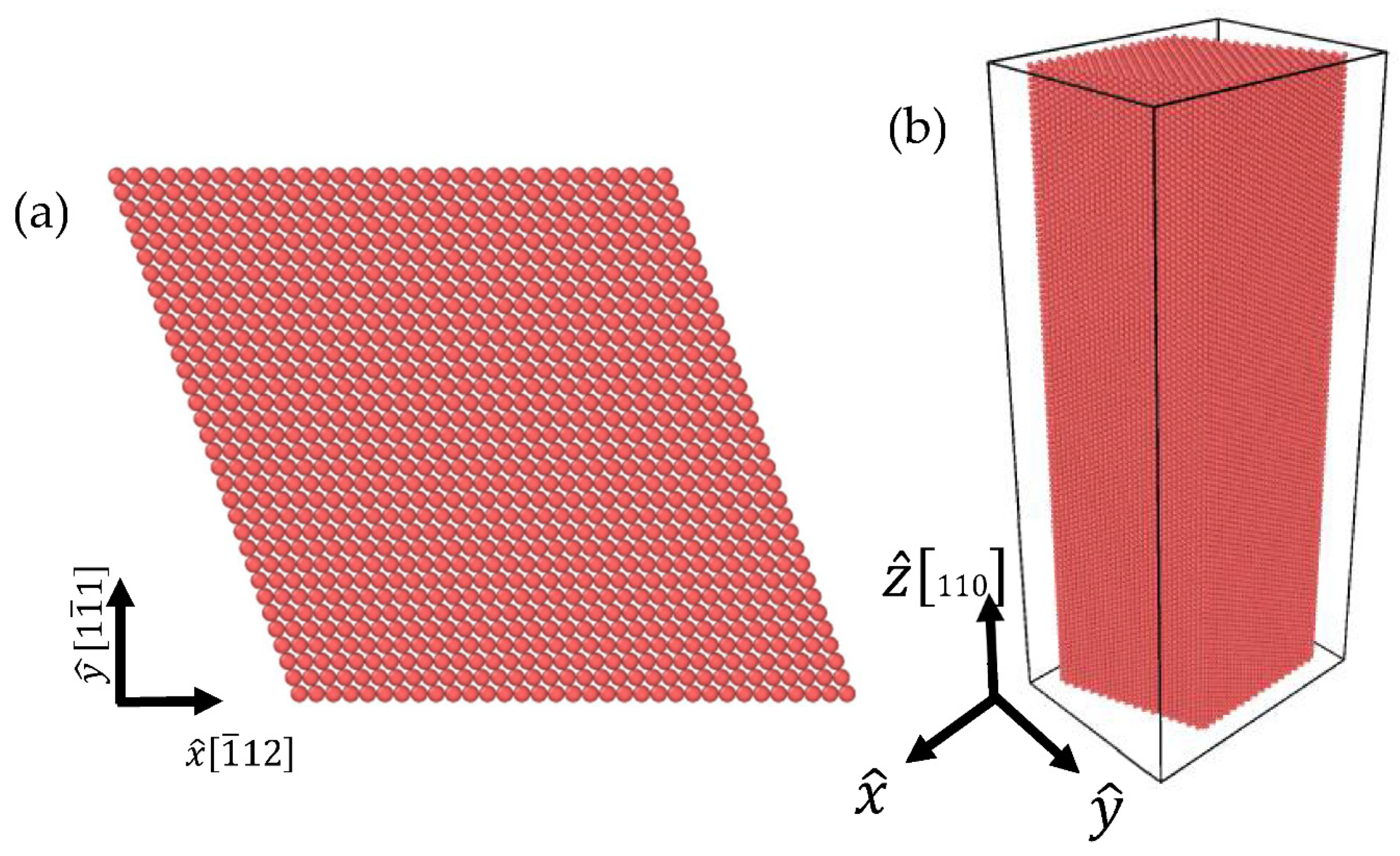
2.1. Molecular Dynamics Simulations
2.2. Nudged Elastic Band Simulations
3. Results
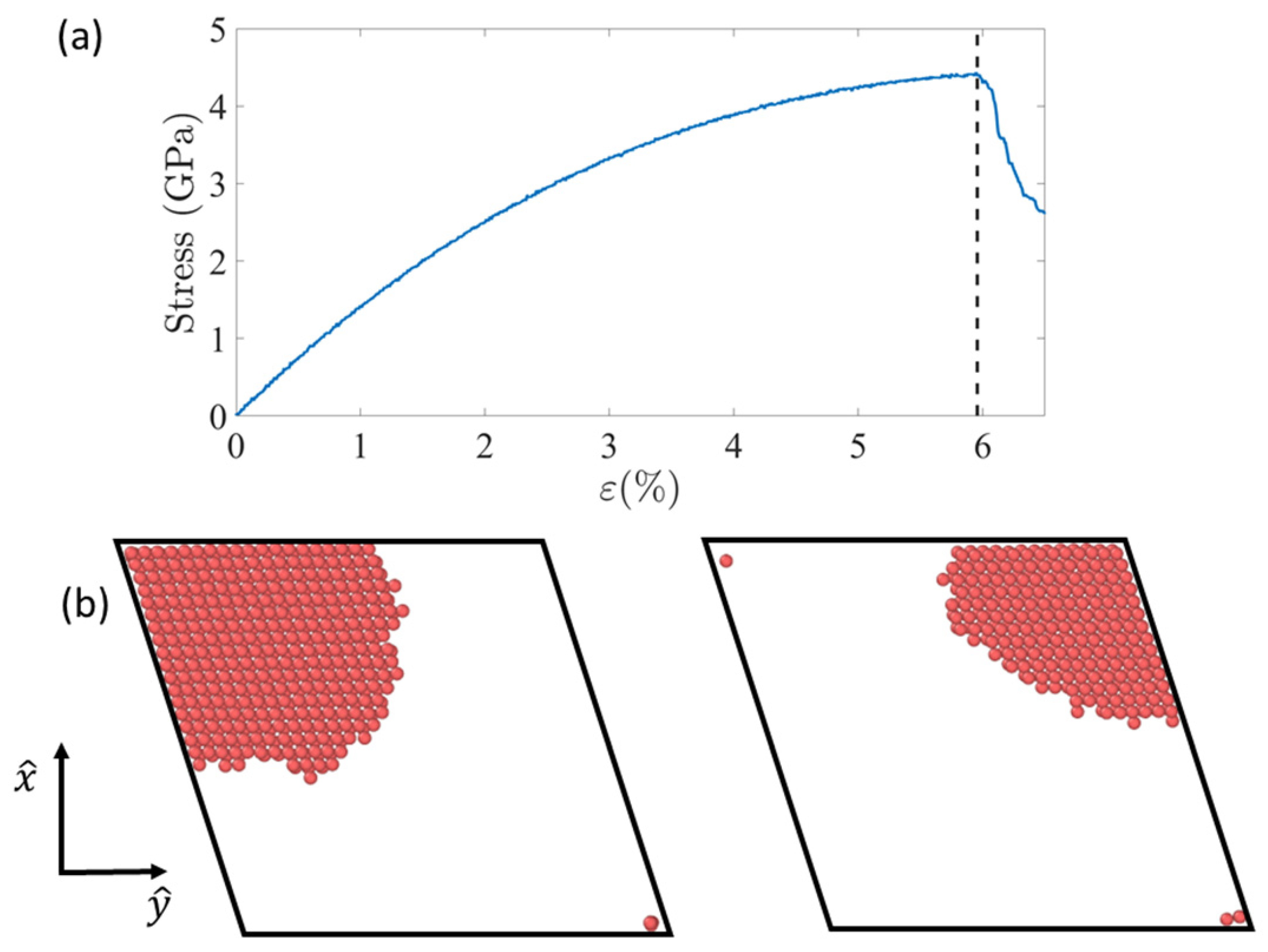
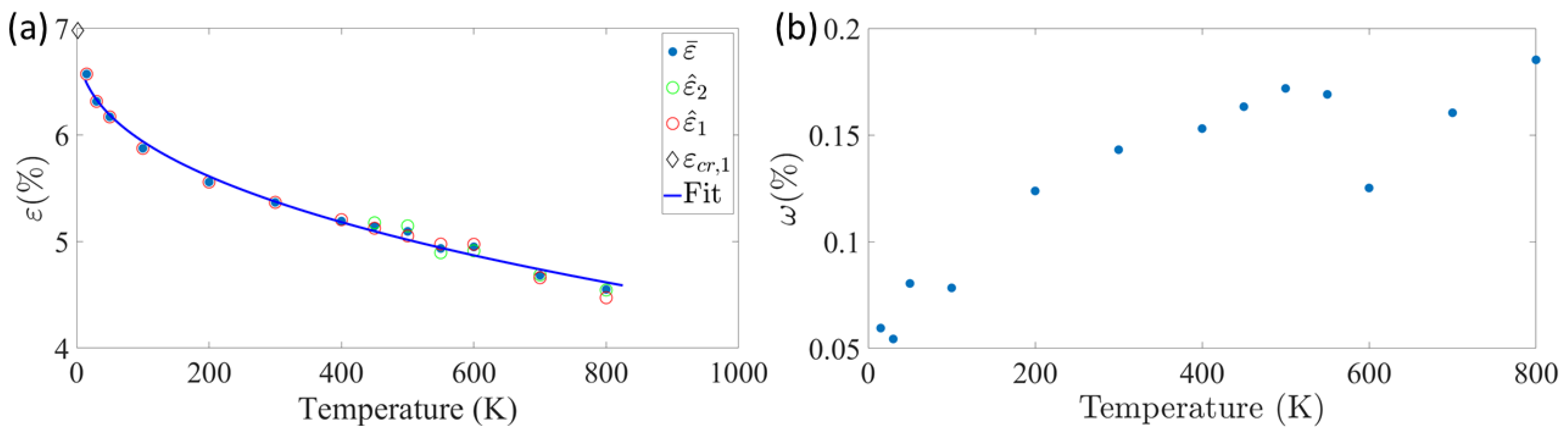
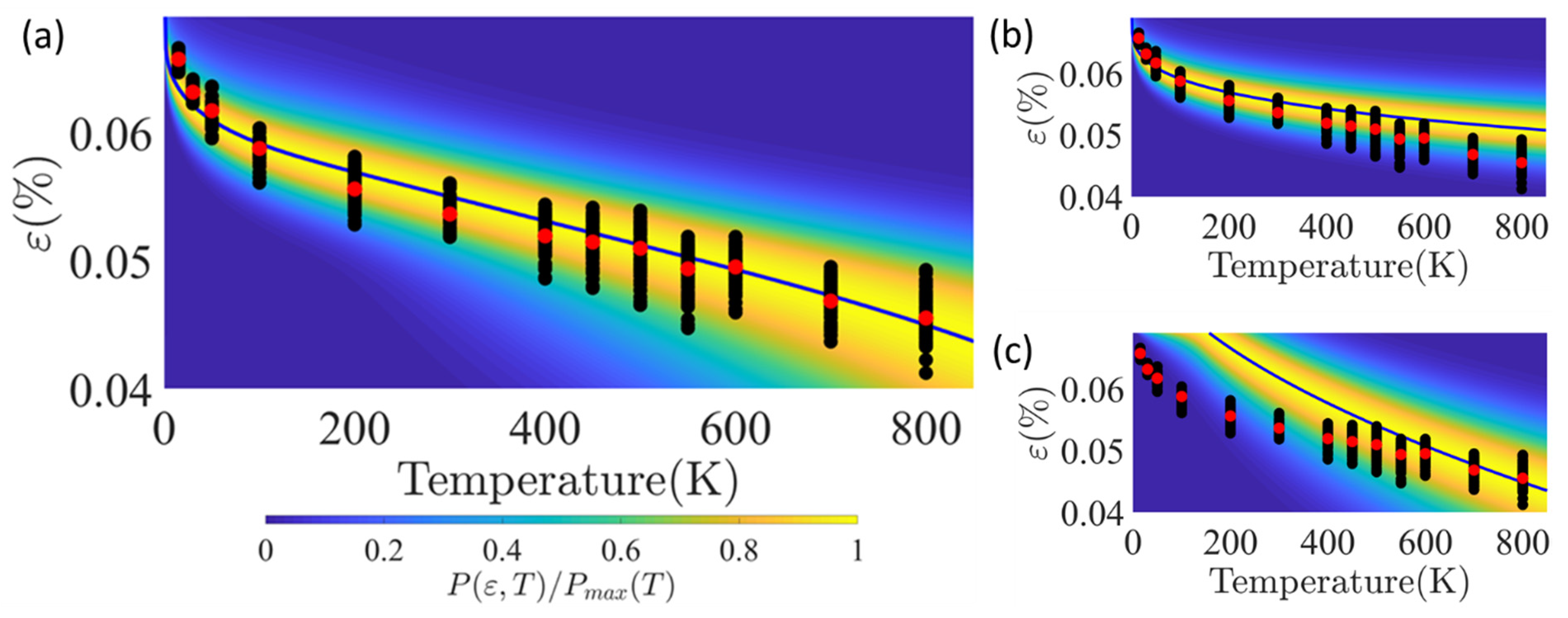
3.1. MD Simulations of Nucleation-Controlled Plasticity in Pd Nanowires
3.2. Multiple Site type Nucleation Model
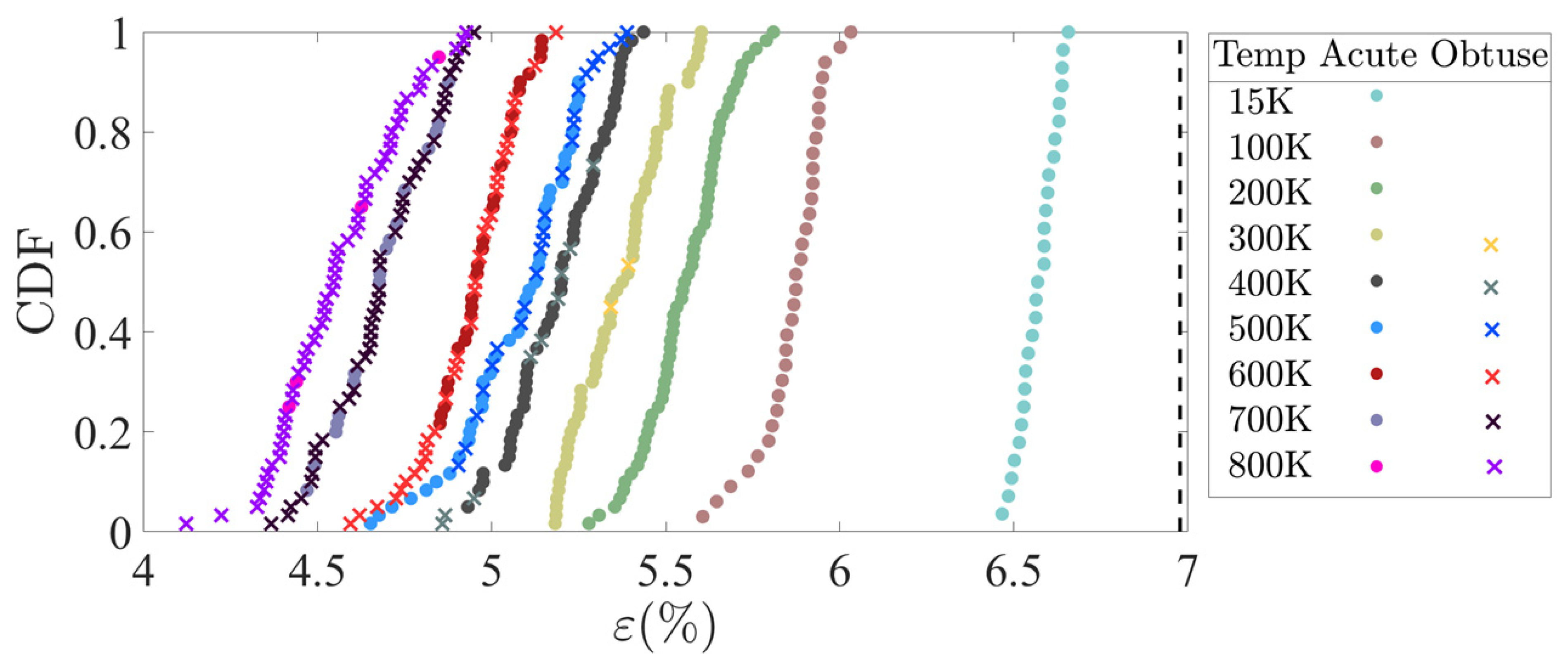
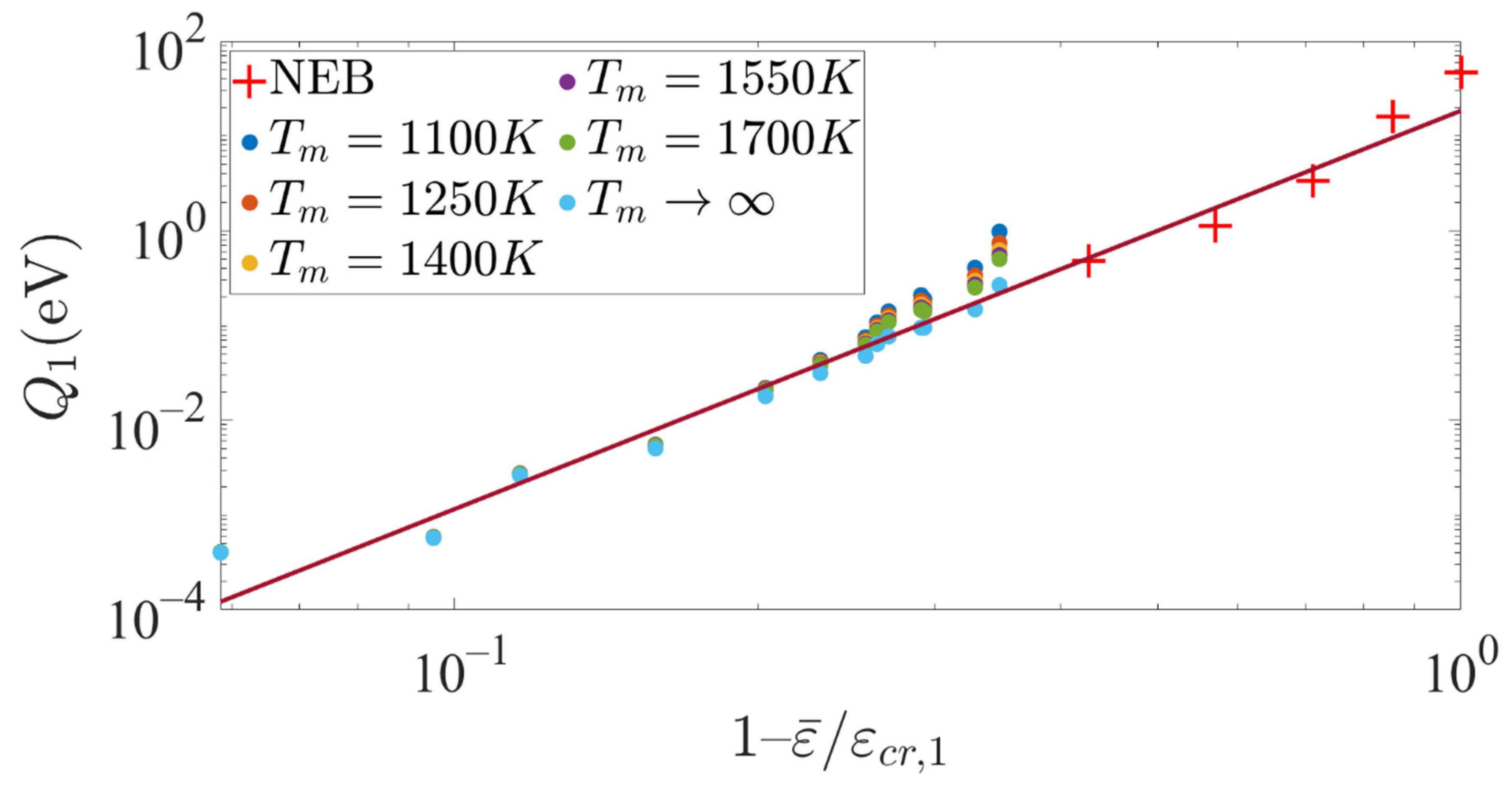
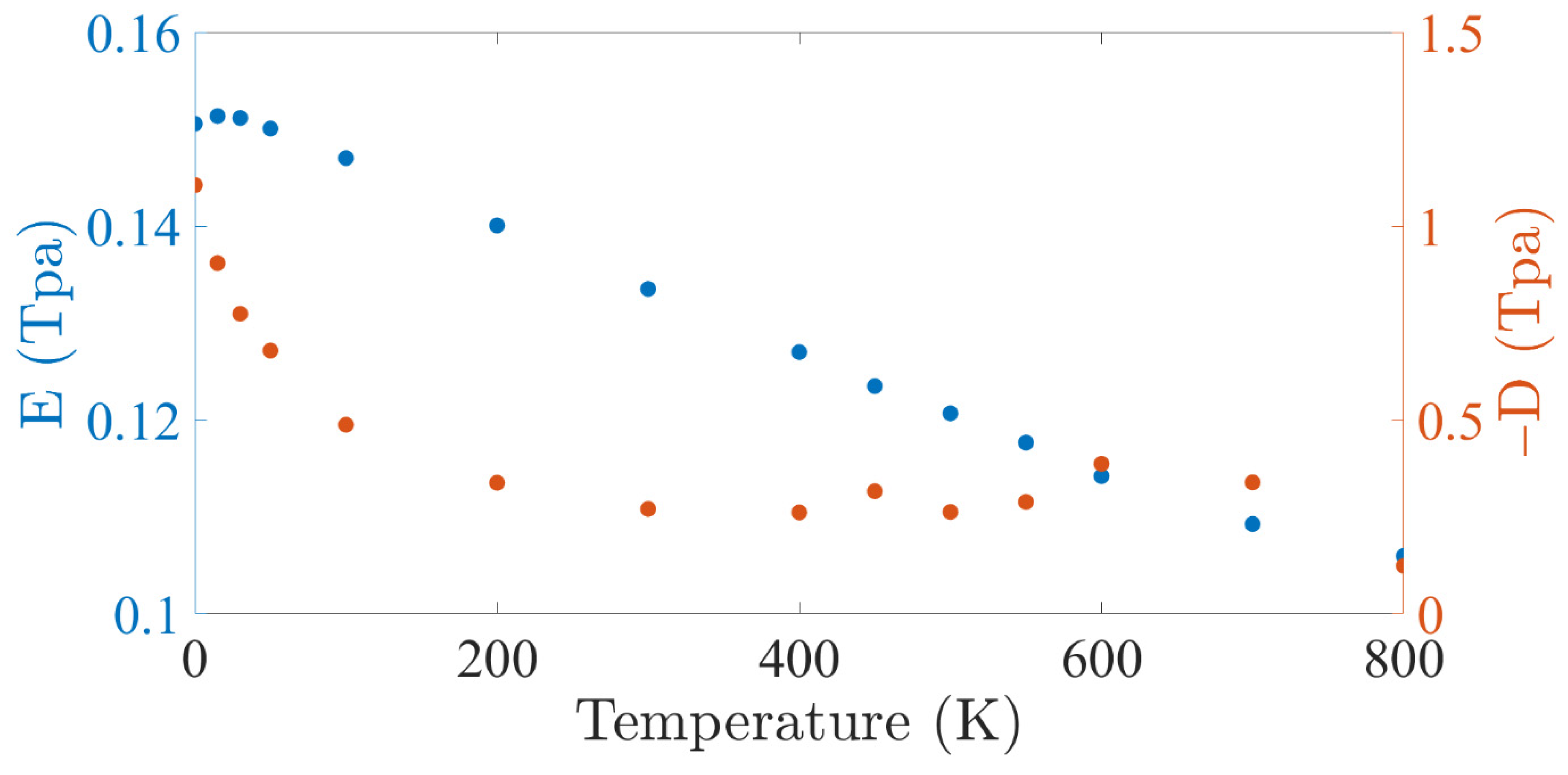
3.3. Calculation of the Activation Parameter from the Two Types of Edges
3.3.1. Extracting the Values of and Its Derivatives from the MD Simulation Results
3.3.2. Finding the Value of
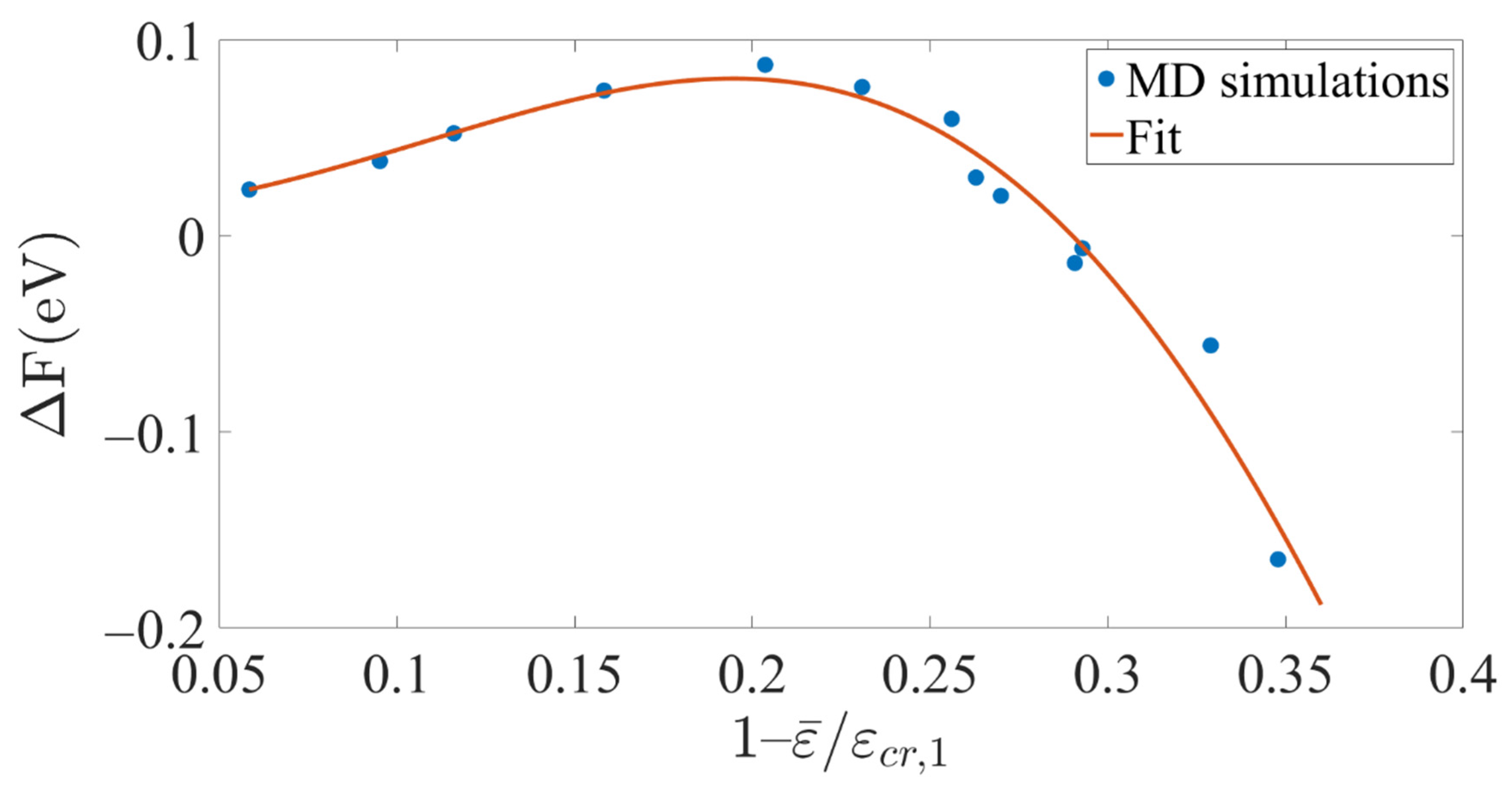
3.3.3. Finding the Free-Energy Barriers
4. Discussion
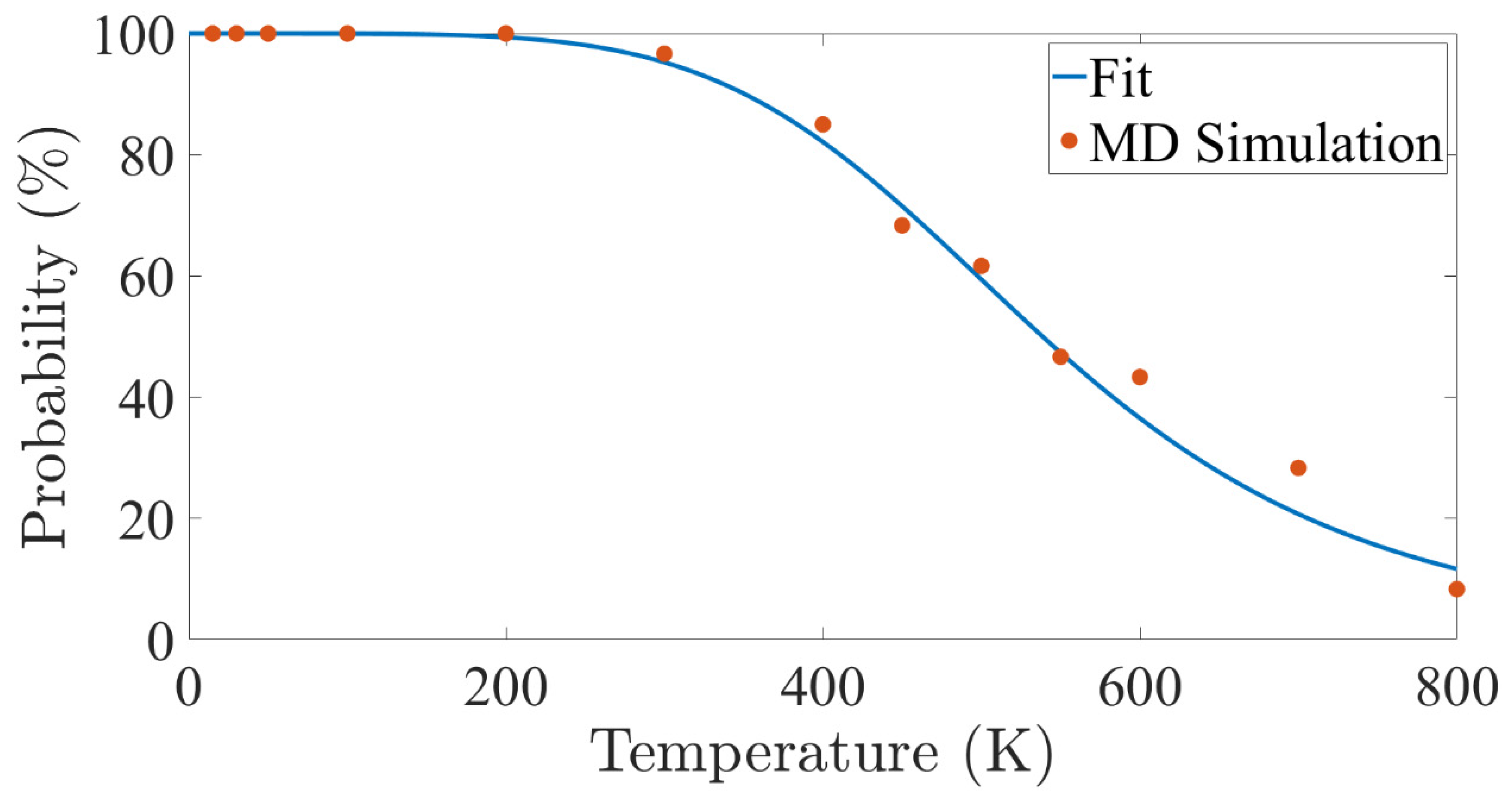
4.1. The Most Probable Strain as a Function of Temperature for Multiple Nucleation Site Types
4.2. The Exponents near the Critical Nucleation Strain
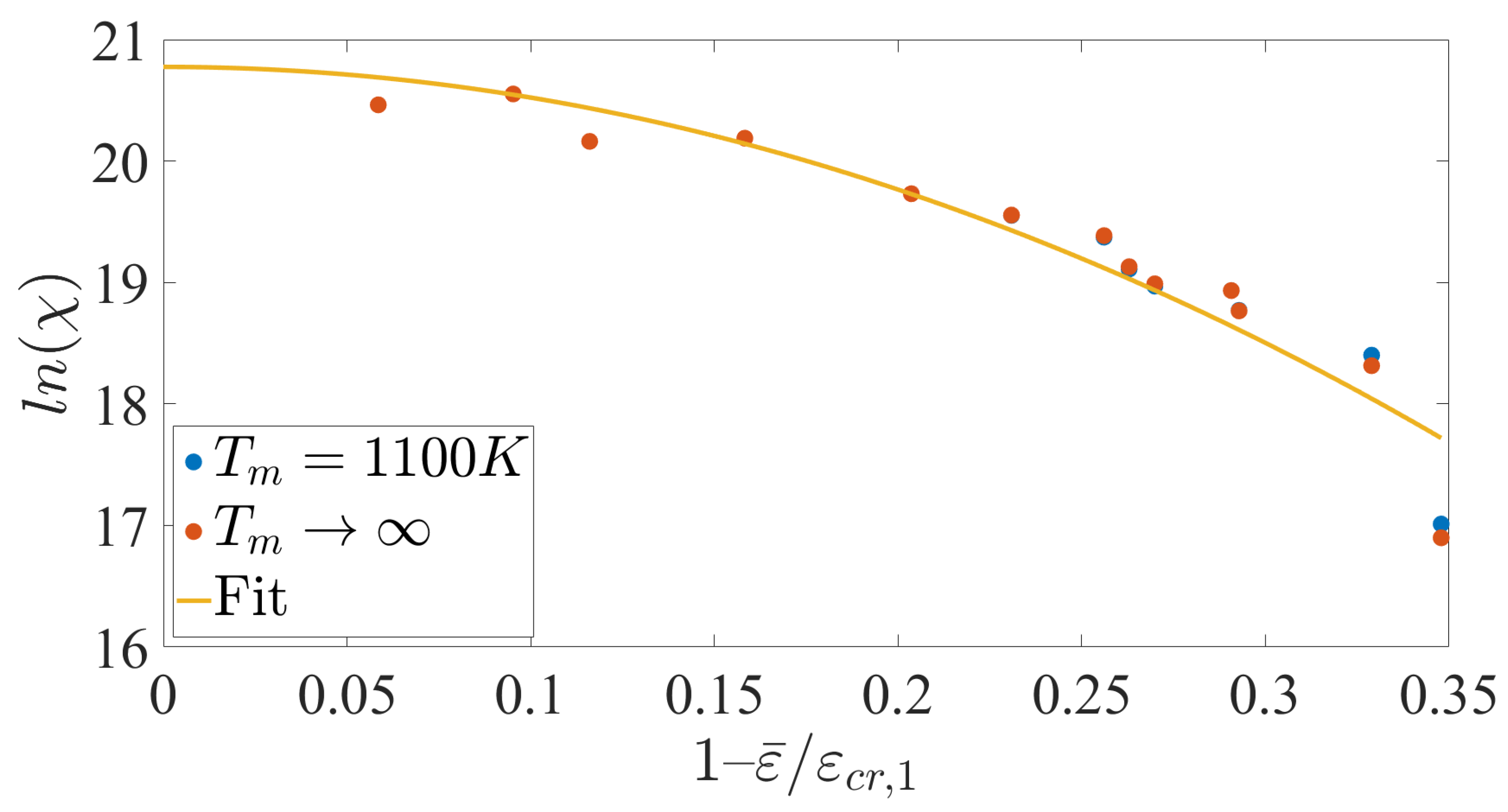
4.3. The Activation Entropy
4.4. Generalization of the Fitting Process
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wu, B.; Heidelberg, A.; Boland, J. Mechanical properties of ultrahigh-strength gold nanowires. Nat. Mater. 2005, 4, 525–529. [Google Scholar] [CrossRef]
- Bin Wu, B.; Heidelberg, A.A.; Boland, J.J.; Sader, J.E.; Sun, X.; Li, Y. Microstructure-hardened silver nanowires. Nano Lett. 2006, 6, 468–472. [Google Scholar] [CrossRef]
- Richter, G.; Hillerich, K.; Gianola, D.S.; Mönig, R.; Kraft, O.; Volkert, C.A. Ultrahigh strength single crystalline nanowhiskers grown by physical vapor deposition. Nano Lett. 2009, 9, 3048–3052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Mao, S.X. Atomistic perspective on in situ nanomechanics. Extreme Mech. Lett. 2016, 8, 127–139. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-J.; Gao, G.-J.J.; Ogata, S. Size-dependent transition of deformation mechanism, and nonlinear elasticity in Ni3Al nanowires. Appl. Phys. Lett. 2013, 102, 041902. [Google Scholar] [CrossRef]
- Mordehai, D.; David, O.; Kositski, R. Nucleation-controlled plasticity of metallic nanowires and nanoparticles. Adv. Mater. 2018, 30, 1706710. [Google Scholar] [CrossRef] [PubMed]
- Schuh, C.A.; Mason, J.; Lund, A.C. Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nat. Mater. 2005, 4, 617–621. [Google Scholar] [CrossRef]
- Mason, J.; Lund, A.C.; Schuh, C.A. Determining the activation energy and volume for the onset of plasticity during nanoindentation. Phys. Rev. B 2006, 73, 054102. [Google Scholar] [CrossRef]
- Mordehai, D.; Lee, S.-W.; Backes, B.; Srolovitz, D.J.; Nix, W.D.; Rabkin, E. Size effect in compression of single-crystal gold microparticles. Acta Mater. 2011, 59, 5202–5215. [Google Scholar] [CrossRef]
- Issa, I.; Amodeo, J.; Réthoré, J.; Joly-Pottuz, L.; Esnouf, C.; Morthomas, J.; Perez, M.; Chevalier, J.; Masenelli-Varlot, K. In situ investigation of MgO nanocube deformation at room temperature. Acta Mater. 2015, 86, 295–304. [Google Scholar] [CrossRef]
- Kositski, R.; Kovalenko, O.; Lee, S.-W.; Greer, J.R.; Rabkin, E.; Mordehai, D. Cross-split of dislocations: An athermal and rapid plasticity mechanism. Sci. Rep. 2016, 6, 25966. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Hickman, J.; Gazit, N.; Rabkin, E.; Mishin, Y. Nickel nanoparticles set a new record of strength. Nat. Commun. 2018, 9, 4102. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Kositski, R.; Kovalenko, O.; Mordehai, D.; Rabkin, E. Giant shape- and size-dependent compressive strength of molybdenum nano- and microparticles. Acta Mater. 2020, 198, 72–84. [Google Scholar] [CrossRef]
- Sedlmayr, A.; Bitzek, E.; Gianola, D.S.; Richter, G.; Mönig, R.; Kraft, O. Existence of two twinning-mediated plastic deformation modes in Au nanowhiskers. Acta Mater. 2012, 60, 3985–3993. [Google Scholar] [CrossRef]
- Weinberger, C.R.; Cai, W. Plasticity of metal nanowires. J. Mater. Chem. 2012, 22, 3277–3292. [Google Scholar] [CrossRef]
- Seo, J.-H.; Park, H.S.; Yoo, Y.; Seong, T.-Y.; Li, J.; Ahn, J.-P.; Kim, B.; Choi, I.-S. Origin of size dependency in coherent-twin-propagation-mediated tensile deformation of noble metal nanowires. Nano Lett. 2013, 13, 5112–5116. [Google Scholar] [CrossRef]
- Seo, J.-H.; Yoo, Y.; Park, N.-Y.; Yoon, S.-W.; Lee, H.; Han, S.; Lee, S.-W.; Seong, T.-Y.; Lee, S.-C.; Lee, K.-B.; et al. Superplastic deformation of defect-free au nanowires via coherent twin propagation. Nano Lett. 2011, 11, 3499–3502. [Google Scholar] [CrossRef]
- Chen, L.Y.; He, M.-R.; Shin, J.; Richter, G.; Gianola, D.S. Measuring surface dislocation nucleation in defect-scarce nanostructures. Nat. Mater. 2015, 14, 707–713. [Google Scholar] [CrossRef]
- Yin, S.; Cheng, G.; Richter, G.; Gao, H.; Zhu, Y. Transition of deformation mechanisms in single-crystalline metallic nanowires. ACS Nano 2019, 13, 9082–9090. [Google Scholar] [CrossRef]
- Roos, B.; Kapelle, B.; Richter, G.; Volkert, C.A. Surface dislocation nucleation controlled deformation of Au nanowires. Appl. Phys. Lett. 2014, 105, 201908. [Google Scholar] [CrossRef]
- Weinberger, C.; Jennings, A.T.; Kang, K.; Greer, J.R. Atomistic simulations and continuum modeling of dislocation nucleation and strength in gold nanowires. J. Mech. Phys. Solids 2012, 60, 84–103. [Google Scholar] [CrossRef]
- Jennings, A.T.; Weinberger, C.R.; Lee, S.-W.; Aitken, Z.H.; Meza, L.; Greer, J.R. Modeling dislocation nucleation strengths in pristine metallic nanowires under experimental conditions. Acta Mater. 2013, 61, 2244–2259. [Google Scholar] [CrossRef]
- Wu, D.; Nieh, T. Incipient plasticity and dislocation nucleation in body-centered cubic chromium. Mater. Sci. Eng. A 2014, 609, 110–115. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, X.; Hang, W.; Liu, M.; Song, Y.; Yuan, J.; Zhang, T. Nanoindentation size effect on stochastic behavior of incipient plasticity in a LiTaO3 single crystal. Eng. Fract. Mech. 2020, 226, 106877. [Google Scholar] [CrossRef]
- Ramalingam, S.; Reimanis, I.E.; Packard, C.E. Determining activation volume for the pressure-induced phase transformation in β-eucryptite through nanoindentation. J. Am. Ceram. Soc. 2012, 95, 2051–2058. [Google Scholar] [CrossRef]
- Wang, S.-P.; Xu, J. Incipient plasticity and activation volume of dislocation nucleation for TiZrNbTaMo high-entropy alloys characterized by nanoindentation. J. Mater. Sci. Technol. 2019, 35, 812–816. [Google Scholar] [CrossRef]
- Chen, L.Y.; Richter, G.; Sullivan, J.P.; Gianola, D.S. Lattice anharmonicity in defect-free Pd nanowhiskers. Phys. Rev. Lett. 2012, 109, 125503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shin, J.; Chen, L.Y.; Sanli, U.T.; Richter, G.; Labat, S.; Richard, M.-I.; Cornelius, T.; Thomas, O.; Gianola, D.S. Controlling dislocation nucleation-mediated plasticity in nanostructures via surface modification. Acta Mater. 2019, 166, 572–586. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Samanta, A.; Leach, A.; Gall, K. Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 2008, 100, 025502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ryu, S.; Kang, K.; Cai, W. Predicting the dislocation nucleation rate as a function of temperature and stress. J. Mater. Res. 2011, 26, 2335–2354. [Google Scholar] [CrossRef] [Green Version]
- Ryu, S.; Kang, K.; Cai, W. Entropic effect on the rate of dislocation nucleation. Proc. Natl. Acad. Sci. USA 2011, 108, 5174–5178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meyer, W.V.; Neldel, H. Relation between the energy constant and the quantity constant in the conductivity—Temperature formula of oxide semiconductors. Z. Tech. Phys. 1937, 18, 588–593. [Google Scholar]
- Chachamovitz, D.; Mordehai, D. The stress-dependent activation parameters for dislocation nucleation in molybdenum nanoparticles. Sci. Rep. 2018, 8, 3915. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.-W.; Mordehai, D.; Rabkin, E.; Nix, W.D. Effects of focused-ion-beam irradiation and prestraining on the mechanical properties of FCC Au microparticles on a sapphire substrate. J. Mater. Res. 2011, 26, 1653–1661. [Google Scholar] [CrossRef]
- Amodeo, J.; Maras, E.; Rodney, D. Site dependence of surface dislocation nucleation in ceramic nanoparticles. NPJ Comput. Mater. 2021, 7, 60. [Google Scholar] [CrossRef]
- Derlet, P.; Maas, R. A probabilistic explanation for the size-effect in crystal plasticity. Philos. Mag. 2014, 95, 1829–1844. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Eastman, D.W.; Hemker, K.J.; El-Awady, J.A. A statistical model for predicting size effects on the yield strength in dislocation-mediated crystal plasticity. J. Mech. Phys. Solids 2020, 147, 104245. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.W.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.T.; Zhou, H.; Zou, G.; Gao, H. Transition from source- to stress-controlled plasticity in nanotwinned materials below a softening temperature. NPJ Comput. Mater. 2019, 5, 2. [Google Scholar] [CrossRef]
- Zhou, Y.; Fichthorn, K.A. Internal stress-induced orthorhombic phase in 5-fold-twinned noble metal nanowires. J. Phys. Chem. C 2014, 118, 18746–18755. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Zhou, X.W.; Wadley, H.N.G.; Johnson, R.A.; Larson, D.J.; Tabat, N.; Cerezo, A.; Petford-Long, A.K.; Smith, G.D.W.; Clifton, P.H.; Martens, R.L.; et al. Atomic scale structure of sputtered metal multilayers. Acta Mater. 2001, 49, 4005–4015. [Google Scholar] [CrossRef]
- Zhang, J.-M.; Zhang, Y.; Xu, K.-W.; Ji, V. Young’s modulus surface and Poisson’s ratio curve for cubic metals. J. Phys. Chem. Solids 2007, 68, 503–510. [Google Scholar] [CrossRef]
- Rabkin, E.; Srolovitz, D.J. Onset of plasticity in gold nanopillar compression. Nano Lett. 2007, 7, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Cottrell, A.H. Thermally activated plastic glide. Philos. Mag. Lett. 2002, 82, 65–70. [Google Scholar] [CrossRef]
- Xie, Z.; Shin, J.; Renner, J.; Prakash, A.; Gianola, D.S.; Bitzek, E. Origins of strengthening and failure in twinned Au nanowires: Insights from in-situ experiments and atomistic simulations. Acta Mater. 2020, 187, 166–175. [Google Scholar] [CrossRef]
- Rodney, D.; Schuh, C. Distribution of thermally activated plastic events in a flowing glass. Phys. Rev. Lett. 2009, 102, 235503. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nisany, S.; Mordehai, D. A Multiple Site Type Nucleation Model and Its Application to the Probabilistic Strength of Pd Nanowires. Metals 2022, 12, 280. https://doi.org/10.3390/met12020280
Nisany S, Mordehai D. A Multiple Site Type Nucleation Model and Its Application to the Probabilistic Strength of Pd Nanowires. Metals. 2022; 12(2):280. https://doi.org/10.3390/met12020280
Chicago/Turabian StyleNisany, Stav, and Dan Mordehai. 2022. "A Multiple Site Type Nucleation Model and Its Application to the Probabilistic Strength of Pd Nanowires" Metals 12, no. 2: 280. https://doi.org/10.3390/met12020280
APA StyleNisany, S., & Mordehai, D. (2022). A Multiple Site Type Nucleation Model and Its Application to the Probabilistic Strength of Pd Nanowires. Metals, 12(2), 280. https://doi.org/10.3390/met12020280




