Calibration of the Flow Curve Up to Large Strain Range by Incremental Sheet Forming Coupled with FEM Simulation
Abstract
:1. Introduction
2. Experiments
2.1. Material Properties
2.2. ISF Experiment
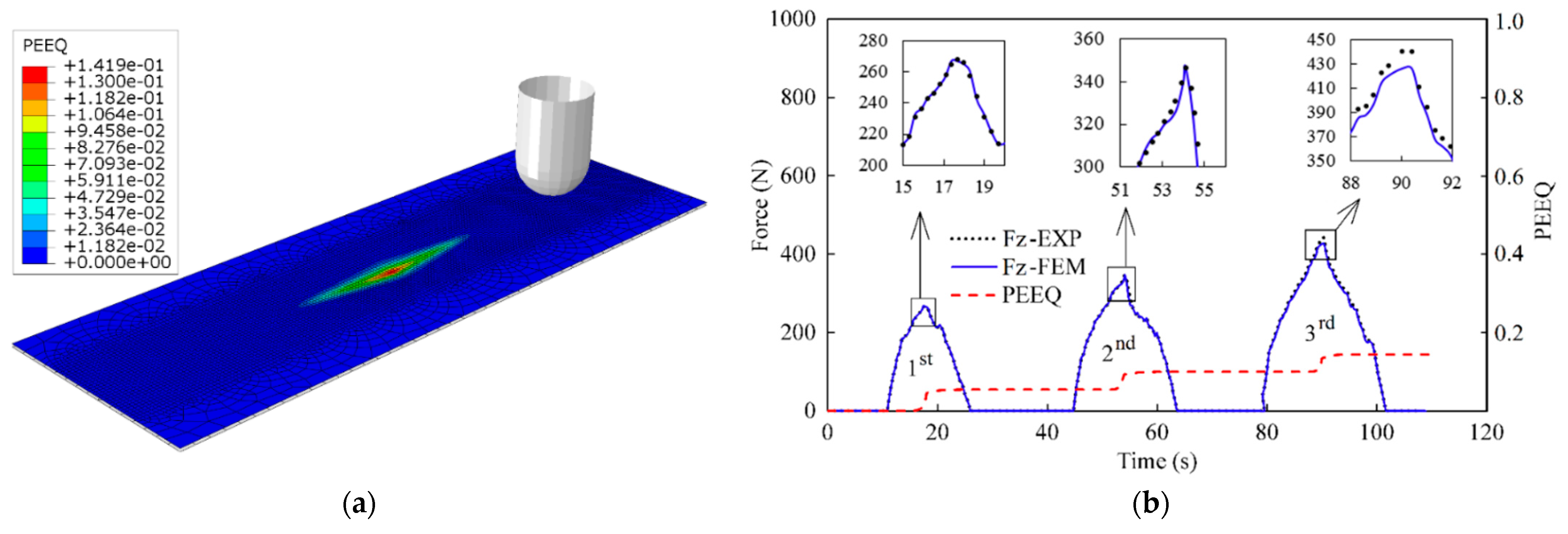
2.3. Forming Force Measurement
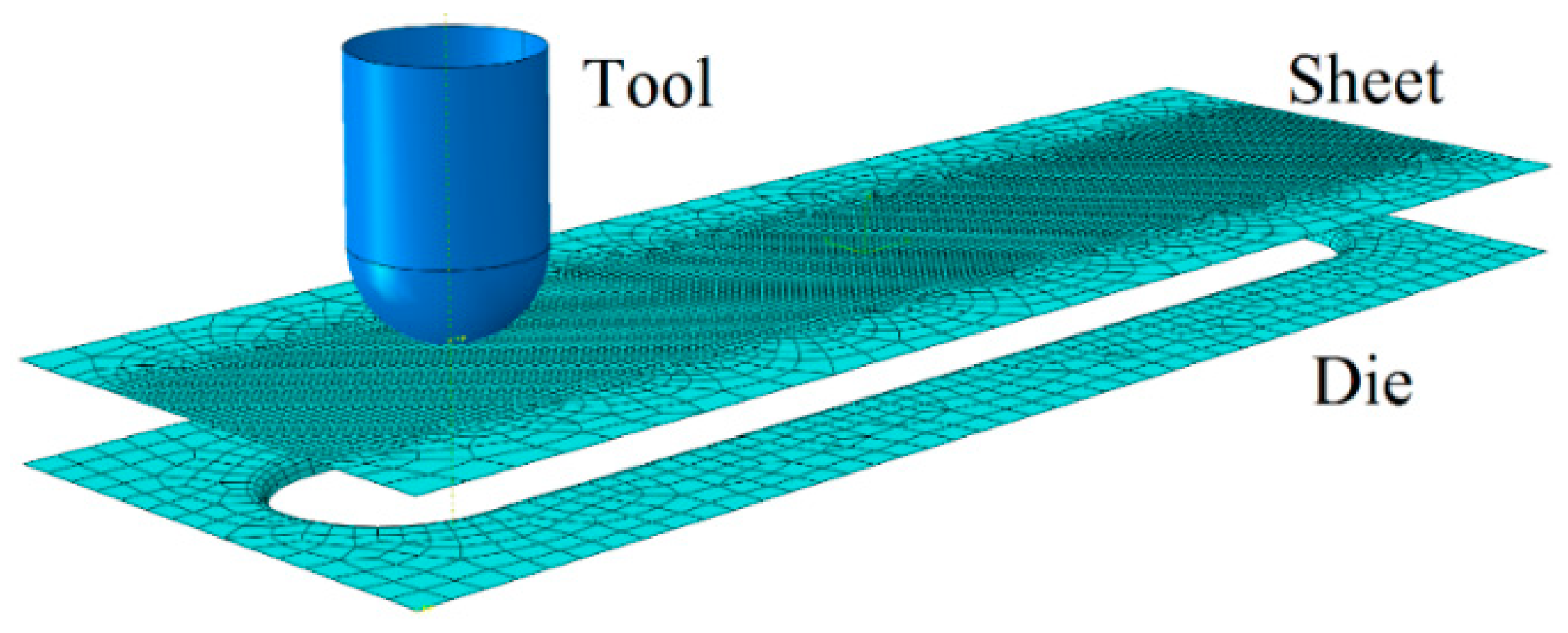
3. Finite Element Simulation
3.1. The Associated Flow Rule with Mixed Hardening
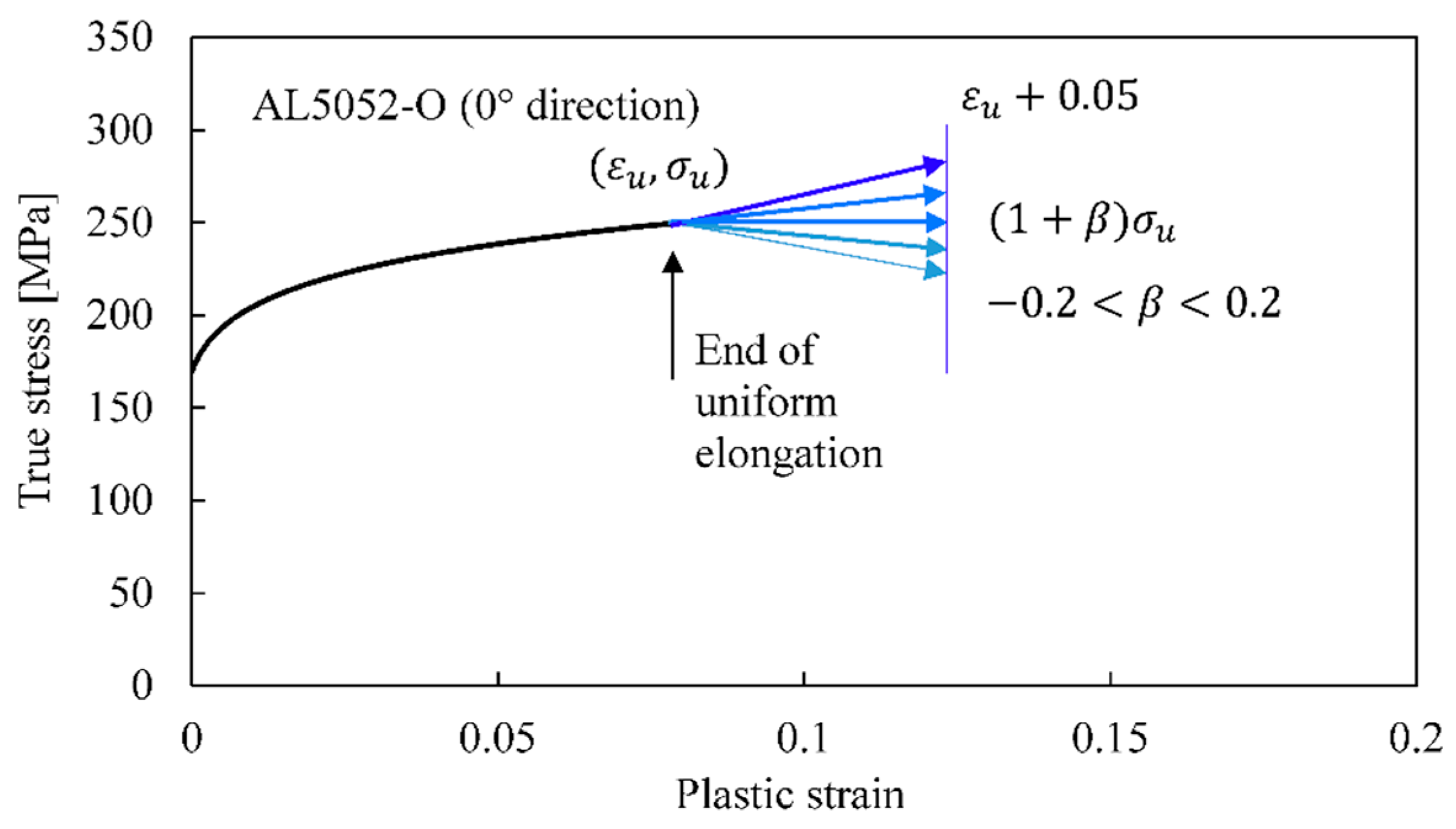
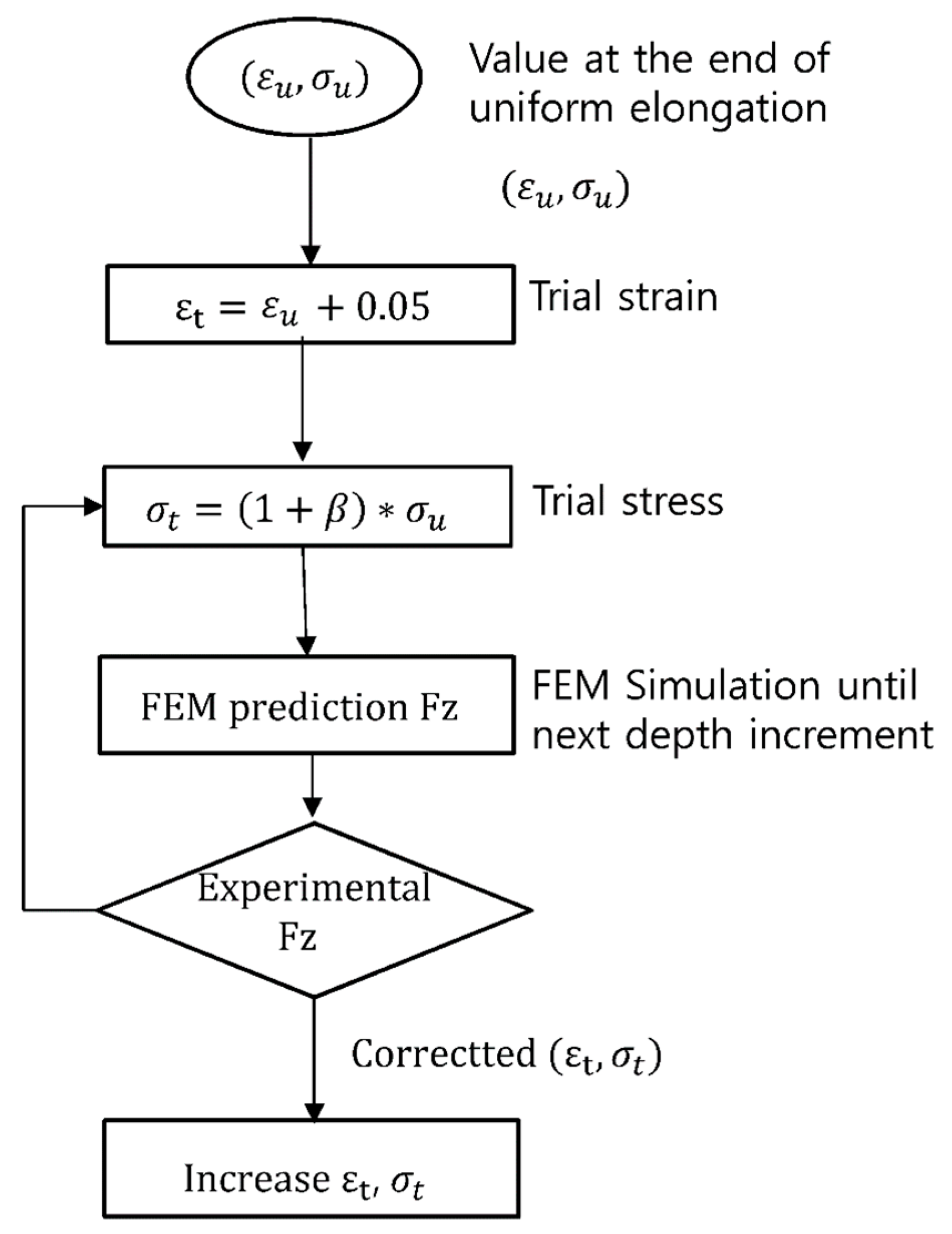
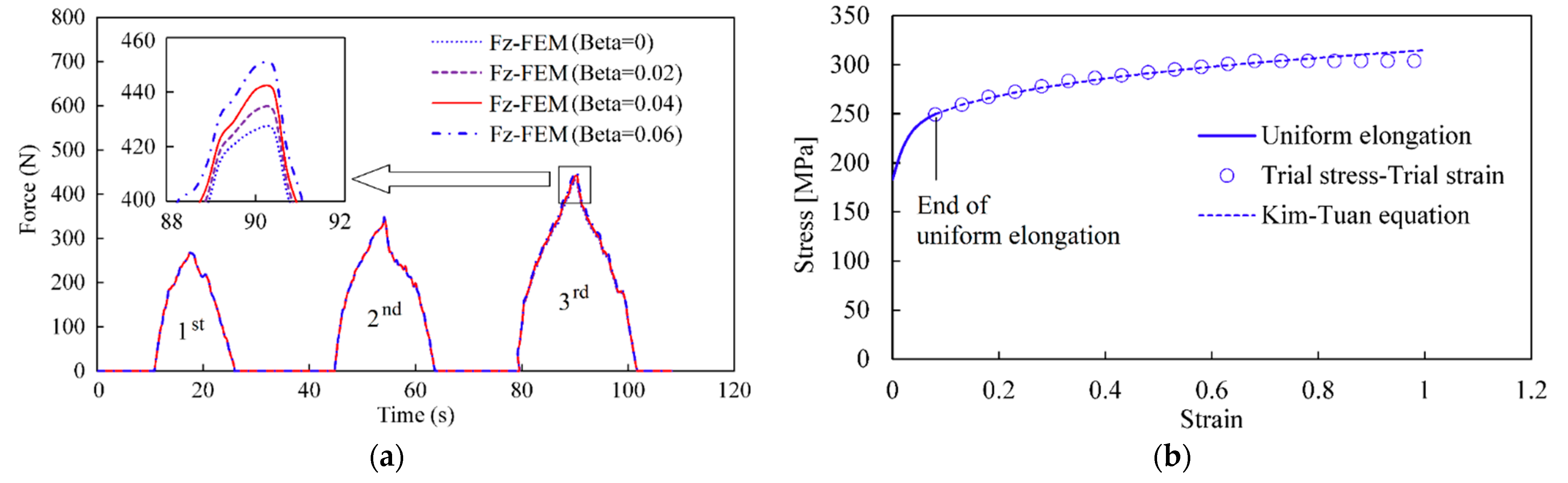
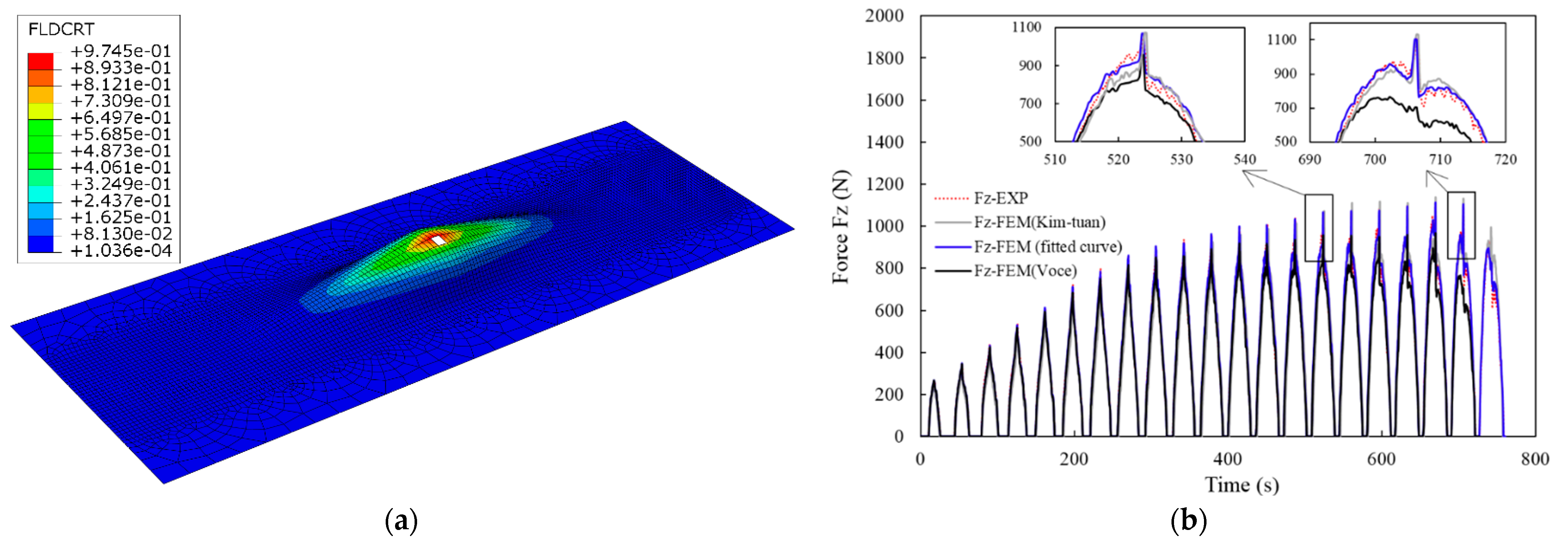
3.2. Calibration of Stress–Strain Curve Up to Large Strain Range
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hollomon, J.H. Tensile deformation. Trans. Metall. Soc. AIME 1945, 162, 268–290. [Google Scholar]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, J.H.; Wagoner, R.H. A plastic constitutive equation incorporating strain, strain-rate, and temperature. Int. J. Plast. 2010, 26, 1746–1771. [Google Scholar] [CrossRef]
- Pham, Q.T.; Kim, Y.S. Identification of the plastic deformation characteristics of AL5052-O sheet based on the non-associated flow rule. Met. Mater. Int. 2017, 23, 254–263. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, B.H.; Park, K.C.; Kim, Y.S. Influence of the post-necking prediction of hardening law on the theoretical forming limit curve of aluminium sheets. Int. J. Mech. Sci. 2018, 140, 521–536. [Google Scholar] [CrossRef]
- Coppieters, S.; Kuwabara, T. Identification of Post-Necking Hardening Phenomena in Ductile Sheet Metal. Exp. Mech. 2014, 54, 1355–1371. [Google Scholar] [CrossRef] [Green Version]
- Saboori, M.; Champliaud, H.; Gholipour, J.; Gakwaya, A.; Savoie, J.; Wanjara, P. Extension of flow stress–strain curves of aerospace alloys after necking. Int. J. Adv. Manf. Technol. 2016, 83, 313–323. [Google Scholar] [CrossRef]
- Pham, Q.T.; Lee, M.G.; Kim, Y.S. New procedure for determining the strain hardening behavior of sheet metals at large strains using the curve fitting method. Mech. Mater. 2021, 154, 103729. [Google Scholar] [CrossRef]
- Joun, M.S.; Eom, J.G.; Lee, M.C. A new method for acquiring true stress–strain curves over a large range of strains using a tensile test and finite element method. Mech. Mat. 2008, 40, 586–593. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, L.; Chang, Y.; Yan, J. Identification of post-necking stress–strain curve for sheet metals by inverse method. Mech. Mat. 2016, 92, 107–118. [Google Scholar] [CrossRef]
- Mei, H.; Lang, L.H.; Liu, K.N.; Yang, X.Q. Evaluation Study on Iterative Inverse Modeling Procedure for Determining Post-Necking Hardening Behavior of Sheet Metal at Elevated Temperature. Metals 2018, 8, 1044. [Google Scholar] [CrossRef] [Green Version]
- Kweon, H.D.; Kim, J.W.; Song, O.; Oh, D. Determination of true stress-strain curve of type 304 and 316 stainless steels using a typical tensile test and finite element analysis. Nucl. Eng. Technol. 2021, 53, 647–656. [Google Scholar] [CrossRef]
- Pham, Q.T.; Thoi, T.N.; Ha, J.J.; Kim, Y.S. Hybrid fitting-numerical method for determining strain-hardening behavior of sheet metals. Mech Mater. 2021, 161, 104031. [Google Scholar] [CrossRef]
- Behera, A.K.; Sousa, R.A.; Ingarao, G.; Oleksik, V. Single point incremental forming: An assessment of the progress and technology trends from 2005 to 2015. J. Manuf. Process. 2017, 27, 37–62. [Google Scholar] [CrossRef] [Green Version]
- Ai, S.; Long, H. A review on material fracture mechanism in incremental sheet forming. Int. J. Adv. Manuf. Technol. 2019, 104, 33–61. [Google Scholar] [CrossRef] [Green Version]
- Do, V.C.; Pham, Q.T.; Kim, Y.S. Identification of forming limit curve at fracture in incremental sheet forming. Int. J. Adv. Manuf. Technol. 2017, 92, 4445–4455. [Google Scholar] [CrossRef]
- Mirnia, M.J.; Shamsari, M. Numerical prediction of failure in single point incremental forming using a phenomenological ductile fracture criterion. J. Mater. Proc. Technol. 2017, 244, 17–43. [Google Scholar] [CrossRef]
- Duflou, J.; Tunckol, Y.; Szekeres, A.; Vanherck, P. Experimental study on force measurements for single point incremental forming. J. Mat. Proc. Technol. 2007, 189, 65–72. [Google Scholar] [CrossRef]
- Aerens, R.; Eyckens, P.; Van Bael, A.; Duflou, J.R. Force prediction for single point incremental forming deduced from experimental and FEM observations. Int. J. Adv. Manuf. Technol. 2010, 46, 969–982. [Google Scholar] [CrossRef]
- Bansal, A.; Lingam, R.; Yadav, S.K.; Reddy, N.V. Prediction of forming forces in single point incremental forming. J. Manuf. Proc. 2017, 28, 486–493. [Google Scholar] [CrossRef]
- Flores, P.; Duchene, L.; Bouffioux, C.; Lelotte, T.; Henrard, C.; Pernin, N.; Van Bael, A.; He, S.; Duflou, J.; Habraken, A.M. Model identification and FE simulations: Effect of different yield loci and hardening laws in sheet forming. Int. J. Plast. 2007, 23, 420–449. [Google Scholar] [CrossRef] [Green Version]
- Henrard, C.; Bouffioux, C.; Eychens, P.; Sol, H.; Duflou, J.R.; Van Houtte, P.; Van Bael, A.; Duchene, L.; Habraken, A.M. Forming forces in single point incremental forming: Prediction by finite element simulations, validation and sensitivity. Comput. Mech. 2011, 47, 573–590. [Google Scholar] [CrossRef]
- Tamura, S.; Sumikawa, S.; Uemori, T.; Hamasaki, H.; Yoshida, F. Experimental Observation of Elasto-Plasticity Behavior of Type 5000 and 6000 Aluminum Alloy Sheets. Mater. Trans. 2011, 52, 868–875. [Google Scholar] [CrossRef] [Green Version]
- Taherizadeh, A.; Green, D.E.; Ghaei, A.; Whan, Y.J. A non-associated constitutive model with mixed iso-kinematic hardening for finite element simulation of sheet metal forming. Int. J. Plast. 2010, 26, 288–309. [Google Scholar] [CrossRef]
- Fang, Y.; Lu, B.; Chen, J.; Xu, D.K.; Ou, H. Analytical and experimental investigations on deformation mechanism and fracture behavior in single point incremental forming. J. Mater. Process. Technol. 2014, 214, 1503–1515. [Google Scholar] [CrossRef]
- Zobeiry, N.; Vaziri, R.; Poursartip, A. Characterization of strain-softening behavior and failure mechanisms of composites under tension and compression. Compos. Part A Appl. Sci. Manuf. 2015, 68, 29–41. [Google Scholar] [CrossRef]
- Kassner, M.E.; Ermagan, R. Large-Strain Softening of Metals at Elevated Temperatures by Deformation Texture Development. Metals 2021, 11, 1059. [Google Scholar] [CrossRef]
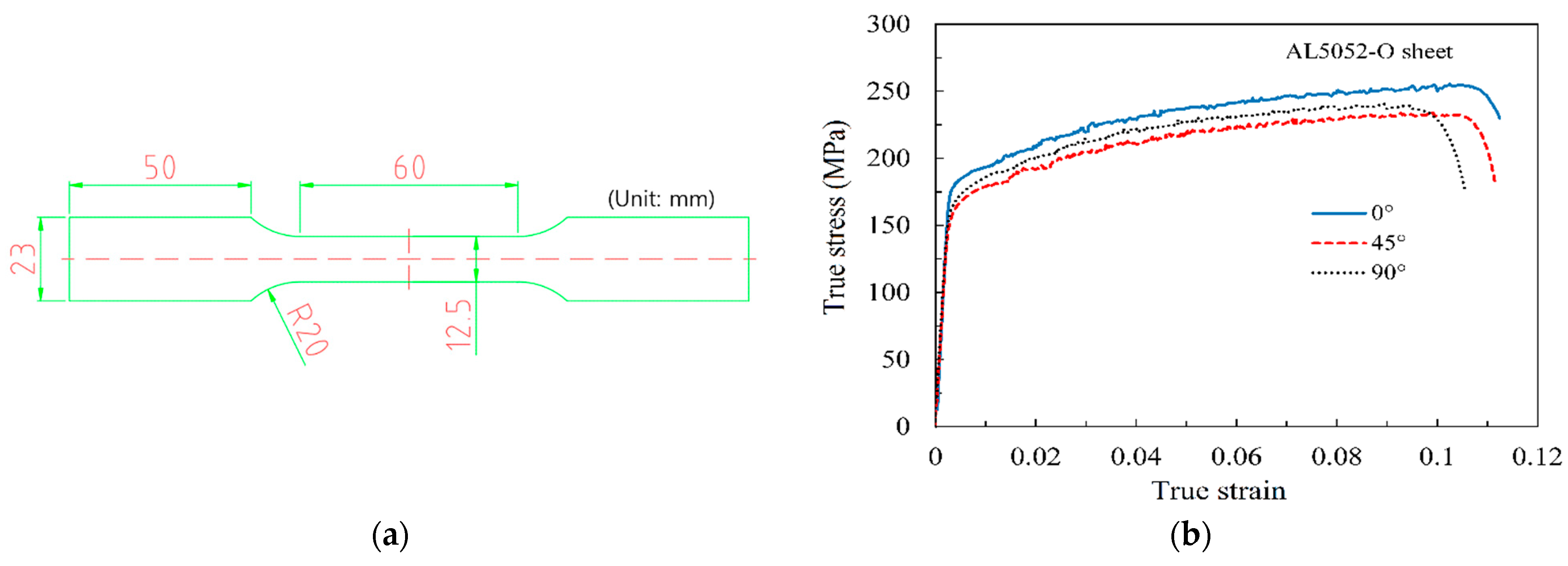
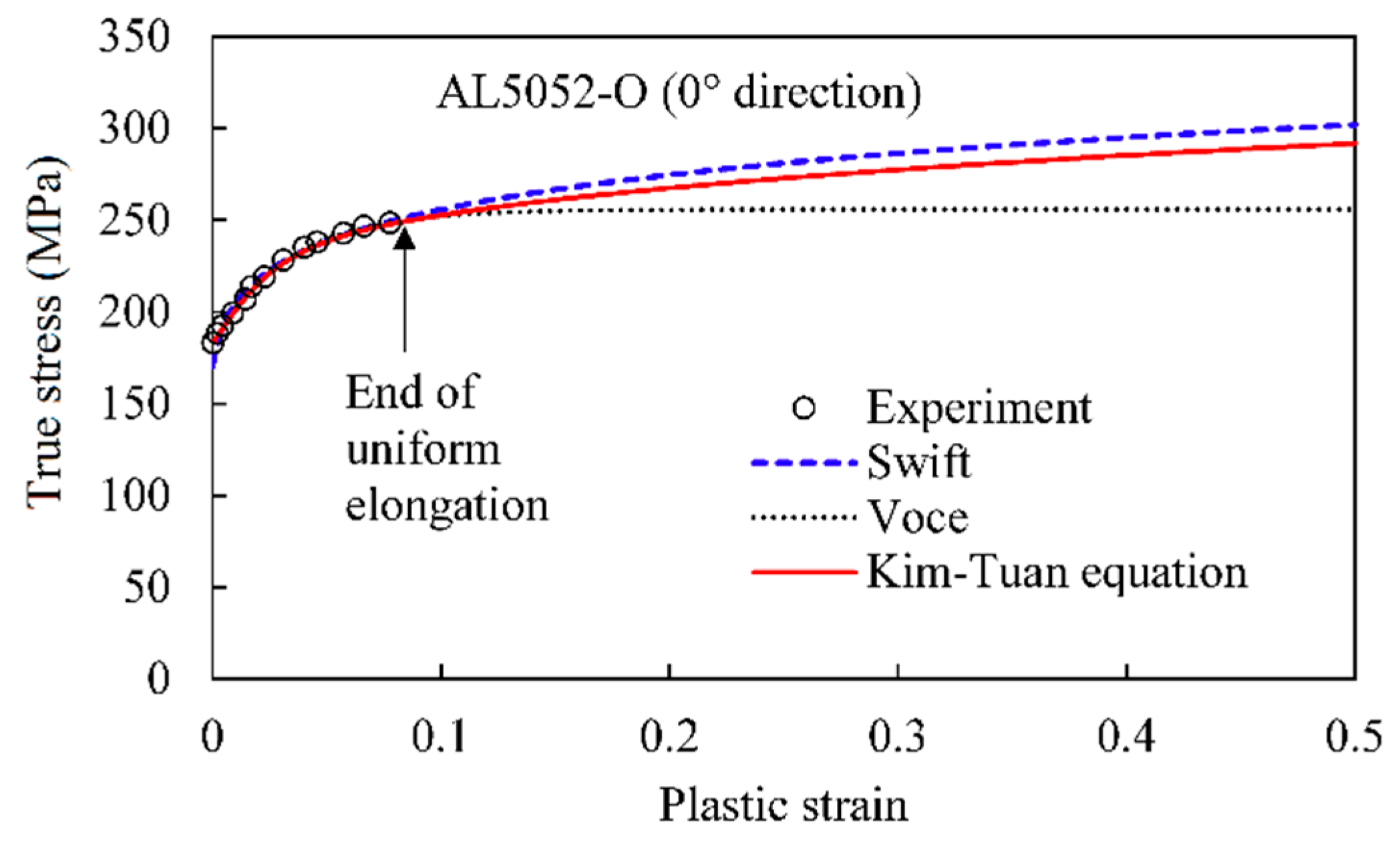
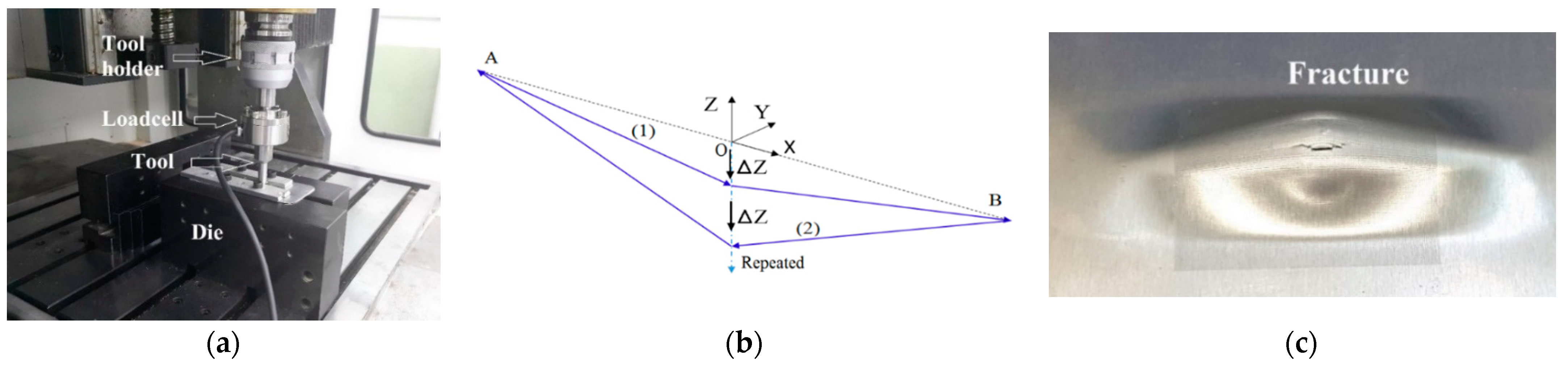
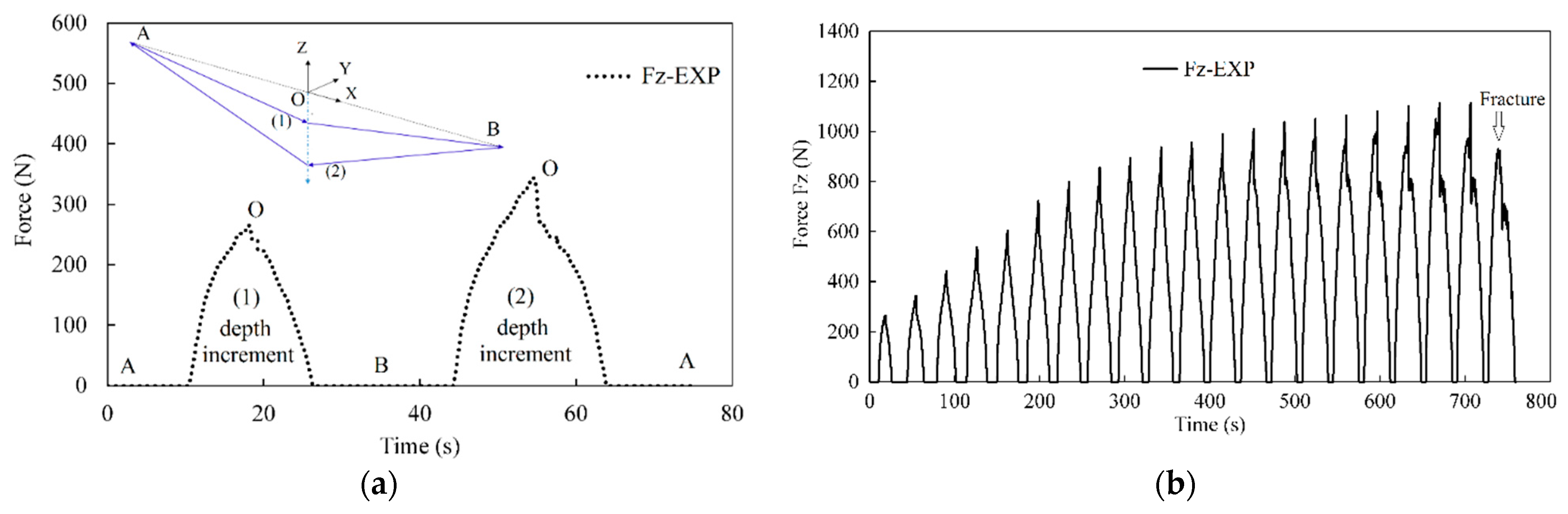
| Direction | 0 | ||
|---|---|---|---|
| Young’s modulus [GPa] | 73.2 | 71.2 | 74.1 |
| Yield stress [MPa] | 183.3 | 172.5 | 173.6 |
| Ultimate tensile strength [MPa] | 229.8 | 216.6 | 220.1 |
| Elongation [%] | 11.0 | 13.6 | 10.5 |
| R-value | 0.758 | 0.646 | 0.863 |
| KT | 131.580 | 124.809 | 124.268 |
| m | 0.271 | 0.278 | 0.251 |
| c | 61.163 | 75.433 | 69.521 |
| Yield Function Hill48 | |||
|---|---|---|---|
| F | G | H | N |
| 0.4996 | 0.5688 | 0.4312 | 1.2244 |
| Increment | Experimental (N) | FEM Using the Fitted Curve (N) | FEM Using Voce Curve (N) |
|---|---|---|---|
| 15th | 1050.3 | 1065.73 | 956.39 |
| 20th | 1095.97 | 1104.38 | 766.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-S.; Tuan, P.-Q.; Xiao, X.; Kim, J.-j. Calibration of the Flow Curve Up to Large Strain Range by Incremental Sheet Forming Coupled with FEM Simulation. Metals 2022, 12, 252. https://doi.org/10.3390/met12020252
Kim Y-S, Tuan P-Q, Xiao X, Kim J-j. Calibration of the Flow Curve Up to Large Strain Range by Incremental Sheet Forming Coupled with FEM Simulation. Metals. 2022; 12(2):252. https://doi.org/10.3390/met12020252
Chicago/Turabian StyleKim, Young-Suk, Pham-Quoc Tuan, Xiao Xiao, and Jin-jae Kim. 2022. "Calibration of the Flow Curve Up to Large Strain Range by Incremental Sheet Forming Coupled with FEM Simulation" Metals 12, no. 2: 252. https://doi.org/10.3390/met12020252
APA StyleKim, Y.-S., Tuan, P.-Q., Xiao, X., & Kim, J.-j. (2022). Calibration of the Flow Curve Up to Large Strain Range by Incremental Sheet Forming Coupled with FEM Simulation. Metals, 12(2), 252. https://doi.org/10.3390/met12020252






