Abstract
Dislocation dynamics has been an intensive research subject in materials science and engineering due to the significant roles it plays in plastic deformation and the hardening of metals, fracture mechanics, and the fabrication of semiconductor thin films. However, a long-standing problem from the three-dimensional dislocation dynamics is that the motion and interaction of dislocation loops heavily depend on the loop-segment sizes, which substantially reduces the accuracy of simulation. We herein propose a new three-dimensional dislocation dynamics model together with its physical background. The proposed model incorporates the inherent interactions among differential dislocation segments. The simulation results on motion of Frank–Read sources demonstrate that the proposed model can resolve the paradoxical segment-dependent phenomenon in dislocation dynamics.
1. Introduction
Metallic materials contain crystal defects in their microstructures, which can be point, line, surface, or volume defects. These defects locally disturb the regular arrangement of atoms. Their presence, especially the presence of the line defects (dislocation loops), essentially determines the strength and plastic deformation of crystalline solids.
Partly because the macroscopic plastic responses of metals are primarily controlled by the nucleation, motion, annihilation, and interaction of dislocations in them, dislocation dynamics has been of great interest to researchers and engineers in the past several decades. Analytical solutions to this problem are impossible in most cases due to the inherent complexity of dislocation loops. Various discretization techniques are widely employed instead, which are known as discrete dislocation dynamics. With the rapid development of computational technology, a lot of important research work on dislocation dynamics has been made since the 1980s. Dislocation dynamics was first applied to two-dimensional (2D) straight, infinitely long dislocations [1,2,3,4], and then to the much more complicated three-dimensional (3D) dislocation loops in the infinite domain [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].
While computational methods have been proposed to model the motion, evolution, and interactions of 3D dislocation arrays, an open question associated with these methods is how to discretize dislocation loops, since inappropriate selection of dislocation segments causes unrealistic responses, as indicated by Gómez-García, Devincre, and Kubin [21]. Ghoniem et al. [11] also showed a strange “velocity jump” phenomenon, illustrated in Figure 1a, in which the movements near the two pinning points of a straight dislocation loop can jump as the number of line segments increases. Such an unreasonable phenomenon contradicts with the numerical approaches that finer discretized meshes employ in order to obtain more accurate solutions. As a matter of fact, simulation results are influenced by the artificial selection of the number of segments and meshes, as shown in Figure 1b, which casts doubts on the reliability of simulations in dislocation dynamics. The current paper aims to investigate the reasons behind such abnormal appearances and to develop a novel model of dislocation motion and dynamics.
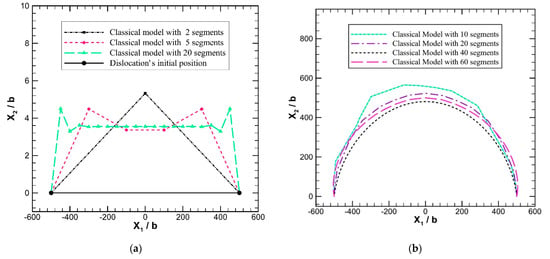
Figure 1.
Simulation results from a classical dislocation dynamics model for a straight dislocation loop: (a) the dislocation segment jumps near the pinning points in the first time-step as the number of segment increases; (b) dislocation positions are dependent on the number of segments during the dislocation loop’s motion and evolution processes.
2. Methodology
With a given three-dimensional dislocation loop, the conventional dislocation-dynamics methods are based on the following governing equation [22]:
where Fi (i = 1, 2, 3) represents the local glide force per unit length exerting on the dislocation loop, Bij (i, j = 1, 2, 3) is the second-rank tensor of dislocation drag coefficients, and Vj (j = 1, 2, 3) is the local velocity of the dislocation. Furthermore, BijVj is also called the drag force of the dislocation. It is noted that all equations are written with tensorial indicial notation (i.e., the free indices take values from 1 to 3 and the repeated indices are summed from 1 to 3 unless explicit statements are indicated [23,24]). From the Peach–Koehler formula [25], glide force Fi can be expressed as follows:
where is the second-rank stress tensor, the Burgers vector of the dislocation, the unit normal to the slip plane, and the in-plane unit normal to the dislocation loop. It is noted that the Peach–Koehler formula-based glide force Fi is always in the same direction of , perpendicular to the dislocation loop. Contributions to the stresses may come from the applied stresses and the self-stresses due to the dislocation loop itself. The self-stresses induced by a dislocation itself is best found using Brown’s formula [26] or Gavazza and Barnett’s equation [27] to avoid singularity issues.
Mathematically, the combination of Equations (1) and (2) indicates that the dislocation velocity Vj is determined by the glide force Fi, as long as the size of the dislocation and applied loads are given. Further investigation shows that the glide force Fi is completely derived, independent of the velocity variation along the dislocation line. Therefore, Equation (1) is essentially an algebraic equation rather than differential equation, from which the velocity Vj can be calculated without the need of discretization processes. If the entire dislocation loop is segmented into many pieces of lines, the nodes at the ends of segments may jump because of the certain averaging approaches involved. That is the reason why the abnormal appearance occurs in Figure 1a causing the dislocation positions in Figure 1b dependent on the number and size of segments during its motion processes.
From a physical point of view, the abnormal phenomenon that dislocation motion is dependent on segment size is due to the fact that only a minor portion of the interaction between adjacent segments is taken into consideration in Equation (1). In the mechanics theory of dislocations, a dislocation is considered as a continuous tube. Because of the stress field external to the tube, the elastic interaction between adjacent dislocation segments is represented by the contribution of self-stresses in Equation (2). However, as illustrated in Figure 2a, the local interaction due to the core structure of the tube is not taken into account in Equation (2). Such local interactions have been exemplified by the Finnis–Sinclair interatomic potential [28] and the interatomic bondings in dislocation cores [29], implying that the local interactions be taken into account in the framework of dislocation dynamics.
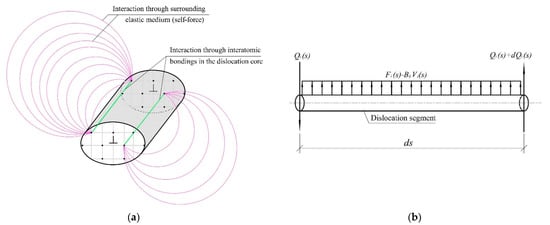
Figure 2.
(a) Interactions of adjacent differential dislocation segments can be divided into two parts. (b) Free-body diagram of a differential dislocation segment with forces acting on it.
Based on the above arguments, the local interaction can be assumed to adhere to the viscous law as follows:
where Qi signifies the shear force between adjacent differential segments, ηij denotes the second-rank tensor of the local interaction of dislocation segments, and s represents a local one-dimensional coordinate along the dislocation loop. From the free-body diagram for a tubed dislocation segment, as shown in Figure 2b, a revised governing equation of dislocation dynamics can be derived as follows:
It is noted that the above governing equation considers both the elastic and local interactions between dislocation segments.
3. Numerical Implementation
Similar to the standard finite element method, the numerical approach applied herein discretizes the dislocation loop into M curved segments, each of which has nodes. The coordinates and velocities at any point on a segment are given as follows:
where ri is the coordinate of a point on the segment, rjs is the node coordinate of the segment, Vjs is the velocity vector of the segment, and Nij (u) is the interpolation function dependent on the parameter . The weak form of Equation (4) for each segment can then be rewritten as follows:
where , , with being the Jacobian and as the local force at the nodes. With the assembly processes, the corresponding global equation is obtained as follows:
where Mp is the total number of nodes of the dislocation loop, and and are obtained by assembling and , respectively. Solving Equation (7) with appropriate constraints on , the node velocities, as well as the velocity of the entire dislocation loop, can be computed.
The time span is also discretized into many time steps. If the velocity Vj at time step ti, say, , has already been obtained by solving Equation (7), then the dislocation position at the next time step ti+1 can be obtained as follows:
4. Results and Discussion
The critical stress necessary to activate a Frank–Read source of dislocation and its evolution have been a major topic in the theory of dislocation dynamics. Foreman [30] was the first to employ computer technology to determine the equilibrium shape and critical stress of a Frank–Read source by continuously adjusting node positions until the dislocation reached an equilibrium state. This method, however, cannot simulate the evolution of a Frank–Read source with any great degree of precision. Devincre and Condat [31] applied a 3D dislocation dynamics model to simulate the evolution and evaluate the critical stress of a Frank–Read source. While various dislocation dynamics models have been actively researched since then, the ability to simulate the evolution of dislocations is still limited by the inherent complexity of this problem, as previously indicated in Section 1.
With the newly developed governing equations and numerical scheme derived in this paper, the motion, bowing, evolution, and critical stress of a Frank–Read source are examined herein. Without losing any generality, the parameters are selected as follows: the Burgers vector , the distance between the two pinning points , shear modulus GPa, Poisson’s ratio , drag coefficient Pa·S, local interaction N·S, and time step s (second). Figure 3 shows the direct comparison between the current model and classical dislocation dynamics simulation. Figure 3a shows the shapes of a Frank–Read source after the first-time step simulated using the classical model and the current model, respectively, demonstrating that the current model is robust, while the classical simulation maintains a peculiar “velocity jump” phenomenon at the beginning steps. Also, Figure 3b shows that the current model quickly stabilizes and converges when the number of dislocation segments approaches 20; yet, for the classical model, dislocation positions are heavily dependent on the number of segments during the motion and evolution processes of the Frank–Read source.
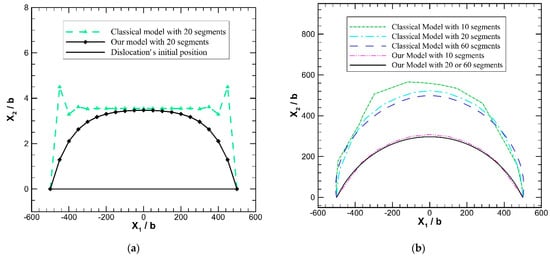
Figure 3.
Comparison between the current model and classical dislocation dynamics simulation at (a) the first-time step of a straight dislocation loop and at (b) the 200th time-step during the evolution process of the dislocation.
Furthermore, Figure 4 illustrates the simulation results for the equilibrium bowing-out of the Frank–Read source and its motion and evolution processes. Specifically, Figure 4a demonstrates that, for an initial edge dislocation Frank–Read source subject to an applied stress no greater than the critical stress, the equilibrium positions are dependent on applied stresses. The results are in good agreement with those given by Foreman [30]. If the applied stress is greater than the critical stress, the annihilation mechanism of Frank–Read source is activated. The entire dislocation evolution of such a case is shown in Figure 4b, exhibiting that the dislocation decelerates, accelerates, and then remains at an almost constant speed during the entire expansion process. For a Frank–Read source with a smaller length, our model can still converge quickly and accurately predict the critical stress, as shown in Figure 4c. The effect of local interaction in a dislocation core is also investigated with the change of η values of the Frank–Read source, showing in Figure 4d that weak interaction yields early evolution and annihilation of the Frank–Read dislocation loop.
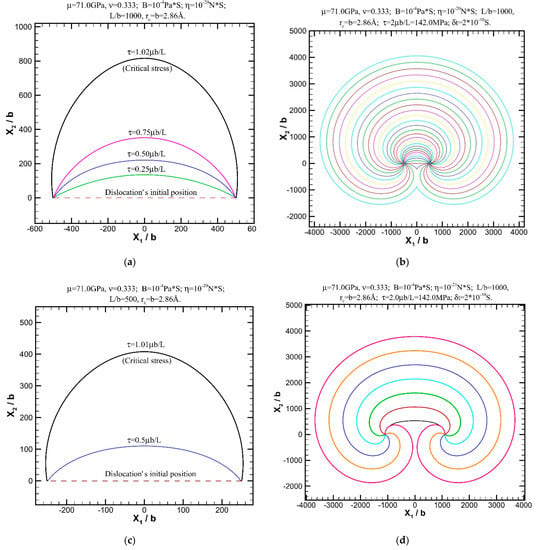
Figure 4.
Simulation results for equilibrium bowing-out of the Frank–Read source and its motion and evolution processes: (a) Equilibrium positions of an initial edge dislocation of relative length L/b = 1000 under different applied stresses; (b) Evolution of the dislocation with strong local interaction under the action of an applied stress of μb/L; (c) Equilibrium positions of the dislocation of relative length L/b = 500 under different applied stresses; (d) Evolution of the dislocation with weak local interaction under the action of an applied stress of μb/L. The time between neighboring evolution lines is S.
Figure 5 demonstrates the relationship between calculated critical stresses and segment numbers. The new model demonstrates excellent stability for various segment sizes. The calculated critical stresses quickly converge to the solution given by Foreman [30], while the results from the classical model heavily depend on the segment size and the artificial ‘manipulations’ during the simulation processes.
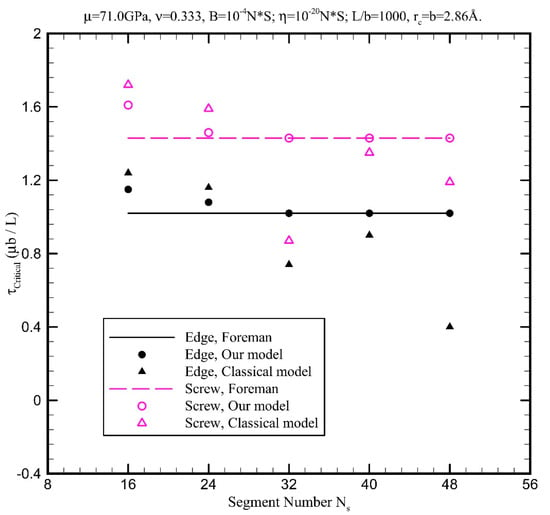
Figure 5.
Relationship between calculated critical stresses and segment numbers.
5. Conclusions
In our proposed model, we fully take into account the local interaction between dislocation segments to resolve the long-standing paradoxical problem mentioned in the literature [11,21]. As expected, the determinations of equilibrium shape and critical stress are insensitive to the values of drag coefficient tensor Bij and local interaction tensor ηij of the dislocation, provided that they vary within a reasonable range. For example, it is Pa·S for Bij and N·S for ηij in our simulation of the Frank–Read source. In contrast, the evolution profiles of the dislocation from the conventional models are heavily dependent on the values of Bij. Under the action of applied stresses larger than, but comparable to, the critical stress, the dislocation expansion speed varies greatly in the multiplication process. However, the dislocation velocity does not vary appreciably if the applied stress is sufficiently large. It is interesting that if we divide N·S by the cross-sectional area of the dislocation tube, we can find Pa·S, which falls into the normal range of material viscosity coefficients. It can be surmised that the intrinsic local interaction within a dislocation loop may be determined with the molecular dynamics methods. Yet, experimental approaches to determining the interaction parameter ηij would surely be of significant benefit. Finally, it should be noted that the new dislocation dynamics model applies not only to the Frank–Read sources but also to general dislocation dynamics problems.
Author Contributions
X.T.: Investigation, Formal Analysis, Data Curation, Writing—Reviewing and Editing. E.T.: Methodology, Investigation, Data Curation, Writing—Original Draft Preparation. L.S.: Conceptualization, Methodology, Supervision, Writing—Reviewing and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partly supported by the U.S. National Science Foundation under Grant No. DMR 0113172.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lepinoux, J.; Kubin, L.P. The dynamic organization of dislocation structures: A simulation. Scr. Metall. 1987, 21, 833–838. [Google Scholar] [CrossRef]
- Amodeo, R.J.; Ghoniem, N.M. Dislocation dynamics I, a proposed methodology for deformation micromechanics. Phys. Rev. B 1990, 41, 6958–6967. [Google Scholar] [CrossRef] [PubMed]
- Amodeo, R.J.; Ghoniem, N.M. Dislocation dynamics I, applications to the formation of persistent slip bands, planar arrays, and dislocation cells. Phys. Rev. B 1990, 41, 6968–6976. [Google Scholar] [CrossRef] [PubMed]
- Van der Giessen, E.; Needleman, A. Discrete dislocation plasticity: A simple planar model. Model. Simul. Mater. Sci. Eng. 1995, 3, 689–735. [Google Scholar] [CrossRef]
- Kubin, L.P.; Canova, G.; Condat, M.; Devincre, B.; Pontikis, V.; Brechet, Y. Dislocation microstructures and plastic flow: A 3D simulation. Solid State Phenom. 1992, 23–24, 455–472. [Google Scholar] [CrossRef]
- Schwarz, K.W.; Tersoff, J. Interaction of threading and misfit dislocations in a strained epitaxial layer. Appl. Phys. Lett. 1996, 69, 1220–1222. [Google Scholar] [CrossRef]
- Schwarz, K.W. Interaction of dislocations on crossed glide planes in a strained epitaxial layer. Phys. Rev. Lett. 1997, 78, 4785–4788. [Google Scholar] [CrossRef]
- Tang, M.; Kubin, L.P.; Canova, G.R. Dislocation mobility and the mechanical response of b.c.c. single crystals: A mesoscopic approach. Acta Mater. 1998, 46, 3221–3235. [Google Scholar] [CrossRef]
- Zbib, H.M.; Rhee, M.; Hirth, J.P. On the plastic deformation and the dynamics of 3D dislocations. Inter. J. Mech. Sci. 1998, 40, 113–127. [Google Scholar] [CrossRef]
- Ghoniem, N.M.; Sun, L.Z. Fast-sum method for the elastic field of three-dimensional dislocation ensembles. Phys. Rev. B 1999, 60, 128–140. [Google Scholar] [CrossRef]
- Ghoniem, N.M.; Tong, S.-H.; Sun, L.Z. Parametric dislocation dynamics: A thermaldynamics-based approach to investigations of mesoscopic plastic deformation. Phys. Rev. B 2000, 61, 913–927. [Google Scholar] [CrossRef]
- Diaz de la Rubia, T.; Zbib, H.M.; Khraishi, T.A.; Wirth, B.D.; Victoria, V.; Caturla, M.J. Multiscale modeling of plastic flow localization in irradiated materials. Nature 2000, 406, 871–874. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Bulatov, V.V. Mobility laws in dislocation dynamics simulations. Mater. Sci. Eng. A 2004, 387–389, 277–281. [Google Scholar] [CrossRef]
- Cui, Y.; Ghoniem, N.M. Influence of Size on the Fractal Dimension of Dislocation Microstructure. Metals 2019, 9, 478. [Google Scholar] [CrossRef]
- Gao, S.; Yang, Z.; Grabowski, M.; Rogal, J.; Drautz, R.; Hartmaier, A. Influence of Excess Volumes Induced by Re and W on Dislocation Motion and Creep in Ni-Base Single Crystal Superalloys: A 3D Discrete Dislocation Dynamics Study. Metals 2019, 9, 637. [Google Scholar] [CrossRef]
- Fan, H.; Wang, Q.; El-Awady, J.A.; Raabe, D.; Zaiser, M. Strain rate dependency of dislocation plasticity. Nat. Commun. 2021, 12, 1845. [Google Scholar] [CrossRef]
- Muraishi, S. Internal Stress and Dislocation Interaction of Plate-Shaped Misfitting Precipitates in Aluminum Alloys. Materials 2021, 14, 5811. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, J.; Muraishi, S. Dislocation Topological Evolution and Energy Analysis in Misfit Hardening of Spherical Precipitate by the Parametric Dislocation Dynamics Simulation. Materials 2021, 14, 6368. [Google Scholar] [CrossRef]
- Pachaury, Y.; Po, G.; El-Azab, A. Discrete Dislocation Dynamics for Crystal RVEs Part I: Periodic Network Kinematics. J. Mech. Phys. Solids 2022, 163, 104861. [Google Scholar] [CrossRef]
- Schneider, Y.; Rapp, D.-M.; Yang, Y.; Wasserbach, W.; Schmauder, S. Many-scale Investigations of Deformation Behavior of Polycrystalline Composites: II Micro-Macro Simultaneous FE and Discrete Dislocation Dynamics Simulation. Materials 2022, 15, 2852. [Google Scholar] [CrossRef]
- Gómez-García, D.; Devincre, B.; Kubin, L.P. Dislocation dynamics in confined geometry. J. Comput.-Aided Mater. Des. 1999, 6, 157–164. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Cai, W. Computer Simulations of Dislocations; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Yin, H.M.; Sun, L.Z. Magnetoelasticity of chain-structured ferromagnetic composites. Appl. Phys. Lett. 2005, 86, 261901. [Google Scholar] [CrossRef]
- Liu, H.T.; Sun, L.Z.; Ju, J.W. Elastoplastic modeling of progressive interfacial debonding for particle-reinforced metal-matrix composites. Acta Mech. 2006, 181, 1–17. [Google Scholar] [CrossRef]
- Peach, M.; Koehler, J.S. The forces exerted on dislocations and the stress fields produced by them. Phys. Rev. 1950, 80, 436–439. [Google Scholar] [CrossRef]
- Brown, L.M. The self-stress of dislocations and the shape of extended nodes. Phil. Mag. 1964, 10, 441–466. [Google Scholar] [CrossRef]
- Gavazza, S.D.; Barnett, D.M. The self-force on a planar dislocation loop in an anisotropic linear-elastic medium. J. Mech. Phys. Solids 1976, 24, 171–185. [Google Scholar] [CrossRef]
- Finnis, M.W.; Sinclair, J.E. A simple empirical N-body potential for transition metals. Phil. Mag. A 1984, 50, 45–55. [Google Scholar] [CrossRef]
- Telling, R.H.; Ewels, C.P.; El-Barbary, A.A.; Heggie, M.I. Wigner defects bridge the graphite gap. Nat. Mater. 2003, 2, 333–337. [Google Scholar] [CrossRef]
- Foreman, A.J.E. The bowing of a dislocation segment. Phil. Mag. 1967, 15, 1011–1021. [Google Scholar] [CrossRef]
- Devincre, B.; Condat, M. Model validation of a 3D simulation of dislocation dynamics: Discretization and line tension effects. Acta Metall. Mater. 1992, 40, 2629–2637. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).