Influence of Weld-Porosity Defects on Fatigue Strength of AH36 Butt Joints Used in Ship Structures
Abstract
1. Introduction
2. Materials
- type-C-1, butt joints without defect and thickness nominal value t = 5.5 mm;
- type-NC-2, butt joints with defect and thickness nominal value t = 5.5 mm;
- type-C-3, butt joints without defect and thickness nominal value t = 6.5 mm;
- type-NC-4, butt joints with defect and thickness nominal value t = 6.5 mm.
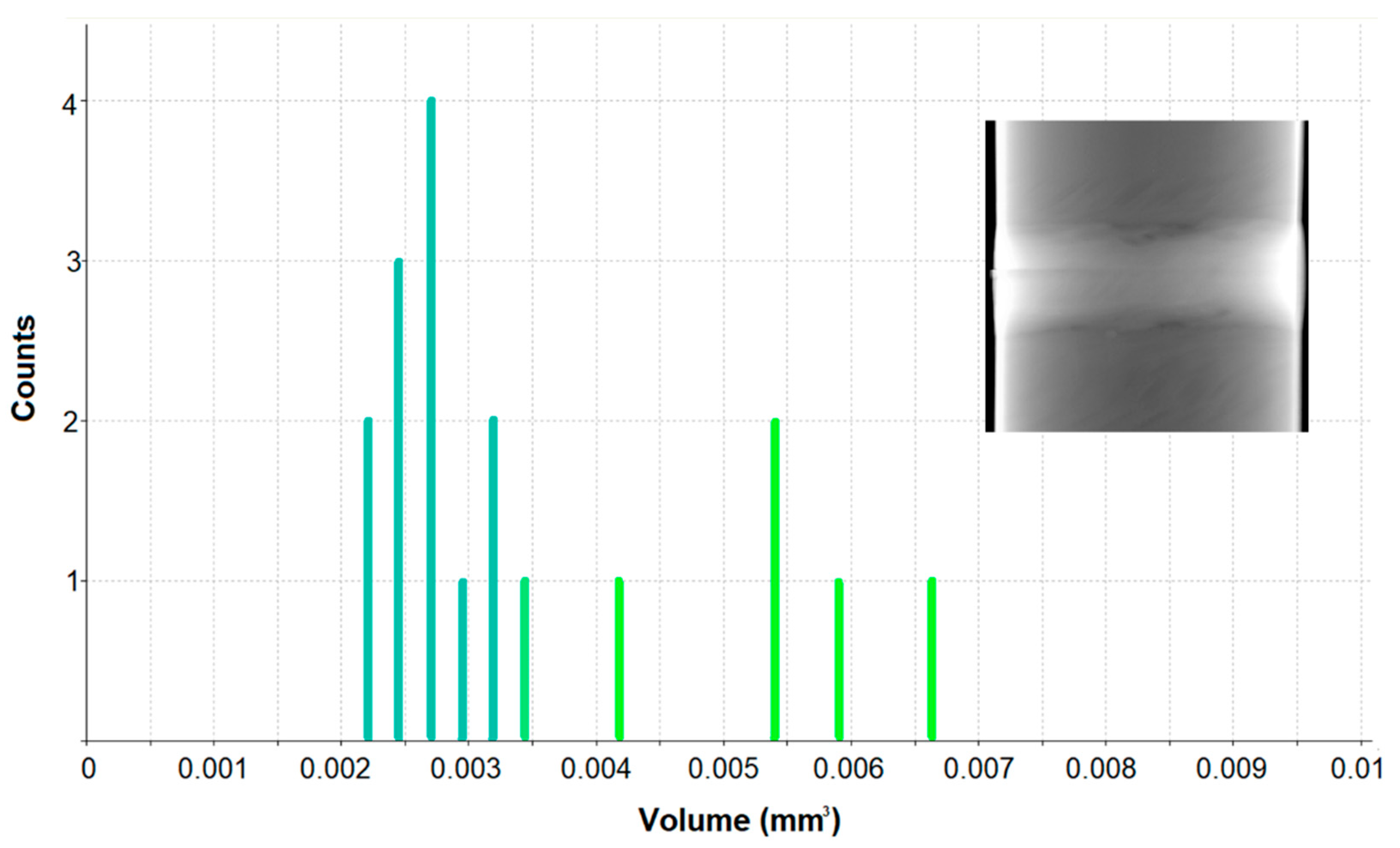
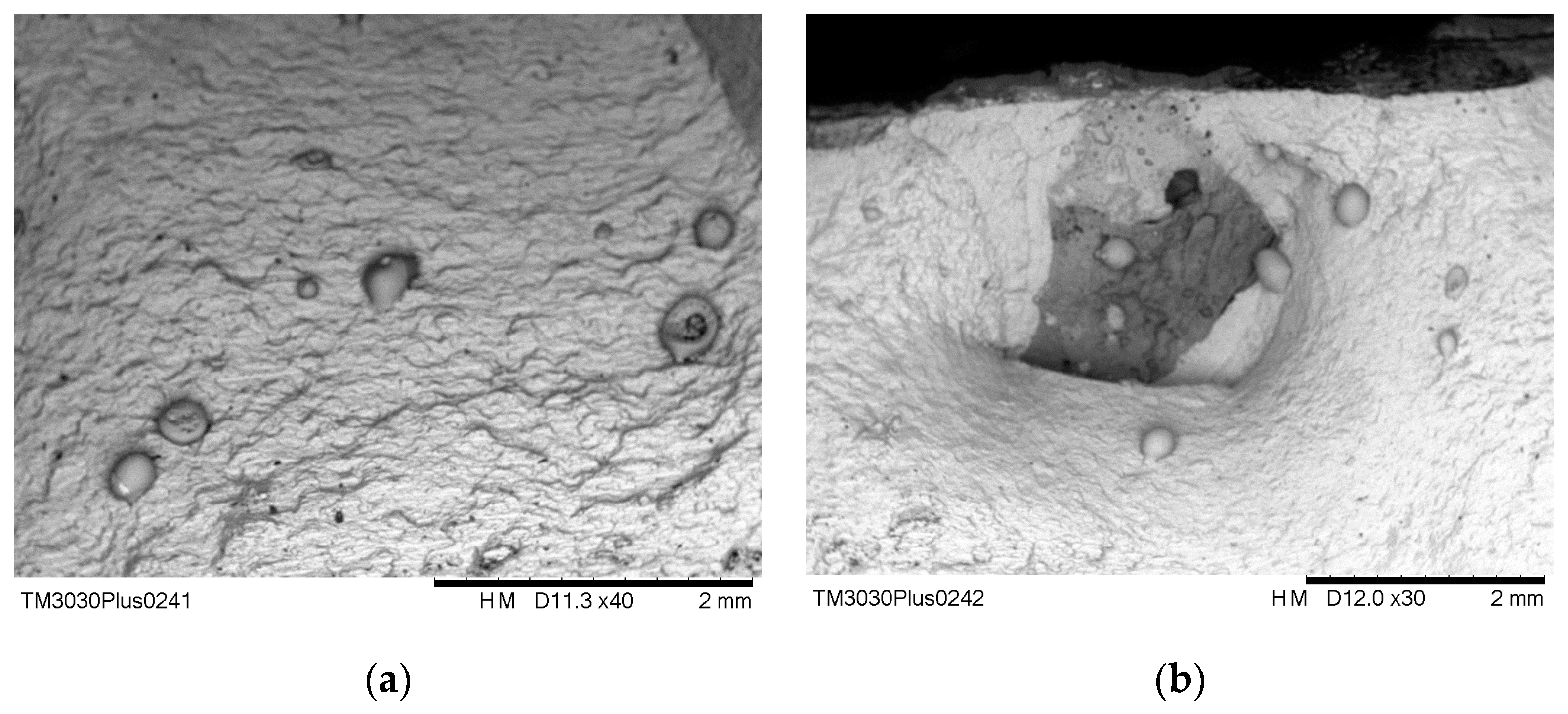
Defect Detection by Computed Tomography
3. Methods
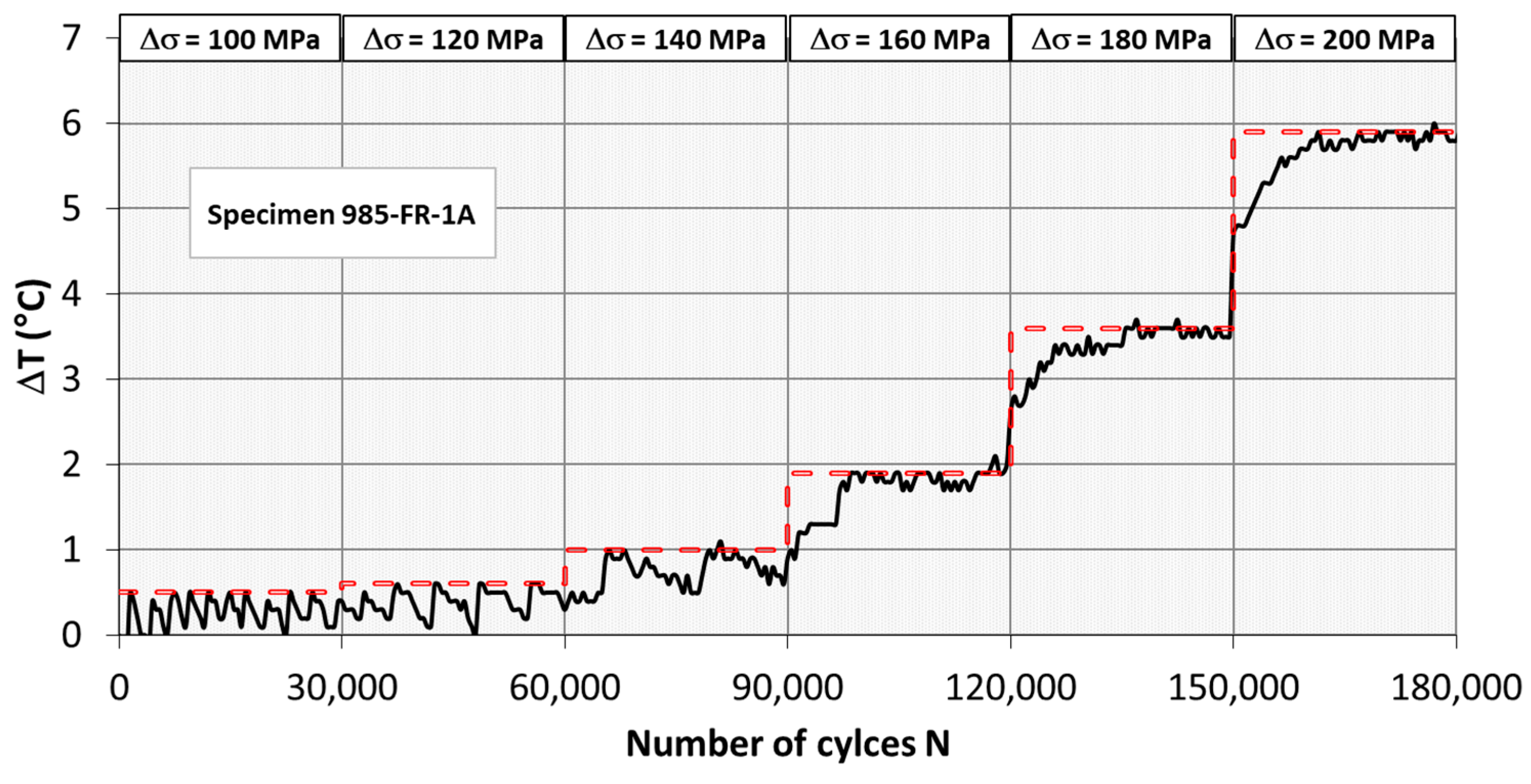
3.1. Rapid Thermographic Method
3.2. Energy Approach
4. Results and Discussion
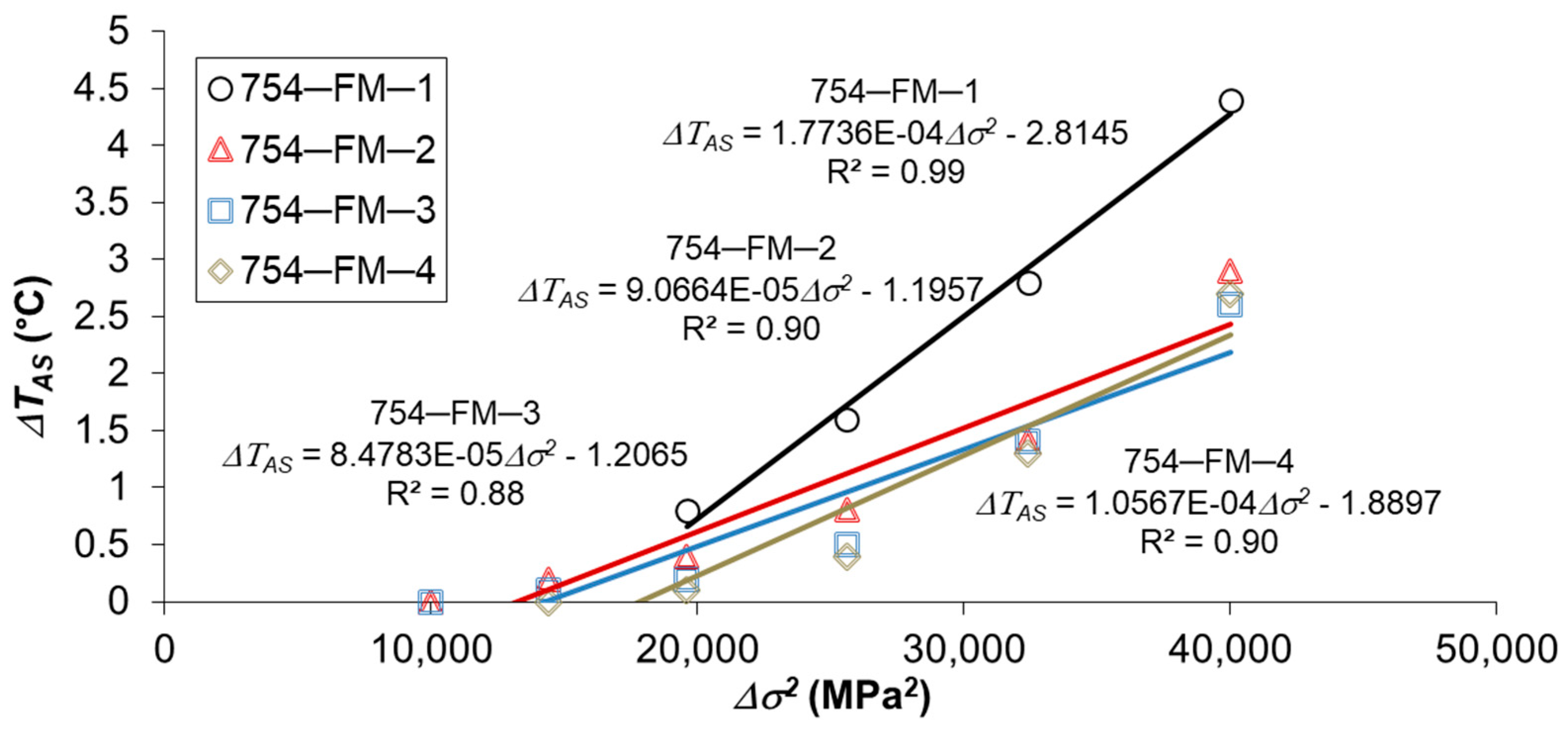
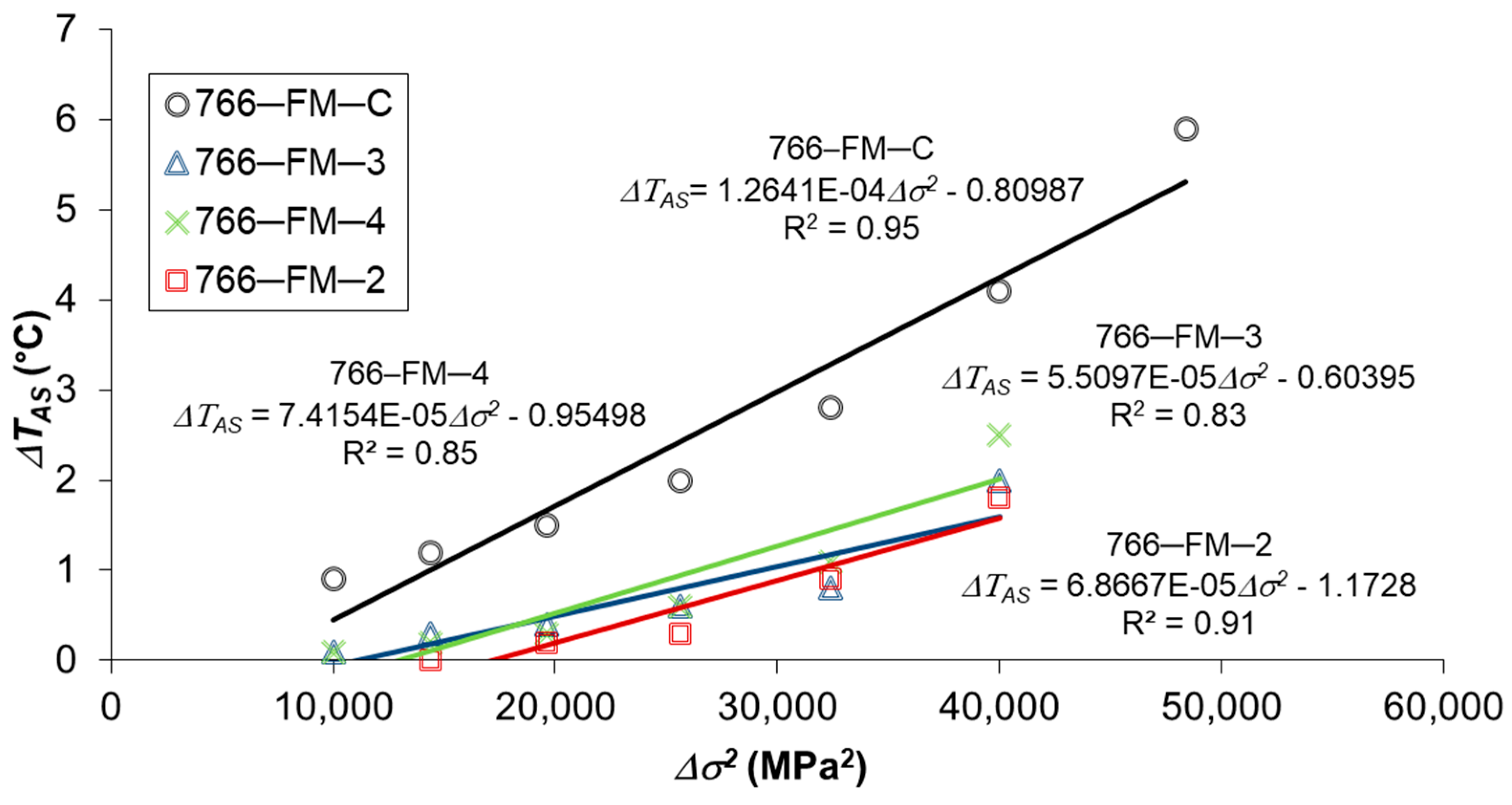
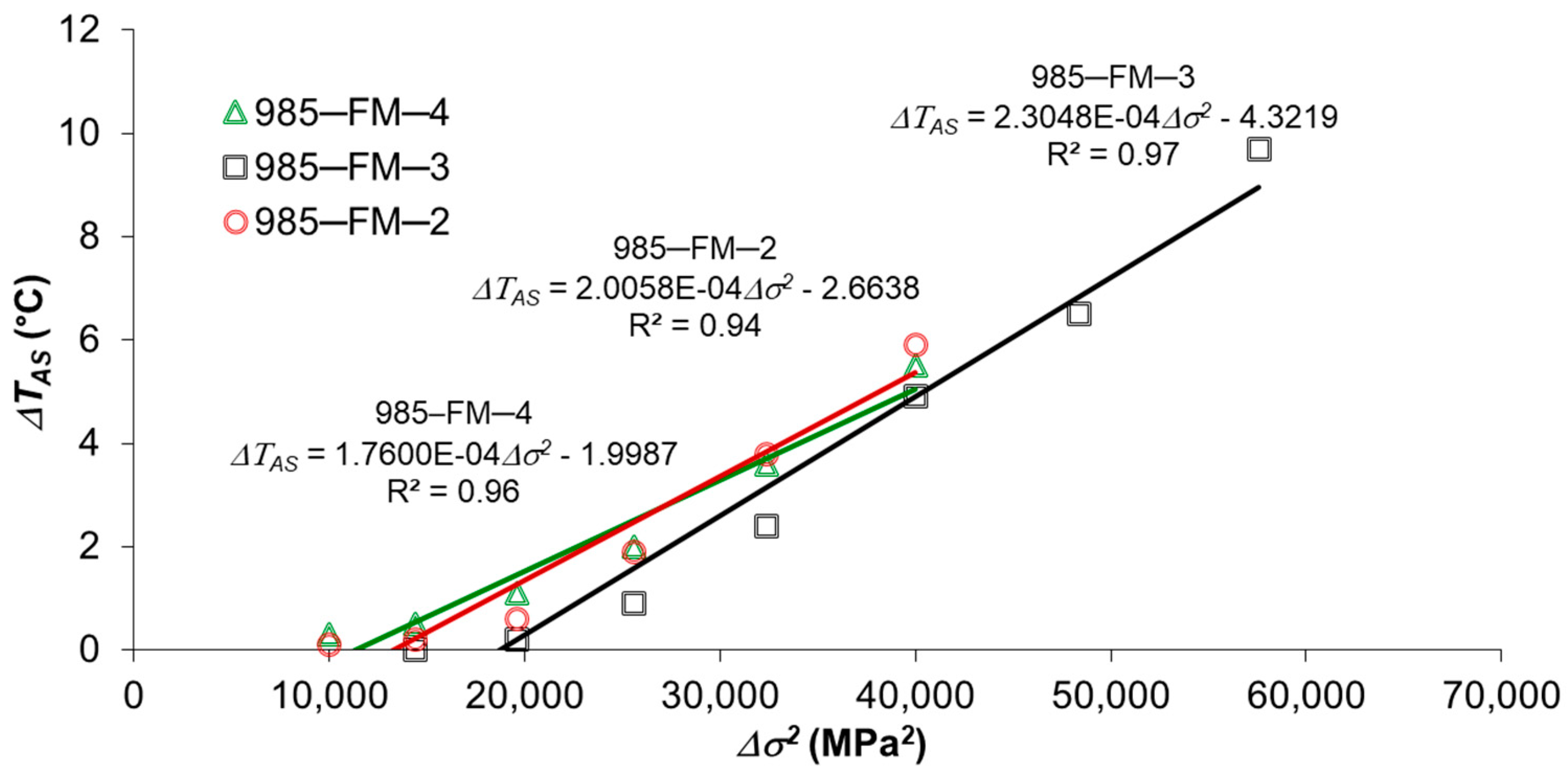
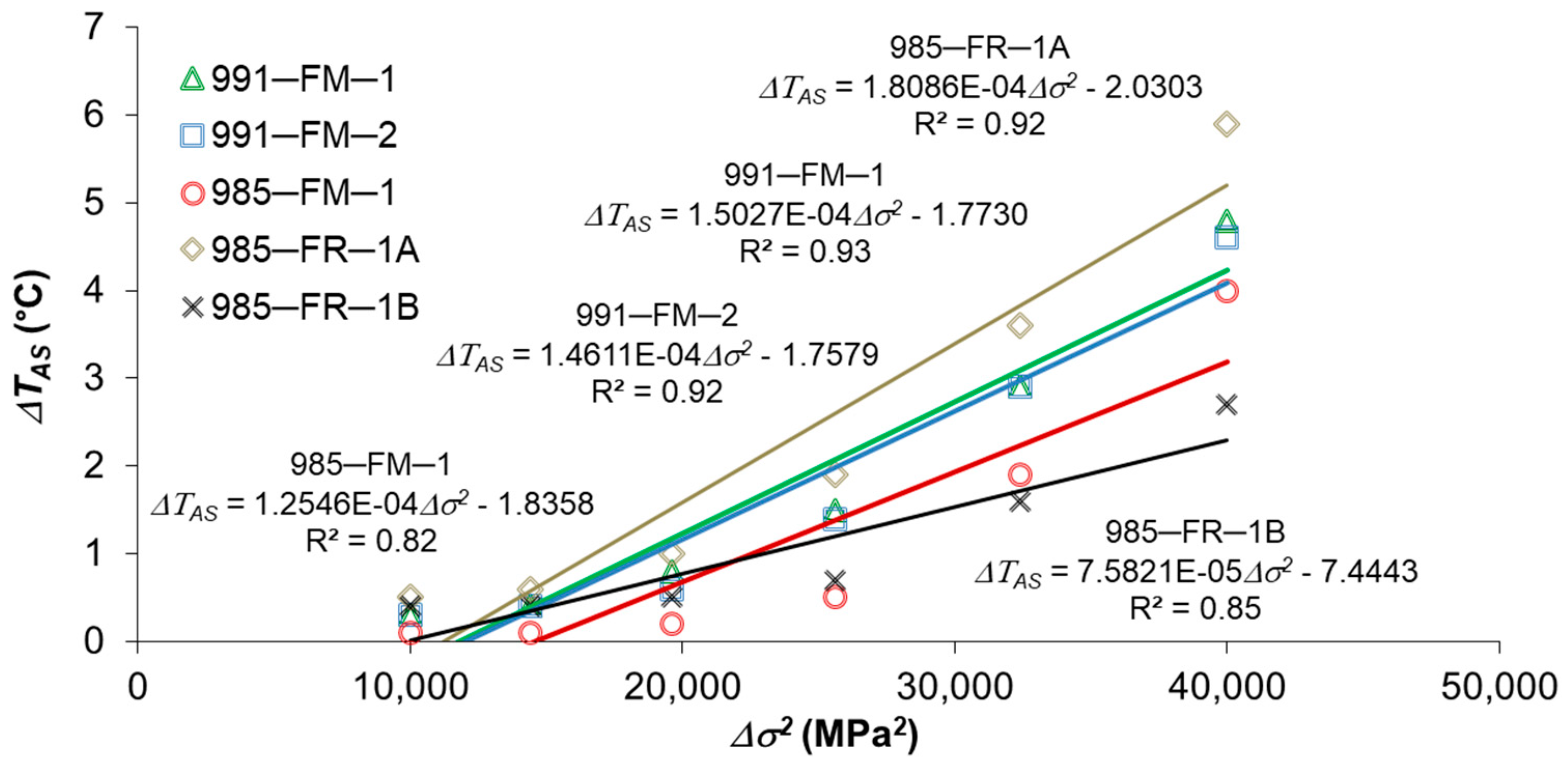
- asymptotic temperature values (ΔTAS) relative to the corresponding applied stress range (Δσ);
- ΔTAS-Δσ2 curves;
- fatigue limit (ΔσeTM) (according to the thermographic method);
- S-N curve predicted by the energy approach;
- fatigue limit (ΔσeSN) (drawn from the predicted S-N curves at 5 × 106 cycles).
4.1. Fatigue Prediction by Rapid Thermographic Method
4.2. S-N Curve Prediction by Energy Approach
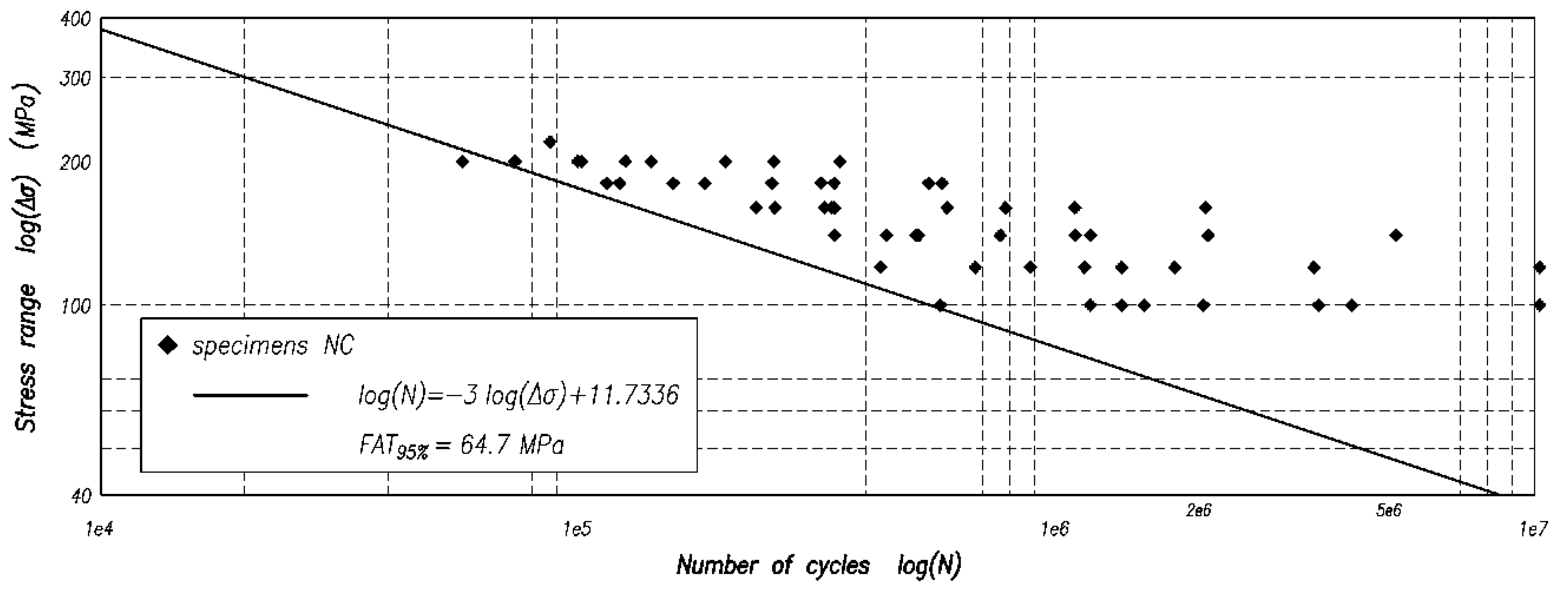
4.3. S-N Curves with m = 3 Predicted by Energy Approach
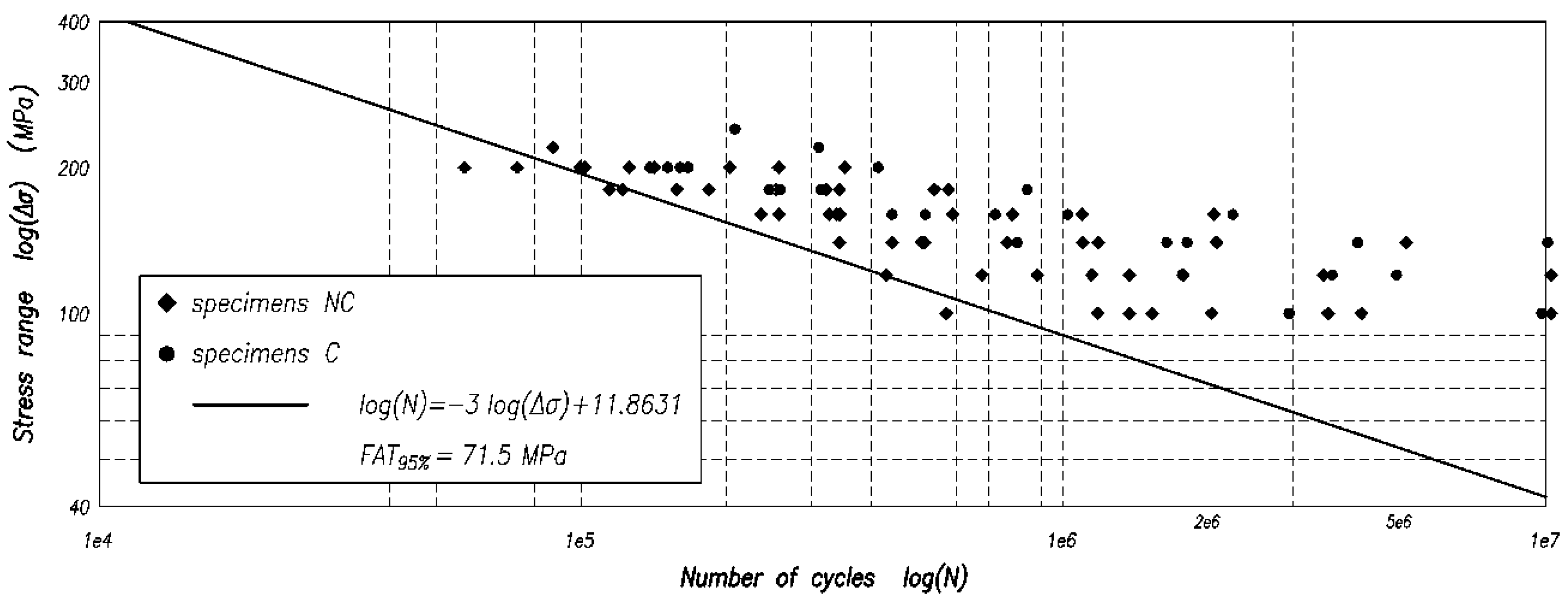
- the type-NC joints have lower value of FAT, equal to 64.7 MPa, and, as expected, higher scatter of experimental data (standard deviation = 0.3196 MPa);
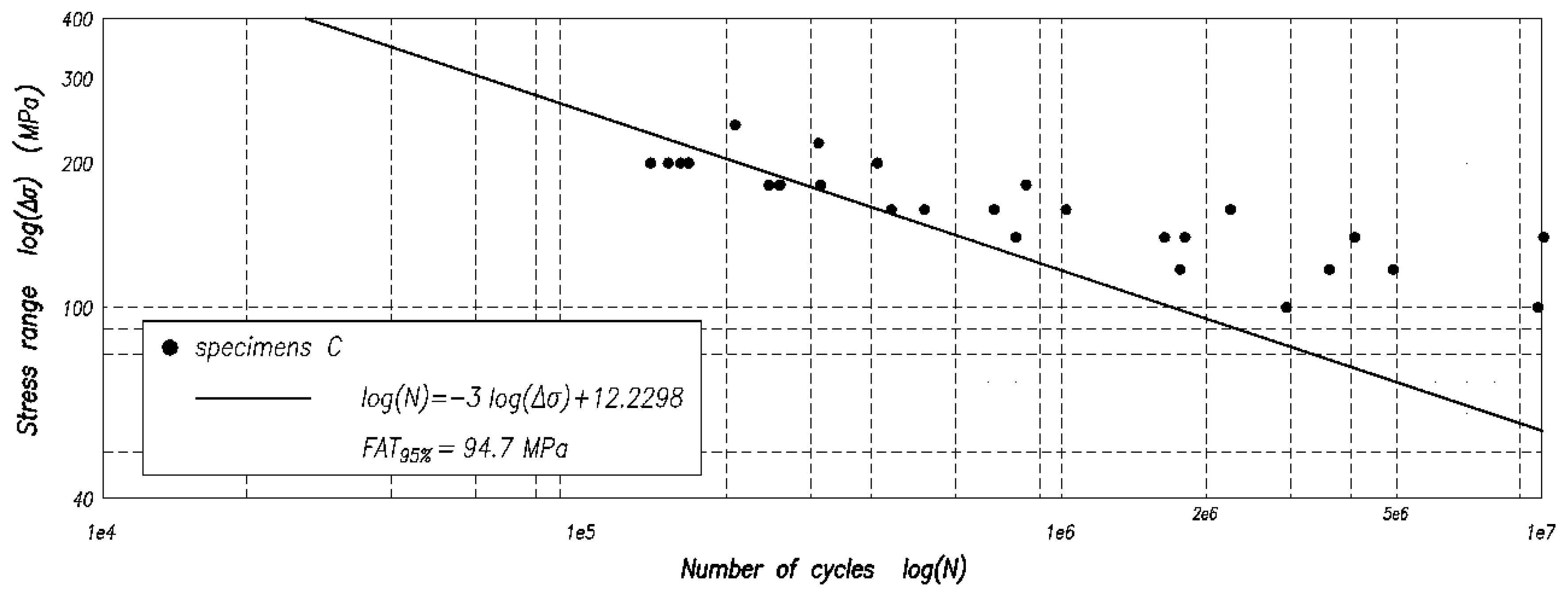
- the type-C joints have higher value of FAT, equal to 94.7 MPa, and lower scatter of experimental data (standard deviation = 0.1692 MPa);
- considering the data for both the type-NC and -C joints, the following values are obtained, FAT = 71.5 MPa and standard deviation = 0.2950 MPa.
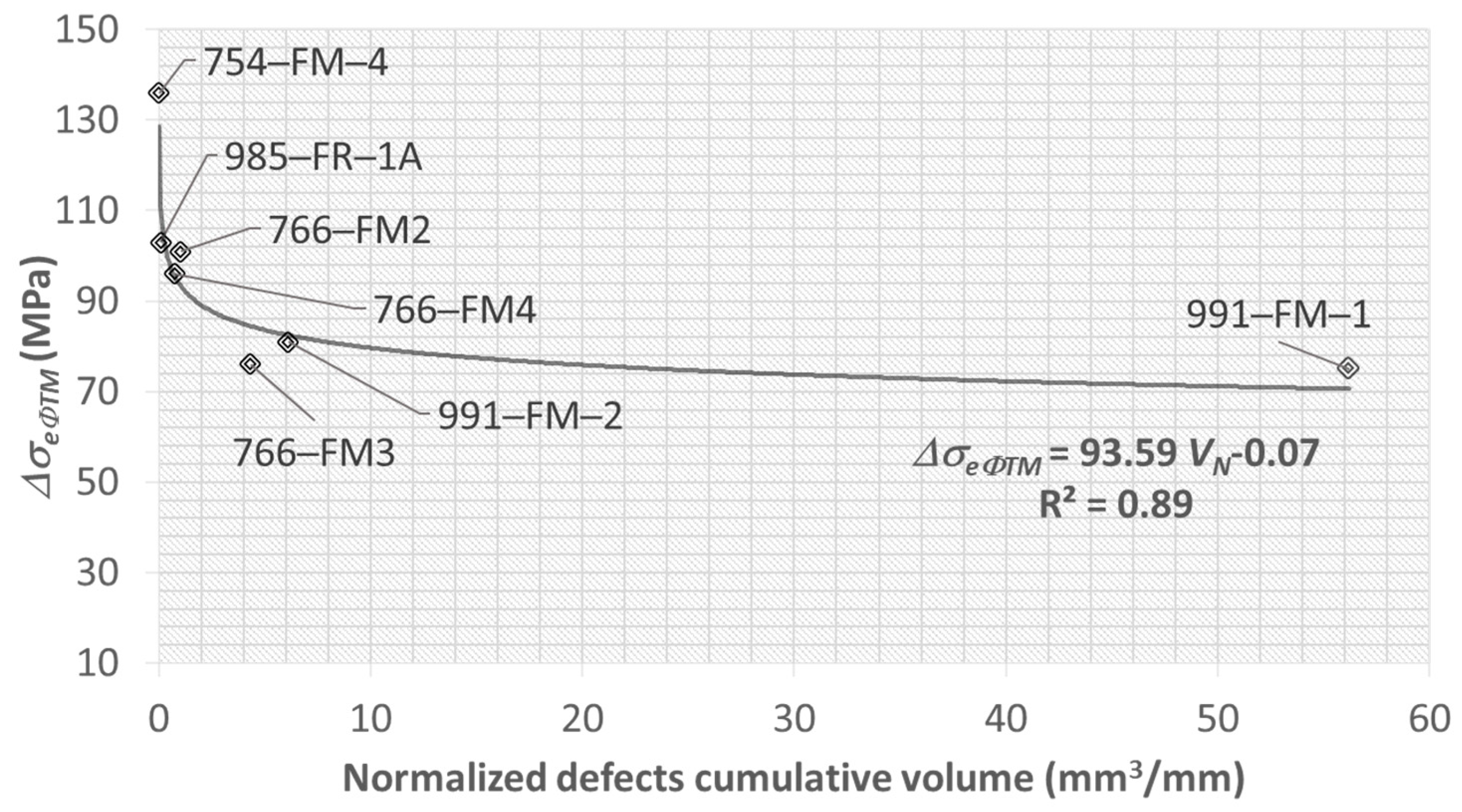
4.4. Defects Influence on Fatigue Strength
5. Conclusions
- according to the rapid thermographic method, the fatigue limit corresponds to the highest stress range (Δσ) for which there is no temperature increase at any point of a cyclically loaded specimen; this definition is correlated to the physical phenomenon;
- according to the energy approach, the fatigue limit is obtained by the S-N curve as the stress range at 5 × 106 cycles; this definition leads to an “agreement” which refers implicitly to pieces that somehow can be considered homogeneous (base material, welds without defects).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| f | frequency (s−1) |
| m | inverse slope of the S-N curve in bi-logarithmic scale |
| t | thickness (mm) |
| C | constant term of the S-N curve in bi-logarithmic scale |
| DMAX | maximum defect size (mm) |
| DMAX,N | ratio between maximum defect size and specimen thickness |
| Ec | energy to failure per unit volume (J m−3) |
| FAT | fatigue class as expected with the S-N curve at 2 × 106 cycles (N mm−2) |
| IIW | International Institute of Welding |
| N | number of cycles |
| Nf | number of cycles to failure |
| Ps | survival probability |
| R | stress ratio |
| RTM | rapid thermographic method |
| TM | thermographic method |
| V | defects cumulative volume (mm3) |
| VN | ratio between defects cumulative volume and specimen thickness (mm3/mm) |
| ΔT | temperature increment (°C) |
| ΔTAS | asymptotic temperature increment (°C) |
| Δσ | stress range (N mm−2) |
| ΔσeTM | fatigue limit predicted by TM (N mm−2) |
| ΔσeSN | fatigue limit as expected with the S-N curve at 5 × 106 cycles (N mm−2) |
| ΔσeΦTM | fatigue limit predicted using energy approach (N mm−2) |
| Φ | thermal increment to failure (°C) |
References
- Dengel, D.; Harig, H. Estimation of the fatigue limit by progressively-increasing load tests. Fatigue Fract. Eng. Mater. Struct. 1980, 3, 113–128. [Google Scholar] [CrossRef]
- Curti, G.; La Rosa, G.; Orlando, M.; Risitano, A. Analisi Tramite Infrarosso Termico della “Temperatura Limite” in Prove di Fatica. In Proceedings of the XIV AIAS National Congress, Catania, Italy, 23–27 September 1986; pp. 211–220. [Google Scholar]
- Wang, X.G.; Crupi, V.; Jiang, C.; Feng, E.S.; Guglielmino, E.; Wang, C.S. Energy-based approach for fatigue life prediction of pure copper. Int. J. Fatigue 2017, 104, 243–250. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, X.; Fan, J.; Syed, R.; Wu, C. An energy method for rapid evaluation of high-cycle fatigue parameters based on intrinsic dissipation. Int. J. Fatigue 2015, 80, 136–144. [Google Scholar] [CrossRef]
- De Finis, R.; Palumbo, D.; Ancona, F.; Galietti, U. Fatigue limit evaluation of various martensitic stainless steels with new robust thermographic data analysis. Int. J. Fatigue 2015, 74, 88–96. [Google Scholar] [CrossRef]
- Lipski, A. Rapid Determination of the S-N Curve for Steel by means of the Thermographic Method. Adv. Mater. Sci. Eng. 2016, 2016, 4134021. [Google Scholar] [CrossRef]
- Teng, Z.; Wu, H.; Boller, C.; Starke, P. A unified fatigue life calculation based on intrinsic thermal dissipation and microplasticity evolution. Int. J. Fatigue 2020, 131. [Google Scholar] [CrossRef]
- Acosta, R.; Wu, H.; Venkat, R.S.; Weber, F.; Tenkamp, J.; Walther, F.; Starke, P. SteBLife, a New Approach for the Accelerated Generation of Metallic Materials’ Fatigue Data. Metals 2020, 10, 798. [Google Scholar] [CrossRef]
- Guo, S.; Liu, X.; Zhang, H.; Yan, Z.; Fang, H. Fatigue Limit Evaluation of AZ31B Magnesium Alloy Based on Temperature Distribution Analysis. Metals 2020, 10, 1331. [Google Scholar] [CrossRef]
- Jirandehi, A.P.; Khonsari, M.M. Microstructure-sensitive estimation of fatigue life using cyclic thermodynamic entropy as an index for metals. Theor. Appl. Fract. Mech. 2021, 112, 102854. [Google Scholar] [CrossRef]
- Luong, M.P. Infrared thermographic scanning of fatigue in metals. Nucl. Eng. Des. 1995, 158, 363–376. [Google Scholar] [CrossRef]
- Luong, M.P. Fatigue limit evaluation of metals using an infrared thermographic technique. Mech. Mater. 1998, 28, 155–163. [Google Scholar] [CrossRef]
- La Rosa, G.; Risitano, A. Thermographic methodology for rapid determination of the fatigue limit of materials and mechanical components. Int. J. Fatigue 2000, 22, 65–73. [Google Scholar] [CrossRef]
- Fargione, G.; Geraci, A.; La Rosa, G.; Risitano, A. Rapid determination of the fatigue curve by the thermographic method. Int. J. Fatigue 2002, 24, 11–19. [Google Scholar] [CrossRef]
- Curà, F.; Curti, G.; Sesana, R. A new iteration method for the thermographic determination of fatigue limit in steels. Int. J. Fatigue 2005, 27, 453–459. [Google Scholar] [CrossRef]
- Meneghetti, G. Analysis of the fatigue strength of a stainless steel based on the energy dissipation. Int. J. Fatigue 2007, 29, 81–94. [Google Scholar] [CrossRef]
- Plekhov, O.A.; Saintier, N.; Palin-Luc, T.; Uvarov, S.V.; Naimark, O.B. Theoretical analysis, infrared and structural investigations of energy dissipation in metals under cyclic loading. Mater. Sci. Eng. A 2007, 462, 367–369. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. Rapid determination of fatigue failure based on temperature evolution: Fully reversed bending load. Int. J. Fatigue 2010, 32, 382–389. [Google Scholar] [CrossRef]
- Wei, W.; Li, C.; Sun, Y.; Xu, H.; Yang, X. Investigation of the Self-Heating of Q460 Butt Joints and an S-N Curve Modeling Method based on Infrared Thermographic Data for High-Cycle Fatigue. Metals 2021, 11, 232. [Google Scholar] [CrossRef]
- Williams, P.; Liakat, M.; Khonsari, M.M.; Kabir, O.M. A thermographic method for remaining fatigue life prediction of welded joints. Mater. Des. 2013, 51, 916–923. [Google Scholar] [CrossRef]
- Fan, J.L.; Guo, X.L.; Wu, C.W.; Zhao, Y.G. Research on fatigue behavior evaluation and fatigue fracture mechanisms of cruciform welded joints. Mater. Sci. Eng. A 2011, 528, 8417–8427. [Google Scholar] [CrossRef]
- Crupi, V.; Guglielmino, E.; Risitano, A.; Taylor, D. Different Methods for Fatigue Assessment of T Welded Joints Used in Ship Structures. J. Ship Res. 2007, 51, 150–159. [Google Scholar] [CrossRef]
- Crupi, V.; Guglielmino, E.; Maestro, M.; Marinò, A. Fatigue analysis of butt welded AH36 steel joints: Thermographic Method and design S-N curve. Mar. Struct. 2009, 22, 373–386. [Google Scholar] [CrossRef]
- Nourian-Avval, A.; Fatemi, A. Fatigue life prediction of cast aluminum alloy based on porosity characteristics. Theor. Appl. Fract. Mech. 2020, 109, 102774. [Google Scholar] [CrossRef]
- Bonneric, M.; Brugger, C.; Saintier, N. Investigation of the sensitivity of the fatigue resistance to defect position in aluminium alloys obtained by Selective laser melting using artificial defects. Int. J. Fatigue 2020, 134, 105505. [Google Scholar] [CrossRef]
- Chen, Y.; He, C.; Yang, K.; Zhang, H.; Wang, C.; Wang, Q.; Liu, Y. Effects of microstructural inhomogeneities and micro-defects on tensile and very high cycle fatigue behaviors of the friction stir welded ZK60 magnesium alloy joint. Int. J. Fatigue 2019, 122, 218–227. [Google Scholar] [CrossRef]
- Amirafshari, P.; Barltrop, N.; Wright, M.; Kolios, A. Weld defect frequency, size statistics and probabilistic models for ship structures. Int. J. Fatigue 2021, 145, 106069. [Google Scholar] [CrossRef]
- Bucci, V.; Corigliano, P.; Crupi, V.; Epasto, G.; Guglielmino, E.; Marinò, A. Experimental investigation on Iroko wood used in shipbuilding. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 128–139. [Google Scholar] [CrossRef]
- Corigliano, P.; Crupi, V.; Epasto, G.; Guglielmino, E.; Maugeri, N.; Marinò, A. Experimental and theoretical analyses of Iroko wood laminates. Compos. Part B Eng. 2017, 112, 251–264. [Google Scholar] [CrossRef]
- Astarita, A.; Campatelli, G.; Corigliano, P.; Epasto, G.; Montevecchi, F.; Scherillo, F.; Venturini, G. Microstructure and mechanical properties of specimens produced using the wire-arc additive manufacturing process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Epasto, G.; Palomba, G.; D’Andrea, D.; Guglielmino, E.; Di Bella, S.; Traina, F. Ti-6Al-4V ELI microlattice structures manufactured by electron beam melting: Effect of unit cell dimensions and morphology on mechanical behaviour. Mater. Sci. Eng. A 2019, 753, 31–41. [Google Scholar] [CrossRef]
- Han, X.; Yang, Z.; Ma, Y.; Shi, C.; Xin, Z. Porosity distribution and mechanical response of laser-MIG hybrid butt welded 6082-T6 aluminum alloy joint. Opt. Laser Technol. 2020, 132, 106511. [Google Scholar] [CrossRef]
- Wu, S.C.; Song, Z.; Kang, G.Z.; Hu, Y.N.; Fu, Y.N. The Kitagawa-Takahashi fatigue diagram to hybrid welded AA7050 joints via synchrotron X-ray tomography. Int. J. Fatigue 2019, 125, 210–221. [Google Scholar] [CrossRef]
- Hartl, R.; Vieltorf, F.; Zaeh, M.F. Correlations between the Surface Topography and Mechanical Properties of Friction Stir Welds. Metals 2020, 10, 890. [Google Scholar] [CrossRef]
- Akbulut, M. Parametric investigation into fatigue life behaviour of spot welded tensile shear test samples. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Hobbacher, A.F. Recommendations for Fatigue Design of Welded Joints and Components; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-319-23757-2. [Google Scholar]
- Fan, J.; Guo, X.; Wu, C.; Crupi, V.; Guglielmino, E. Influence of Heat Treatments on Mechanical Behavior of FV520B Steel. Exp. Tech. 2015, 39, 55–64. [Google Scholar] [CrossRef]








| Joint Type | Specimen ID | Width b (mm) | Thickness t (mm) | Cross-Sectional Area A (mm2) | Defect Type |
|---|---|---|---|---|---|
| C-1 | 754-FM-1 | 46.8 | 5.6 | 262 | - |
| C-1 | 754-FM-2 | 45.8 | 5.5 | 252 | - |
| C-1 | 754-FM-3 | 39.0 | 5.5 | 215 | - |
| C-1 | 754-FM-4 | 40.6 | 5.6 | 227 | - |
| NC-2 | 766-FM-C | 45.2 | 5.6 | 253 | slag inclusions |
| NC-2 | 766-FM-3 | 39.0 | 5.5 | 215 | slag inclusions |
| NC-2 | 766-FM-4 | 53.5 | 5.5 | 294 | slag inclusions, pores |
| NC-2 | 766-FM-2 | 45.0 | 5.5 | 248 | pore clusters |
| C-3 | 985-FM-4 | 42.7 | 6.5 | 278 | - |
| C-3 | 985-FM-3 | 49.6 | 6.7 | 332 | - |
| C-3 | 985-FM-2 | 47.0 | 6.7 | 315 | - |
| NC-4 | 991-FM-1 | 40.0 | 6.7 | 268 | worm holes |
| NC-4 | 991-FM-2 | 43.0 | 6.7 | 288 | worm holes |
| NC-4 | 985-FR-1A | 47.0 | 6.7 | 315 | slag inclusions |
| NC-4 | 985-FR-1B | 47.5 | 6.7 | 318 | slag inclusions |
| NC-4 | 985-FM-1 | 43.6 | 6.6 | 288 | pores |
| Content | C | Mn | Si | P | S | Cu | Ni | Cr | Mo | Al | V | Nb | Ti | N | C Eq | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | 0.16 | 1.43 | 0.27 | 0.012 | 0.009 | 0.04 | 0.02 | 0.02 | 0.00 | 0.044 | 0.00 | 0.00 | 0.00 | 0.005 | 0.406 | balance |
| min | 0.90 | 0.015 | 0.05 | 0.02 | ||||||||||||
| max | 0.18 | 1.60 | 0.50 | 0.035 | 0.035 | 0.35 | 0.40 | 0.20 | 0.08 | 0.10 | 0.05 | 0.02 |
| Yield Stress σy (MPa) | Rupture Stress σr (MPa) | Elongation A5 (%) |
|---|---|---|
| 400 | 545 | 32 |
| 355 (min) | 490/620 (min/max) | 21 (min) |
| Joint Type | Specimen ID | Defect Type by X-ray | Maximum Defect Size by CT DMAX (mm) | Cumulative Volume by CT V (mm3) |
|---|---|---|---|---|
| C-1 | 754-FM-4 | - | - | 0.06 |
| NC-2 | 766-FM-C | slag inclusions | 4.72 | not available |
| NC-2 | 766-FM-3 | slag inclusions | 3.07 | 23.82 |
| NC-2 | 766-FM-4 | slag inclusions, pores | 2.64 | 4.18 |
| NC-2 | 766-FM-2 | pore clusters | 1.64 | 5.74 |
| NC-4 | 991-FM-1 | worm holes | 4.53 | 365.20 |
| NC-4 | 991-FM-2 | worm holes | 3.13 | 39.65 |
| NC-4 | 985-FR-1A | slag inclusions | 1.46 | 0.54 |
| NC-4 | 985-FR-1B | slag inclusions | not available | - |
| NC-4 | 985-FM-1 | pores | not available | - |
| Type Joint | Specimen ID | Thickness t (mm) | Fatigue Limit Predictions by RTM ΔσeTM (MPa) |
|---|---|---|---|
| C-1 | 754-FM-1 | 5.5 | 126 |
| C-1 | 754-FM-2 | 5.5 | 115 |
| C-1 | 754-FM-3 | 5.5 | 119 |
| C-1 | 754-FM-4 | 5.5 | 134 |
| NC-2 | 766-FM-C | 5.5 | 80 |
| NC-2 | 766-FM-3 | 5.5 | 105 |
| NC-2 | 766-FM-4 | 5.5 | 113 |
| NC-2 | 766-FM-2 | 5.5 | 131 |
| C-3 | 985-FM-4 | 6.5 | 107 |
| C-3 | 985-FM-3 | 6.5 | 137 |
| C-3 | 985-FM-2 | 6.5 | 115 |
| NC-4 | 991-FM-1 | 6.5 | 109 |
| NC-4 | 991-FM-2 | 6.5 | 110 |
| NC-4 | 985-FR-1A | 6.5 | 106 |
| NC-4 | 985-FR-1B | 6.5 | 99 |
| NC-4 | 985-FM-1 | 6.5 | 121 |
| Type Joint | Specimen ID | m | log(C) Ps = 50% | FAT Ps = 50% (MPa) | FAT Ps = 97.7% (MPa) | ΔσeΦTM Ps = 50% (MPa) | ΔσeΦTM Ps = 97.7% (MPa) | Std.Dev.(log(N)) |
|---|---|---|---|---|---|---|---|---|
| C-1 | 754-FM-3 | 6.6 | 20.36 | 134 | 128 | 117 | 111 | 0.0737 |
| C-1 | 754-FM-4 | 9.3 | 26.65 | 150 | 145 | 136 | 132 | 0.0631 |
| NC-2 | 766-FM-C | 2.3 | 10.51 | 62 | 55 | 42 | 37 | 0.0632 |
| NC-2 | 766-FM-3 | 3.8 | 13.84 | 97 | 85 | 76 | 67 | 0.1070 |
| NC-2 | 766-FM-4 | 4.5 | 15.57 | 118 | 107 | 96 | 87 | 0.0954 |
| NC-2 | 766-FM2 | 6.4 | 19.57 | 116 | 108 | 101 | 93 | 0.1054 |
| C-3 | 985-FM-4 | 4.4 | 15.22 | 113 | 107 | 91 | 87 | 0.0463 |
| C-3 | 985-FM-3 | 7.0 | 21.98 | 167 | 151 | 146 | 133 | 0.1500 |
| C-3 | 985-FM-2 | 6.3 | 19.65 | 133 | 124 | 115 | 107 | 0.0924 |
| NC-4 | 991-FM-1 | 4.2 | 14.54 | 94 | 85 | 75 | 68 | 0.0904 |
| NC-4 | 991-FM-2 | 4.2 | 14.63 | 101 | 88 | 81 | 71 | 0.1251 |
| NC-4 | 985-FR-1A | 3.7 | 14.21 | 132 | 115 | 103 | 90 | 0.1089 |
| NC-4 | 985-FR-1B | 2.8 | 11.88 | 100 | 76 | 72 | 55 | 0.1616 |
| NC-4 | 985-FM-1 | 5.7 | 18.63 | 150 | 123 | 127 | 104 | 0.2465 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crupi, V.; Epasto, G.; Guglielmino, E.; Marinò, A. Influence of Weld-Porosity Defects on Fatigue Strength of AH36 Butt Joints Used in Ship Structures. Metals 2021, 11, 444. https://doi.org/10.3390/met11030444
Crupi V, Epasto G, Guglielmino E, Marinò A. Influence of Weld-Porosity Defects on Fatigue Strength of AH36 Butt Joints Used in Ship Structures. Metals. 2021; 11(3):444. https://doi.org/10.3390/met11030444
Chicago/Turabian StyleCrupi, Vincenzo, Gabriella Epasto, Eugenio Guglielmino, and Alberto Marinò. 2021. "Influence of Weld-Porosity Defects on Fatigue Strength of AH36 Butt Joints Used in Ship Structures" Metals 11, no. 3: 444. https://doi.org/10.3390/met11030444
APA StyleCrupi, V., Epasto, G., Guglielmino, E., & Marinò, A. (2021). Influence of Weld-Porosity Defects on Fatigue Strength of AH36 Butt Joints Used in Ship Structures. Metals, 11(3), 444. https://doi.org/10.3390/met11030444








