The Effect of Fiber Waviness on the Residual Stress State and Its Prediction by the Hole Drilling Method in Fiber Metal Laminates: A Global-Local Finite Element Analysis
Abstract
1. Introduction
2. Simulation of Residual Stress States in Metal/CFRP Hybrids and Its Prediction by the Simulated Hole Drilling Method
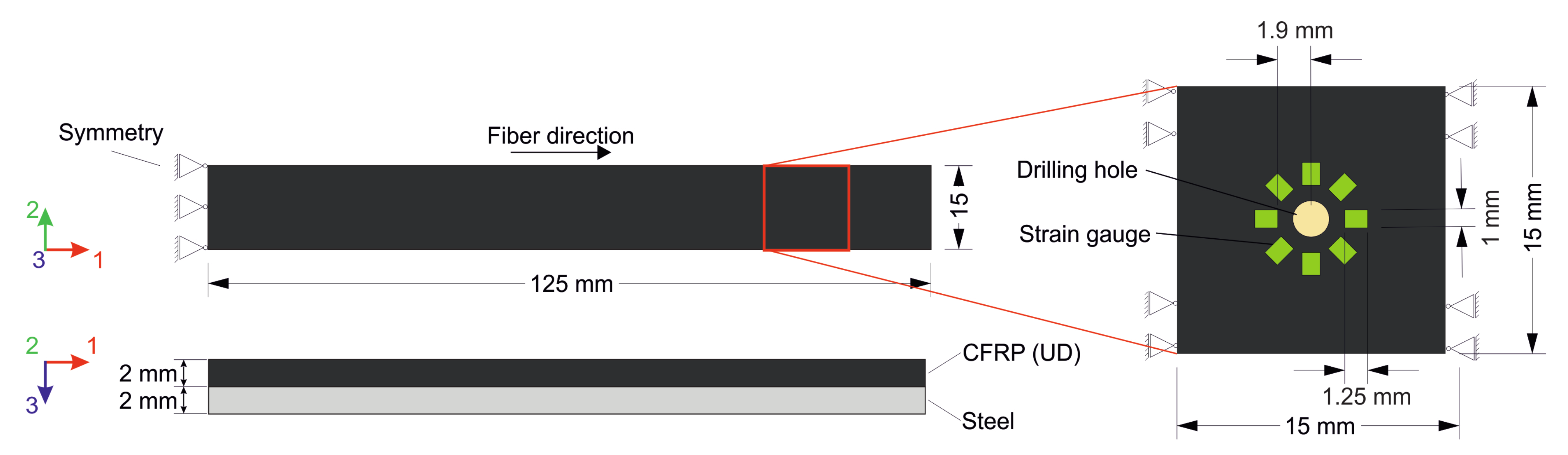
2.1. Global-Local Finite Element Analysis
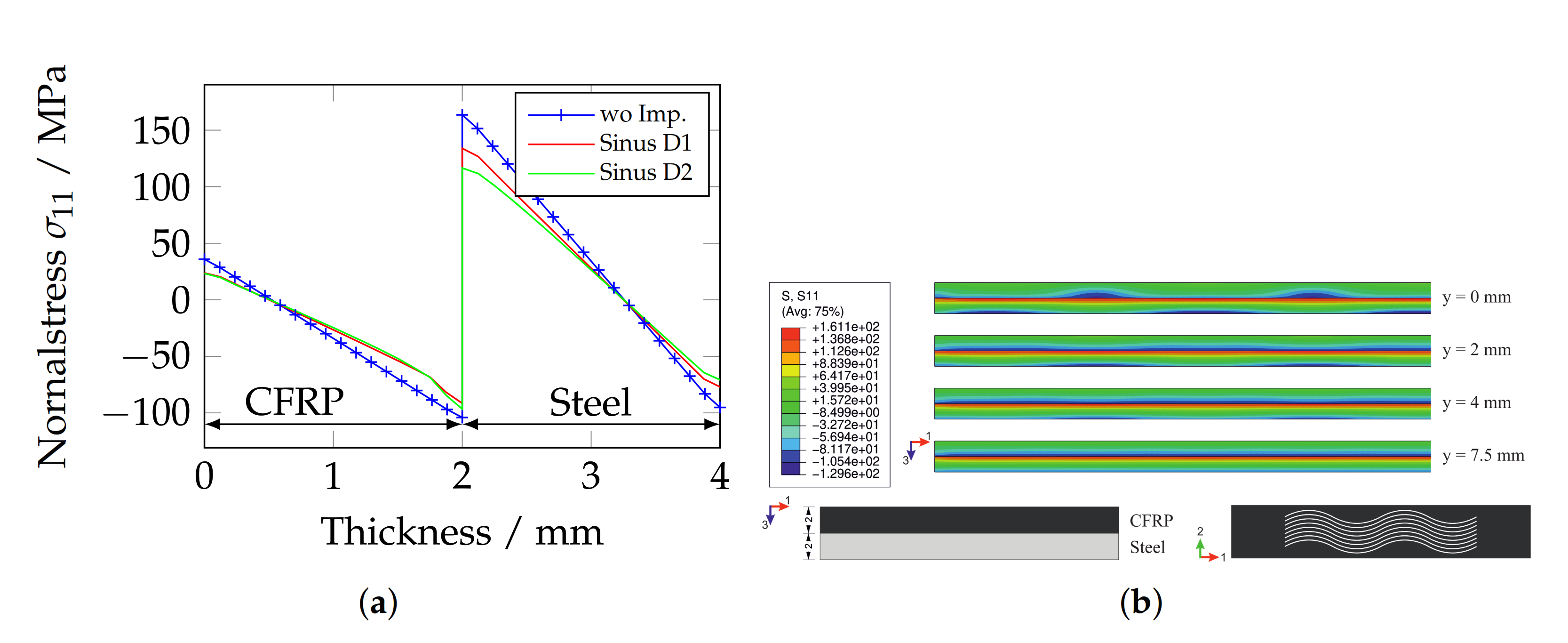
2.2. Comparison between Experimental Data and Numerical Modeling
3. Analysis of Fiber Waviness on the Residual Stress State and the Reliability of the HDM
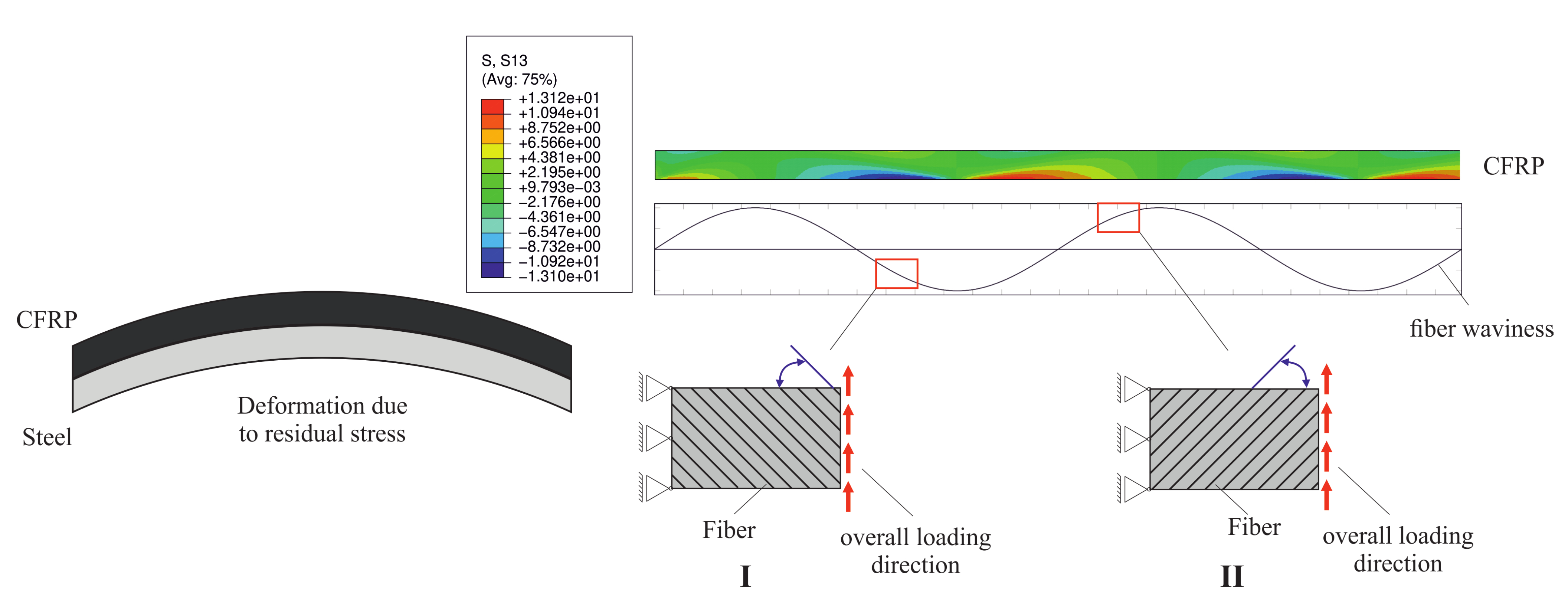
3.1. Definition of Fiber Waviness
3.2. Analysis Results
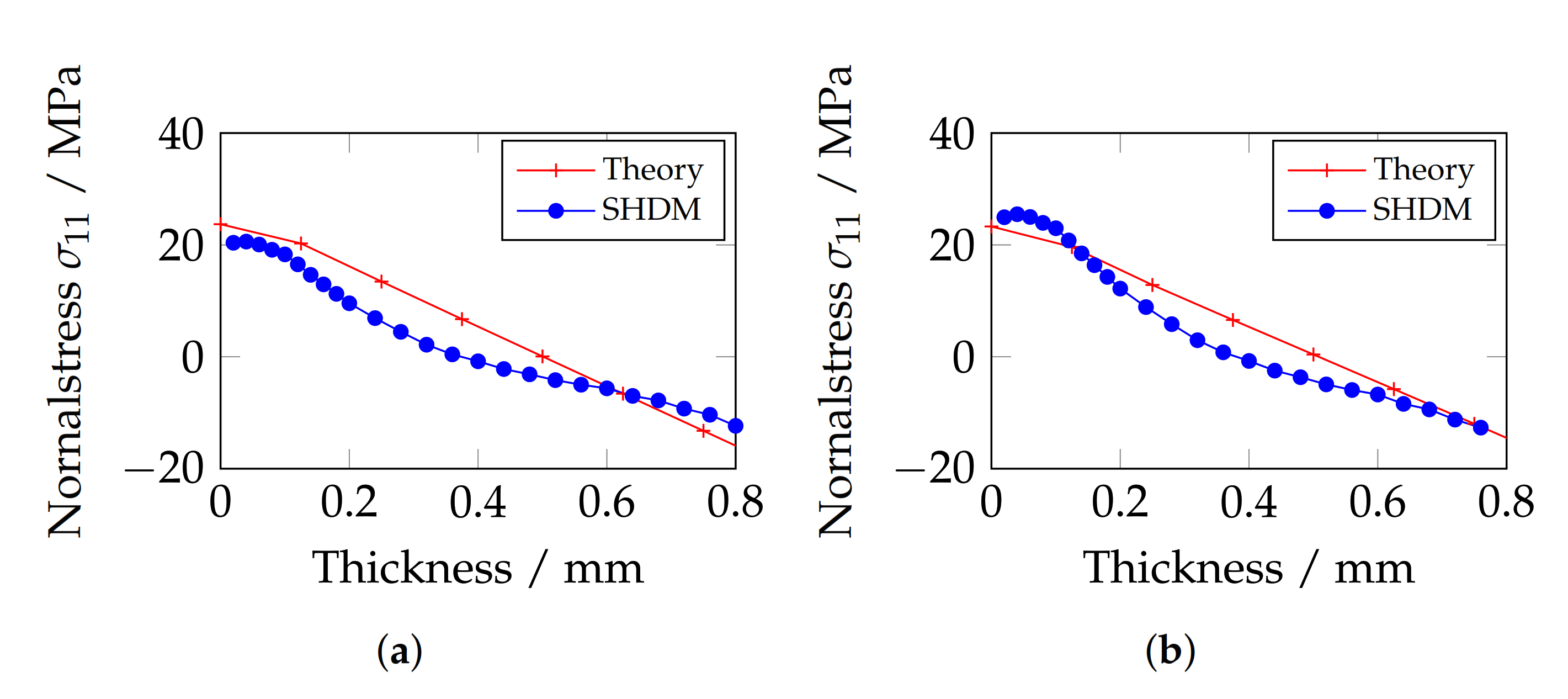
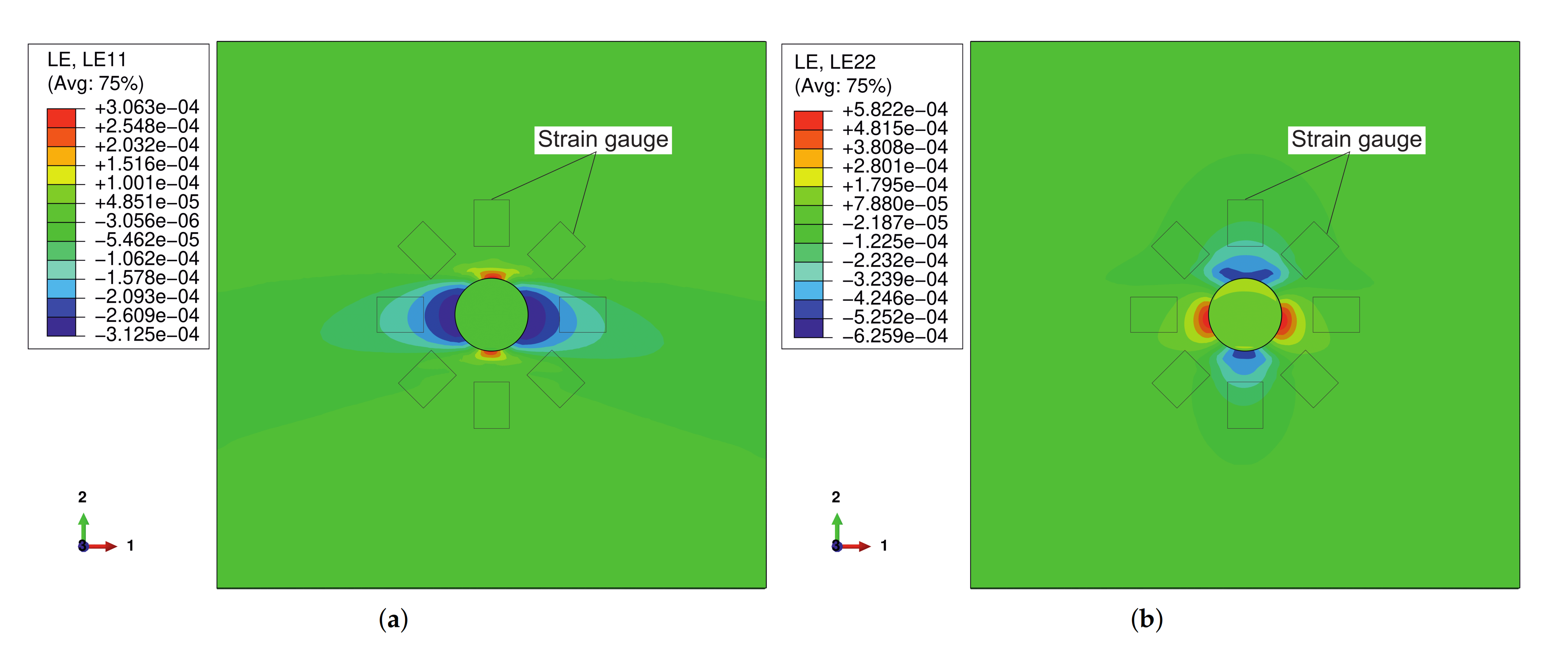
3.2.1. In-Plane Fiber Waviness
3.2.2. Out-of-Plane Fiber Waviness
4. Conclusions
- (1)
- In-plane fiber waviness leads to a rather low variance of residual stresses over thickness. Furthermore, oscillation of residual stresses occurs only at the boundaries of the samples section, which, however, quickly fades away. The simulated hole drilling method has proven that the residual stresses along the thickness direction can still be determined precisely in the case of such an in-plane waviness. The results indicated that the residual stress is not sensitive to the wave length and amplitude, if the waviness is in-plane.
- (2)
- Out-of-plane fiber waviness is much more critical with regard to the distribution and variance of residual stresses. The oscillation of residual stresses occurs over the entire sample width and is not limited to the boundary layers, as in the case of the in-plane fiber waviness described above. In addition, the investigation of two kinds of sinusoidal fiber waviness indicated that the long-wave profile with higher amplitude leads to significantly higher scattering of residual stresses, especially at the metal-CFRP interface. Applying the simulated hole drilling method, it was shown that the fiber waviness in thickness direction is a challenge for the determination of residual stress states such that the approach could not provide satisfactory results in the form of correct residual stress predictions.
- (3)
- Additionally it could be shown that the waviness in loading direction leads to a varying shear stiffness. This can be related to the kinematic of the fiber orientation, which can be with or against the overall loading direction. If shear stresses are present (e.g., in Timoshenko-Theory, multimaterial layup), this kind of fiber waviness leads to the oscillation of deformation fields.
- (4)
- The current limits of the incremental hole drilling method could be pointed out by the presented investigations. Without further adjustment of the calibration coefficients the oscillating stress and strain fields lead, in particular fiber waviness in thickness direction, to unreliable predictions. For the experimental application it can be concluded that the specimens have to be carefully examined with regard to fiber waviness, which, however, in most cases will be difficult to determine.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHSS | Advanced high strength steels |
| BIW | Body in white |
| CFRP | Carbon fiber reinforced plastics |
| FML | Fiber metal laminates |
| CTE | Coefficient of thermal expansion |
| CCS | Coefficient of chemical shrinkage |
| HDM | Incremental hole drilling method |
| RVE | Representative volume element |
| DOC | Degree of cure |
| FEA | Finite element analysis |
| SHDM | Simulated hole drilling method |
| Normal stress in x direction [MPa] | |
| Shear stress in x–z [MPa] | |
| Entry of fourth order linear elasticity tensor [MPa] | |
| Coefficient of thermal expansion (CTE) [] | |
| Coefficient of chemical shrinkage (CCS) [-] | |
| Angle of slope | |
| a | Amplitude of fiber waviness [mm] |
| L | Wavelength of fiber waviness [mm] |
| ORIENT | User subroutine to prescribe an orientation for defining local material directions |
| USDFLD | User subroutine to define field variables |
| GLARE | Glass fiber aluminum reinforced epoxy |
References
- Reuter, C.; Tröster, T. Crashworthiness and numerical simulation of hybrid aluminium-CFRP tubes under axial impact. Thin-Walled Struct. 2017, 117, 1–9. [Google Scholar] [CrossRef]
- Shanmugam, K.; Gadhamshetty, V.; Yadav, P.; Athanassiadis, D.; Tysklind, M.; Upadhyayula, V.K. Advanced High-Strength Steel and Carbon Fiber Reinforced Polymer Composite Body in White for Passenger Cars: Environmental Performance and Sustainable Return on Investment under Different Propulsion Modes. ACS Sustain. Chem. Eng. 2019, 7, 4951–4963. [Google Scholar] [CrossRef]
- Wang, Z.; Lauter, C.; Sanitther, B.; Camberg, A. Manufacturing and investigation of steel-CFRP hybrid pillar structures for automotive applications by intrinsic resin transfer moulding technology. Int. J. Automot. Compos. 2016, 2, 229–243. [Google Scholar] [CrossRef]
- Sinmazçelik, T.; Avcu, E.; Bora, M.Z.; Çoban, O. A review: Fibre metal laminates, background, bonding types and applied test methods. Mater. Des. 2011, 32, 3671–3685. [Google Scholar] [CrossRef]
- Koch, S.F.; Barfuss, D.; Bobbert, M.; Groß, L.; Grützner, R.; Riemer, M.; Stefaniak, D.; Wang, Z. Intrinsic Hybrid Composites for Lightweight Structures: New Process Chain Approaches. Adv. Mater. Res. 2016, 1140, 239–246. [Google Scholar] [CrossRef]
- Schimanski, K.; Schumacher, J.; Wottschel, V.; von Hehl, A.; Zoch, H.W.; Vollertsen, F. Characterization of Ti6Al4V for Integral Transition Structures in FRP–Aluminum Compounds. Steel Res. Int. 2012, 83, 964–971. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.; Beukers, A. Residual stresses in thermoplastic composites— A study of the literature— Part I: Formation of residual stresses. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1847–1857. [Google Scholar] [CrossRef]
- Zahlan, N.; O’Neill, J. Design and fabrication of composite components; the spring-forward phenomenon. Composites 1989, 20, 77–81. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.; Beukers, A. Residual stresses in thermoplastic composites— A study of the literature. Part III: Effects of thermal residual stresses. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1581–1596. [Google Scholar] [CrossRef]
- Tinkloh, S.; Wu, T.; Niendorf, T. A micromechanical-based finite element simulation of process-induced residual stresses in metal-CFRP-hybrid structures. Compos. Struct. 2020, 238, 111926. [Google Scholar] [CrossRef]
- White, S.; Hahn, H. Process Modeling of Composite Materials: Residual Stress Development during Cure. Part I. Model Formulation. J. Compos. Mater. 1992, 26, 2402–2422. [Google Scholar] [CrossRef]
- Bogetti, T.A.; Gillespie, J.W.J. Process-Induced Stress and Deformation in Thick-Section Thermoset Composite Laminates. J. Compos. Mater. 1992, 26, 626–660. [Google Scholar] [CrossRef]
- Wu, T.; Tinkloh, S.; Tröster, T.; Zinn, W.; Niendorf, T. Determination and Validation of Residual Stresses in CFRP/Metal Hybrid Components Using the Incremental Hole Drilling Method. J. Compos. Sci. 2020, 4, 143. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, H.; Zhang, R.; Pei, Y.; Fang, D. Measuring residual stress and its influence on properties of porous ZrO2/(ZrO2+Ni) ceramics. Mater. Sci. Eng. A 2015, 622, 82–90. [Google Scholar] [CrossRef][Green Version]
- Guo, J.; Fu, H.; Pan, B.; Kang, R. Recent progress of residual stress measurement methods: A review. Chin. J. Aeronaut. 2019. [Google Scholar] [CrossRef]
- Prussak, R.; Stefaniak, D.; Hühne, C.; Sinapius, M. Evaluation of residual stress development in FRP-metal hybrids using fiber Bragg grating sensors. Prod. Eng. 2018, 12, 259–267. [Google Scholar] [CrossRef]
- Schajer, G.S.; Yang, L. Residual-stress measurement in orthotropic materials using the hole-drilling method. Exp. Mech. 1994, 34, 324–333. [Google Scholar] [CrossRef]
- ASTM. E837-01 Standard Test Method for Determining Residual Stresses by the Hole Drilling Strain-Gage Method; American Society for Testing and Materials: New York, NY, USA, 2001. [Google Scholar]
- Wang, G.D.; Melly, S. Three-dimensional finite element modeling of drilling CFRP composites using Abaqus/CAE: A review. Int. J. Adv. Manuf. Technol. 2018, 94. [Google Scholar] [CrossRef]
- Phadnis, V.A.; Makhdum, F.; Roy, A.; Silberschmidt, V.V. Drilling in carbon/epoxy composites: Experimental investigations and finite element implementation. Compos. Part A Appl. Sci. Manuf. 2013, 47, 41–51. [Google Scholar] [CrossRef]
- Phadnis, V.A.; Roy, A.; Silberschmidt, V.V. Finite element analysis of drilling in carbon fiber reinforced polymer composites. J. Phys. Conf. Ser. 2012, 382, 012014. [Google Scholar] [CrossRef]
- Giasin, K.; Ayvar-Soberanis, S.; French, T.; Phadnis, V. Erratum to: 3D Finite Element Modelling of Cutting Forces in Drilling Fibre Metal Laminates and Experimental Hole Quality Analysis. Appl. Compos. Mater. 2016, 24, 139–140. [Google Scholar] [CrossRef]
- Ameur, M.F.; Zitoune, R.; Habak, M.; Kenane, M. Multi-Scales Analysis of the Damage Induced During One-Shot Drilling of CFRP/Titanium Alloy. In Proceedings of the 18th European Conference on Composite Materials (ECCM-18), Athens, Greece, 25–28 June 2018. [Google Scholar]
- Nobre, J.; Stiffel, J.H.; Nau, A.; Outeiro, J.; Batista, A.; Van Paepegem, W.; Scholtes, B. Induced drilling strains in glass fibre reinforced epoxy composites. CIRP Ann. 2013, 62, 87–90. [Google Scholar] [CrossRef]
- Nobre, J.P.; Stiffel, J.H.; Paepegem, W.V.; Nau, A.; Batista, A.C.; Marques, M.J.; Scholtes, B. Quantifying the Drilling Effect during the Application of Incremental Hole-Drilling Technique in Laminate Composites. Mater. Sci. Forum 2011, 681, 510–515. [Google Scholar] [CrossRef]
- Aamir, M.; Tolouei-Rad, M.; Giasin, K.; Nosrati, A. Recent advances in drilling of carbon fiber reinforced polymers for aerospace applications: A review. Int. J. Adv. Manuf. Technol. 2019. [Google Scholar] [CrossRef]
- Rohwer, K. Models for Intralaminar Damage and Failure of Fiber Composites - A Review. Facta Univ. Ser. Mech. Eng. 2016, 14, 1–19. [Google Scholar] [CrossRef]
- Ameen, M.; Peerlings, R.; Geers, M. A quantitative assessment of the scale separation limits of classical and higher-order asymptotic homogenization. Eur. J. Mech. A Solids 2018, 71, 89–100. [Google Scholar] [CrossRef]
- Zitoune, R.; Krishnaraj, V.; Collombet, F.; Le Roux, S. Experimental and numerical analysis on drilling of carbon fibre reinforced plastic and aluminium stacks. Compos. Struct. 2016, 146, 148–158. [Google Scholar] [CrossRef]
- Iliescu, D.; Gehin, D.; Iordanoff, I.; Girot, F.; Gutiérrez, M. A discrete element method for the simulation of CFRP cutting. Compos. Sci. Technol. 2010, 70, 73–80. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Ghasemi, K.A.R. Simulation of Central Hole Drilling Process for Measurement of Residual Stresses in Isotropic, Orthotropic, and Laminated Composite Plates. J. Compos. Mater. 2007, 41, 435–452. [Google Scholar] [CrossRef]
- Schuster, S.; Steinzig, M.; Gibmeier, J. Incremental Hole Drilling for Residual Stress Analysis of Thin Walled Components with Regard to Plasticity Effects. Exp. Mech. 2017, 57, 1–11. [Google Scholar] [CrossRef]
- Garnich, M.R.; Karami, G. Localized Fiber Waviness and Implications for Failure in Unidirectional Composites. J. Compos. Mater. 2005, 39, 1225–1245. [Google Scholar] [CrossRef]
- Kugler, D.; Moon, T.J. Identification of the Most Significant Processing Parameters on the Development of Fiber Waviness in Thin Laminates. J. Compos. Mater. 2002, 36, 1451–1479. [Google Scholar] [CrossRef]
- Kulkarni, P.; Mali, K.D.; Singh, S. An overview of the formation of fibre waviness and its effect on the mechanical performance of fibre reinforced polymer composites. Compos. Part A Appl. Sci. Manuf. 2020, 137, 106013. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Jones, M.I.; Hallett, S.R. Compressive failure of laminates containing an embedded wrinkle; experimental and numerical study. Compos. Part A Appl. Sci. Manuf. 2015, 73, 132–142. [Google Scholar] [CrossRef]
- Altmann, A.; Gesell, P.; Drechsler, K. Strength prediction of ply waviness in composite materials considering matrix dominated effects. Compos. Struct. 2015, 127, 51–59. [Google Scholar] [CrossRef]
- Hsiao, H.; Daniel, I. Effect of fiber waviness on stiffness and strength reduction of unidirectional composites under compressive loading. Compos. Sci. Technol. 1996, 56, 581–593. [Google Scholar] [CrossRef]
- Karami, G.; Garnich, M. Micromechanical study of thermoelastic behavior of composites with periodic fiber waviness. Compos. Part B Eng. 2005, 36, 241–248. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, J.; Zu, L. Influence of out-of-plane ply waviness on elastic properties of composite laminates under uniaxial loading. Compos. Struct. 2015, 132, 440–450. [Google Scholar] [CrossRef]
- Abaqus/CAE User’s Manual Version 6.5; Abaqus: Providence, RI, USA, 2004.
- Nau, A.; Scholtes, B. Evaluation of the High-Speed Drilling Technique for the Incremental Hole-Drilling Method. Exp. Mech. 2012, 53, 531–542. [Google Scholar] [CrossRef]







| E | ||
|---|---|---|
| 1.2 × 10 |
| Label | a [mm] | L [mm] |
|---|---|---|
| Sinus D1 | ||
| Sinus D2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinkloh, S.; Wu, T.; Tröster, T.; Niendorf, T. The Effect of Fiber Waviness on the Residual Stress State and Its Prediction by the Hole Drilling Method in Fiber Metal Laminates: A Global-Local Finite Element Analysis. Metals 2021, 11, 156. https://doi.org/10.3390/met11010156
Tinkloh S, Wu T, Tröster T, Niendorf T. The Effect of Fiber Waviness on the Residual Stress State and Its Prediction by the Hole Drilling Method in Fiber Metal Laminates: A Global-Local Finite Element Analysis. Metals. 2021; 11(1):156. https://doi.org/10.3390/met11010156
Chicago/Turabian StyleTinkloh, Steffen, Tao Wu, Thomas Tröster, and Thomas Niendorf. 2021. "The Effect of Fiber Waviness on the Residual Stress State and Its Prediction by the Hole Drilling Method in Fiber Metal Laminates: A Global-Local Finite Element Analysis" Metals 11, no. 1: 156. https://doi.org/10.3390/met11010156
APA StyleTinkloh, S., Wu, T., Tröster, T., & Niendorf, T. (2021). The Effect of Fiber Waviness on the Residual Stress State and Its Prediction by the Hole Drilling Method in Fiber Metal Laminates: A Global-Local Finite Element Analysis. Metals, 11(1), 156. https://doi.org/10.3390/met11010156






