Modeling of Fluid Flow and Residence-Time Distribution in a Five-Strand Tundish
Abstract
1. Introduction
2. CFD Model Description
- The model is based on a 3D standard set of the Navier–Stokes equations. The continuous phase is treated by a Eulerian framework (using averaged equations);
- The liquid flow was assumed to be isothermal and in steady state;
- Two additional passive scalar-transport equations are solved to separately describe the E-curve and the F-curve. Transient solver is applied to calculate the transportation of the passive scalars;
- The realizable k-ε model was used to describe the turbulence;
- The free surface is flat and kept at a fixed level. The slag layer is not included in the tundish.
2.1. Governing Equation
2.1.1. Fluid Flow
2.1.2. Tracer Dispersion
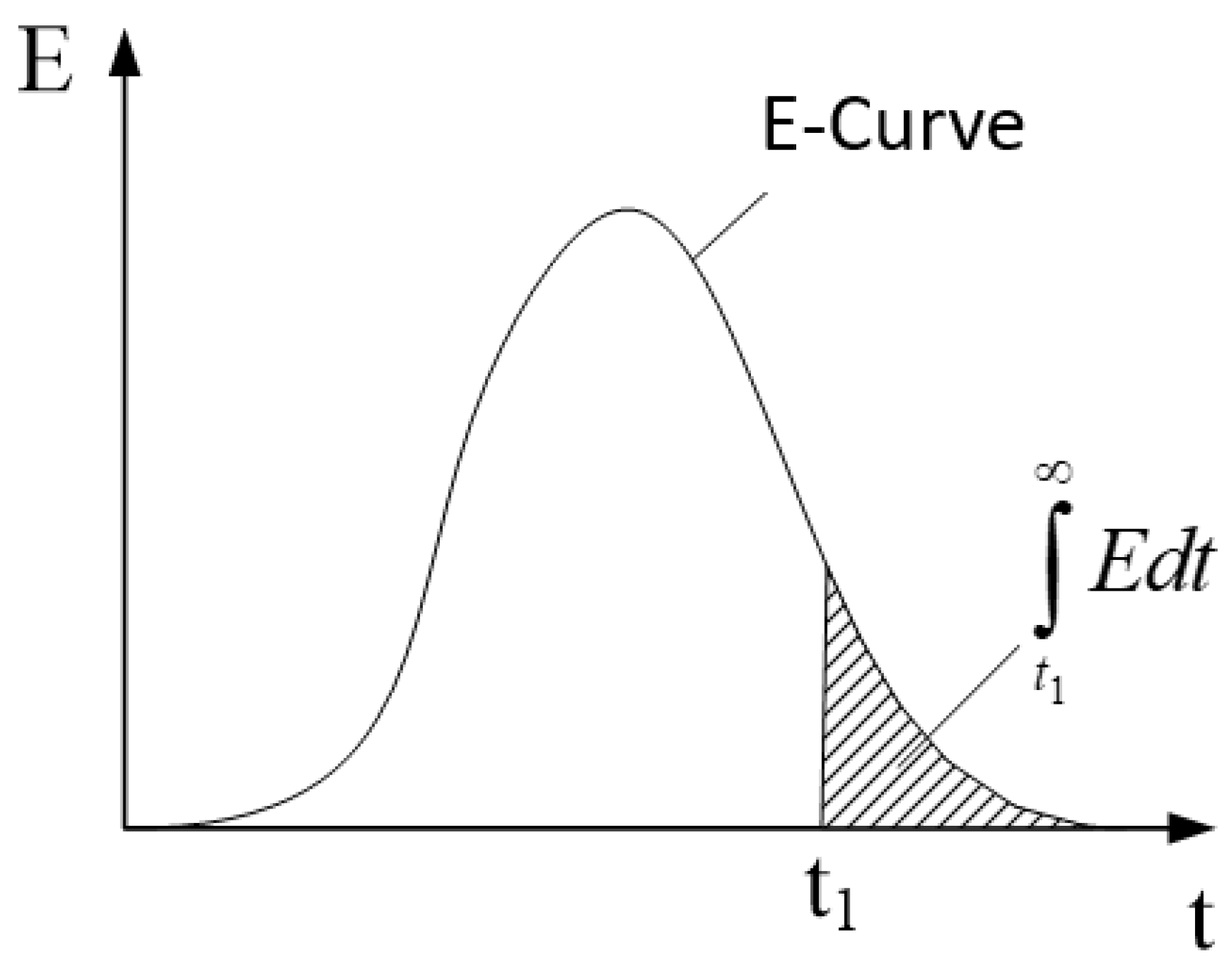
2.1.3. Characteristic Volumes Calculation from RTD Curves
2.2. Geometry and Mesh
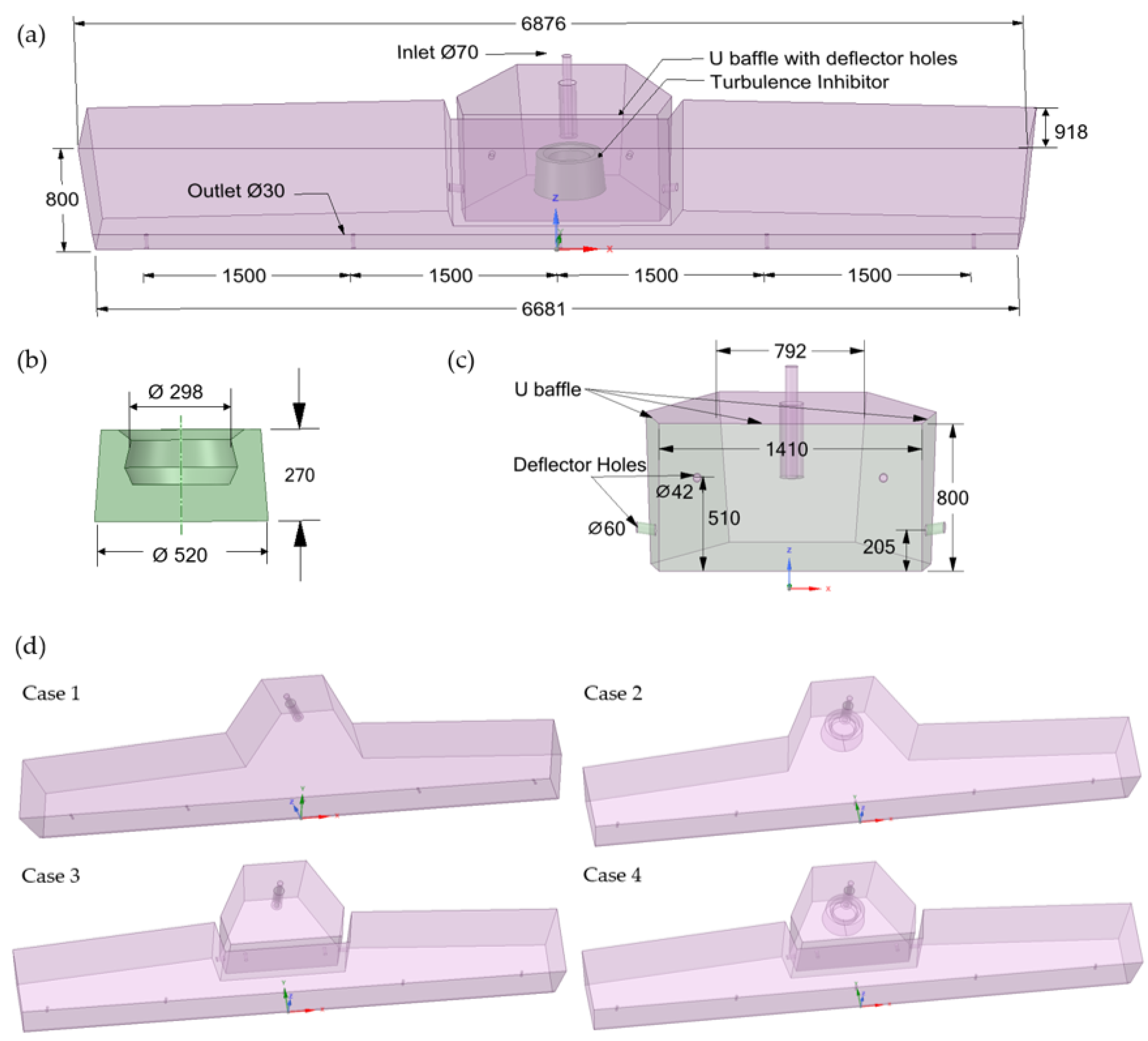
2.2.1. Tundish Geometry
- Case 1—bare tundish;
- Case 2—tundish with turbulence inhibitor (TI);
- Case 3—tundish with U-baffle with deflector holes(UB);
- Case 4—tundish with U-baffle with deflector holes and turbulence inhibitor (UB + TI).
2.2.2. Computational Domain and Mesh
2.3. Initial and Boundary Conditions
2.3.1. Liquid Phase
2.3.2. Tracer
2.4. Solution Procedure
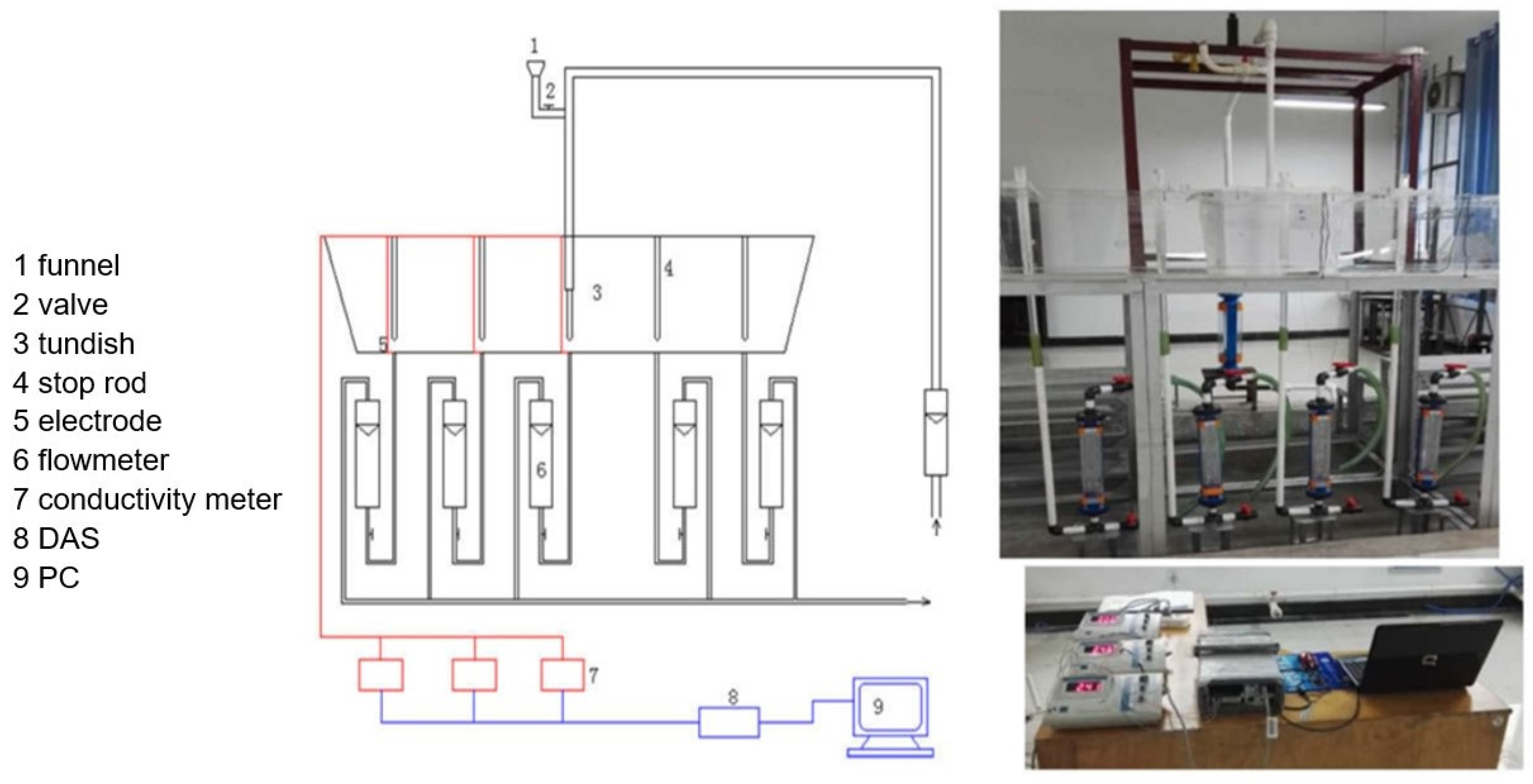
3. Water Model
4. Results and Discussion
4.1. Validation of CFD Model
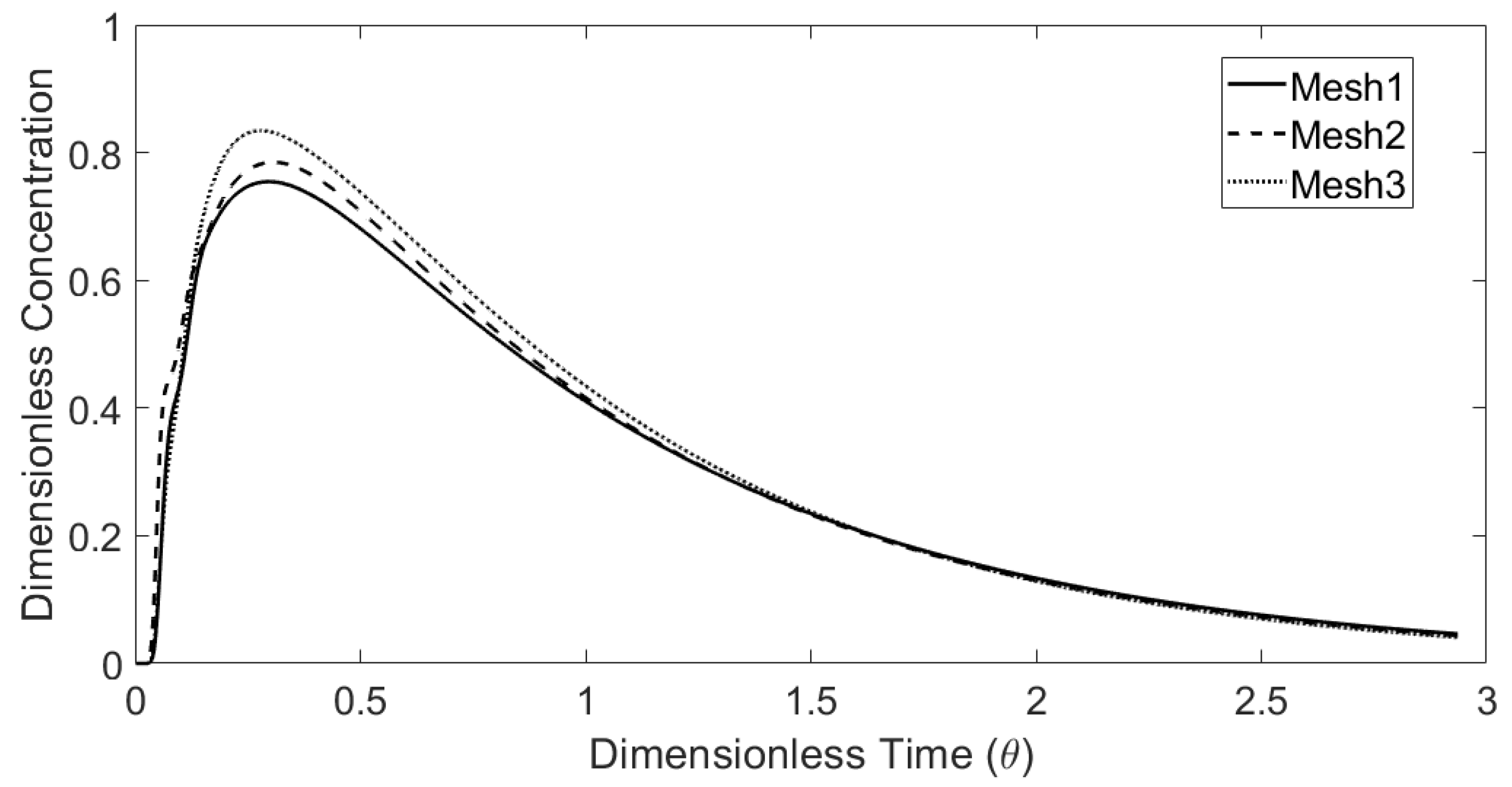
4.1.1. Independent of Computational Mesh
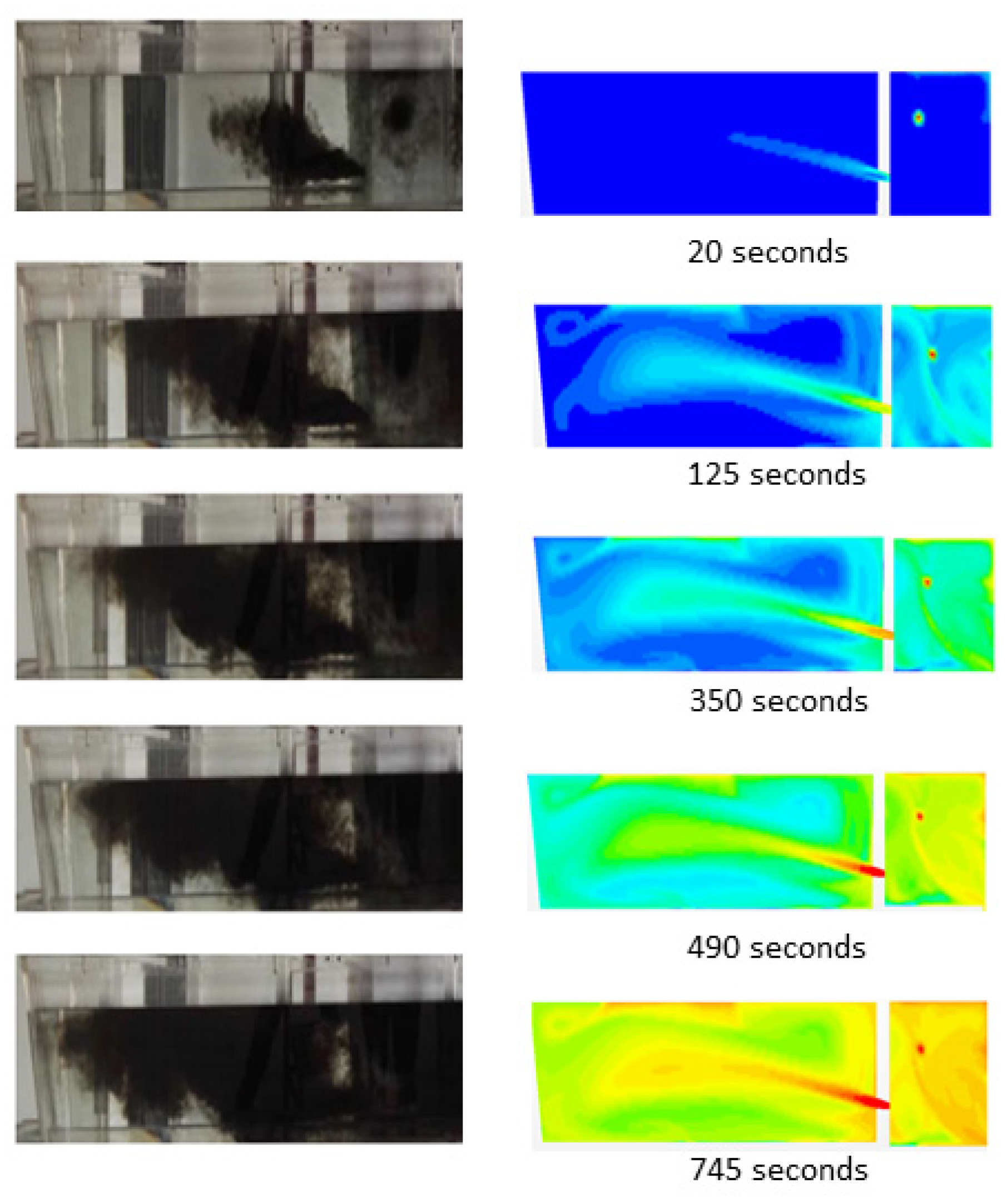
4.1.2. Numeric vs. Physical Modeling
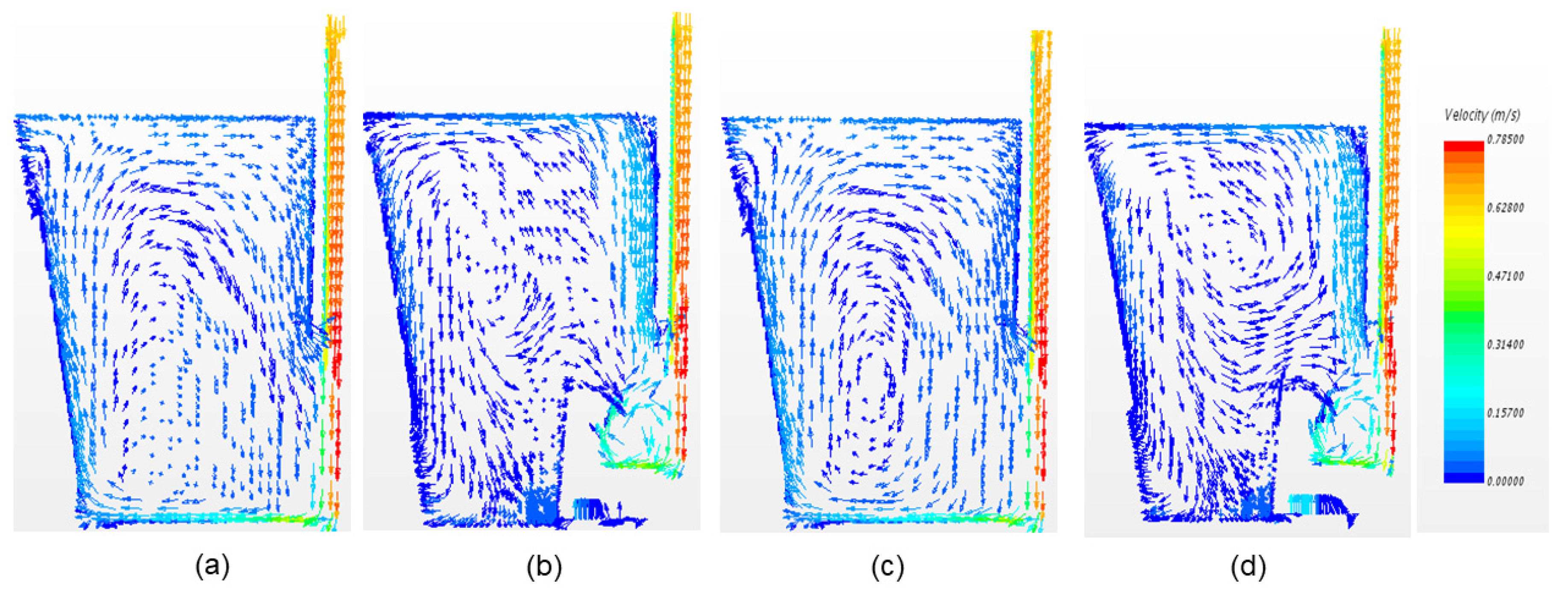
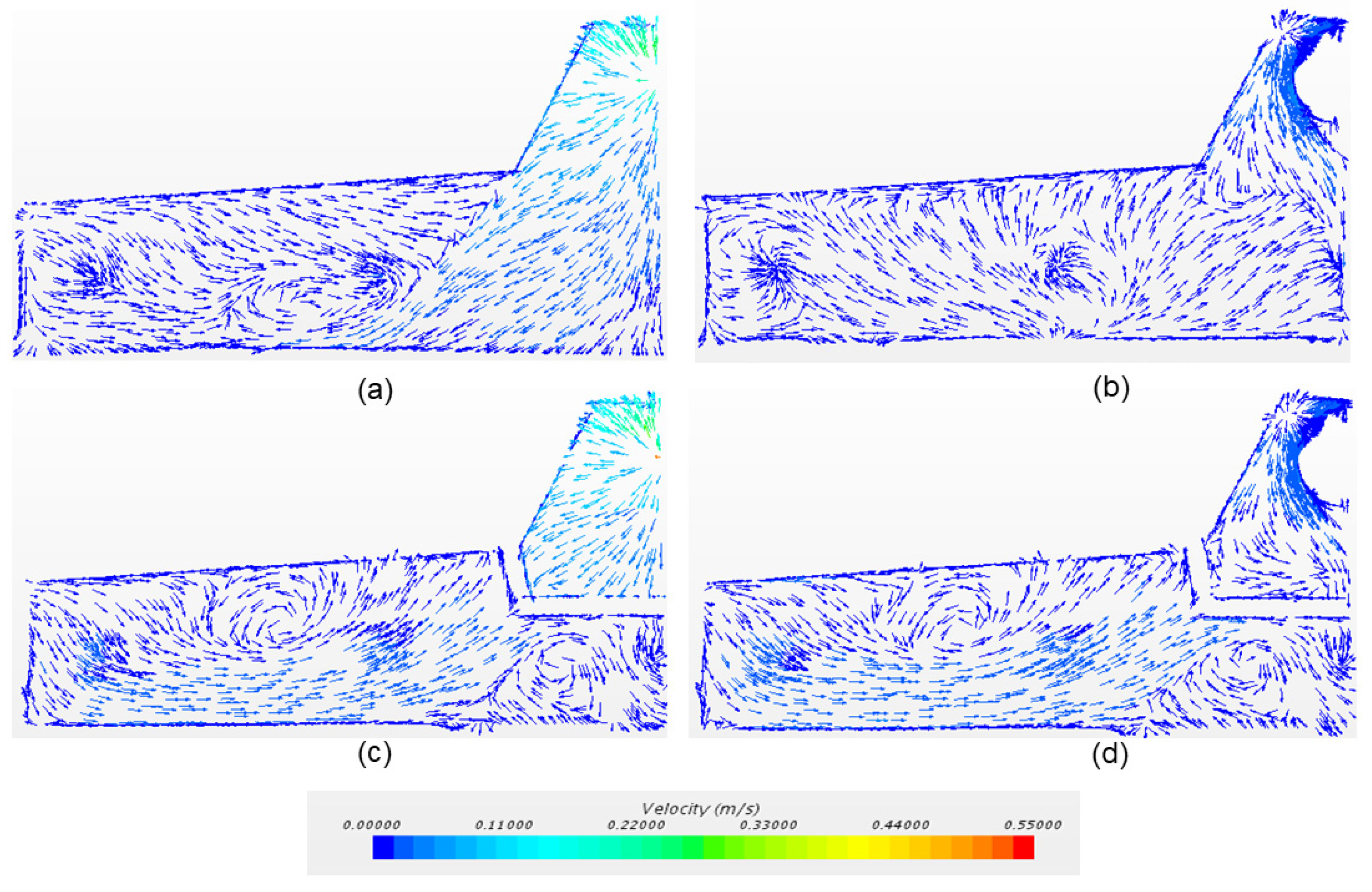
4.2. Liquid Flow in Tundish with Different FCD
- View A: Longitudinal plane of inlet;
- View B: Horizontal plane (close to bottom);
- View C: Longitudinal plane of all the outlets.
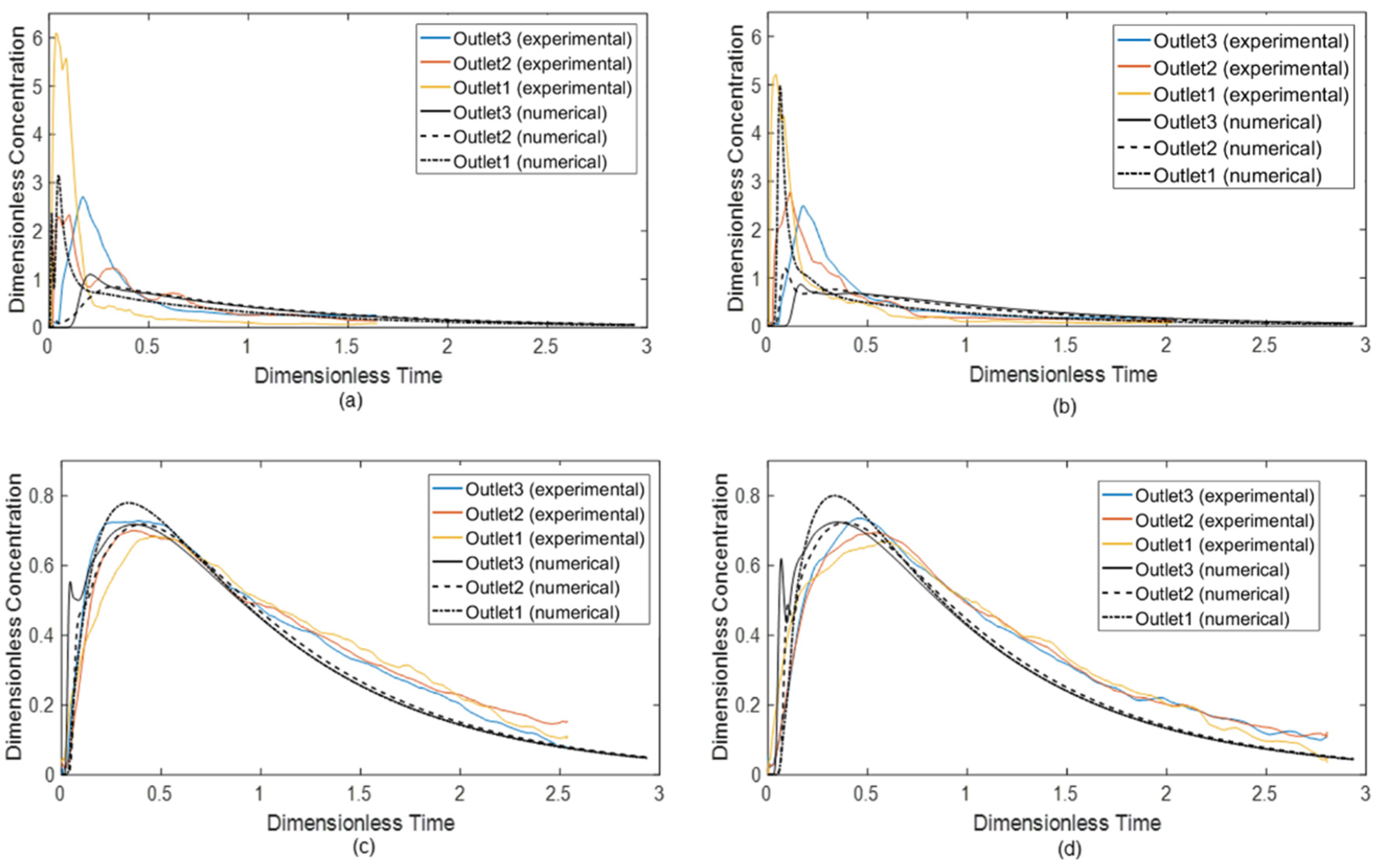
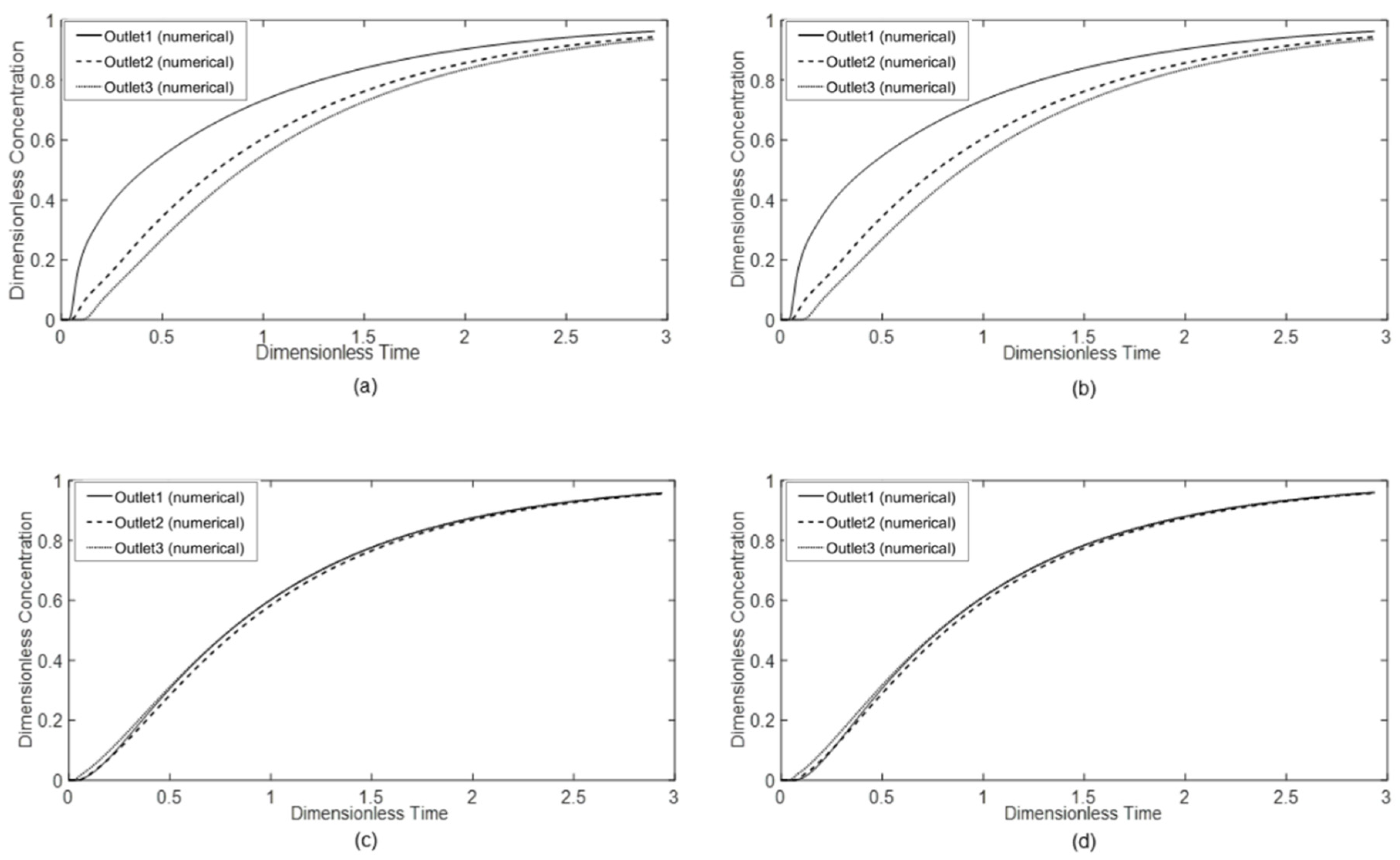
4.3. E-Curve
4.4. F-Curve
5. Conclusions
- A combination of the U-baffle with deflector holes and turbulence inhibitor was proposed for a five-strand tundish. The existence of turbulence inhibitor impaired the turbulence zone in the outlet chamber due to the redirection of the incoming flow. Additionally, the U-type baffle with deflector holes could reorient the flow and extend the flow path, which was predicted by the numeric flow simulation and visualized through tracer dispersion in the water modeling;
- A sharp increase in the tracer concentration suggests the short-circuiting phenomena in the bare tundish, resulting in a relatively high dead volume fraction, up to 27%. High dead volume fraction was an undesirable feature in the tundish design;
- The tundish equipped with the U-baffle with deflector holes could improve the flow characteristics in the E-curve analysis. The dead volume fractions were less than 10% and the plug volume fractions were around 20% for all the outlets. The deviation around E-curves indicated a lowered difference of the flow characteristics among the outlets. The comparison of two U-baffle cases showed that the existence of turbulence inhibitor delays the breakthrough time, but shortened the mean residence time;
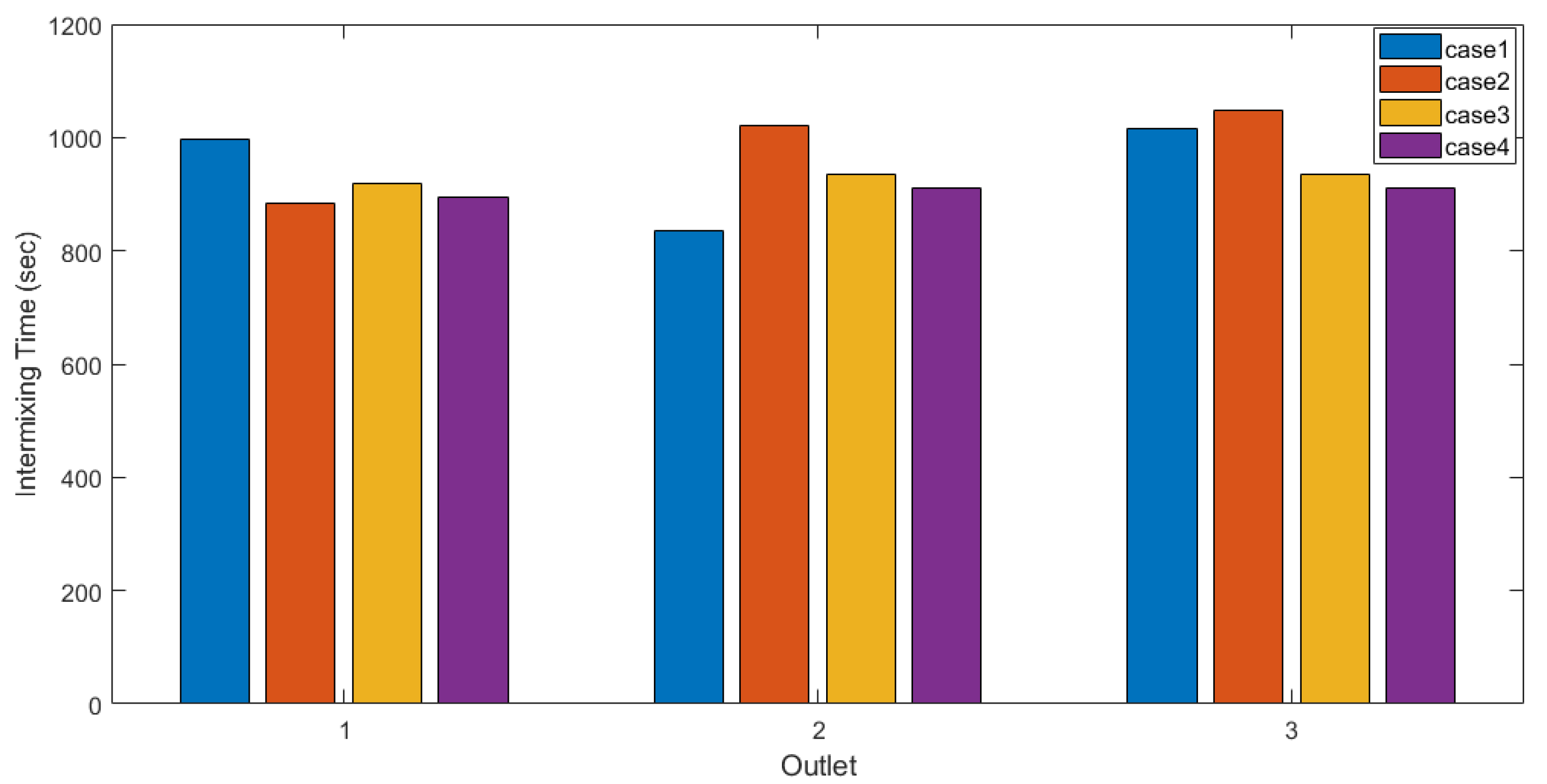
- Intermixing time of the mixed grade casting were numerically investigated for the ladle changeover operation by the analysis of the F-curve. A slope change of F-curve was observed when there was a short-circuiting phenomenon. The tundish equipped with U-baffle and turbulence inhibitor generated the shortest intermixing time and the lowest deviation at the outlets.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mazumdar, D.; Guthrie, R.I.L. The physical and mathematical modelling of continuous casting tundish systems. ISIJ Int. 1999, 39, 524–547. [Google Scholar] [CrossRef]
- Chattopadhyay, K.; Isac, M.; Guthrie, R.I.L. Physical and mathematical modelling of steelmaking tundish operations: A review of the last decade (1999–2009). ISIJ Int. 2010, 50, 331–348. [Google Scholar] [CrossRef]
- Mazumdar, D. Review, analysis, and modeling of continuous casting tundish systems. Steel Res. Int. 2019, 90, 1800279. [Google Scholar] [CrossRef]
- Szekely, J.; Ilegbusi, O. The Physical and Mathematical Modeling of Tundish Operations; Springer: New York, NY, USA, 1989. [Google Scholar]
- López-Ramírez, S.; Palafox-Ramos, J.; Morales, R.D.; Barrón-Meza, M.A.; Toledo, M.V. Effects of tundish size, tundish design and casting flow rate on fluid flow phenomena of liquid steel. Steel Res. 1998, 69, 423–428. [Google Scholar]
- Vargas-Zamora, A.; Palafox-Ramos, J.; Morales, R.D.; Díaz-Cruz, M.; Barreto-Sandoval, J.D.J. Inertial and buoyancy driven water flows under gas bubbling and thermal stratification conditions in a tundish model. Metall. Mater. Trans. B 2004, 35, 247–257. [Google Scholar] [CrossRef]
- Zhong, L.C.; Li, L.Y.; Wang, B.; Zhang, L.; Zhu, L.X.; Zhang, Q.F. Fluid flow behaviour in slab continuous casting tundish with different configurations of gas bubbling curtain. Ironmak. Steelmak. 2008, 35, 436–440. [Google Scholar] [CrossRef]
- Bensouici, M.; Bellaouar, A.; Talbi, K. Numerical investigation of the fluid flow in continuous casting tundish using analysis of RTD curves. J. Iron Steel Res. Int. 2009, 16, 22–29. [Google Scholar] [CrossRef]
- Zheng, M.J.; Gu, H.Z.; Ao, H.; Zhang, H.X.; Deng, C.J. Numerical simulation and industrial practice of inclusion removal from molten steel by gas bottom blowing in continuous casting tundish. J. Min. Metall. Sec. B Metall. 2011, 47, 137–147. [Google Scholar]
- Chen, D.F.; Xie, X.; Long, M.J.; Zhang, M.; Zhang, L.L.; Liao, Q. Hydraulics and mathematics simulation on the weir and gas curtain in tundish of ultrathick slab continuous casting. Metall. Mater. Trans. B 2013, 45, 200. [Google Scholar] [CrossRef]
- Chen, C.; Jonsson, L.T.I.; Tilliander, A.; Cheng, G.G.; Jönsson, P.G. A mathematical modeling study of tracer mixing in a continuous casting tundish. Metall. Mater. Trans. B 2015, 46, 169–190. [Google Scholar] [CrossRef]
- Chang, S.; Zhong, L.; Zou, Z. Simulation of flow and heat fields in a seven-strand tundish with gas curtain for molten steel continuous-casting. ISIJ Int. 2015, 55, 837–844. [Google Scholar] [CrossRef]
- Devi, S.; Singh, R.; Paul, A. Role of tundish argon diffuser in steelmaking tundish to improve inclusion flotation with CFD and water modelling studies. Int. J. Eng. Res. Technol. 2015, 4, 213–218. [Google Scholar]
- He, F.; Zhang, L.Y.; Xu, Q.Y. Optimization of flow control devices for a T-type five-strand billet caster tundish: Water modeling and numerical simulation. Chin. Foundry 2016, 13, 166–175. [Google Scholar] [CrossRef]
- Neves, L.; Tavares, R.P. Analysis of the mathematical model of the gas bubbling curtain injection on the bottom and the walls of a continuous casting tundish. Ironmak. Steelmak. 2017, 44, 559–567. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhao, D.T.; Qiu, S.T.; Zou, Z.S. Effect of tunnel filters on flow characteristics in an eight-strand tundish. ISIJ Int. 2017, 57, 1990–1999. [Google Scholar] [CrossRef]
- Aguilar-Rodriguez, C.E.; Ramos-Banderas, J.A.; Torres-Alonso, E.; Solorio-Diaz, G.; Hernández-Bocanegra, C.A. Flow characterization and inclusions removal in a slab tundish equipped with bottom argon gas feeding. Metallurgist 2018, 61, 1055–1066. [Google Scholar] [CrossRef]
- Yang, B.; Lei, H.; Zhao, Y.; Xing, G.; Zhang, H. Quasi-symmetric transfer behavior in an asymmetric two-strand tundish with different turbulence inhibitor. Metals 2019, 9, 855. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Huang, A.; Yan, W.; Gu, H.; Li, G. CFD Investigation of effect of multi-hole ceramic filter on inclusion removal in a two-strand tundish. Metall. Mater. Trans. B 2020, 51, 276–292. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corporation, Taylor & Francis Group: New York, NY, USA, 1980; ISBN 0-89116-522-3. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-ε eddy viscosity model for high reynolds number turbulent flows-model development and validation. Comput. Fluids 1994, 24, 227–238. [Google Scholar] [CrossRef]
- Siemens. STAR-CCM+ Version 13.04 User Guide; Siemens PLM Software: Munich, Germany, 2019. [Google Scholar]
- Ghirelli, F.; Hermansson, S.; Thunman, H.; Leckner, B. Reactor residence time analysis with CFD. Prog. Comput. Fluid Dyn. 2006, 6, 241–247. [Google Scholar] [CrossRef]
- Spalding, D.B. A note on mean residence-times in steady flows of arbitrary complexity. Chem. Eng. Sci. 1958, 9, 74–77. [Google Scholar] [CrossRef]
- Jha, P.K.; Dash, S.K. Effect of outlet positions and various turbulence models on mixing in a single and multi strand tundish. Int. J. Numer. Methods Heat Fluid Flow 2002, 12, 560–584. [Google Scholar] [CrossRef]
- Sahai, Y.; Emi, T. Criteria for water modeling of melt flow and inclusion removal in continuous casting tundishes. ISIJ Int. 1996, 36, 1166–1173. [Google Scholar] [CrossRef]
- Michalek, K.; Gryc, K.; Tkadleckova, M.; Bocek, D. Model study of tundish steel intermixing and operational verification. Arch. Metall. Mater. 2012, 57, 291–296. [Google Scholar] [CrossRef]


| Reference | Model 1 | Code | Design | Numeric Model | Parameter Study 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Strand | Fluid 3 | FCD 4 | Gas | Fluid 5 | Turb. 6 | Inclu. 7 | RTD 8 | ||||
| S. López-Ramirez (1998) [5] | N | - | 2 | S | B, TI | - | - | k-ε | - | E | SFR, FCD, TC |
| Vargas-Zamora (2004) [6] | N, P | - | 1 | W | TI, D | - | - | - | - | F | GFR |
| Zhong (2008) [7] | P | - | 2 | W | TI, D, W | N2 | - | - | - | E | TC, FCD, GFR |
| Bensouici (2009) [8] | N, P | Fluent | 1 | W | W, D | - | - | k-ε | - | E | MS, FCD |
| Zheng (2011) [9] | N, P | CFX | 2 | S | TI, B | Ar | Eu | k-ε | La | E | TC, GFR, IS |
| Chen (2013) [10] | N, P | Fluent | 1 | S, W | W | Ar | Eu | k-ε | La | E | TC, FCD, IS |
| Chen (2015) [11] | N, P | Phoenics | 1 | W | SR, D, W, TI | - | - | k-ε | - | E | MS, TS, TP |
| Chang (2015) [12] | N, P | Fluent | 7 | S, W | TI, B | Ar | Eu | k-ε | La | E | GFR, FCD |
| Devi (2015) [13] | N, P | Fluent | 2 | S, W | D | Ar | Eu | k-ε | - | E | FCD, GFR |
| He (2016) [14] | N, P | Fluent | 5 | S, W | TI, B | - | - | E | TC, SFR | ||
| Neves (2017) [15] | N, P | CFX | 2 | W | SR, D, W | Air | Eu | k-ε | - | E | GFR, FCD |
| Wang (2017) [16] | N, P | Fluent | 8 | S | TI, F | - | - | k-ε | La | E | TC, FCD, IS |
| Aguilar–Rodriguez (2018) [17] | N | Fluent | 1 | S | - | Ar | VOF | k-ε | La | E | GFR, TC, FCD |
| Yang (2019) [18] | N | CFX | 2 | S | D, TI | - | - | k-ε | La | E | FCD, TC |
| Wang (2020) [19] | N | Fluent | 2 | S | W, TI, F | - | Eu | k-ε | La | E | IS, FCD, TC |
| Water density | 998 kg/m3 |
| Water viscosity | 0.00089 Pa·s |
| Reference Pressure | 101,325 Pa |
| Inlet flow rate | 0.00028 m3/s |
| Outlet (outflow ratio) | 0.2:0.4:0.4 (Outlet 1/2/3) |
| Wall | No slip |
| Free surface | Free slip |
| Tracer inlet (E-curve) | 1 (t <= 0–2 s), 0 (t > 2 s) |
| Tracer inlet (F-curve) | 1 |
| Mesh | Mesh Number | Mesh Size (m) | ttheo (s) 1 | tmin (s) | tmax (s) | tmean (s) | Vp/V (%) | Vm/V (%) | Vd/V (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 Million | 0.002 | 749 | 31 | 222 | 685 | 17 | 75 | 9 |
| 2 | 2 Million | 0.003 | 749 | 26 | 229 | 669 | 17 | 72 | 11 |
| 3 | 1 Million | 0.004 | 749 | 30 | 208 | 664 | 16 | 73 | 11 |
| Case | ttheo (s) | tmin (s) | tmax (s) | tmean (s) | Vp/V (%) | Vm/V (%) | Vd/V (%) |
|---|---|---|---|---|---|---|---|
| 1—Outlet 1 | 749 | 4 | 36 | 544 | 3 | 70 | 27 |
| 1—Outlet 2 | 749 | 13 | 239 | 733 | 17 | 81 | 2 |
| 1—Outlet 3 | 749 | 78 | 155 | 711 | 16 | 79 | 5 |
| 2—Outlet 1 | 749 | 22 | 46 | 482 | 5 | 60 | 36 |
| 2—Outlet 2 | 749 | 28 | 65 | 673 | 6 | 84 | 10 |
| 2—Outlet 3 | 749 | 69 | 123 | 748 | 13 | 86 | 1 |
| 3—Outlet 1 | 749 | 27 | 252 | 696 | 19 | 74 | 7 |
| 3—Outlet 2 | 749 | 32 | 304 | 716 | 22 | 73 | 4 |
| 3—Outlet 3 | 749 | 15 | 274 | 690 | 19 | 73 | 8 |
| 4—Outlet 1 | 749 | 44 | 250 | 692 | 20 | 73 | 8 |
| 4—Outlet 2 | 749 | 44 | 291 | 707 | 22 | 72 | 6 |
| 4—Outlet 3 | 749 | 27 | 261 | 682 | 19 | 72 | 9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, D.-Y.; Yue, Q. Modeling of Fluid Flow and Residence-Time Distribution in a Five-Strand Tundish. Metals 2020, 10, 1084. https://doi.org/10.3390/met10081084
Sheng D-Y, Yue Q. Modeling of Fluid Flow and Residence-Time Distribution in a Five-Strand Tundish. Metals. 2020; 10(8):1084. https://doi.org/10.3390/met10081084
Chicago/Turabian StyleSheng, Dong-Yuan, and Qiang Yue. 2020. "Modeling of Fluid Flow and Residence-Time Distribution in a Five-Strand Tundish" Metals 10, no. 8: 1084. https://doi.org/10.3390/met10081084
APA StyleSheng, D.-Y., & Yue, Q. (2020). Modeling of Fluid Flow and Residence-Time Distribution in a Five-Strand Tundish. Metals, 10(8), 1084. https://doi.org/10.3390/met10081084






