Resonance Effects in Variable Practice for Handball, Basketball, and Volleyball Skills: A Study on Contextual Interference and Differential Learning
Abstract
1. Introduction
2. Materials and Methods
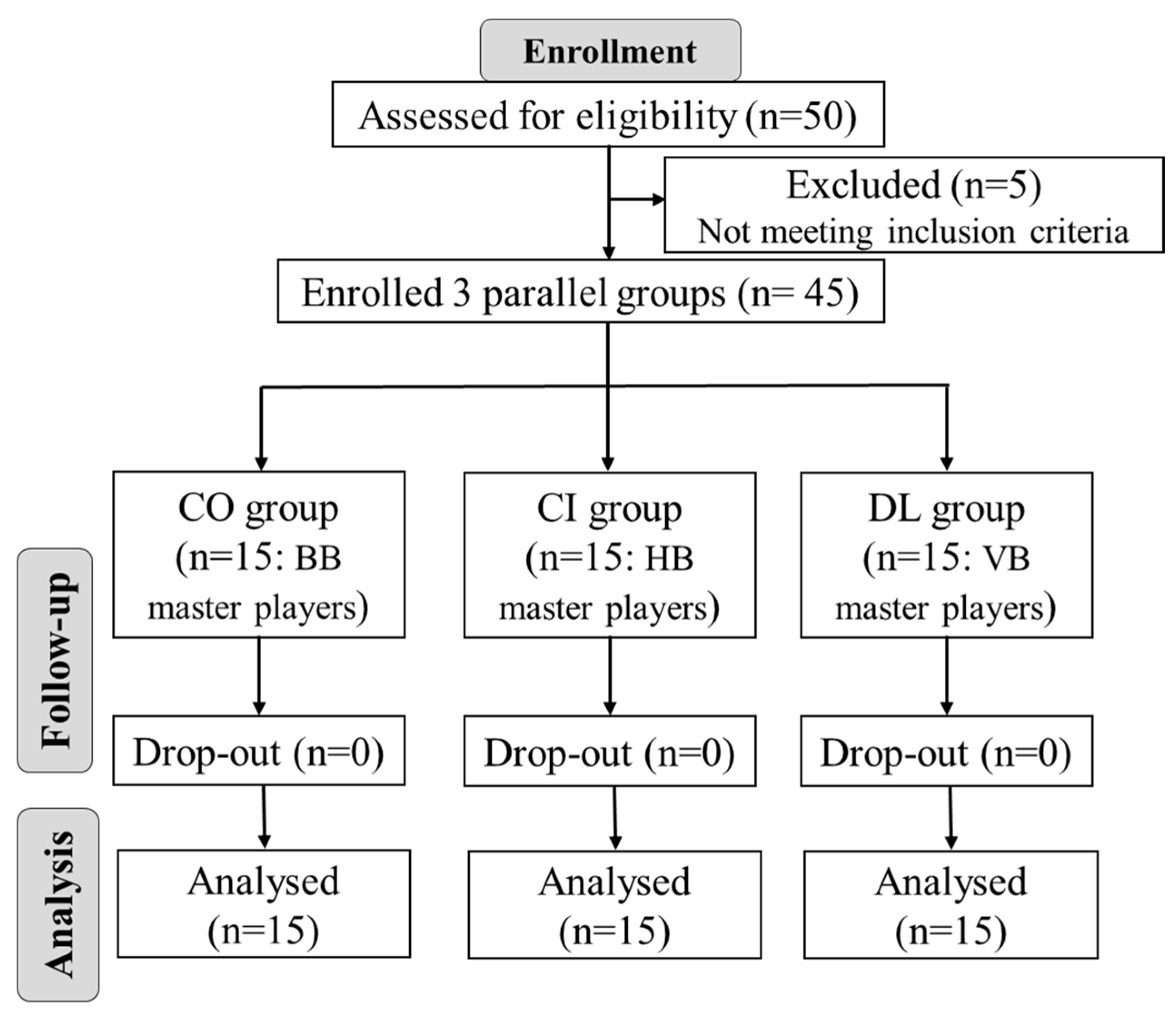
2.1. Participants
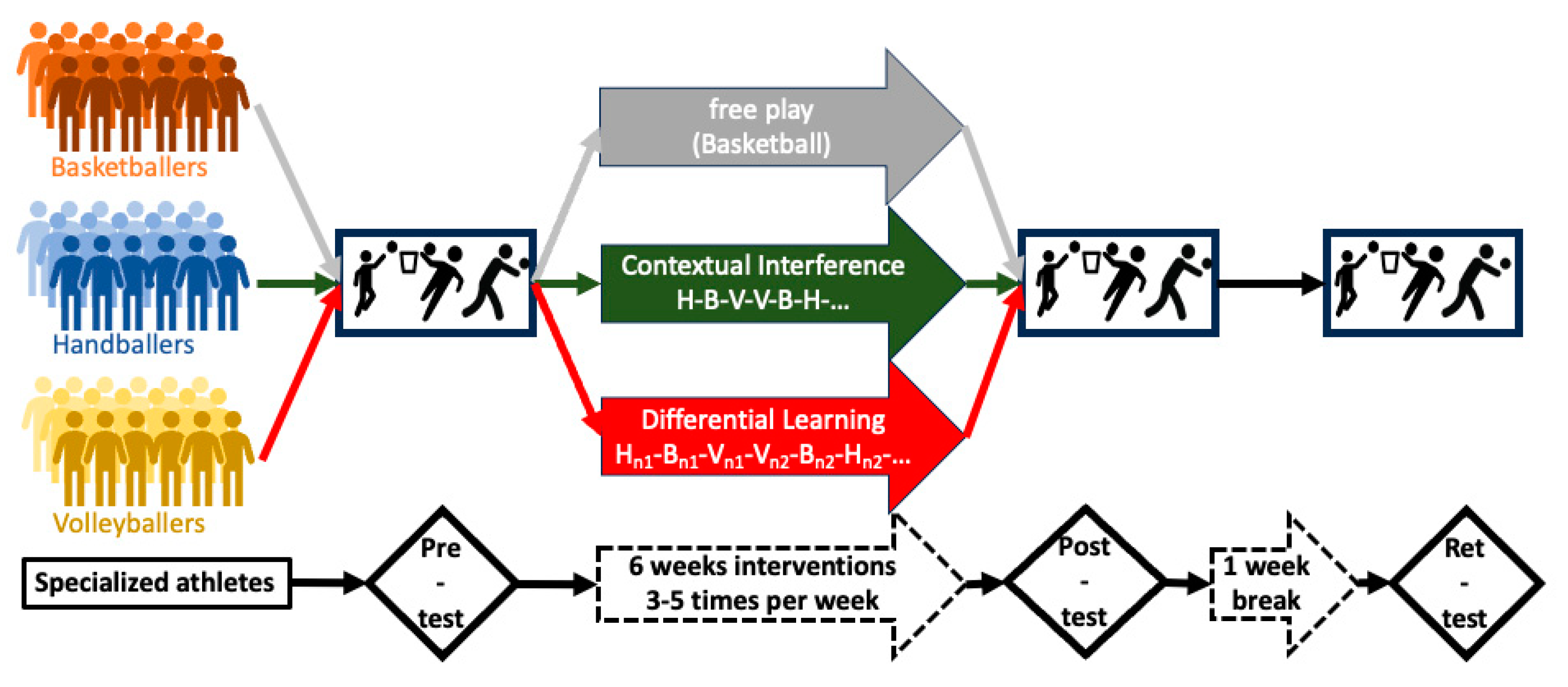
2.2. Experimental Design
2.3. Test Design
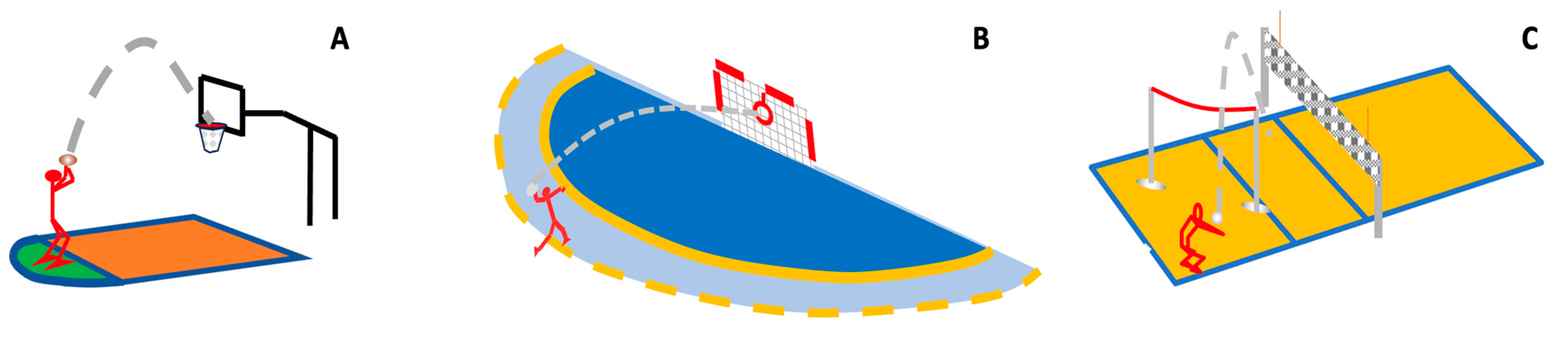
2.3.1. Test 1 A: Basketball Free-Throw
2.3.2. Test 1 B: Handball Shooting
2.3.3. Test 1 C: Volleyball Underarm Pass
2.4. Training-Interventions
2.5. Data Analysis
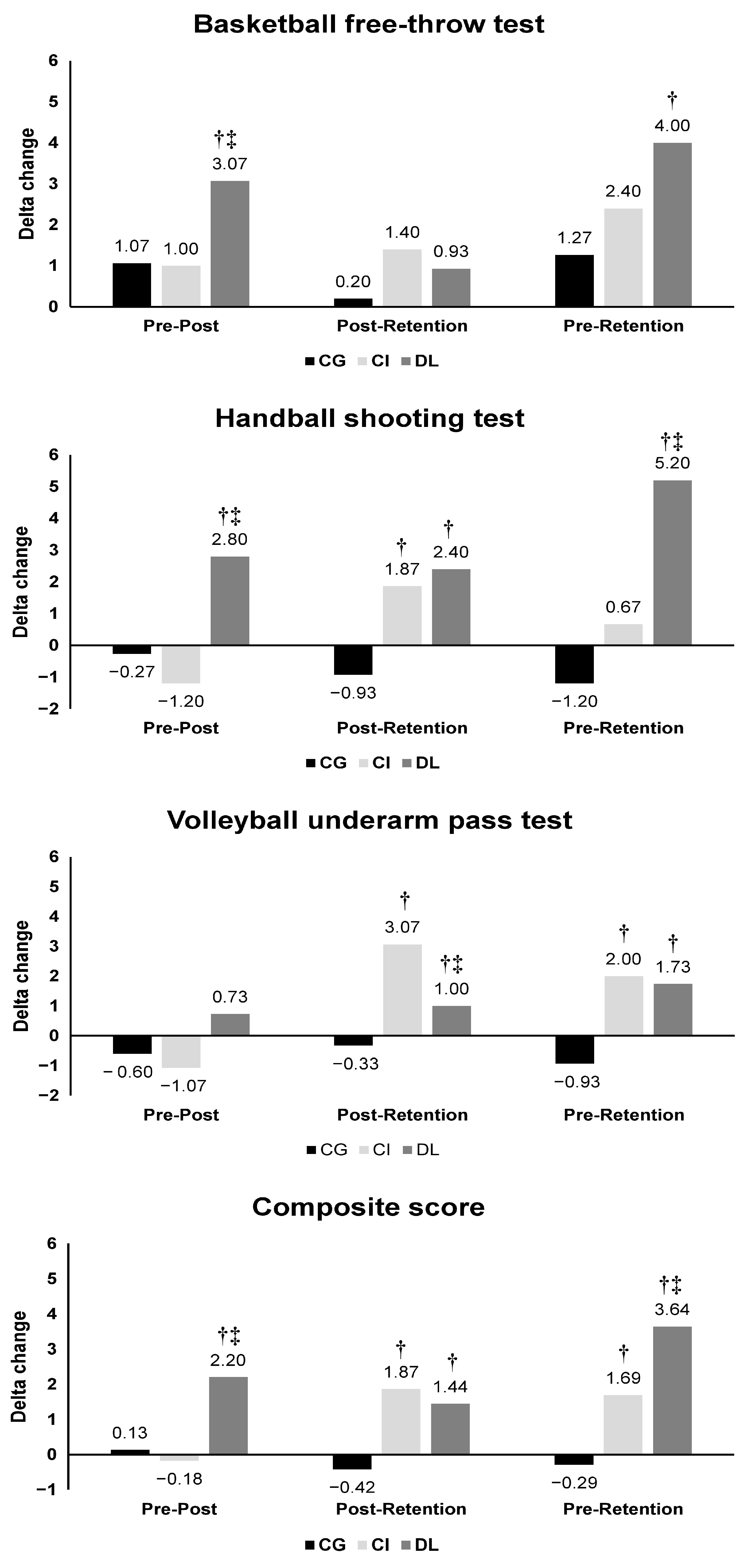
3. Results
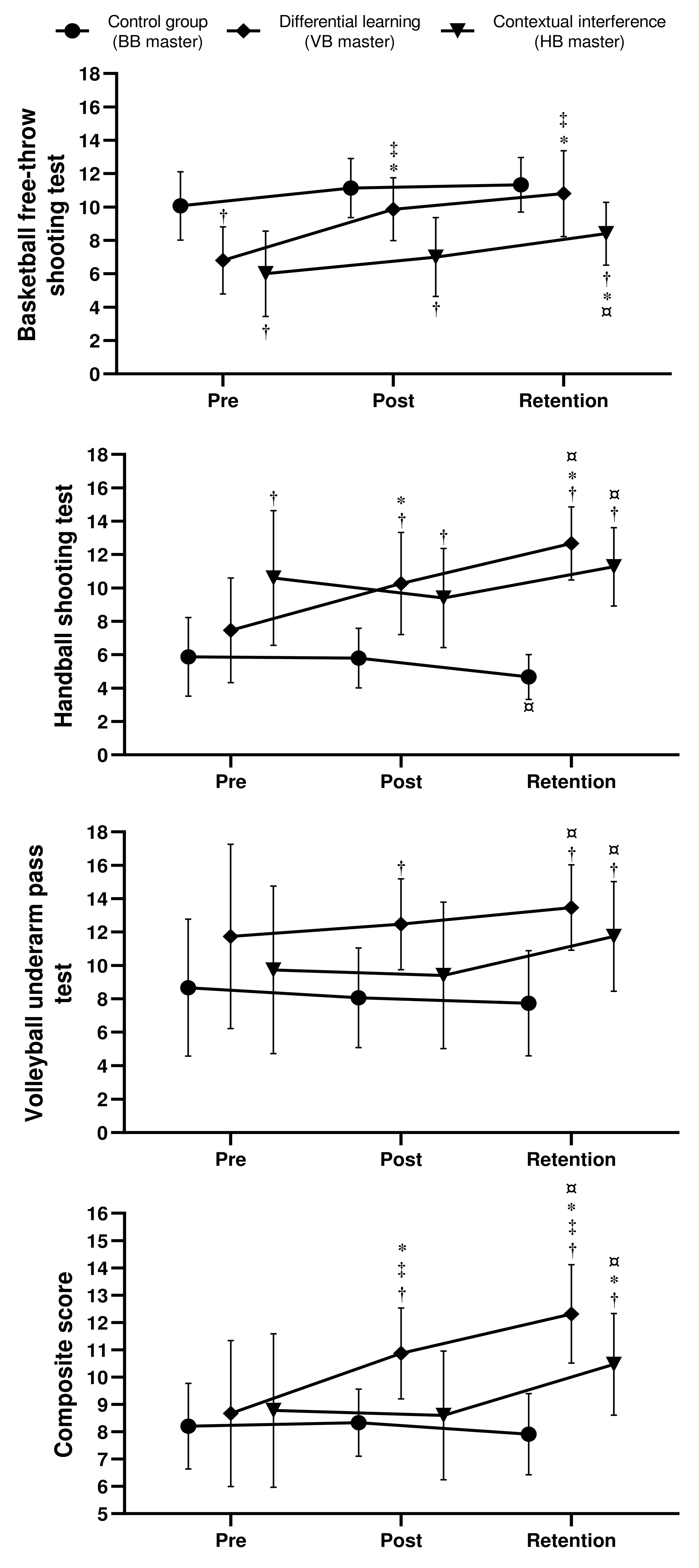
3.1. Comparative Analysis across Single Skills
3.2. Comparative Analysis across the Composite Score
3.3. Comparative Analysis across the Short-Term and Relatively Permanent Gains
3.3.1. Group Effect on the Short-Term Gain (Δ Pre–Post)
3.3.2. Group Effect on the Relatively Permanent Gain (Δ Post–Retention and Δ Pre–Retention)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Braun, D.A.; Aertsen, A.; Wolpert, D.M.; Mehring, C. Motor task variation induces structural learning. Curr. Biol. 2009, 19, 352–357. [Google Scholar] [CrossRef] [PubMed]
- Manley, H.; Dayan, P.; Diedrichsen, J. When money is not enough: Awareness, success, and variability in motor learning. PLoS ONE 2014, 9, e86580, Erratum in PLoS ONE 2014, 9, e97058. [Google Scholar] [CrossRef] [PubMed]
- Corrêa, U.C.; Benda, R.N.; de Oliveira, D.L.; Ugrinowitsch, H.; Freudenheim, A.M.; Tani, G. Different Faces of Variability in the Adaptive Process of Motor Skill Learning. Nonlinear Dyn. Psychol. Life Sci. 2015, 19, 465–487. [Google Scholar]
- Van Rossum, J.H. Schmidt’s schema theory: The empirical base of the variability of practice hypothesis: A critical analysis. Hum. Mov. Sci. 1990, 9, 387–435. [Google Scholar] [CrossRef]
- Buszard, T.; Reid, M.; Krause, L.; Kovalchik, S.; Farrow, D. Quantifying Contextual Interference and Its Effect on Skill Transfer in Skilled Youth Tennis Players. Front. Psychol. 2017, 8, 1931. [Google Scholar] [CrossRef] [PubMed]
- Newell, K.M.; Kugler, P.N.; Van Emmerik, R.E.A.; Mcdonald, P.V. Search strategies and the acquisition of coordination. In Advances in Psychology: Perspectives on the Coordination of Movement; Wallace, S., Ed.; North-Holland: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Brady, F. Contextual Interference: A Meta-Analytic Study. Percept. Mot. Ski. 2004, 99, 116–126. [Google Scholar] [CrossRef]
- Morrison, S.; Newell, K.M. Strength training as a dynamical model of motor learning. J. Sport. Sci. 2023, 41, 408–423. [Google Scholar] [CrossRef]
- Ammar, A.; Trabelsi, K.; Boujelbane, M.A.; Boukhris, O.; Glenn, J.M.; Chtourou, H.; Schöllhorn, W.I. The myth of contextual interference learning benefit in sports practice: A systematic review and meta-analysis. Educ. Res. Rev. 2023, 39, 100537. [Google Scholar] [CrossRef]
- Schmidt, R.A. Motor Schema Theory after 27 Years: Reflections and Implications for a New Theory. Res. Q. Exerc. Sport 2003, 74, 366–375. [Google Scholar] [CrossRef]
- Schöllhorn, W.I.; Rizzi, N.; Slapšinskaitė-Dackevičienė, A.; Leite, N. Always Pay Attention to Which Model of Motor Learning You Are Using. Int. J. Environ. Res. Public Health 2022, 19, 711. [Google Scholar] [CrossRef]
- Wulf, G.; Shea, C.H. Principles derived from the study of simple skills do not generalize to complex skill learning. Psychon. Bull. Rev. 2002, 9, 185–211. [Google Scholar] [CrossRef] [PubMed]
- Gaulhofer, K.; Streicher, M. Grundzüge des Österreichischen Schulturnens; Deutscher Verlag für Jugend und Volk: Wien, Austria, 1924. [Google Scholar]
- Mester, L. Gemeinschaftserziehung und Mannschaftsspiel. In Kongressbericht, Das Spiel: Kongress für Leibeserziehung, 3–5 Oktober 1958 in Osnabrück; Dt. Leibeserzieher, A., Ed.; Limpert: Frankfurt, Germany, 1959. [Google Scholar]
- Schmidt, R.A. A schema theory of discrete motor skill learning. Psychol. Rev. 1975, 82, 225–260. [Google Scholar] [CrossRef]
- Moxley, S.E. Schema. J. Mot. Behav. 1979, 11, 65–70. [Google Scholar] [CrossRef] [PubMed]
- Battig, W.F. The flexibility of human memory. In Levels of Processing in Human Memory; Cermak, L.S., Craik, F.I., Eds.; Erlbaum: Hillsdale, NJ, USA, 1979; pp. 23–44. [Google Scholar]
- Shea, J.B.; Morgan, R.L. Contextual interference effects on the acquisition, retention, and transfer of a motor skill. J. Exp. Psychol. Hum. Learn. Mem. 1979, 5, 179–187. [Google Scholar] [CrossRef]
- Ludgate, K.E. The effect of manual guidance upon maze learning. Psychol. Monogr. Gen. Appl. 1923, 33, i-65. [Google Scholar] [CrossRef]
- Koch, H.L. The influence of mechanical guidance upon maze learning. Psychol. Monogr. Gen. Appl. 1923, 32, i-113. [Google Scholar] [CrossRef]
- Größing, S. Einführung in Die Sportdidaktik: Lehren und Lernen im Sportunterricht; Limpert: Wiesbaden, Germany, 1988. [Google Scholar]
- Wood, C.A.; Ging, C.A. The Role of Interference and Task Similarity on the Acquisition, Retention, and Transfer of Simple Motor Skills. Res. Q. Exerc. Sport 1991, 62, 18–26. [Google Scholar] [CrossRef]
- Wulf, G.; Lee, T.D. Contextual interference in movements of the same class: Differential effects on program and parameter learning. J. Mot. Behav. 1993, 25, 254–263. [Google Scholar] [CrossRef]
- Shea, J.B.; Zimny, S.T. Context effects in memory and learning movement information. In Memory and Control of Action; Magill, R.A., Ed.; North-Holland: New York, NY, USA, 1983; pp. 345–366. [Google Scholar]
- Schöllhorn, W.I.; Bauer, H.U. Assessment of running patterns using neural networks. In Sport und Informatik; Mester, J., Perl, J., Eds.; Sport & Buch Strauss: Cologne, Germany, 1998; pp. 208–309. [Google Scholar]
- Horst, F.; Rupprecht, C.; Schmitt, M.; Hegen, P.; Schöllhorn, W.I. Muscular Activity in Conventional and Differential Back Squat Exercise. In Proceedings of the 21st Annual Congress of the European College of Sport Science, Vienna, Austria, 6–9 July 2016; Baca, A., Wessner, B., Diketmüller, R., Tschan, H., Hofmann, M., Kornfeind, P., Tsolakidis, E., Eds.; European College of Sport Science: Cologne, Germany, 2016; p. 516. [Google Scholar]
- Horst, F.; Eekhoff, A.; Newell, K.M.; Schöllhorn, W.I. Intra-individual gait patterns across different time-scales as revealed by means of a supervised learning model using kernel-based discriminant regression. PLoS ONE 2017, 12, e0179738. [Google Scholar] [CrossRef]
- Aragonés, D.; Eekhoff, A.; Horst, F.; Schöllhorn, W.I. Fatigue-related changes in technique emerge at different timescales during repetitive training. J. Sport. Sci. 2018, 36, 1296–1304. [Google Scholar] [CrossRef]
- Horst, F.; Lapuschkin, S.; Samek, W.; Müller, K.-R.; Schöllhorn, W.I. Explaining the unique nature of individual gait patterns with deep learning. Sci. Rep. 2019, 9, 2391. [Google Scholar] [CrossRef] [PubMed]
- Horst, F.; Hoitz, F.; Slijepcevic, D.; Schons, N.; Beckmann, H.; Nigg, B.M.; Schöllhorn, W.I. Identification of subject-specific responses to footwear during running. Sci. Rep. 2019, 13, 11284. [Google Scholar] [CrossRef] [PubMed]
- Schöner, G.; Haken, H.; Kelso, J.A.S. A stochastic theory of phase transitions in human hand movement. Biol. Cybern. 1989, 53, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Schöllhorn, W.I. Practical consequences of biomechanically determined individuality and fluctuations on motor learning. In Proceedings of the XVII Conference of the International Society of Biomechanics, Calgary, AB, Canada, 8–13 August 1999; University Press: Calgary, AB, Canada, 1999. [Google Scholar]
- Schöllhorn, W.I. Topology and metrics of a ballistic gross motor movement during a learning process. In Proceedings of the Poster Presentation on the International Bernstein Conference on Motor Control in Penn State, State College, PA, USA, 23–25 August 1996. [Google Scholar]
- Apidogo, J.B.; Burdack, J.; Schöllhorn, W.I. Learning Multiple Movements in Parallel—Accurately and in Random Order, or Each with Added Noise? Int. J. Environ. Res. Public Health 2022, 19, 10960. [Google Scholar] [CrossRef] [PubMed]
- Bortoli, L.; Robazza, C.; Durigon, V.; Carra, C. Effects of contextual interference on learning technical sports skills. Percept. Mot. Ski. 1992, 75, 555–562. [Google Scholar] [CrossRef] [PubMed]
- French, K.E.; Rink, J.E.; Werner, P.H. Effects of contextual interference on retention of three volleyball skills. Percept. Mot. Ski. 1990, 71, 179–189. [Google Scholar] [CrossRef]
- Jones, L.L.; French, K.E. Effects of contextual interference on acquisition and retention of three volleyball skills. Percept. Mot. Ski. 2007, 105, 883–890. [Google Scholar] [CrossRef]
- Lee, T.D.; Magill, R.A. The locus of contextual interference in motor-skill acquisition. J. Exp. Psychol. Learn. Mem. Cogn. 1983, 9, 730–746. [Google Scholar] [CrossRef]
- Lee, T.D.; Magill, R.A. Can Forgetting Facilitate Skill Acquisition? In Advances in Psychology; Elsevier: Amsterdam, The Netherlands, 1985; pp. 3–22. [Google Scholar] [CrossRef]
- Baddeley, A.D. Exploring Working Memory: Selected Works of Alan Baddeley, 1st ed.; Routledge: London, UK, 2018. [Google Scholar]
- Lin, C.H.; Winstein, C.J.; Fisher, B.E.; Wu, A.D. Neural Correlates of the Contextual Interference Effect in Motor Learning: A Tran-scranial Magnetic Stimulation Investigation. J. Mot. Behav. 2010, 42, 223–232. [Google Scholar] [CrossRef]
- Lage, G.M.; Ugrinowitsch, H.; Apolinário-Souza, T.; Vieira, M.M.; Albuquerque, M.R.; Benda, R.N. Repetition and variation in motor practice: A review of neural correlates. Neurosci. Biobehav. Rev. 2015, 57, 132–141. [Google Scholar] [CrossRef]
- Jaitner, T.; Schöllhorn, W.I. Prozessorientierte Bewegungsanalyse am Beispiel des Stabhochsprungs. In Sport im Lebenslauf; Schmidtbleicher, D., Bös, K., Müller, A., Eds.; Czwalina: Hamburg, Germany, 1995; pp. 293–298. [Google Scholar]
- Horst, F.; Janssen, D.; Beckmann, H.; Schöllhorn, W.I. Can Individual Movement Characteristics Across Different Throwing Dis-ciplines Be Identified in High-Performance Decathletes? Front. Psychol. 2020, 11, 2262. [Google Scholar] [CrossRef] [PubMed]
- Burdack, J.; Giesselbach, S.; Simak, M.L.; Ndiaye, M.L.; Marquardt, C.; Schöllhorn, W.I. Identifying underlying individuality across running, walking, and handwriting patterns with conditional cycle–consistent generative adversarial networks. Front. Bioeng. Biotechnol. 2023, 11, 1204115. [Google Scholar] [CrossRef]
- Janssen, D.; Schöllhorn, W.I.; Lubienetzki, J.; Fölling, K.; Kokenge, H.; Davids, K. Recognition of emotions in gait patterns by means of artificial neural nets. J. Nonverbal Behav. 2008, 32, 79–92. [Google Scholar] [CrossRef]
- Janssen, D.; Schöllhorn, W.I.; Newell, K.M.; Jäger, J.M.; Rost, F.; Vehof, K. Diagnosing fatigue in gait patterns by support vector machines and self-organizing maps. Hum. Mov. Sci. 2011, 30, 966–975. [Google Scholar] [CrossRef] [PubMed]
- Burdack, J.; Horst, F.; Aragonés, D.; Eekhoff, A.; Schöllhorn, W.I. Fatigue-Related and Timescale-Dependent Changes in Individual Movement Patterns Identified Using Support Vector Machines. Front. Psychol. 2020, 11, 551548. [Google Scholar] [CrossRef]
- Albrecht, S.; Janssen, D.; Quarz, E.; Newell, K.M.; Schöllhorn, W.I. Individuality of movements in music—Finger and body movements during playing of the flute. Hum. Mov. Sci. 2014, 35, 131–144. [Google Scholar] [CrossRef]
- Schöllhorn, W.I. Applications of systems dynamic principles to technique and strength training. Acta Acad. Olymp. Est. 2000, 8, 67–85. [Google Scholar]
- Ashby, W.R. An Introduction to Cybernetics; Chapman & Hall Ltd.: London, UK, 1956. [Google Scholar]
- GelFand, I.M.; Tsetlin, M.L. Some methods of control for complex systems. Russ. Math. Surv. 1962, 17, 95–117. [Google Scholar] [CrossRef]
- Gros, C. Generating Functionals for Guided Self-Organization. In Guided Self-Organization; Prokopenko, M., Ed.; Inception: Springer: Berlin/Heidelberg, Germany, 2014; pp. 53–66. [Google Scholar] [CrossRef]
- Schöllhorn, W.I. Applications of artificial neural nets in clinical biomechanics. Clin. Biomech. 2004, 19, 876–898. [Google Scholar] [CrossRef]
- Schöllhorn, W.I. Biomechanische Einzelfallanalyse im Diskuswurf: Prozess und Produktorientierte Technikanalyse mecha-nischer Energieformen. In Biomechanical Single Case Analysis in Discus Throwing: Process and Product Oriented Technique Analysis of Mechanical Energy Forms; Harri Deutsch: Frankfurt am Main, Germany, 1993. [Google Scholar]
- Schöllhorn, W.I.; Schaper, H.; Kimmeskamp, S.; Milani, T. Inter- and intra-individual differentiation of dynamic foot pressure patterns by means of artificial neural nets. Gait Posture 2002, 16, 172–173. [Google Scholar]
- Beckmann, H.; Schöllhorn, W.I. Differencial learning in shot put. In 1st European Workshop on Movement Science Book of Abstracts; Schöllhorn, W.I., Bohn, C., Jäger, J.M., Schaper, H., Alichmann, M., Eds.; Sport & Buch Strauß: Köln, Germany, 2003; p. 68. [Google Scholar]
- Trockel, M.; Schöllhorn, W.I. Differencial Training in Soccer. In Book of Abstracts, Proceedings of the EWOMS. 1st European Workshop on Movement Science; Sport & Buch Strauß: Cologne, Germany, 2003; p. 64. [Google Scholar]
- Vainauskas, E.; Slapšinskaitė, A. Repetitive or differential exercises are better for elderly women with lower back osteochon-drosis? In Proceedings of the 4th International Scientific-Practical Conference Lithuanian University of Health Sciences, Institute of Sports, Kaunas, Lithuania, 20 December 2018; pp. 42–43. [Google Scholar]
- Hegen, P.; Schöllhorn, W.I. Gleichzeitig in verschiedenen Bereichen besser werden, ohne zu wiederholen? Fußball 2012, 42, 17–23. [Google Scholar]
- Apidogo, J.B.; Burdack, J.; Schöllhorn, W.I. Repetition without repetition or differential learning of multiple techniques in volleyball? Int. J. Environ. Res. Public Health 2021, 18, 10499. [Google Scholar] [CrossRef] [PubMed]
- Hegen, P.; Polywka, G.; Schöllhorn, W.I. The Differiential Learning Approach in Strength Training. In Proceedings of the 20th annual Congress of the European College of Sport Science, Malmö, Sweden, 24–27 June 2015; Radmann, A., Hedenborg, S., Tsolakidis, E., Eds.; European College of Sport Science: Cologne, Germany, 2015; p. 590. [Google Scholar]
- Ammar, A.; Boujelbane, M.A.; Simak, M.L.; Fraile-Fuente, I.; Rizzi, N.; Boukhris, O.; Trabelsi, K.; Chtourou, H.; Washif, J.A.; Driss, T.; et al. Unveiling the acute neurophysiological responses to strength training: An exploratory study on novices performing weightlifting bouts with different motor learning models. Biol. Sport 2024, 41, 249–274. [Google Scholar] [CrossRef]
- Hegen, P. Krafttraining auf der Basis systemdynamischer Prinzipien; Dr. Kovač: Hamburg, Germany, 2018. [Google Scholar]
- Schöllhorn, W.I.; Paschke, M.; Beckmann, H. Differenzielles Training im Volleyball beim Erlernen von zwei Techniken. In Volleyball 2005—Beach-WM; Langolf, K., Roth, R., Eds.; Czwalina: Hamburg, Germany, 2006; pp. 97–105. [Google Scholar]
- Schöllhorn, W.I. Differenzielles Lehren und Lernen von Bewegung—Durch veränderte Annahmen zu neuen Konsequenzen. In Zur Vernetzung von Forschung und Lehre in Biomechanik, Sportmotorik und Trainingswissenschaft. Deutsche Vereinigung für Sportwissenschaf; Gabler, H., Göhner, U., Schiebl, F., Eds.; Czwalina: Hamburg, Germany, 2005; pp. 125–135. [Google Scholar]
- Tutu, H. Frequency adaptation in controlled stochastic resonance utilizing delayed feedback method: Two-pole approximation for response function. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2011, 83, 061106. [Google Scholar] [CrossRef] [PubMed]
- Krauss, P.; Metzner, C.; Schilling, A.; Schütz, C.; Tziridis, K.; Fabry, B.; Schulze, H. Adaptive stochastic resonance for unknown and variable input signals. Sci. Rep. 2017, 7, 2450. [Google Scholar] [CrossRef] [PubMed]
- Schöllhorn, W.I.; Hegen, P.; Eekhoff, A. Differenzielles Lernen und andere motorische Lerntheorien (Differential learning and other motor learning theories). Spectr. der Sportwiss. 2014, 2, 35–55. [Google Scholar]
- Henz, D.; Schöllhorn, W.I. Differential Training Facilitates Early Consolidation in Motor Learning. Front. Behav. Neurosci. 2016, 10, 199. [Google Scholar] [CrossRef]
- Henz, D.; John, A.; Merz, C.; Schöllhorn, W.I. Post-task Effects on EEG Brain Activity Differ for Various Differential Learning and Contextual Interference Protocols. Front. Hum. Neurosci. 2018, 12, 19. [Google Scholar] [CrossRef]
- Wulf, G.; Lewthwaite, R. Optimizing performance through intrinsic motivation and attention for learning: The OPTIMAL theory of motor learning. Psychon. Bull. Rev. 2016, 23, 1382–1414. [Google Scholar] [CrossRef]
- Hacking, I. Review of The Methodology of Scientific Research Programmes. J. Philos. Sci. 1979, 30, 381–402. [Google Scholar] [CrossRef]
- Beck, T.W. The Importance of A Priori Sample Size Estimation in Strength and Conditioning Research. J. Strength Cond. Res. 2013, 27, 2323–2337. [Google Scholar] [CrossRef] [PubMed]
- Faul, F.; Erdfelder, E.; Lang, A.-G.; Buchner, A. G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef] [PubMed]
- Gebkenjans, F.; Beckmann, H.; Schöllhorn, W.I. Does low and high contextual interference lead to different levels of noise. In 3rd European Workshop on Movement Sciences. Book of Abstract; Beek, P., van den Langenberg, R., Eds.; Sportverlag Strauß: Köln, Germany, 2007; pp. 153–154. [Google Scholar]
- Ammar, A.; Chtourou, H.; Souissi, N. Effect of Time-of-Day on Biochemical Markers in Response to Physical Exercise. J. Strength Cond. Res. 2017, 31, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Michalsik, L.B.; Madsen, K.; Aagaard, P. Technical Match Characteristics and Influence of Body Anthropometry on Playing Performance in Male Elite Team Handball. J. Strength Cond. Res. 2015, 29, 416–428. [Google Scholar] [CrossRef] [PubMed]
- Bauer, J.; Schedler, S.; Fischer, S.; Muehlbauer, T. Relationship between Upper Quarter Y Balance Test performance and throwing proficiency in adolescent Olympic handball players. BMC Sport. Sci. Med. Rehabil. 2020, 12, 50. [Google Scholar] [CrossRef]
- American Association for Health, Physical Education, and Recreation (AAHPERD). AAHPER Skills Test Manual; Volleyball: Washington, DC, USA, 1969. [Google Scholar]
- Feghhi, I.; Abode, B.; Valizadeh, R. Compare contextual interference effect and practice specificity in learning basketball free throw. Procedia-Soc. Behav. Sci. 2011, 15, 2176–2180. [Google Scholar] [CrossRef]
- Brace, D.K.; Shay, C.; American Association for Health, Physical Education, and Recreation Sports Skills Project Committee. AAHPER Sports Skills Tests; American Association for Health, Physical Education, and Recreation: Washington, DC, USA, 1965–1969. [Google Scholar]
- Cohen, J. The Concepts of Power Analysis BT—Statistical Power Analysis for the Behavioral Sciences (Revised Edition). In Statistical Power Analysis for the Behavioral Sciences; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2020. [Google Scholar]
- Singmann, H.; Klauer, K.C.; Beller, S. Probabilistic conditional reasoning: Disentangling form and content with the dual-source model. Cogn. Psychol. 2016, 88, 61–87. [Google Scholar] [CrossRef]
- Length, R. Estimated Marginal Means, aka Least-Squares Means. 2023. Available online: https://cran.r-project.org/web/packages/emmeans/emmeans.pdf (accessed on 12 December 2023).
- Kassambara, A. rstatix: Pipe-Friendly Framework for Basic Statistical Tests. 2023. Available online: https://rpkgs.datanovia.com/rstatix/ (accessed on 12 December 2023).
- Noguchi, K.; Gel, Y.R.; Brunner, E.; Konietschke, F. nparLD: An R Software Package for the Nonparametric Analysis of Longitudinal Data in Factorial Experiments. Anal. Longitud. Data Factorial 2012, 12, 1–23. [Google Scholar] [CrossRef]
- Benda, J. Neural adaptation. Curr. Biol. 2021, 31, R110–R116. [Google Scholar] [CrossRef]
- Newell, K.M.; Liu, Y.T.; Mayer-Kress, G. Time scales in motor learning and development. Psychol. Rev. 2001, 108, 57–82. [Google Scholar] [CrossRef]
- Coutinho, D.; Kelly, A.L.; Santos, S.; Figueiredo, P.; Pizarro, D.; Travassos, B. Exploring the Effects of Tasks with Different Decision-Making Levels on Ball Control, Passing Performance, and External Load in Youth Football. Children 2023, 10, 220. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, A. Functional neuroanatomy of altered states of consciousness: The transient hypofrontality hypothesis. Conscious. Cogn. 2003, 12, 231–256. [Google Scholar] [CrossRef] [PubMed]
- Henz, D.; Kenville, R.; Simon, M.; Leinberger, O.; Schöllhorn, W.I. EEG brain activity in differential, contextual interference, and classical repetition-oriented badminton serve training. In Book of Abstract of the 20th Annual Congress of the European College of Sport Science in Malmö; Radmann, A., Hedenborg, S., Tsolakidis, E., Eds.; European College of Sport Science: Cologne, Germany, 2015; p. 53. [Google Scholar]
- Masters, R.S.W.; Poolton, J.S.; Maxwell, J.P. Stable implicit motor processes despite aerobic locomotor fatigue. Conscious. Cogn. 2008, 17, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 1st ed.; McMaster University: Hamilton, ON, Canada, 1994. [Google Scholar]
- Broadbent, D.P.; Ford, P.R.; O’hara, D.A.; Williams, A.M.; Causer, J. The effect of a sequential structure of practice for the training of perceptual-cognitive skills in tennis. PLoS ONE 2017, 12, e0174311. [Google Scholar] [CrossRef] [PubMed]
- Cube, F.V. Kybernetische Grundlagen des Lernens und Lehrens, 1st ed.; Ernst Klett Verlag: Stuttgart, Germany, 1965. [Google Scholar]
- Abernethy, B.; Baker, J.; Côté, J. Transfer of pattern recall skills may contribute to the development of sport expertise. Appl. Cogn. Psychol. 2005, 19, 705–718. [Google Scholar] [CrossRef]
- O’Keeffe, S.L.; Harrison, A.J.; Smyth, P.J. Transfer or specificity? An applied investigation into the relationship between fundamental overarm throwing and related sport skills. Phys. Educ. Sport Pedagog. 2007, 12, 89–102. [Google Scholar] [CrossRef]
- Gutsmuths, J.C.F. Spiele zur Uebung und Erholung des Koerpers und Geistes, für die Jugend, Ihre Erzieher und Alle Freunde Unschuldiger Jugendfreuden; Buchhandlung der Erziehungsanstalt: Schnepfenthal, Germany, 1804. [Google Scholar]
- Beerwald, K.; Brauer, G. Das Turnen im Hause. Leibesübungen zur Förderung und Erhalt der Gesundheit für Jung und Alt; Oldenbourgverlag: München, Germany, 1902. [Google Scholar]
- Eichberg, H. Der Beginn des modernen Leistens. In Terminologische Verschiebungen in der Bewertung von Leibesübungen um 1800, 4th ed.; Sportwissenschaft: Karlsruhe, Germany, 1974; pp. 21–48. [Google Scholar]
- Eekhoff, A.; Aragonés, D.; Horst, F.; Schöllhorn, W.I. Changes of Postural Stability during a Repeated Karate Kick Task identified by Means of Support Vector Machines. In Proceedings of the 21st Annual Congress of the European College of Sport Science, Vienna, Austria, 6–9 July 2016; Baca, A., Wessner, B., Diketmüller, R., Tschan, H., Hofmann, M., Kornfeind, P., Tsolakidis, E., Eds.; European College of Sport Science: Cologne, Germany, 2016; p. 529. [Google Scholar]
- Schöllhorn, W.I.; Jäger, J. A Survey on Various Applications of Artificial Neural Networks in Selected Fields of Healthcare. In Neural Networks in Healthcare; IGI Global: Hershey, PA, USA, 2006; pp. 20–58. [Google Scholar] [CrossRef]
- Humpert, V.; Schöllhorn, W.I. Vergleich von Techniktrainingsansätzen zum Tennisaufschlag (Comparison of technical training approaches to the tennis serve). In Trainingswissenschaft im Freizeitsport; Ferrauti, A., Remmert, H., Eds.; Czwalina: Hamburg, Germany, 2006; pp. 121–124. [Google Scholar]
- Schöllhorn, W.I.; Beckmann, H.; Janssen, D.; Drepper, J. Stochastic perturbations in athletics field events enhance skill acquisition. In Motor Learning in Practice: A Constraints-Led Approach; Renshaw, I., Davids, K., Savelsbergh, G.J.P., Eds.; Routledge: London, UK, 2010; pp. 69–82. [Google Scholar]
- Qiu, X.; Sun, T.; Xu, Y.; Shao, Y.; Dai, N.; Huang, X. Pre-trained models for natural language processing: A survey. Sci. China Technol. Sci. 2020, 63, 1872–1897. [Google Scholar] [CrossRef]
- Han, X.; Zhang, Z.; Ding, N.; Gu, Y.; Liu, X.; Huo, Y.; Qiu, J.; Yao, Y.; Zhang, A.; Zhang, L.; et al. Pre-trained models: Past, present, and future. AI Open 2021, 2, 225–250. [Google Scholar] [CrossRef]
- Gigerenzer, G. Mindless statistics. J. Socio-Econ. 2004, 33, 587–606. [Google Scholar] [CrossRef]
- Fisher, R.A. On the Mathematical Foundations of Theoretical Statistics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1922, 222, 309–368. [Google Scholar] [CrossRef]
- John, A.T.; Barthel, A.; Wind, J.; Rizzi, N.; Schöllhorn, W.I. Acute Effects of Various Movement Noise in Differential Learning of Rope Skipping on Brain and Heart Recovery Analyzed by Means of Multiscale Fuzzy Measure Entropy. Front. Behav. Neurosci. 2022, 16, 816334. [Google Scholar] [CrossRef] [PubMed]
- Horst, F.; Slijepcevic, D.; Simak, M.; Horsak, B.; Schöllhorn, W.I.; Zeppelzauer, M. Modeling biological individuality using machine learning: A study on human gait. Comput. Struct. Biotechnol. J. 2023, 21, 3414–3423. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apidogo, J.B.; Ammar, A.; Salem, A.; Burdack, J.; Schöllhorn, W.I. Resonance Effects in Variable Practice for Handball, Basketball, and Volleyball Skills: A Study on Contextual Interference and Differential Learning. Sports 2024, 12, 5. https://doi.org/10.3390/sports12010005
Apidogo JB, Ammar A, Salem A, Burdack J, Schöllhorn WI. Resonance Effects in Variable Practice for Handball, Basketball, and Volleyball Skills: A Study on Contextual Interference and Differential Learning. Sports. 2024; 12(1):5. https://doi.org/10.3390/sports12010005
Chicago/Turabian StyleApidogo, Julius Baba, Achraf Ammar, Atef Salem, Johannes Burdack, and Wolfgang Immanuel Schöllhorn. 2024. "Resonance Effects in Variable Practice for Handball, Basketball, and Volleyball Skills: A Study on Contextual Interference and Differential Learning" Sports 12, no. 1: 5. https://doi.org/10.3390/sports12010005
APA StyleApidogo, J. B., Ammar, A., Salem, A., Burdack, J., & Schöllhorn, W. I. (2024). Resonance Effects in Variable Practice for Handball, Basketball, and Volleyball Skills: A Study on Contextual Interference and Differential Learning. Sports, 12(1), 5. https://doi.org/10.3390/sports12010005









