Determining Physiological and Energetic Demands during High-Level Pommel Horse Routines Using a Modified Method Based on Heart Rate–Oxygen Uptake Functions
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Approach
2.2. Subjects
2.3. Part 1: Validation of the Modified Method
2.3.1. Procedure and Physiological Measurements of the Modified Method
2.3.2. Calculation of VO2 during PH Routine
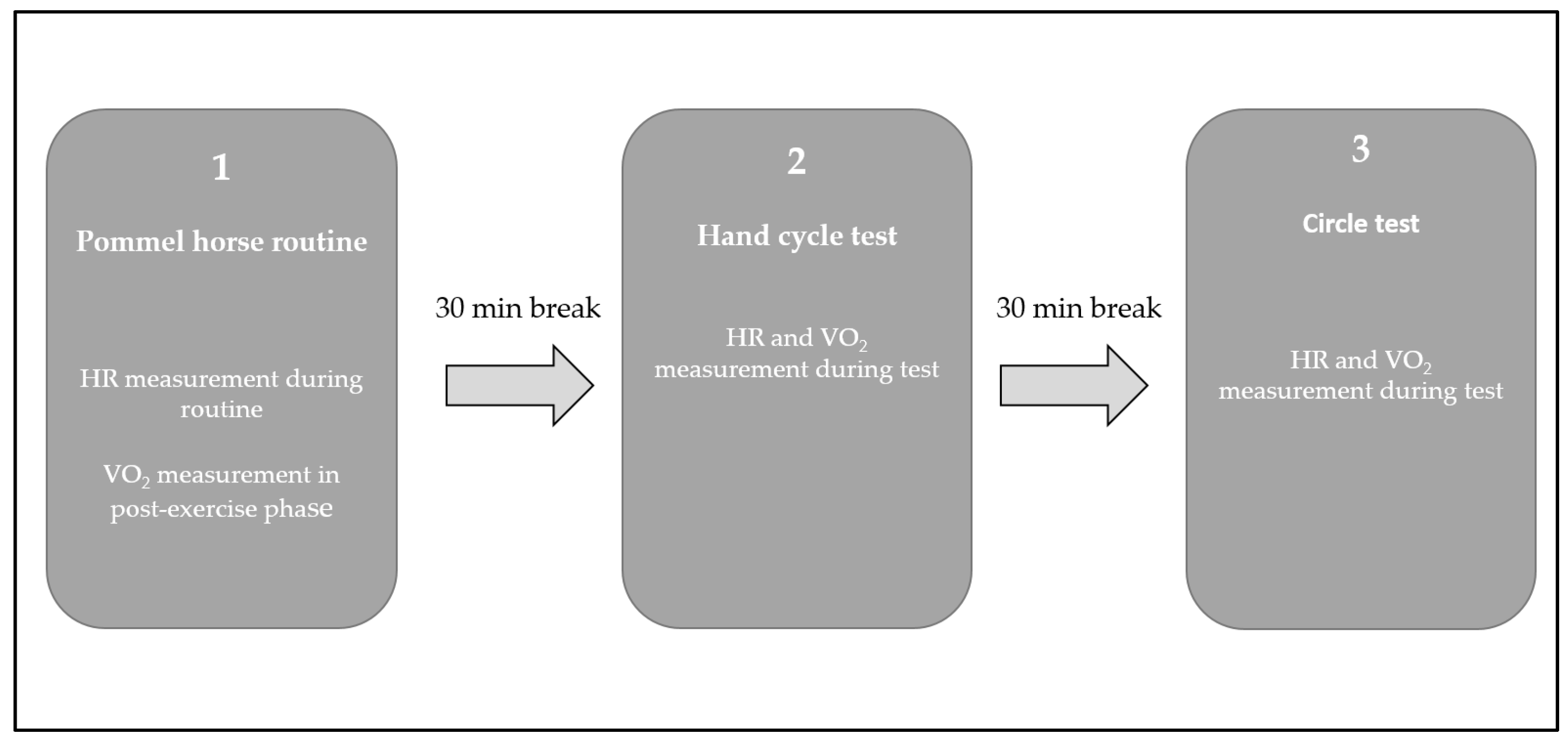
2.4. Part 2: Determination of Physiological and Energetic Demands for High-Level Pommel Horse Routines
2.4.1. Graded Exercise Test
2.4.2. Procedure and Physiological Measurements for Determination of Physiological and Energetic Demands
2.5. Calculation of Energy Contributions
2.6. Statistical Analysis
3. Results
3.1. Part 1: Validity of the Modified Method
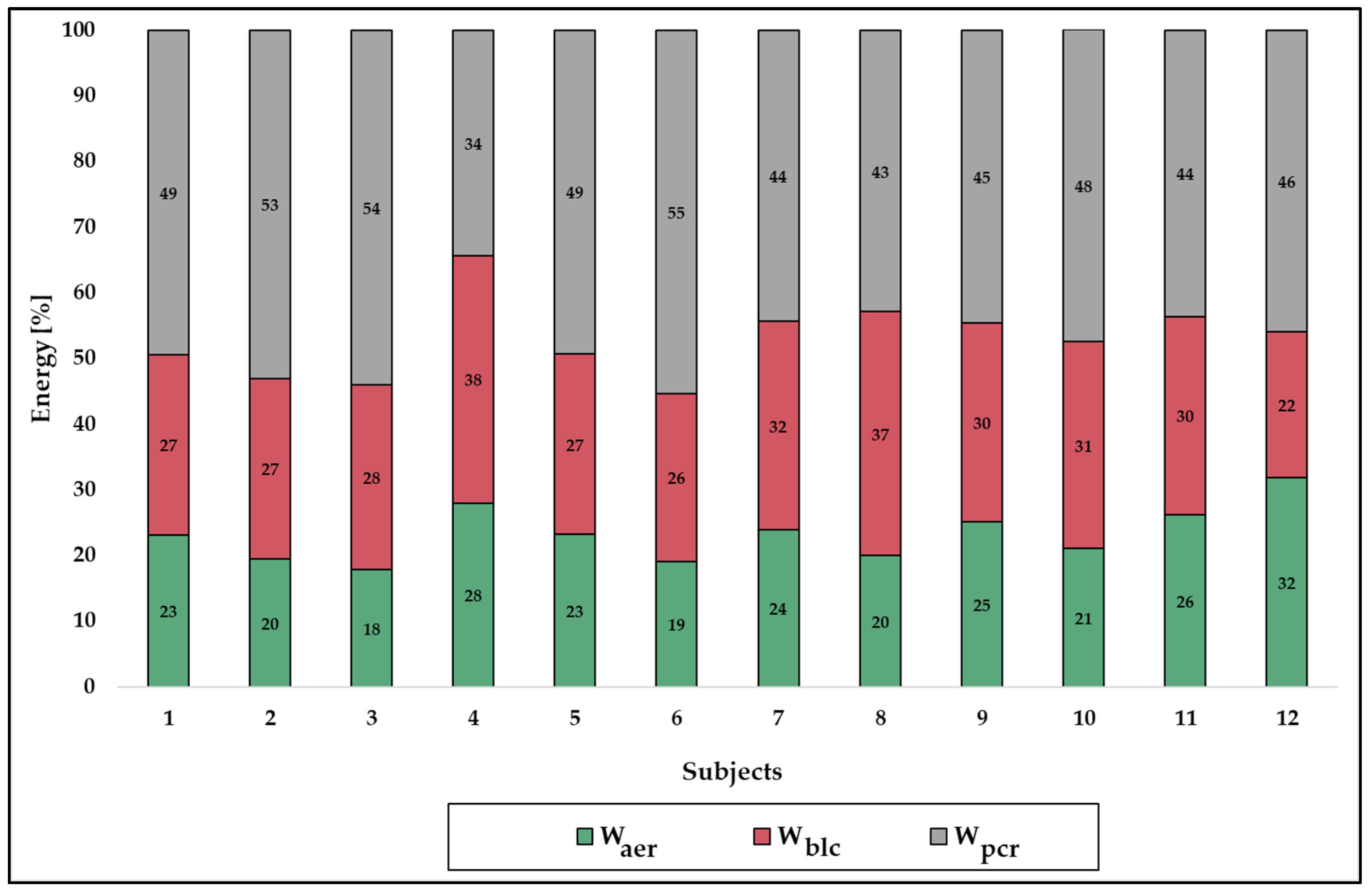
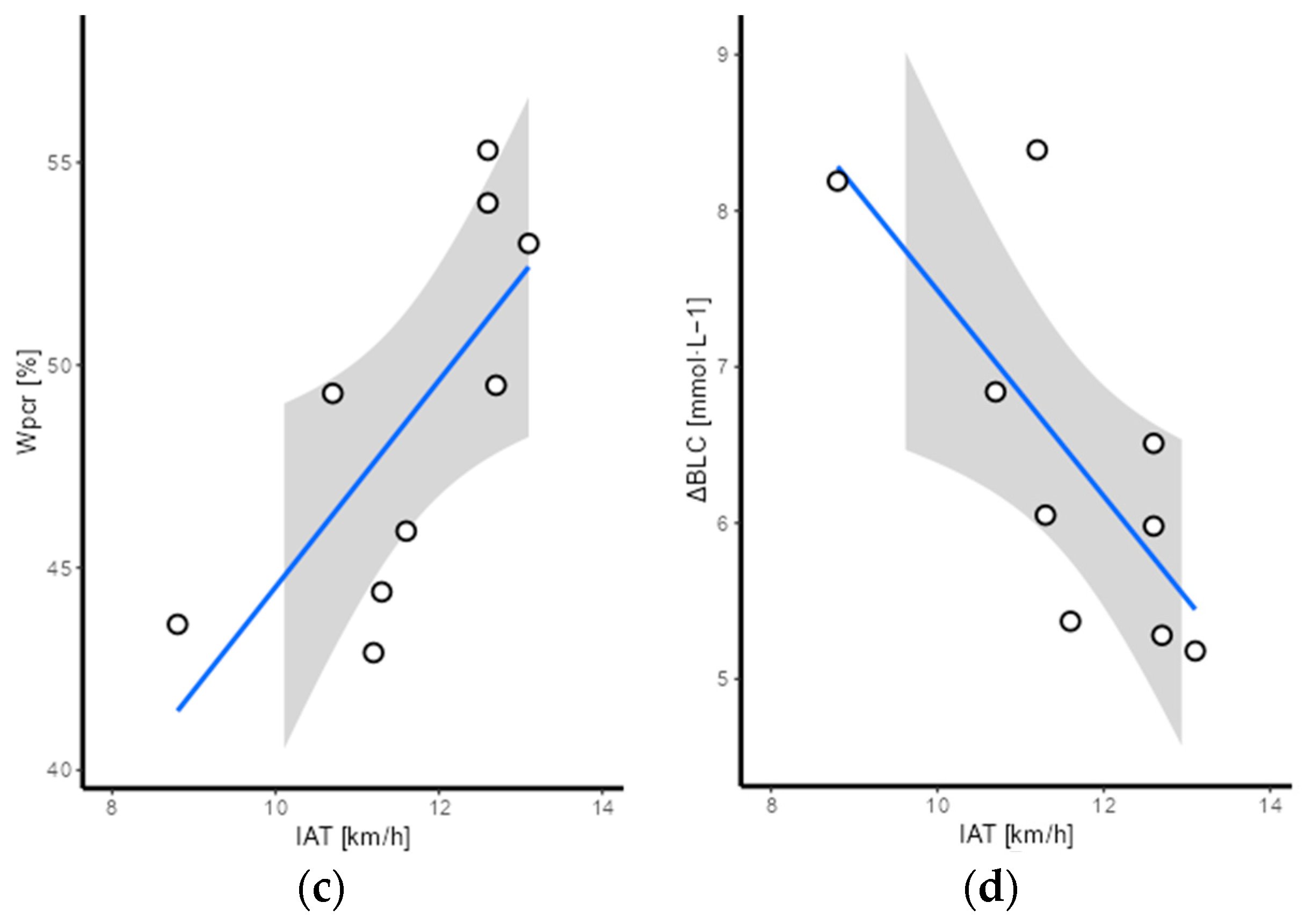
3.2. Part 2: Physiological and Energetic Data of High-Level Pommel Horse Routines
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brueggemann, G.-P.; Hume, P.A. Biomechanics related to injury. In Handbook of Sports Medicine and Science: Gymnastics; Caine, D.J., Russell, K., Lim, L., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 63–74. [Google Scholar]
- Jemni, M. Energetics of gymnastics. In The Science of Gymnastics, 2nd ed.; Jemni, M., Ed.; Routledge: Abingdon, UK, 2018; pp. 5–23. [Google Scholar]
- Seemann-Sinn, A.; Brehmer, S.; Naundorf, F.; Wolfarth, B. Development of the routine duration in artistic gymnastics from 1997 to 2019. Int. J. Perform. Anal. Sport 2021, 21, 250–262. [Google Scholar] [CrossRef]
- Kaufmann, S.; Ziegler, M.; Werner, J.; Noe, C.; Latzel, R.; Witzany, S.; Beneke, R.; Hoos, O. Energetics of floor gymnastics: Aerobic and anaerobic share in male and female sub-elite gymnasts. Sports Med. 2022, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Seemann-Sinn, A.; Rudrich, P.; Gorges, T.; Naundorf, F.; Wolfarth, B. Physiological and energetic demands during still-rings routines of elite artistic gymnasts. Int. J. Sports Physiol. Perform. 2023, 18, 704–710. [Google Scholar] [CrossRef] [PubMed]
- Julio, U.F.; Panissa, V.L.; Esteves, J.V.; Cury, R.L.; Agostinho, M.F.; Franchini, E. Energy-system contributions to simulated judo matches. Int. J. Sports Physiol. Perform. 2017, 12, 676–683. [Google Scholar] [CrossRef] [PubMed]
- Bertuzzi, R.C.d.M.; Franchini, E.; Kokubun, E.; Kiss, M.A.P.D.M. Energy system contributions in indoor rock climbing. Eur. J. Appl. Physiol. 2007, 101, 293–300. [Google Scholar] [CrossRef]
- Guidetti, L.; Baldari, C.; Capranica, L.; Persichini, C.; Figura, F. Energy cost and energy sources of ball routine in rhythmic gymnasts. Int. J. Sports Med. 2000, 21, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Solcanu, M.; Bidiugan, S.; Corlaci, I. Specific demands of the effort on the pommel horse in artistic gymnastics. In Eur. Proc. Soc. Behav. Sci.; 2019; Volume 55, pp. 215–224. [Google Scholar]
- Fédération Internationale de Gymnastique. 2022–2024 Code of Points Men’s Artistic Gymnastics; Fédération Internationale de Gymnastique: Lausanne, Switzerland, 2020. [Google Scholar]
- Seemann-Sinn, A.; Rüdrich, P.; Naundorf, F.; Wolfarth, B. Modifiziertes Verfahren zur Bestimmung der Energiebereitstellung bei Pauschenpferdübungen. Dtsch. Z. Sport. 2021, 72, 90. [Google Scholar]
- Gastin, P.B. Energy system interaction and relative contribution during maximal exercise. Sports Med. 2001, 31, 725–741. [Google Scholar] [CrossRef]
- Mkaouer, B.; Jemni, M.; Chaabene, H.; Amara, S.; Njah, A.; Chtara, M. Effect of two different types of olympic rotation order on cardiovascular and metabolic variables in men’s artistic gymnastics. J. Hum. Kinet. 2018, 61, 179–187. [Google Scholar] [CrossRef]
- Armstrong, N.; Sharp, C. Gymnastics physiology. In Handbook of Sports Medicine and Science: Gymnastics; Caine, D.J., Russell, K., Lim, L., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 85–97. [Google Scholar]
- Baiget, E.; Iglesias, X.; Rodriguez, F.A. Validity of heart rate-based models for estimating oxygen uptake during tennis play. J. Strength Cond. Res. 2020, 34, 3208–3216. [Google Scholar] [CrossRef]
- Scribbans, T.D.; Berg, K.; Narazaki, K.; Janssen, I.; Gurd, B.J. Heart rate during basketball game play and volleyball drills accurately predicts oxygen uptake and energy expenditure. J. Sports Med. Phys. Fit. 2015, 55, 905–913. [Google Scholar]
- Wong, D.P.; Carling, C.; Chaouachi, A.; Dellal, A.; Castagna, C.; Chamari, K.; Behm, D.G. Estimation of oxygen uptake from heart rate and ratings of perceived exertion in young soccer players. J. Strength. Cond. Res. 2011, 25, 1983–1988. [Google Scholar] [CrossRef] [PubMed]
- Maas, S.; Kok, M.L.; Westra, H.G.; Kemper, H.C. The validity of the use of heart rate in estimating oxygen consumption in static and in combined static/dynamic exercise. Ergonomics 1989, 32, 141–148. [Google Scholar] [CrossRef]
- Novas, A.M.; Rowbottom, D.G.; Jenkins, D.G. A practical method of estimating energy expenditure during tennis play. J. Sci. Med. Sport 2003, 6, 40–50. [Google Scholar] [CrossRef] [PubMed]
- Castagna, C.; Belardinelli, R.; Impellizzeri, F.M.; Abt, G.A.; Coutts, A.J.; D’Ottavio, S. Cardiovascular responses during recreational 5-a-side indoor-soccer. J. Sci. Med. Sport. 2007, 10, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Beneke, R.; Pollmann, C.; Bleif, I.; Leithäuser, R.; Hütler, M. How anaerobic is the wingate anaerobic test for humans? Eur. J. Appl. Physiol. 2002, 87, 388–392. [Google Scholar] [PubMed]
- Guidetti, L.; Meucci, M.; Bolletta, F.; Emerenziani, G.P.; Gallotta, M.C.; Baldari, C. Validity, reliability and minimum detectable change of COSMED K5 portable gas exchange system in breath-by-breath mode. PLoS ONE 2018, 13, e0209925. [Google Scholar] [CrossRef]
- Borg, G.A. Psychophysical bases of perceived exertion. Med. Sci. Sports Exerc. 1982, 14, 377–381. [Google Scholar] [CrossRef]
- Dickhuth, H.-H.; Huonker, M.; Münzel, T.; Drexler, H.; Berg, A.; Keul, J. Individual anaerobic threshold for evaluation of competitive athletes and patients with left ventricular dysfunction. In Advances in Ergometry; Bachl, N., Graham, T.E., Löllgen, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 173–179. [Google Scholar]
- Cerretelli, P.; di Prampero, P.E. Gas exchange in exercise. In Handbook of Physiology, Section 3; Fahri, L.E., Tenney, S.M., Eds.; American Physiological Society: Rockville, MD, USA, 1987; Volume 4, pp. 297–339. [Google Scholar]
- Harris, J.A.; Benedict, F.G. A Biometric study of human basal metabolism. Proc. Natl. Acad. Sci. USA 1918, 4, 370–373. [Google Scholar] [CrossRef]
- McBride, G. A Proposal for Strength-of-Agreement Criteria for Lin’s Concordance Correlation Coefficient; NIWA: Auckland, New Zealand, 2005; pp. 307–310. [Google Scholar]
- Hoeger, W.; Fisher, G. Energy costs for men’s gymnastic routines. IG Tech. Suppl. 1981, 5, 1–3. [Google Scholar]
- Jemni, M.; Sands, W.; Friemel, F.; Cooke, C.; Stone, M. Effect of gymnastics training on aerobic and anaerobic components in elite and sub elite men gymnasts. J. Strength. Cond. Res. 2006, 20, 899–907. [Google Scholar] [PubMed]
- Zinner, C.; Morales-Alamo, D.; Ørtenblad, N.; Larsen, F.J.; Schiffer, T.A.; Willis, S.J.; Gelabert-Rebato, M.; Perez-Valera, M.; Boushel, R.; Calbet, J.A.; et al. The physiological mechanisms of performance enhancement with sprint interval training differ between the upper and lower extremities in humans. Front. Physiol. 2016, 7, 426. [Google Scholar] [CrossRef] [PubMed]
- Koppo, K.; Bouckaert, J.; Jones, A.M. Oxygen uptake kinetics during high-intensity arm and leg exercise. Respir. Physiol. Neurobiol. 2002, 133, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Guidetti, L.; Emerenziani, G.P.; Gallotta, M.C.; Da Silva, S.G.; Baldari, C. Energy cost and energy sources of a ballet dance exercise in female adolescents with different technical ability. Eur. J. Appl. Physiol. 2008, 103, 315–321. [Google Scholar] [CrossRef]
- Sahlin, K. Muscle energetics during explosive activities and potential effects of nutrition and training. Sports Med. 2014, 44, 167–173. [Google Scholar] [CrossRef]



| Part of the Study | Subjects | Age (Years) | Height (cm) | Body Mass (kg) | Years of Experience | Weekly Training Hours | VO2peak (mL·kg−1·min−1) | IAS (km/h) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 20 | 174 | 68 | 14 | 10–15 | - | - |
| 2 | 27 | 177 | 72 | 23 | 20–25 | - | - | |
| 3 | 27 | 174 | 68 | 23 | 20–25 | - | - | |
| 4 | 35 | 160 | 62 | 31 | 15–20 | - | - | |
| 5 | 28 | 174 | 68 | 23 | 5–10 | - | - | |
| 6 | 32 | 174 | 67 | 28 | 15–20 | - | - | |
| 7 | 25 | 177 | 67 | 20 | 15–20 | - | - | |
| 8 | 20 | 178 | 74 | 14 | 10–15 | - | - | |
| 9 | 24 | 176 | 68 | 18 | 10–15 | - | - | |
| 2 | 1 | 27 | 167 | 63.0 | 23 | ≥28 | 58.7 | 12.7 |
| 2 | 18 | 179 | 62.0 | 14 | ≥28 | 59.0 | 13.1 | |
| 3 | 19 | 176 | 61.0 | 15 | ≥28 | 53.0 | 12.6 | |
| 4 | 20 | 178 | 66.0 | 15 | ≥28 | - | - | |
| 5 | 23 | 175 | 68.0 | 19 | ≥28 | 48.7 | 10.7 | |
| 6 | 22 | 160 | 61.0 | 17 | ≥28 | 55.6 | 12.6 | |
| 7 | 23 | 173 | 72.5 | 19 | ≥28 | 49.2 | 11.3 | |
| 8 | 19 | 181 | 70.0 | 15 | ≥28 | 52.6 | 11.2 | |
| 9 * | 32 | 174 | 67.0 | 28 | 15–20 | - | - | |
| 10 * | 25 | 177 | 67.0 | 20 | 15–20 | - | - | |
| 11 * | 27 | 177 | 72.0 | 23 | 20–25 | - | 8.8 | |
| 12 * | 27 | 174 | 68.0 | 23 | 20–25 | 49.0 | 12.1 |
| Parameters | Morg | Mmod |
|---|---|---|
| Waer (kJ) | 20.37 ± 9.58 | 21.77 ± 10.55 |
| Wpcr (kJ) | 36.06 ± 8.98 | 36.06 ± 9.07 |
| Wtotal (kJ) | 79.08 ± 22.65 | 80.48 ± 24.00 |
| Parameters | Intercept | Slope | SDD | lLOA | uLOA | CCC |
|---|---|---|---|---|---|---|
| (95% CI) | (95% CI) | (95% CI) | 95% CI | (95% CI) | ||
| Waer | 0.669 | 0.905 | 2.661 | −6.611 | 3.819 | 0.955 |
| (−5.736; 7.070) | (0.579; 1.230) | (−10.247; −2.974) | (0.183; 7.456) | (0.833; 0.988) | ||
| Wpcr | 0.339 | 0.991 | 0.412 | −0.811 | 0.806 | 0.999 |
| (−1.369; 2.050) | (0.941; 1.040) | (−1.374; 0.247) | (0.242; 1.369) | (0.996; 1.000) | ||
| Wtotal | 3.162 | 0.943 | 2.882 | −7.047 | 4.251 | 0.990 |
| (−6.795; 13.12) | (0.818; 1.070) | (−10.986; −3.108) | (0.312; 8.189) | (0.964; 0.997) |
| Parameter | Mean ± SD | 95% CI |
|---|---|---|
| routine duration (s) | 39.50 ± 4.03 | 36.9–42.1 |
| D-score (Ppoints) | 4.72 ± 0.48 | 4.4–5.0 |
| HRmean (bpm) | 149 ± 10.1 | 142–155 |
| HRpeak (bpm) | 172 ± 8.37 | 166–177 |
| VO2mean (mL·min−1·kg−1) | 30.70 ± 5.39 | 27.3–34.1 |
| VO2peak (mL·min−1·kg−1) | 45.4 ± 5.03 | 42.2–48.6 |
| BLCpre (mmol·L−1) | 1.45 ± 0.82 | 0.93–1.97 |
| BLCpost (mmol·L−1) | 7.92 ± 1.25 | 7.12–8.71 |
| ΔBLC, (mmol·L−1) | 6.47 ± 1.11 | 5.77–7.17 |
| Rating of perceived exertion | 15.5 ± 1.27 | 14.6–16.4 |
| Absolute Energy [kJ] | Relative Energy [%] | Metabolic Power [W·kg−1] | ||||
|---|---|---|---|---|---|---|
| Mean ± SD | 95% CI | Mean ± SD | 95% CI | Mean ± SD | 95% CI | |
| Waer | 21.40 ± 6.07 | 17.60–25.30 | 23.30 ± 4.08 | 20.70–25.80 | 8.05 ± 1.50 | 7.10–9.00 |
| Wblc | 27.10 ± 5.68 | 23.50–30.70 | 29.70 ± 4.45 | 26.90–32.60 | 10.30 ± 1.22 | 9.48–11.00 |
| Wpcr | 42.80 ± 7.65 | 37.90–47.60 | 47.00 ± 5.79 | 43.30–50.7 | 16.50 ± 3.31 | 14.40–18.60 |
| Wtotal | 91.30 ± 14.50 | 82.10–101.00 | 100 | - | 34.80 ± 3.49 | 32.6–37.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seemann-Sinn, A.; Rüdrich, P.; Gorges, T.; Sandau, I.; Naundorf, F.; Wolfarth, B. Determining Physiological and Energetic Demands during High-Level Pommel Horse Routines Using a Modified Method Based on Heart Rate–Oxygen Uptake Functions. Sports 2024, 12, 27. https://doi.org/10.3390/sports12010027
Seemann-Sinn A, Rüdrich P, Gorges T, Sandau I, Naundorf F, Wolfarth B. Determining Physiological and Energetic Demands during High-Level Pommel Horse Routines Using a Modified Method Based on Heart Rate–Oxygen Uptake Functions. Sports. 2024; 12(1):27. https://doi.org/10.3390/sports12010027
Chicago/Turabian StyleSeemann-Sinn, Alexander, Peter Rüdrich, Tom Gorges, Ingo Sandau, Falk Naundorf, and Bernd Wolfarth. 2024. "Determining Physiological and Energetic Demands during High-Level Pommel Horse Routines Using a Modified Method Based on Heart Rate–Oxygen Uptake Functions" Sports 12, no. 1: 27. https://doi.org/10.3390/sports12010027
APA StyleSeemann-Sinn, A., Rüdrich, P., Gorges, T., Sandau, I., Naundorf, F., & Wolfarth, B. (2024). Determining Physiological and Energetic Demands during High-Level Pommel Horse Routines Using a Modified Method Based on Heart Rate–Oxygen Uptake Functions. Sports, 12(1), 27. https://doi.org/10.3390/sports12010027






