Predictive Study on the Occurrence of Wheat Blossom Midges Based on Gene Expression Programming with Support Vector Machines
Abstract
Simple Summary
Abstract
1. Introduction
2. Construction of GEP-SVM-Based Model for Plant Pest Prediction
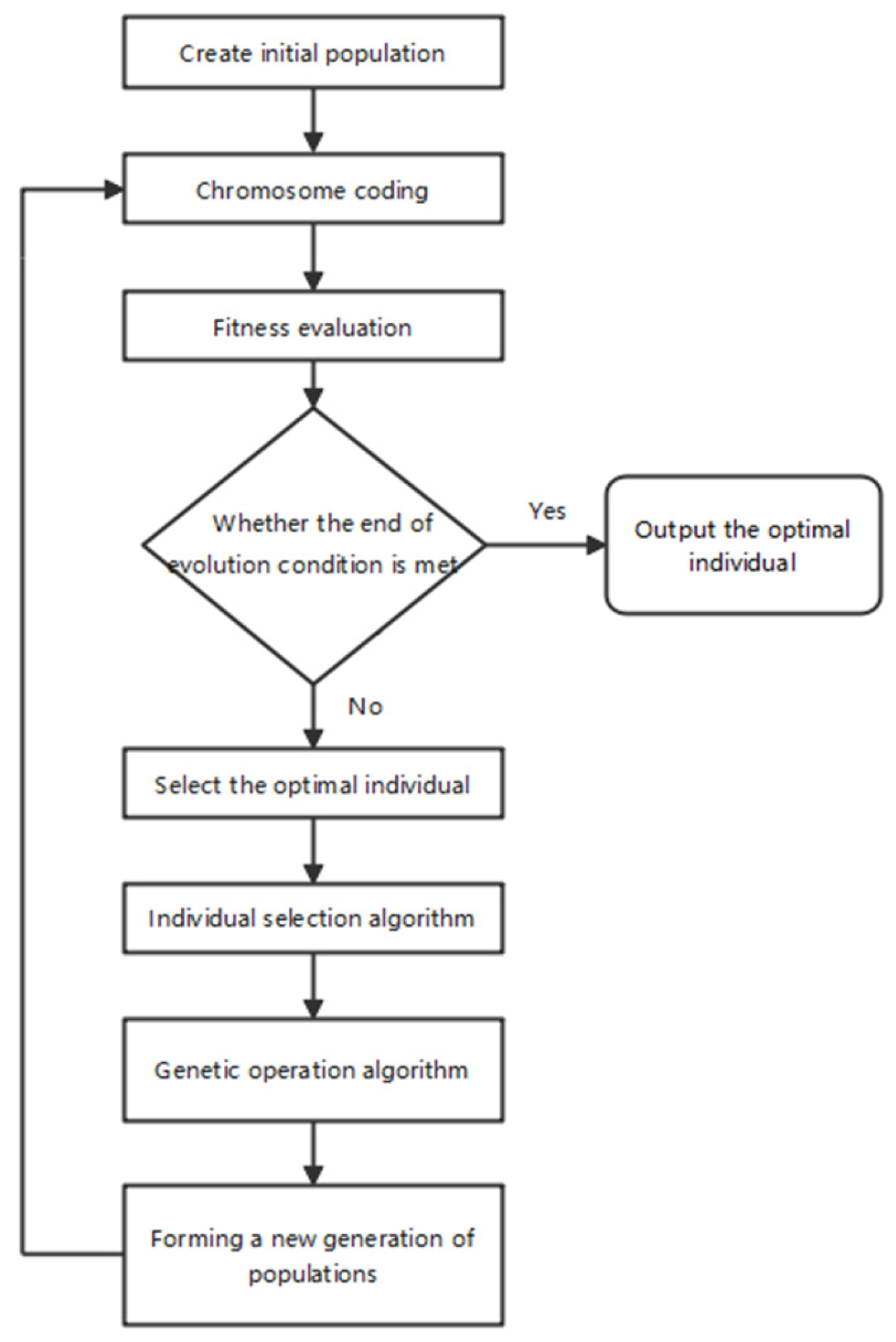
2.1. Theory of GEP Algorithm
2.1.1. GEP Algorithm
2.1.2. Fitness Functions
2.1.3. Genetic Operators
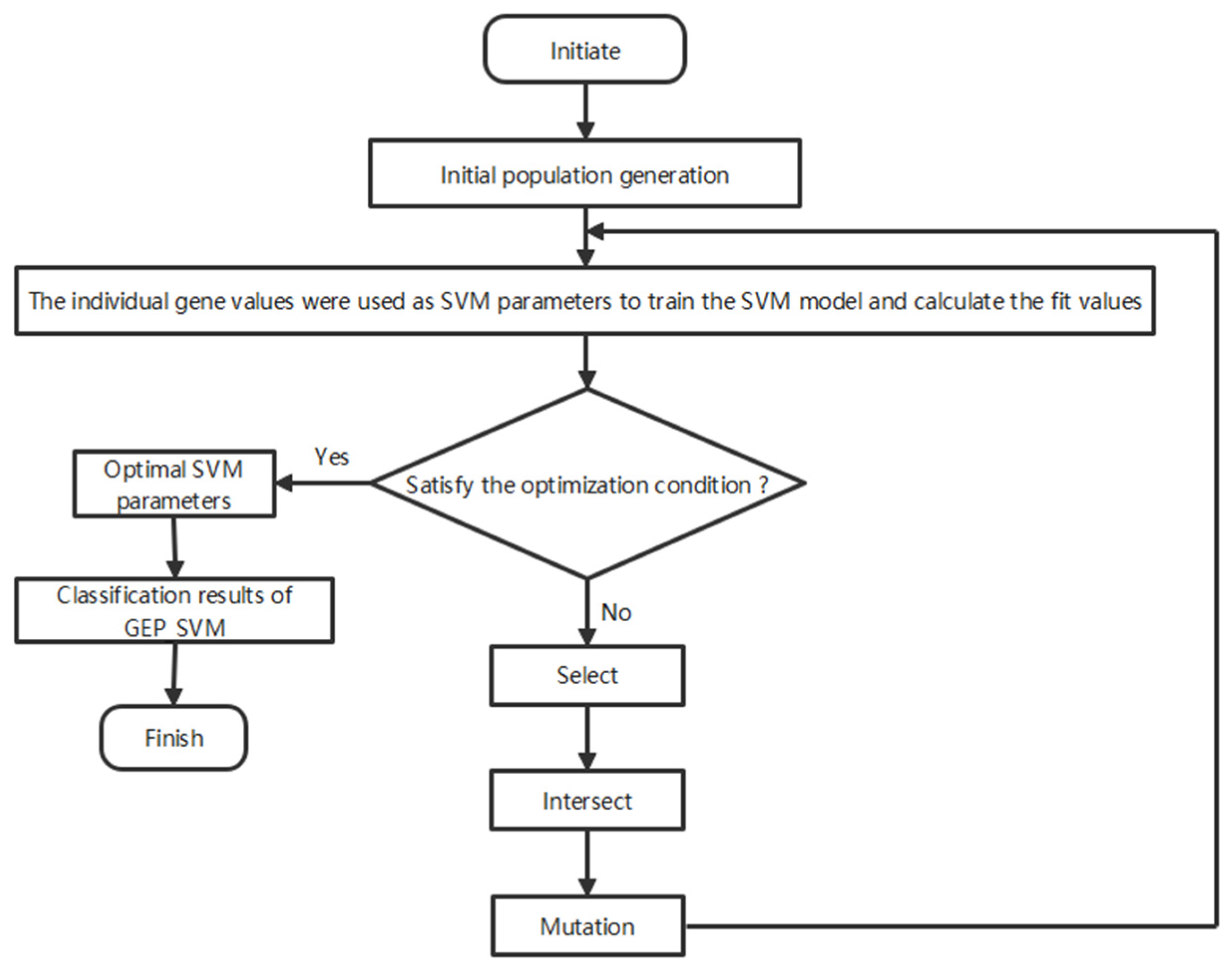
2.2. GEP-SVM Algorithm
2.2.1. Gene Expression Programming–Support Vector Machine Algorithm
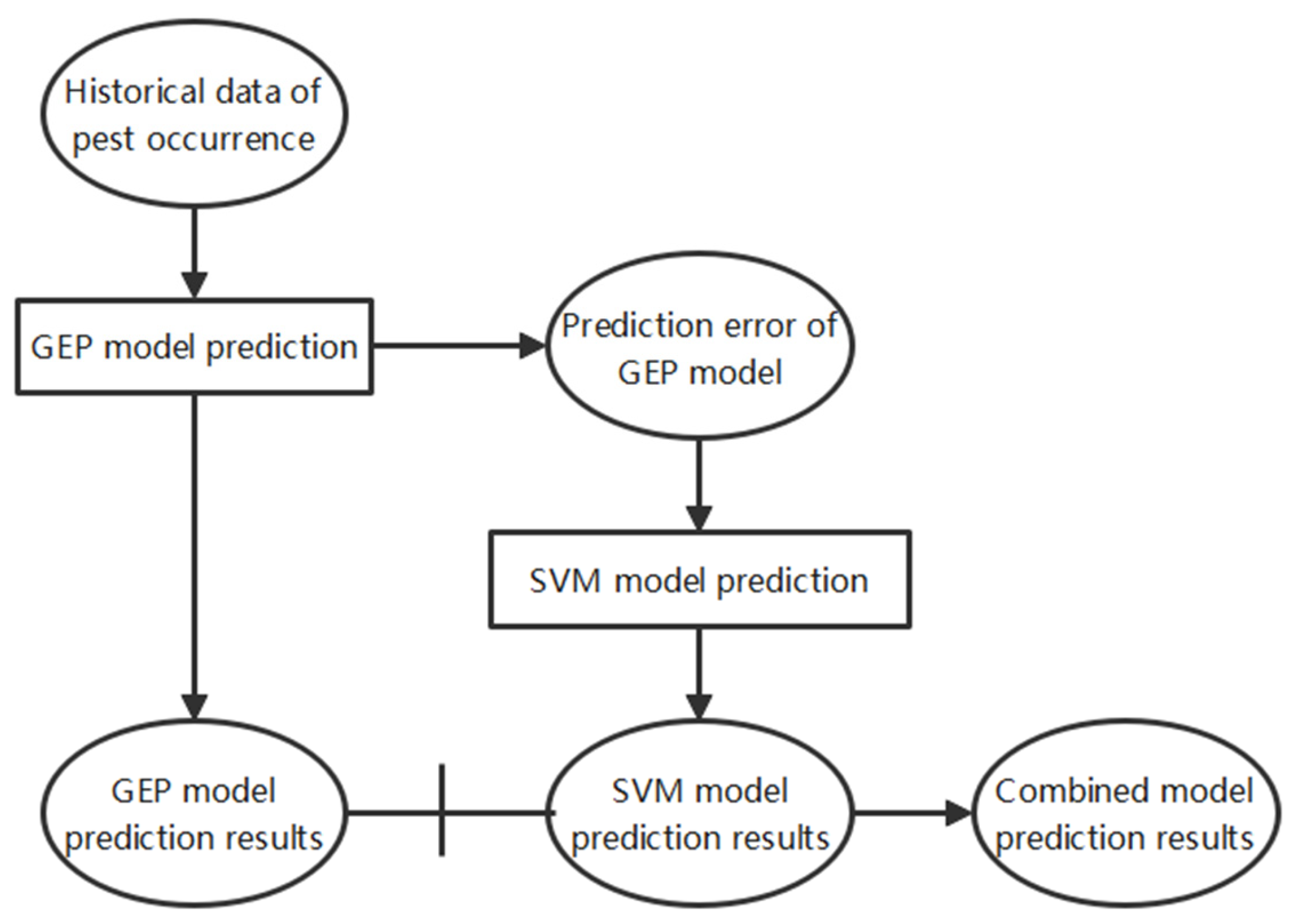
2.2.2. Integration and Data Processing in GEP-SVM
2.2.3. Model Evaluation Metrics
3. Experimental Results and Analyses
3.1. Data Preparation and Data Description
3.2. Experimental Environment
3.3. Data Pre-Processing
3.4. Parameter Setting
3.5. Experimental Analysis
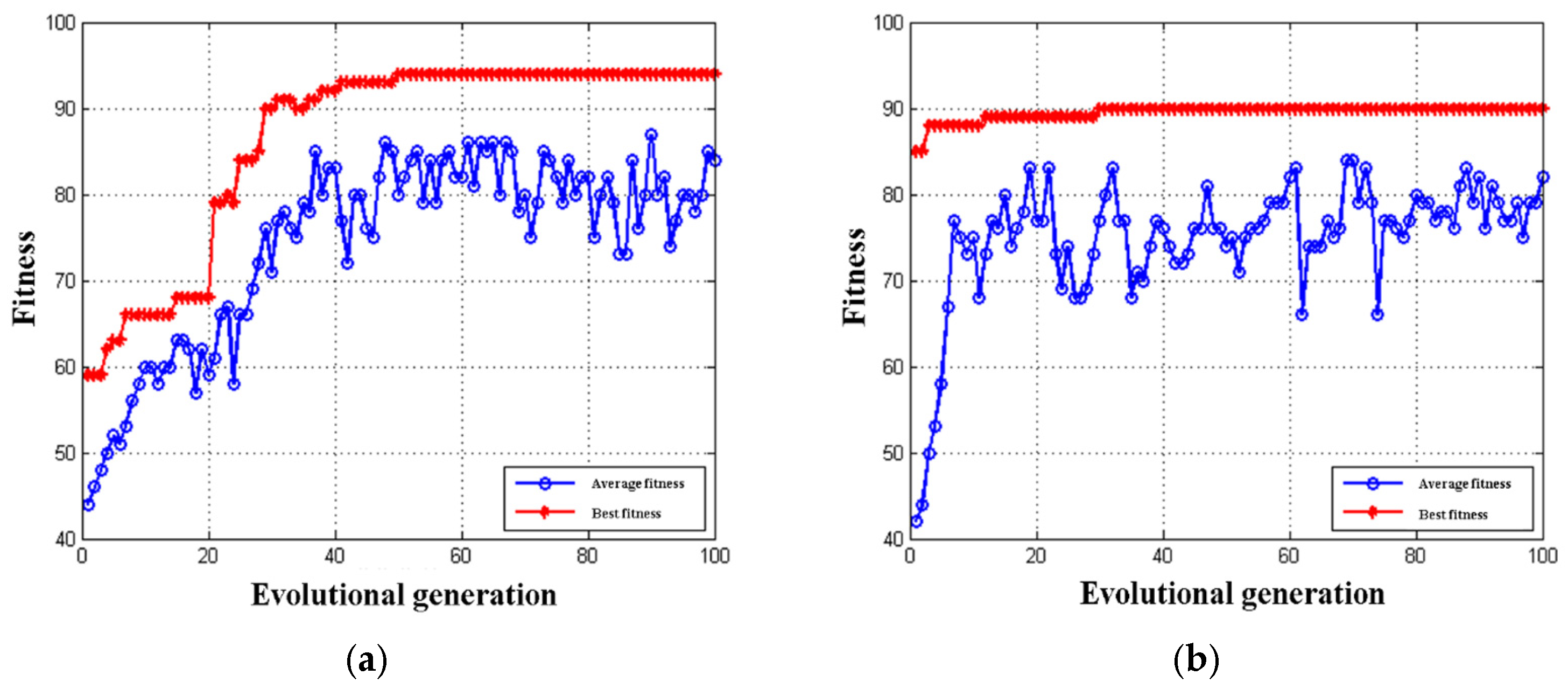
3.5.1. Optimization of GEP-SVM Parameters
3.5.2. Model Performance Analysis
4. Performance Analysis of GEP-SVM Algorithm on Other Datasets
4.1. Experimental Environment
4.2. Datasets
4.3. Algorithm Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, F.; Qiao, R.; Yang, X.; Gong, P.; Zhou, X. Occurrence, distribution, and management of tomato yellow leaf curl virus in China. Phytopathol. Res. 2022, 4, 28. [Google Scholar] [CrossRef]
- Patra, J.; Chakraborty, M.; Gupta, S. Random Forest Algorithm for Plant Disease Prediction. In AI to Improve e-Governance and Eminence of Life. Studies in Big Data; Mukhopadhyay, S., Sarkar, S., Mandal, J.K., Roy, S., Eds.; Springer: Singapore, 2023; Volume 130. [Google Scholar] [CrossRef]
- Ramesh, S.; Hebbar, R.; Niveditha, M.; Pooja, R.; Shashank, N.; Vinod, P.V. Plant disease detection using machine learning. In Proceedings of the 2018 International Conference on Design Innovations for 3Cs Compute Communicate Control (ICDI3C), Bangalore, India, 25–28 April 2018; pp. 41–45. [Google Scholar]
- Kranth GP, R.; Lalitha, M.H.; Basava, L.; Mathur, A. Plant disease prediction using machine learning algorithms. Int. J. Comput. Appl. 2018, 18, 0975–8887. [Google Scholar]
- Ahmed, I.; Yadav, P.K. Plant disease detection using machine learning approaches. Expert Syst. 2023, 40, e13136. [Google Scholar] [CrossRef]
- Rumpf, T.; Mahlein, A.K.; Steiner, U.; Oerke, E.C.; Dehne, H.W.; Plümer, L. Early detection and classification of plant diseases with Support Vector Machines based on hyperspectral reflectance. Comput. Electron. Agric. 2010, 74, 91–99. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Zhang, H.M. Research on crop disaster prediction based on deep learning algorithms. Mod. Electron. Tech. 2021, 4, 107–110. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2021&filename=XDDJ202104024&uniplatform=OVERSEA&v=rq2Iv1DUQDdWJAFhSNf5-it2RG0zZFa9LnfcZLa0NNR4I9PNckDw8ilqSThjkqVm (accessed on 26 May 2024). [CrossRef]
- Hang, L.; Che, J.; Song, P.Y.; Wang, C.Y.; Tian, B. Pest prediction based on machine learning and image processing techniques. J. Southwest Univ. (Nat. Sci. Ed.) 2020, 1, 134–141. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2020&filename=XNND202001020&uniplatform=OVERSEA&v=rPFjTndswnVyEl8zUt_0V8f9Zc-dcaT2FsdL3Xku5bv9ID4ITRurvoDr1fHZ4kOZ (accessed on 26 May 2024). [CrossRef]
- Ubalanka, V.; Jose, A.; Viswanath, D. Machine Learning Strategies for Predicting Crop Diseases. J. Phys. Conf. Ser. 2021, 1850, 012119. [Google Scholar] [CrossRef]
- Goel, L.; Nagpal, J. A systematic review of recent machine learning techniques for plant disease identification and classification. IETE Tech. Rev. 2023, 40, 423–439. [Google Scholar] [CrossRef]
- Fang, T.; Chen, P.; Zhang, J.; Wang, B. Identification of Apple Leaf Diseases Based on Convolutional Neural Network. In Intelligent Computing Theories and Application; Huang, D.S., Bevilacqua, V., Premaratne, P., Eds.; ICIC 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11643. [Google Scholar] [CrossRef]
- Shafik, W.; Tufail, A.; Liyanage, C.D.S.; Apong, R.A.A.H.M. Using a novel convolutional neural network for plant pests detection and disease classification. J. Sci. Food Agric. 2023, 103, 5849–5861. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.L. Application research of an improved RBF neural network in pest prediction. Sci. Technol. Eng. 2013, 1, 136–139+156. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2013&filename=KXJS201301030&uniplatform=OVERSEA&v=kMnLlpqYpOkKC18Wn7xijJbfdfcTGaUvdctSA8J9MZkLrqt8lpMoA5PnOSiVWuYK (accessed on 26 May 2024).
- Wu, C.C. Pest Prediction Application Research Based on Rough Sets and Artificial Neural Networks. Master’s Thesis, Jilin University, Changchun, China, 2011. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD2011&filename=1011099267.nh&uniplatform=OVERSEA&v=SiPXTz9ik7_nmi--wF7HmnRZeM7-YopaU5pXOlJALHSKLjV7lu8yGctCYOfeML6m (accessed on 26 May 2024).
- Yu, X.D.; Yang, M.J.; Zhang, H.Q.; Li, D.; Tang, Y.Q.; Yu, X. Research and application of crop pest detection methods based on transfer learning. Trans. Chin. Soc. Agric. Mach. 2020, 10, 252–258. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2020&filename=NYJX202010028&uniplatform=OVERSEA&v=JZVKi2VZLz_VTPXjSjDXxfyhydE_njuX43gRXD14ylc_HcohTUQtkvmfooAMAcBL (accessed on 26 May 2024).
- Chen, Z. Research on Crop Disease Classification Algorithms Based on Deep Learning. Master’s Thesis, Qilu University of Technology, Jinan, Shandong, 2022. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD202301&filename=1022602569.nh&uniplatform=OVERSEA&v=f9T1xWAXGx7XtGTa-DgrBMJQBGc1wF7-7G0KW90RZdhXPFrI2_JdMEuwakhdIsSi (accessed on 26 May 2024).
- Chen, J. Research on Pest Detection Methods Based on Convolutional Neural Networks and Metric Learning. Ph.D. Dissertation, Zhejiang University, Hangzhou, China, 2021. (In Chinese). Available online: https://chn.oversea.cnki.net/KCMS/detail/detail.aspx?dbcode=CDFD&dbname=CDFDLAST2022&filename=1021699825.nh&uniplatform=OVERSEA&v=t94Zaaj4XJXYSNVUTt_npwBizEcTW8TvjP9UpZJVB1x6KilztwXwGt32n6rmOdSe (accessed on 26 May 2024).
- Avsec, Ž.; Agarwal, V.; Visentin, D.; Ledsam, J.R.; Grabska-Barwinska, A.; Taylor, K.R.; Assael, Y.; Jumper, J.; Kohli, P.; Kelley, D.R. Effective gene expression prediction from sequence by integrating long-range interactions. Nat. Methods 2021, 18, 1196–1203. [Google Scholar] [CrossRef] [PubMed]
- Applalanaidu, M.V.; Kumaravelan, G. A Review of Machine Learning Approaches in Plant Leaf Disease Detection and Classification. In Proceedings of the 2021 Third International Conference on Intelligent Communication Technologies and Virtual Mobile Networks (ICICV), Tirunelveli, India, 4–6 February 2021; pp. 716–724. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming in Problem Solving. In Soft Computing and Industry; Roy, R., Köppen, M., Ovaska, S., Furuhashi, T., Hoffmann, F., Eds.; Springer: London, UK, 2002. [Google Scholar] [CrossRef]
- Nawaz, M.N.; Qamar, S.U.; Alshameri, B.; Nawaz, M.M.; Hassan, W.; Awan, T.A. A robust prediction model for evaluation of plastic limit based on sieve # 200 passing material using gene expression programming. PLoS ONE 2022, 17, e0275524. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wu, X.; Cheng, W. The Relationship between Population Changes of Wheat Red Midge and Meteorological Factors. J. Wheat Crops. 1994. (In Chinese). Available online: https://www.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFD&dbname=CJFD9495&filename=MLZW402.017&uniplatform=OVERSEA&v=fZYpz51-tAMaR64PtZNjRYloSO8XDSqet0CX97BFDf1CK0ubO3gTcju0oAH8sbA1 (accessed on 24 May 2024).
- Valle, D.; Ben Toh, K.; Laporta, G.Z.; Zhao, Q. Ordinal regression models for zero-inflated and/or over-dispersed count data. Sci. Rep. 2019, 9, 3046. [Google Scholar] [CrossRef] [PubMed]
- Ananth, C.V.; Kleinbaum, D.G. Regression models for ordinal responses: A review of methods and applications. Int. J. Epidemiol. 1997, 26, 1323–1333. [Google Scholar] [CrossRef]
- Osei, P.P.; Reiss, P.T. Ordinal state-trait regression for intensive longitudinal data. Br. J. Math. Stat. Psychol. 2023, 76, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Jacobucci, R.; Ammerman, B.A.; Li, X. Using ordinal regression for advancing the understanding of distinct suicide outcomes. Suicide Life Threat. Behav. 2021, 51, 65–75. [Google Scholar] [CrossRef] [PubMed]
- Chen, B. Research and Application of Combined Forecasting Model. Ph.D. Dissertation, Shandong University, Jinan, China, 2017. [Google Scholar]
- Fan, T. Short-Term Traffic Flow Forecasting Research for Urban Roads. Ph.D. Dissertation, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Marković, D.; Vujičić, D.; Tanasković, S.; Đorđević, B.; Ranđić, S.; Stamenković, Z. Prediction of Pest Insect Appearance Using Sensors and Machine Learning. Sensors 2021, 21, 4846. [Google Scholar] [CrossRef] [PubMed]
- Saleem, R.M.; Kazmi, R.; Bajwa, I.S.; Ashraf, A.; Ramzan, S.; Anwar, W. IOT-Based Cotton Whitefly Prediction Using Deep Learning. Sci. Program. 2021, 2021, 8824601. [Google Scholar] [CrossRef]
- Tsai, M.-F.; Lan, C.-Y.; Wang, N.-C.; Chen, L.-W. Time Series Feature Extraction Using Transfer Learning Technology for Crop Pest Prediction. Agronomy 2023, 13, 792. [Google Scholar] [CrossRef]
- Saleem, R.M.; Bashir, R.N.; Faheem, M.; Haq, M.A.; Alhussen, A.; Alzamil, Z.S.; Khan, S. Internet of Things Based Weekly Crop Pest Prediction by Using Deep Neural Network. IEEE Access 2023, 11, 85900–85913. [Google Scholar] [CrossRef]
- Al-Anni, R.; Hou, J.; Abdu-aljabar RD, A.; Xiang, Y. Prediction of NSCLC recurrence from microarray data with GEP. IET Syst. Biol. 2017, 11, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Aquino, N.M.R.; Gutoski, M.; Lopes, H.S. A Gene Expression Programming Approach for Evolving Multi-Class Image Classifiers. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Arequipa, Peru, 8–10 November 2017. [Google Scholar]

| Target value on fitness samples | |
| Chromosome return value on the fitness sample | |
| Selection range |
| Transfer Operator | Transfer Factor | Target Location |
|---|---|---|
| Gene transfer | Entire gene | Multigene chromosome |
| Insertion sequence elements (IS elements) | Short sequences where the first position is a function or endpoint | Gene head anywhere except the root |
| Root insertion sequence element (RIS element) | Short sequence where the first position is a function | Root of the gene |
| Input: | ||
| cases | The sample data set. | |
| N | Population size. | |
| h | Gene head length. | |
| e | Gene tail length. | |
| n | Maximum number of operations of the function. | |
| k | The number of genes. | |
| MaxGeneration | Fitness of termination iteration. | |
| Pmu | The mutation probability | |
| Ptr | Probability of string insertion | |
| Pre | Recombination probability | |
| Pex | Extraction probability | |
| Output: | ||
| Y | Optimal individual (classifier) | |
| 1: | Pretreat cases; | |
| 2: | S = InitialPopulation; | |
| 3: | Best_Ind = null; | |
| 4: | m = MaxGeneration; | |
| 5: | repeat | |
| 6: | analyze chromosome; | |
| 7: | fitness (); | |
| 8: | S = Selection(S); | |
| 9: | S = Mutation(S) by Pmu; | |
| 10: | S = Transpostion(S) by Ptr; | |
| 11: | S = Recombinations(S) by Pre; | |
| 12: | S = Extraction(S) by Pex; | |
| 13: | S = Invertion(S) by Pin; | |
| 14: | S = Adjustment(S) by Pad; | |
| 15: | Retain (Best_Ind); | |
| 16: | m = m − 1; | |
| 17: | until m = 0; | |
| 18: | return (Best_Ind); | |
| Indicator | Expression |
|---|---|
| MSE | |
| MAPE |
| Year | Average Temperature | Average Rainfall | Annual Total Accumulated Temperature | Annual Total Precipitation | Incidence Level or Occurrence Level | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | February | March | July | August | September | January | February | March | July | August | September | ||||
| 1933 | 2.4 | 3.7 | 7.3 | 28.3 | 27.9 | 20.5 | 1.8 | 0.8 | 34.5 | 47.4 | 77.0 | 48.3 | 5409.4 | 285.2 | 1 |
| 1934 | 1.7 | 1.8 | 7.7 | 28.4 | 27.0 | 21.3 | 3.5 | 20.6 | 24.7 | 98.0 | 75.1 | 49.1 | 5312.2 | 527.7 | 1 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 2009 | 2.5 | 6.1 | 9.7 | 27.0 | 24.9 | 22.5 | 5.4 | 0.0 | 14.8 | 155.6 | 124.0 | 31.5 | 5522.6 | 482.5 | 2 |
| 2010 | 0.5 | 3.4 | 12.0 | 26.6 | 26.4 | 22.3 | 9.2 | 4.9 | 9.8 | 90.6 | 97.4 | 49.3 | 5534.0 | 593.0 | 1 |
| Input: training dataset T | |
| Output: prediction formula f | |
| 1: | begin |
| 2: | While there are still data in the data set T; |
| 3: | Read w data from T; |
| 4: | Add the first w-1 data to the GEP parameter table and add the remaining data to the target table; |
| 5: | End while |
| 6: | Initialize the GEP run; while |
| 7: | End while Initialize the GEP run; while Terminate condition is met; |
| 8: | Output the optimal chromosome in the population; |
| 9: | end while |
| 10: | Return the formula f found by the GEP. |
| 11: | end |
| Operating Parameters | Detailed Description |
|---|---|
| Evolutionary generation | 1000 |
| Population size | 30 |
| Fitness function | Mean Squared Error |
| Set of functions | +, , ×, , Sqrt, Exp, Ln, Abs, Sin, Cos |
| Organization of chromosomes | The gene head is 6 genes in length and the chromosome is made up of 5 genes |
| Mutation probability | 0.044 |
| Inversion probability | 0.1 |
| IS transformation probability, RIS transformation probability | 0.1, 0.1 |
| Single-point recombination probability, two-point recombination probability | 0.3, 0.3 |
| Recombination probability, gene change probability | 0.1, 0.1 |
| Connection function | + |
| Model | Training Set | Test Set | ||
|---|---|---|---|---|
| MSE | MAPE | MSE | MAPE | |
| GEP-SVM | 1.57 | 5.51% | 4.39 | 16.57% |
| GEP | 1.89 | 5.98% | 4.75 | 16.93% |
| SVM | 5.33 | 10.53% | 6.78 | 17.49% |
| K Nearest Neighbors | 5.69 | 11.16% | 6.83 | 17.83% |
| Simple Bayes | 5.51 | 10.91% | 6.46 | 17.62% |
| BP Neural Network | 5.74 | 11.77% | 8.58 | 18.93% |
| Model | Train/Test | M | D | AC | Precision | Recall | F1-Score | MCC |
|---|---|---|---|---|---|---|---|---|
| GEP-SVM | Train | 49 | 11 | 90.83% | 0.870 | 0.889 | 0.880 | 0.501 |
| GEP | 48 | 10 | 88.33% | 0.829 | 0.906 | 0.866 | 0.477 | |
| SVM | 47 | 11 | 87.50% | 0.826 | 0.883 | 0.853 | 0.440 | |
| K Nearest Neighbors | 46 | 12 | 86.66% | 0.804 | 0.880 | 0.840 | 0.412 | |
| Simple Bayes | 45 | 12 | 85.00% | 0.782 | 0.878 | 0.827 | 0.386 | |
| BP Neural Network | 46 | 12 | 86.66% | 0.787 | 0.902 | 0.840 | 0.424 | |
| GEP-SVM | Test | 15 | 2 | 88.89% | 0.857 | 0.923 | 0.888 | 0.563 |
| GEP | 13 | 3 | 80.55% | 0.714 | 0.909 | 0.800 | 0.395 | |
| SVM | 13 | 3 | 80.55% | 0.769 | 0.833 | 0.800 | 0.350 | |
| K Nearest Neighbors | 12 | 4 | 77.78% | 0.642 | 0.900 | 0.750 | 0.328 | |
| Simple Bayes | 12 | 4 | 77.78% | 0.692 | 0.818 | 0.750 | 0.268 | |
| BP Neural Network | 11 | 5 | 75.00% | 0.615 | 0.800 | 0.695 | 0.194 |
| Time | Actual Value of Shipments (in Millions of USD) |
|---|---|
| 1992.2 | 11,567 |
| 1992.3 | 11,345 |
| 1992.4 | 11,987 |
| 1992.5 | 11,674 |
| … | … |
| 2015.4 | 482,323 |
| 2015.5 | 481,347 |
| 2015.6 | 484,363 |
| Time | Traffic Flow (in Trolleys) |
|---|---|
| 7:00–7:15 | 141 |
| 7:15–7:30 | 138 |
| 7:30–7:45 | 147 |
| 7:45–8:00 | 155 |
| 8:00–8:15 | 167 |
| 8:15–8:30 | 233 |
| 8:30–8:45 | 245 |
| 8:45–9:00 | 288 |
| … | … |
| 19:15–19:30 | 267 |
| 19:30–19:45 | 221 |
| 19:45–20:00 | 216 |
| Model | MSE | MAPE |
|---|---|---|
| KNN | 1187 | 0.0037 |
| SVM | 688.4 | 0.0026 |
| GEP | 564.2 | 0.0017 |
| GEP-SVM | 90.3 | 0.00098 |
| Model | MSE | MAPE |
|---|---|---|
| KNN | 1.86 | 0.0369 |
| SVM | 1.47 | 0.0253 |
| GEP | 1.32 | 0.0350 |
| GEP-SVM | 1.29 | 0.0290 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lv, Y.; Guo, J.; Wang, Y.; Tian, Y.; Gao, H.; He, J. Predictive Study on the Occurrence of Wheat Blossom Midges Based on Gene Expression Programming with Support Vector Machines. Insects 2024, 15, 463. https://doi.org/10.3390/insects15070463
Li Y, Lv Y, Guo J, Wang Y, Tian Y, Gao H, He J. Predictive Study on the Occurrence of Wheat Blossom Midges Based on Gene Expression Programming with Support Vector Machines. Insects. 2024; 15(7):463. https://doi.org/10.3390/insects15070463
Chicago/Turabian StyleLi, Yin, Yang Lv, Jian Guo, Yubo Wang, Youjin Tian, Hua Gao, and Jinrong He. 2024. "Predictive Study on the Occurrence of Wheat Blossom Midges Based on Gene Expression Programming with Support Vector Machines" Insects 15, no. 7: 463. https://doi.org/10.3390/insects15070463
APA StyleLi, Y., Lv, Y., Guo, J., Wang, Y., Tian, Y., Gao, H., & He, J. (2024). Predictive Study on the Occurrence of Wheat Blossom Midges Based on Gene Expression Programming with Support Vector Machines. Insects, 15(7), 463. https://doi.org/10.3390/insects15070463






