Characteristics of Trees Infested by the Invasive Primary Wood-Borer Aromia bungii (Coleoptera: Cerambycidae)
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
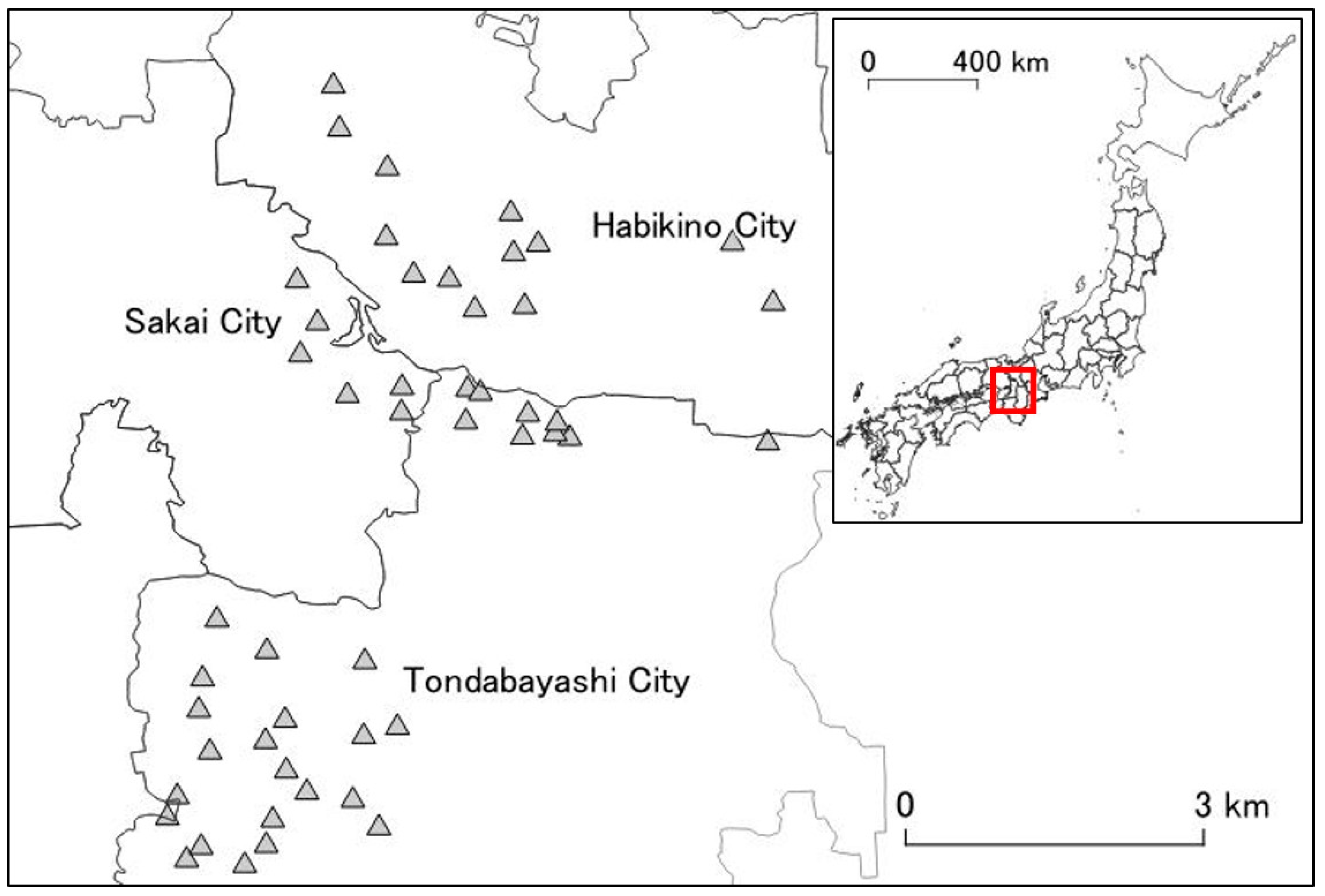
2.1. Study Sites and Monitoring Trees
2.2. Survey of Infestation and Tree Characteristics
2.3. Trees of Interest by Study Site Category
2.4. Data Processing for Statistical Analysis
2.5. Statistical Analysis
3. Results
3.1. Number of Study Sites and Monitoring Trees Categorized by A. bungii Infestation
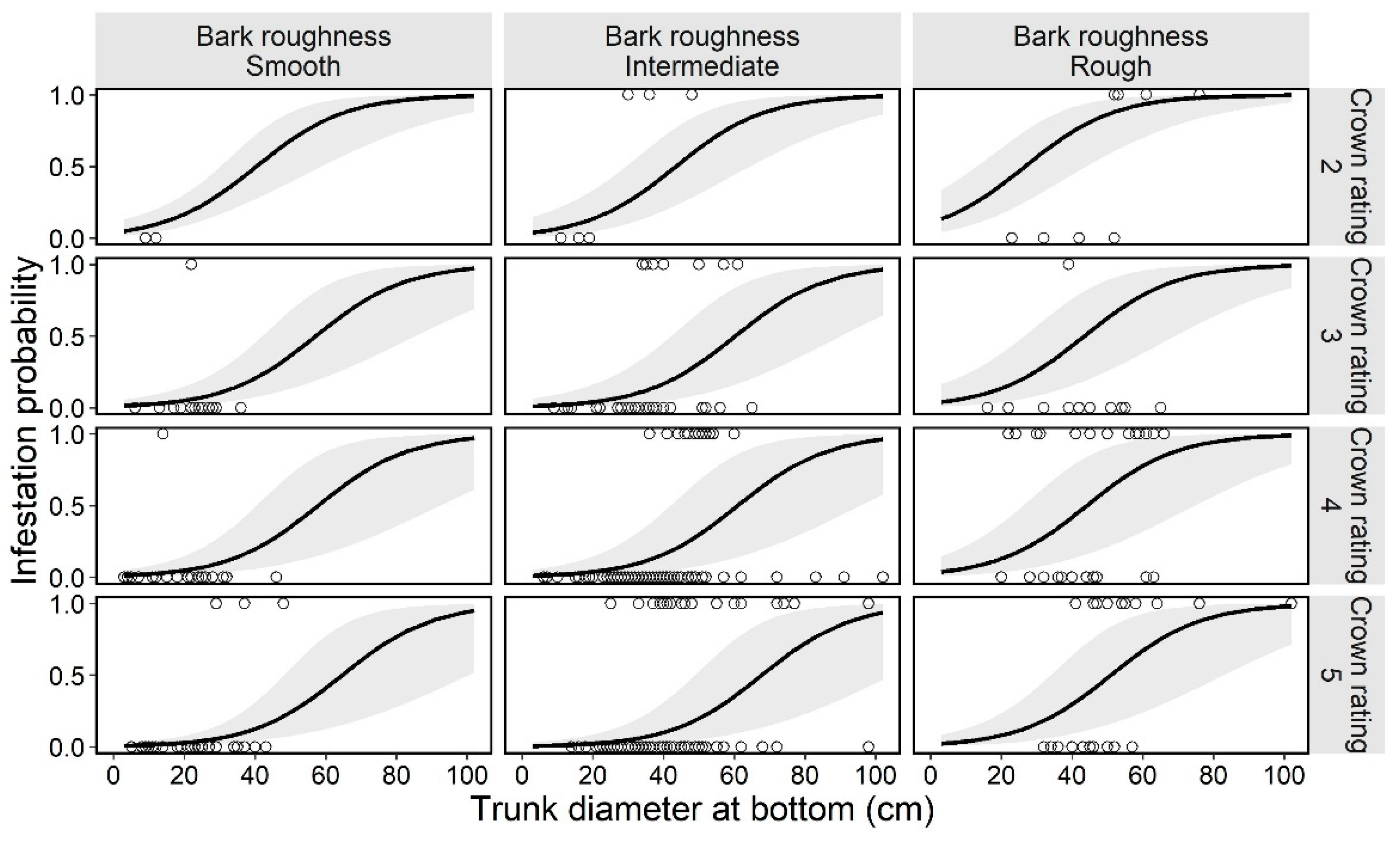
3.2. First Trees Model
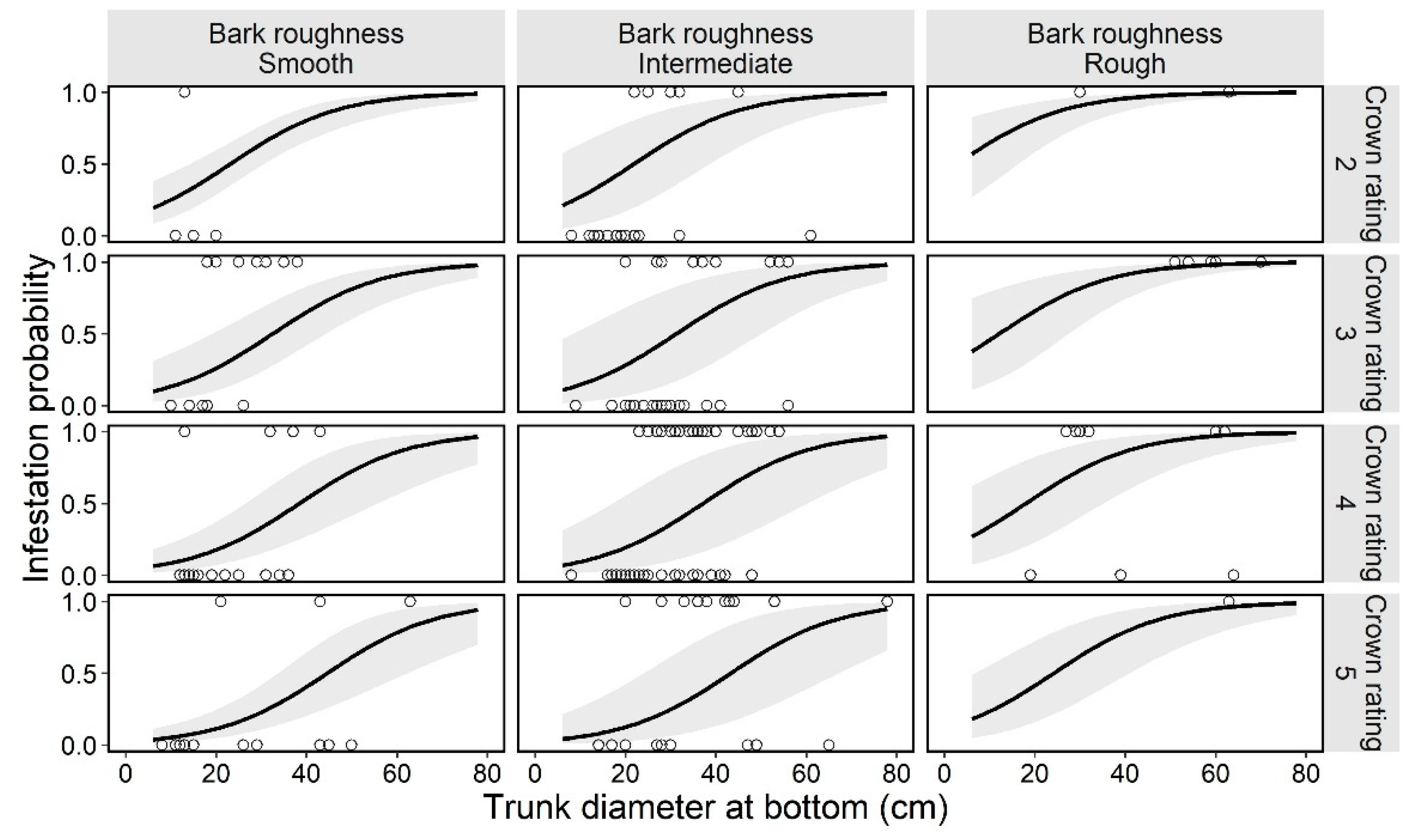
3.3. Next Trees Model
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Tree Characteristic | Level or Class | Number of Monitoring Trees | ||||||
|---|---|---|---|---|---|---|---|---|
| Study Site Category 1 | Study Site Category 3 | |||||||
| Infested in Post- Survey | Uninfested in Post- Survey | Total for Analysis | Infested in Pre- Survey | Infested in Post- Survey | Uninfested in Post- Survey | Total for Analysis | ||
| Bark roughness | Smooth | 5 | 70 | 75 | 12 | 17 | 56 | 73 |
| Intermediate | 48 | 194 | 242 | 90 | 67 | 107 | 174 | |
| Rough | 32 | 40 | 72 | 30 | 21 | 8 | 29 | |
| Species | Cerasus jamasakura | 1 | 7 | 8 | 0 | 2 | 12 | 14 |
| C. Sato-zakura group | 1 | 44 | 45 | 15 | 10 | 44 | 54 | |
| C. speciosa | 8 | 37 | 45 | 4 | 7 | 11 | 18 | |
| C. × yedoensis ‘Somei-yoshino’ | 75 | 216 | 291 | 113 | 86 | 104 | 190 | |
| Tree size (cm) | 1–10 | 0 | 15 | 15 | 0 | 0 | 11 | 11 |
| 11–20 | 1 | 37 | 38 | 9 | 12 | 56 | 77 | |
| 21–30 | 7 | 83 | 90 | 29 | 25 | 48 | 102 | |
| 31–40 | 15 | 82 | 97 | 43 | 32 | 38 | 113 | |
| 41–50 | 30 | 52 | 82 | 27 | 16 | 14 | 57 | |
| 51–60 | 18 | 21 | 39 | 13 | 13 | 1 | 27 | |
| 61–70 | 7 | 8 | 15 | 5 | 6 | 3 | 14 | |
| 71–80 | 5 | 2 | 7 | 2 | 1 | 0 | 3 | |
| 81–90 | 0 | 1 | 1 | 2 | 0 | 0 | 2 | |
| 91–100 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | |
| 101–110 | 1 | 1 | 2 | 1 | 0 | 0 | 1 | |
| 111–120 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| Tree vigor (crown rating) | Level 2 | 7 | 10 | 17 | 27 | 17 | 20 | 37 |
| Level 3 | 11 | 62 | 73 | 49 | 28 | 45 | 73 | |
| Level 4 | 32 | 112 | 144 | 46 | 42 | 66 | 108 | |
| Level 5 | 35 | 120 | 155 | 10 | 18 | 40 | 58 | |
Appendix B
| Species, Varieties, or Cultivars (Scientific Name) | Study Site Category 1 | Study Site Category 3 | Total Number of Monitoring Trees in Pre- Survey | |||
|---|---|---|---|---|---|---|
| Infested in Post- Survey | Uninfested in Post- Survey | Infested in Pre- Survey | Infested in Post- Survey | Uninfested in Post- Survey | ||
| Cerasus itosakura ‘Pendula’ | 0 | 5 | 0 | 0 | 1 | 6 |
| C. jamasakura | 1 | 7 | 0 | 2 | 12 | 22 |
| C. leveilleana | 0 | 3 | 0 | 0 | 3 | 6 |
| C. leveilleana ‘Juzukakezakura’ | 0 | 1 | 0 | 0 | 0 | 1 |
| C. sargentii | 0 | 2 | 2 | 1 | 4 | 9 |
| C. Sato-zakura Group | 0 | 15 | 8 | 7 | 31 | 61 |
| C. Sato-zakura Group ‘Albo-rosea’ | 0 | 8 | 0 | 0 | 0 | 8 |
| C. Sato-zakura Group ‘Beni-yutaka’ | 0 | 1 | 0 | 0 | 0 | 1 |
| C. Sato-zakura Group ‘Hisakura’ | 0 | 0 | 0 | 1 | 0 | 1 |
| C. Sato-zakura Group ‘Sekiyama’ | 1 | 4 | 0 | 0 | 0 | 5 |
| C. speciosa | 8 | 37 | 4 | 7 | 11 | 67 |
| C. speciosa ‘Surugadai-odora’ | 0 | 5 | 0 | 0 | 5 | 10 |
| C. × yedoensis ‘Somei-yoshino’ | 75 | 216 | 113 | 86 | 104 | 594 |
| N.A. | 0 | 0 | 5 | 1 | 0 | 6 |
Appendix C
| Explanatory Variable | Estimate | Std. Error | z Value | Pr (>|z|) | |
|---|---|---|---|---|---|
| Bark roughness.L. | 0.763 | 0.461 | 1.653 | 0.098 | . |
| Bark roughness.Q. | 0.642 | 0.326 | 1.971 | 0.049 | * |
| Tree vigor.L. | −1.295 | 0.520 | −2.489 | 0.013 | * |
| Tree vigor.Q. | 0.395 | 0.420 | 0.939 | 0.348 | |
| Tree vigor.C. | −0.393 | 0.352 | −1.117 | 0.264 | |
Appendix D
| Fixed Effect | Df | Sum of Squares for Variance | Mean Squares for Variance | Chi-Square Values | Pr (>Chisq) |
|---|---|---|---|---|---|
| Bark roughness | 2 | 13.02 | 6.51 | 9.44 | 0.007 |
| Tree size | 1 | 15.18 | 15.18 | 19.48 | <0.001 |
| Tree vigor | 3 | 6.88 | 2.29 | 6.74 | 0.081 |
Appendix E
| Explanatory Variable | Estimate | Std. Error | z Value | Pr (>|z|) | |
|---|---|---|---|---|---|
| Bark roughness.L. | 1.205 | 0.504 | 2.392 | 0.017 | * |
| Bark roughness.Q. | 0.609 | 0.326 | 1.867 | 0.062 | . |
| Cerasus × yedoensis ‘Somei-yoshino’ | 0.402 | 0.618 | 0.651 | 0.515 | |
| C. Sato-zakura group | −0.490 | 0.765 | −0.641 | 0.522 | |
| C. jamasakura | −1.695 | 1.146 | −1.480 | 0.139 | |
| Tree vigor.L. | −1.312 | 0.421 | −3.114 | 0.002 | ** |
| Tree vigor.Q. | 0.135 | 0.344 | 0.394 | 0.694 | |
| Tree vigor.C. | −0.072 | 0.296 | −0.242 | 0.809 | |
Appendix F
| Fixed Effect | Df | Sum of Squares for Variance | Mean Squares for Variance | Chi-Square Values | Pr (>Chisq) |
|---|---|---|---|---|---|
| Bark roughness | 2 | 11.82 | 5.91 | 6.48 | 0.039 |
| Species | 3 | 6.21 | 2.07 | 6.93 | 0.074 |
| Tree size | 1 | 16.53 | 16.53 | 22.63 | <0.001 |
References
- EPPO. EPPO datasheet on pests recommended for regulation Aromia bungii. EPPO Bull. 2015, 45, 4–8. [Google Scholar] [CrossRef]
- Iwata, R. Aromia bungii (Coleoptera: Cerambycidae): Taxonomy, distribution, biology and eradication. For. Pests 2018, 67, 7–34. (In Japanese) [Google Scholar]
- EFSA. Aromia bungii Pest Report to Support Ranking of EU Candidate Priority Pests; Pest Report EN-1639; EFSA: Parma, Italy, 2019; pp. 1–33. [CrossRef]
- Russo, E.; Nugnes, F.; Vicinanza, F.; Garonna, A.P.; Bernardo, U. Biological and molecular characterization of Aromia bungii (Faldermann, 1835) (Coleoptera: Cerambycidae), an emerging pest of stone fruits in Europe. Sci. Rep. 2020, 10, 7112. [Google Scholar] [CrossRef] [PubMed]
- Lockwood, J.L.; Hoopes, M.F.; Marchetti, M.P. Eradication and control of invaders. In Invasion Ecology, 2nd ed.; Wiley-Blackwell: Chichester, UK, 2013; pp. 335–355. [Google Scholar]
- Fan, J.T.; Denux, O.; Courtin, C.; Bernard, A.; Javal, M.; Millar, J.G.; Hanks, L.M.; Roques, A. Multi-component blends for trapping native and exotic longhorn beetles at potential points-of-entry and in forests. J. Pest Sci. 2019, 92, 281–297. [Google Scholar] [CrossRef]
- Millar, J.G.; Zou, Y.; Barringer, L.; Hanks, L.M. Field trials with blends of pheromones of native and invasive Cerambycid beetle species. Environ. Entomol. 2021, 50, 1294–1298. [Google Scholar] [CrossRef]
- Xu, T.; Yasui, H.; Teale, S.A.; Fujiwara-Tsujii, N.; Wickham, J.D.; Fukaya, M.; Hansen, L.; Kiriyama, S.; Hao, D.; Nakano, A.; et al. Identification of male-produced sex-aggregation pheromone for a highly invasive cerambycid beetle, Aromia bungii. Sci. Rep. 2017, 7, 7330. [Google Scholar] [CrossRef] [PubMed]
- Di Palma, A.; Pistillo, M.; Griffo, R.; Garonna, A.P.; Germinara, G.S. Scanning electron microscopy of the antennal sensilla and their secretion analysis in adults of Aromia bungii (Faldermann, 1835) (Coleoptera, Cerambycidae). Insects 2019, 10, 88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Germinara, G.S.; Pistillo, M.; Griffo, R.; Garonna, A.P.; Di Palma, A. Electroantennographic responses of Aromia bungii (Faldermann, 1835) (Coleoptera, Cerambycidae) to a range of volatile compounds. Insects 2019, 10, 274. [Google Scholar] [CrossRef] [Green Version]
- Fukaya, M.; Kiriyama, S.; Yasui, H. Mate-location flight of the red-necked longicorn beetle, Aromia bungii (Coleoptera: Cerambycidae): An invasive pest lethal to Rosaceae trees. Appl. Entomol. Zool. 2017, 52, 559–565. [Google Scholar] [CrossRef]
- Yasui, H.; Fujiwara-Tsujii, N.; Kugimiya, S.; Haruyama, N. Extension of sustained pheromone release for monitoring an emerging invader, red-necked longicorn Beetle Aromia bungii (Coleoptera: Cerambycidae). Appl. Entomol. Zool. 2021, 56, 291–297. [Google Scholar] [CrossRef]
- Ito, K. Differential host residence of adult cryptomeria bark borer, Semanotus japonicus Lacordaire (Coleoptera: Cerambycidae), in relation to tree size of Japanese cedar, Cryptomeria japonica D. Don. J. For. Res. 1999, 4, 151–156. [Google Scholar] [CrossRef]
- Nahrung, H.F.; Smith, T.E.; Wiegand, A.N.; Lawson, S.A.; Debuse, V.J. Host tree influences on longicorn beetle (Coleoptera: Cerambycidae) attack in subtropical Corymbia (Myrtales: Myrtaceae). Environ. Entomol. 2014, 43, 37–46. [Google Scholar] [CrossRef]
- Nelson, T.D.; Sweeney, J.D.; Hillier, N.K. Do visual cues associated with larger diameter trees influence host selection by Tetropium fuscum (Coleoptera: Cerambycidae)? Can. Entomol. 2017, 149, 487–490. [Google Scholar] [CrossRef]
- Morewood, W.D.; Neiner, P.R.; McNeil, J.R.; Sellmer, J.C.; Hoover, K. Oviposition preference and larval performance of Anoplophora glabripennis (Coleoptera: Cerambycidae) in four eastern North American hardwood tree species. Environ. Entomol. 2003, 32, 1028–1034. [Google Scholar] [CrossRef]
- Hanks, L.M. Influence of the larval host plant on reproductive strategies of Cerambycid beetles. Annu. Rev. Entomol. 1999, 44, 483–505. [Google Scholar] [CrossRef] [Green Version]
- Saint-Germain, M.; Buddle, C.M.; Drapeau, P. Primary attraction and random landing in host selection by wood-feeding insects: A matter of scale? Agric. For. Entomol. 2007, 9, 227–235. [Google Scholar] [CrossRef]
- Flaherty, L.; Quiring, D.; Pureswaran, D.; Sweeney, J. Preference of an exotic wood borer for stressed trees is more attributable to pre-alighting than post-alighting behaviour. Ecol. Entomol. 2013, 38, 546–552. [Google Scholar] [CrossRef]
- Shibata, E.; Waguchi, Y.; Yoneda, Y. Role of tree diameter in the damage caused by the sugi bark borer (Coleoptera: Cerambycidae) to the Japanese cedar, Cryptomeria japonica. Environ. Entomol. 1994, 23, 76–79. [Google Scholar] [CrossRef]
- Menzel, F.; Kitching, R.L.; Boulter, S.L. Host specificity or habitat structure? The epicortical beetle assemblages in an Australian subtropical rainforest. Eur. J. Entomol. 2004, 101, 251–259. [Google Scholar] [CrossRef] [Green Version]
- Kašák, J.; Foit, J. Shortage of declining and damaged sun-exposed trees in European mountain forests limits saproxylic beetles: A case study on the endangered longhorn beetle Ropalopus ungaricus (Coleoptera: Cerambycidae). J. Insect Conserv. 2018, 22, 171–181. [Google Scholar] [CrossRef]
- Haruyama, N.; Yaita, S.; Fukuda, T.; Yamazaki, K.; Watanabe, H.; Handa, M. Peach orchard damages caused by the red-necked longhorn beetle Aromia bungii (Faldermann) in Tochigi Prefecture. Ann. Rep. Kanto-Tosan. Plant. Prot. Soc. 2019, 66, 106–109. (In Japanese) [Google Scholar] [CrossRef]
- Yamamoto, Y.; Ishikawa, Y. Occurrence of Aromia bungii in Osaka Prefecture. Ann. Rept. Kansai. Plant Prot. 2018, 60, 17–21. [Google Scholar] [CrossRef] [Green Version]
- Tamura, S.; Sunamura, E.; Shoda-Kagaya, E. Seasonal changes in frass ejection by larval red-necked longicorn beetles, Aromia bungii (Coleoptera: Cerambycidae), infesting cherry trees. Jpn. J. Appl. Entomol. Zool. 2021, 65, 57–61. [Google Scholar] [CrossRef]
- Shoda-Kagaya, E. Cherry tree damages associated with the invasion of red-necked longhorn beetle Aromia bungii in Japan. Tree Health 2015, 19, 37–40. (In Japanese) [Google Scholar] [CrossRef]
- Yamamoto, Y.; Uehara, K.; Ishikawa, Y.; Tsuyoshi, Y. Survey on the actual damage by the invasive red-necked longhorn beetle (Aromia bungii) harmful to trees such as the Japanese flowering cherries. A. R. Pro. Nat. Found. Ja. 2019, 8, 24–35. (In Japanese) [Google Scholar] [CrossRef]
- Rizzo, D.; Luchi, N.; Da Lio, D.; Bartolini, L.; Nugnes, F.; Cappellini, G.; Bruscoli, T.; Salemi, C.; Griffo, R.V.; Garonna, A.P.; et al. Development of a loop-mediated isothermal amplification (LAMP) assay for the identification of the invasive wood borer Aromia bungii (Coleoptera: Cerambycidae) from frass. 3 Biotech 2021, 11, 85. [Google Scholar] [CrossRef]
- Ishikawa, Y. Notes on the frass of longicorn beetles on Cerasus (Prunus) tree. Plant Prot. 2021, 75, 557–563. (In Japanese) [Google Scholar]
- Yasuoka, T. Efficacy of insecticides against larvae of red necked longhorn beetle Aromia bungii (Faldermann) (Coleoptera: Cerambycidae). Res. Bull. Plant Prot. Japan. 2017, 53, 51–62. (In Japanese) [Google Scholar]
- Yamamoto, Y. Invasion and control strategy of the red-necked longhorn beetle Aromia bungii. J. Pestic. Sci. 2010, 45, 127–133. [Google Scholar] [CrossRef]
- Hishinuma, S.; Coleman, T.W.; Flint, M.L.; Seybold, S.J. Goldspotted Oak Borer: Field Identification Guide. University of California Agriculture and Natural Resources, Statewide Integrated Pest Management Program. 2011. Available online: https://www.fs.fed.us/psw/publications/seybold/psw_2011_seybold(hishinuma)001.pdf (accessed on 31 October 2021).
- Oohara, T. The Handbook of Flowering Cherries in Japan, 1st ed.; Bun-Ichi Co., Ltd.: Tokyo, Japan, 2009; pp. 1–88. (In Japanese) [Google Scholar]
- Katsuki, T. Taxonomy and identification by morphology for Japanese flowering cherries. Tree Health 2017, 21, 93–104. (In Japanese) [Google Scholar] [CrossRef]
- R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 31 March 2021).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Hardersen, S.; Cuccurullo, A.; Bardiani, M.; Bologna, M.A.; Maura, M.; Maurizi, E.; Roversi, P.F.; Sabbatini Peverieri, G.; Chiari, S. Monitoring the saproxylic longhorn beetle Morimus asper: Investigating season, time of the day, dead wood characteristics and odour traps. J. Insect Conserv. 2017, 21, 231–242. [Google Scholar] [CrossRef]
- Byers, J.A. An encounter rate model of bark beetle populations searching at random for susceptible host trees. Ecol. Model. 1996, 91, 57–66. [Google Scholar] [CrossRef]
- Ferrenberg, S.; Mitton, J.B. Smooth bark surfaces can defend trees against insect attack: Resurrecting a “slippery” hypothesis. Funct. Ecol. 2014, 28, 837–845. [Google Scholar] [CrossRef]
- Eyre, D.; Haack, R.A. Invasive cerambycid pests and biosecurity measures. In Cerambycidae of the World: Biology and Pest Management; Wang, Q., Ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 563–618. [Google Scholar]
- Faccoli, M.; Favaro, R. Host preference and host colonization of the Asian long-horned beetle, Anoplophora glabripennis (Coleoptera Cerambycidae), in Southern Europe. Bull. Entomol. Res. 2016, 106, 359–367. [Google Scholar] [CrossRef]



| Category of Study Site | Infested Trees in Study Site | Total Number of Study Sites | Number of Trees | Total Number of Monitoring Trees | ||||
|---|---|---|---|---|---|---|---|---|
| In Pre-Survey | In Post-Survey | Infested in Pre-Survey | Infested in Post-Survey | Uninfested in Post-Survey | Cut or Dead before Post-Survey | |||
| 1 | Absence | Presence | 12 | 0 | 85 | 304 | 4 | 393 |
| 2 | Absence | Absence | 13 | 0 | 0 | 182 | 3 | 185 |
| 3 | Presence | Presence | 22 | 132 | 105 | 171 | 9 | 417 |
| 4 | Presence | Absence | 2 | 14 | 0 | 22 | 1 | 37 |
| Rank | Random Effect Term | ΔAIC |
|---|---|---|
| 1 | Slope (tree size) by study sites | 0 |
| 2 | Independent intercept and slope (tree size) by study site | 0.44 |
| Rank | ΔAIC | R2 | Regression Coefficient | Standard Deviation of Coefficient | |||||
|---|---|---|---|---|---|---|---|---|---|
| Conditional | Marginal | Bark Roughness | Species | Tree Size | Tree Vigor | Intercept | Tree Size (Random Slope) | ||
| 1 | 0 | 0.567 | 0.307 | + | − | 0.079 | + | −4.054 | 0.035 |
| 2 | 0.65 | 0.529 | 0.275 | + | − | 0.069 | − | −4.069 | 0.033 |
| Rank | Random Effect Term | ΔAIC |
|---|---|---|
| 1 | Slope (tree size) by study sites | 0 |
| 2 | Independent intercept and slope (tree size) by study sites | 2.00 |
| Rank | ΔAIC | R2 | Regression Coefficient | Standard Deviation of Coefficient | |||||
|---|---|---|---|---|---|---|---|---|---|
| Conditional | Marginal | Bark Roughness | Species | Tree Size | Tree Vigor | Intercept | Tree Size (Random Slope) | ||
| 1 | 0 | 0.471 | 0.382 | + | + | 0.083 | + | −2.689 | 0.022 |
| 2 | 1.83 | 0.481 | 0.338 | + | − | 0.089 | + | −2.632 | 0.029 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, Y.; Ishikawa, Y.; Uehara, K. Characteristics of Trees Infested by the Invasive Primary Wood-Borer Aromia bungii (Coleoptera: Cerambycidae). Insects 2022, 13, 54. https://doi.org/10.3390/insects13010054
Yamamoto Y, Ishikawa Y, Uehara K. Characteristics of Trees Infested by the Invasive Primary Wood-Borer Aromia bungii (Coleoptera: Cerambycidae). Insects. 2022; 13(1):54. https://doi.org/10.3390/insects13010054
Chicago/Turabian StyleYamamoto, Yuichi, Yosuke Ishikawa, and Kazuhiko Uehara. 2022. "Characteristics of Trees Infested by the Invasive Primary Wood-Borer Aromia bungii (Coleoptera: Cerambycidae)" Insects 13, no. 1: 54. https://doi.org/10.3390/insects13010054
APA StyleYamamoto, Y., Ishikawa, Y., & Uehara, K. (2022). Characteristics of Trees Infested by the Invasive Primary Wood-Borer Aromia bungii (Coleoptera: Cerambycidae). Insects, 13(1), 54. https://doi.org/10.3390/insects13010054






