Lubricated Loaded Tooth Contact Analysis and Non-Newtonian Thermoelastohydrodynamics of High-Performance Spur Gear Transmission Systems
Abstract
1. Introduction
2. Methodology
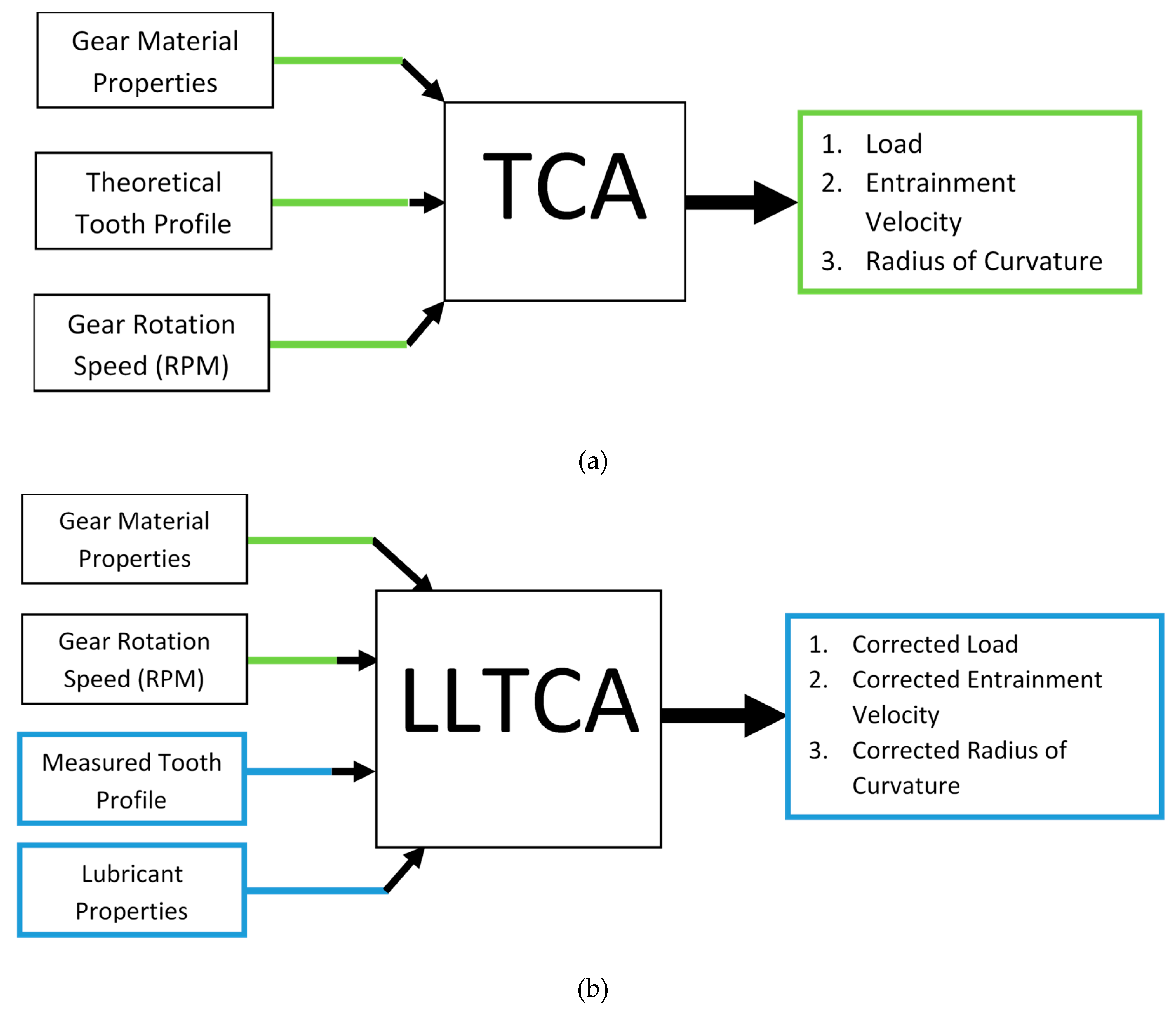
2.1. Tooth Contact Analysis (TCA) and Lubricated Loaded Tooth Contact Analysis (LLTCA)
2.2. Elastohydrodynamic Lubrication (EHL)
2.3. Tractive Analysis
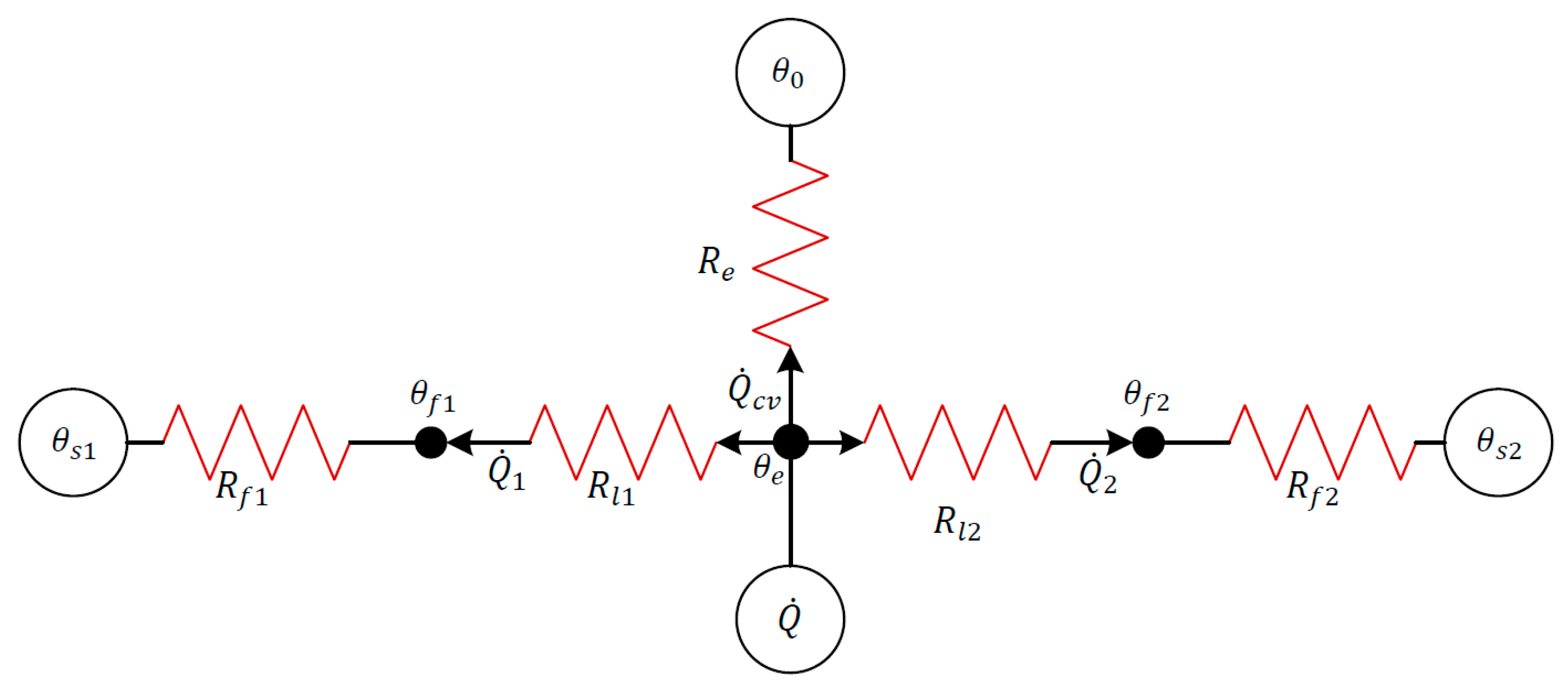
2.4. Thermal Network Model
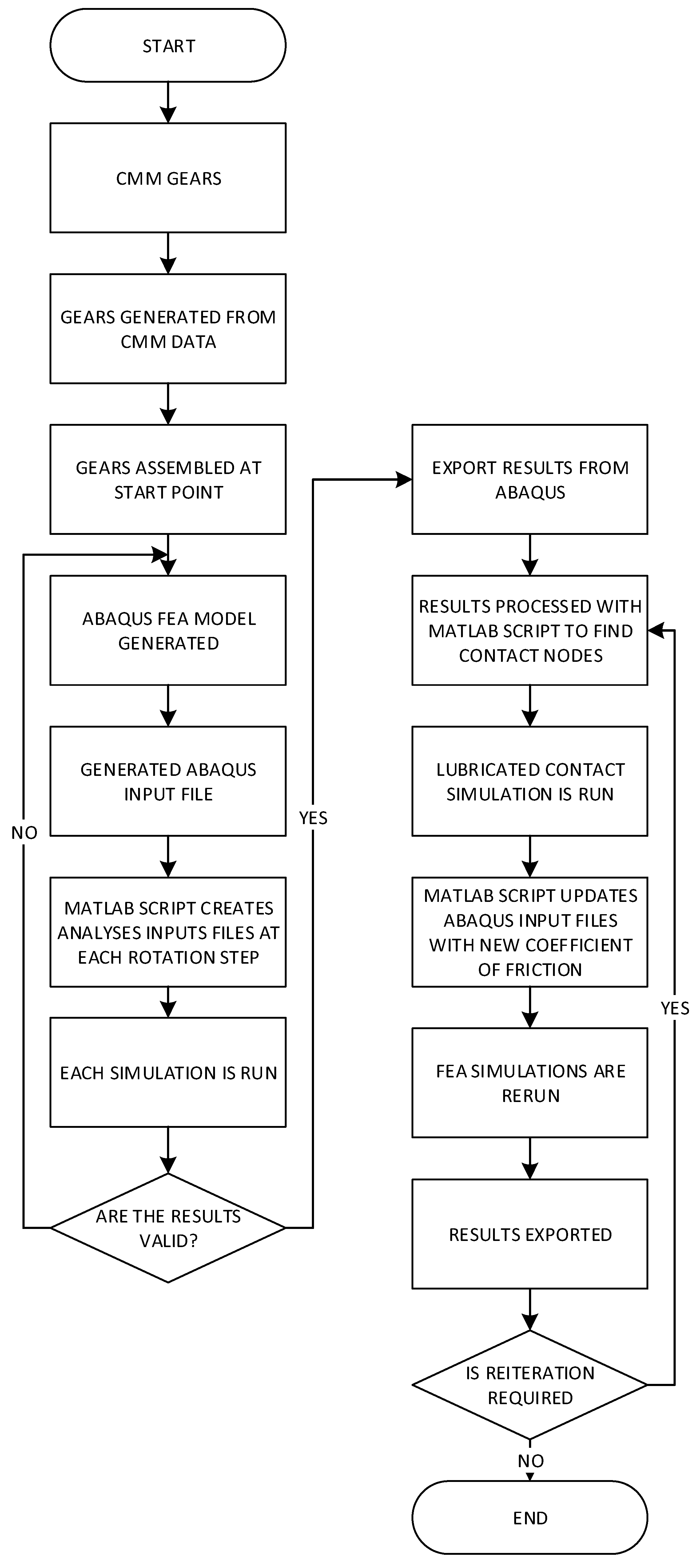
3. Method of Solution
- Inputs from LLTCA at the start of the meshing cycle are used.
- An initial guess is made for the film thickness at the center of the contact.
- The computational domain is set with an inlet length of and contact exit position of . The number of elements used in the direction of lubricant entrainment is 2051.
- Iterative pressure residuals are found using the under-relaxed Effective Influence Newton (EIN) method, including local surface deflection calculated through the use of Equation (9), which is based on Equation (38), where n denotes the iteration step and is the under-relaxation factor, typically –:
- The iterative procedure evaluates the contact pressure and continues until the pressure convergence criterion is satisfied:
- When pressure convergence is satisfied, the contact load-carrying capacity is calculated through the integration of pressure distribution over the computational domain as:
- The following equilibrium condition should be satisfied in order to achieve a load balance condition where is the applied load:
- If Equation (41) is not satisfied, the film thickness is updated through modification of the undeformed gap, using Equation (42):where is termed the damping (load relaxation) factor, and for the current analysis, the value of is used. Subsequently, the density and viscosity are updated using the newly found pressure. Then, Steps 4 to 8 are repeated until Step 7 is satisfied.
- Once the film thickness is determined, the thermal network model (highlighted in Section 2.4) is used to find the temperature of the lubricant as well as those of the adjacent meshing surfaces.
- Steps 2 to 9 are repeated for each point on the meshing cycle until the entire meshing cycle is completed.
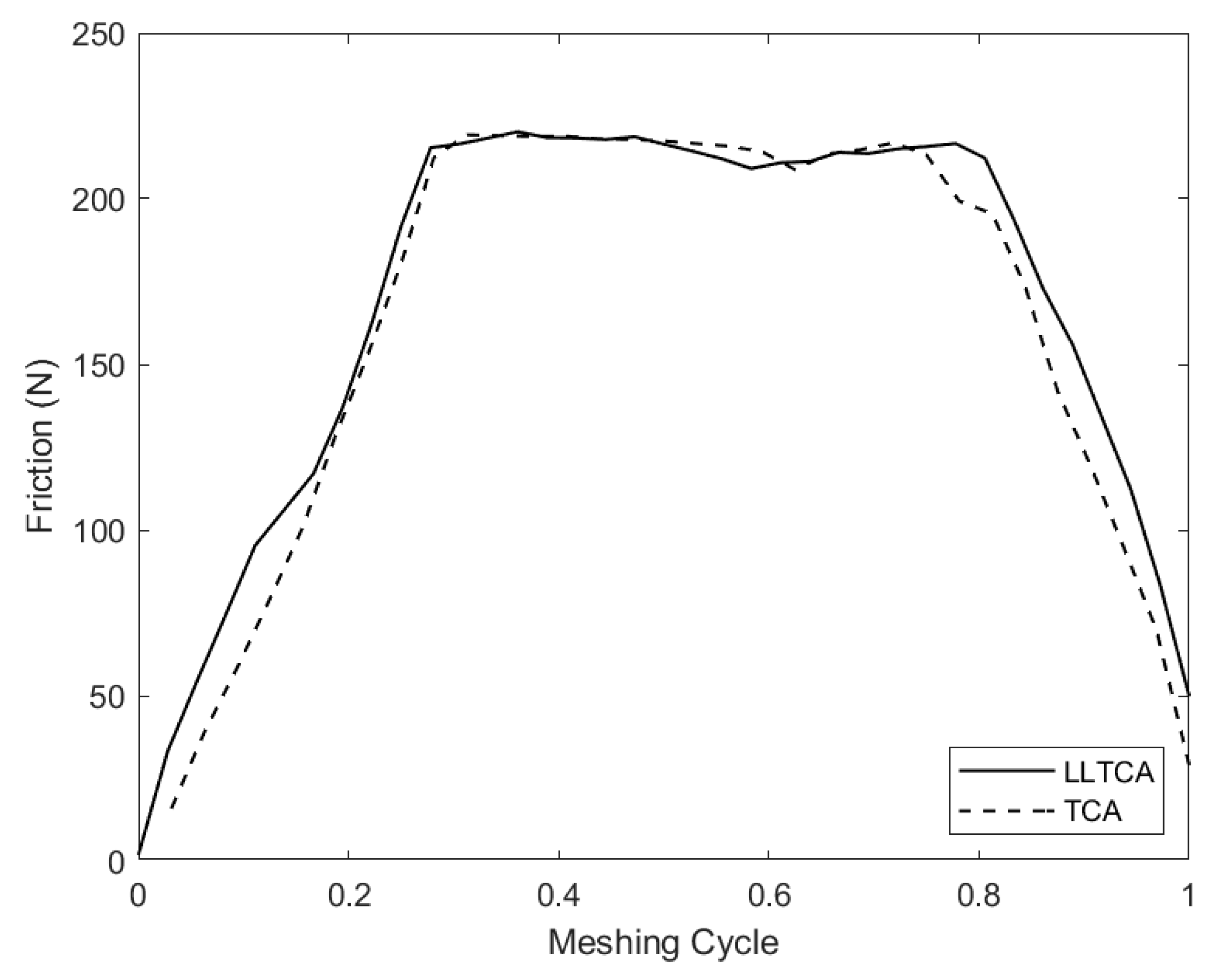
4. Shear Stress and Friction
5. Sub-Surface Stress Field
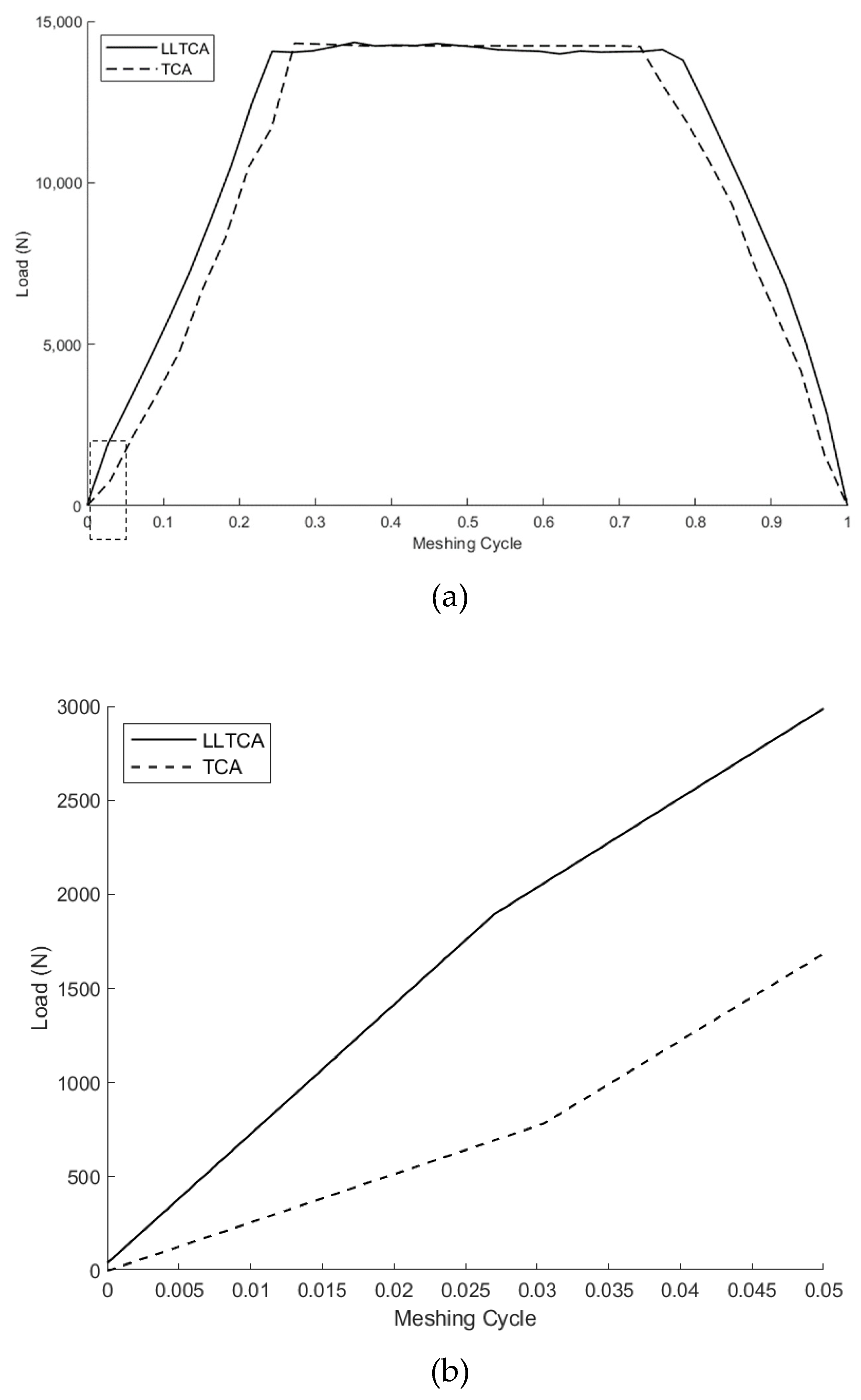
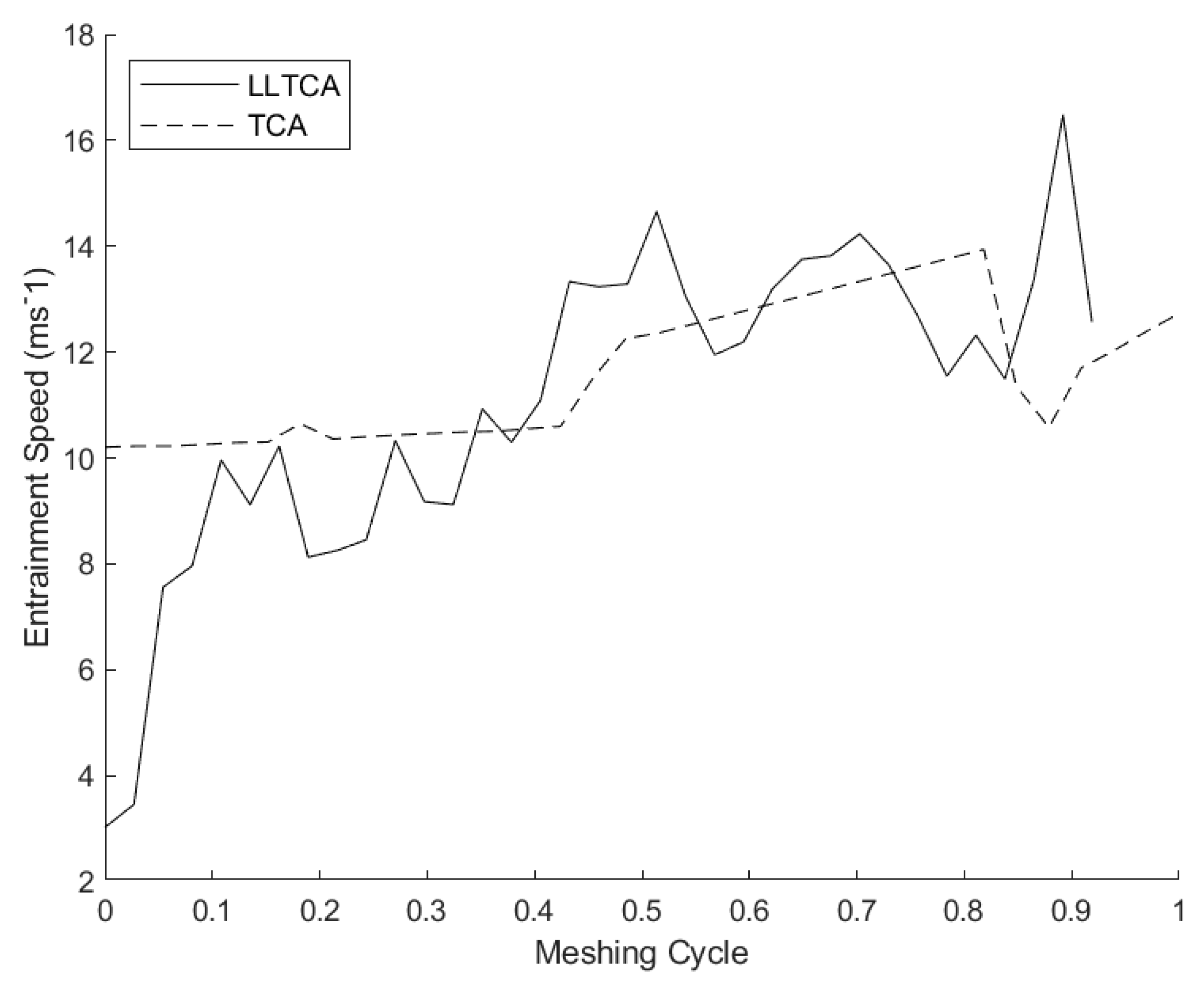
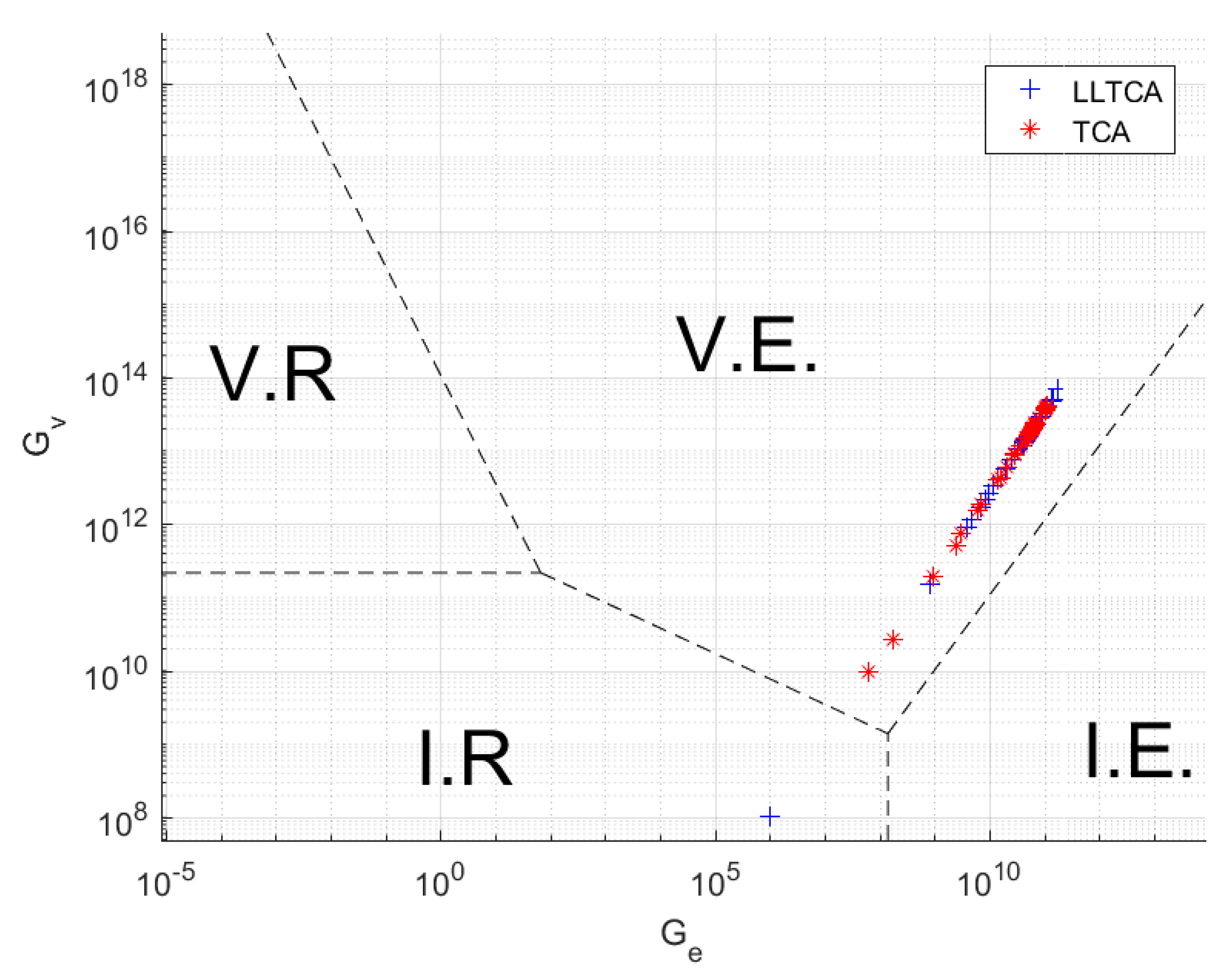
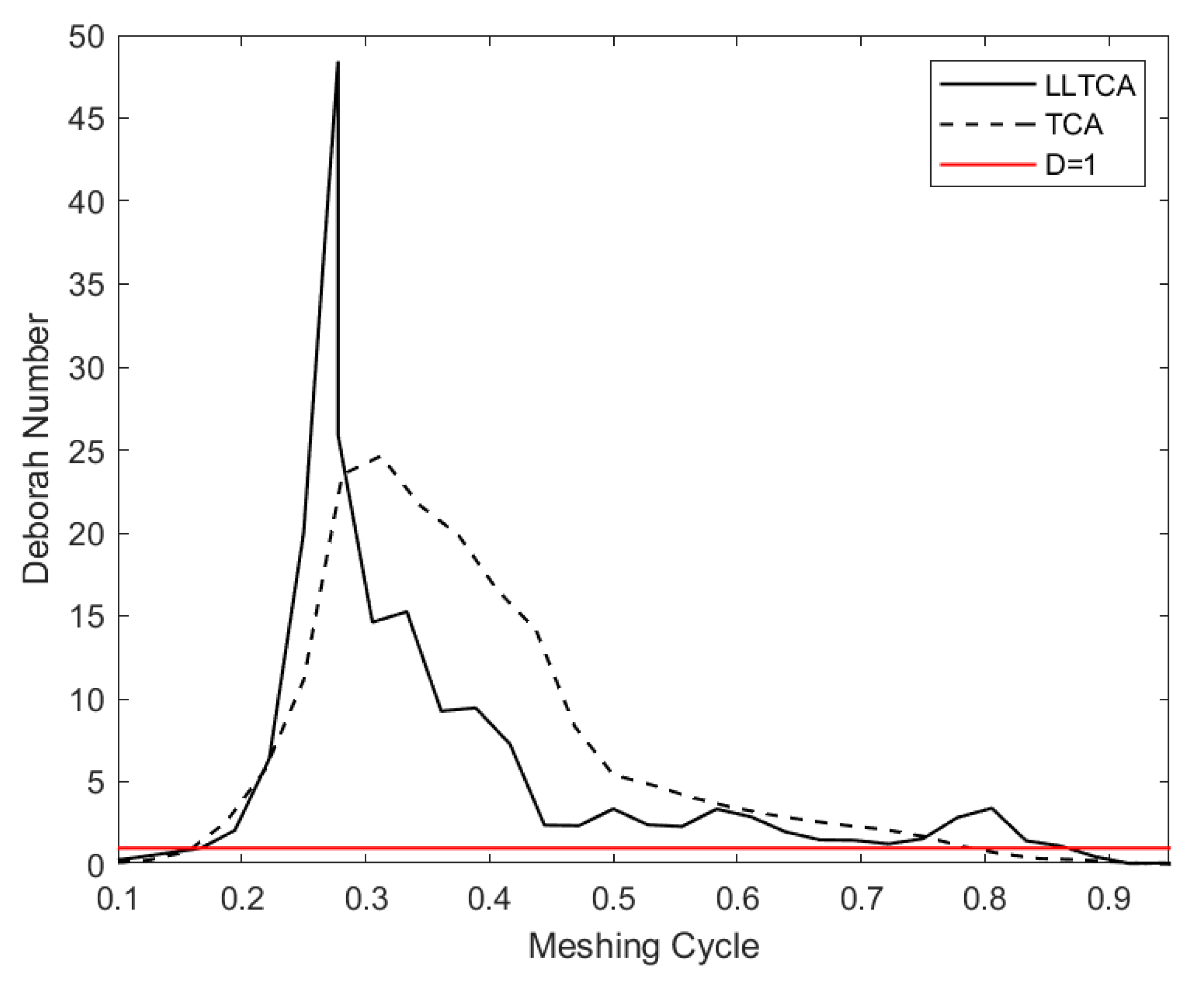
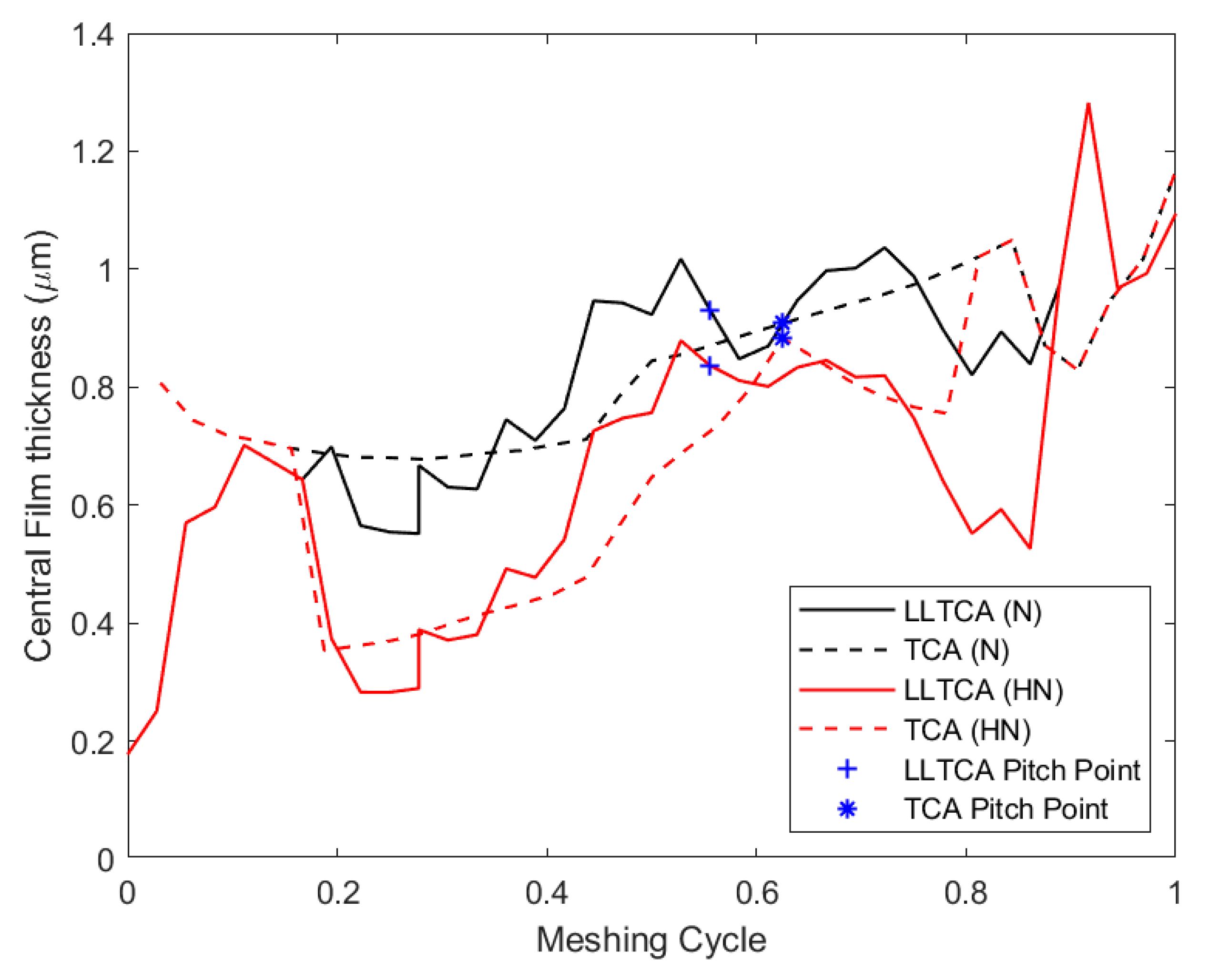
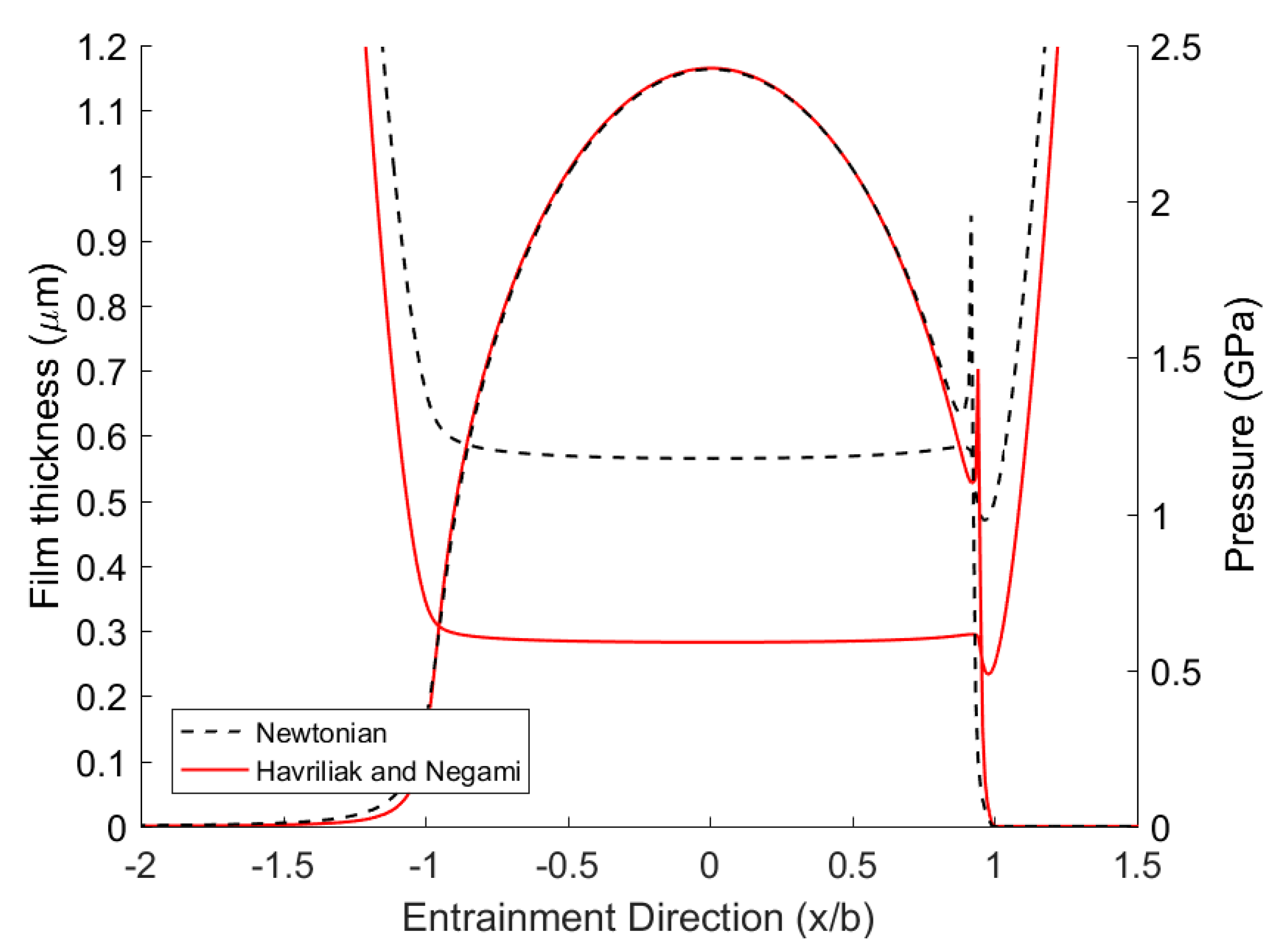
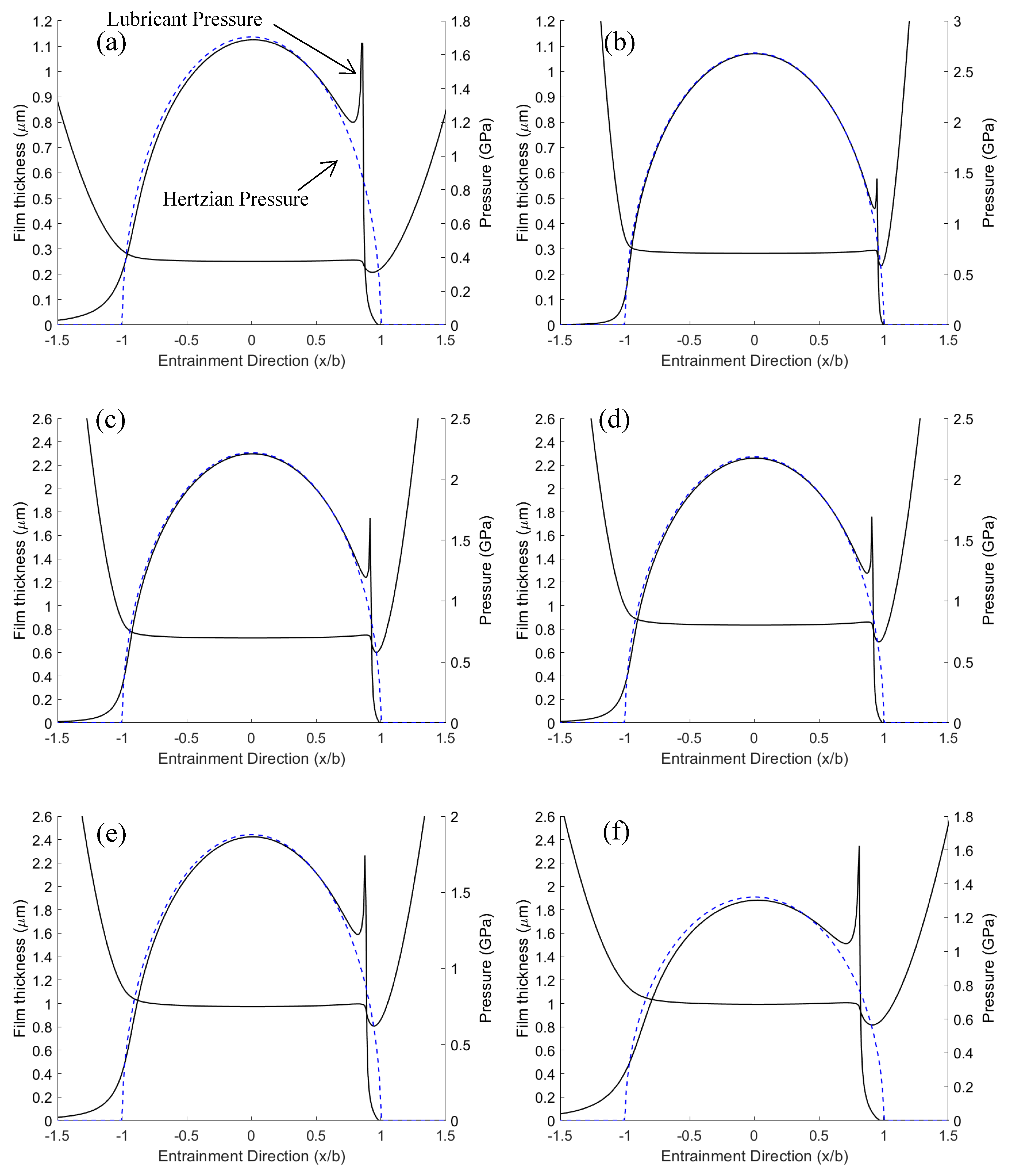
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Area of contact | |
| Vogel viscosity constant | |
| Hertzian semi-half-width of the contact | |
| , | Vogel viscosity constants |
| Specific heat capacity of the lubricant | |
| Specific heat capacity of the solids body | |
| Deborah number | |
| Equivalent/reduced Young’s modulus of elasticity: | |
| Havriliak and Negami non-Newtonian function | |
| Friction | |
| , | Parameters for the Greenwood chart |
| Dimensionless materials’ parameter | |
| Dimensionless film thickness | |
| Film thickness | |
| Minimum film thickness for the undeformed (rigid) profile | |
| Central contact film thickness | |
| Nodal position identifier | |
| Thermal conductivity of the lubricant | |
| Thermal conductivity of the solids | |
| Contact length | |
| Lubricant mass flow rate | |
| Iteration counter | |
| Pressure | |
| Average contact pressure | |
| Maximum Hertzian elastic line contact pressure | |
| Rate of heat generation | |
| Heat conducted away through the bounding surfaces | |
| Heat convected away by the lubricant | |
| Shear field | |
| Radius of curvature of equivalent solid | |
| Conductive thermal resistivity of the lubricant | |
| Convective thermal resistivity of the lubricant | |
| Radius of curvature in the direction of entraining motion | |
| Radius of curvature in the side leakage direction | |
| Rolling velocity in the direction of lubricant entrainment | |
| Speed of entraining motion | |
| Relative sliding velocity | |
| Dimensionless (rolling) velocity parameter | |
| Velocity in the slide leakage direction | |
| Applied load | |
| Load carrying capacity of the lubricant | |
| Dimensionless load parameter | |
| Undeformed geometrical contact profile | |
| Cartesian coordinate set | |
| Bulk temperature | |
| Atmospheric reference temperature | |
| Time |
Greek Symbols
| Piezoviscosity coefficient at ambient temperature | |
| Piezoviscosity coefficient at specified temperature | |
| , | Havriliak and Negami parameters |
| Shear rate | |
| Localized elastic deflection | |
| Evans and Johnson’s friction parameter | |
| Viscosity at rest temperature and atmospheric pressure | |
| Dynamic viscosity of the lubricant | |
| Dynamic viscosity at the center of the contact | |
| Piezoviscosity of the lubricant (solely dependent on pressure) | |
| Bulk flow temperature | |
| Temperature rise | |
| Relaxation time | |
| Coefficient of friction | |
| Density of the lubricant | |
| Density at the center of the contact | |
| Density of the solid bodies | |
| Load relaxation parameter | |
| Equivalent stress | |
| Shear stress | |
| Limiting shear stress | |
| Characteristic shear stress | |
| Pressure relaxation parameter | |
| Thermal partitioning coefficient |
Abbreviations
| 1D | One-Dimensional |
| CMM | Coordinate Measuring Machine |
| EHL | Elastohydrodynamic Lubrication |
| EIN | Effective Influence Newton–Raphson |
| FEA | Finite Element Analysis |
| HN | Havriliak–Negami |
| LLTCA | Lubricated Loaded Tooth Contact Analysis |
| NVH | Noise, Vibration, and Harshness |
| TCA | Tooth Contact Analysis |
Appendix A
| Gear Type | Spur |
|---|---|
| Pinion No. Teeth | 13 |
| Wheel No. Teeth | 35 |
| Gear Module | 3.8 |
| Center Distance | 90 mm |
| Gear Width | 13.3 mm |
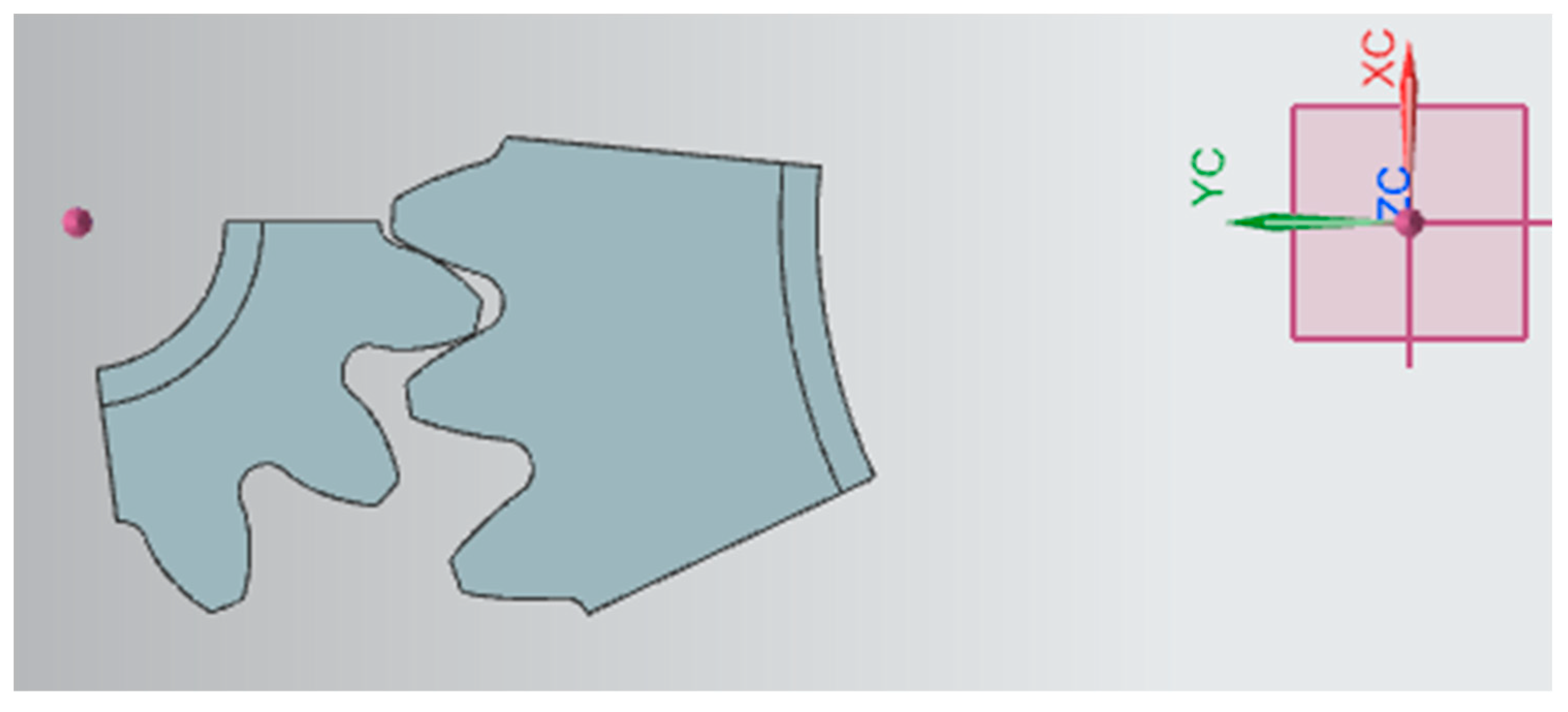
References
- Mohammadpour, M.; Theodossiades, S.; Rahnejat, H.; Kelly, P. Transmission efficiency and noise, vibration and harshness refinement of differential hypoid gear pairs. J. Multi-Body Dynamics 2014, 228, 19–33. [Google Scholar] [CrossRef]
- Wu, S.; Cheng, H.S. A Friction Model of Partial-EHL Contacts and its Application to Power Loss in Spur Gears. Tribol. Trans. 1991, 34, 398–407. [Google Scholar] [CrossRef]
- Diab, Y.; Ville, F.; Velex, P. Investigations on power losses in high-speed gears. J. Eng. Tribol. 2006, 220, 191–198. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. Prediction of Spur Gear Mechanical Power Losses Using a Transient Elastohydrodynamic Lubrication Model. Tribol. Trans. 2010, 53, 554–563. [Google Scholar] [CrossRef]
- Petry-Johnson, T.T.; Kahraman, A.; Anderson, N.E.; Chase, D.R. An Experimental Investigation of Spur Gear Efficiency. J. Mech. Des. 2008, 130, 062601. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. A tribo-dynamic model of a spur gear pair. J. Sound Vib. 2013, 332, 4963–4978. [Google Scholar] [CrossRef]
- Velex, P.; Maatar, M. A mathematical model for analyzing the influence of shape deviations and mounting errors on gear dynamic behaviour. J. Sound Vib. 1996, 191, 629–660. [Google Scholar] [CrossRef]
- Kahraman, A.; Blankenship, G.W. Effect of Involute Tip Relief on Dynamic Response of Spur Gear Pairs. J. Mech. Des. 1999, 121, 313–315. [Google Scholar] [CrossRef]
- Parker, R.; Vijayakar, S.; Imajo, T. Non-linear dynamic response of a spur gear pair: Modelling and experimental comparisons. J. Sound Vib. 2000, 237, 435–455. [Google Scholar] [CrossRef]
- Cooley, C.G.; Liu, C.; Dai, X.; Parker, R.G. Gear tooth mesh stiffness: A comparison of calculation approaches. Mech. Mach. Theory 2016, 105, 540–553. [Google Scholar] [CrossRef]
- Johns-Rahnejat, P.M.; Gohar, R. Point contact elastohydrodynamic pressure distribution and sub-surface stress field. In Int. Tri-Annual Conf. on Multi-Body Dynamics: Monitoring and Simulation Techniques; Bradford: Yorkshire, UK, 1997; pp. 161–177. [Google Scholar]
- Ding, Y.; Rieger, N.F. Spalling formation mechanism for gears. Wear 2003, 254, 1307–1317. [Google Scholar] [CrossRef]
- Tao, J.; Hughes, T.G.; Evans, H.P.; Snidle, R.W.; Hopkinson, N.A.; Talks, M.; Starbuck, J.M. Elastohydrodynamic Lubrication Analysis of Gear Tooth Surfaces from Micropitting Tests. J. Tribol. 2003, 125, 267–274. [Google Scholar] [CrossRef][Green Version]
- Moss, J.; Kahraman, A.; Wink, C. An Experimental Study of Influence of Lubrication Methods on Efficiency and Contact Fatigue Life of Spur Gears. J. Tribol. 2018, 140, 051103. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press (CUP): Cambridge, UK, 2004. [Google Scholar]
- Vijayakar, S.M. Tooth Contact Analysis Software: CALYX; Advanced Numerucal Solutions: Hilliard, OH, USA, 1998. [Google Scholar]
- Karagiannis, I.; Theodossiades, S.; Rahnejat, H. On the dynamics of lubricated hypoid gears. Mech. Mach. Theory 2012, 48, 94–120. [Google Scholar] [CrossRef]
- Fatourehchi, E.; Elisaus, V.; Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Efficiency and Durability Predictions of High Performance Racing Transmissions. SAE Int. J. Passeng. Cars Mech. Syst. 2016, 9, 1117–1124. [Google Scholar] [CrossRef]
- Oglieve, C.; Sivayogan, G.; Mohammadpour, M.; Rahnejat, H. Lubricated loaded tooth contact analysis for spur gear pair. Int. J. Powertrains 2019, 8, 23–39. [Google Scholar] [CrossRef]
- Radzevich, S.P.; Dudley, D.W. Handbook of Practical Gear Design; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- And, P.S.; Velex, P.; Duverger, O.; Sainsot, P. Contribution of Gear Body to Tooth Deflections—A New Bidimensional Analytical Formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar]
- Elisaus, V.; Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Effect of teeth micro-geometrical form modification on contact kinematics and efficiency of high performance transmissions. J. Multi-body Dyn. 2017, 231, 538–555. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A.; Hayasaka, K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears. Mech. Mach. Theory 2006, 41, 83–118. [Google Scholar] [CrossRef]
- Evans, C.R.; Johnson, K.L. Regimes of Traction in Elastohydrodynamic Lubrication. J. Mech. Eng. Sci. 1986, 200, 313–324. [Google Scholar] [CrossRef]
- Chittenden, R.J.; Dowson, D.; Dunn, J.F.; Taylor, C.M. A theoretical analysis of the isothermal elastohydrodynamic lubrication of concentrated contacts. I. Direction of lubricant entrainment coincident with the major axis of the Hertzian contact ellipse. Proc. R. Soc. London Ser. A. Math. Phys. Sci. 1985, 397, 245–269. [Google Scholar]
- Olver, A.V. Gear lubrication—A review. J. Eng. Tribol. 2002, 216, 255–267. [Google Scholar] [CrossRef]
- Gohar, R. Elastohydrodynamics; World Scientific Pub Co Pte Lt: Singapore, Singapore, 2001. [Google Scholar]
- Hamrock, B.J.; Jacobson, B.O. Elastohydrodynamic Lubrication of Line Contacts. ASLE Trans. 1984, 27, 275–287. [Google Scholar] [CrossRef]
- Paouris, L.; Rahmani, R.; Theodossiades, S.; Rahnejat, H.; Hunt, G.; Barton, W. An Analytical Approach for Prediction of Elastohydrodynamic Friction with Inlet Shear Heating and Starvation. Tribol. Lett. 2016, 64, 10. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Houpert, L. New Results of Traction Force Calculations in Elastohydrodynamic Contacts. J. Tribol. 1985, 107, 241–245. [Google Scholar] [CrossRef]
- Vogel, H. The temperature dependence law of the viscosity of fluids. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Crouch, R.F.; Cameron, A. Viscosity-temperature equations for lubricants. J. Inst. Pet 1961, 47, 307–313. [Google Scholar]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology; World Scientific Pub Co Pte Lt: Singapore, Singapore, 2008. [Google Scholar]
- Yang, P.; Cui, J.; Jin, Z.M.; Dowson, D. Transient elastohydrodynamic analysis of elliptical contacts. Part 2: Thermal and Newtonian lubricant solution. J. Eng. Tribol. 2005, 219, 187–200. [Google Scholar] [CrossRef]
- Greenwood, J.A. Presentation of Elastohydrodynamic Film-Thickness Results. J. Mech. Eng. Sci. 1969, 11, 128–132. [Google Scholar] [CrossRef]
- Reiner, M. The Deborah Number. Phys. Today 1964, 17, 62. [Google Scholar] [CrossRef]
- Bezot, P.; Hesse-Bezot, C.; Dalmaz, G.; Taravel, P.; Vergne, P.; Berthe, D. A study of traction in elastohydrodynamic lubrication: Experimental and simulated curves for a point contact lubricated by a silicone fluid. Wear 1988, 123, 13–31. [Google Scholar] [CrossRef]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.; Fitzsimons, B. Tribology of piston compression ring conjunction under transient thermal mixed regime of lubrication. Tribol. Int. 2013, 59, 248–258. [Google Scholar] [CrossRef]
- Paouris, L.; Rahmani, R.; Theodossiades, S.; Rahnejat, H.; Hunt, G.; Barton, W. Inefficiency predictions in a hypoid gear pair through tribodynamics analysis. Tribol. Int. 2018, 119, 631–644. [Google Scholar] [CrossRef]
- Olver, A.V.; Spikes, H.A. Prediction of traction in elastohydrodynamic lubrication. J. Eng. Tribol. 1998, 212, 321–332. [Google Scholar] [CrossRef]
- Sharif, K.J.; Evans, H.P.; Snidle, R.W.; Newall, J.P. Modeling of Film Thickness and Traction in a Variable Ratio Traction Drive Rig. J. Tribol. 2004, 126, 92–104. [Google Scholar] [CrossRef][Green Version]
- Jalali-Vahid, D.; Gohar, R.; Rahnejat, H.; Jin, Z.M. Prediction of oil-film thickness and shape in elliptical point contacts under combined rolling and sliding motion. J. Eng. Tribol. 2000, 214, 427–437. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, Plasticity, and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283. [Google Scholar] [CrossRef]
- Hoglund, E.; Jacobson, B. Experimental Investigation of the Shear Strength of Lubricants Subjected to High Pressure and Temperature. J. Tribol. 1986, 108, 571–577. [Google Scholar] [CrossRef]
- Rahnejat, H.; Johns-Rahnejat, P.M. Mechanics of Contacting Surfaces. In Encyclopedia of Automotive Engineering; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press (CUP): Cambridge, UK, 1985. [Google Scholar]
- Ioannides, E.; Harris, T.A. A New Fatigue Life Model for Rolling Bearings. J. Tribol. 1985, 107, 367–377. [Google Scholar] [CrossRef]
- Rahnejat, H.; Rahmani, R.; Mohammadpour, M.; Johns-Rahnejat, P.M. Tribology of power train systems. ASM Handb. 2017, 18, 916–934. [Google Scholar]
- Paouris, L.; Theodossiades, S.; De la Cruz, M.; Rahnejat, H.; Kidson, A.; Hunt, G.; Barton, W. Lubrication analysis and sub-surface stress field of an automotive differential hypoid gear pair under dynamic loading. J. Mech. Eng. Sci. 2016, 230, 1183–1197. [Google Scholar] [CrossRef]
- Hamilton, G.M.; Moore, S.L. Deformation and pressure in an elastohydrodynamic contact. Proc. R. Soc. London Ser. A. Math. Phys. Sci. 1971, 322, 313–330. [Google Scholar]
- Johns-Rahnejat, P.M. Pressure and Stress Distribution under Elastohydrodynamic Point Contacts. Ph.D. Thesis, Imperial College, University of London, London, UK, 1988. [Google Scholar]
- Jalali-Vahid, D.; Rahnejat, H.; Gohar, R.; Jin, Z.M. Comparison between experiments and numerical solutions for isothermal elastohydrodynamic point contacts. Appl. Phys. 1998, 31, 2725–2732. [Google Scholar] [CrossRef]
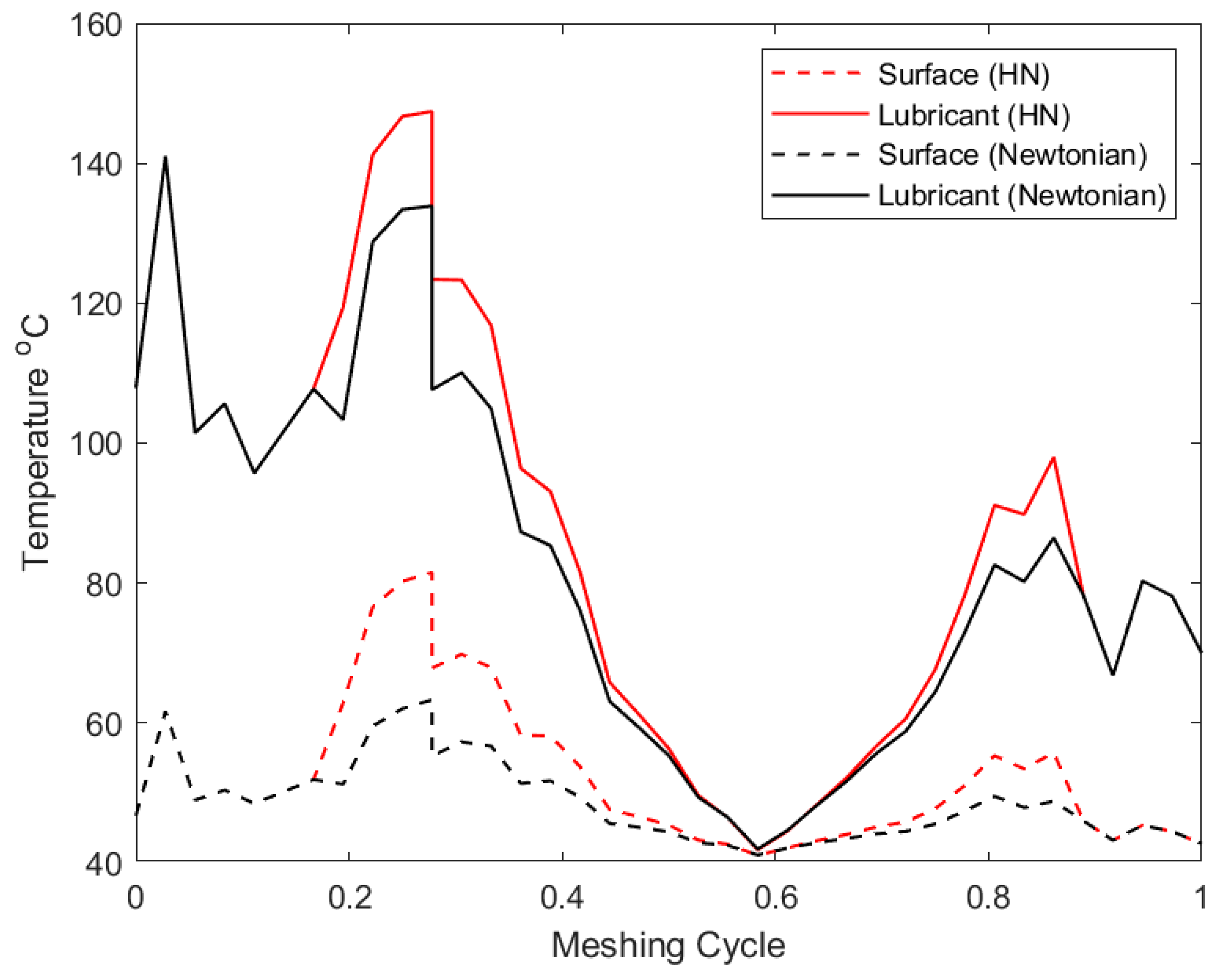

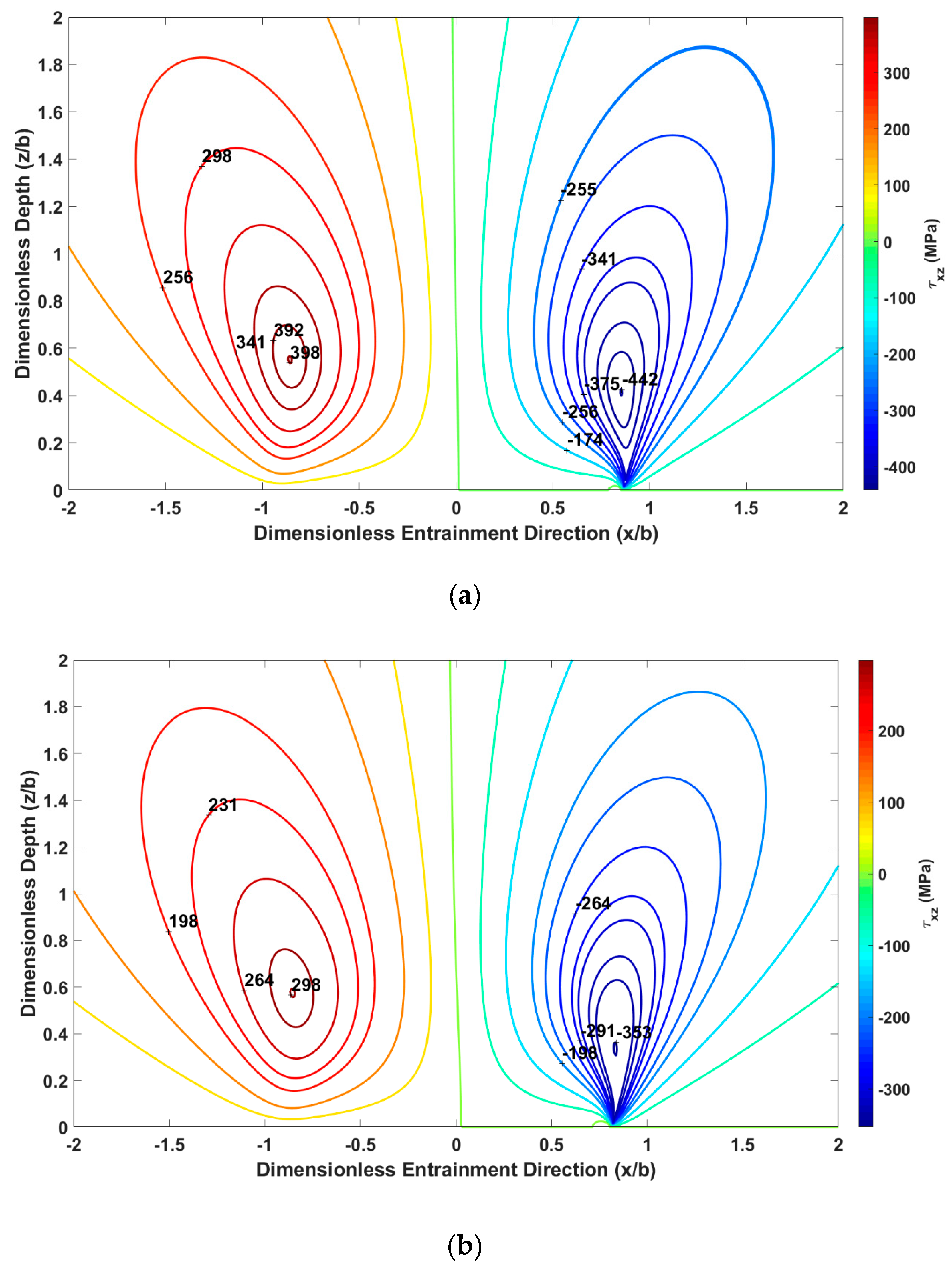
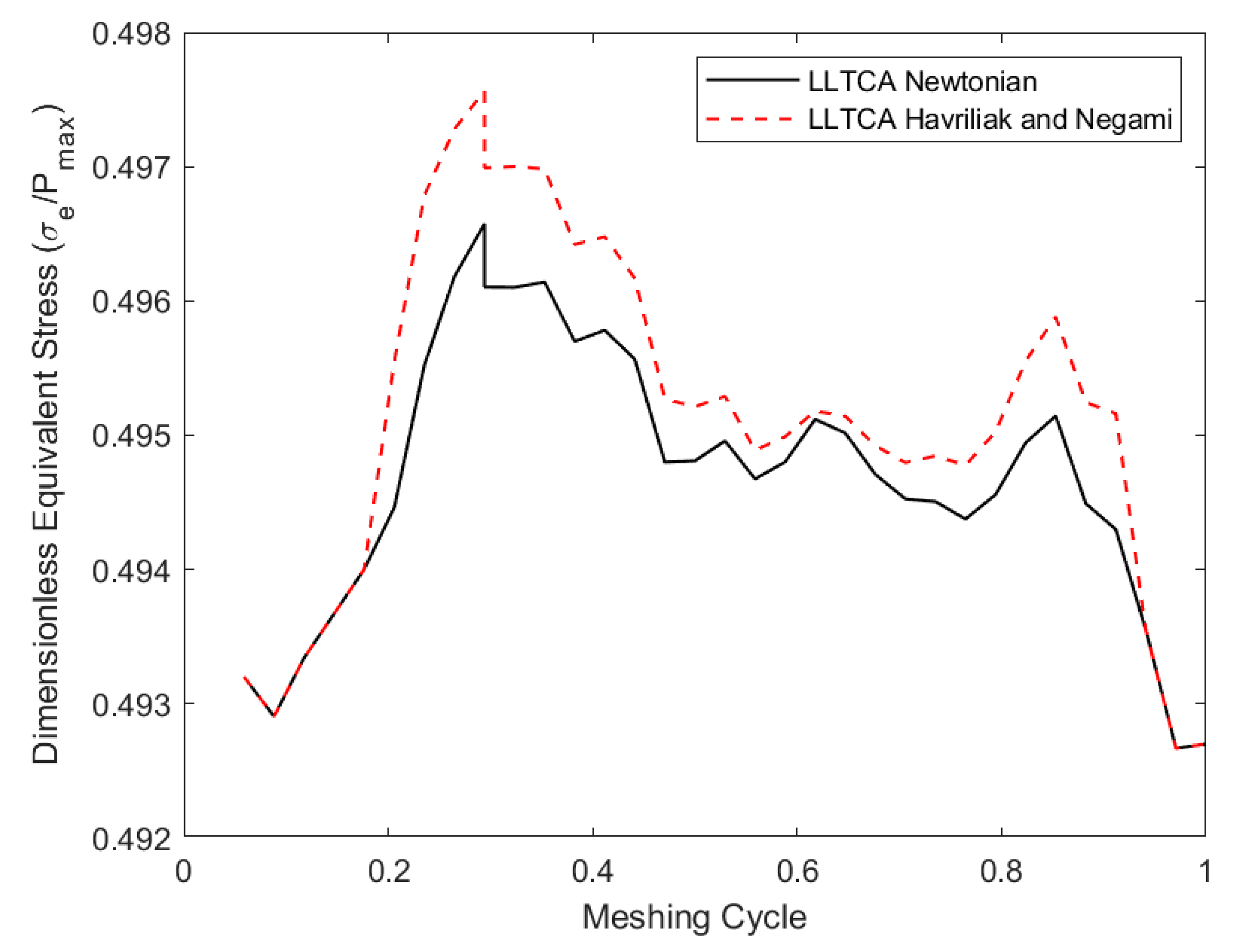
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Young’s modulus (both pinion and wheel) | , | 206 | GPa |
| Poisson ratio (both pinion and wheel) | , | 0.3 | - |
| Dynamic viscosity (at 40 °C) | 0.0304 | Pa·s | |
| Lubricant density (at 40 °C) | 851 | kg/m3 | |
| Pressure coefficient of viscosity (at 40 °C) | 1.69 × 10−8 | 1/Pa | |
| Density of the solid | 7800 | kg/m3 | |
| Limiting shear stress | 2 | MPa | |
| Specific heat capacity of lubricant | 1670 | J/kg·K | |
| Specific heat capacity of solid | 470 | J/kg·K | |
| Thermal conductivity of lubricant | 0.137 | W/m·K | |
| Thermal conductivity of the solid | 46.7 | W/m·K |
| Parameter | Value | Units |
|---|---|---|
| 7.9 × 10−8 | S | |
| 0.7 | - | |
| 1 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivayogan, G.; Rahmani, R.; Rahnejat, H. Lubricated Loaded Tooth Contact Analysis and Non-Newtonian Thermoelastohydrodynamics of High-Performance Spur Gear Transmission Systems. Lubricants 2020, 8, 20. https://doi.org/10.3390/lubricants8020020
Sivayogan G, Rahmani R, Rahnejat H. Lubricated Loaded Tooth Contact Analysis and Non-Newtonian Thermoelastohydrodynamics of High-Performance Spur Gear Transmission Systems. Lubricants. 2020; 8(2):20. https://doi.org/10.3390/lubricants8020020
Chicago/Turabian StyleSivayogan, Gajarajan, Ramin Rahmani, and Homer Rahnejat. 2020. "Lubricated Loaded Tooth Contact Analysis and Non-Newtonian Thermoelastohydrodynamics of High-Performance Spur Gear Transmission Systems" Lubricants 8, no. 2: 20. https://doi.org/10.3390/lubricants8020020
APA StyleSivayogan, G., Rahmani, R., & Rahnejat, H. (2020). Lubricated Loaded Tooth Contact Analysis and Non-Newtonian Thermoelastohydrodynamics of High-Performance Spur Gear Transmission Systems. Lubricants, 8(2), 20. https://doi.org/10.3390/lubricants8020020






