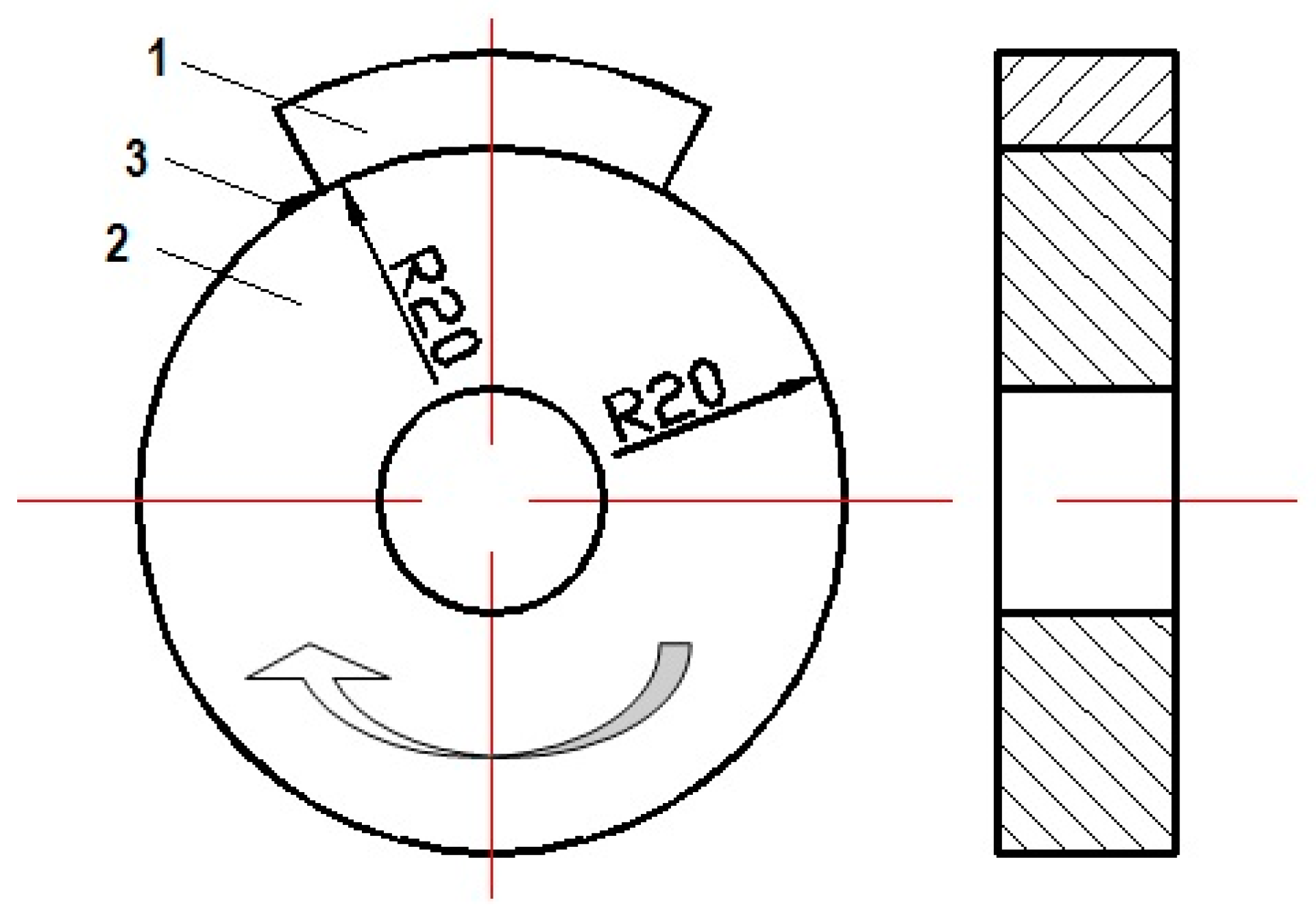
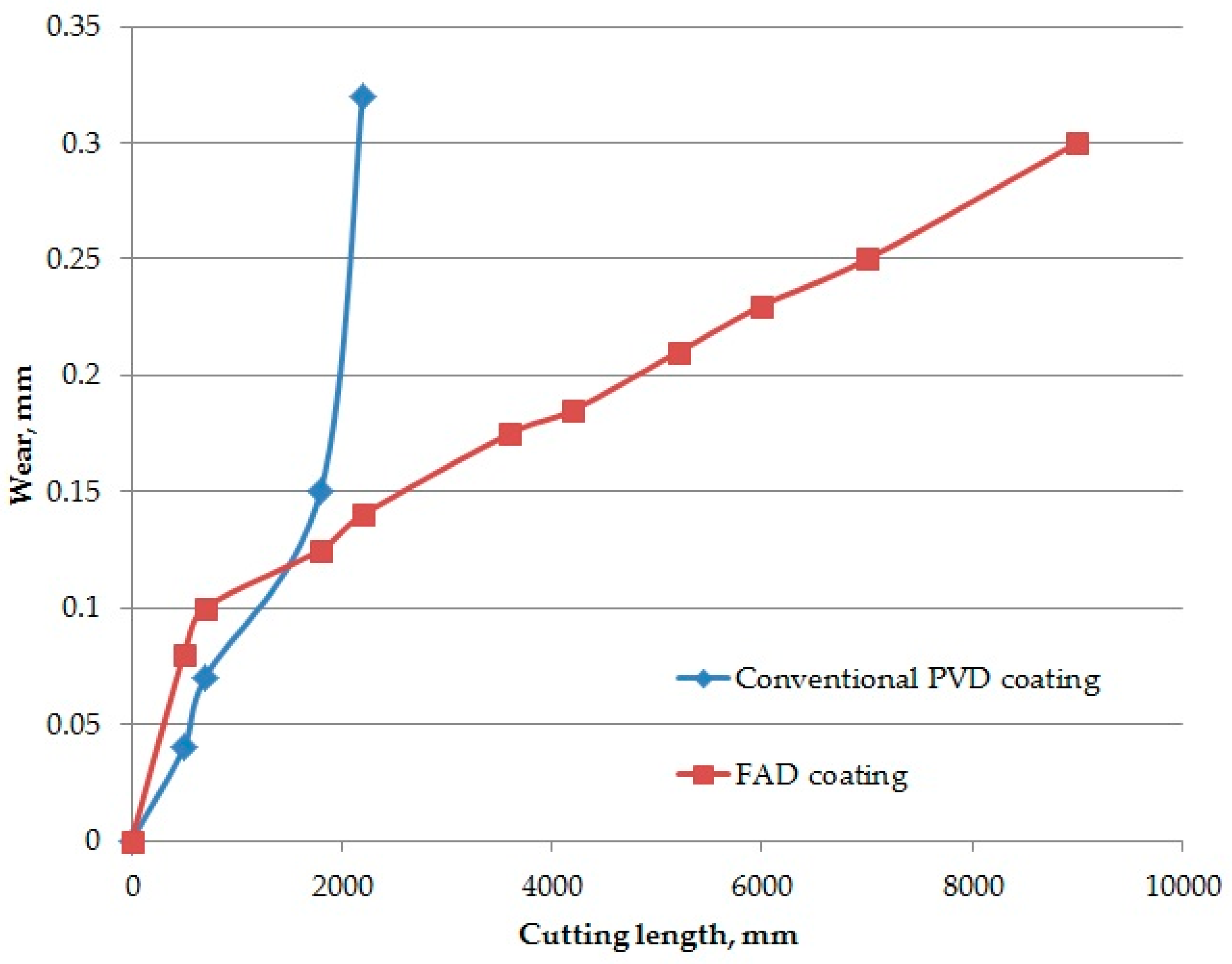
In [
6,
7,
8,
9,
10] it is stated that materials enter a nonequilibrium state during friction due to the formation of secondary structures on the surface. In [
2] the analyzed tribosystem deviated significantly from the equilibrium state. State analysis was based on the concept of reserved energy, the entropy of the system and entropy production. If energy delivered to the system has insufficient time to be dissipated by channels such as thermal conductivity, heterogeneous secondary structures that affect the state of the contacting surfaces are expected to manifest and grow in sliding bodies. Therefore, entropy might decrease, and the system will shift to a non-equilibrium state. According to [
6], once secondary structures are formed, friction energy gets unevenly distributed within the rubbing body and becomes mostly concentrated in secondary structures.
As a consequence, the secondary structures perform protective functions, limiting the spread of interactions inside the rubbing bodies and reducing their intensity. Their appearance, therefore, corresponds to the Le Chatelier principle [
11]. All other conditions being equal, increasing the degree of uneven distribution of energy within the rubbing body leads to a decrease in its entropy [
12].
In a rubbing body, the friction energy is distributed according to a monotonically decreasing function with distance from the friction zone [
6]. Conversely, the distribution of friction energy becomes abrupt as secondary structures form. Most of the friction energy is concentrated within the secondary structures, sharply decreasing at their boundary. This energy distribution has a greater degree of non-equilibrium compared to the case of a rubbing body where secondary structures are not present. Under equal friction energies, the entropy of a friction body with secondary structures will be less than the entropy of a friction body without them. Thus, as the material reacts to friction, it will enter a non-equilibrium state. There are processes which strive to reduce entropy within the rubbing material, i.e., through negative entropy production. The material reacts to friction by dissociating from the equilibrium state, which leads to a decrease in the wear rate [
13]. In this context, it becomes necessary to investigate the wear rate behavior of materials initially present in a state of non-equilibrium.
Theory
From [
5,
11], it follows that the wear rate decreases along with entropy production. In [
11,
13], it is noted that the production of entropy markedly decreases under tougher friction conditions due to self-organization and the formation of dissipative structures in the friction zone. Dissipative structures are characterized by processes with increased free energy and negative entropy production. The latter contributes to a decrease in the total entropy production of a friction body compared to its state under the same conditions without self-organization.
The entropy production of a rubbing body without self-organization is given in expression (1):
where
is the sum of entropy production processes occurring in the rubbing body as a result of friction without self-organization. It should be noted that
.
The production of entropy after self-organization is given in (2):
where:
is the production of the entropy in the rubbing body following self-organization;
is the sum of entropy production processes contributed by dissipative structures.
The second term on the right-hand side of (2) is expressed in terms of absolute value with a negative sign to emphasize the negative entropy production of dissipative structure processes.
Comparing (1) and (2) it can be concluded that:
Thus, according to [
11], all other conditions being equal, the wear rate of the rubbing body during the course of self-organization is less than that of the rubbing body where self organization is absent.
From the point of view of thermodynamics, the nonequilibrium state of a material is characterized by the relatively high value of internal energy and the relatively low value of entropy. Examples of such materials include hardened alloys as compared to quenched and annealed materials, alloys with a high value of internal stresses as compared to annealed materials and others. Relaxation processes occur in these materials during heating, which bring it closer to the equilibrium state. In quenched materials, such processes can be the decomposition of a supersaturated solid solution, a decrease of the density of vacancies or recrystallization, whereas in materials that have increased internal stresses, these processes include the movement of dislocations with increasing uniformity of distribution by volume. Different relaxation processes can proceed through various mechanisms. Increasing entropy and decreasing internal energy are common features of these processes. Relaxation processes are accompanied by positive entropy production.
During the course of relaxation processes under friction, the entropy production of the rubbing body will increase in both cases with (4) and without self-organization (5):
where:
are the entropy production relaxation processes.
Comparing (5) and (4) with (1) and (2) respectively, it can be concluded that entropy production increases during the passage of the relaxation processes. Therefore, an increase in the wear rate is anticipated.
However, it was noted in [
14] that the probability of self-organization rises along with the increasing complexity of the system. In [
15,
16], the probability of self-organization and the formation of dissipative structures with regard to friction processes on the surface of a rubbing body is estimated depending on the number of thermodynamic flows interacting with the rubbing body. In (6), the probability of thermodynamic stability loss of a rubbing body is given, which is a prerequisite for the initiation of self-organization:
where:
P isthe probability of loss of thermodynamic stability,
n is the number of thermodynamic fluxes.
From (6) it follows that the probability of thermodynamic stability loss increases alongside the number of flows. Consequently, the probability of self-organization also increases.
During friction of relatively non-equilibrium materials, thermodynamic flows of matter, energy, dislocations and accompanying relaxation processes are added to the thermodynamic flows caused by friction. According to (6), this increases the probability of self-organization
In non-equilibrium materials, self-organization will take place under less severe friction conditions than in equilibrium materials. Given the same friction conditions, self-organization is unlikely to commence in equilibrium materials but may take place in non-equilibrium ones. Self-organization in non-equilibrium materials will reduce the wear rate several times compared to relatively equilibrium materials without self-organization [
13].
It should be noted that all previous arguments only apply if the properties of equilibrium and non-equilibrium materials are similar.