High-Speed Measurements of Steel–Ice Friction: Experiment vs. Calculation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ice Tribometry-Setup, Materials and Test Program
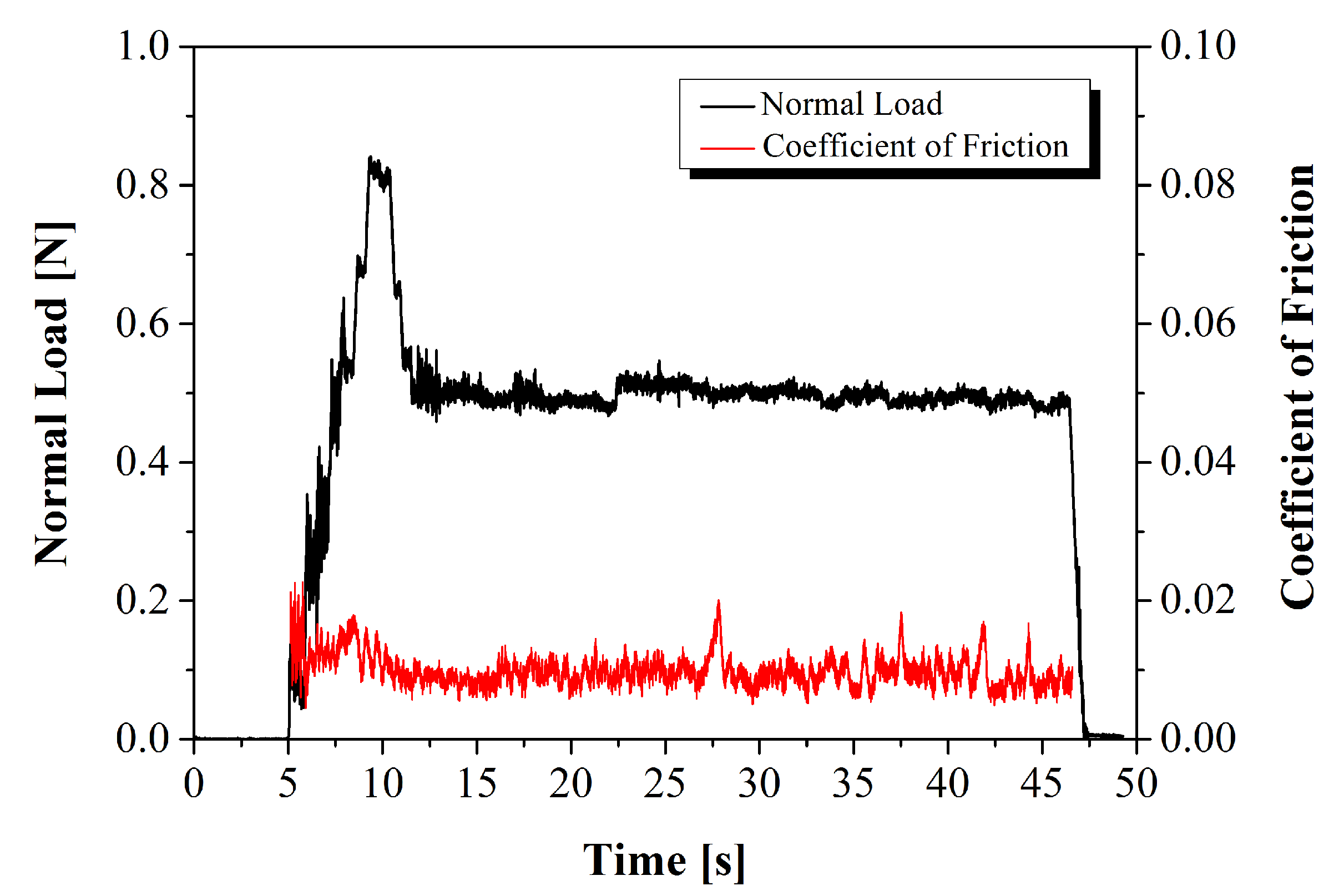
2.1.1. Tribometry
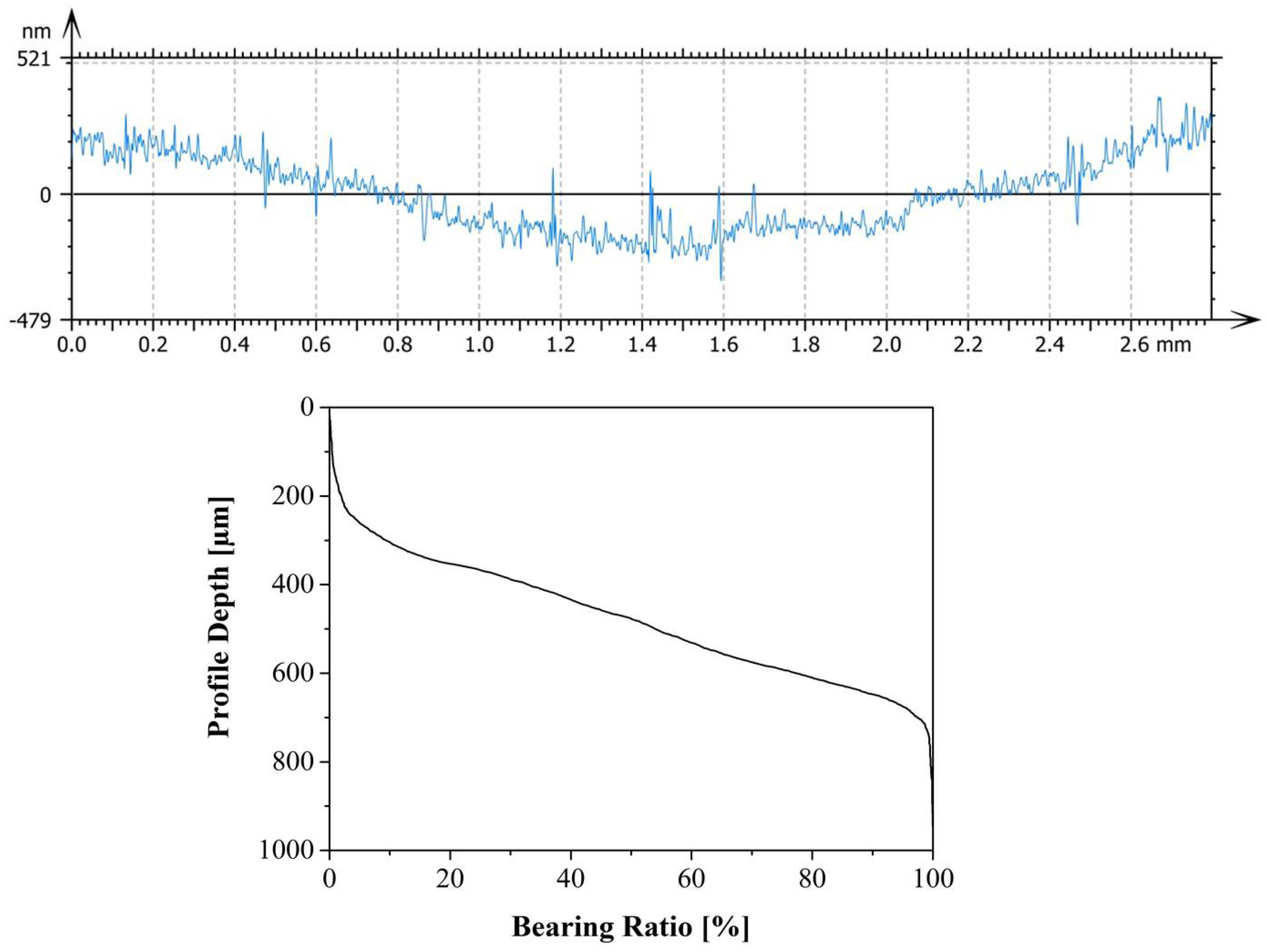
2.1.2. Ice and Steel Sample Preparation
2.1.3. Test Program
2.2. Basics of Friction Calculation
3. Results
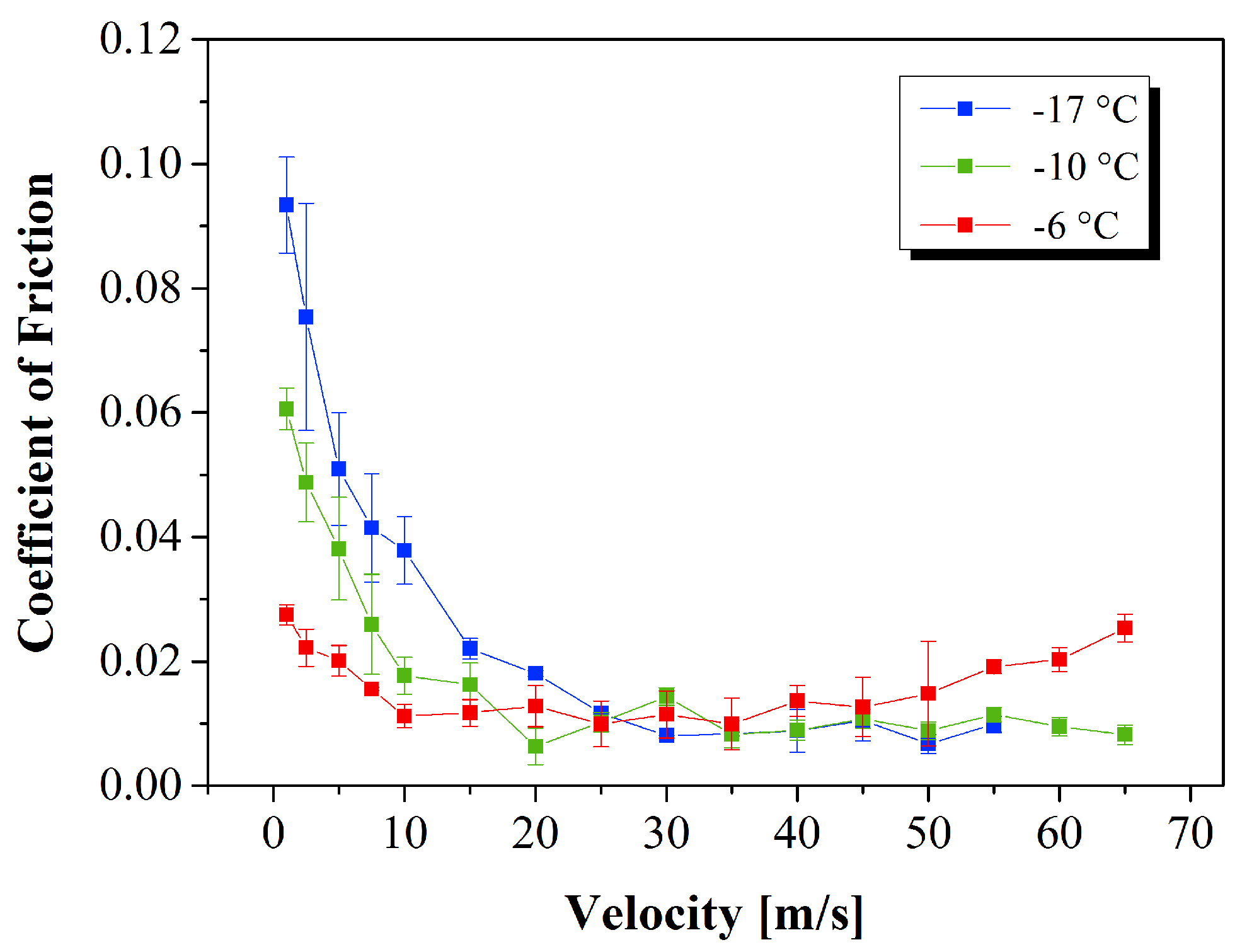
3.1. Friction Measurements
3.2. Calculations
4. Discussion
5. Conclusions
- Coefficients of friction between steel and ice were successfully measured up to high velocities of 240 km/h by means of a custom-built tribometer.
- Using the model of Makkonen et al., friction coefficients of the steel–ice interface can be calculated with very good precision. The model is ready to be implemented into modern calculation tools of bobsleigh track designers.
- For highest sliding velocities, the coefficients of friction do not become lower than 0.008.
Author Contributions
Conflicts of Interest
References
- Scherge, M.; Böttcher, R.; Richter, M.; Gurgel, U. High-Speed Ice Friction Experiments under Lab Conditions: On the Influence of Speed and Normal Force. ISRN Tribol. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Itagaki, K.; Huber, N.P.; Lemieux, G.E. Dynamic Friction of a Metal Runner on Ice; CRREL Report; 1989. [Google Scholar]
- Penny, A.; Lozowski, E.; Forest, T.; Fong, C.; Maw, S.; Montgomery, P.; Sinha, N. Speedskate ice friction: Review and numerical model - FAST 1.0. In Physics and Chemistry of Ice; Kuhs, W.F., Ed.; The Royal Society of Chemistry: Cambridge, UK, 2007; pp. 495–502. [Google Scholar]
- Dumm, M.; Hainzlmaier, C.; Boerboom, S.; Wintermantel, E. The Effect of Pressure on Friction of Steel and Ice and Implementation to Bobsleigh Runners. In The Engineering of Sport 6; Springer: New York, NY, USA, 2006; pp. 103–106. [Google Scholar]
- Mills, A. The coefficient of friction, particularly of ice. Phys. Educ. 2008, 43, 392. [Google Scholar] [CrossRef]
- Kobayashi, T. Studies of the properties of ice in speed-skating rinks. ASHRAE J. 1973, 15, 51–56. [Google Scholar]
- Böttcher, R.; Seidelmann, M.; Scherge, M. Sliding of UHMWPE on ice: Experiment vs. modeling. Cold Reg. Sci. Technol. 2017, 141, 171–180. [Google Scholar] [CrossRef]
- Marmo, B.A.; Blackford, J.R.; Jeffree, C.E. Ice friction, wear features and their dependence on sliding velocity and temperature. J. Glaciol. 2005, 51, 391–398. [Google Scholar] [CrossRef]
- Ovaska, M.; Tuononen, A.J. Multiscale imaging of wear tracks in ice skate friction. Tribol. Int. 2018, 121, 280–286. [Google Scholar]
- Spagni, A.; Berardo, A.; Marchetto, D.; Gualtieri, E.; Pugno, N.M.; Valeri, S. Friction of rough surfaces on ice: Experiments and modeling. Wear 2016, 368–369, 258–266. [Google Scholar] [CrossRef]
- De Koning, J.J.; de Groot, G.; van Ingen Schenau, G.J. Ice friction during speed skating. J. Biomech. 1992, 25, 565–571. [Google Scholar] [CrossRef]
- Federolf, P.A.; Mills, R.; Nigg, B. Ice friction of flared ice hockey skate blades. J. Sports Sci. 2008, 26, 1201–1208. [Google Scholar] [CrossRef] [PubMed]
- Poirier, L. Ice Friction in the Sport of Bobsleigh. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2011. [Google Scholar]
- Makkonen, L.; Tikanmäki, M. Modeling the friction of ice. Cold Reg. Sci. Technol. 2014, 102, 84–93. [Google Scholar] [CrossRef]
- Oksanen, P.; Keinonen, J. The mechanism of friction of ice. Wear 1982, 78, 315–324. [Google Scholar] [CrossRef]
- Yen, Y.C. Review of thermal properties of snow, ice and sea ice. Cold Reg. Res. Eng. Lab. 1981, 81, 1–27. [Google Scholar]

| Entity | Unit | Value |
|---|---|---|
| temperatures | −17 / −10 / −6 | |
| velocities | m/s | 1 / 2.5 / 5 / 7.5 / 10 / 15 / 20 / 25 / 30 / 35 / 40 / 45 |
| 50 / 55 / 60 / 65 | ||
| applied load | mN | 500 |
| average track radius | mm | 7.5 |
| pin diameter | mm | 3 |
| nominal pressure | MPa | 0.07 |
| step duration | s | 30 |
| (nm) | (nm) | Rsk | Rku |
|---|---|---|---|
| 33.8 ± 3.72 | 47.37 ± 5.51 | 0.61 ± 0.71 | 7.12 ± 1.08 |
| Unit | Ice | Steel | |
|---|---|---|---|
| thermal conductivity | W/m/K | 55 | |
| specific heat | J/kg/K | 1962 | 460 |
| density at = −20 | kg/m3 | 919.7 | 7900 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scherge, M.; Böttcher, R.; Spagni, A.; Marchetto, D. High-Speed Measurements of Steel–Ice Friction: Experiment vs. Calculation. Lubricants 2018, 6, 26. https://doi.org/10.3390/lubricants6010026
Scherge M, Böttcher R, Spagni A, Marchetto D. High-Speed Measurements of Steel–Ice Friction: Experiment vs. Calculation. Lubricants. 2018; 6(1):26. https://doi.org/10.3390/lubricants6010026
Chicago/Turabian StyleScherge, Matthias, Roman Böttcher, Alberto Spagni, and Diego Marchetto. 2018. "High-Speed Measurements of Steel–Ice Friction: Experiment vs. Calculation" Lubricants 6, no. 1: 26. https://doi.org/10.3390/lubricants6010026
APA StyleScherge, M., Böttcher, R., Spagni, A., & Marchetto, D. (2018). High-Speed Measurements of Steel–Ice Friction: Experiment vs. Calculation. Lubricants, 6(1), 26. https://doi.org/10.3390/lubricants6010026





