Degradation Law Analysis and Life Estimation of Transmission Accuracy of RV Reducer Based on Tooth Surface and Bearing Wear
Abstract
1. Introduction
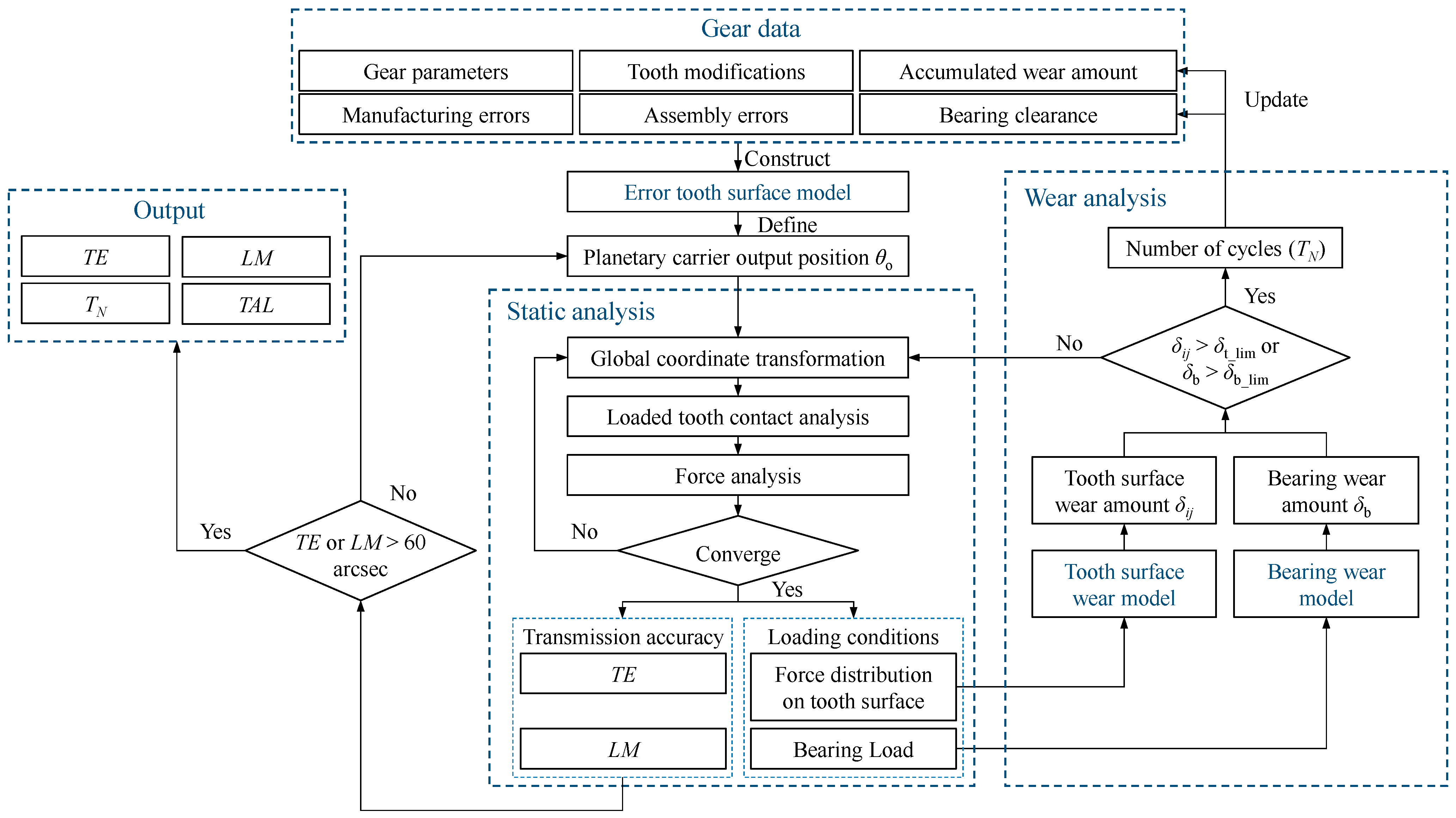
2. Static Analysis Model of RV Reducer
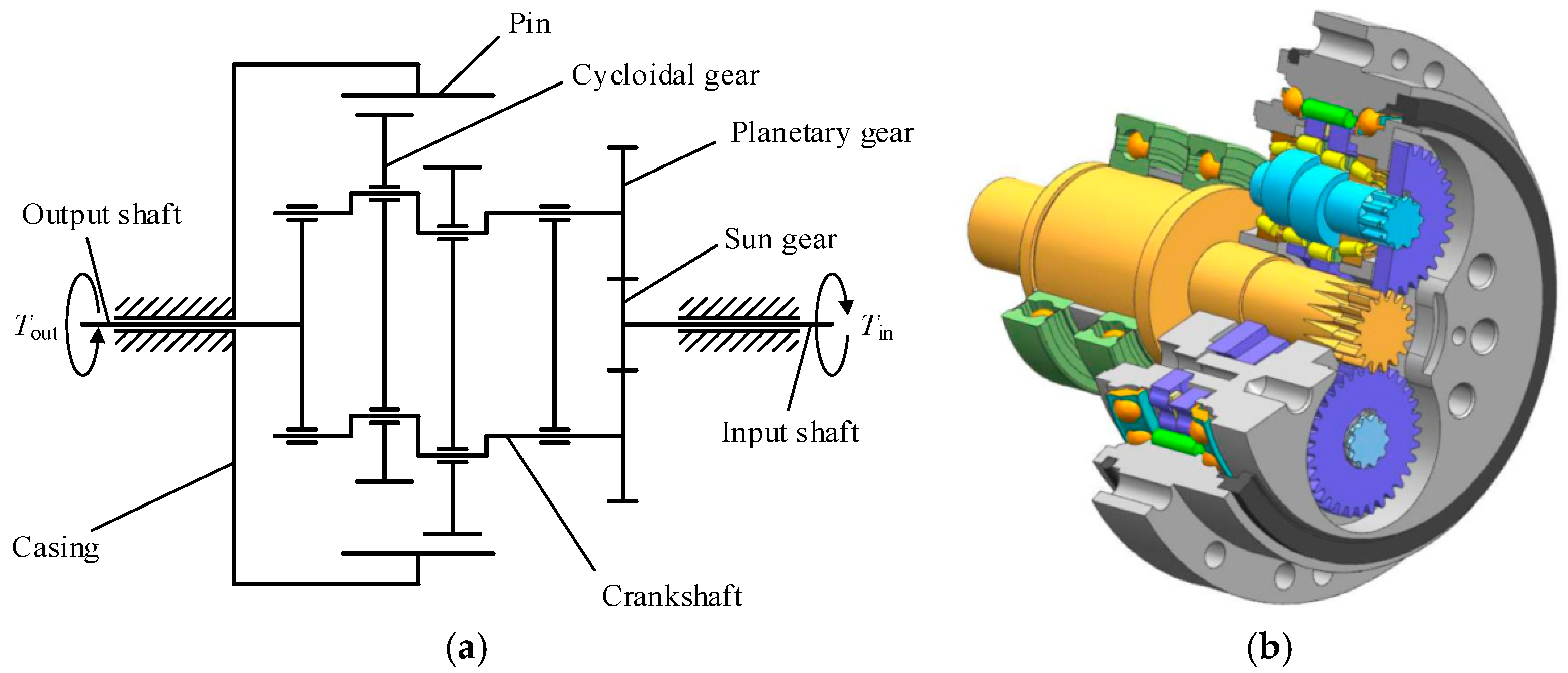
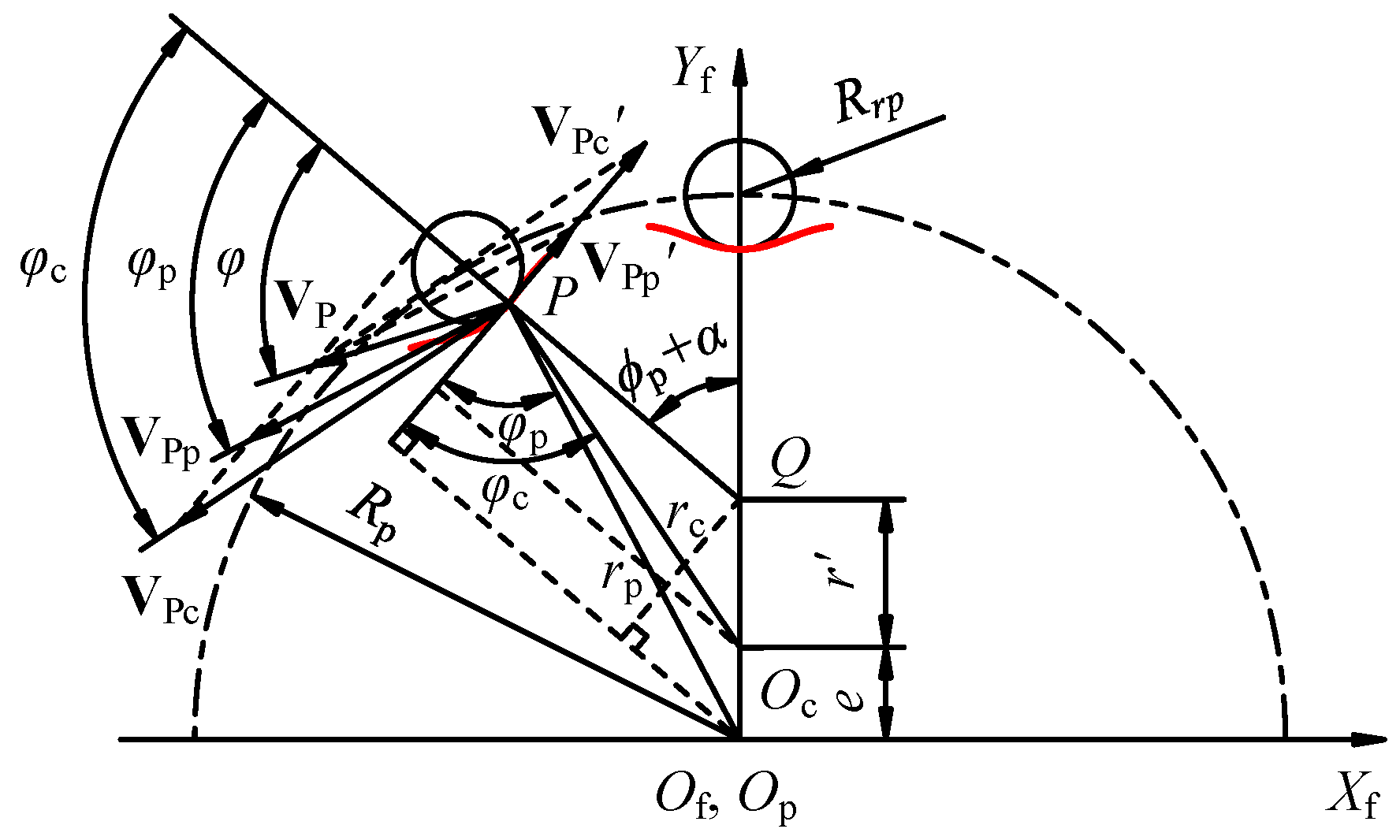
2.1. Transmission Principle
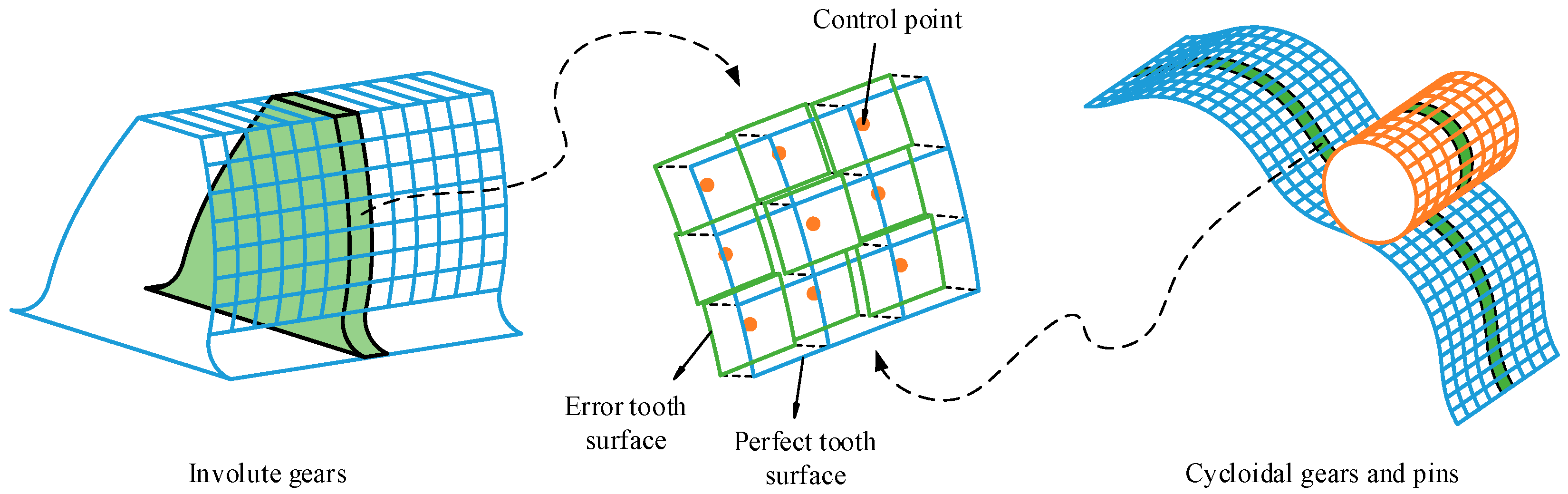
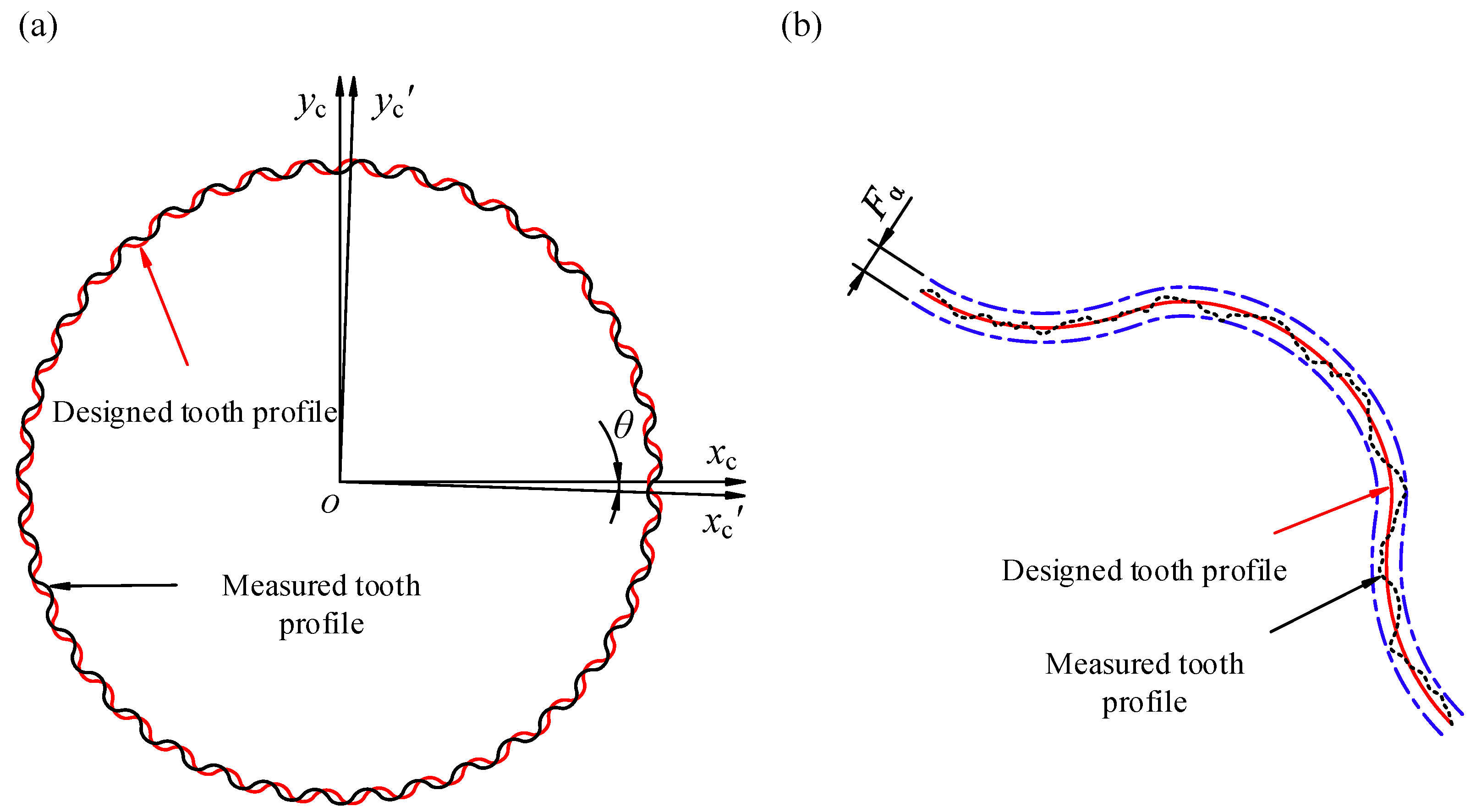
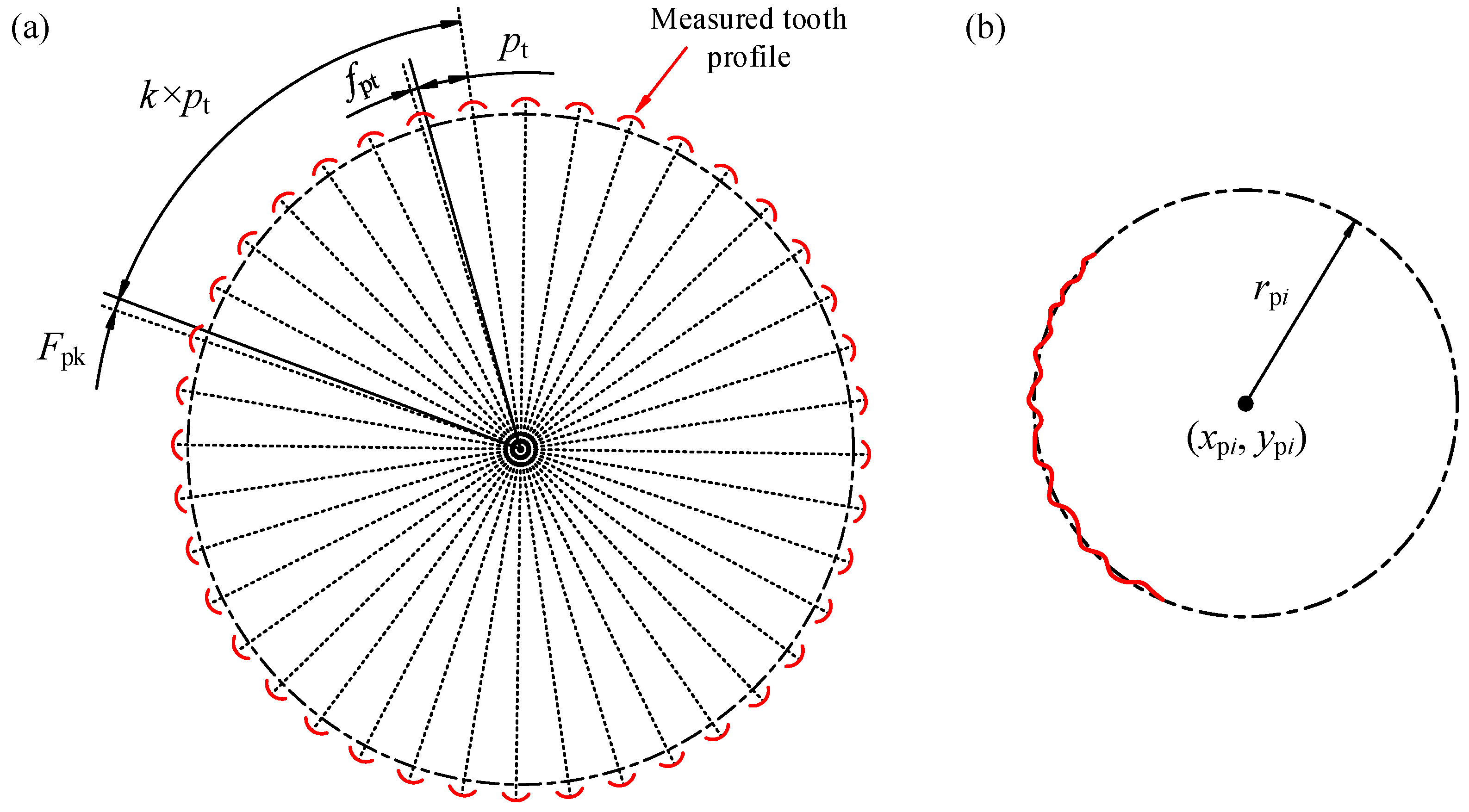
2.2. Error Tooth Surface Model
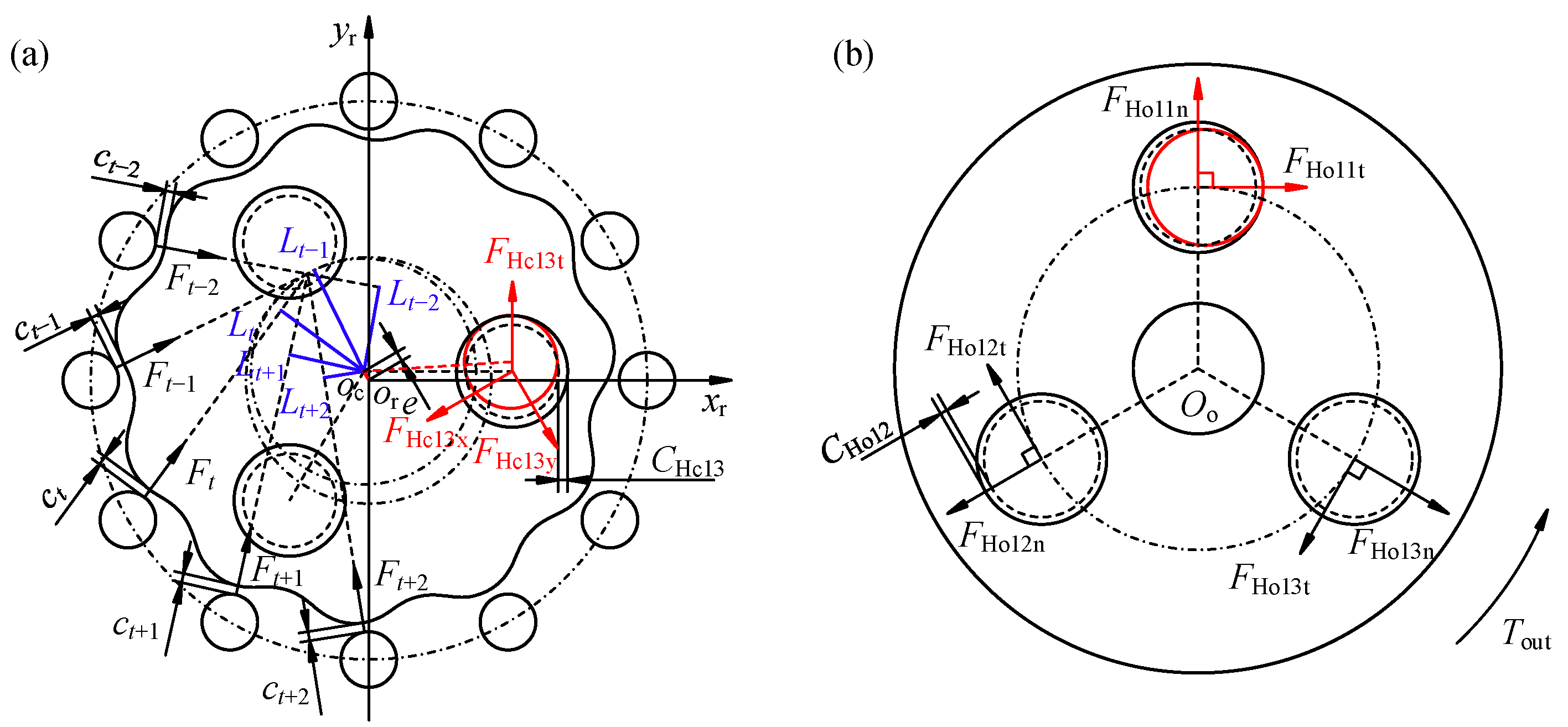
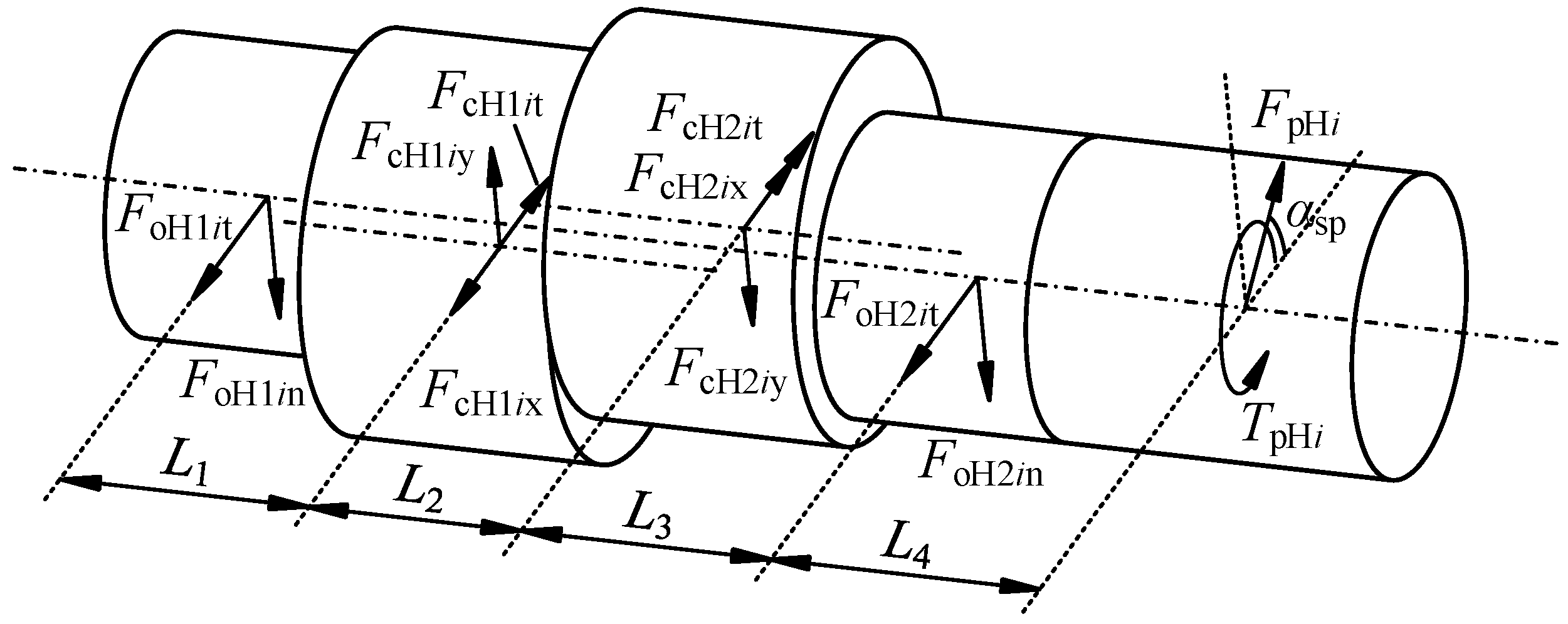
2.3. Static Equilibrium and Deformable Compatibility Conditions
2.4. Calculation Method for Transmission Accuracy and TAL
3. Wear Model of the Tooth Surface and Bearing
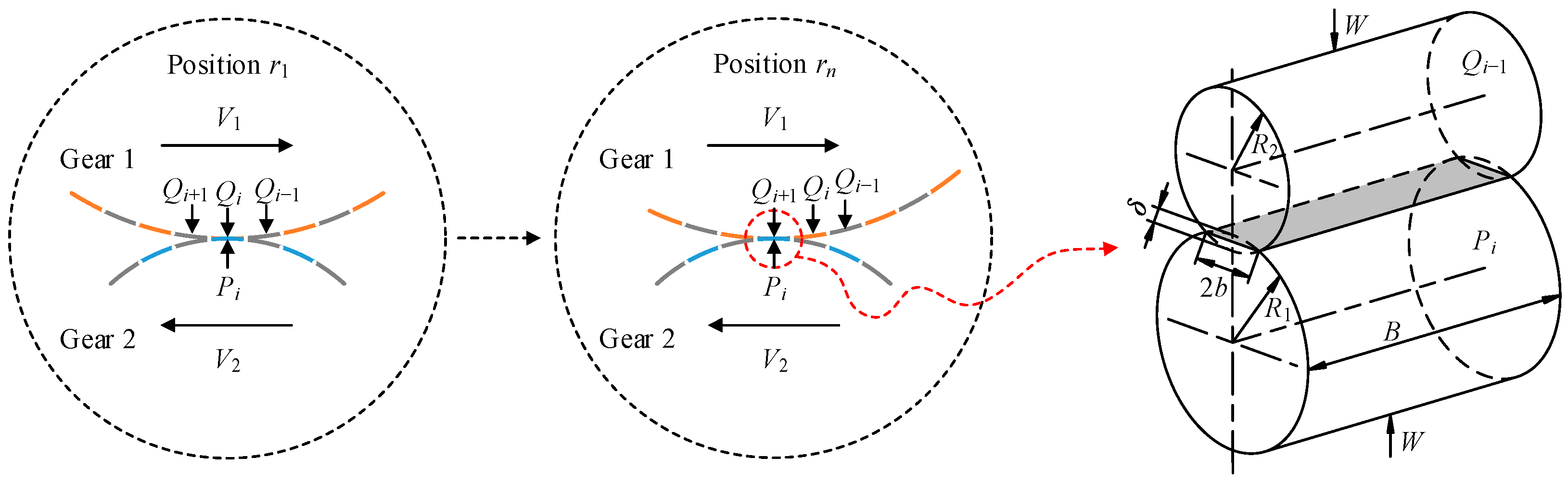
3.1. Tooth Surface Wear Model
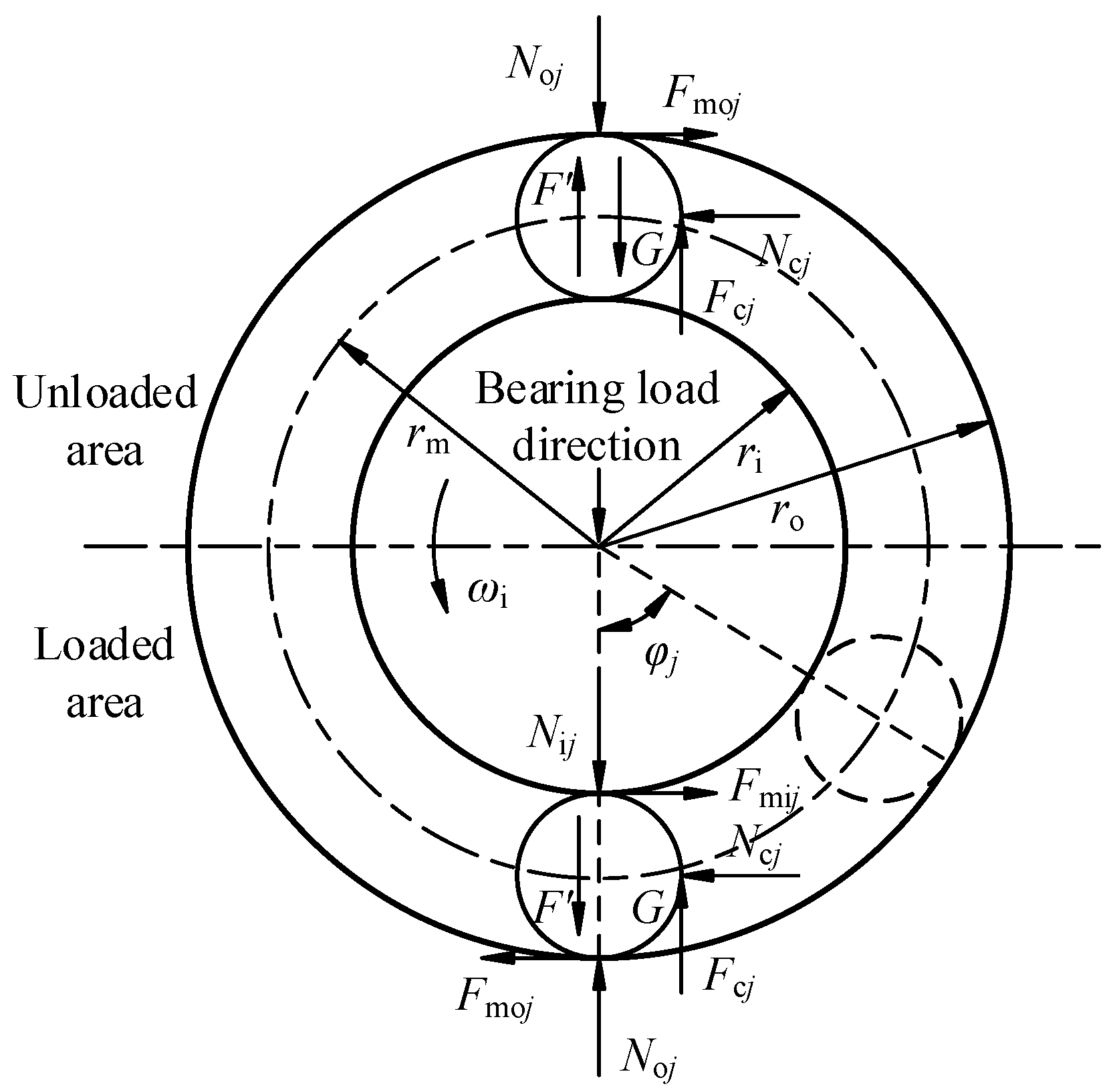
3.2. Rolling Bearing Wear Model
4. Degradation Law Analysis of Transmission Accuracy
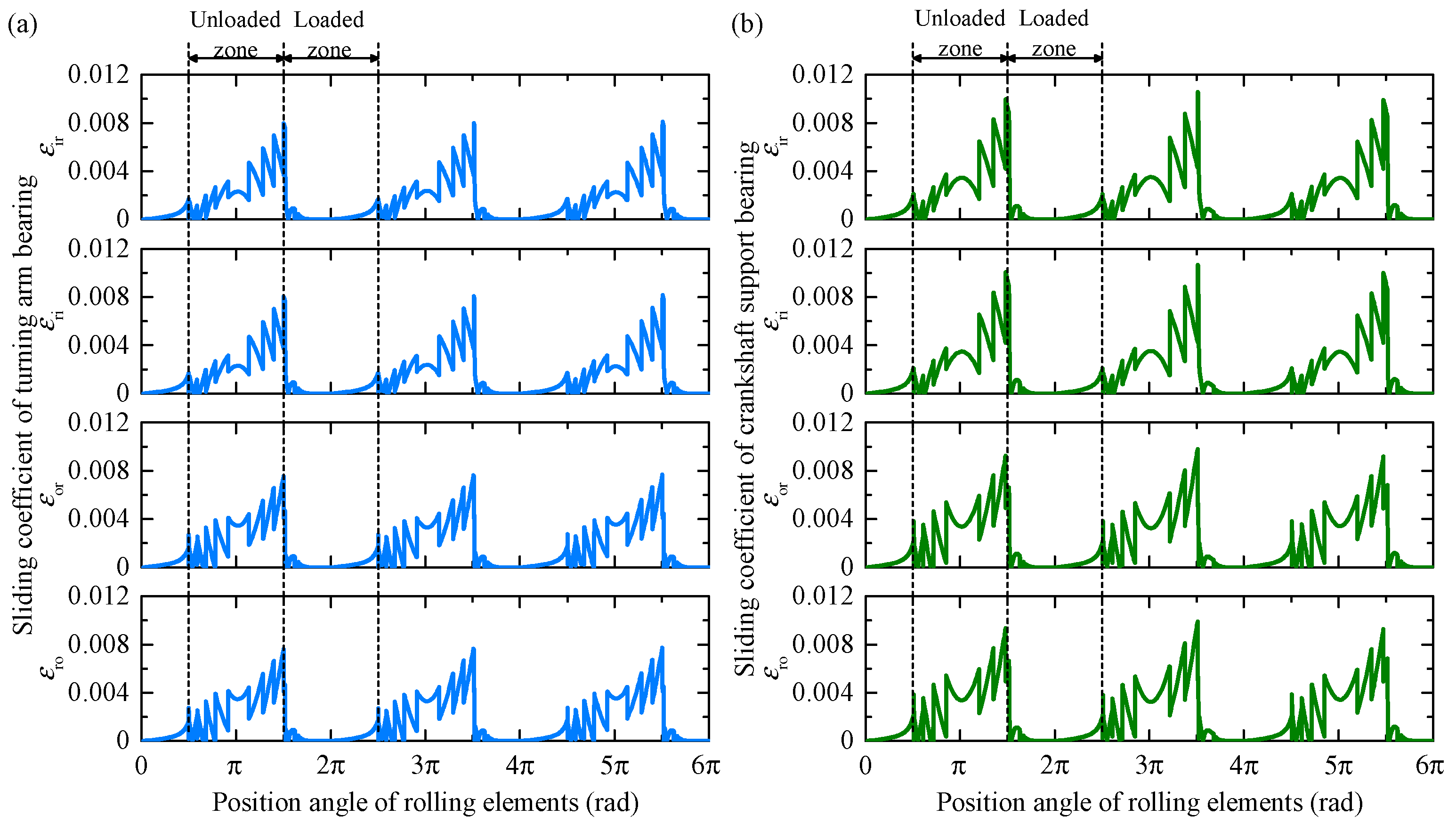
4.1. Sliding Coefficients of Tooth Surfaces and Rolling Bearings
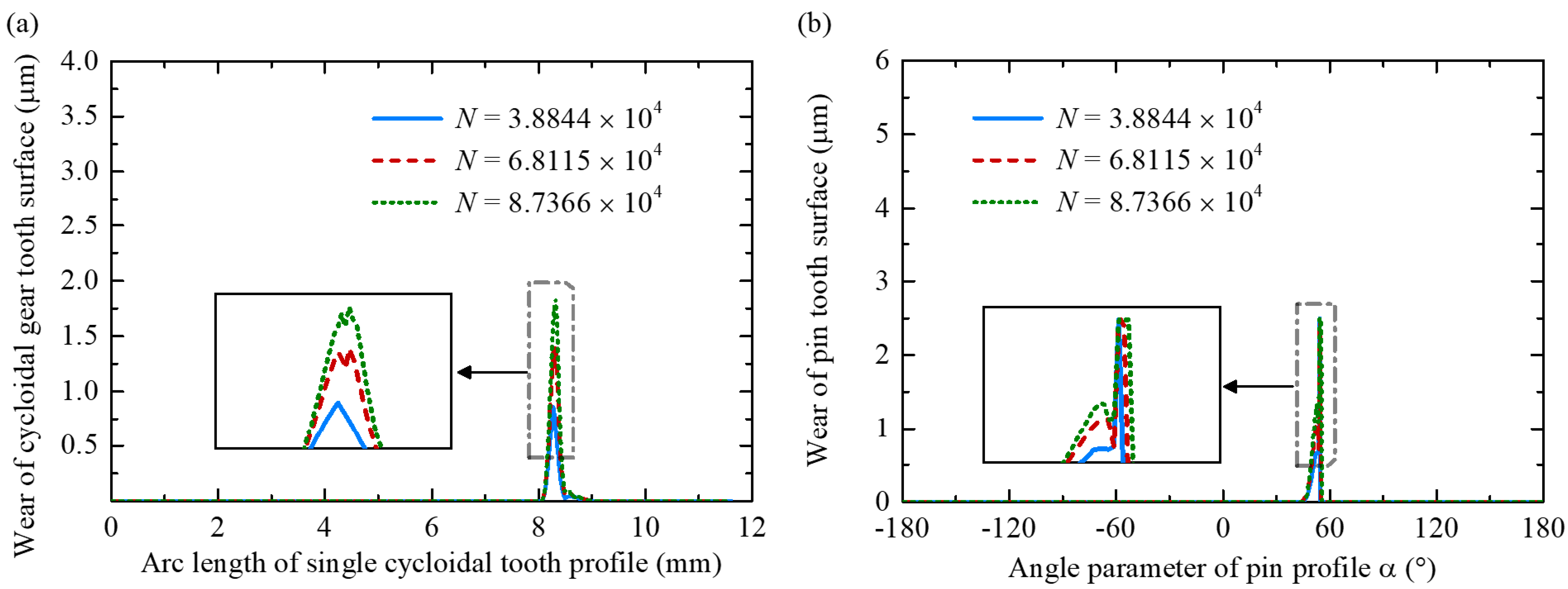
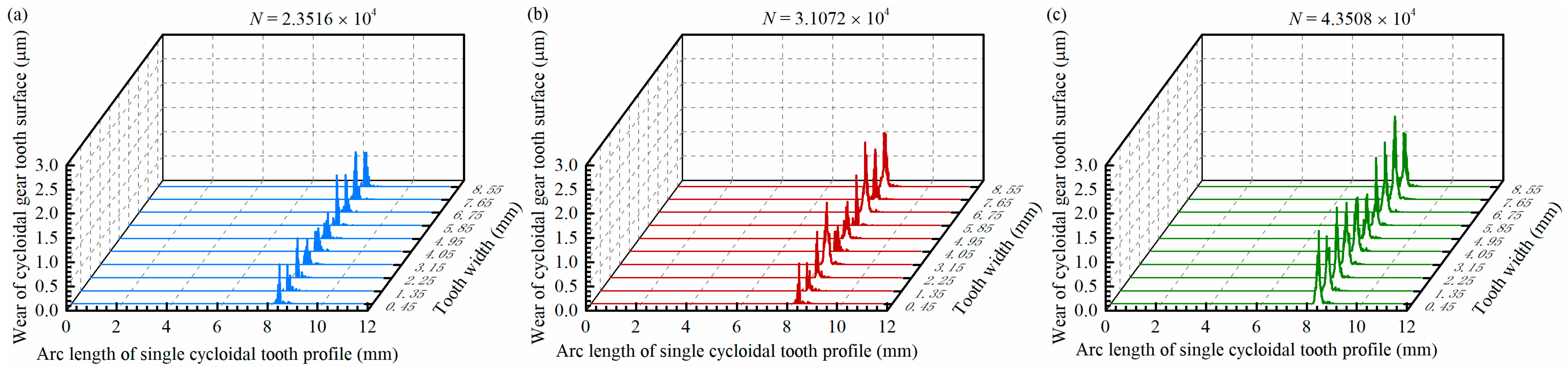
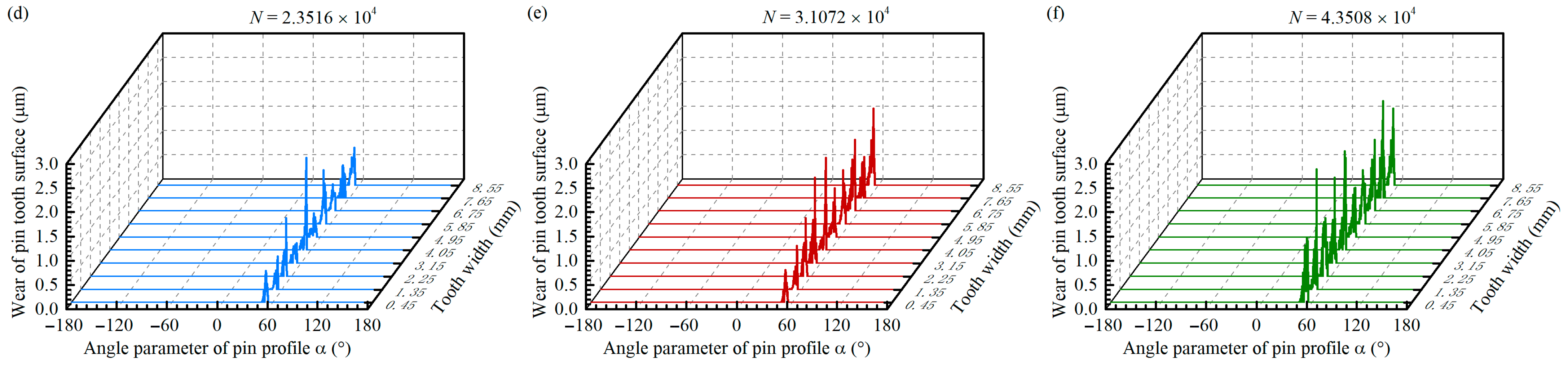
4.2. Wearing Law of Tooth Surfaces and Rolling Bearings
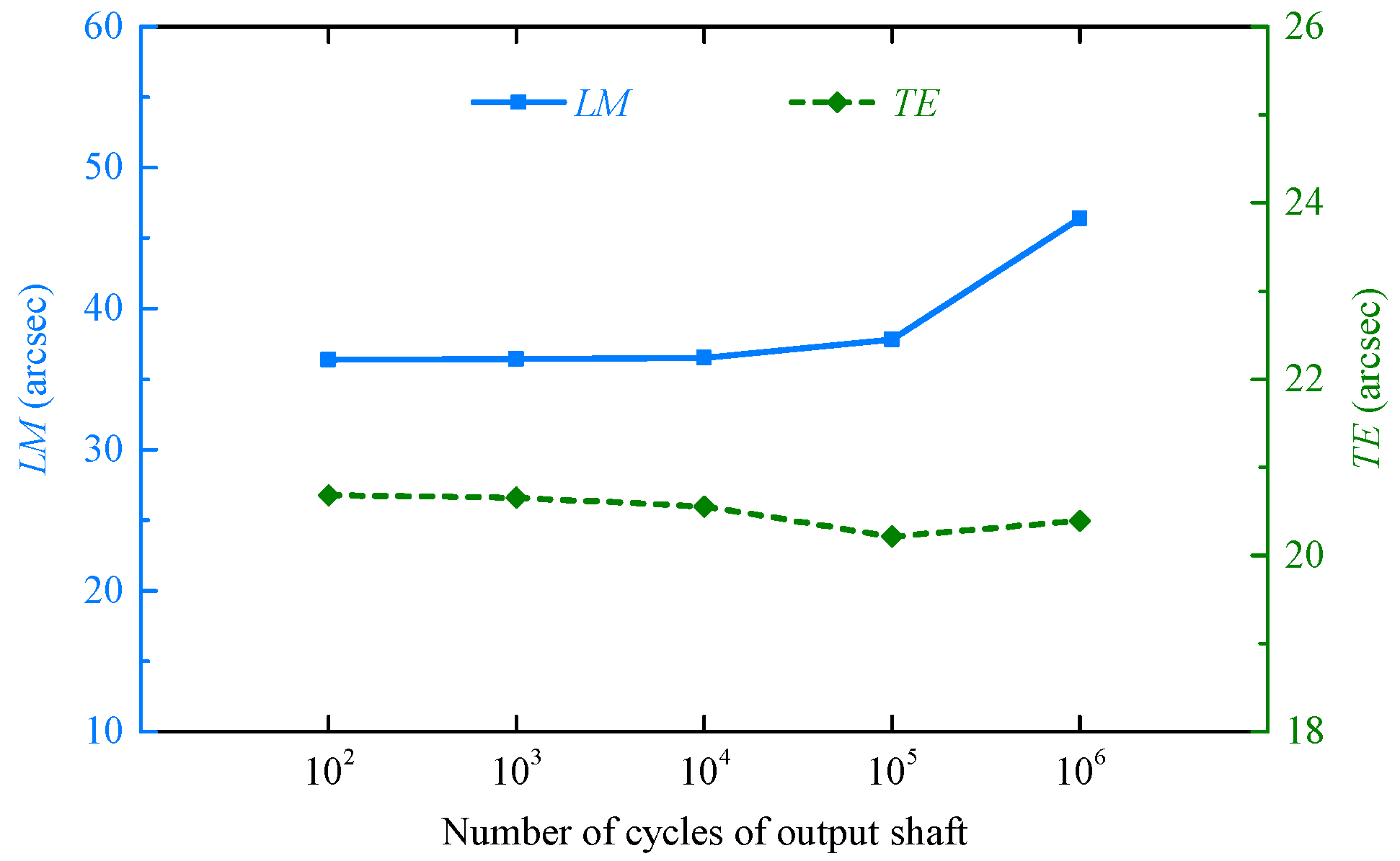
4.3. Degradation Law of Transmission Accuracy
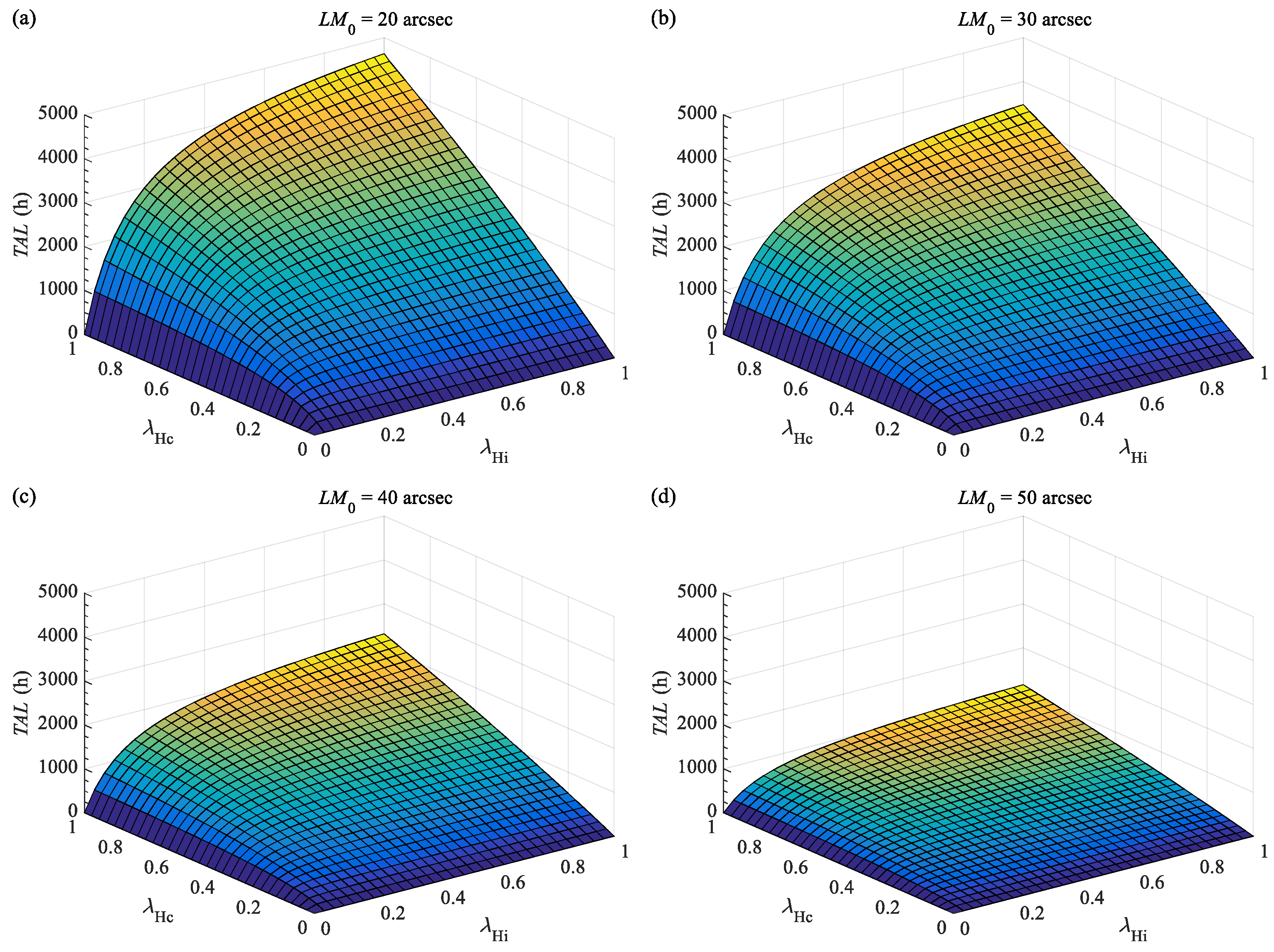
4.4. Estimation Model of Transmission Accuracy Life
5. Experimental Validation
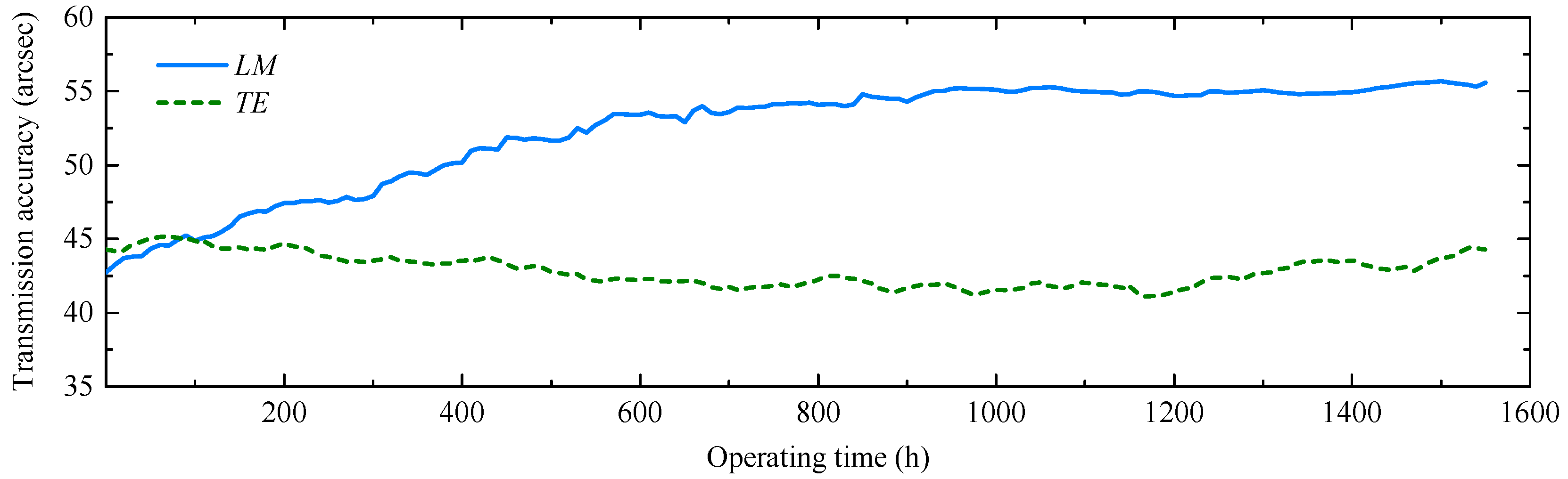
5.1. TAL Test of RV Reducers
5.2. Validation of TAL Estimation Model
6. Conclusions
- (1)
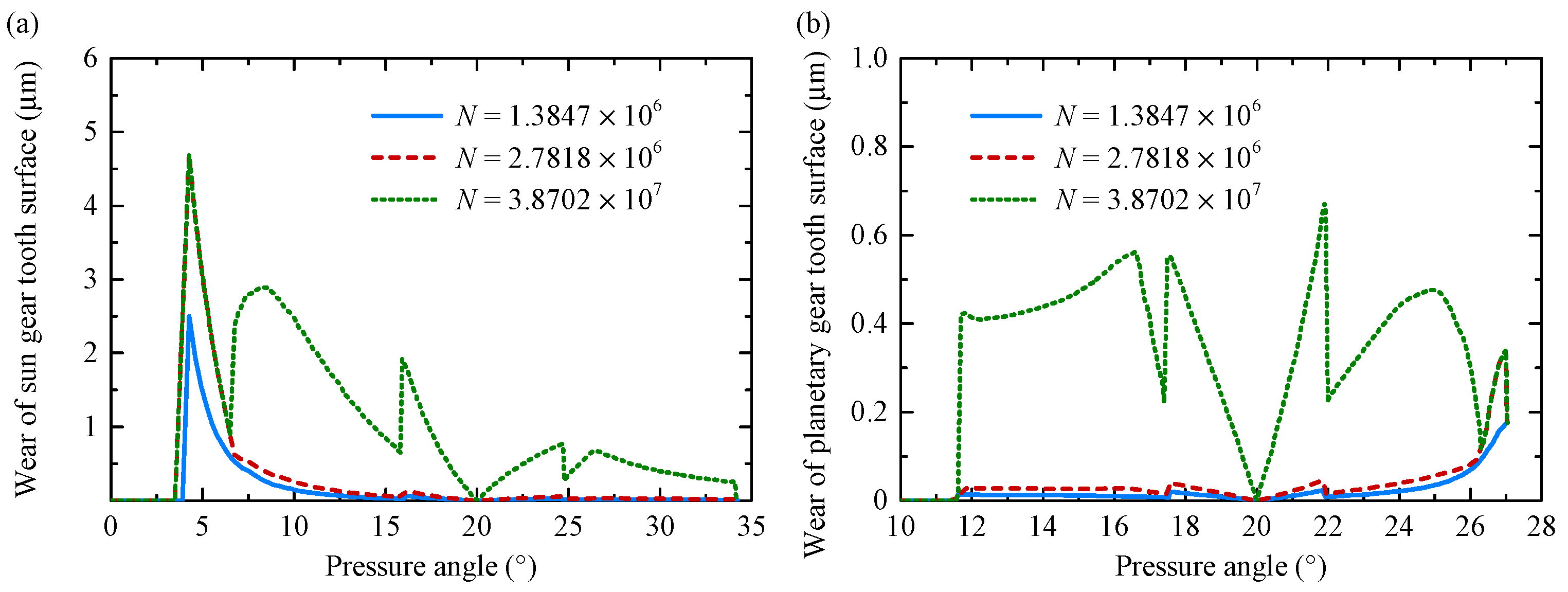
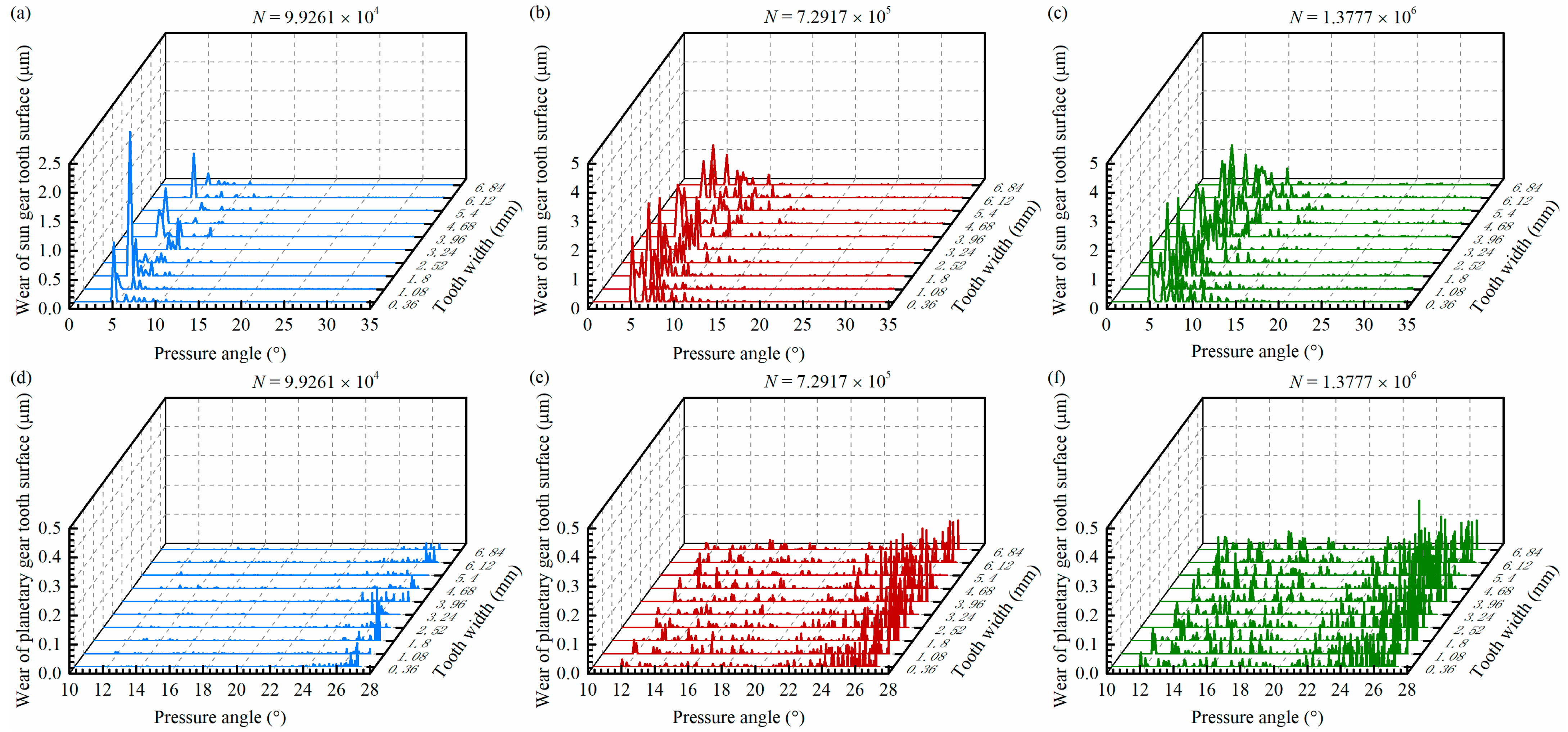
- In cycloid-pin transmission, the wear of cycloidal gears mainly occurs on the convex tooth surfaces, while the tooth surface wear of pins increases sharply at the edge of its contact area. In the involute gear drive, the sun gear tooth surface experiences more wear than the planetary gears, with minimal wear observed at the pitch point.
- (2)
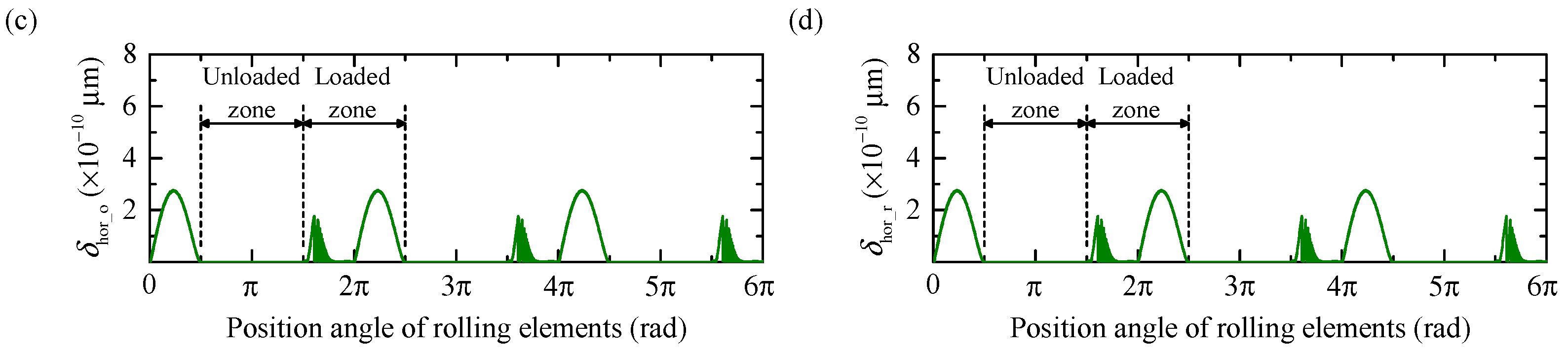
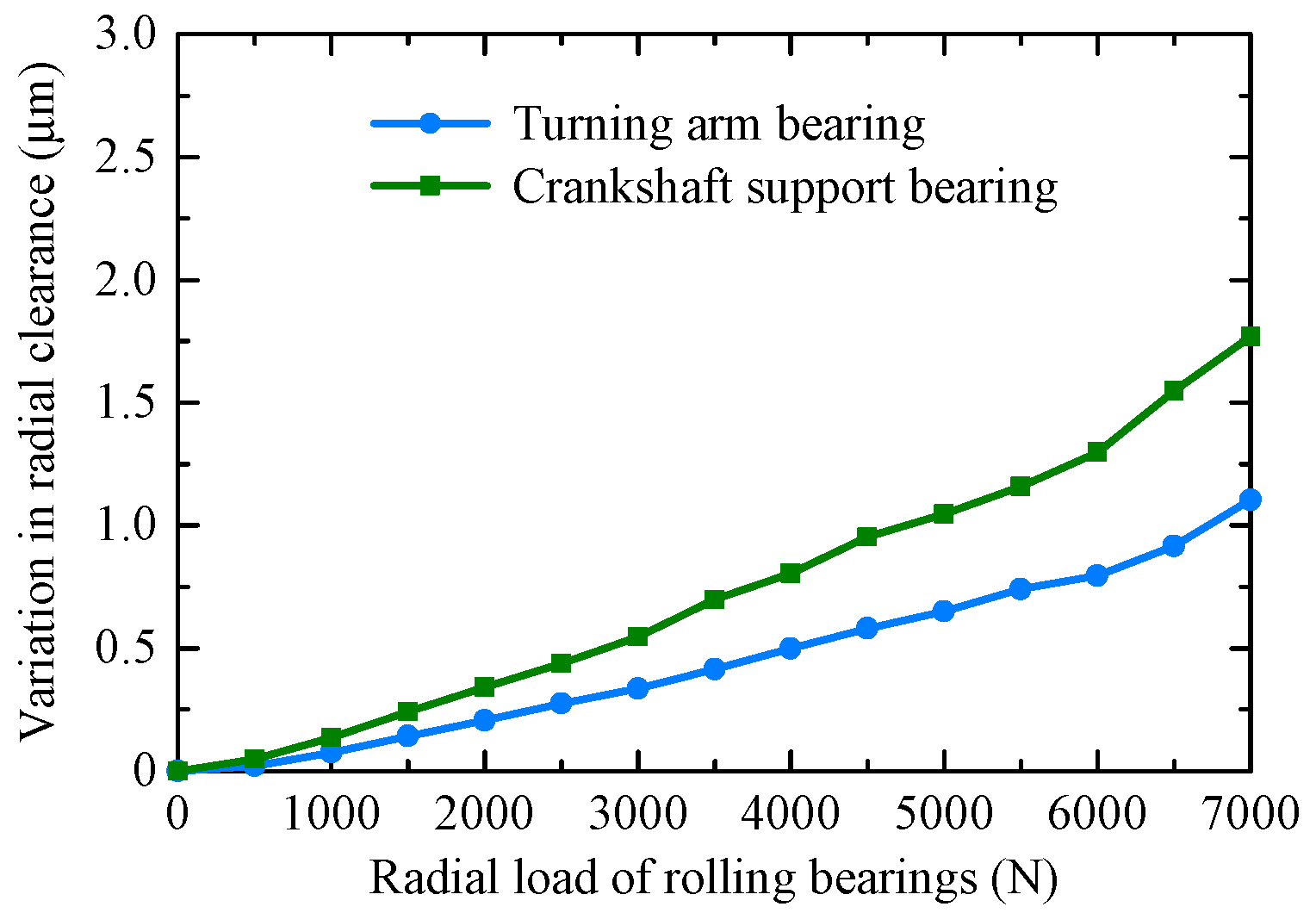
- Rolling bearing wear is concentrated at the points where rolling elements enter and exit the loaded region. Bearing radial clearance increases approximately linearly with bearing radial load. Under identical radial loads, crankshaft support bearings exhibit greater radial clearance variation than turning-arm bearings.
- (3)
- Both theoretical and experimental results have revealed that the TE of RV reducers remain relatively stable during operation, while the LM increases notably due to the influence of tooth surface and bearing wear, particularly during the first 600 h of test. Beyond 600 h, LM increases at 0.0024 arcsecs/h. Over the 1550 h test, the LM exhibited a total growth of 12.9209 arcsec, representing a 30.23% growth relative to initial LM, with its growth rate substantially surpassing that of TE. Based on these findings, the progressive increase in LM is the primary cause of transmission accuracy degradation in RV reducers, and LM is recommended as the primary evaluation index for TAL of RV reducers.
- (4)
- The deviation between the estimated TAL of RV reducers and the experimental results is 11.06%, which verifies the feasibility of the estimation model proposed in this study.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blanche, J.G.; Yang, D.C.H. Cycloid drives with machining tolerances. J. Mech. Trans. Autom. 1989, 111, 337–344. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Blanche, J.G. Design and application guidelines for cycloid drives with machining tolerances. Mech. Mach. Theory 1990, 25, 487–501. [Google Scholar] [CrossRef]
- Hidaka, T.; Wang, H.; Ishida, T. Rotational transmission error of K-H-V planetary gears with cycloid gear (1st report, analytical method of the rotational transmission error). Trans. Jpn. Soc. Mech. Eng. Ser. C 1994, 60, 645–653. [Google Scholar] [CrossRef]
- Ishida, T.; Wang, H.; Hidaka, T. Rotational transmission error of K-H-V planetary gears with cycloid gear (2nd report, effects of manufacturing and assembly errors on rotational transmission error). Trans. Jpn. Soc. Mech. Eng. Ser. C 1994, 60, 3510–3517. [Google Scholar] [CrossRef]
- Wang, H.; Ishida, T.; Hidaka, T. Rotational transmission error of K-H-V planetary gears with cycloid gear (3rd report, mutual effects of errors of the elements on the rotational transmission error. Trans. Jpn. Soc. Mech. Eng. Ser. C 1994, 60, 286–293. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Wang, Y.; Chen, B.; Lim, T.C. Analysis of a cycloid speed reducer considering tooth profile modification and clearance-fit output mechanism. ASME J. Mech. Des. 2017, 139, 033303. [Google Scholar] [CrossRef]
- Lin, K.S.; Chan, K.Y.; Lee, J.J. Kinematic error analysis and tolerance allocation of cycloidal gear reducers. Mech. Mach. Theory 2018, 124, 73–91. [Google Scholar] [CrossRef]
- Li, T.; Tian, M.; Xu, H.; Deng, X.; An, X.; Su, J. Meshing contact analysis of cycloidal-pin gear in RV reducer considering the influence of manufacturing error. J. Braz. Soc. Mech. Sci. 2020, 42, 133. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, G.; Chang, L.; Chen, G. A modelling approach for kinematic equivalent mechanism and rotational transmission error of RV reducer. Mech. Mach. Theory 2021, 163, 104384. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Hao, L.; Wang, H. Positioning accuracy prediction of precision cycloid reducer based on a BDDTE model and use in design optimization. Precis. Eng. 2024, 88, 27–43. [Google Scholar] [CrossRef]
- Huang, J.; Li, C.; Zhang, Y.; Wang, Y.; Chen, B. Transmission error analysis of cycloidal pinwheel meshing pair based on rolling-sliding contact. J. Braz. Soc. Mech. Sci. 2021, 43, 355. [Google Scholar] [CrossRef]
- Xie, Y.H.; Xu, L.X.; Deng, Y.Q. A dynamic approach for evaluating the moment rigidity and rotation precision of a bearing-planetary frame rotor system used in RV reducer. Mech. Mach. Theory 2022, 173, 104851. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.; Huang, J.; Li, X.; Sun, L. Theoretical analysis and performance prediction of a NN-type precision cycloidal reducer. Forsch. Ingenieurwes. 2024, 88, 44. [Google Scholar] [CrossRef]
- Xu, L.; Wu, Y. Investigation of the dynamic transmission accuracy of an industrial robot joint RV reducer under variable situations. Multibody Syst. Dyn. 2025, 1–38. [Google Scholar] [CrossRef]
- Wu, S.; Cheng, H.S. A sliding wear model for partial-EHL contacts. J. Tribol. 1991, 113, 134–141. [Google Scholar] [CrossRef]
- Wu, S.; Cheng, H.S. Sliding wear calculation in spur gears. J. Tribol. 1993, 115, 493–500. [Google Scholar] [CrossRef]
- Wojnarowski, J.; Onishchenko, V. Tooth wear effects on spur gear dynamics. Mech. Mach. Theory 2003, 38, 161–178. [Google Scholar] [CrossRef]
- Bajpai, P.; Kahraman, A.; Andersson, N.E. A surface wear prediction methodology for parallel-axis gear pairs. J. Tribol. 2004, 126, 597–605. [Google Scholar] [CrossRef]
- Kahraman, A.; Bajpai, P.; Andersson, N.E. Influence of tooth profile deviations on helical gear wear. ASME J. Mech. Des. 2005, 127, 656–663. [Google Scholar] [CrossRef]
- Ding, H.; Kahraman, A. Interactions between nonlinear spur gear dynamics and surface wear. J. Sound Vib. 2007, 307, 662–679. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, J.; Wei, Z. Study on transmission error and torsional stiffness of RV reducer under wear. J. Mech. Sci. Technol. 2022, 36, 4067–4081. [Google Scholar] [CrossRef]
- Ahn, H.J.; Choi, B.M.; Lee, Y.H.; Pham, A.D. Impact analysis of tolerance and contact friction on a RV reducer using FE method. Int. J. Precis. Eng. Manuf. 2021, 22, 1285–1292. [Google Scholar] [CrossRef]
- Han, J.; Li, W.; Qiao, Z. Analysis of mixed lubrication characteristics of cycloid pin-wheel transmission. Int. J. Precis. Eng. Manuf. 2021, 22, 453–472. [Google Scholar] [CrossRef]
- Han, J.; Li, W.; Qiao, Z. Lubrication characteristics of cycloid pin wheel transmission of RV reducer. J. Cent. South Univ. 2021, 28, 398–417. [Google Scholar] [CrossRef]
- Qi, L.; Yang, D.; Cao, B.; Li, Z.; Liu, H. Design principle and numerical analysis for cycloidal drive considering clearance, deformation, and friction. Alex. Eng. J. 2024, 91, 403–418. [Google Scholar] [CrossRef]
- Sun, H.; Yang, J.; Wei, S.; Dong, P.; Zhao, N. Load-carrying analysis for turning arm bearings of cycloidal gear reducers with manufacturing errors. J. Braz. Soc. Mech. Sci. 2025, 47, 117. [Google Scholar] [CrossRef]
- Sheng, W.; Li, Z.; Yu, X.; Xi, R. Active design method and performance prediction of internal gear pairs with low sliding ratio. Meccanica 2024, 59, 1121–1137. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Y.; Li, T.; Ding, X.; Ji, S.; Cao, Z. Influence of cycloid pinwheel reducer structure parameters on transmission performance and optimized design with considering friction loss. Optim. Eng. 2025, 26, 507–541. [Google Scholar] [CrossRef]
- Orlov, A.V. Ball-bearing wear in real loading conditions. Russ. Eng. Res. 2009, 29, 884–890. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor. J. Sound Vib. 2000, 238, 723–756. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity. Eur. J. Mech. A/Solids 2010, 29, 1022–1033. [Google Scholar] [CrossRef]
- Qiu, Z.; Xue, J. Review of performance testing of high precision reducers for industrial robots. Measurement 2021, 183, 109794. [Google Scholar] [CrossRef]
- Ge, J.; Lu, B.; Wang, Y.; Jiang, X. Research on accelerated degradation test of RV reducer. Int. J. Control Autom. 2017, 10, 209–216. [Google Scholar] [CrossRef]
- Chen, B.; Peng, C.; Huang, J. A new error model and compensation strategy of angle encoder in torsional characteristic measurement system. Sensors 2019, 19, 3772. [Google Scholar] [CrossRef] [PubMed]
- Peng, P.; Wang, J. NOSCNN: A robust method for fault diagnosis of RV reducer. Measurement 2019, 138, 652–658. [Google Scholar] [CrossRef]
- Wang, H.; Fu, W.; Fang, K.; Chen, T. Transmission characteristics of an RV reducer based on ADAMS. J Mech. Sci. Technol. 2024, 38, 787–802. [Google Scholar] [CrossRef]
- Ghorbel, F.H.; Gandhi, P.S.; Alpeter, F. On the kinematic error in harmonic drive gears. ASME J. Mech. Des. 2001, 123, 90–97. [Google Scholar] [CrossRef]
- Jia, H.; Li, J.; Xiang, G.; Wang, J.; Xiao, K.; Han, Y. Modeling and analysis of pure kinematic error in harmonic drive. Mech. Mach. Theory 2021, 155, 104122. [Google Scholar] [CrossRef]
- Liu, C.; Shi, W.; Liu, K. Calculation method of mesh stiffness for helical gear pair with manufacturing errors, assembly errors and tooth modifications. Meccanica 2022, 57, 541–565. [Google Scholar] [CrossRef]
- Liu, C.; Shi, W.; Xu, L.; Liu, K. A novel approach to calculating the transmission accuracy of a cycloid-pin gear pair based on error tooth surfaces. Appl. Sci. 2021, 11, 8671. [Google Scholar] [CrossRef]
- Janakiraman, V. An Investigation of the Impact of Contact Parameters on the Wear Coefficient; The Ohio State University: Columbus, OH, USA, 2013. [Google Scholar]
- Liu, C.; Tang, M.; Yang, X.; Ying, J. Influence of tooth surface wear on dynamic characteristics of gear systems considering three-dimensional tooth surface errors. Shock Vib. 2025, 2025, 2539671. [Google Scholar] [CrossRef]
- Ghaisas, N.; Wassgren, C.R.; Sadeghi, F. Cage instabilities in cylindrical roller bearings. J. Tribol. 2004, 126, 681–689. [Google Scholar] [CrossRef]
- Zhang, J.; Bian, S.; Qing, L.; Liu, X. Quasi-static-model-based wear analysis of spur gears. J. Mech. Eng. 2017, 53, 136–145. [Google Scholar] [CrossRef]




| Involute Planetary Gear Transmission at the First Stage | Cycloid-Pin Gear Transmission at the Second Stage | ||||
|---|---|---|---|---|---|
| Parameters | Sun gear | Planet gear | Parameters | Cycloidal gear | Pin |
| Number of teeth | 16 | 32 | Number of teeth | 39 | 40 |
| Modulus (mm) | 1.5 | Radius of pins (mm) | - | 3 | |
| Pressure angle at reference circle (°) | 20 | 20 | Radius of pin center circle (mm) | - | 64 |
| Tooth width (mm) | 7.2 | 7.2 | Tooth width (mm) | 9 | - |
| Profile shift coefficient | 0.1 | −0.1 | Eccentricity (mm) | 1.3 | - |
| Fillet radius (mm) | 0.57 | 0.57 | Isometric modification (mm) | 0.005 | - |
| Hub radius (mm) | - | 8 | Offset modification (mm) | 0.003 | - |
| Poisson’s ratio | 0.3 | 0.3 | Poisson’s ratio | 0.3 | 0.3 |
| Young’s modulus (N/mm2) | 2.068 × 105 | 2.068 × 105 | Young’s modulus (N/mm2) | 2.12 × 105 | 2.12 × 105 |
| Parameter | Parameter Values | |
|---|---|---|
| Turning-Arm Bearing | Crankshaft Support Bearing | |
| Radius of outer raceway (mm) | 18 | 14.89 |
| Radius of inner raceway (mm) | 13 | 10.31 |
| Bearing pitch radius (mm) | 15.5 | 12.60 |
| Rolling element mass (kg) | 1.38 × 10−3 | 0.98 × 10−3 |
| Rolling element moment of inertia (kg∙m2) | 4.31 × 10−9 | 2.58 × 10−9 |
| Number of rolling elements | 14 | 13 |
| Effective length of rolling element (mm) | 9 | 7.58 |
| Rolling element radius (mm) | 2.5 | rr1 = 2.16 (small end); rr2 = 2.42 (large end) |
| Contact angle between rolling elements and raceways (°) | - | αi = 9 (inner raceway); αo = 13 (outer raceway) |
| Gap of cage pocket (mm) | 0.01 | 0.01 |
| LM0 (arcsec) | a0 | a1 | a2 | a3 | a4 | a5 |
|---|---|---|---|---|---|---|
| 20 | −138.4 | −960.9 | −745.1 | 1544.5 | 4154.0 | 796.4 |
| 30 | −104.2 | −730.3 | −588.4 | 1163.6 | 3127.2 | 598.4 |
| 40 | −69.4 | −490.8 | −392.0 | 778.5 | 2089.7 | 399.0 |
| 50 | −34.4 | −246.6 | −196.5 | 390.6 | 1046.0 | 199.8 |
| Parameters | Sun Gear | Planetary Gear 1 | Planetary Gear 2 | |||
|---|---|---|---|---|---|---|
| Left Surface | Right Surface | Left Surface | Right Surface | Left Surface | Right Surface | |
| Total profile deviation (Fα/μm) | 4.3 | 4.6 | 4.7 | 4.2 | 4.8 | 4.1 |
| Total helix deviation (Fβ/μm) | 5.6 | 5.9 | 5.4 | 4.7 | 5.0 | 5.6 |
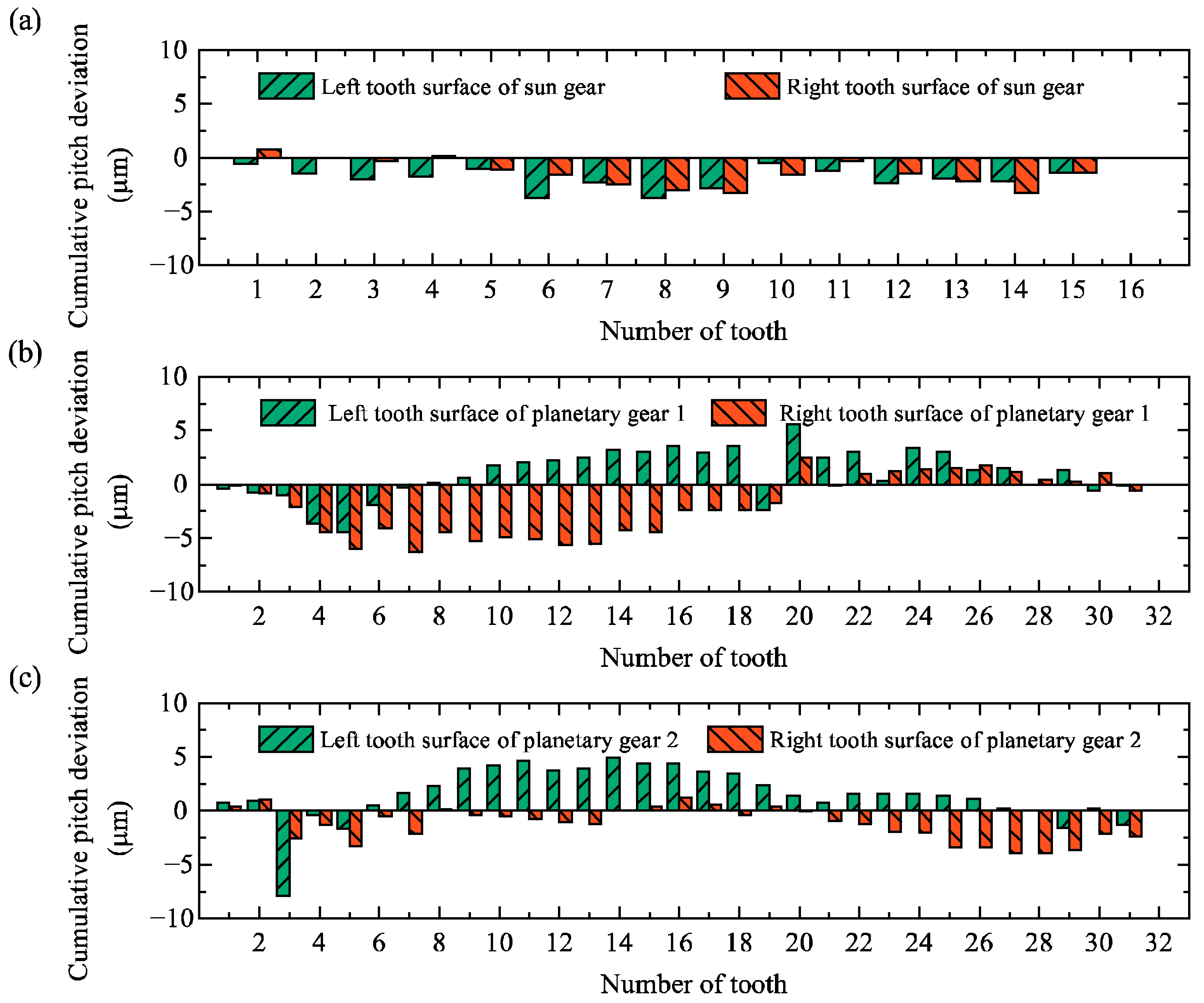
| Total cumulative pitch deviation (Fp/μm) | 3.8 | 4.1 | 10.0 | 8.8 | 12.8 | 5.1 |
| Cycloidal Gear 1 | Cycloidal Gear 2 | ||
|---|---|---|---|
| Profile Modification Amount (μm) | Profile Deviation (μm) | Profile Modification Amount (μm) | Profile Deviation (μm) |
| ΔRrp = −0.012 | ΔRrp = −0.013 | ||
| ΔRp = −0.009 | ΔRp = −0.013 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Shi, W.; Yu, H.; Liu, K. Degradation Law Analysis and Life Estimation of Transmission Accuracy of RV Reducer Based on Tooth Surface and Bearing Wear. Lubricants 2025, 13, 362. https://doi.org/10.3390/lubricants13080362
Liu C, Shi W, Yu H, Liu K. Degradation Law Analysis and Life Estimation of Transmission Accuracy of RV Reducer Based on Tooth Surface and Bearing Wear. Lubricants. 2025; 13(8):362. https://doi.org/10.3390/lubricants13080362
Chicago/Turabian StyleLiu, Chang, Wankai Shi, He Yu, and Kun Liu. 2025. "Degradation Law Analysis and Life Estimation of Transmission Accuracy of RV Reducer Based on Tooth Surface and Bearing Wear" Lubricants 13, no. 8: 362. https://doi.org/10.3390/lubricants13080362
APA StyleLiu, C., Shi, W., Yu, H., & Liu, K. (2025). Degradation Law Analysis and Life Estimation of Transmission Accuracy of RV Reducer Based on Tooth Surface and Bearing Wear. Lubricants, 13(8), 362. https://doi.org/10.3390/lubricants13080362





