Dynamic Modeling of 5-DOF Aerostatic Bearing Rotor System with Adjustable Gas Film Gap
Abstract
:1. Introduction
2. Mathematical Modeling
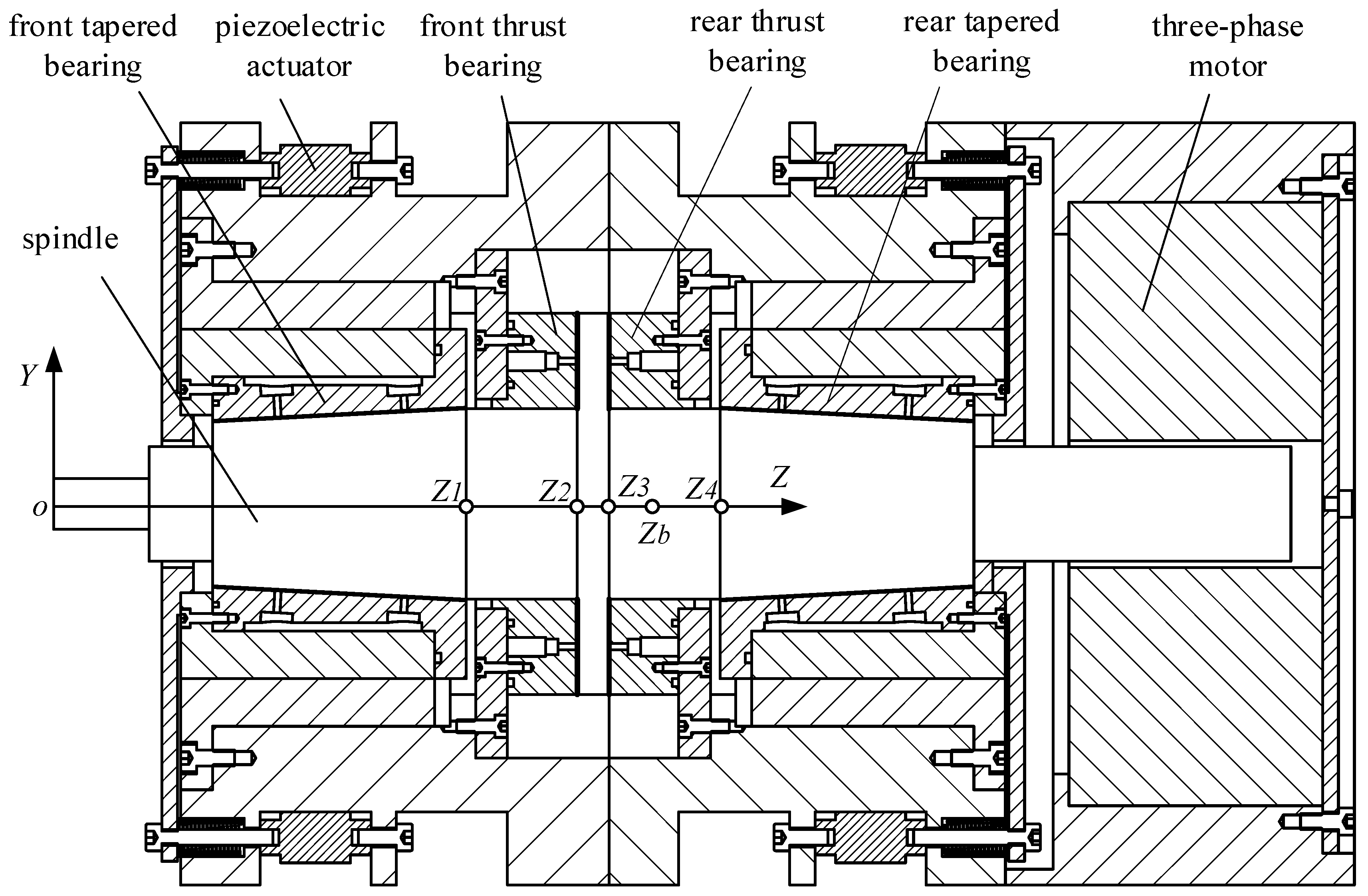
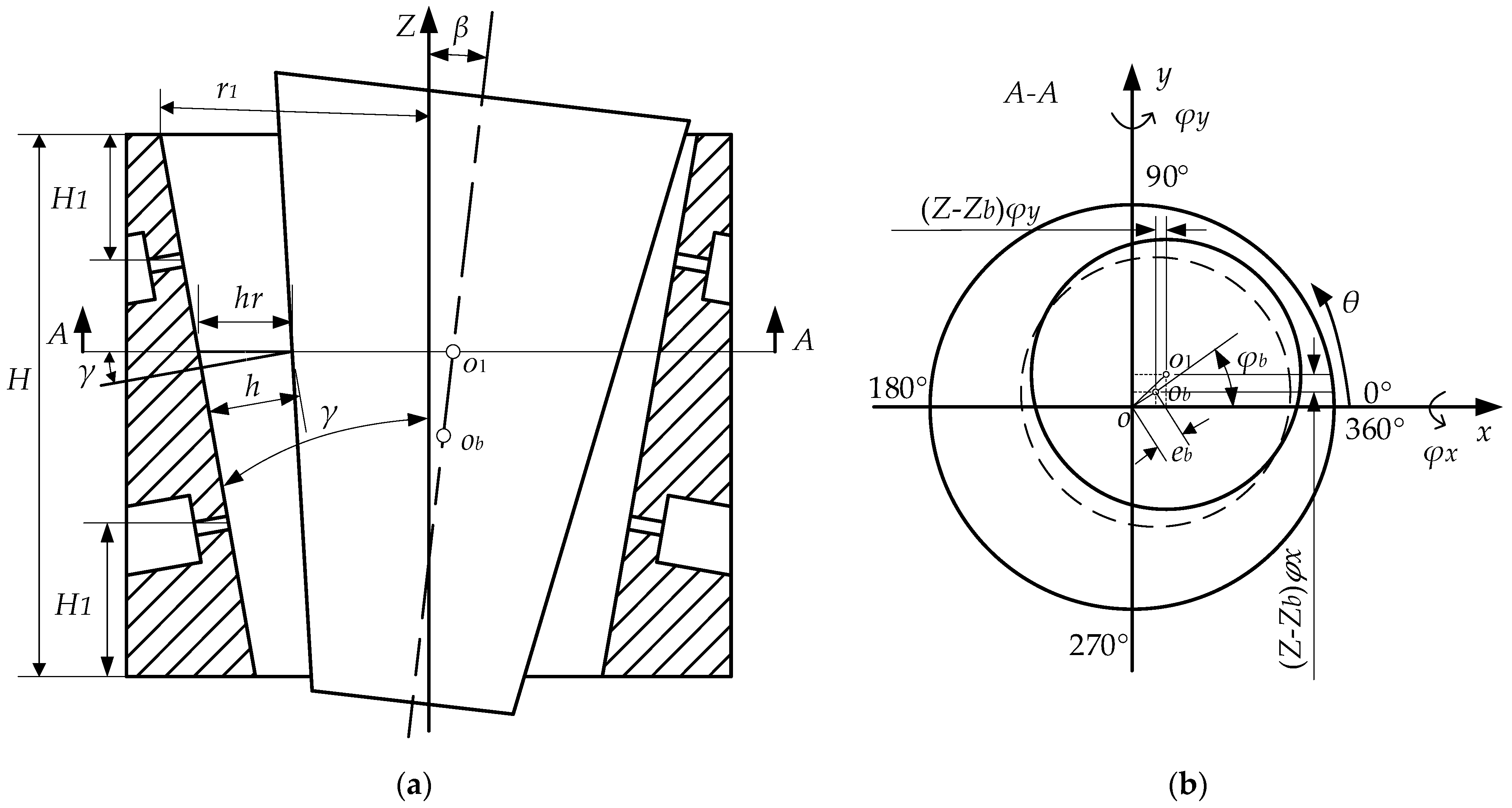
2.1. The Structure of the Aerostatic Motorized Spindle
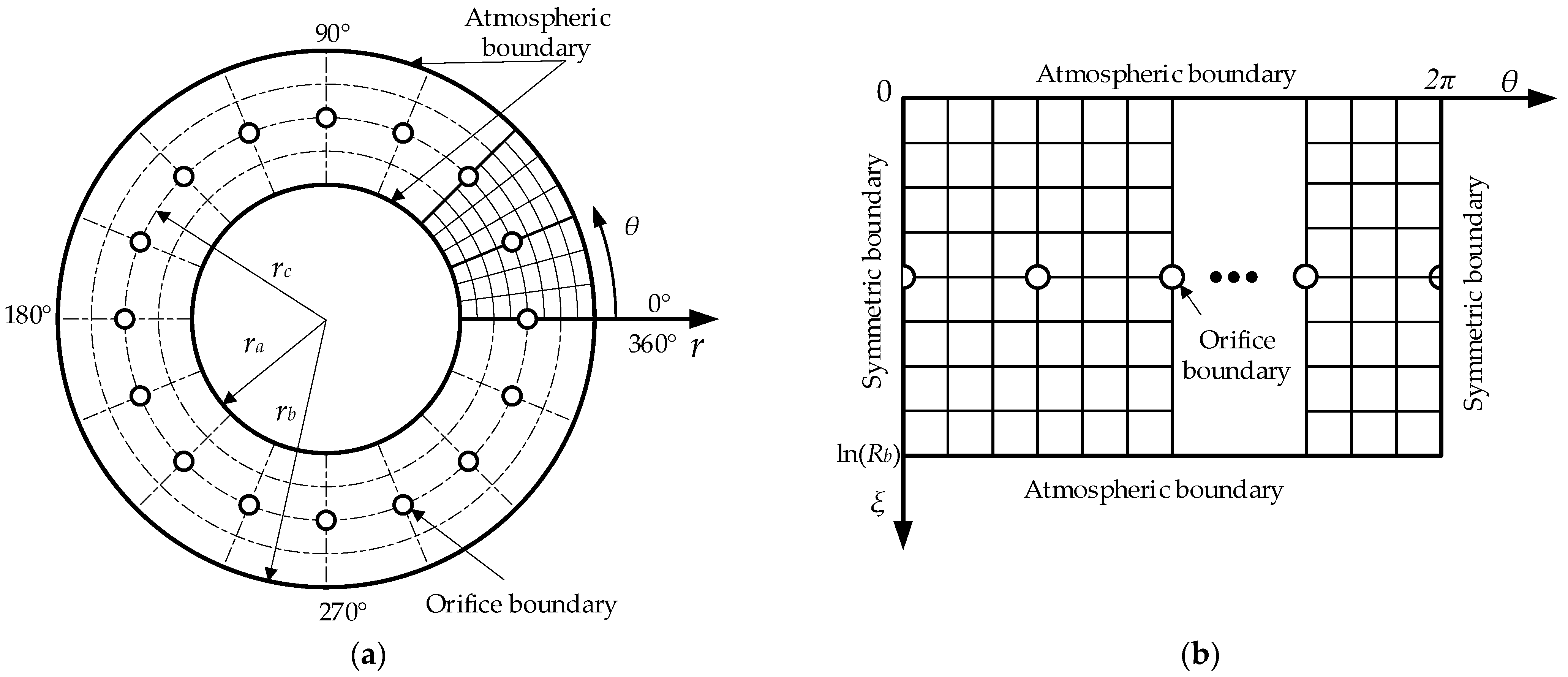
2.2. Mathematical Model of Aerostatic Thrust Bearing
2.2.1. Control Equation of Thrust Bearing
2.2.2. Flow Balance Equation
2.2.3. Gas Film Thickness Equation of Thrust Bearing
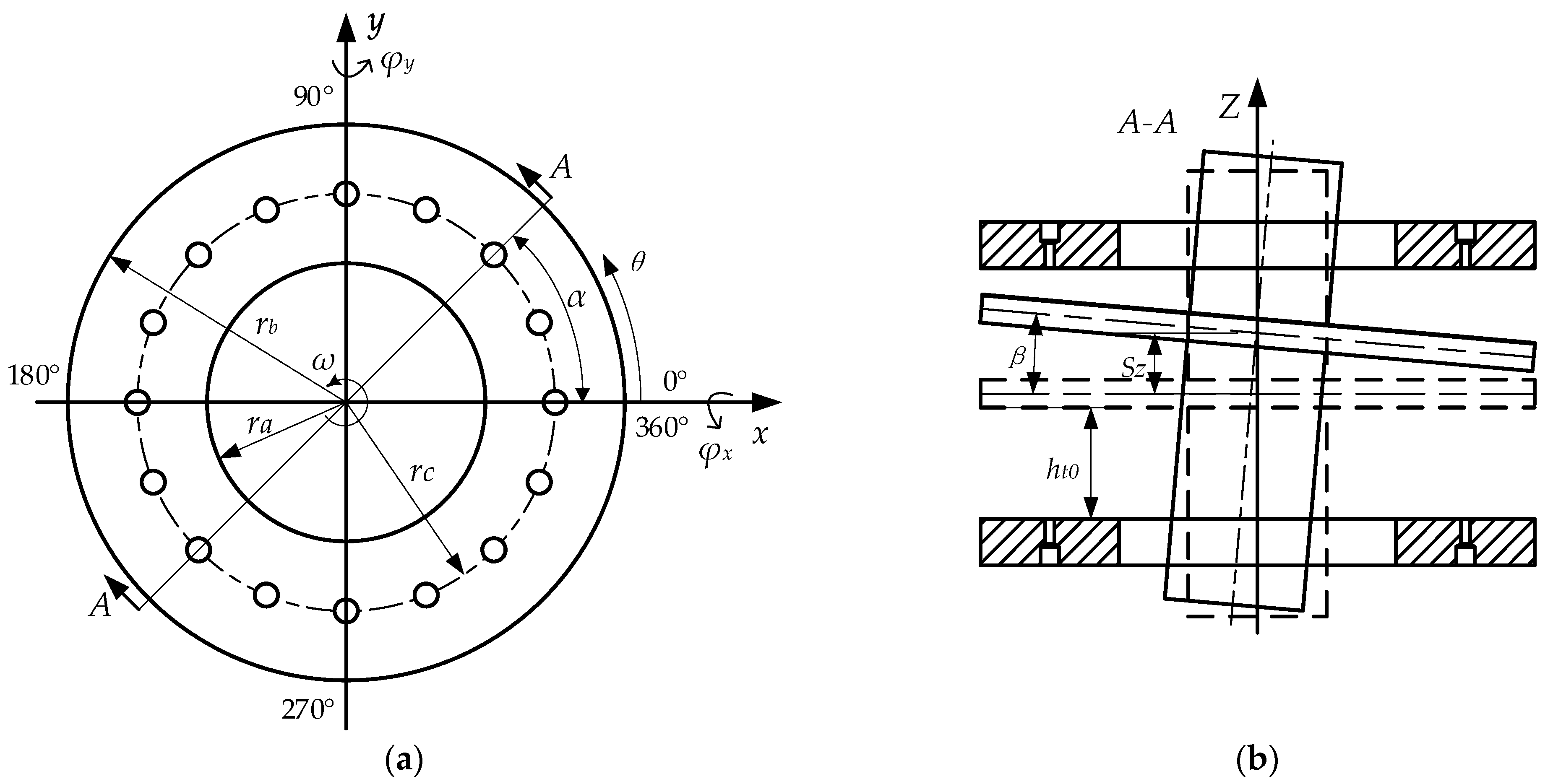
2.2.4. Force and Torque Equation of Thrust Bearing
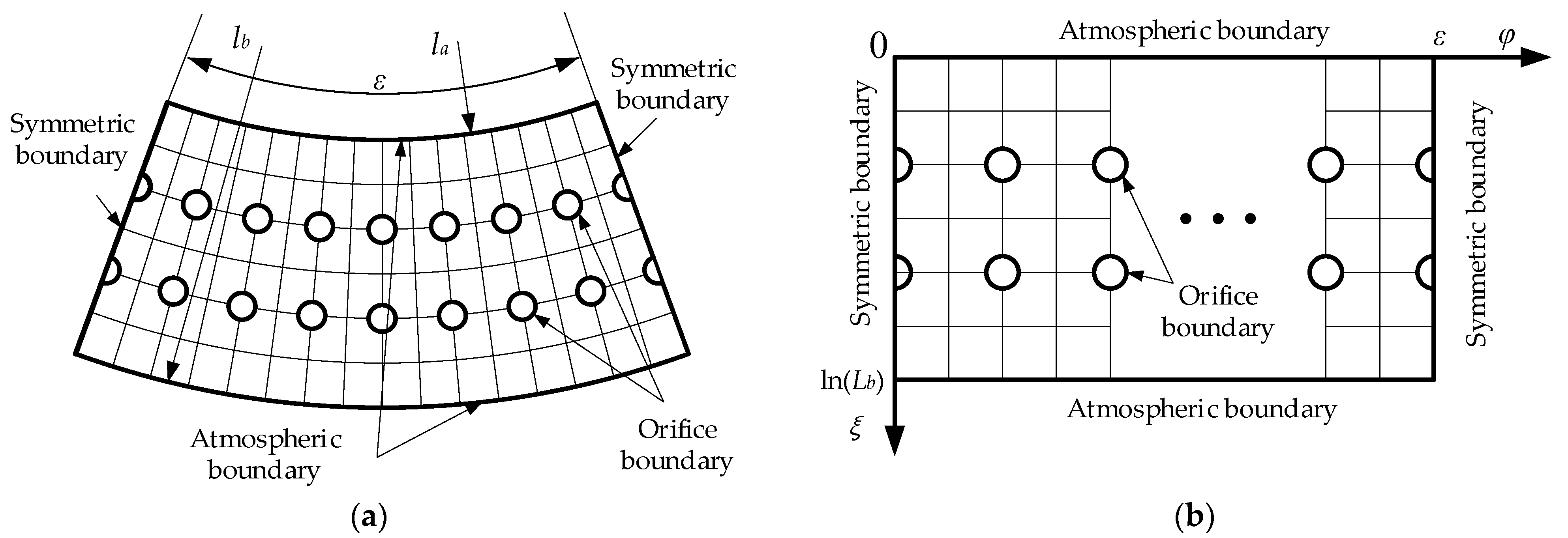
2.3. Mathematical Model of Aerostatic Tapered Bearing
2.3.1. Control Equation of Tapered Bearing
2.3.2. Gas Film Thickness Equation of Tapered Bearing
2.3.3. Force and Torque Equation of Tapered Bearing
2.4. Spindle Motion Equation
3. Numerical Solution
3.1. Model Parameters
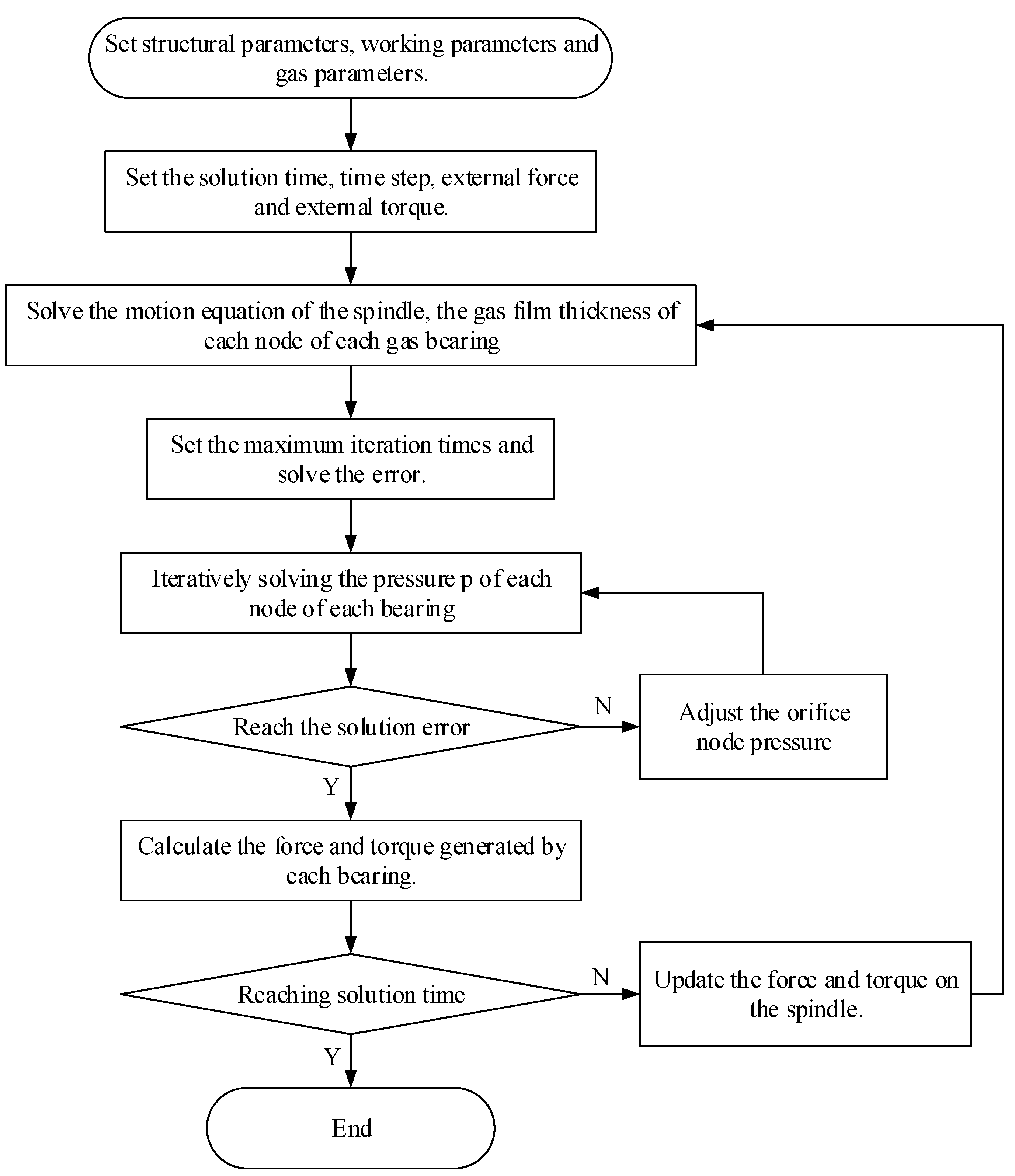
3.2. Calculation Process
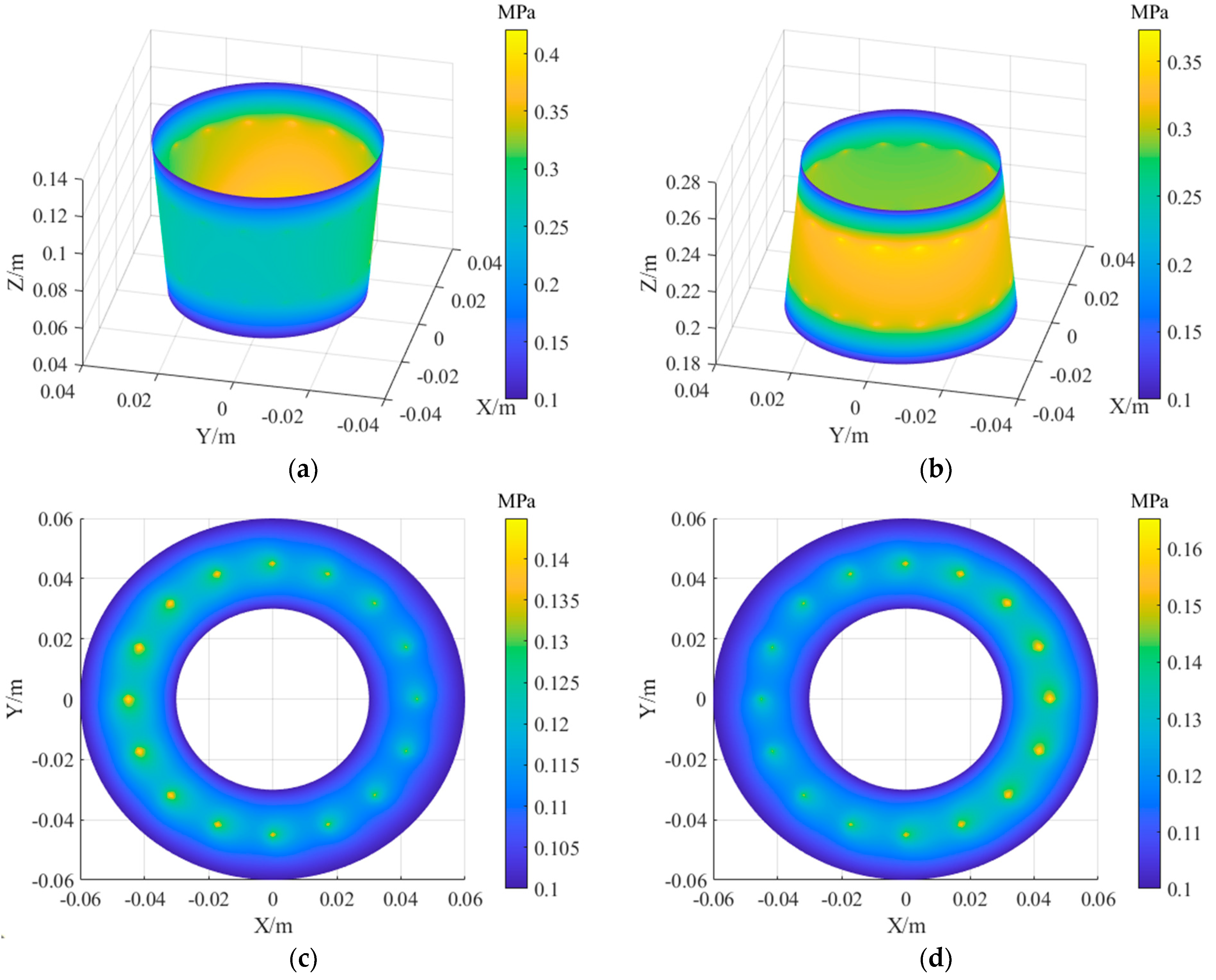
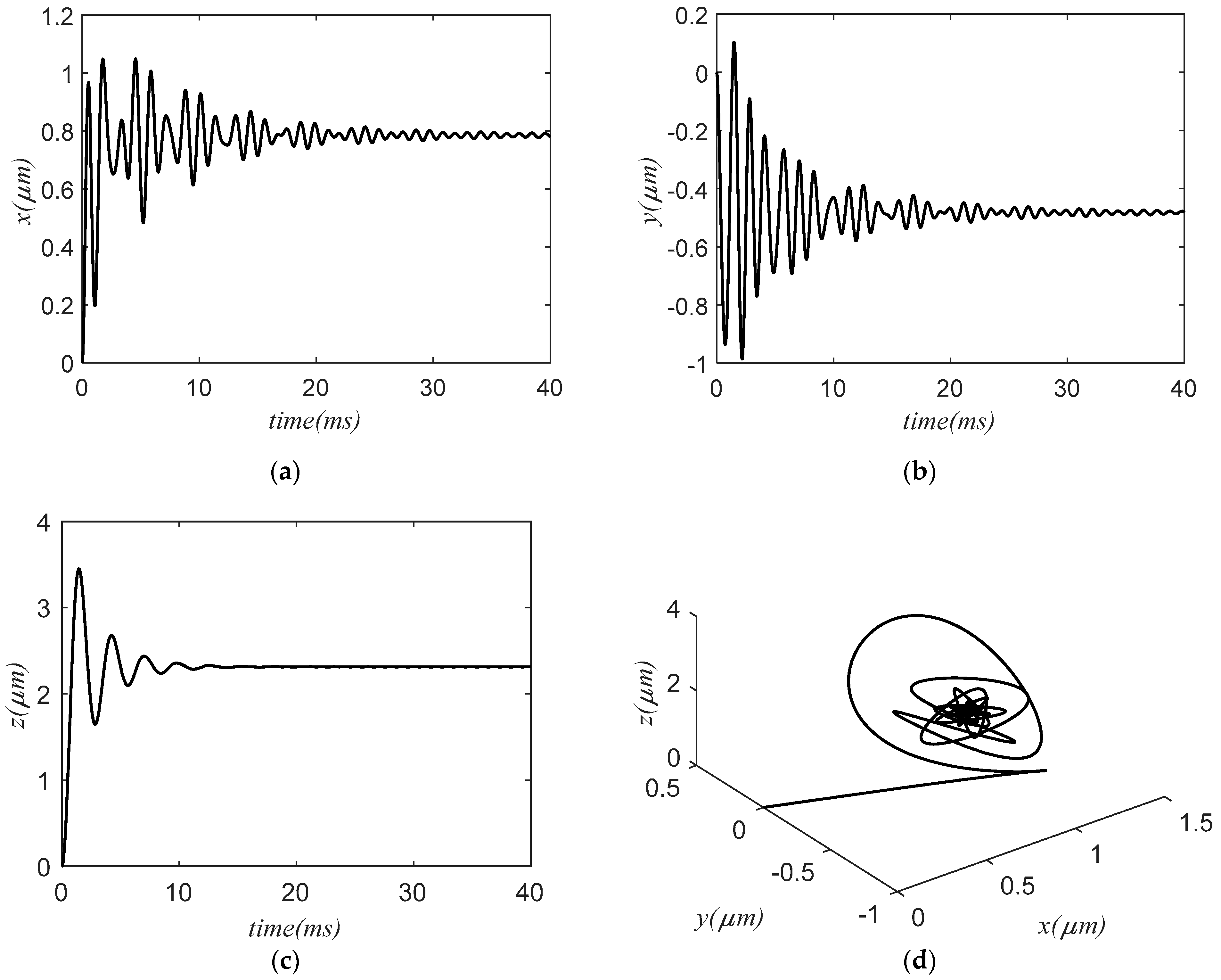
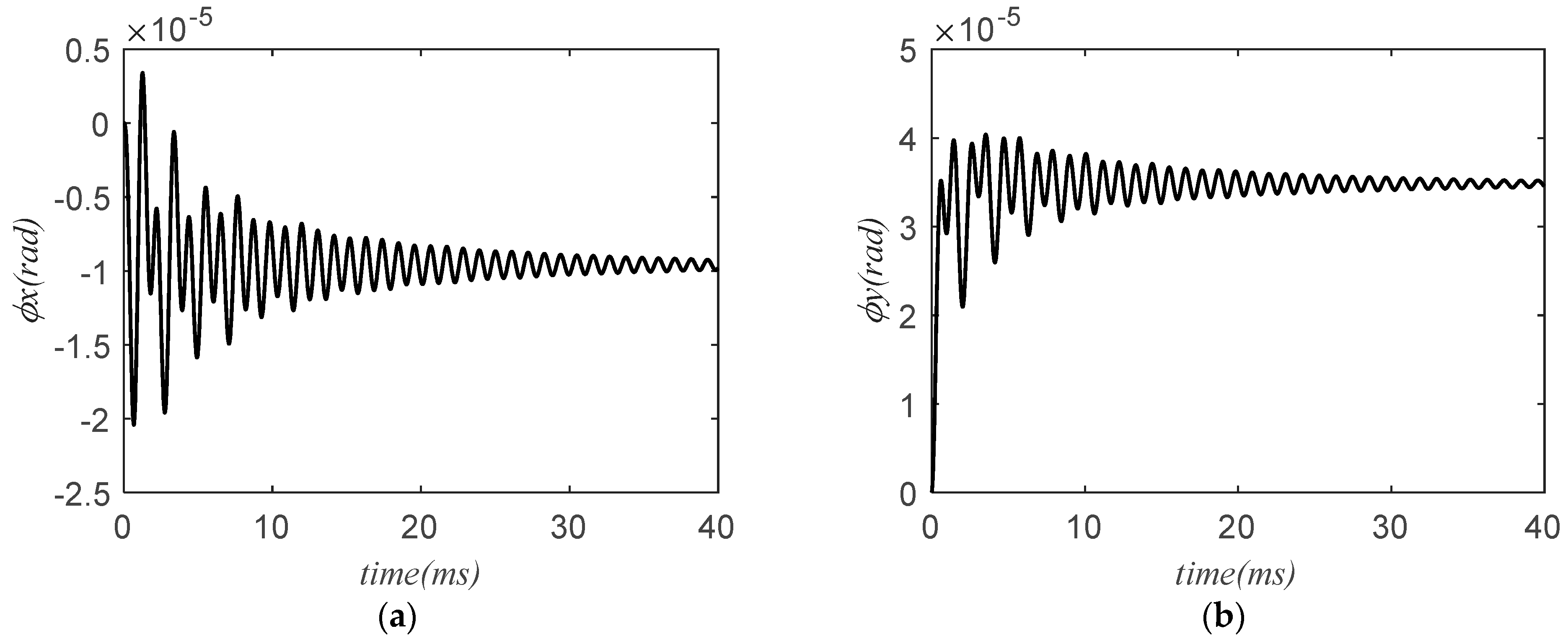
3.3. Result and Analysis
3.3.1. Situation 1
3.3.2. Situation 2
3.3.3. Situation 3
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.F.; Wang, Y.M.; Cai, L.G.; Zhao, Y.S.; Cheng, Q.; Dong, X.M. A review of hydrostatic bearing system: Researches and applications. Adv. Mech. Eng. 2017, 9, 168781401773053. [Google Scholar] [CrossRef]
- Chen, G.; Ju, B.; Fang, H.; Chen, Y.; Yu, N.; Wan, Y. Air bearing: Academic insights and trend analysis. Int. J. Adv. Manuf. Technol. 2019, 106, 1191–1202. [Google Scholar] [CrossRef]
- Gao, Q.; Chen, W.Q.; Lu, L.H.; Huo, D.H.; Cheng, K. Aerostatic bearings design and analysis with the application to precision engineering: State-of-the-art and future perspectives. Tribol. Int. 2019, 135, 1–17. [Google Scholar] [CrossRef]
- Zhang, J.B.; Deng, Z.F.; Zhang, K.; Jin, H.L.; Yuan, T.; Chen, C.; Su, Z.M.; Cao, Y.T.; Xie, Z.L.; Wu, D.Y.; et al. The Influences of Different Parameters on the Static and Dynamic Performances of the Aerostatic Bearing. Lubricants 2023, 11, 130. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, J.; To, S.; Xiong, Z. A theoretical and experimental study of spindle imbalance induced forced vibration and its effect on surface generation in diamond turning. Int. J. Mach. Tools Manuf. 2018, 133, 61–71. [Google Scholar] [CrossRef]
- Chen, D.J.; Huo, C.; Cui, X.X.; Pan, R.; Fan, J.W.; An, C.H. Investigation the gas film in micro scale induced error on the performance of the aerostatic spindle in ultra-precision machining. Mech. Syst. Signal Proc. 2018, 105, 488–501. [Google Scholar] [CrossRef]
- Zhang, S.J.; To, S.; Cheung, C.F.; Wang, H.T. Dynamic characteristics of an aerostatic bearing spindle and its influence on surface topography in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2012, 62, 1–12. [Google Scholar] [CrossRef]
- Wen, Z.P.; Gu, H.; Shi, Z.Y. Key Technologies and Design Methods of Ultra-Precision Aerostatic Bearings. Lubricants 2023, 11, 315. [Google Scholar] [CrossRef]
- Li, J.; Liu, P. Dynamic analysis of 5-DOFs aerostatic spindles considering tilting motion with varying stiffness and damping of thrust bearings. J. Mech. Sci. Technol. 2019, 33, 5199–5207. [Google Scholar] [CrossRef]
- Zhao, X.L.; Dong, H.; Fang, Z.; Chen, D.D.; Zhang, J.A. Study on Dynamic Characteristics of Aerostatic Bearing with Elastic Equalizing Pressure Groove. Shock Vib. 2018, 2018, 989. [Google Scholar] [CrossRef]
- Chen, D.; Li, N.; Pan, R.; Han, J. Analysis of aerostatic spindle radial vibration error based on microscale nonlinear dynamic characteristics. J. Vib. Control. 2019, 25, 2043–2052. [Google Scholar] [CrossRef]
- Lei, Q.; Yuan, Y.; Du, J.; LI, L. Study on Rotor Dynamics Characteristics of High Speed Aerostatic Motorized Spindle during Fly-cutter Milling Process. J. Mech. Eng. 2021, 57, 45–54. [Google Scholar]
- Shi, J.H.; Cao, H.R.; Jin, X.L. Dynamics of 5-DOF aerostatic spindle with time-varying coefficients of air bearing. Mech. Syst. Signal Proc. 2022, 172, 109005. [Google Scholar] [CrossRef]
- Zhang, G.-H.; Sun, Y.; Liu, Z.-S.; Zhang, M.; Yan, J.-J. Dynamic characteristics of self-acting gas bearing–flexible rotor coupling system based on the forecasting orbit method. Nonlinear Dyn. 2011, 69, 341–355. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, K.; Zhang, Y.; Liu, W.; Li, W. Nonlinear dynamic analysis of a rotor-bearing system with porous tilting pad bearing support. Nonlinear Dyn. 2018, 94, 1391–1408. [Google Scholar] [CrossRef]
- Chen, G.D.; Chen, Y.J. Multi-Field Coupling Dynamics Modeling of Aerostatic Spindle. Micromachines 2021, 12, 251. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; Li, J.; Li, W.; Huang, J.; Gao, F.; Sun, J. A novel parallel capillary-cavity model for the analysis of pneumatic hammer vibration in porous aerostatic bearings. Tribol. Int. 2023, 189, 108993. [Google Scholar] [CrossRef]
- Gao, S.; Cheng, K.; Chen, S.; Ding, H.; Fu, H. Computational design and analysis of aerostatic journal bearings with application to ultra-high speed spindles. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 231, 1205–1220. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Y.; Lu, Q.; Wu, Q.; Wang, M. Multi-Physics Fields Based Nonlinear Dynamic Behavior Analysis of Air Bearing Motorized Spindle. Micromachines 2020, 11, 723. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, Y.; Chen, W.; Wang, Q.; Chen, G. Theoretical prediction and experimental verification of the unbalanced magnetic force in air bearing motor spindles. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2019, 233, 2330–2344. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, X.; Wang, X.; Su, Z.; Wang, D. Effects of Shaft Shape Errors on the Dynamic Characteristics of a Rotor-Bearing System. J. Tribol. 2019, 141, 101701. [Google Scholar] [CrossRef]
- Zhang, G.; Zheng, J.; Yu, H.; Chen, T.; Zhang, K.; Dou, G. Evaluation of the Influence of Shaft Shape Errors on the Rotation Accuracy of Aerostatic Spindle—Part 1: Modeling. Electronics 2022, 11, 1304. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Spindle length () | 340 mm |
| Spindle mass () | 5.6 Kg |
| X direction torque of inertia () | 31.18 g.m2 |
| Y direction torque of inertia () | 31.18 g.m2 |
| Z direction torque of inertia () | 3.27 g.m2 |
| Center of mass position () | 167 mm |
| Position of front tapered bearing () | 130 mm |
| Position of front thrust bearing () | 150 mm |
| Position of rear thrust bearing () | 160 mm |
| Position of rear tapered bearing () | 180 mm |
| Parameter | Value |
|---|---|
| Radius of the inner circle () | 30 mm |
| Radius of the external circle () | 60 mm |
| Radius of distribution circle () | 45 mm |
| Number of orifices () | 16 |
| Orifice diameter () | 0.12 mm |
| Average film thickness () | 20 μm |
| Parameter | Value |
|---|---|
| Big end radius () | 30 mm |
| Height (H) | 80 mm |
| Half-cone angle () | 3° |
| Number of orifices () | 16 |
| Orifice diameter () | 0.12 mm |
| Radial maximum film thickness () | 25 μm |
| Axial adjustment () | 0~100 μm |
| Distance from orifice to end face () | 20 mm |
| Parameter | Value |
|---|---|
| Gas supply pressure ) | 0.3~0.8 MPa |
| Atmospheric pressure ) | 0.1 MPa |
| Gas density at ambient pressure ) | 1.204 Kg/m3 |
| Gas dynamic viscosity () | |
| Ratio of Specific Heat () | 1.4 |
| Gas temperature () | 293 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Jia, C.; Lu, Y. Dynamic Modeling of 5-DOF Aerostatic Bearing Rotor System with Adjustable Gas Film Gap. Lubricants 2024, 12, 424. https://doi.org/10.3390/lubricants12120424
Jia S, Jia C, Lu Y. Dynamic Modeling of 5-DOF Aerostatic Bearing Rotor System with Adjustable Gas Film Gap. Lubricants. 2024; 12(12):424. https://doi.org/10.3390/lubricants12120424
Chicago/Turabian StyleJia, Shuo, Chenhui Jia, and Yanhui Lu. 2024. "Dynamic Modeling of 5-DOF Aerostatic Bearing Rotor System with Adjustable Gas Film Gap" Lubricants 12, no. 12: 424. https://doi.org/10.3390/lubricants12120424
APA StyleJia, S., Jia, C., & Lu, Y. (2024). Dynamic Modeling of 5-DOF Aerostatic Bearing Rotor System with Adjustable Gas Film Gap. Lubricants, 12(12), 424. https://doi.org/10.3390/lubricants12120424




