Comment on Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178
Conflicts of Interest
References
- Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Effect of Pressure on the Viscosity of Forty-Three Pure Liquids. Proc. Amer. Acad. 1926, 61, 57–99. [Google Scholar] [CrossRef]
- Thoms, E.; Grzybowski, A.; Pawlus, S.; Paluch, M. Breakdown of the Simple Arrhenius Law in the Normal Liquid State. J. Phys. Chem. Lett. 2018, 9, 1783–1787. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L.; Tevaarwerk, J.L. Shear behaviour of elastohydrodynamic oil films. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 356, 215–236. [Google Scholar]
- Bair, S.; Winer, W.O. Some observations in high pressure rheology of lubricants. J. Lubr. Technol. 1982, 104, 357–364. [Google Scholar] [CrossRef]
- Houpert, L. New results of traction force calculations in elastohydrodynamic contacts. J. Tribol. 1985, 107, 241–248. [Google Scholar] [CrossRef]
- Ree, F.; Ree, T.; Eyring, H. Relaxation theory of transport problems in condensed systems. Ind. Eng. Chem. 1958, 50, 1036–1040. [Google Scholar] [CrossRef]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 1966. [Google Scholar]
- Prentice, I.J.; Liu, X.; Nerushev, O.A.; Balakrishnan, S.; Pulham, C.R.; Camp, P.J. Experimental and simulation study of the high-pressure behavior of squalane and poly-α-olefins. J. Chem. Phys. 2020, 152, 074504. [Google Scholar] [CrossRef] [PubMed]
- Bair, S.; Kotzalas, M. The contribution of roller compliance to elastohydrodynamic traction. Tribol. Trans. 2006, 49, 218–224. [Google Scholar] [CrossRef]
- Hooke, C.; Šperka, P.; Bair, S.; Morales-Espejel, G.E. A comparison of measured film thicknesses with quantitative predictions from an elastohydrodynamic, perturbation analysis at high slide-roll ratios. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 870–880. [Google Scholar] [CrossRef]
- Lower, G.W.; Walker, W.C.; Zettlemoyer, A.C. The rheology of printing inks. II. temperature control studies in the rotational viscometer. J. Colloid Sci. 1953, 8, 116–129. [Google Scholar] [CrossRef]
- Floudas, G.; Paluch, M.; Grzybowski, A.; Ngai, K. Molecular Dynamics of Glass-Forming Systems: Effects of Pressure; Springer Science & Business Media: Heidelburg, Germany, 2010; Volume 1, pp. 7–8. [Google Scholar]
- Drozd-Rzoska, A. Pressure-related universal previtreous behavior of the structural relaxation time and apparent fragility. Front. Mater. 2019, 6, 103. [Google Scholar] [CrossRef]
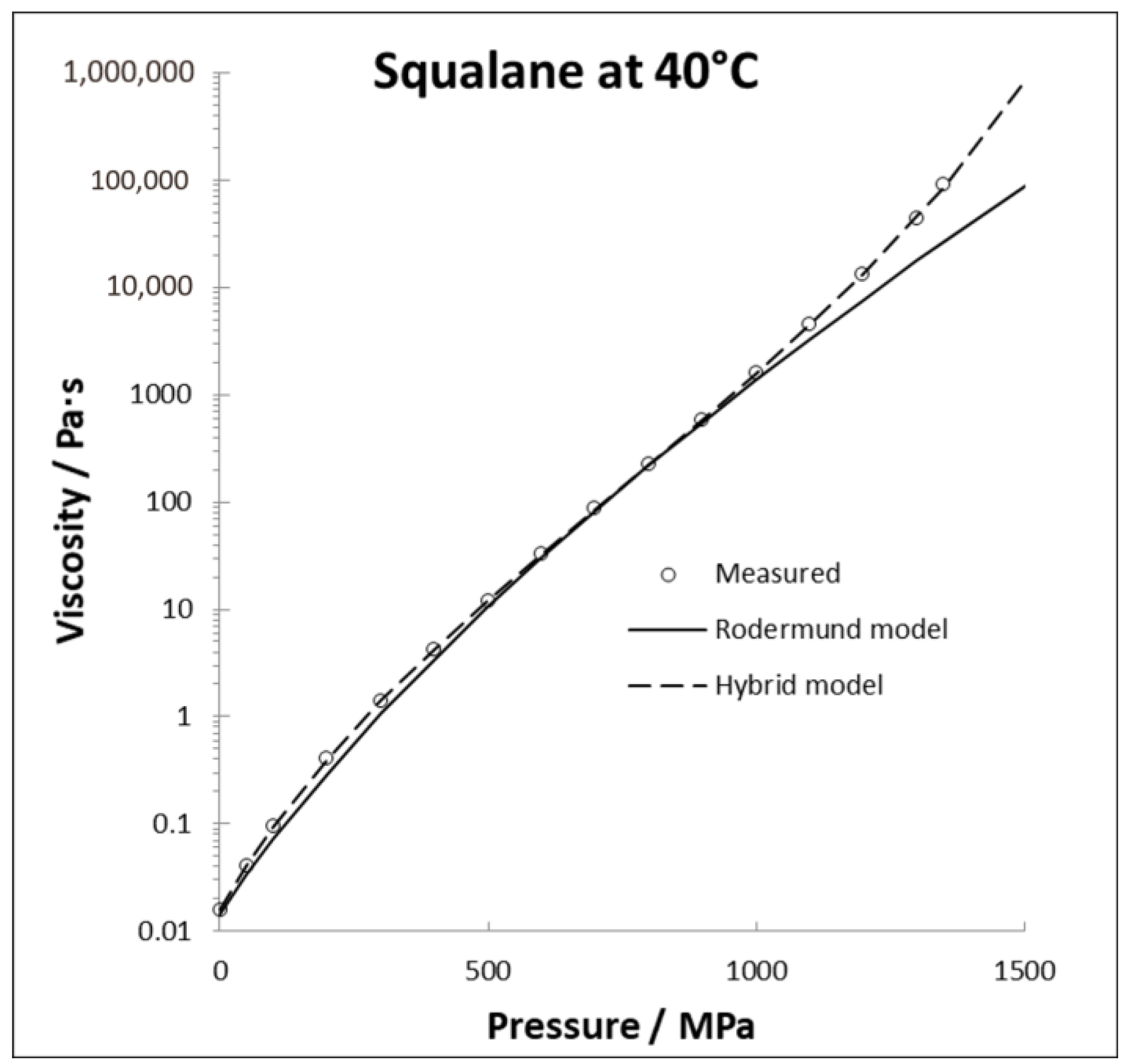
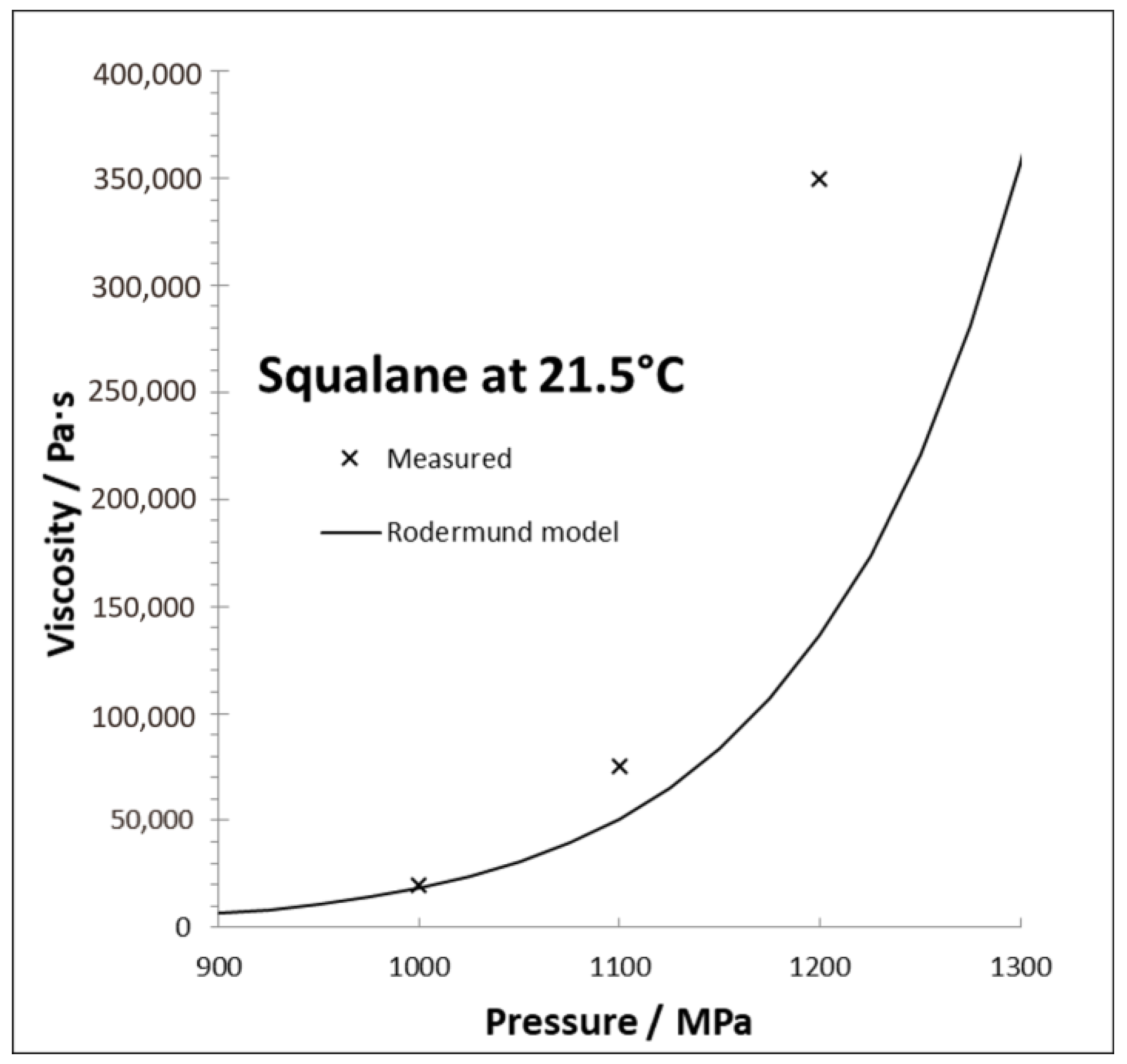
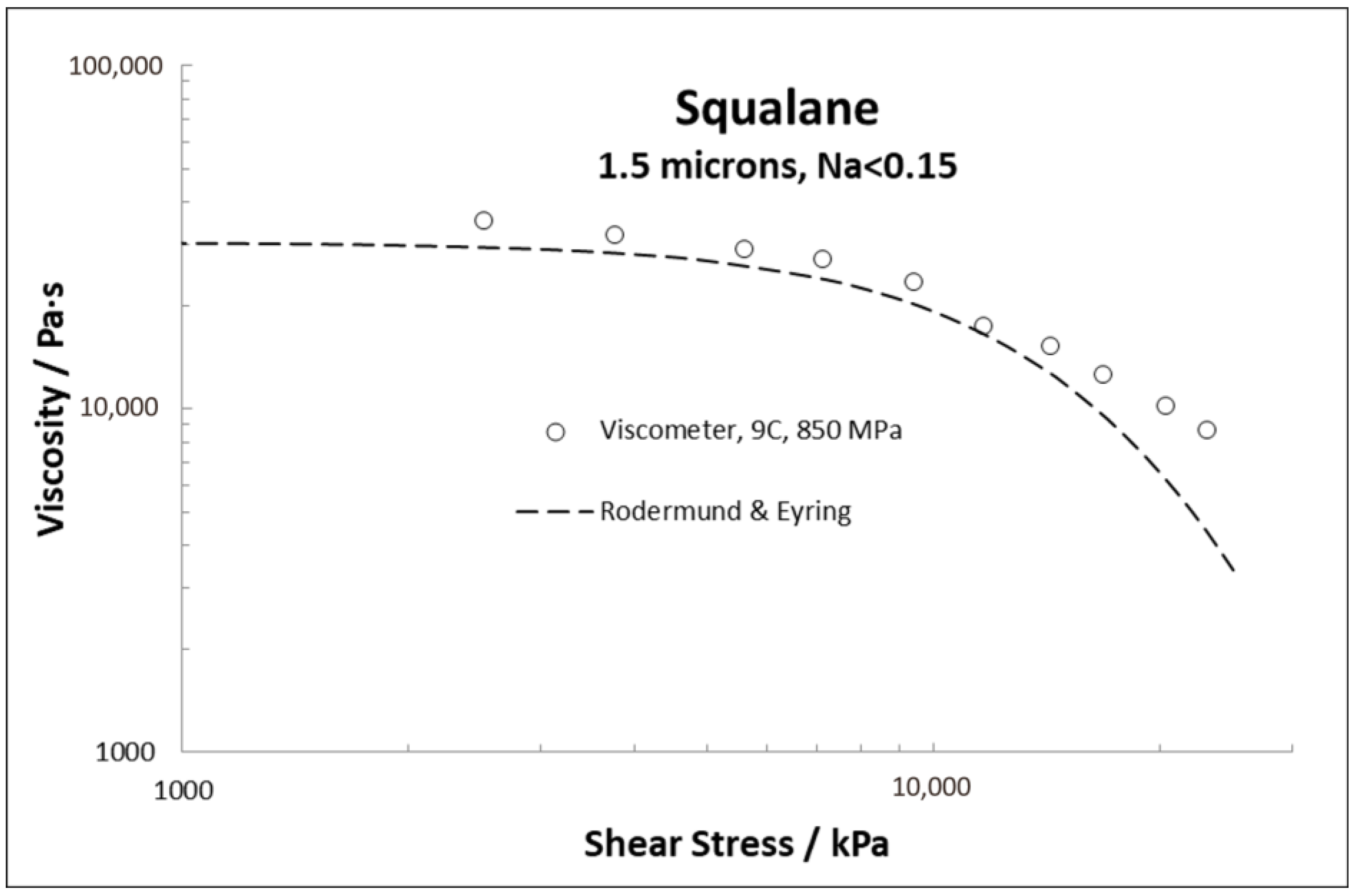
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bair, S. Comment on Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178. Lubricants 2023, 11, 393. https://doi.org/10.3390/lubricants11090393
Bair S. Comment on Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178. Lubricants. 2023; 11(9):393. https://doi.org/10.3390/lubricants11090393
Chicago/Turabian StyleBair, Scott. 2023. "Comment on Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178" Lubricants 11, no. 9: 393. https://doi.org/10.3390/lubricants11090393
APA StyleBair, S. (2023). Comment on Neupert, T.; Bartel, D. Evaluation of Various Shear-Thinning Models for Squalane Using Traction Measurements, TEHD and NEMD Simulations. Lubricants 2023, 11, 178. Lubricants, 11(9), 393. https://doi.org/10.3390/lubricants11090393




