A GMRT Narrowband vs. Wideband Analysis of the ACT−CL J0034.4+0225 Field Selected from the ACTPol Cluster Sample
Abstract
1. Introduction
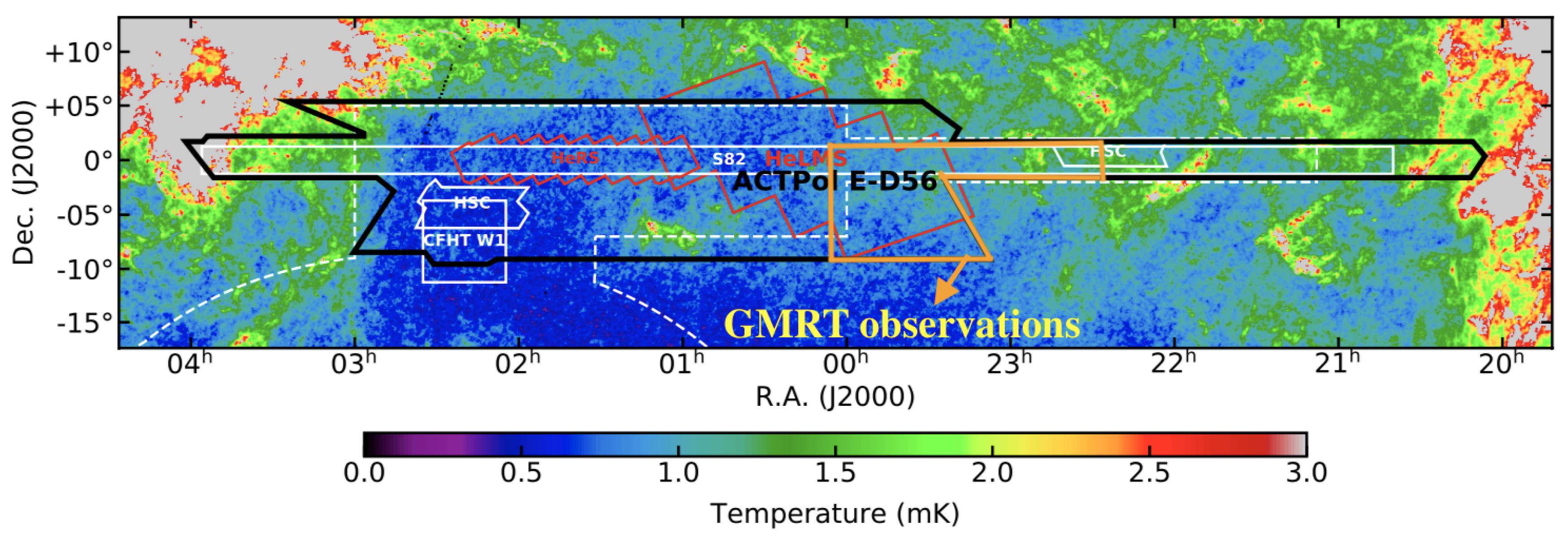
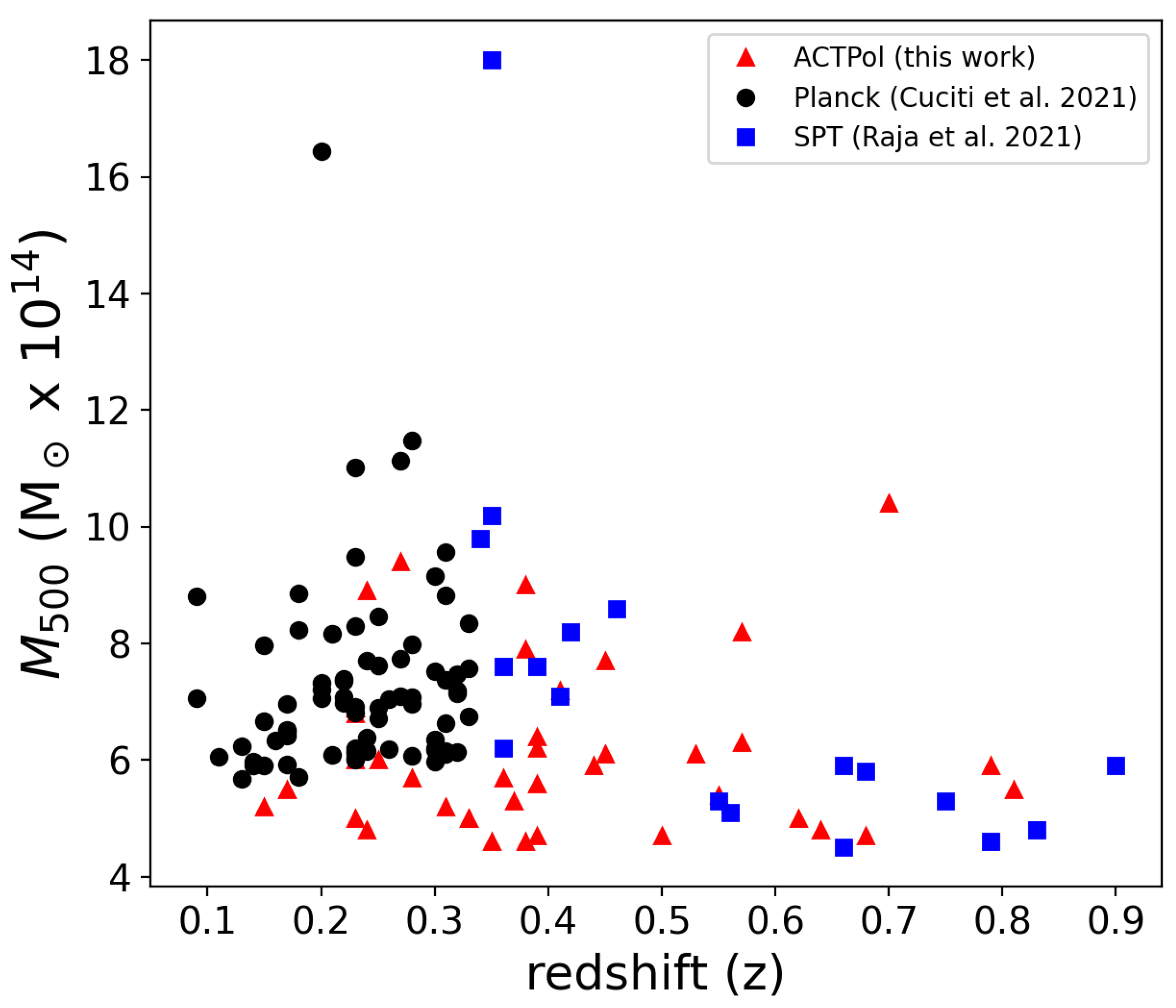
2. The ACTPol Sample
3. Data Reduction
3.1. Legacy GMRT GSB
- The ‘pre-calibrate target’ step performs the cross-calibration step of the standard calibration procedure. The pipeline uses the primary calibrator(s) to determine the channels affected by RFI, determine the flux scale, and to produce cross calibration tables. The flags and calibration tables are then applied to the target source. Finally, the calibrator and target visibilities are split into separate UVFITS files.
- The ‘process target’ step begins by taking the cross-calibrated (1GC) target data and applying 2GC (or self calibration). For 2GC, the target visibilities are imaged using the facet-based method established by Cornwell and Perley [69]. The point sources covering the primary beam are obtained from a sky model extracted from the VLA low-frequency sky survey (VLSS; [70]) and the NRAO VLA sky survey (NVSS; [71]). The observed field is then faceted based on the sky model. The deconvolution is done using the Cotton-Schwab clean algorithm [71]. The cleaned visibilities are calibrated using the sky model. Then the calibrated visibilities are imaged to produce a better sky model and improved calibration solutions. This self calibration cycle is applied three times. For the wide-field imaging, the pipeline performs a single-scale CLEAN deconvolution down to 3 times the central background noise (), using automated CLEAN boxes placed at positive peaks of at least 5.
- The second part of the ‘process target’ step is to correct for DDEs (3GC), which include ionospheric effects [72]. For each 3GC cycle, the brightest source in the field is peeled. The ionospheric effects of the brightest source are modelled and phase corrected solutions for the peeled model are obtained. spam uses a phase screen model to extend the ionospheric phase solutions of the single source to the full field. Then the solutions are applied to each facet during imaging. This cycle is repeated six times, and each time the brightest source is selected and corrected for DDEs. This repeats until all the bright sources are corrected for DDEs. Finally, the astrometric corrections are applied to the DDEs corrected image and the image is primary beam corrected thereafter.
3.2. uGMRT Data Reduction
3.2.1. CASA Pipeline
3.2.2. DDFacet/killMS Pipeline
3.2.3. Experimental SPAM Wideband Pipeline
3.3. Flux Density and P Calculations
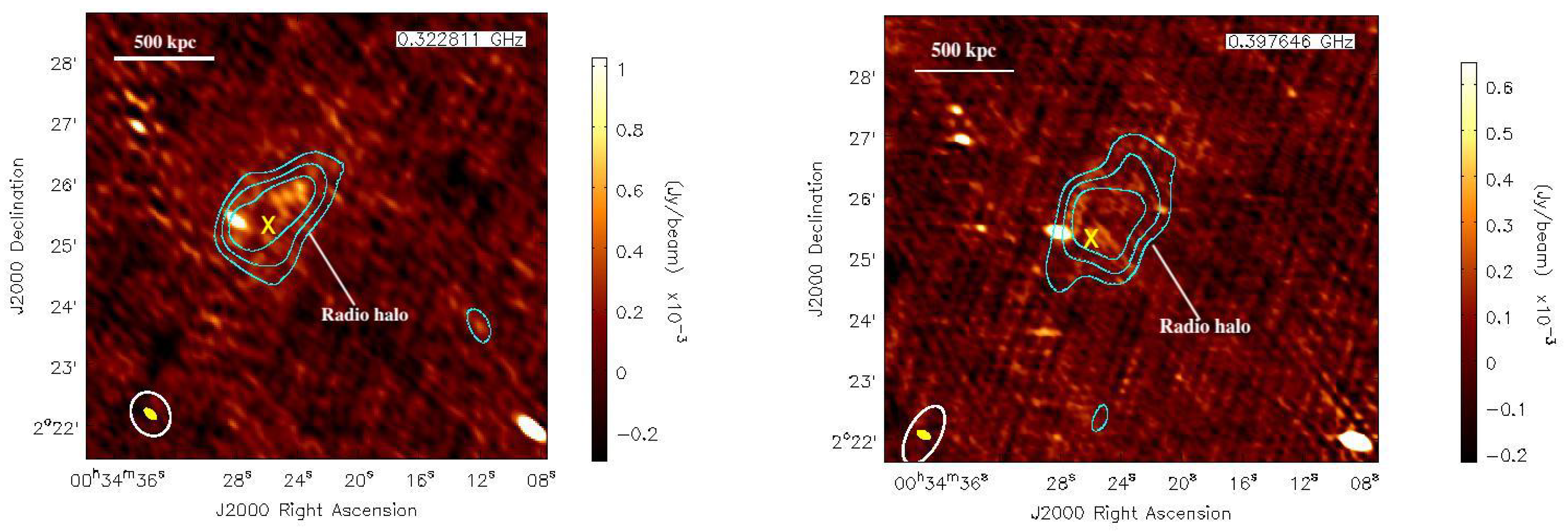
4. Case Study: ACT-CL J0034.4+0225
5. Summary and Future Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | S |
| 2 | https://github.com/saopicc/killMS, accessed on 30 November 2020. |
| 3 | http://www.intema.nl/doku.php?id=huibintemaspampipeline, accessed on 30 November 2020. |
References
- Large, M.I.; Mathewson, D.S.; Haslam, C.G.T. A High-resolution Survey of the Andromeda Nebula at 408 Mc./S. Nature 1959, 183, 1250–1251. [Google Scholar] [CrossRef]
- Brown, S.; Rudnick, L. Diffuse radio emission in/around the Coma cluster: Beyond simple accretion. Mon. Not. R. Astron. Soc. 2011, 412, 2–12. [Google Scholar] [CrossRef]
- Bonafede, A.; Brunetti, G.; Vazza, F.; Simionescu, A.; Giovannini, G.; Bonnassieux, E.; Shimwell, T.W.; Brüggen, M.; van Weeren, R.J.; Botteon, A.; et al. The Coma cluster at LOFAR frequencies I: Insights into particle acceleration mechanisms in the radio bridge. arXiv 2020, arXiv:2011.08856. [Google Scholar]
- Sarazin, C.L. Book-Review—X-ray Emissions from Clusters of Galaxies. Sky Telesc. 1988, 76, 639. [Google Scholar]
- Kravtsov, A.V.; Borgani, S. Formation of Galaxy Clusters. Annu. Rev. Astron. Astrophys. 2012, 50, 353–409. [Google Scholar] [CrossRef]
- Enßlin, T.; Pfrommer, C.; Miniati, F.; Subramanian, K. Cosmic ray transport in galaxy clusters: Implications for radio halos, gamma-ray signatures, and cool core heating. Astron. Astrophys. 2011, 527, A99. [Google Scholar] [CrossRef]
- Dennison, B. Cosmic Rays in Clusters of Galaxies and the Formation of Extended Radio Halos. Bull. Am. Astron. Soc. 1980, 12, 471. [Google Scholar]
- Pfrommer, C.; Enßlin, T.A.; Springel, V. Simulating cosmic rays in clusters of galaxies—II. A unified scheme for radio haloes and relics with predictions of the γ-ray emission. Mon. Not. R. Astron. Soc. 2008, 385, 1211–1241. [Google Scholar] [CrossRef]
- Reimer, O.; Pohl, M.; Sreekumar, P.; Mattox, J.R. EGRET Upper Limits on the High-Energy Gamma-ray Emission of Galaxy Clusters. Astrophys. J. 2003, 588, 155–164. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, A.F. Fermi LAT observations of cosmic-ray electrons from 7 GeV to 1 TeV. Phys. Rev. D 2010, 82, 092004. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, F. Search for Gamma-Ray Emission from the Coma Cluster with Six Years of Fermi-LAT Data. Astrophys. J. 2016, 819, 149, Erratum in 2018, 860, 85. [Google Scholar] [CrossRef]
- Brunetti, G.; Blasi, P. Alfvénic reacceleration of relativistic particles in galaxy clusters in the presence of secondary electrons and positrons. Mon. Not. R. Astron. Soc. 2005, 363, 1173–1187. [Google Scholar] [CrossRef]
- Brunetti, G.; Zimmer, S.; Zandanel, F. Relativistic protons in the Coma galaxy cluster: First gamma-ray constraints ever on turbulent reacceleration. Mon. Not. R. Astron. Soc. 2017, 472, 1506–1525. [Google Scholar] [CrossRef]
- Pinzke, A.; Oh, S.P.; Pfrommer, C. Turbulence and particle acceleration in giant radio haloes: The origin of seed electrons. Mon. Not. R. Astron. Soc. 2017, 465, 4800–4816. [Google Scholar] [CrossRef]
- Brunetti, G.; Setti, G.; Feretti, L.; Giovannini, G. Particle reacceleration in the Coma cluster: Radio properties and hard X-ray emission. Mon. Not. R. Astron. Soc. 2001, 320, 365–378. [Google Scholar] [CrossRef]
- Feretti, L.; Giovannini, G.; Govoni, F.; Murgia, M. Clusters of galaxies: Observational properties of the diffuse radio emission. Astron. Astrophys. Rev. 2012, 20, 54. [Google Scholar] [CrossRef]
- Donnert, J.; Brunetti, G. An efficient Fokker-Planck solver and its application to stochastic particle acceleration in galaxy clusters. Mon. Not. R. Astron. Soc. 2014, 443, 3564–3577. [Google Scholar] [CrossRef]
- Markevitch, M.; Govoni, F.; Brunetti, G.; Jerius, D. Bow Shock and Radio Halo in the Merging Cluster A520. Astrophys. J. 2005, 627, 733–738. [Google Scholar] [CrossRef]
- Lindner, R.R.; Baker, A.J.; Hughes, J.P.; Battaglia, N.; Gupta, N.; Knowles, K.; Marriage, T.A.; Menanteau, F.; Moodley, K.; Reese, E.D.; et al. The Radio Relics and Halo of El Gordo, a Massive z = 0.870 Cluster Merger. Astrophys. J. 2014, 786, 49. [Google Scholar] [CrossRef]
- Kale, R.; Venturi, T.; Giacintucci, S.; Dallacasa, D.; Cassano, R.; Brunetti, G.; Cuciti, V.; Macario, G.; Athreya, R. The Extended GMRT Radio Halo Survey. II. Further results and analysis of the full sample. Astron. Astrophys. 2015, 579, A92. [Google Scholar] [CrossRef]
- Cassano, R.; Ettori, S.; Brunetti, G.; Giacintucci, S.; Pratt, G.W.; Venturi, T.; Kale, R.; Dolag, K.; Markevitch, M. Revisiting Scaling Relations for Giant Radio Halos in Galaxy Clusters. Astrophys. J. 2013, 777, 141. [Google Scholar] [CrossRef]
- Brunetti, G.; Jones, T.W. Cosmic Rays in Galaxy Clusters and Their Nonthermal Emission. Int. J. Mod. Phys. D 2014, 23, 1430007-98. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Observations of Relic Radiation as a Test of the Nature of X-ray Radiation from the Clusters of Galaxies. Comments Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Cuciti, V.; Cassano, R.; Brunetti, G.; Dallacasa, D.; Kale, R.; Ettori, S.; Venturi, T. Occurrence of radio halos in galaxy clusters. Insight from a mass-selected sample. Astron. Astrophys. 2015, 580, A97. [Google Scholar] [CrossRef]
- Cuciti, V.; Cassano, R.; Brunetti, G.; Dallacasa, D.; de Gasperin, F.; Ettori, S.; Giacintucci, S.; Kale, R.; Pratt, G.W.; van Weeren, R.J.; et al. Radio halos in a mass-selected sample of 75 galaxy clusters. II. Statistical analysis. arXiv 2021, arXiv:2101.01641. [Google Scholar]
- van Weeren, R.J.; de Gasperin, F.; Akamatsu, H.; Brüggen, M.; Feretti, L.; Kang, H.; Stroe, A.; Zandanel, F. Diffuse Radio Emission from Galaxy Clusters. Space Sci. Rev. 2019, 215, 16. [Google Scholar] [CrossRef]
- Gitti, M.; Brunetti, G.; Setti, G. Modeling the interaction between ICM and relativistic plasma in cooling flows: The case of the Perseus cluster. Astron. Astrophys. 2002, 386, 456–463. [Google Scholar] [CrossRef]
- Bonafede, A.; Intema, H.T.; Bruggen, M.; Russell, H.R.; Ogrean, G.; Basu, K.; Sommer, M.; van Weeren, R.J.; Cassano, R.; Fabian, A.C.; et al. A giant radio halo in the cool core cluster CL1821+643. Mon. Not. R. Astron. Soc. 2014, 444, L44–L48. [Google Scholar] [CrossRef]
- Parekh, V.; Laganá, T.F.; Kale, R. Substructure analysis of the RXCJ0232.2-4420 galaxy cluster. Mon. Not. R. Astron. Soc. 2021, 504, 610–620. [Google Scholar] [CrossRef]
- Jaffe, W.J.; Rudnick, L. Observations at 610 MHz of radio halos in clusters of galaxies. Astrophys. J. 1979, 233, 453–462. [Google Scholar] [CrossRef]
- Enßlin, T.A.; Biermann, P.L.; Klein, U.; Kohle, S. Cluster radio relics as a tracer of shock waves of the large-scale structure formation. Astron. Astrophys. 1998, 332, 395–409. [Google Scholar]
- Bonafede, A.; Brüggen, M.; van Weeren, R.; Vazza, F.; Giovannini, G.; Ebeling, H.; Edge, A.C.; Hoeft, M.; Klein, U. Discovery of radio haloes and double relics in distant MACS galaxy clusters: Clues to the efficiency of particle acceleration. Mon. Not. R. Astron. Soc. 2012, 426, 40–56. [Google Scholar] [CrossRef]
- Botteon, A.; Gastaldello, F.; Brunetti, G.; Dallacasa, D. A shock at the radio relic position in Abell 115. Mon. Not. R. Astron. Soc. 2016, 460, L84–L88. [Google Scholar] [CrossRef]
- Locatelli, N.T.; Rajpurohit, K.; Vazza, F.; Gastaldello, F.; Dallacasa, D.; Bonafede, A.; Rossetti, M.; Stuardi, C.; Bonassieux, E.; Brunetti, G.; et al. Discovering the most elusive radio relic in the sky: Diffuse shock acceleration caught in the act? Mon. Not. R. Astron. Soc. 2020, 496, L48–L53. [Google Scholar] [CrossRef]
- Stuardi, C.; Bonafede, A.; Wittor, D.; Vazza, F.; Botteon, A.; Locatelli, N.; Dallacasa, D.; Golovich, N.; Hoeft, M.; van Weeren, R.J.; et al. Particle re-acceleration and Faraday-complex structures in the RXC J1314.4-2515 galaxy cluster. Mon. Not. R. Astron. Soc. 2019, 489, 3905–3926. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts—II. Mon. Not. R. Astron. Soc. 1978, 182, 443–455. [Google Scholar] [CrossRef]
- Jones, F.C.; Ellison, D.C. The plasma physics of shock acceleration. Space Sci. Rev. 1991, 58, 259–346. [Google Scholar] [CrossRef]
- Pinzke, A.; Oh, S.P.; Pfrommer, C. Giant radio relics in galaxy clusters: Reacceleration of fossil relativistic electrons? Mon. Not. R. Astron. Soc. 2013, 435, 1061–1082. [Google Scholar] [CrossRef]
- Kang, H.; Ryu, D.; Jones, T.W. Shock Acceleration Model for the Toothbrush Radio Relic. Astrophys. J. 2017, 840, 42. [Google Scholar] [CrossRef]
- de Gasperin, F.; van Weeren, R.J.; Brüggen, M.; Vazza, F.; Bonafede, A.; Intema, H.T. A new double radio relic in PSZ1 G096.89+24.17 and a radio relic mass-luminosity relation. Mon. Not. R. Astron. Soc. 2014, 444, 3130–3138. [Google Scholar] [CrossRef]
- Shimwell, T.W.; Markevitch, M.; Brown, S.; Feretti, L.; Gaensler, B.M.; Johnston-Hollitt, M.; Lage, C.; Srinivasan, R. Another shock for the Bullet cluster, and the source of seed electrons for radio relics. Mon. Not. R. Astron. Soc. 2015, 449, 1486–1494. [Google Scholar] [CrossRef]
- van Weeren, R.J.; Andrade-Santos, F.; Dawson, W.A.; Golovich, N.; Lal, D.V.; Kang, H.; Ryu, D.; Brìggen, M.; Ogrean, G.A.; Forman, W.R.; et al. The case for electron re-acceleration at galaxy cluster shocks. Nat. Astron. 2017, 1, 0005. [Google Scholar] [CrossRef]
- Bonafede, A.; Intema, H.T.; Brüggen, M.; Girardi, M.; Nonino, M.; Kantharia, N.; van Weeren, R.J.; Röttgering, H.J.A. Evidence for Particle Re-acceleration in the Radio Relic in the Galaxy Cluster PLCKG287.0+32.9. Astrophys. J. 2014, 785, 1. [Google Scholar] [CrossRef]
- van Weeren, R.J.; Ogrean, G.A.; Jones, C.; Forman, W.R.; Andrade-Santos, F.; Pearce, C.J.J.; Bonafede, A.; Brüggen, M.; Bulbul, E.; Clarke, T.E.; et al. Chandra and JVLA Observations of HST Frontier Fields Cluster MACS J0717.5+3745. Astrophys. J. 2017, 835, 197. [Google Scholar] [CrossRef]
- Zimbardo, G.; Perri, S. Superdiffusive shock acceleration at galaxy cluster shocks. Nat. Astron. 2017, 1, 0163. [Google Scholar] [CrossRef]
- Zimbardo, G.; Perri, S. Understanding the radio spectral indices of galaxy cluster relics by superdiffusive shock acceleration. Mon. Not. R. Astron. Soc. 2018, 478, 4922–4930. [Google Scholar] [CrossRef]
- Guo, X.; Sironi, L.; Narayan, R. Non-thermal Electron Acceleration in Low Mach Number Collisionless Shocks. II. Firehose-mediated Fermi Acceleration and its Dependence on Pre-shock Conditions. Astrophys. J. 2014, 797, 47. [Google Scholar] [CrossRef]
- Caprioli, D.; Spitkovsky, A. Simulations of Ion Acceleration at Non-relativistic Shocks. III. Particle Diffusion. Astrophys. J. 2014, 794, 47. [Google Scholar] [CrossRef]
- van Haarlem, M.P.; Wise, M.W.; Gunst, A.W.; Heald, G.; McKean, J.P.; Hessels, J.W.T.; de Bruyn, A.G.; Nijboer, R.; Swinbank, J.; Fallows, R.; et al. LOFAR: The LOw-Frequency ARray. Astron. Astrophys. 2013, 556, A2. [Google Scholar] [CrossRef]
- Jonas, J.; MeerKAT Team. The MeerKAT Radio Telescope. In Proceedings of the MeerKAT Science: On the Pathway to the SKA, Stellenbosch, South Africa, 25–27 May 2016; p. 1. [Google Scholar]
- Gupta, Y.; Ajithkumar, B.; Kale, H.S.; Nayak, S.; Sabhapathy, S.; Sureshkumar, S.; Swami, R.V.; Chengalur, J.N.; Ghosh, S.K.; Ishwara-Chandra, C.H.; et al. The upgraded GMRT: Opening new windows on the radio Universe. Curr. Sci. 2017, 113, 707–714. [Google Scholar] [CrossRef]
- de Gasperin, F.; Intema, H.T.; Shimwell, T.W.; Brunetti, G.; Brüggen, M.; Enßlin, T.A.; van Weeren, R.J.; Bonafede, A.; Röttgering, H.J.A. Gentle reenergization of electrons in merging galaxy clusters. Sci. Adv. 2017, 3, e1701634. [Google Scholar] [CrossRef]
- Knowles, K.; Baker, A.J.; Bond, J.R.; Gallardo, P.A.; Gupta, N.; Hilton, M.; Hughes, J.P.; Intema, H.; López-Caraballo, C.H.; Moodley, K.; et al. GMRT 610 MHz observations of galaxy clusters in the ACT equatorial sample. Mon. Not. R. Astron. Soc. 2019, 486, 1332–1349. [Google Scholar] [CrossRef]
- Giovannini, G.; Cau, M.; Bonafede, A.; Ebeling, H.; Feretti, L.; Girardi, M.; Gitti, M.; Govoni, F.; Ignesti, A.; Murgia, M.; et al. Diffuse radio sources in a statistically complete sample of high-redshift galaxy clusters. Astron. Astrophys. 2020, 640, A108. [Google Scholar] [CrossRef]
- Raja, R.; Rahaman, M.; Datta, A.; van Weeren, R.J.; Intema, H.T.; Paul, S. A low-frequency radio halo survey of the South Pole Telescope SZ-selected clusters with the GMRT. Mon. Not. R. Astron. Soc. 2021, 500, 2236–2249. [Google Scholar] [CrossRef]
- Venturi, T.; Giacintucci, S.; Dallacasa, D.; Cassano, R.; Brunetti, G.; Bardelli, S.; Setti, G. GMRT radio halo survey in galaxy clusters at z = 0.2 − 0.4. II. The eBCS clusters and analysis of the complete sample. Astron. Astrophys. 2008, 484, 327–340. [Google Scholar] [CrossRef]
- Andrade-Santos, F.; Jones, C.; Forman, W.R.; Lovisari, L.; Vikhlinin, A.; van Weeren, R.J.; Murray, S.S.; Arnaud, M.; Pratt, G.W.; Démoclès, J.; et al. The Fraction of Cool-core Clusters in X-ray versus SZ Samples Using Chandra Observations. Astrophys. J. 2017, 843, 76. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Baker, M.; Balbi, A.; Banday, A.J.; et al. Planck early results. I. The Planck mission. Astron. Astrophys. 2011, 536, A1. [Google Scholar] [CrossRef]
- Carlstrom, J.E.; Ade, P.A.R.; Aird, K.A.; Benson, B.A.; Bleem, L.E.; Busetti, S.; Chang, C.L.; Chauvin, E.; Cho, H.M.; Crawford, T.M.; et al. The 10 Meter South Pole Telescope. Publ. Astron. Soc. Pac. 2011, 123, 568. [Google Scholar] [CrossRef]
- Louis, T.; Grace, E.; Hasselfield, M.; Lungu, M.; Maurin, L.; Addison, G.E.; Ade, P.A.R.; Aiola, S.; Allison, R.; Amiri, M.; et al. The Atacama Cosmology Telescope: Two-season ACTPol spectra and parameters. J. Cosmol. Astropart. Phys. 2017, 2017, 031. [Google Scholar] [CrossRef]
- Hilton, M.; Hasselfield, M.; Sifón, C.; Battaglia, N.; Aiola, S.; Bharadwaj, V.; Bond, J.R.; Choi, S.K.; Crichton, D.; Datta, R.; et al. The Atacama Cosmology Telescope: The Two-season ACTPol Sunyaev-Zel’dovich Effect Selected Cluster Catalog. Astrophys. J. Suppl. Ser. 2018, 235, 20. [Google Scholar] [CrossRef]
- Arnaud, M.; Pratt, G.W.; Piffaretti, R.; Böhringer, H.; Croston, J.H.; Pointecouteau, E. The universal galaxy cluster pressure profile from a representative sample of nearby systems (REXCESS) and the YSZ − M500 relation. Astron. Astrophys. 2010, 517, A92. [Google Scholar] [CrossRef]
- Knowles, K.; Baker, A.J.; Basu, K.; Bharadwaj, V.; de Gasperin, F.; Deane, R.; Devlin, M.; Dicker, S.; Ferrari, C.; Hilton, M.; et al. MERGHERS: An SZ-selected cluster survey with MeerKAT. In Proceedings of the MeerKAT Science: On the Pathway to the SKA, Stellenbosch, South Africa, 25–27 May 2016; p. 30. [Google Scholar]
- Gupta, N.; Srianand, R.; Baan, W.; Baker, A.J.; Beswick, R.J.; Bhatnagar, S.; Bhattacharya, D.; Bosma, A.; Carilli, C.; Cluver, M.; et al. The MeerKAT Absorption Line Survey (MALS). In Proceedings of the MeerKAT Science: On the Pathway to the SKA, Stellenbosch, South Africa, 25–27 May 2016; p. 14. [Google Scholar]
- Intema, H.T. SPAM: A data reduction recipe for high-resolution, low-frequency radio-interferometric observations. Astron. Soc. India Conf. Ser. 2014, 13, 469. [Google Scholar]
- Intema, H.T.; Jagannathan, P.; Mooley, K.P.; Frail, D.A. The GMRT 150 MHz all-sky radio survey. First alternative data release TGSS ADR1. Astron. Astrophys. 2017, 598, A78. [Google Scholar] [CrossRef]
- Kettenis, M.; van Langevelde, H.J.; Reynolds, C.; Cotton, B. ParselTongue: AIPS Talking Python. In Astronomical Data Analysis Software and Systems XV; Gabriel, C., Arviset, C., Ponz, D., Enrique, S., Eds.; Astronomical Society of the Pacific Conference Series; ADASS: San Lorenzo de El Escorial, Spain, 2005; Volume 351, p. 497. [Google Scholar]
- van Moorsel, G.; Kemball, A.; Greisen, E. AIPS Developments in the Nineties. In Astronomical Data Analysis Software and Systems V; Jacoby, G.H., Barnes, J., Eds.; Astronomical Society of the Pacific Conference Series; ADASS: Tucson, AZ, USA, 1995; Volume 101, p. 37. [Google Scholar]
- Cornwell, T.J.; Perley, R.A. Radio-interferometric imaging of very large fields. The problem of non-coplanar arrays. Astron. Astrophys. 1992, 261, 353–364. [Google Scholar]
- Cohen, A.S.; Lane, W.M.; Cotton, W.D.; Kassim, N.E.; Lazio, T.J.W.; Perley, R.A.; Condon, J.J.; Erickson, W.C. The VLA Low-Frequency Sky Survey. Astron. J. 2007, 134, 1245–1262. [Google Scholar] [CrossRef]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA Sky Survey. Astron. J. 1998, 115, 1693–1716. [Google Scholar] [CrossRef]
- Lonsdale, C.J. Configuration Considerations for Low Frequency Arrays. In From Clark Lake to the Long Wavelength Array: Bill Erickson’s Radio Science; Kassim, N., Perez, M., Junor, W., Henning, P., Eds.; Astronomical Society of the Pacific Conference Series; ADASS: Cambridge, MA, USA, 2005; Volume 345, p. 399. [Google Scholar]
- Kale, R.; Ishwara-Chandra, C.H. CAPTURE: Interferometric Pipeline for Image Creation from GMRT Data. Exp. Astron. 2020, 51, 95–108. [Google Scholar] [CrossRef]
- McMullin, J.P.; Waters, B.; Schiebel, D.; Young, W.; Golap, K. CASA Architecture and Applications. In Astronomical Data Analysis Software and Systems XVI; Shaw, R.A., Hill, F., Bell, D.J., Eds.; Astronomical Society of the Pacific Conference Series; ADASS: Austin, TX, USA, 2007; Volume 376, p. 127. [Google Scholar]
- Perley, R.A.; Butler, B.J. An Accurate Flux Density Scale from 1 to 50 GHz. Astrophys. J. Suppl. Ser. 2013, 204, 19. [Google Scholar] [CrossRef]
- Offringa, A.R.; van de Gronde, J.J.; Roerdink, J.B.T.M. A morphological algorithm for improving radio-frequency interference detection. Astron. Astrophys. 2012, 539, A95. [Google Scholar] [CrossRef]
- Tasse, C.; Hugo, B.; Mirmont, M.; Smirnov, O.; Atemkeng, M.; Bester, L.; Hardcastle, M.J.; Lakhoo, R.; Perkins, S.; Shimwell, T. Faceting for direction-dependent spectral deconvolution. Astron. Astrophys. 2018, 611, A87. [Google Scholar] [CrossRef]
- Joye, W.A.; Mandel, E. New Features of SAOImage DS9. In Astronomical Data Analysis Software and Systems XII; Payne, H.E., Jedrzejewski, R.I., Hook, R.N., Eds.; Astronomical Society of the Pacific Conference Series; ADASS: Princeton, NJ, USA, 2003; Volume 295, p. 489. [Google Scholar]
- Knowles, K.; Intema, H.T.; Baker, A.J.; Bharadwaj, V.; Bond, J.R.; Cress, C.; Gupta, N.; Hajian, A.; Hilton, M.; Hincks, A.D.; et al. A giant radio halo in a low-mass SZ-selected galaxy cluster: ACT-CL J0256.5+0006. Mon. Not. R. Astron. Soc. 2016, 459, 4240–4258. [Google Scholar] [CrossRef][Green Version]
- Chandra, P.; Ray, A.; Bhatnagar, S. The Late-Time Radio Emission from SN 1993J at Meter Wavelengths. Astrophys. J. 2004, 612, 974–987. [Google Scholar] [CrossRef]
- Knowles, K.; Pillay, D.S.; Amodeo, S.; Baker, A.J.; Basu, K.; Crichton, D.; de Gasperin, F.; Devlin, M.; Ferrari, C.; Hilton, M.; et al. MERGHERS Pilot: MeerKAT discovery of diffuse emission in nine massive Sunyaev-Zel’dovich-selected galaxy clusters from ACT. arXiv 2020, arXiv:2012.15088. [Google Scholar] [CrossRef]
- Carrasco, M.; Barrientos, L.F.; Anguita, T.; García-Vergara, C.; Bayliss, M.; Gladders, M.; Gilbank, D.; Yee, H.K.C.; West, M. VLT/Magellan Spectroscopy of 29 Strong Lensing Selected Galaxy Clusters. Astrophys. J. 2017, 834, 210. [Google Scholar] [CrossRef]
- Appenzeller, I.; Fricke, K.; Fürtig, W.; Gässler, W.; Häfner, R.; Harke, R.; Hess, H.J.; Hummel, W.; Jürgens, P.; Kudritzki, R.P.; et al. Successful commissioning of FORS1—The first optical instrument on the VLT. Messenger 1998, 94, 1–6. [Google Scholar]

| Pipeline | MHz | Flags % | Synthesised Beam “×”, PA() | RMS Jy/beam | Peak Brightness Jy/beam |
|---|---|---|---|---|---|
| casa | 397 | 46.8 | 8.0 × 4.9, 60.3 | 38.9 | 0.13 |
| ddfacet/killms | 397 | 35.6 | 7.9 × 4.5, 52.4 | 40.5 | 0.19 |
| spam GWB | 398 | 24.4 | 14.0 × 7.6, 65.3 | 45.9 | 0.27 |
| spam GSB | 323 | 14.7 | 18.1 × 14.2, 48.2 | 75.8 | 0.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sikhosana, S.P.; Knowles, K.; Ishwara-Chandra, C.H.; Hilton, M.; Moodley, K.; Gupta, N. A GMRT Narrowband vs. Wideband Analysis of the ACT−CL J0034.4+0225 Field Selected from the ACTPol Cluster Sample. Galaxies 2021, 9, 117. https://doi.org/10.3390/galaxies9040117
Sikhosana SP, Knowles K, Ishwara-Chandra CH, Hilton M, Moodley K, Gupta N. A GMRT Narrowband vs. Wideband Analysis of the ACT−CL J0034.4+0225 Field Selected from the ACTPol Cluster Sample. Galaxies. 2021; 9(4):117. https://doi.org/10.3390/galaxies9040117
Chicago/Turabian StyleSikhosana, Sinenhlanhla P., Kenda Knowles, C. H. Ishwara-Chandra, Matt Hilton, Kavilan Moodley, and Neeraj Gupta. 2021. "A GMRT Narrowband vs. Wideband Analysis of the ACT−CL J0034.4+0225 Field Selected from the ACTPol Cluster Sample" Galaxies 9, no. 4: 117. https://doi.org/10.3390/galaxies9040117
APA StyleSikhosana, S. P., Knowles, K., Ishwara-Chandra, C. H., Hilton, M., Moodley, K., & Gupta, N. (2021). A GMRT Narrowband vs. Wideband Analysis of the ACT−CL J0034.4+0225 Field Selected from the ACTPol Cluster Sample. Galaxies, 9(4), 117. https://doi.org/10.3390/galaxies9040117






