Abstract
The suspended test masses of gravitational-wave (GW) detectors require precise alignment to be able to operate the detector stably and with high sensitivity. This includes the continuous counter-acting of seismic disturbances, which, below a few Hertz, are not sufficiently reduced by the seismic isolation system. The residual angular motion of suspended test masses is further suppressed by the Angular Sensing and Control (ASC) system. However, in doing so, the angular motion can be enhanced by the ASC at higher frequencies where the seismic isolation system is very effective. This has led to sensitivity limitations between about 10 Hz and 25 Hz of the LIGO detectors in past observation runs. The observed ASC noise was larger than simple models predict, which means that more accurate detector models and new simulation tools are required. In this article, we present Lightsaber, a new time-domain simulator of the ASC in LIGO. Lightsaber is a nonlinear simulation of the optomechanical system consisting of the high-power cavity laser beam and the last two stages of suspension in LIGO including the ASC. The main noise inputs are power fluctuations of the laser beam at the input of the arm cavities, read-out noise of sensors used for the ASC, displacement noise from the suspension platforms, and noise introduced by the suspension damping loops. While the plant simulation uses local degrees of freedom of individual suspension systems, the control is applied on a global angular basis, which requires a conversion between the local and global bases for sensing and actuation. Some of the studies that can be done with this simulation concern mis-centering of the beam-spot (BS) position on the test masses, the role of laser power fluctuations for angular dynamics, and the role of the various nonlinear dynamics. The next important step following this work will be a detailed comparison between Lightsaber results and data from the control channels of the LIGO detectors.
1. Introduction
The seismic isolation system of Advanced LIGO detectors consists of an active stage providing a low-vibration platform, from which a passive isolation system is suspended in the form of a quadruple pendulum stage (QUAD) [1,2]. The QUAD takes over the vibration noise from the suspension platform, reducing its level by several orders of magnitude to achieve LIGO’s desired displacement sensitivity of below of m above 10 Hz. In this way, LIGO uses both active and passive vibration isolation systems to smooth the way for its ability to detect gravitational waves (GWs) [3,4], but this system does not fully solve the problem of vibrational noise in LIGO.
The LIGO interferometer is a complex optomechanical system whose angular mechanics are dominated by radiation pressure (RP) effects [5]. More light power in the arm cavities is desirable since strain sensitivity improves by in the high frequency (>200 Hz) shot-noise-limited band. With increasing power, optomechanical coupling becomes stronger, leading to RP noise and to additional challenges with interferometer control. More power introduces, apart from the RP effects, the thermal side effects that must all be addressed for effective interferometer (IFO) operation [6]. Radiation pressure creating torque is a long-known issue, but the optical torque’s ability to de-stabilize optical cavities was first observed in 1991 [7]. The theory of the RP’s effect on angular mechanical transfer functions (tfs) was not completely modeled until 2006 and presented in the paper by Sidles and Sigg [8]. More elaboration of this topic can also be found in [9,10,11]. The concern arose that RP might be a factor limiting LIGO’s ability to increase the light power inside the arm cavities.
In order to have the stable operation of the IFO at high power, to have the beams in the right spatial mode, to maintain the good quality of interference at the antisymmetric port, and to limit couplings to technical noise sources, it is important to have the test masses (TMs) steady at low frequencies (below 3 Hz) [12]. An important part of the control system to achieve this goal is angular sensing and control (ASC). Apart from reducing the angular displacements, ASC is also deployed to handle optomechanical instabilities up to a few Hertz [13]. One of the most important measures of efficiency for the ASC is how much noise it contributes to the differential arm (DARM) channel. DARM is the differential length change between the long Fabry–Perot arm cavities, and this is the most important degree of freedom, as it is most sensitive to the passage of GWs [14]. For the IFO to reach the desired sensitivity, DARM residual motion must be suppressed. The coherence between the DARM and ASC signals is low, implying that this coupling is, in essence, nonlinear. The combination of beam-spot (BS) motion on the mirror together with the angular motion of the mirror creates a nonlinear angle to length coupling [15,16]. As long as the DARM noise due to this coupling is well below the desired displacement sensitivity, and as long as the overall angular motion is sufficiently small so that the interferometer can be operated stably, the ASC performs well.
The issue is that in the process of controlling TMs at low frequencies, high-frequency noise is introduced in the observation band originating mostly from the readout noise of sensors and less by imperfections of actuators at the penultimate mass (PUM) of the QUAD [5,6,17]. This noise interferes directly with GW measurements. In ASC, requirements are to reduce root mean square (RMS) of angular TM motion below 1 nrad and to introduce the lowest possible noise in the angular TM motion above 10 Hz in order to meet the sensitivity target [17]. Since the controls noise, during the Third Observing Run (O3), dominated the noise budget approximately between 10 Hz and 25 Hz, where it was 10–100 times higher than quantum noise and being a significant noise source up to 55 Hz [13,16], it is important to mitigate this noise to achieve sensitivity improvements. Reducing it, the signal to noise ratio of observable GW signals will increase and therefore enhance the astrophysical impact of the GW observatories [18,19]. Specifically, early observation of the inspiral of neutron star binaries can be used to alert observatories of an upcoming merger [20], and detection of intermediate-mass black-hole binaries would be greatly facilitated [19,21,22,23]. It is possible to follow the waveform evolution for a longer amount of time, which means more accurate estimates of some of the parameters of the binary systems including sky location [24].
In this paper, we present a time-domain simulator of the ASC. It incorporates the dominant nonlinear couplings of the optomechanical system consisting of the high-power cavity laser beam and the last two stages of suspension in LIGO with the control system. Input noises are laser power fluctuations, the motion of the Internal Seismic Isolation (ISI) platform, noise from the suspension damping loops, and the readout noises of the angular control. The local degrees of freedom are simulated and converted into a global angular basis for the angular control as done in the real system. Most input noises are simulated by spectral methods, and state-space [25] models cover the last two stages of the suspension system and the angular control. Nonlinear optomechanical couplings are included explicitly through equations of motion, i.e., not as effective time-variant state-space models. The feed-forward radiation pressure compensation (RPC) path is implemented.
In Section 2, the general overview of the Lightsaber is given. In Section 3, LIGO’s seismic isolation system is described briefly including the active and passive isolation systems and the relevant noise inputs. In Section 4, radiation-pressure effects and optomechanical couplings are introduced. In Section 5, the feedback control of the ASC and the radiation pressure compensation path are described. In Section 6, we present the main results of our simulation involving nonlinear angular mirror pitch motion to strain noise coupling.
2. Overview of the Lightsaber
The Lightsaber is the time-domain simulator of the ASC in LIGO. The way in which the Lightsaber is constructed is that most of the input noises are simulated by spectral methods to avoid an unnecessarily large dimension of the state-space model. The linear couplings of the simulation are based on zero-pole-gain (ZPK) models converted to the state-space models, which cover the last two stages of the suspension system and the angular controls. This also means that the ZPK specifications of control filters are internally converted into state-space models. State-space models are convenient for continuous sampling of system coordinates. The main mechanical degree of freedom simulated in Lightsaber is the pitch motion of the test masses, which introduces the dominant angular noise in GW measurements. Pitch dynamics between PUM and TM are constructed by combining state-space models and non-linear optical features. So, the Lightsaber plant model is constructed from several static state-space models representing the mechanical and feedback system together with several nonlinear optomechanical couplings:
- Fluctuations of arm-cavity power depend nonlinearly on cavity length changes;
- Radiation-pressure torque is a bilinear term that contains the beam-spot motion as well as power fluctuations;
- Strain noise is produced as a bilinear coupling between angular motion of test masses and beam-spot motion.
The readout of the TM pitch motion is given a readout noise. A linear ASC feedback filter in a global basis is implemented as used at LIGO Hanford Observatory (LHO) during the O3 run. The filtered signal is fed back to PUM. The mechanical system is simulated in its local degrees of freedom, while the control is produced with respect to the global angular modes. There is the feed-forward radiation pressure compensation implemented as it was during the O3 run at the LHO. For now, Lightsaber simulates one arm-cavity. Light propagation times inside the arm cavities are neglected, which means that the noise estimates are only accurate below 45 Hz corresponding to the arm-cavity pole [16].
The simulation is run with a sampling frequency of 256 Hz and the duration of the entire simulation run (as used for here presented results) is 1024 s. The Lightsaber is written completely in Python. Some of the libraries, apart from standard ones, needed to run the simulation are control, slycot, absl-py, json5, tqdm. On a PC with 12 processors, it takes approximately one hour for one simulation run.
3. Mechanical System
The first line of defense against unwanted vibrations is LIGO’s active seismic isolation system. Seismic sensors monitor displacements of the mechanical system, and feedback forces are calculated from these signals to counter and suppress displacements in the range 0.1–10 Hz. Residual displacement can be reduced to less than m/ above 10 Hz [3,26,27], and is subsequently passed through the QUAD also causing angular motion of the TM. The spectra of ISI displacements along the direction of the interferometer arm (longitudinal) are shown in Figure 1a 1. Using a spectral representation of this noise as the basis for its simulation means that non-stationarities are neglected, but this is a valid approximation for most of the time. In our notation, L represents longitudinal displacements along the arm direction and P pitch rotations. We focus on L motion, since this is the most important ISI degree of freedom (DOF), i.e., the one expected to produce the strongest pitch motion of the test mass.

Figure 1.
Noise inputs passing through the QUAD. The spectra in (a) are directly obtained from LIGO Hanford O3 channel recordings. Plot (b) depends on a transfer function model from ISI L and TOP P to TOP L. The OSEM noise in (b) is simulated based on the spectral model shown in (c).
The suspensions of the test masses consist of a four-stage pendulum QUAD system providing passive seismic isolation. The masses of the four stages shown in Figure 2 are called top mass (TOP), upper-intermediate mass (UIM), PUM, and the TM. The QUAD is suspended from a platform of the ISI reducing displacements by 10 Hz by seven orders of magnitude [28]. Steel wires are used for the suspension except for LIGO’s ‘Main Chain’ test masses, which are suspended from 0.4 mm thick fused-silica fibers bonded to PUM and TM. This final monolithic stage provides a high mechanical quality factor to lower thermal noise [4]. The first two masses of the ‘Main Chain’ are made out of steel, while PUM and TM are made of fused silica. The 40 kg TM is cylindrical with radius of 17 cm and thickness of 20 cm. In addition to the ‘Main Chain’, which faces the light beam and supports the TM, there is a nearly identical ‘Reaction Chain’ placed 5 mm behind it for the ETMs and 20 mm for the ITMs. The purpose of this chain is to be a quiet platform for applying control forces for longitudinal and angular DOFs. In LIGO, digital servo systems are used to feed control signals back. Forces are applied using either electromagnetic coils or electrostatic actuators [4,16,17,29,30,31,32]. Gentle control forces are applied on the TM with the electrostatic drive [3,16,33,34].

Figure 2.
Schematic of the quadruple pendulum stage in LIGO.
The QUAD is designed to place the frequencies of its fundamental modes in different DOFs close to each other and well below 10 Hz to yield effective noise reduction in the GW observation band [35]. Above the pendulum resonant frequencies each pendulum stage provides isolation [32]. The length change of the arm cavities should not fluctuate more than a fraction of picometre in order to operate IFO effectively [3,29]. The suspended test masses respond like free masses to horizontal longitudinal forces above 10 Hz effectively. Pitch motion is the rotation of a mirror about its horizontal axis, and yaw angular motion is the rotation of a mirror about its vertical axis [12], with the main pitch and yaw resonances being set to 0.55 Hz and 0.6 Hz, respectively [17,36]. Pitch and length DOFs are coupled, which leaves an imprint of the longitudinal resonance at approximately 0.45 Hz in the pitch motion. The longitudinal to pitch coupling is also responsible for larger pitch motion compared to yaw (3–5 times larger) being excited by longitudinal motion of the ISI [13,37].
Local damping of all the low-frequency suspension modes is done with co-located optical sensors and electromagnetic actuators (OSEMs) on the TOP mass [30,31,32]. These damping sensors and actuators are placed on the ‘Main Chain’, while the ASC signal, and other control signals, are applied from the ‘Reaction Chain’ [4,16]. The four-stage pendulum QUAD system has many DOFs with low-frequency resonances. Fibers can ring up, there are rotational and translational resonances, in total 24. Out of these, 22 resonances between 0.5 Hz and 5 Hz are actively damped using feedback to TOP mass. Two additional resonances exist at 9.7 and 13.8 Hz, which couple weakly to the TM and are damped by tuned-mass dampers [29,32,33,38,39]. Damping low-frequency resonances using OSEMs to avoid amplification of motion, noise is introduced over a broad band of frequencies. This noise mostly comes from shadow sensors that are used to monitor the motion of a mass with a spectral density of about m/Hz at 1 Hz per OSEM [28,30,32,33]. Another source of noise comes from the electromagnetic actuators. These noises are to be injected at the TOP mass and transferred to the TM (contribute to its pitch motion). The spectra of these noises are shown in Figure 1b,c, respectively. For comparison, also the ISI L contributions to the TOP L motion at ITM and ETM are shown in Figure 1b. Seismic noise dominates approximately below 1 Hz and OSEM noises above 1 Hz. Together they form the main mechanical drivers of TM pitch motion. To get the noise spectra at the TM level, transfer functions from ISI and TOP to TM are required, which are shown in Figure 3a–c. Note that while most angular transfer functions are in units rad/Nm, i.e., the angular motion produced by a certain torque input, the transfer function for the OSEM noise in Figure 3c has unit rad/rad since the noise is provided as an effective angular displacement produced by a damping loop that is not explicitly modeled in Lightsaber. The spectra of the overall noise injected at ITM and ETM are shown in Figure 4. These spectra are being used to produce a time series of Gaussian noise added sample-wise to the angular motion of the test mass during a time-domain simulation.

Figure 3.
QUAD suspension transfer functions. For OSEMs the transfer function magnitude is with respect to 1 rad/Nm.

Figure 4.
Simulated total noise passing through the suspension system for input and end test mass.
Another mechanical transfer function is required from PUM pitch torque to TM P angular motion. Since this part of the suspension system needs to be included in the dynamics of the time-domain simulation, it is represented as a state-space model. We use as a starting point a ZPK model, which approximates the full dynamics of the QUAD suspension influencing this stage, i.e., incorporating the effect of cross-couplings between DOFs and transmission from TM to PUM. The ZPK model is converted into a state-space model for the time-domain simulation, which requires six internal states (see Figure 5 for a bode plot). The parameter values of the ZPK model are summarized in Table 1.
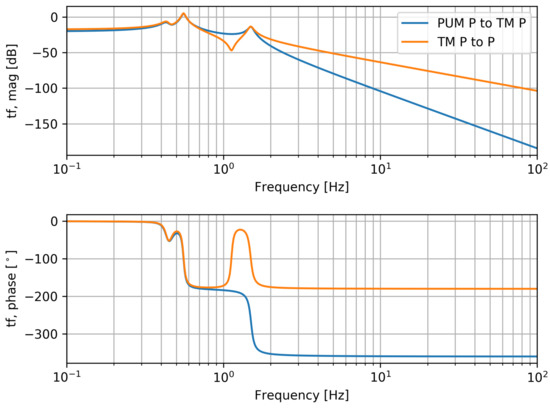
Figure 5.
Bode plots of QUAD’s last stage transfer functions. The transfer function magnitude is with respect to 1 rad/Nm.

Table 1.
ZPK model describing the transfer function from PUM P torque to TM P angular motion.
4. Optomechanical System
In the current generation of GW detectors, the light power inside arm cavities is high (200 kW assumed in this simulation). It is important to examine the interaction between light field and mechanical system. In the regime of high circulating power, RP modifies the pendula dynamics and couples the angular motion of different suspended optics [11]. Since the amount of power stored in the arm cavities is much higher than in other parts of the IFO, optomechanical couplings in the recycling cavities can be neglected as a first step [14]. The basic RP coupling considered in this paper is the torque produced by the light onto the suspended TMs [15],
assuming that all of the light is being reflected from the TMs. Torque fluctuations can be caused by power fluctuations and/or BS motion . Since the torque creates angular motion, which, in turn, creates BS motion on the other TM, a feedback is established, leading to an optomechanical angular spring [5,14]. The cavity arms are long, which means that small angular motion of one TM can create significant BS motion on the other TM.
To understand how the cavity dynamics are affected by RP, it is useful to diagonalize the coupled equations of the mirror motions into normal modes. The resulting decoupled equations of motion govern specific combinations of angular motions of the two TMs, the global modes, instead of the pitch or yaw of an individual TM. For pitch and yaw, we can thereby define the so-called soft and hard modes [5,6]. The soft mode corresponds to a lateral offset of the cavity axis, and the hard mode to a rotation of the cavity axis, as shown in Figure 6.
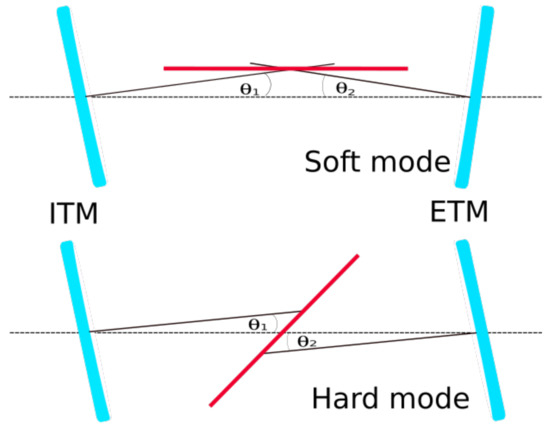
Figure 6.
Visualization of global basis angles diagonalizing the torque stiffness matrix.
Since in the soft mode RP torque works against suspension torque (softens mechanical spring), its eigenfrequency is lower than the eigenfrequency of the suspension itself. The hard mode situation is opposite so the eigenfrequency of the hard mode is higher than the eigenfrequency of suspension (hardens mechanical spring). Shifting of resonant frequencies increasing the arm-cavity power is shown in Figure 7a,b for soft and hard mode, respectively.

Figure 7.
Bode plot of Sidles–Sigg feedback transfer function with changing arm-cavity power.
Increasing the light power inside the arm cavities, RP torque can exceed suspension restoring torque, at which point the total torsional spring constant becomes negative making the resonance frequency of the soft mode imaginary and the entire system statically unstable. This creates a run-away situation where motion grows exponentially [5,11,15,40]. The control filter has to be properly shaped to guarantee stability [14]. In particular, the unity gain frequency (UGF) of the loop needs to be about 10 times higher than the frequency of the unstable resonance in order to provide overall stability [17,40]. On the other hand, the hard mode is always stable at DC, but external control is also required to suppress the hard mode at its shifted resonance [36]. The complete derivation of the RP torsional spring constants is given in [8]. The torques of soft and hard mode are
where plus sign corresponds to the soft mode and minus sign to the hard mode and
with P being the light power inside the cavity assumed to fluctuate around 200 kW, c is the speed of light, L is the arm-cavity length (3994.5 m) and, are the radii of curvature of the ITM (1934 m) and the ETM (2245 m), respectively. With these values for the radii of curvature and corresponding g-factor, the soft mode is suppressed [17]. The condition for the optical stability of a Fabry–Perot cavity is [8].
The torque eigenvalues quantify the magnitude of the RP torsional spring constant for each of the modes and they are −2.7579 Nm/rad for the soft mode and 60.6795 Nm/rad for the hard mode for a cavity power of 200 kW. The eigenfrequencies for soft and hard mode can be then written as:
where is the restoring torque of the TM suspension and it is 9.72 Nm/rad for pitch and 9.41 Nm/rad for yaw. I is the TM’s equivalent moment of inertia and for pitch it is 0.757 kgm and for yaw it is equal to 0.663 kgm [17]. Resonant frequencies for pitch soft and hard mode are 0.4827 Hz and 1.5348 Hz, respectively, and for yaw soft and hard mode are 0.5041 Hz and 1.6364 Hz, respectively. The critical arm-cavity power, for which the pitch soft mode becomes unstable, is 705 kW, and for yaw it is 682 kW. One more important coefficient is the beam offset to angle coefficient, which tells us how much beam offset is produced on a TM due to angular motion of the other TM. It is given by the following formula:
For the soft mode, it is approximately −2100 m/rad and for the hard mode, it is approximately 45,000 m/rad [36,41].
These modifications due to RP are referred to as the Sidles–Sigg effect: a mirror’s angular motion causes beam-spot motion on the other mirror, which in turn creates a torque that may lead to either less or more angular motion depending on the phase of the feedback. Fluctuations of the RP torque on the TM can be also caused by power fluctuations, which is referred to as the effect. It is generally assumed to that power fluctuations contribute less to the torque than the Sidles–Sigg effect, but according to Equation (1), it might depend on whether there are any static beam offsets maintained during the interferometer operation, and the difference in feedback mechanisms for these two couplings also influences the overall impact [36]. In our simulation, where we use the precise nonlinear coupling in time domain, they are both incorporated in the same time-domain equation for the RP torque, and if they form, will appear automatically.
5. The Angular Control System
The fundamental requirement for the angular sensing and control scheme is to suppress the angular mirror motion at low frequencies, to overcome RP induced angular instabilities, without reintroducing noise in the GW signal [40,42]. Quadrant photodiodes (QPDs) and wavefront sensors (WFSs) monitor beam positions and shapes. The signal that they collect is filtered and fed back to PUM by means of four electromagnetic actuators producing torque to align the TMs. This process containing the last two stages of suspension in LIGO with the control system is sketched in Figure 8, and a more detailed description of angular controls process can be found in [5]. Together with the desired control signal, readout noise of the sensors is injected. It is a combination of optical shot noise, photodetector electronics noise, and vibration noise, e.g., from the acoustic field for components outside the vacuum system [5,28]. Furthermore, actuators produce additional noise, which is significantly lower than readout noise of the sensors, and neglected in current Lightsaber simulations. The TM is not pushed directly for angular control since at PUM the actuation range is larger, and therefore we use this stage instead of the TM stage, which has a very small actuation range. If feedback is put higher in the QUAD chain, control authority would be significantly reduced. Knowing also that, by actuating the PUM, any actuation noise is filtered by the final stage’s , making the pushing at PUM the optimal solution. The ASC requirement is to reduce the RMS of the mirror angular motion to below 1 nrad and at the same time inject the lowest possible noise above 10 Hz. In fact, the sensors’ readout noises dominate pitch motion of the TMs at higher frequencies. It limits strain sensitivity in the band 10 Hz to 25 Hz, and it remains significant to higher frequencies [5,16]. Instead, the noise coming from the ISI and OSEMs is weak at 10 Hz [31], because of the very efficient QUAD suspension. Apart from the ASC, optical levers are used for angular stabilization, but these are not engaged in low-noise operation [5,11,43].

Figure 8.
Diagram representing the simulated optomechanical system consisting of the high-power cavity laser beam and the last two stages of suspension in LIGO with the control system.
The Lightsaber time-domain simulation uses local degrees of freedom. As in the real ASC, a transformation to the global basis is required for the simulation of the feedback control, which implements filters acting on soft and hard modes. The filter outputs are transformed back to the local basis for the actuator output at the two PUMs. The transformation into the global basis is also useful for stability analyses of the optomechanical system [5]. The transformation matrix connecting angular motion of the TMs with the angle motion of the soft and hard modes is given by:
where is the angular displacement of the ITM, is the angle of the ETM, is soft mode angle, hard mode angle, and r is defined as
The equation used for calculating beam-spots on ITM and ETM is:
In order to get optical torque noise, we need the response of TM pitch motion to RP torque, which in Lightsaber is given by the ZPK model shown in Table 2 (TM P to P transfer function). The bode plot of this transfer function is shown in Figure 5. The dynamics of this system are described with six internal states in the state-space model. The Sidles–Sigg effect results from torque fluctuations due to BS motion perturbing the TM angular motion, which causes BS motion on the other TM, where the process repeats. These optomechanical dynamics form a loop that alters resonance frequencies as discussed earlier. Optical torque noise superposes with external noise reaching the TMs from ISI and OSEMs. The controls signal is transferred from PUM to TM (PUM P to TM P in Figure 5), and then summed with the other contributions to TM pitch motion. Another feedback path to consider is the radiation pressure compensation, which is described below.

Table 2.
ZPK model describing optical torque to TM pitch angle transfer function (torque-to-angle response).
With all contributions to the TM angular motion summed up, Lightsaber then simulates the readout of these motions in the global angular basis using the transformation in Equation (6). WFSs sense the angular misalignment of the cavities with respect to their input beams, and QPDs see the beam transmitted through the arm cavities. QPDs maintain the alignment at low frequencies, mainly controlling BS positions, while WFSs are doing it at frequencies up to several Hz [5,14]. More about WFS and QPD sensors and their placing and usage in IFOs can be found in [33,36]. The sensing noise of the soft mode is rad/Hz , and for the hard mode it is rad/Hz . The bandwidth of soft mode loops is smaller, and therefore their sensing noise contribution to the DARM noise is less severe than in the case of the hard modes [36]. This signal is used for the ASC control signal, including the radiation pressure compensation (both contained in the feedback ‘C’ in Figure 8). The sensor outputs in our simulation have spectra shown in Figure 9a,b, for the soft and hard mode, respectively.
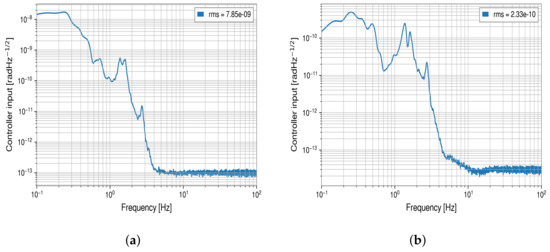
Figure 9.
Simulated spectra of the sensor outputs for the (a) soft and (b) hard mode.
5.1. Radiation Pressure Compensation
Since for 200 kW, arm-cavity RP effects are significant and hard mode resonant frequency is high (Figure 7b), at the LHO site, the feed-forward radiation pressure compensation was implemented during the 03 run. The solution for stabilization of Sidles–Sigg effects comes from the fact that the torsional stiffness is a frequency-independent quantity that depends only on the cavity geometry (i.e., the arm length and the radius of curvature of TMs) and the arm-cavity power,
and the Sidles–Sigg feedback can be modeled precisely. The compensation is then just to add a parallel digital torque with the same shape, but with the sign inverted as shown in Figure 10. With this radiation pressure compensation path, with arm-cavity power variations, the only parameter that needs to be adjusted is the DC gain [36]. As a result, it is only needed to design a single controller that optimally stabilizes the system, and this filter will stay valid over at least a large range of input power levels. This will greatly simplify the commissioning of the ASC at high-power operations [16]. While in the LIGO detectors, the compensation path is fed back onto PUM with the feedback filter containing an inversion of the PUM P to TM P mechanical transfer function, in Lightsaber the compensation is directly given to TM P to avoid the transfer function inversion.
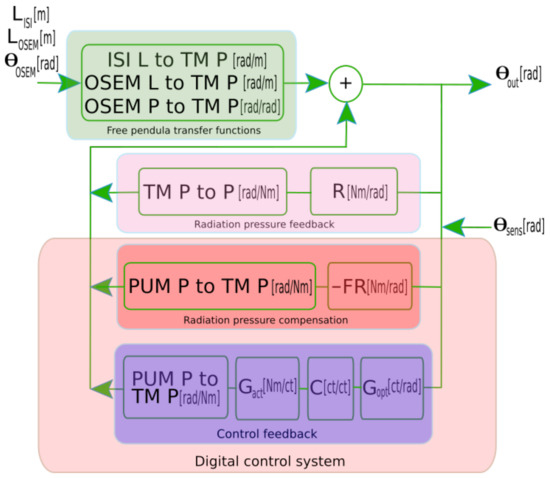
Figure 10.
Diagram illustrating the components of the Lightsaber simulation including RPC and feedback control. F is the gain-adjustment factor, converts angular motion into digital counts, and converts digital counts into actuation torque.
Both soft and hard Sidles–Sigg torques could be canceled completely, but in reality, introduction of a gain-adjustment factor in the path is necessary. This is because, when the compensation is done for the hard mode, a digital torque corresponding to the soft mode is also sent to the suspension. If over-compensation accidentally happens, it can cause destabilization of the system with the digital soft mode. To avoid such a situation, what is performed is under-compensation for the hard mode. In RPC, the gain-adjustment factor is such that 200 kW is effectively reduced to 56.7 kW. In other words, with respect to the Sidles–Sigg optomechanics, the response function looks like a hard mode pendulum at an arm-cavity power of 56.7 kW, and small errors in the compensation path will not turn it into a destabilizing soft mode. The soft mode can be perfectly compensated, i.e., reducing the arm-cavity power effectively to 0 W [36]. In Lightsaber, the ZPK model used in this compensation path is the same as the ZPK model describing optical torque to TM pitch angle transfer function, but with the gain obtained using Equation (9) multiplied with needed gain-adjustment factor (for soft mode equal to 1, for hard mode approximately 0.72). Before feeding back to the plant, this compensation signal is transformed into local basis. Using this RPC technique is a much easier way of tackling the Sidles–Sigg effect than designing different frequency-dependent control filters at different power levels. This technique works well, and it successfully removes the RP dependence in the response functions. More about it can be found in [36].
The sensing noise injection in the compensation path is actually quite low compared to the regular control path, but to avoid this noise contaminating the GW readout, an extra high-frequency cut-off filter is introduced. The design of this low-pass filter is quite flexible. Requirements are to have a phase delay < 10 at 3 Hz. What is used in our simulation is a second-order elliptic filter at 17 Hz with 40 dB attenuation above 17 Hz and 1 dB of ripple below 17 Hz. With this low-pass filter, the compensation path also meets aLIGO’s requirement on the noise roll-off [36].
5.2. Feedback Control
Filter design is typically obtained by a half-quantitative, half-intuitive method. It is difficult to make a filter that is stable over a relatively large span of input power and maintaining a high noise suppression at the same time. The controller is a linear filter leading to stable feedback. It essentially takes the shape of a low-pass filter, with UGF tuned to the lowest possible value, but providing sufficient gain at lower frequencies (below 1 Hz) in order to reduce the motion of the mirrors and with a relatively steep cut-off around 20–30 Hz, where the sensor noise dominates. Steepening the cut-off can in principle reduce the noise introduced in the GW band, but with every pole used to reach the steeper drop-off, an extra 90 of phase loss is introduced [6,28]. The resulting need for a low-pass filter limits the achievable bandwidth of the loops. One important thing to keep in mind during design is that the reduction of noise in the GW band is proportional to the UGF raised to the minus third or even minus fourth power [5].
There are ASC feedback filters at LIGO for soft and hard mode. The gain is chosen by the control designers and must be chosen to obtain a stable system and sufficient RMS reduction. The more complicated shape of the current control filters for the hard modes is partially to maintain the system’s stability over a wide range of different input powers [36]. It is not so difficult to control the soft mode, because the decreasing resonance naturally moves deeper into the control bandwidth towards frequencies where the gain is higher [33]. The hard, stable mode is the one that poses the greater control challenge. Since the eigenfrequency of the hard mode increases with power, it can potentially make the overall control loop unstable [5]. The price is that the control filter does not roll off fast enough to meet the LIGO noise requirement in the 10–25 Hz band. A significant amount of control noise is injected in this band, contaminating the GW sensitivity [36,42].
The ZPK model for the soft mode controller is given in Table 3 and for the hard mode controller in Table 4. They have three components: control, low pass filter, and boosting component. Actually, most of the low-frequency actuation is sent to the upper stages of the suspensions to ensure a sufficient actuation range. In addition, the hard-mode readout is filtered and passed to the TOP mass to avoid instabilities in the reaction chain [16]. In Lightsaber, this path is also directly given to PUM. The state vector of the soft controller needs 14 internal states, and for the hard controller, 19 internal states to represent these dynamics. The bode plots of the feedback soft and hard controllers are given in the Figure 11. The controller output in our simulation has spectra shown in Figure 12a,b for the soft and hard mode, respectively. The control signals are transformed to the local basis using Equation (6). Then, transfer functions from PUM pitch input torque to TM pitch angular motion is used to calculate this signal at the level of the test mass, and the loop is closed as shown in Figure 10.

Table 3.
ZPK model of the soft mode controller.

Table 4.
ZPK model of the hard mode controller.

Figure 11.
Bode plots of feedback control filters.

Figure 12.
Simulated spectra of the controller output for the (a) soft and (b) hard mode.
6. Results
In Lightsaber simulations, the ASC needs about a second to engage as shown in Figure 13 for the hard mode. The spectra of simulated residual pitch angular motion for soft and hard mode are shown in Figure 14.

Figure 13.
Demonstration of controls engagement in Lightsaber in the case of the hard mode angular motion.
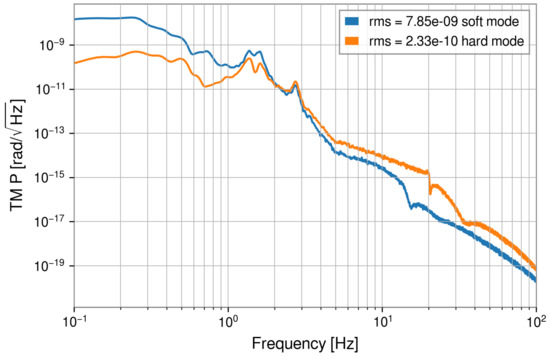
Figure 14.
Simulated spectra of TM pitch motion for the soft and hard mode.
As explained earlier, the strain noise coming from angular motion results as a product of BS motion and angular motion. The BS motion is relatively slow (mainly below 0.5 Hz), while angular motion is relevant at frequencies higher than 10 Hz [15,40]. One of the issues here is that frequency components of spot position and angular motion could beat, creating hard-to-subtract noise [44]. The formula describing this bilinear process in the time domain using local angles is [17]
This coupling can be easily understood geometrically, as shown in Figure 15. If the beam-spot position does not correspond to the mirror’s rotational pivot, a length signal is created [15]. To evaluate angular noise coupled to the strain noise, we need to compute and add the length variation produced by each mirror. Beam spots are determined by angular motion (Equation (8)), and the coefficient for LIGO is about m/rad. The eigenvalues of the matrix determine the coupling coefficients between beam-spot and angular motion for the soft and hard mode. According to the RMS values given in Figure 14, the soft mode RMS is higher, but it produces smaller beam-spot motion and ultimately less strain noise as shown in Figure 16a.
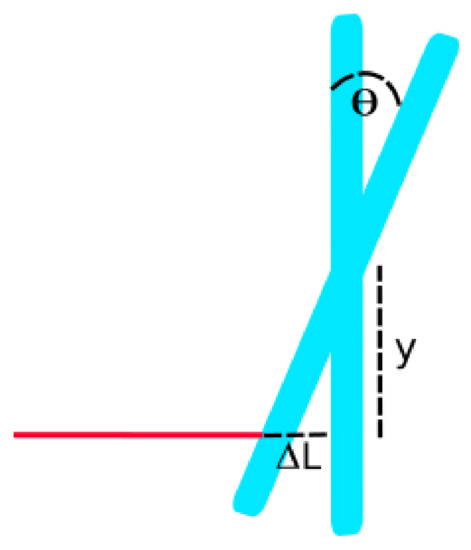
Figure 15.
Angle-to-length coupling due to beam-spot miscentering.

Figure 16.
(a) Simulated strain noise without static beam offset and (b) simulated strain noise obtained assuming a static beam offset of 3 mm in hard mode, in the case of both linear and nonlinear coupling, with radiation pressure compensation and 200 kW arm-cavity power.
The length change affects the arm-cavity power according to
where is the input power that pumps the arm-cavity, assuming are the transmissivity and reflectivity of the ITM, and nm is the wavelength of the laser light [33]. The average input power is 705 W and the spectrum of its relative fluctuations characteristic for the O3 run, commonly expressed as relative intensity noise (RIN), is given in Figure 17a 2. Since Lightsaber currently does not implement a length control, a simulation run, with DC offset, produces excess power fluctuations due to high length fluctuations entering Equation (11). As a temporary solution, a high-pass filter is applied before inserting the length fluctuations into Equation (11), so the arm-cavity relative power fluctuations match input relative power fluctuations. Without beam offset, the power-to-angle-to-length-to-power loop is suppressed, and excess power fluctuations cannot build up. The RIN with high-pass filter satisfies the requirements on power stability in control band given in [45]. In the 0.1–0.4 Hz band, the RMS of RIN is approximately and in the 0.4–10 Hz band, it is approximately . A typical simulated BS motion has an RMS of about 0.02 mm with spectrum shown in Figure 17b. Taking into consideration the ASC loops and the seismic inputs that are used, the RMS of BS motion should be ≲0.1 , which is in agreement with the simulated result [36].

Figure 17.
(a) Spectrum of simulated relative power fluctuations, and (b) spectrum of simulated beam-spot motion.
The main result of Lightsaber is a model of the strain noise produced by the ASC. The first set of simulations concern the case without static beam offset. The result of such a model is shown in Figure 16a with 200 kW of light power inside the arm-cavity (orange curve). The second ASC spectrum (blue curve) represents a 56.7 kW simulation without RPC. Since it is equivalent to the 200 kW simulation with RPC with respect to the Sidles-Sigg coupling, it allows us to infer the role of cavity-power fluctuations, which is overall minor at frequencies where ASC noise is important. The third ASC spectrum (green curve) is obtained including only the soft mode readout noise. As you can see, the hard mode readout noise contributes much more to the overall strain noise than the soft mode readout noise.
The next set of simulations is with static beam offset. Intentional steering of the beam from the center of rotation of the TM by as much as 3–5 mm (hard mode) offset was done in LIGO to reduce optical scatter and losses, i.e., avoiding overlap of the laser beam with major point defects on the TMs. In this case, the impact of power fluctuations on angular motion of the TMs is enhanced, and the dynamics are strongly determined by a single angular mode (depending on whether the static offset is in hard or soft mode). Since Lightsaber currently does not implement a cancellation of a DC torque, a simulation run, with DC offset, produces DC term in angular mirror motion. As a temporary solution, a DC torque is subtracted before entering optical torque noise calculation. In Figure 16b, it can be seen that 3 mm beam offset in hard mode is sufficient to raise the ASC noise quite high in the case of linear coupling (blue curve). This is easily explained through the strain–noise coupling given in Equation (10), but, in reality, linear noise couplings are subtracted. In the case of nonlinear coupling (orange curve), having DC torque optical pitch noise subtracted, the level of noise is much lower. The Lightsaber simulation predicts angular noise to be an important contribution to detector noise, but the level of predicted noise is lower than in some of the past noise projections.
7. Conclusions
In this paper, we presented the time-domain simulation Lightsaber of the Angular Sensing and Control (ASC) system in LIGO. The ASC system is a complex component of the detector, which has proven to be difficult to model. This made it challenging to understand ASC noise in LIGO detectors, which however is known to be an important contribution to instrument noise below 25 Hz. The complexity of the angular motion comes from the nonlinear optomechanical couplings between the suspended test masses and the high-power laser beam inside the arm cavities. Moreover, the angular motion of test masses couples nonlinearly to differential arm length. The Lightsaber is a nonlinear simulation of the optomechanical system consisting of the high-power cavity laser beam and the last two stages of suspension in LIGO with the feedback control. Main noise inputs are power fluctuations from the input beam to the arm-cavity, readout noise of sensors of angular motion, seismic noise, and noise from dampers of suspension modes. The mechanical system is simulated in its local degrees of freedom, while the control is produced with respect to the global angular modes.
Lightsaber produces time series of all single arm ASC observables of the LIGO detectors, which makes it possible to carry out detailed comparisons between simulation and real system at various levels. In the future, it will be very interesting to make these comparisons and their matching. Without very precise comparisons, at the moment, we see that, overall, the simulation reproduces the main characteristics of the actual data, but the match is not completely satisfactory pointing to aspects of the noise inputs or ASC dynamics, which are not fully understood yet. Nonetheless, even in its present state, Lightsaber is sufficiently accurate to serve as a useful modeling tool, especially when high precision is not required, i.e., for noise budget calculations of current and future GW detectors. While the plant model is for the LIGO detectors, it is straightforward to modify the mechanical system, angular readouts, etc., to represent other detectors. The main work here is not on the simulation side, but for commissioners to have a sufficient understanding of the optomechanical plant and control system to feed the models.
As another application of Lightsaber, which has not been explored in this paper, the fully nonlinear, time-domain representation allows researchers to test ASC controllers before implementing them in a detector. This can be especially valuable for certain nonstationary modern control schemes. In this context, Lightsaber serves as a development tool possibly leading to performance enhancements of future ASC systems parallel to nonlinear noise-cancellation techniques as another possible approach to reduce angular noise. As pointed out abundantly in the past, the ASC remains one of the big challenges of detector control, which needs to be addressed to be able to improve the low-frequency sensitivity of current detectors, and a detailed understanding of noise produced by the ASC is crucial to plan future generations of GW detectors.
Author Contributions
Conceptualization, J.H.; methodology, J.H.; software, T.A. and J.H.; validation, T.A.; formal analysis, T.A.; investigation, T.A. and J.H.; writing—original draft preparation, T.A.; writing—review and editing, J.H.; visualization, T.A. and J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This is a simulation paper. Data needed to replicate our results come from personal communication as stated in the Acknowledgments. The LIGO suspension models are under more or less continuous development and are not publicly available.
Acknowledgments
We thank Hang Yu and Rana Adhikari for their support providing most of the information about the LIGO Hanford detector, which we used for the construction of the angular controls model. This material is based upon work supported by NSF’s LIGO Laboratory, which is a major facility fully funded by the National Science Foundation. The work was supported by the GSSI’s Centre for Urban Informatics and Modelling (CUIM) project.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GW | Gravitational wave |
| ASC | Angular Sensing and Control |
| BS | Beam-spot |
| QUAD | Quadruple pendulum stage |
| RP | Radiation pressure |
| IFO | Interferometer |
| tf | Transfer function |
| TM | Test mass |
| PUM | Penultimate mass |
| RMS | Root mean square |
| DARM | Differential arm |
| ISI | Internal Seismic Isolation |
| RPC | Radiation pressure compensation |
| ZPK | Zero-pole-gain |
| LHO | LIGO Hanford Observatory |
| ITM | Input test mass |
| ETM | End test mass |
| DOF | Degree of freedom |
| TOP | Top mass |
| UIM | Upper-intermediate mass |
| OSEM | Optical Sensors and Electro-Magnetic actuator |
| UGF | Unity gain frequency |
| QPD | Quadrant photodiode |
| WFS | Wavefront sensor |
| RIN | Relative intensity noise |
Notes
| 1 | The channels used to calculate these spectra are H1:ISI-ITMX_SUSPOINT_ITMX_EUL_L_DQ, and H1:ISI-ETMX_SUSPOINT_ETMX_EUL_L_DQ for input test mass (ITM), and end test mass (ETM), respectively. |
| 2 | RIN spectrum of input beam is calculated from H1:ASC-X_TR_A_NSUM_OUT_DQ (transmission through end mirror), which is possible since the RIN of the simulated arm-cavity power, which generally depends on TM motion, is almost the same as the RIN of the simulated input power. |
References
- Matichard, F.; Lantz, B.; Mason, K.; Mittleman, R.; Abbott, B.; Abbott, S.; Allwine, E.; Barnum, S.; Birch, J.; Biscans, S.; et al. Advanced LIGO two-stage twelve-axis vibration isolation and positioning platform. Part 1: Design and production overview. Precis. Eng. 2014, 40, 273–286. [Google Scholar] [CrossRef] [Green Version]
- Matichard, F.; Lantz, B.; Mason, K.; Mittleman, R.; Abbott, B.; Abbott, S.; Allwine, E.; Barnum, S.; Birch, J.; Biscans, S.; et al. Advanced LIGO two-stage twelve-axis vibration isolation and positioning platform. Part 2: Experimental investigation and tests results. Precis. Eng. 2015, 40, 287–297. [Google Scholar] [CrossRef] [Green Version]
- Vibration Isolation. Available online: https://www.ligo.caltech.edu/page/vibration-isolation (accessed on 24 March 2021).
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: The Advanced LIGO Detectors in the Era of First Discoveries. Phys. Rev. Lett. 2016, 116, 131103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dooley, K.; Barsotti, L.; Adhikari, R.; Evans, M.; Fricke, T.; Fritschel, P.; Frolov, V.; Kawabe, K.; Smith-Lefebvre, N. Angular control of optical cavities in a radiation-pressure-dominated regime: The Enhanced LIGO case. J. Opt. Soc. Am. A 2013, 30, 2618–2626. [Google Scholar] [CrossRef] [Green Version]
- Dooley, L.K. Design and Performance of High Laser Power Interferometers for Gravitational-Wave Detection. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2011. [Google Scholar]
- Solimeno, S.; Barone, F.; de Lisio, C.; Di Fiore, L.; Milano, L.; Russo, G. Fabry-Pérot resonators with oscillating mirrors. Phys. Rev. A 1991, 43, 6227–6240. [Google Scholar] [CrossRef]
- Sidles, J.A.; Sigg, D. Optical torques in suspended Fabry-Pérot interferometers. Phys. Lett. A 2006, 354, 167–172. [Google Scholar] [CrossRef]
- Fan, Y.; Merrill, L.; Zhao, C.; Ju, L.; Blair, D.; Slagmolen, B.; Hosken, D.; Brooks, A.; Veitch, P.; Mudge, D.; et al. Observation of optical torsional stiffness in a high optical power cavity. Appl. Phys. Lett. 2009, 94, 081105. [Google Scholar] [CrossRef] [Green Version]
- Driggers, J. Optomechanical Alignment Instability in LIGO Mode Cleaners; Technical Report T060240-00-R; LIGO Laboratory: Washington, WA, USA, 2006. [Google Scholar]
- Hirose, E.; Kawabe, K.; Sigg, D.; Adhikari, R.; Saulson, P. Angular instability due to radiation pressure in the LIGO gravitational-wave detector. Appl. Opt. 2010, 49, 3474–3484. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fritschel, P.; Mavalvala, N.; Shoemaker, D.; Sigg, D.; Zucker, M.; Gonzalez, G. Alignment of an Interferometric Gravitational Wave Detector. Appl. Opt. 1998, 37, 6734–6747. [Google Scholar] [CrossRef]
- Kasprzack, M. Seismic Motion to Angular Control: Challenges and Prospects in Advanced LIGO; Low-Frequency Workshop: Birmingham, UK, 2018. [Google Scholar]
- Allocca, A.; Bersanetti, D.; Diaz, J.; Rossi, C.; Mantovani, M.; Masserot, A.; Rolland, L.; Ruggi, P.; Swinkels, B.; Martin, E.; et al. Interferometer Sensing and Control for the Advanced Virgo Experiment in the O3 Scientific Run. Galaxies 2020, 8, 85. [Google Scholar] [CrossRef]
- Seymour, B.C.; Kasprzack, M.; Pelé, A.; Mullavey, A. Characterization of Nonlinear Angular Noise Coupling into Differential Arm Length of the LIGO Livingston Detector; Technical Report LIGO-T1700343-v1; LIGO: Washington, WA, USA, 2017. [Google Scholar]
- Buikema, A.; Cahillane, C.; Mansell, G.L.; Blair, C.D.; Abbott, R.; Adams, C.; Adhikari, R.X.; Ananyeva, A.; Appert, S.; Arai, K.; et al. Sensitivity and performance of the Advanced LIGO detectors in the third observing run. Phys. Rev. D 2020, 102, 062003. [Google Scholar] [CrossRef]
- Barsotti, L.; Evans, M. Modeling of Alignment Sensing and Control for Advanced LIGO; Technical Report LIGO-T0900511-v4; LIGO-MIT: Washington, WA, USA, 2011. [Google Scholar]
- Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity studies for third-generation gravitational wave observatories. Class. Quantum Grav. 2011, 28, 094013. [Google Scholar] [CrossRef]
- Maggiore, M.; Broeck, C.V.D.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science case for the Einstein telescope. J. Cosmol. Astropart. Phys. 2020, 2020, 050. [Google Scholar] [CrossRef] [Green Version]
- Chan, M.L.; Messenger, C.; Heng, I.S.; Hendry, M. Binary neutron star mergers and third generation detectors: Localization and early warning. Phys. Rev. D 2018, 97, 123014. [Google Scholar] [CrossRef] [Green Version]
- Sathyaprakash, B.; Abernathy, M.; Acernese, F.; Ajith, P.; Allen, B.; Amaro-Seoane, P.; Andersson, N.; Aoudia, S.; Arun, K.; Astone, P.; et al. Scientific objectives of Einstein Telescope. Class. Quantum Gravity 2012, 29, 124013. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; Agathos, M.; et al. Properties and Astrophysical Implications of the 150 SM Binary Black Hole Merger GW190521. Astrophys. J. 2020, 900, L13. [Google Scholar] [CrossRef]
- Jani, K.; Shoemaker, D.; Cutler, C. Detectability of intermediate-mass black holes in multiband gravitational wave astronomy. Nat. Astron. 2019, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Grimm, S.; Harms, J. Multiband gravitational-wave parameter estimation: A study of future detectors. Phys. Rev. D 2020, 102, 022007. [Google Scholar] [CrossRef]
- Williamson, D. Discrete-time Signal Processing; Springer-Verlag: London, UK, 1999. [Google Scholar] [CrossRef]
- Marrocchesi, A.; Dooley, K.; Arai, K.; Adhikari, R. A Prototype for a Tilt-Free Seismometer; Technical Report LIGO-T1500485–v1; LIGO-Caltech-MIT: Washington, WA, USA, 2015. [Google Scholar]
- Schwartz, E.; Pele, A.; Warner, J.; Lantz, B.; Betzwieser, J.; Dooley, K.; Biscans, S.; Coughlin, M.; Mukund, N.; Abbott, R.; et al. Improving the robustness of the advanced LIGO detectors to earthquakes. Class. Quantum Grav. 2020, 37, 235007. [Google Scholar] [CrossRef]
- Martynov, D. Lock Acquisition and Sensitivity Analysis of Advanced LIGO Interferometers. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2015. [Google Scholar]
- Aston, S.; Barton, M.; Bell, A.; Beveridge, N.; Bland, B.; Brummitt, A.; Gianpietro, C.; Cantley, C.; Carbone, L.; Cumming, A.; et al. Update on quadruple suspension design for Advanced LIGO. Class. Quantum Grav. 2012, 29, 235004. [Google Scholar] [CrossRef]
- Carbone, L.; Aston, S.; Cutler, R.; Freise, A.; Greenhalgh, J.; Heefner, J.; Hoyland, D.; Lockerbie, N.; Lodhia, D.; Robertson, N.; et al. Sensors and Actuators for the Advanced LIGO Mirror Suspensions. Class. Quantum Grav. 2012, 29, 115005. [Google Scholar] [CrossRef] [Green Version]
- Harry, G.M.; the LIGO Scientific Collaboration. Advanced LIGO: The next generation of gravitational wave detectors. Class. Quantum Grav. 2010, 27, 084006. [Google Scholar] [CrossRef]
- Shapiro, B.; Adhikari, R.; Driggers, J.; Kissel, J.; Lantz, B.; Rollins, J.; Youcef-Toumi, K. Noise and control decoupling of Advanced LIGO suspensions. Class. Quantum Grav. 2015, 32, 015004. [Google Scholar] [CrossRef]
- Fritschel, P.; the LIGO Scientific Collaboration. Advanced LIGO. Class. Quantum Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Soni, S.; Austin, C.; Effler, A.; Schofield, R.M.S.; González, G.; Frolov, V.V.; Driggers, J.C.; Pele, A.; Urban, A.L.; Valdes, G.; et al. Reducing scattered light in LIGO’s third observing run. Class. Quantum Grav. 2021, 38, 025016. [Google Scholar] [CrossRef]
- About “aLIGO”. Available online: https://www.ligo.caltech.edu/page/about-aligo (accessed on 24 March 2021).
- Hang, Y. Astrophysical Signatures of Neutron Stars in Compact Binaries and Experimental Improvements on Gravitational-Wave Detectors. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2019. [Google Scholar]
- Abbott, R.; Adhikari, R.; Ballmer, S.; Barsotti, L.; Evans, M.; Fritschel, P.; Frolov, V.; Mueller, G.; Slagmole, B.; Waldman, S. AdvLIGO Interferometer Sensing and Control Conceptual Design; Technical Report LIGO-T070247-v1; LIGO-Caltech-MIT: Washington, WA, USA, 2008. [Google Scholar]
- Robertson, N.; Torrie, C. A Tale of Two Dampers: Bounce and Roll Mode Damping for the Quads; Talk for the LVC Meeting, G1600371-v3; LIGO: Washington, WA, USA, 2016. [Google Scholar]
- Fritschel, P. Concept for a Bounce and Roll Mode Damper for the Quad Suspensions; Technical Report T1500343-v1; LIGO-Caltech-MIT: Washington, WA, USA, 2015. [Google Scholar]
- Barsotti, L.; Evans, M.; Fritschel, P. Alignment sensing and control in advanced LIGO. Class. Quantum Grav. 2010, 27, 084026. [Google Scholar] [CrossRef]
- aLIGO LLO Logbook. Available online: https://alog.ligo-la.caltech.edu/aLOG/index.php?callRep=41815 (accessed on 1 April 2021).
- Yu, H.; Martynov, D.; Vitale, S.; Evans, M.; Barr, B.; Carbone, L.; Dooley, K.; Freise, A.; Fulda, P.; Grote, H.; et al. Prospects for Detecting Gravitational Waves at 5 Hz with Ground-Based Detectors. Phys. Rev. Lett. 2017, 120, 141102. [Google Scholar] [CrossRef] [Green Version]
- Adhikari, R. Sensitivity and Noise Analysis of 4 km Laser Interferometric Gravitational Wave Antennae. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Driggers, J. Noise Cancellation for Gravitational Wave Detectors; LIGO Seminar: Pasadena, CA, USA, 2013. [Google Scholar]
- LIGO Laboratory/LIGO Scientific Collaboration. ADVANCED LIGO, Pre-Stabilized Laser Design Requirements; Technical Report LIGO-T050036-00-D; LIGO-Caltech-MIT: Washington, WA, USA, 2005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).