Abstract
In this work, the modulational instability of dust-acoustic (DA) waves (DAWs) is theoretically studied in a four-component plasma medium with electrons, positrons, ions, and negative dust grains. The nonlinear and dispersive coefficients of the nonlinear Schrödinger equation (NLSE) are used to recognize the stable and unstable parametric regimes of the DAWs. It can be seen from the numerical analysis that the amplitude of the DA rogue waves decreases with increasing populations of positrons and ions. It is also observed that the direction of the variation of the critical wave number is independent (dependent) of the sign (magnitude) of q. The applications of the outcomes from the present investigation are briefly addressed.
1. Introduction
Electron–positron–ion-dust (EPID) plasma has been identified in the galactic centre [1], Saturn’s magnetosphere [2,3], Jupiter’s magnetosphere [3,4], the pulsar magneto-sphere [5,6,7,8], supernova environments [8,9], interstellar medium [10,11,12,13,14], cometary tails [15,16,17], the solar atmosphere [17,18,19,20], and laboratory experiments [21,22,23,24,25]. There are many electron–ion plasma systems in which positron or charged dust species or both occur naturally due to many mechanisms (viz., pair production [18], thermal heating [26,27], and radiative heating [28], etc.). The dynamics of the EPID plasma medium (EPIDPM) and associated electrostatic nonlinear waves have rigorously changed due to the existence of the light positron and heavy dust grains in the EPIDPM [29,30,31,32]. The signature of the positron in the EPIDPM has encouraged many authors to examine the nonlinear electrostatic pulses in the EPIDPM [29,30]. Banerjee and Maitra [29] considered a four-component EPIDPM, studied the electrostatic potential structures in the presence of massive dust grains and light positrons, and observed that the height of the potential structures increases with increasing dust number density but decreases with increasing positron number density. Paul and Bandyopadhyay [30] demonstrated dust–ion-acoustic waves in an EPIDPM and showed that only positive super-solitons can exist.
Highly energetic particles have been observed in Saturn’s magnetosphere [2,3], Jupiter’s magnetosphere [3,4], the vicinity of the Moon [33], Earth’s bow-shock [34], and galaxy clusters [35], etc. Renyi [36] first noticed the deviation of these particles from a Maxwellian–Boltzman distribution, and finally Tsallis [37] generalized the non-extensive q-distribution to explain these particles. The parameter q in the q-distribution describes the deviation of these particles from a Maxwellian–Boltzman distribution, and when , Tsallis distribution coincides with the Maxwell–Boltzmann distribution [38,39,40]. Eslami et al. [38] examined the dust-acoustic (DA) solitary waves (DA-SWs) in the presence of non-extensive plasma species. Roy et al. [39] studied the DA shock waves (DA-SHWs) in a three-component dusty plasma featuring non-extensive electrons and observed that the height of the DA-SHWs decreases with q.
The modulational instability (MI) of electrostatic waves and associated rogue waves are governed by the nonlinear Schrödinger equation (NLSE) [41,42,43]. Bains et al. [41] studied the MI of the DA waves (DAWs) by deriving the NLSE in a three-component dusty plasma with non-extensive plasma species and found that the critical wave number (), which determines the stability of the electrostatic waves, increases with increasing non-extensivity of the plasma species. Moslem et al. [42] analyzed the DA rogue waves (DA-RWs) by considering q-distributed plasma species. Rahman et al. [43] examined DA-RWs in a multi-component dusty plasma and observed that the temperature of the ion enhances the height of the DA-RWs.
Recently, Esfandyari-Kalejahi et al. [44] investigated the electrostatic DA-SWs in an EPIDPM and observed that the amplitude of DA-SWs increases with increasing charge of the dust grains. Jehan et al. [45] studied DA-SWs in a four-component dusty plasma by considering inertial massive dust grains and inertialess iso-thermal electrons, positrons, and ions. To the best knowledge of the authors, no theoretical investigation has been made to understand the stability of the DAWs in a four-component EPIDPM. Therefore, in this paper, we study the MIs of DAWs and the formation of DA-RWs in an EPIDPM.
2. Governing Equations
We consider the propagation of DAWs in an unmagnetized EPIDPM with inertial, warm, negatively-charged, massive dust grains (mass ; charge ; temperature ; number density ) and inertialess q-distributed electrons (mass ; charge ; temperature ; number density ), positrons (mass ; charge ; temperature ; number density ), and ions (mass ; charge ; temperature ; number density ), where () is the number of electrons (protons) residing in negatively (positively) charged dust grains (ions). The dynamics of the EPIDPM is governed by these equations:
where is the dust fluid speed, is the pressure of the dust grains, and represents the electrostatic wave potential. To obtain the normalized form of Equations (1)–(3), we introduce the normalized parameters; namely, , , , and , where , , , and are the equilibrium number densities of the dust grains, electrons, positrons, and ions, respectively; , where and is the Boltzmann constant; ; , where ; and , where . The pressure term of the dust grains can be recognized as , with and , where N is the degree of freedom, and for the one-dimensional case, , then . The equilibrium quasi-neutrality condition can be written as . Now, after employing the normalizing parameters, we can write the normalized form of Equations (1)–(3) as
Other plasma parameters are considered as , , and . Now, the non-extensive q-distributed electron, positron, and ion number densities can be expressed as [37,43]
where and . For simplicity, we have considered , where q is the non-extensive parameter defining the degree of non-extensivity of plasma species; i.e., corresponds to the Maxwellian distribution, and () corresponds to the super-extensivity (sub-extensivity). We note that we are interested in DAWs with a frequency of 10 to 100 Hz [20] and that the charging frequency of the dust species in electron–ion plasma is on the order of [20]. This clearly indicates that the dust charge fluctuation is important only for the waves whose frequency is comparable to the dust charging frequency. Thus, the dust charging time scale is completely negligible in comparison with that of the DAWs, and the effect of the dust charge fluctuation can be reasonably neglected in any kind of study of the DAWs. We further note that the electron species is assumed to follow a non-extensive distribution. Thus, the estimation of characteristic times of electron thermalization for the plasma system under consideration is irrelevant. Now, by expanding Equations (7)–(9) to the third-order in and thus substituting these expansions into Equation (6), one can easily write
where
By employing the reductive perturbation method, one can easily derive the NLSE [46,47,48]. For the derivation of the NLSE, the stretched coordinates are considered as and , where is small parameter (i.e., ) and is the group velocity of the DAWs [46,47,48]. The dependent variables can be represented as [46,47,48]
where k () stands for the carrier wave number (frequency). The derivative operators are [46,47,48]
Now, by substituting Equations (11)–(14) into Equations (4), (5), and (10), and under consideration of with , we can write Equations (4) and (5) as
and the dispersion relation of DAWs is
The second-order ( with ) equations are given by
with the compatibility condition
The coefficients of under consideration of and provide the following relations:
where
Now, we consider the expressions for ( with ) and ( with ), which lead to the zeroth harmonic modes. Thus, we obtain
where
3. Modulational Instability and Rogue Waves
When P and Q of the NLSE (22) have the same sign (i.e., ) then the DAWs are modulationally unstable, and when the P and Q values of the NLSE (22) have the opposite sign (i.e., ), then the DAWs are modulationally stable [46,47,48,49]. The point at which transition of the curve intersects with the k-axis is known as the critical wave number k (=). It may be noted here that for typical dusty plasma, a number of authors have considered [19,20,21,50,51,52,53], [18,19,20,21,50,51,52,53], [18,53], [19,20,21,50,51,52,53], [18,53], [19,20,21,50,51,52,53], [19,20,21,50,51,52,53], and [19,20,21,50,51,52,53], and for laboratory edge dusty plasma, , , , and [24,25]. For simplicity, we have considered for our numerical analysis , , , , and .
Now, the modulationally stable and unstable parametric regimes of the DAWs can be seen from Figure 1. It is clear from the left panel of Figure 1 that (a) the DAWs are stable for small values of k () and are unstable for large values of k () under consideration of a sub-extensive q; (b) when , , and , then the corresponding value is (dotted blue curve), (dashed green curve), and (solid red curve); (c) the increases as q increases. Similarly, the right panel of Figure 1 represents the variation of the with k for different values of q under consideration of a super-extensive q: (a) when , , and , then the corresponding value is (dotted blue curve), (dashed green curve), and (solid red curve); (b) a negative q also leads to an increase in the critical wave number. Thus, one can say that the direction of the variation of the critical wave number is independent (dependent) of the sign (magnitude) of the q.
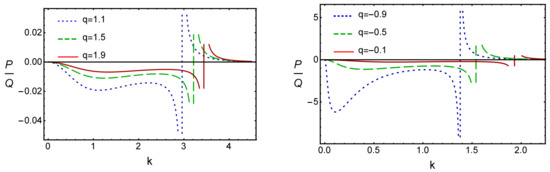
Figure 1.
Plot of versus k for different values of positive q (left panel), and negative q (right panel) when , , , , and .
The modulationally unstable parametric regime (i.e., ) of the DAWs allows the generation of highly energetic DA-RWs [54,55]:
We have also numerically analyzed Equation (23) in Figure 2 to illustrate the influence of the number density and charge state of the plasma species on the formation of DA-RWs associated with DAWs in the unstable parametric regimes (i.e., ). It is clear from the left panel of Figure 2 that (a) the amplitude and width of the DA-RWs decreases with increasing positron number density () for a constant value of and ; (b) the increasing negative dust number density () enhances the amplitude and width of the DA-RWs for a constant value of and dust charge state . The right panel of Figure 2 describes the variation of amplitude and width of the DA-RWs with space for different values of , and it is obvious from this figure that (a) the height and width of the DA-RWs increase (decrease) with an increasing dust (ion) number density for a fixed value of and ; (b) similarly, the nonlinearity of the EPIDPM increases (decreases) with the charge state of the negative dust grains (positive ion) when their number densities remain constant.
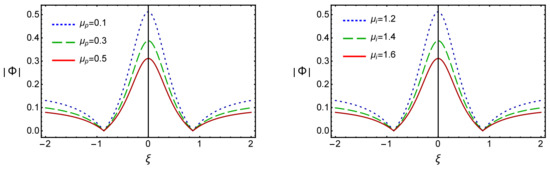
Figure 2.
Plot of versus for different values of and (left panel), and plot of versus for different values of and (right panel) when , , , and .
4. Conclusions
In this paper, we have investigated DW-RW-associated DAWs in an EPIDPM with inertial negative dust grains and inertialess non-extensive electrons, positrons, and ions. The dynamics of the EPIDPM and the DA-RWs are governed by the standard NLSE. The results that have been found in our present investigation can be summarized as follows:
- Both modulationally stable (i.e., ) and unstable (i.e., ) DAWs are observed;
- The direction of the variation of the critical wave number is independent (dependent) of the sign (magnitude) of the q;
- The amplitude of the DA-RWs decreases with increasing population of non-extensive positrons;
- Excess non-extensive ions reduce the height of the DA-RWs.
The results of our present investigation will be useful in future to understand the MIs of DAWs and associated DA-RWs in the galactic centre [1], Saturn’s magnetosphere [2,3], Jupiter’s magnetosphere [3,4], the pulsar magneto-sphere [5,6,7,8], supernova environments [8,9], interstellar medium [10,11,12,13,14], cometary tails [15,16,17], the solar atmosphere [17,18,19,20], and laboratory experiments [21,22,23,24,25].
Author Contributions
All authors contributed equally to complete this work. All authors have read and agreed to the published version of the manuscript.
Funding
The research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable—no new data generated.
Acknowledgments
The authors are grateful to anonymous reviewers for their constructive suggestions which have significantly improved the quality of our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zurek, W.H. Annihilation radiation from the galactic center-Positrons in dust? Astrophys. J. 1985, 289, 603–608. [Google Scholar] [CrossRef]
- Horányi, M.; Hartquist, T.W.; Havnes, O.; Mendis, D.A.; Morfill, G.E. Dusty plasma effects in saturn’s magnetosphere. Rev. Geophys. 2004, 42, RG4002. [Google Scholar] [CrossRef]
- Krimigis, S.M.; Carbary, J.F.; Keath, E.P.; Armstrong, T.P.; Lanzerotti, L.J.; Gloeckler, G. General characteristics of hot plasma and energetic particles in the Saturnian magnetosphere: Results from the voyager spacecraft. J. Geophys. Res. 1983, 88, 8871–8892. [Google Scholar] [CrossRef]
- Horányi, M.; Morfill, G.E.; Grün, E. Mechanism for the acceleration and ejection of dust grains from Jupiter’s magnetosphere. Nature 1993, 363, 144–146. [Google Scholar] [CrossRef]
- Sturrock, P.A. A model of pulsars. Astrophys. J. 1971, 164, 529–556. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Sutherland, P.G. Theory of pulsars-Polar caps, sparks, and coherent microwave radiation. Astrophys. J. 1975, 196, 51–72. [Google Scholar] [CrossRef]
- Michel, F.C. Theory of pulsar magnetospheres. Rev. Mod. Phys. 1982, 54, 1. [Google Scholar] [CrossRef]
- Shukla, P.K.; Marklund, M. Dust acoustic wave in a strongly magnetized pair-dust plasma. Phys. Scr. 2004, T113, 36. [Google Scholar] [CrossRef]
- Alfvén, H. Cosmic Plasma; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1981. [Google Scholar]
- Spitzer, L., Jr. Physical Processes in the Interstellar Media; John Wiley and Sons: New York, NY, USA, 1978. [Google Scholar]
- Miller, T.J.; Williams, D.A. Dust and Chemistry in Astronomy; Institute of Physics: Bristol, UK, 1993. [Google Scholar]
- Evans, A. The Dusty Universe; John Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Higdon, J.C.; Lingenfelter, R.E.; Rothschild, R.E. The galactic positron annihilation radiation and the propagation of positrons in the interstellar medium. Astrophys. J. 2009, 698, 350. [Google Scholar] [CrossRef][Green Version]
- Shukla, P.K. A note on the formation of large-scale structures in the universe. Phys. Scr. 2008, 77, 068201. [Google Scholar] [CrossRef]
- Ellis, T.A.; Neff, J.S. Numerical simulation of the emission and motion of neutral and charged dust from P/Halley. Icarus 1991, 91, 280–296. [Google Scholar] [CrossRef]
- Mendis, D.A.; Rosenberg, M. Cosmic dusty plasma. Annu. Rev. Astron. Astrophys. 1994, 32, 419–463. [Google Scholar] [CrossRef]
- Horányi, M. Charged dust dynamics in the solar system. Annu. Rev. Astron. Astrophys. 1996, 34, 383–418. [Google Scholar] [CrossRef]
- Murphy, R.J.; Share, G.H.; Skibo, J.G.; Kozlovsky, B. The physics of positron annihilation in the solar atmosphere. Astrophys. J. Suppl. Ser. 2005, 161, 495. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion, 3rd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Shukla, P.K.; Mamun, A.A. Introduction to Dusty Plasma Physics; IOP: London, UK, 2002. [Google Scholar]
- Bandyopadhyay, P.; Prasad, G.; Sen, A.; Kaw, P.K. Experimental study of nonlinear dust acoustic solitary waves in a dusty plasma. Phys. Rev. Lett. 2012, 101, 065006. [Google Scholar] [CrossRef]
- Surko, C.M.; Murphy, T.J. Use of the positron as a plasma particle. Phys. Fluids B 1990, 2, 1372. [Google Scholar] [CrossRef]
- Cho, S.H.; Lee, H.J.; Kim, Y.S. Nonrelativistic electromagnetic surface waves: Dispersion properties in a magnetized dusty electron-positron plasma. Phys. Rev. E 2000, 61, 4357. [Google Scholar] [CrossRef]
- Smirnov, R.D.; Pigarov, A.Y.; Rosenberg, M.; Krasheninnikov, S.I.; Mendis, D.A. Modelling of dynamics and transport of carbon dust particles in tokamaks. Plasma Phys. Control. Fusion 2007, 49, 347. [Google Scholar] [CrossRef]
- Krasheninnikov, S.I.; Pigarov, A.Y.; Smirnov, R.D.; Rosenberg, M.; Tanaka, Y.; Benson, D.J. Recent progress in understanding the behavior of dust in fusion devices. Plasma Phys. Control. Fusion 2008, 50, 124054. [Google Scholar] [CrossRef]
- Nosenko, V.; Zhdanov, S.; Ivlev, A.V.; Morfill, G.; Goree, J.; Piel, A. Heat transport in a two-dimensional complex (dusty) plasma at melting conditions. Phys. Rev. Lett. 2008, 100, 025003. [Google Scholar] [CrossRef]
- Avinash, K.; Merlino, R.L.; Shukla, P.K. Anomalous dust temperature in dusty plasma experiments. Phys. Lett. A 2011, 375, 2854–2857. [Google Scholar] [CrossRef]
- Rosenberg, M.; Mendis, D.A.; Sheehan, D.P. Positively charged dust crystals induced by radiative heating. Phys. Lett. A 1999, 27, 239–242. [Google Scholar] [CrossRef]
- Banerjee, G.; Maitra, S. Arbitrary amplitude dust ion acoustic solitons and double layers in the presence of nonthermal positrons and electrons. Phys. Plasmas 2016, 23, 123701. [Google Scholar] [CrossRef]
- Paul, A.; Bandyopadhyay, A. Dust ion acoustic solitary structures in presence of nonthermal electrons and isothermal positrons. Astrophys. Space Sci. 2016, 361, 172. [Google Scholar] [CrossRef]
- Noman, A.A.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-acoustic envelope solitons in super-thermal plasmas. Contrib. Plasma Phys. 2019, 59, e201900023. [Google Scholar] [CrossRef]
- Khondaker, S.; Mannan, A.; Chowdhury, N.A.; Mamun, A.A. Rogue waves in multi-pair plasma medium. Contrib. Plasma Phys. 2019, 59, e201800125. [Google Scholar] [CrossRef]
- Futaana, Y.; Machida, S.; Saito, Y.; Matsuoka, A.; Hayakawa, H. Moon-related nonthermal ions observed by Nozomi: Species, sources, and generation mechanisms. J. Geophys. Res. 2003, 108, 1025. [Google Scholar] [CrossRef]
- Asbridge, J.R.; Bame, S.J.; Strong, I.B. Outward flow of protons from the Earth’s bow shock. J. Geophys. Res. 1968, 73, 5777–5782. [Google Scholar] [CrossRef]
- Hansen, S.H. Cluster temperatures and non-extensive thermo-statistics. New Astron. 2005, 10, 371–377. [Google Scholar] [CrossRef]
- Renyi, A. On a new axiomatic theory of probability. Acta Math. Acad. Sci. Hung. 1955, 6, 285–335. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Eslami, P.; Mottaghizadeh, M.; Pakzad, H.R. Nonplanar dust acoustic solitary waves in dusty plasmas with ions and electrons following a q-nonextensive distribution. Phys. Plasmas 2011, 18, 102303. [Google Scholar] [CrossRef]
- Roy, K.; Chatterjee, P.; Kausik, S.S.; Wong, C.S. Shock waves in a dusty plasma having q-nonextensive electron velocity distribution. Astrophys. Space Sci. 2014, 350, 599–605. [Google Scholar] [CrossRef]
- Zaman, D.M.S.; Mannan, A.; Chowdhury, N.A.; Mamun, A.A. Dust-acoustic rogue waves in opposite polarity dusty plasma featuring nonextensive statistics. High Temp. 2020, 58, 789–794. [Google Scholar] [CrossRef]
- Bains, A.S.; Tribeche, M.; Ng, C.S. Dust-acoustic wave modulation in the presence of q-nonextensive electrons and/or ions in dusty plasma. Astrophys. Space Sci. 2013, 343, 621–628. [Google Scholar] [CrossRef]
- Moslem, W.M.; Sabry, R.; El-Labany, S.K.; Shukla, P.K. Dust-acoustic rogue waves in a nonextensive plasma. Phys. Rev. E 2011, 84, 066402. [Google Scholar] [CrossRef]
- Rahman, M.H.; Mannan, A.; Chowdhury, N.A.; Mamun, A.A. Generation of rogue waves in space dusty plasmas. Phys. Plasmas 2018, 25, 102118. [Google Scholar] [CrossRef]
- Esfandyari-Kalejahi, A.; Afsari-Ghazi, M.; Noori, K.; Irani, S. Large amplitude dust-acoustic solitary waves in electron-positron-ion plasma with dust grains. Phys. Plasmas 2012, 19, 082308. [Google Scholar] [CrossRef]
- Jehan, N.; Masood, W.; Mirza, A.M. Planar and nonplanar dust acoustic solitary waves in electron–positron–ion–dust plasmas. Phys. Scr. 2009, 80, 035506. [Google Scholar] [CrossRef]
- Banik, S.; Shikha, R.K.; Noman, A.A.; Chowdhury, N.A.; Mannan, A.; Roy, T.S.; Mamun, A.A. First and second-order dust-ion-acoustic rogue waves in non-thermal plasma. Eur. Phys. J. D 2021, 75, 43. [Google Scholar] [CrossRef]
- Shikha, R.K.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Electrostatic dust-acoustic envelope solitons in an electron-depleted plasma. Contrib. Plasma Phys. 2021, 61, e202000117. [Google Scholar] [CrossRef]
- Rajib, T.I.; Tamanna, N.K.; Chowdhury, N.A.; Mannan, A.; Sultana, S.; Mamun, A.A. Dust-ion-acoustic rogue waves in presence of non-extensive non-thermal electrons. Phys. Plasmas 2019, 26, 123701. [Google Scholar] [CrossRef]
- Fedele, R. Envelope Solitons versus Solitons. Phys. Scr. 2002, 65, 502. [Google Scholar] [CrossRef]
- Cousens, S.E.; Sultana, S.; Kourakis, I.; Yaroshenko, V.V.; Verheest, F.; Hellberg, M.A. Nonlinear dust-acoustic solitary waves in strongly coupled dusty plasmas. Phys. Rev. E 2012, 86, 066404. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.; Konopka, U.; Khrapak, S.A.; Morfill, G.E.; Sen, A. Effect of polarization force on the propagation of dust acoustic solitary waves. New J. Phys. 2010, 12, 073002. [Google Scholar] [CrossRef]
- Zadorozhny, A.M. Effects of charged dust on mesospheric electrical structure. Adv. Space Res. 2001, 28, 1059–1064. [Google Scholar] [CrossRef]
- Wang, Y.L.; Guo, X.Y.; Li, Q.S. Nonlinear dust acoustic waves in strongly coupled dusty plasmas with charged dust particles. Commun. Theor. Phys. 2016, 65, 247. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Devine, N.; Akhmediev, N. Are rogue waves robust against perturbations? Phys. Lett. A 2009, 373, 3997–4000. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).