Investigating Multiwavelength Lognormality with Simulations—Case of Mrk 421
Abstract
1. Introduction
2. Observations and Data
3. PDF Estimation Methodology
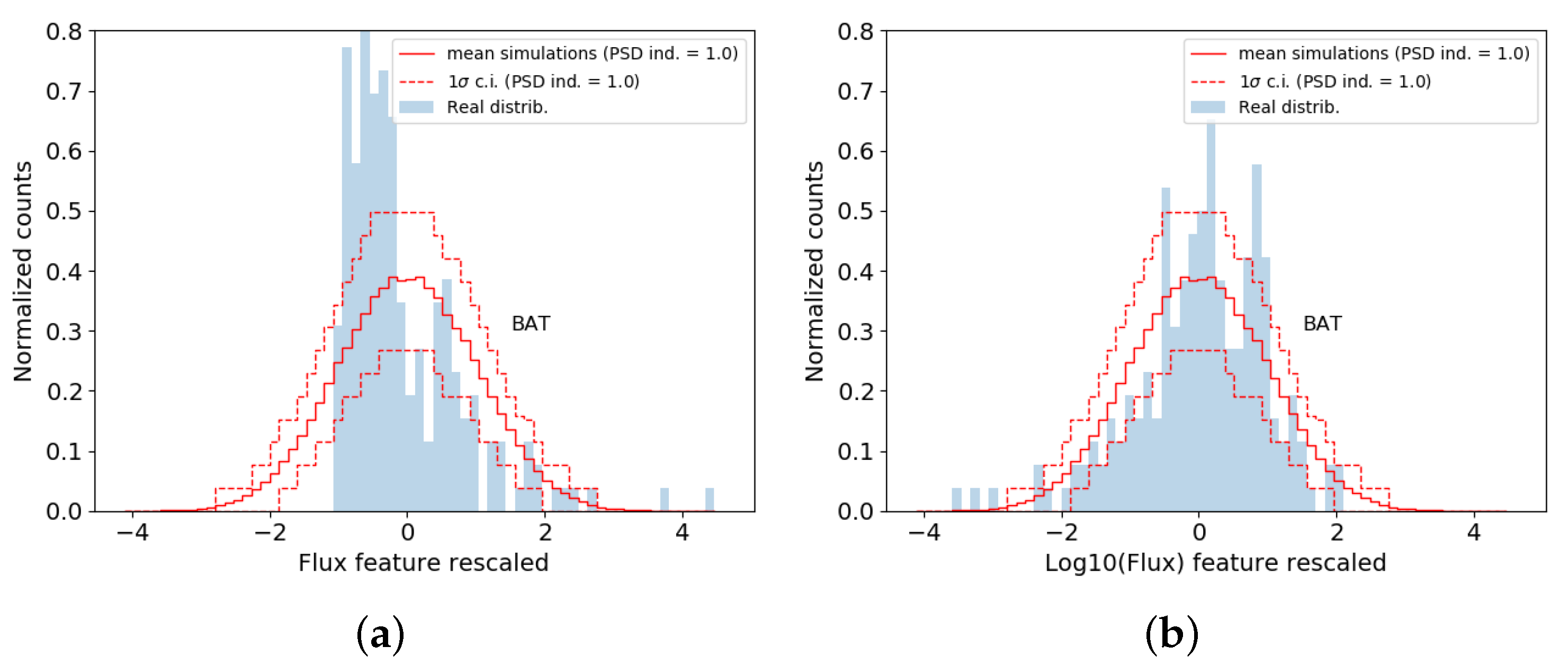
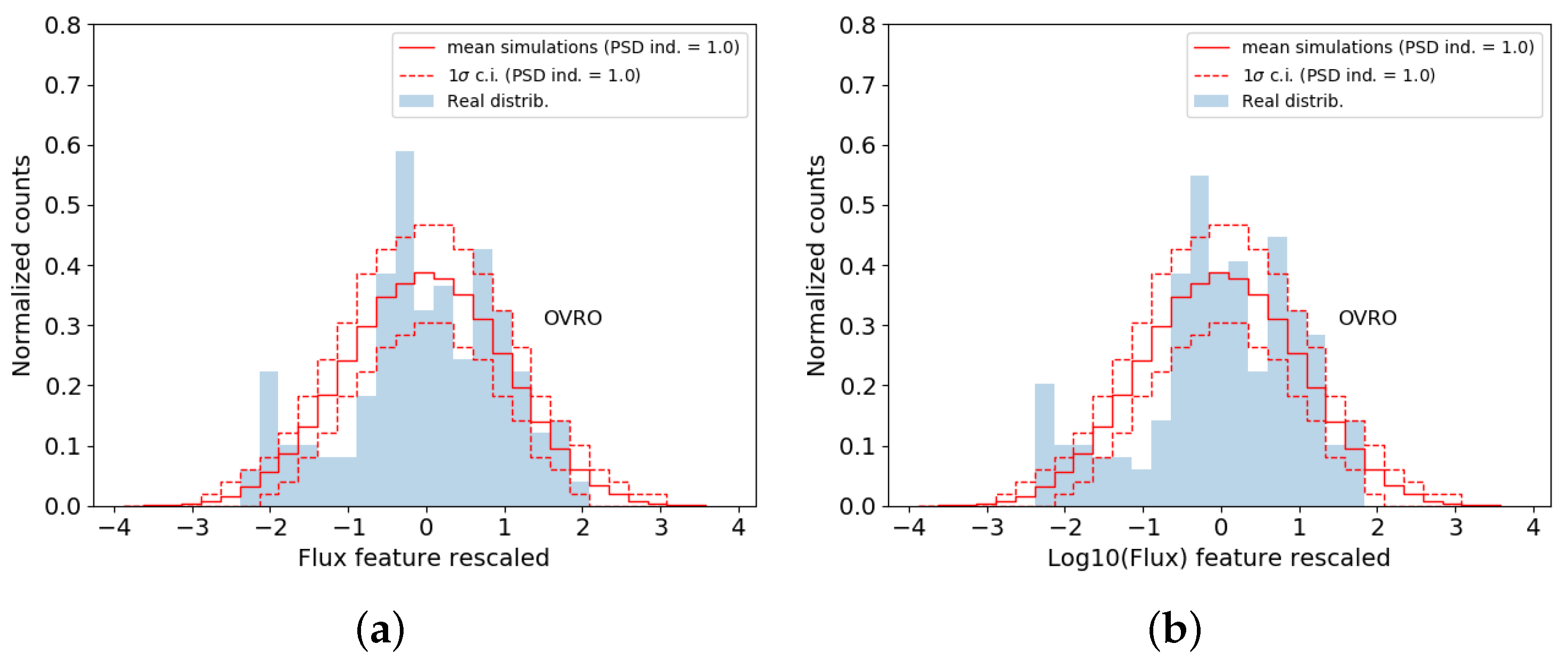
4. Results: Normal vs. Lognormal
5. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Urry, C. AGN Unification: An Update. In Proceedings of the AGN Physics with the Sloan Digital Sky Survey, Princeton, NJ, USA, 27–31 July 2003; Richards, G.T., Hall, P.B., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2004; Volume 311, p. 49. [Google Scholar]
- Lyubarskii, Y.E. Flicker noise in accretion discs. Mon. Not. R. Astron. Soc. 1997, 292, 679–685. [Google Scholar] [CrossRef]
- Uttley, P.; McHardy, I.M.; Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2005, 359, 345–362. [Google Scholar] [CrossRef]
- Romoli, C.; Chakraborty, N.; Dorner, D.; Taylor, A.; Blank, M. Flux Distribution of Gamma-Ray Emission in Blazars: The Example of Mrk 501. Galaxies 2018, 6, 135. [Google Scholar] [CrossRef]
- Sinha, A.; Shukla, A.; Saha, L.; Acharya, B.S.; Anupama, G.C.; Bhattacharjee, P.; Britto, R.J.; Chitnis, V.R.; Prabhu, T.P.; Singh, B.B.; et al. Long-term study of Mkn 421 with the HAGAR Array of Telescopes. Astron. Astrophys. 2016, 591, A83. [Google Scholar] [CrossRef]
- Gorham, P.W.; van Zee, L.; Unwin, S.C.; Jacobs, C. Markarian 421’[CSC]s[/CSC] Unusual Satellite Galaxy. Astron. J. 2000, 119, 1677–1686. [Google Scholar] [CrossRef][Green Version]
- Chevalier, J.; Kastendieck, M.A.; Rieger, F.; Maurin, G.; Lenain, J.P. Long term variability of the blazar PKS 2155-304. arxiv 2015, arXiv:1509.03104. [Google Scholar]
- Richards, J.L.; Max-Moerbeck, W.; Pavlidou, V.; King, O.G.; Pearson, T.J.; Readhead, A.C.S.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Weintraub, L.C.; et al. Blazars in the Fermi Era: The OVRO 40 m Telescope Monitoring Program. Astrophys. J. Suppl. Ser. 2011, 194, 29. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Emmanoulopoulos, D.; McHardy, I.M.; Papadakis, I.E. Generating artificial light curves: Revisited and updated. Mon. Not. R. Astron. Soc. 2013, 433, 907–927. [Google Scholar] [CrossRef]
- Morris, P.J.; Chakraborty, N.; Cotter, G. Deviations from normal distributions in artificial and real time series: A false positive prescription. Mon. Not. R. Astron. Soc. 2019, 489, 2117–2129. [Google Scholar] [CrossRef]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271–1284. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, N. Investigating Multiwavelength Lognormality with Simulations—Case of Mrk 421. Galaxies 2020, 8, 7. https://doi.org/10.3390/galaxies8010007
Chakraborty N. Investigating Multiwavelength Lognormality with Simulations—Case of Mrk 421. Galaxies. 2020; 8(1):7. https://doi.org/10.3390/galaxies8010007
Chicago/Turabian StyleChakraborty, Nachiketa. 2020. "Investigating Multiwavelength Lognormality with Simulations—Case of Mrk 421" Galaxies 8, no. 1: 7. https://doi.org/10.3390/galaxies8010007
APA StyleChakraborty, N. (2020). Investigating Multiwavelength Lognormality with Simulations—Case of Mrk 421. Galaxies, 8(1), 7. https://doi.org/10.3390/galaxies8010007




