1. Introduction
The identification of dark matter (DM) is one of the major endeavours of particle physics and cosmology of the 21st century. Despite theoretical and experimental efforts deployed to detect DM particles, the nature of this elusive form of matter remains mostly unknown. We know cold DM to be successful in describing the universe on large scales [
1]. However, null outcomes of weakly-interacting massive particle (WIMP, [
2]) searches in direct, indirect, and collider experiments, together with deviations from cold DM predictions on small scales [
3], challenge this paradigm and feed the interest for alternative DM scenarios.
However, deviations from cold DM predictions on small scales tantalise this paradigm and cast serious doubts on the weakly-interacting massive particle hypothesis, the most scrutinised model for cold DM so far [
2]. Additionally, searches for DM particle candidates at the weak scale have been until now unsuccessful with current instruments, on ground and in space. In particular, attempts of indirect detection of high-energy photons from WIMP self-annihilation provide some among the strongest limits on WIMP DM [
4,
5]. At this stage, it is unclear if the WIMP (and cold DM) paradigm has to be revised in favour of other, still viable, DM particle models (warm and ultra-light DM models), or if it is instead kinematically outside of the main explored range and can be discovered with the next generation of gamma-ray telescopes, e.g., the Cherenkov telescope array (CTA, [
6]).
Indirect detection constraints on the WIMP parameter space are unavoidably affected by background model systematics. This is particularly severe in the inner region of the galaxy, where the gamma-ray emission is dominated by the interactions of cosmic rays with the interstellar matter and fields (i.e., galactic diffuse emission). “Cleaner” and, in this respect, more promising targets for DM identification are dwarf spheroidal galaxies, optically faint galaxies whose dynamics has been proved to be dominated by large haloes of DM [
7]. Those faintest detectable galaxies can probe the WIMP paradigm with multi wavelength observations, from optical to gamma rays (see for example [
8,
9]). Moreover, the DM haloes hosting dwarf spheroidal galaxies are thought to be the most massive of a vast population of DM subhaloes, overdensities in the DM host halo surrounding our galaxy [
10,
11]. While the majority of these DM subhaloes lacks an optical counterpart, a steady gamma-ray signal from directions where no object can be associated in other wavelengths would be a hint for WIMP annihilation.
Searches for DM subhaloes are typically performed in point-source catalogues of the Large Area Telescope (LAT), aboard the Fermi satellite. Point-source catalogues like the Third Fermi-LAT Source Catalogue (3FGL) [
12], and the Second Catalogue of Hard Fermi-LAT Sources (2FHL) [
13] contain a number of gamma-ray sources which are not associated with any known astrophysical object. Classification algorithms, utilizing in particular spectral information, are applied on these unassociated sources in order to single out potential DM subhalo candidates [
14,
15,
16].
Limits on the DM parameter space (annihilation cross-section vs. mass) are derived by comparing the number of expected DM subhalo candidates in the catalogues with predictions of the number of subhaloes above the Fermi-LAT detection threshold expected from theoretical models of subhaloes [
16,
17,
18,
19,
20,
21,
22]. To this end, one needs to know how many subhaloes are expected to be bright enough in gamma rays to be seen above the standard astrophysical background. This requires, on the one hand, a detailed description of the galactic subhalo population. The complicated physics of subhalo evolution inside the potential of their host leads to different quantitative pictures depending on the models. To bracket these uncertainties, various models, either analytical or based on numerical simulations, are considered in this study, see
Section 2. On the other hand, the number of expected detectable subhaloes is obtained by convolving the DM subhalo signal with the Fermi-LAT detection threshold. The LAT detection threshold depends on the spectral signal that is looked for. Reference [
22] showed that computing the sensitivity of the LAT to DM subhalo signals, adopting the specific spectral energy distribution determined by the particle physics DM model (see also
Section 3), provides more accurate predictions on the number of expected detectable subhalo and that important differences with respect to assuming a fixed sensitivity threshold arise. We will therefore use the Fermi-LAT detection threshold as derived in [
22].
The goal of the present paper is to assess the detectability of DM subhaloes as predicted by state-of-the-art DM subhalo models [
23]. We will do so by using the more accurate Fermi-LAT sensitivity threshold to DM subhalo signals [
22]. In
Section 2 we describe the galactic subhalo models, in
Section 3 we remind the reader the main ingredients to compute the gamma-ray DM signal from dark subhaloes, and in
Section 4 how the LAT sensitivity is computed. We present the results in
Section 5, and conclude in
Section 6.
2. Galactic Subhalo Modelling
Subhaloes are subject to a variety of phenomena, including tidal stripping, gravitational shocking, and dynamical friction, which make their modelling challenging. Subhaloes can be studied by the means of fully-numerical cosmological simulations or simplified analytical models. These different approaches lead to similar qualitative pictures regarding the galactic subhalo population but often differ on a quantitative level. To get a handle on the modelling uncertainties, four models are considered in this study. These models share some common features: spherical symmetry is assumed for the galactic halo, subhaloes all have a Navarro–Frenk–White (NFW) density profile and their mass function is a power law with index
.
1 These assumptions are all verified on the scales resolved by numerical simulations, see e.g., [
10,
26]. Four configurations are considered, which are identical to those used in Hütten et al. [
23], which the reader is referred to for further details.
Our first model is based on the Aquarius DM-only N-body simulation [
26] and as such is called DMonly. The subhalo spatial distribution in Aquarius is found to be well fitted by an Einasto profile with parameters
and
kpc. The core in the distribution is created by tidal interactions which tend to disrupt subhaloes at the center of the host. The total number of subhaloes is fixed by assuming 300 high-mass clumps with masses larger than
, as an upper bound to the Aquarius findings [
26]. Subhaloes are further assumed to follow the mass-concentration relation given by Moliné et al. [
27]. While a well-known effect of tides is to remove matter from the outskirts of subhaloes, this is not accounted for in DMonly and all the subhaloes have their cosmological extension (defined with respect to the critical density of the universe).
The Phat-ELVIS model is based on a suite of DM-only simulations which incorporate a static disc potential [
28]. Through gravitational shocking, the disc is very efficient at disrupting most subhaloes in the inner 30 kpc of the host galaxy. The spatial distribution of the remaining population is well fitted by the following function:
with
,
kpc,
kpc and
kpc. Similar to the DMonly model, the mass-concentration relation is taken from [
27] and the density profile of subhaloes extends to their cosmological extension.
Our next configurations are based on the semi-analytical model of Stref and Lavalle [
29] (SL17 from now on). This model relies on a realistic description of the Milky Way and incorporates the stripping effect due to the gravitational potential of the galaxy as well as the shocking effect from the disc. It is not clear yet whether the efficient disruption of DM subhaloes as observed in simulations is realistic or not [
30,
31,
32]. This can be of importance because it has been shown to impact predictions for indirect searches [
33]. To account for this uncertainty, we consider two scenarios. In the first one, called
SL17-fragile, subhaloes are disrupted when their tidal radius
is equal to their scale radius
. In the second one, called SL17-resilient, subhaloes are more robust and survive unless
. Unlike the DMonly and Phat-ELVIS models, subhaloes in the SL17 configurations are stripped down to their tidal radius.
Knowing the DM subhalo spatial density
, it is possible to compute the so-called astrophysical or
-factor towards the direction—line of sight (l.o.s.)—of the subhalo of interest:
where the integral along the l.o.s. is further integrated over the solid angle
. In what follows, we will set
effectively considering subhaloes as point-like sources. We note that previous works have overestimated the
-factor—and thus got too stringent limits on DM—by integrating up to 0.5
[
22] or, up to the DM profile scale radius, e.g., [
16]. Indeed, as we will explain below, the way in which the LAT sensitivity to DM spectra is computed strictly applies to point-like sources having an angular extension of 0.1–0.3
. Cutting the integration radius up-to 0.1
worsens the final limits on the DM annihilation cross section by a factor of 2, over all the DM mass range. Again, we believe this choice to be truly conservative. The
-factor is one of the crucial ingredients to compute gamma-ray DM fluxes, as we will see below.
Having incorporated these models in the CLUMPY code [
34,
35,
36], we consider 1000 Monte Carlo realisations for each configuration, and we select all subhaloes with
(<0.1
) >10
. The choice of this cut guarantees that the flux from DM annihilation (for e.g., cross-section values ∼10
10
and masses ∼100 GeV is well below the Fermi-LAT catalogues threshold, and therefore that we do not miss any detectable subhalo. As we highlight below, this cut also allows us to study what is the role, if any, of low-mass subhaloes. We note that relying on the simulations done in [
23] guarantees that the subhalo population is complete in brightness.
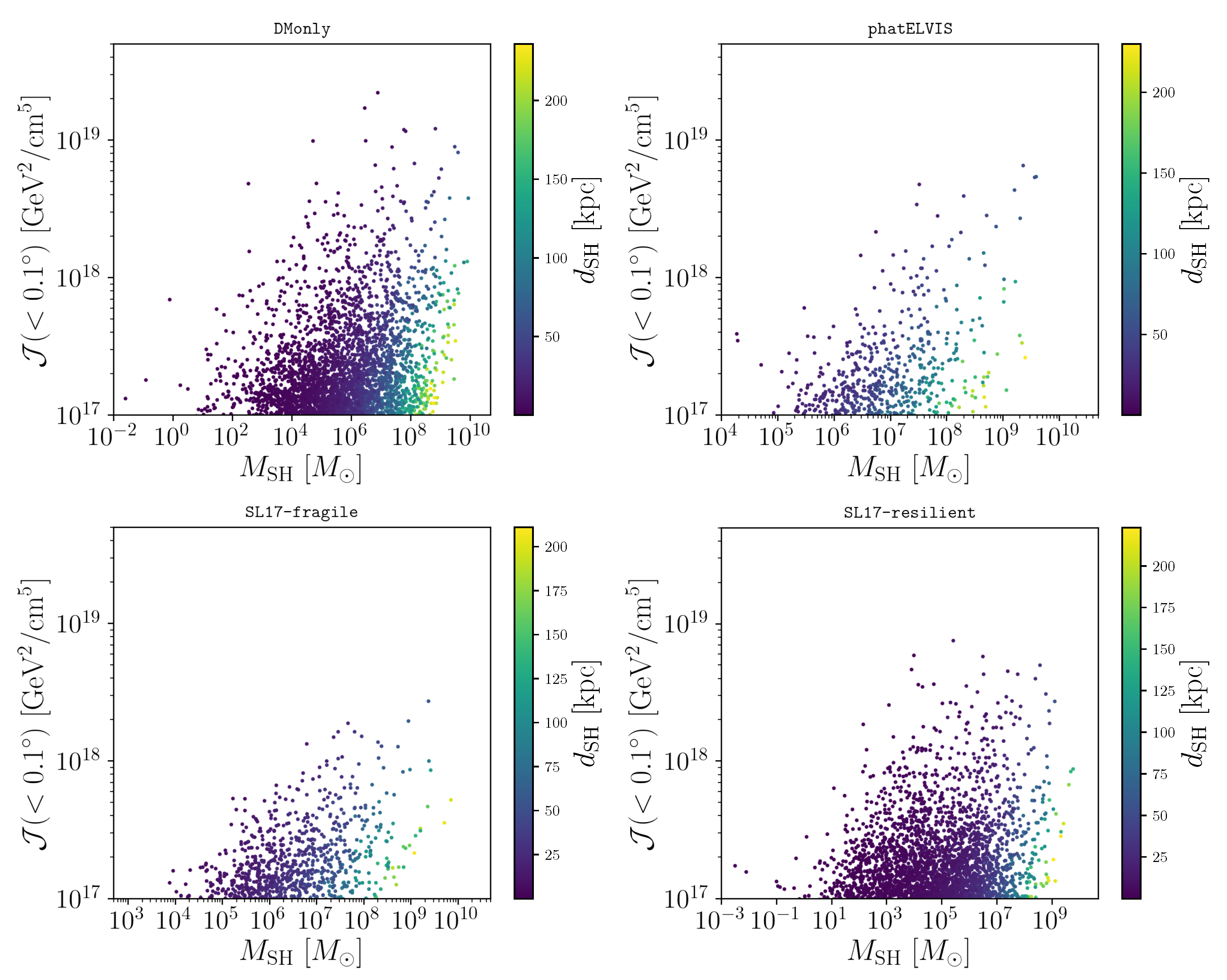
In
Figure 1, we show the scatter plots of
-factor values,
(<0.1
), as a function of subhalo mass,
, in one realisation of the Monte Carlo simulations for each subhalo model.
4. Fermi-LAT Sensitivity to DM Subhalos
We adopt the flux sensitivity calculation of Calore et al. [
22], where the authors provided an accurate calculation of the LAT sensitivity to DM annihilation signals from subhaloes and showed that such a determination of the detection threshold leads to significant differences with respect to adopting a fixed flux threshold. The Fermi-LAT source detection simulation of DM subhaloes was performed for the third Fermi-LAT catalog of point sources (3FGL) [
12], and the second catalog of hard Fermi-LAT sources (2FHL) [
13]. In both catalogues, unassociated sources represent a significant fraction of all detected sources: About 15% in the 2FHL and 30% in the 3FGL.
Interestingly, some gamma-ray emitting DM subhaloes can hide among unassociated sources in the Fermi-LAT catalogues. In the present work, we assess what is the sensitivity to DM subhalo modelling of the Fermi-LAT 3FGL and 2FHL catalogues.
As can be seen from Figures 5–8 in [
22], the flux sensitivity threshold of Fermi-LAT for the 3FGL and 2FHL set-ups depends both on latitude and mass of the DM candidate: Regardless of the annihilation channel, the flux sensitivity threshold decreases by a factor of about 2 between
and
in latitude for all masses, for both the 3FGL and 2FHL set-up. Also, higher (lower) DM masses are more easily detected in the 3FGL (2FHL) set-up, as thoroughly explained in [
22]. We note that our sensitivity threshold for the
and
channels is very similar to the one more recently derived by Coronado-Blazquez et al. [
16]. Given the contamination of the galactic diffuse foreground, the sensitivity calculation of [
22] is truly accurate for
. We will therefore consider only subhlaoes at high latitudes.
5. Results
To derive the number of detectable subhaloes for a given mass and final state annihilation channel, we computed the corresponding gamma-ray flux (Equation (
3)) in the same energy range of the catalogue we want to compare with (
GeV for the 3FGL and
GeV for the 2FHL). For each subhalo in the Monte Carlo simulations, we then compared the DM gamma-ray flux with the Fermi-LAT sensitivity threshold at the position of the subhalo: A subhalo was detected if its gamma-ray flux was larger than the flux threshold at its position.
In general, the number of detectable subhaloes was almost linearly proportional to the annihilation cross section. As found in [
22], the number of detectable subhaloes did not strongly depend on the DM mass for annihilation into bottom quarks, while, because of the harder spectrum, the DM mass was more relevant in the case of annihilation into
leptons. In
Table 1, for each model and catalogue configuration, we provide the annihilation cross section required to have at least one subhalo detectable for annihilation into
b-quarks and
leptons. We note that the minimal cross section needed to detect at least one subhalo was about a few
for annihilation into
in the 3FGL, in the case of the DMonly model. The minimal cross section for SL17-resilient was found to be a factor of ∼2 higher, while it was ∼4–5 higher for the Phat-ELVIS and SL17-fragile models. The hierarchy between the models was similar for the 2FHL catalogue and for annihilation into
. These minimal cross sections exceed current bounds from Fermi-LAT observations towards dwarf spheroidal galaxies, see e.g., [
38]. Dwarf spheroidal galaxies are traditionally believed to give the strongest and most robust limits of the DM parameter space—although several, independent, works addressed the robustness of such a bound showing that it is prone to uncertainties of a factor of a few mainly because on the uncertainty in the modelling of the foreground at the dwarf position [
9] and of the dwarf DM distribution [
39,
40,
41].
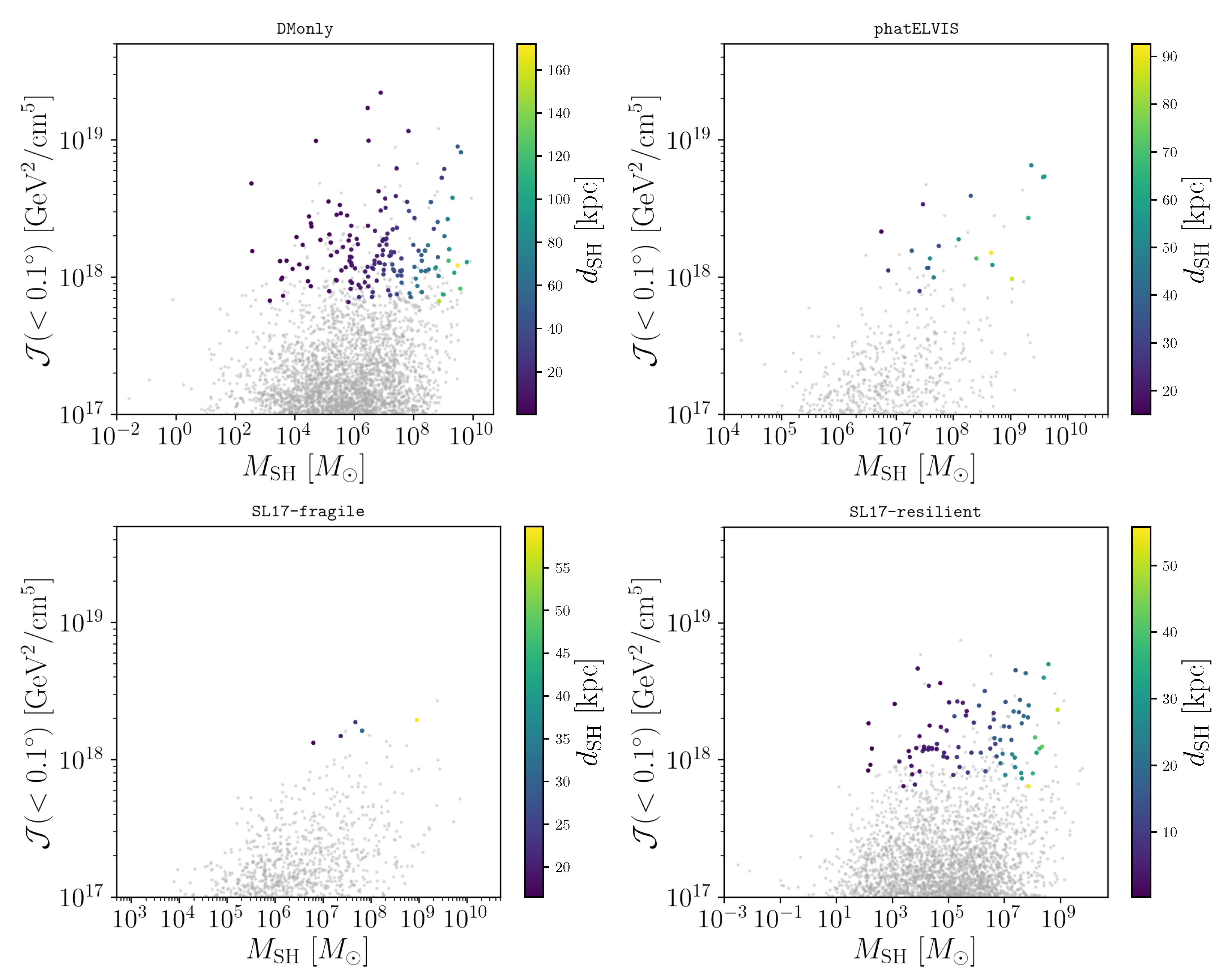
It is of interest to have a look at the distribution of the
-factor of detectable subhaloes versus their mass. This is shown in
Figure 2 for the 3FGL catalogue set-up. In contrast to
Figure 1, all subhaloes are here represented by grey dots, while the ones detectable in the 3FGL catalogue are shown by coloured points. Note that these subhaloes, represented by their
-factors, are detectable for fluxes from a DM particle with mass of 100 GeV and annihilation cross section into
of
cm
/s.
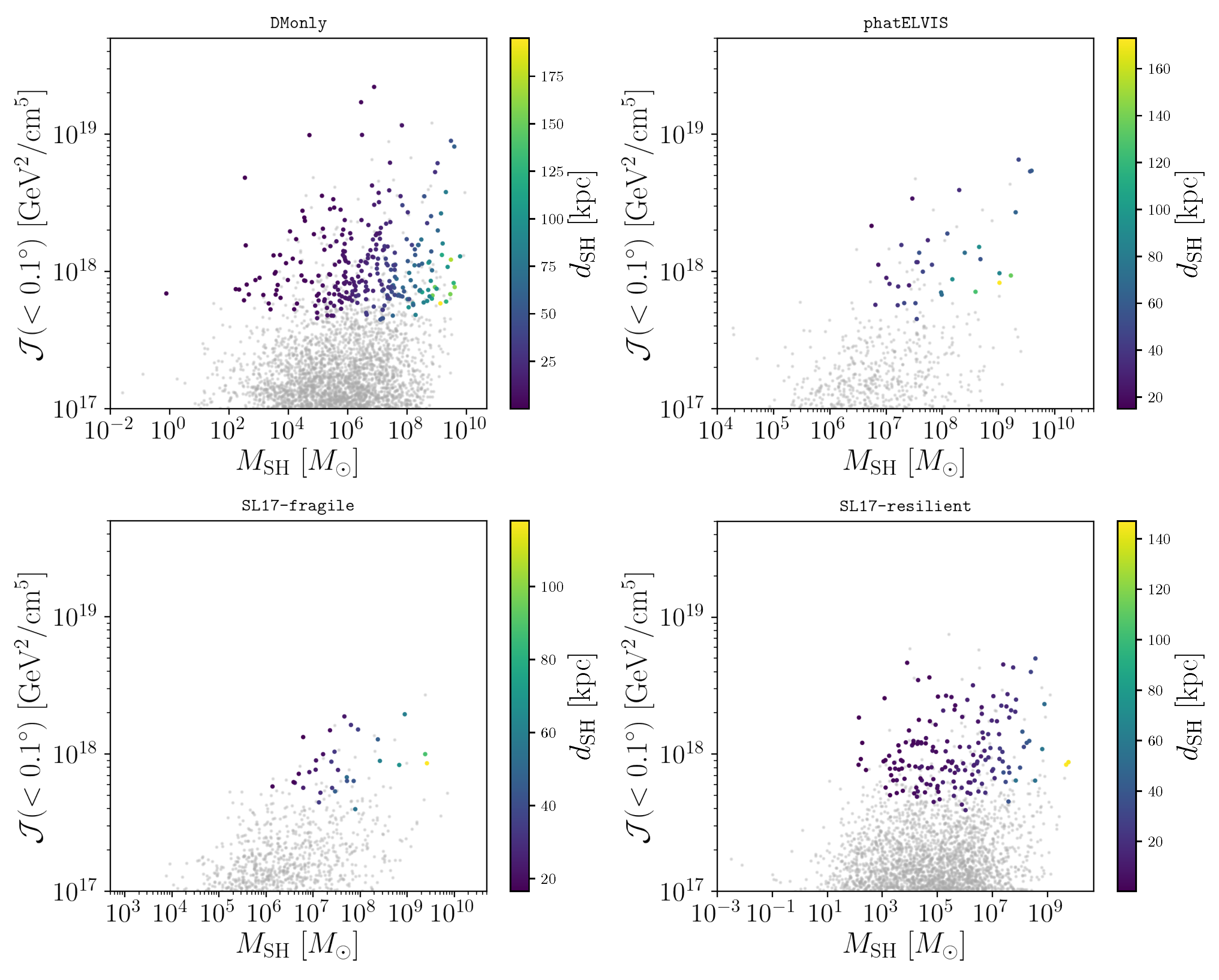
Figure 3 shows the same for the 2FHL catalogue set-up, DM mass of 1.5 TeV and annihilation cross section into
of
cm
/s.
A few considerations are in order. First, for the set of particle physics parameter chosen, for the 3FGL (2FHL) set-up the
-factor threshold for subhalo detection was about
for all four models. However, not all subhaloes with
-factor above this threshold were detectable in the Fermi-LAT catalogues; indeed, the DM mass and latitude dependence of the flux sensitivity threshold implied that the highest
-factor subhaloes were sometimes not the most likely detectable ones with the LAT. This could be clearly seen, for example, in the bottom right panel of
Figure 2: While the brightest gamma-ray subhalo had
, the detectable subhalo with the highest
-factor had
. The same occurred for the 2FHL set-up. Secondly, the mass of detectable subhaloes could span up to seven orders in magnitude (from ∼10
M
to ∼10
M
) depending on the configuration, as was the case for DMonly and SL17-resilient. We concluded that among detectable sources there were both dwarf galaxies and dark subhaloes. Indeed, galaxy formation models agreed that DM haloes with mass
are massive enough to systematically host galaxies. Although the exact threshold for star formation is quite debated and dark subhaloes can even coexist with luminous ones above that star formation threshold [
42], low-mass subhaloes (below
) are almost surely optically dark objects. However, those can still have large
-factor and be among detectable subhaloes. This occurred for our DMonly, but also in a model where the effect of baryons in the galaxy was fully modelled (SL17-resilient). Finally, we note that in subhalo models where tidal disruption was less efficient (DMonly and SL17-resilient), most detectable subhaloes were located at a distance less than 20 kpc from us. Some of them were even closer than 10 kpc. On the other hand, when tidal disruption was efficient (as in Phat-ELVIS and SL17-fragile), a larger fraction of detectable subhaloes was located farther away (see also [
23] for details). This was because the stellar disc disrupted most objects orbiting within the inner ∼20 kpc of the galaxy.
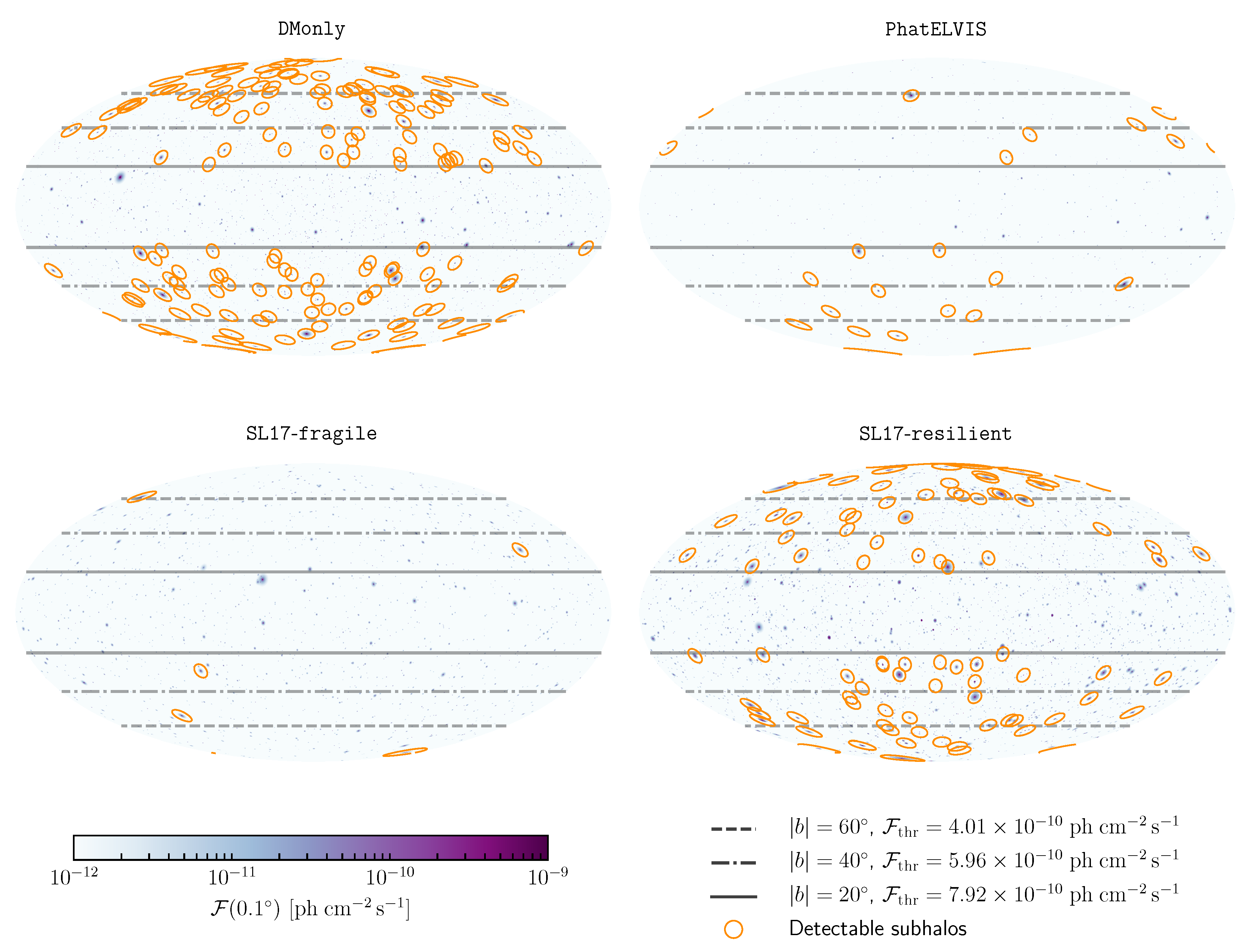
In
Figure 4, we display the all-sky gamma-ray maps of selected haloes corresponding to the realisations shown in
Figure 1. Fluxes were computed again assuming a DM mass of 100 GeV and an annihilation cross section into
of
, for the 3FGL catalogue set-up. Subhaloes whose flux exceeded the sensitivity threshold are highlighted by light orange circles on the skymaps. Besides the latitude cut
, we could see that bright clumps at high latitude remained undetectable because of the latitude (and DM mass dependence) of the LAT detection threshold. We also note that subhaloes could have a very small angular extension on the sky and still be detectable, as could be seen in particular on the SL17-resilient skymap (bottom right). This was due to the cuspy density profile of DM haloes: Even if the structure was stripped off its outer layers by tidal effects, the
-factor was only mildly affected and could remain quite high.
Dedicated searches for DM subhalo candidates among Fermi-LAT unassociated sources have been performed in the past through spectral and spatial analyses, often based on machine learning classification algorithms, see the latest analysis in [
16]. The most recent analysis found 16 (4, 24) DM subhalo candidates in the 3FGL (2FHL, 3FHL) catalogue [
16]. The flux sensitivity threshold inferred from Figure 9 of [
16] was quite similar to the corresponding sensitivity curves of the 2FHL—so we will provide predictions for the 2FHL in the present work. Also, the limits from the 3FGL and 2FHL were completely complementary and the strongest over the full DM mass range considered in [
16].
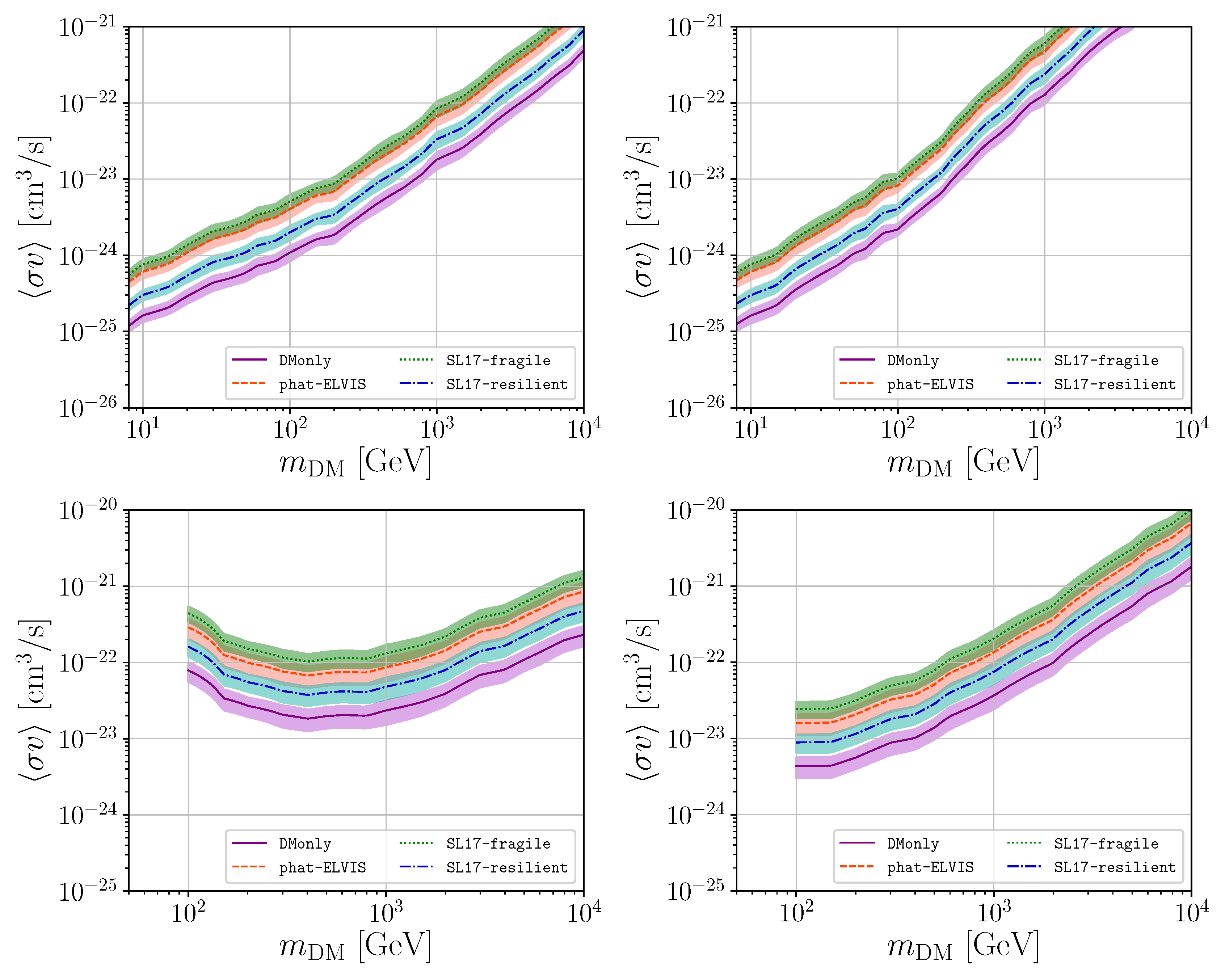
Knowing the number of DM subhalo candidates in Fermi-LAT catalogues, it is possible to infer an upper limit on the DM annihilation cross-section: For a given DM mass, this would be the value of giving a number of detectable subhaloes equal to the number of DM subhalo candidates, . The strongest bounds on DM would of course correspond to the case in which (and therefore the subhalo to be used to set the bound is the one with the largest -factor). On the other hand, the most conservative limits come from the case where is equal to the number of unassociated sources—which is anyhow unrealistic since most likely the largest fraction of these is indeed made up by standard astrophysical objects.
In
Figure 5, we present upper limits on the DM annihilation cross-section as a function of the particle mass that comes from comparing the number of detectable subhaloes in the four models under consideration with the number of DM subhalo candidates from [
16]. The upper limit on the cross section was defined as the maximum value of
for which the predicted subhalo gamma-ray fluxes were equal to the catalogue sensitivity flux threshold. The uncertainty bands corresponded to the uncertainty in the subhalo modelling, propagating the spread in the 1000 Monte Carlo realisations of the subhalo models (namely, the “galactic subhaloes variance”). We found that the DMonly configuration led to the strongest bounds on the annihilation cross-section. The bound from SL17-resilient was a factor of ∼2 weaker, while the bounds from Phat-ELVIS and SL17-fragile are similar and are ∼5–6 times weaker. Unsurprisingly, configurations where tidal disruption was not very efficient led to the strongest bounds. We could compare our bounds from the DMonly model with the limits obtained by [
16] for the 3FGL and 2FHL catalogues (the authors also computed a limit for the updated 3FHL catalogue). Their limits were a factor of ∼3 stronger for both catalogues. For the origin of this difference there could be various reasons: for example, we recall that our DMonly model was based on the Aquarius cosmological simulation while the subhalo model used in [
16] is based on Via Lactea II [
10]. Subhaloes in these simulations have a different spatial distribution and the total number of resolved objects within the virial radius of the galactic halo also differs, hence there is no reason to expect the exact same gamma-ray prediction from both models. Also, [
16] consider
-factor integration angles equal to
, while we integrate only up to
. We note that in the case of the 2FHL our limits were cut at 100 GeV masses; below this mass the limits steeply increased because of a loss of sensitivity of the 2FHL catalogue.
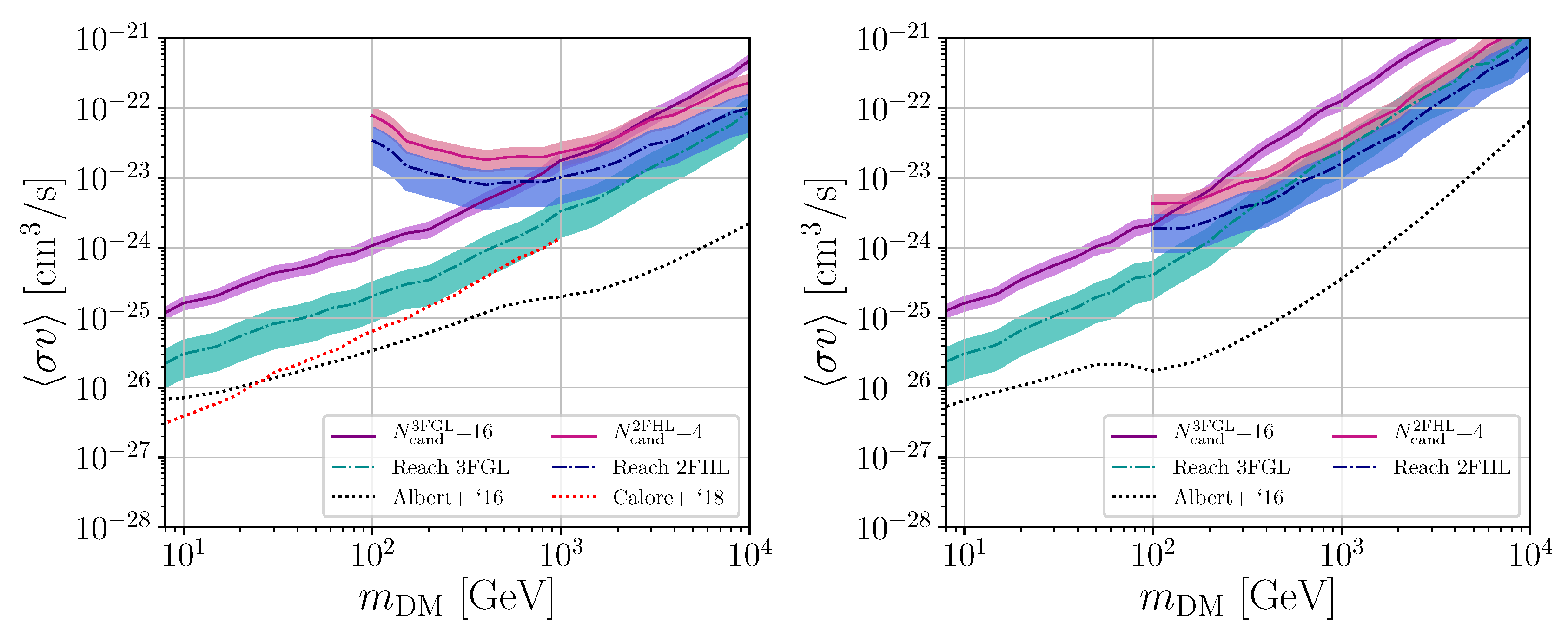
In
Figure 6, we put together the limits from the 3FGL and 2FHL catalogues and compared them to existing limits from gamma-ray observations of dwarf spheroidal galaxies [
9,
38]. We also display the “sensitivity reach” of DM searches towards unassociated gamma-ray sources, namely the limit on the annihilation cross section one gets imposing that no DM subhalo candidate remains among unassociated gamma-ray sources in the 3FGL and 2FHL catalogues. We stress that cutting the integration radius up to 0.1
leads to less strong bounds on the annihilation cross section (about a factor of 2 at all masses). Again, we believe our choice to be truly conservative, against what was done in the past. We can therefore see that the limits on the DM parameter space from the dark subhalo search are not as competitive as the search towards dwarf spheroidal galaxies—at least with present catalogues (and current sensitivity threshold). Indeed, the sensitivity reach for the 3FGL and 2FHL catalogues is always above the current limits from dwarf galaxies.
6. Discussion and Conclusions
In this work we have assessed the detectability of DM subhaloes in Fermi-LAT catalogues taking into account the uncertainties associated to the modelling of the galactic subhalo population. We have investigated four different subhalo models: one based on the Aquarius DMonly simulation [
26], one on the Phat-ELVIS DM simulation which incorporates a disc potential [
28], and two configurations based on an analytical model [
29]. The incorporation of these models in CLUMPY [
34,
35,
36] allowed us to perform 1000 Monte Carlo realisations for each configuration. We then identified among each realisations the detectable subhaloes according to the criterion derived by Calore et al. [
22] for the 3FGL and 2FHL
Fermi point-source catalogues. We obtained the DM annihilation cross-section required to detect at least one subhalo, see
Table 1, to be a few
(
) for the 3FGL (2FHL) catalogue set-up. We found that, irrespective of the subhalo model, the minimal cross section was already ruled out by gamma-ray observation of dwarf galaxies. Using the unassociated point-sources in the Fermi-LAT catalogues, we could derive upper limits on the annihilation cross section as a function of the DM mass. We have done so using the number of subhalo candidates found by Coronado-Blazquez et al. [
16] to get a conservative limit and we have shown the result in
Figure 5. A more stringent bound was obtained if we assumed all the unassociated sources were in fact explained by conventional astrophysical objects. We showed the corresponding bound along with existing limits from dwarf galaxies in
Figure 6. We found that even for the DMonly configuration, which did not include tidal disruption from baryons, the subhalo bound was less stringent than the dwarf galaxy limit.
Comparing the results obtained with the different subhalo configurations, we found that baryonic effects on the subhalo population were significant and lead to DM constraints that were less stringent by a factor of ∼2 to ∼5. This uncertainty came from the unknown resilience of DM subhaloes to tidal disruption.
We note that, compared to previous works, we conservatively adopted a radius of 0.1
for the
-factor integration. This choice was fully consistent with the computation of the Fermi-LAT threshold to subhalo signals as point-like sourcessubhaloes. Unavoidably, this led to limits on the annihilation cross section which were a factor of a few less stringent than what we found in the literature towards dark subhaloes. Nevertheless, we mention that stronger constraints can be set by looking at extended Fermi-LAT-unassociated sources. Spatial extension of a gamma-ray-unassociated source at high-latitude is generally considered a very promising hint for the DM nature of that emission. So far, however, no source has been flagged as extended [
16], and, in general, only a few subhaloes are found to be extended in galaxy formation simulations [
20,
22]. The DM subhalo models studied in the present work instead, depending on the model, predicted from a few up to tens of subhaloes with significant angular extension (>1
). This means that, in order to properly assess their detectability, the sensitivity to the LAT to such a type of extended signals needs to be computed. We leave this work for a future publication, where we will also derive corresponding constraints on the DM parameter space.
In the future, CTA [
6] is expected to boost the search for DM particles with high-energy gamma rays. Sensitivity studies show that we expect at least factor of 10 improvements in the limits from the galactic center analysis [
43,
44]. Also, searches towards dark subhaloes can be competitive, for example, by exploiting the data from a foreseen large-sky survey [
43,
45]. In particular, CTA deep follow-up observations of subhalo candidates or of hints of weak signals in gamma-ray surveys will provide an unprecedented discovery potential for indirect DM signals. Limits from known dwarf satellites with future telescopes will be very promising also because of the revolutionary results promised by the large synoptic survey telescope (LSST) [
46]: tens to hundreds of new faint satellites of the Milky Way are expected to be discovered and their stellar kinematics to be measured with high accuracy, characterising their DM content. This will further accelerate the DM-constraining power of already existing data, such as the ones collected by Fermi-LAT and future CTA observations [
47]. Finally, lower gamma-ray energies (i.e., <100 MeV) represent an almost unexplored territory. Advanced proposals for MeV telescopes exist [
48,
49], and future prospects look very promising, offering new opportunities to discover and/or constrain DM particle models [
50].