Magnetic Fields and Halos in Spiral Galaxies
Abstract
1. Introduction
2. Faraday Rotation and Depolarization Effects
3. Magnetic Field Strength and Star Formation
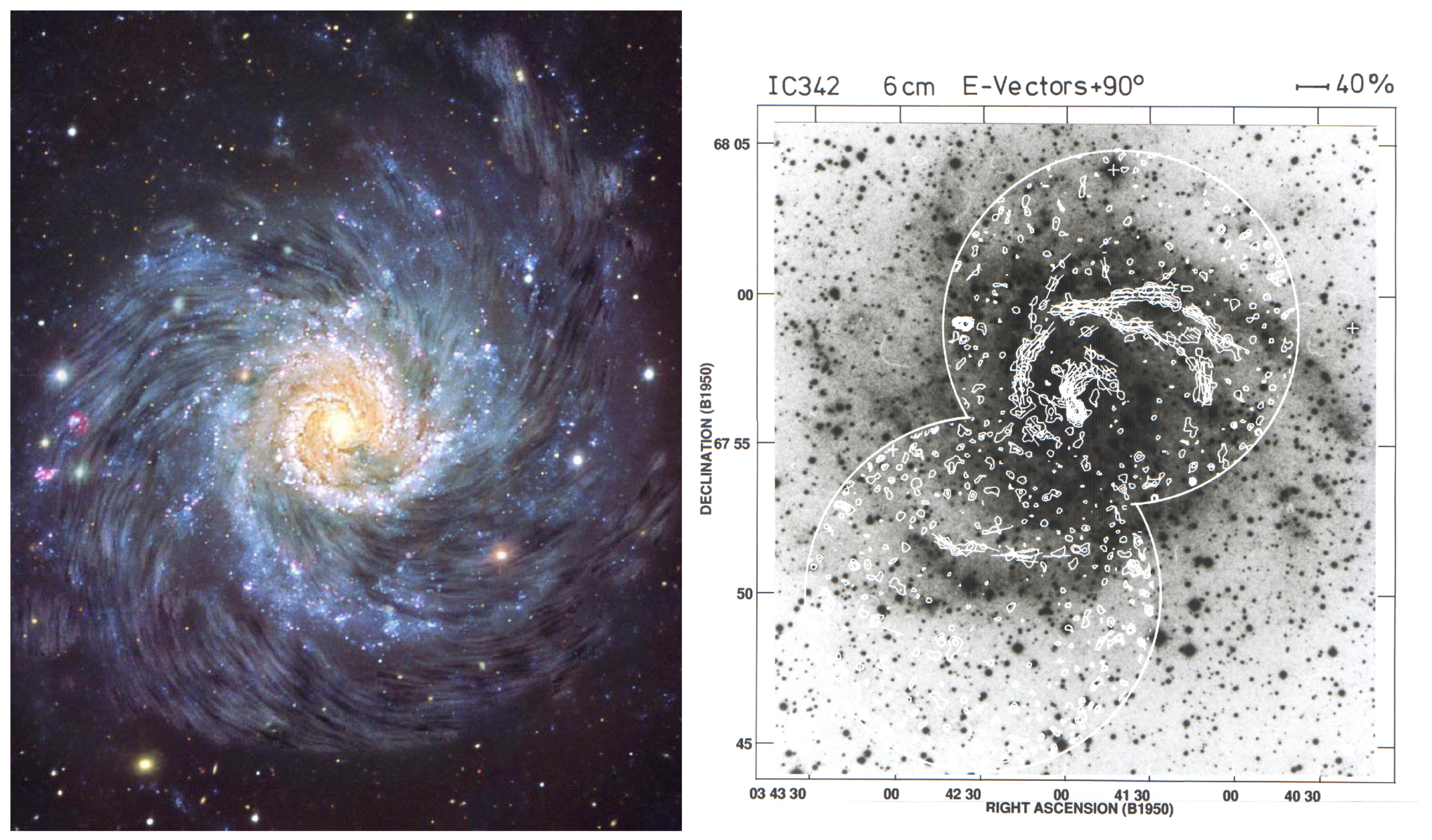
4. Magnetic Field Structure in Spiral Galaxies
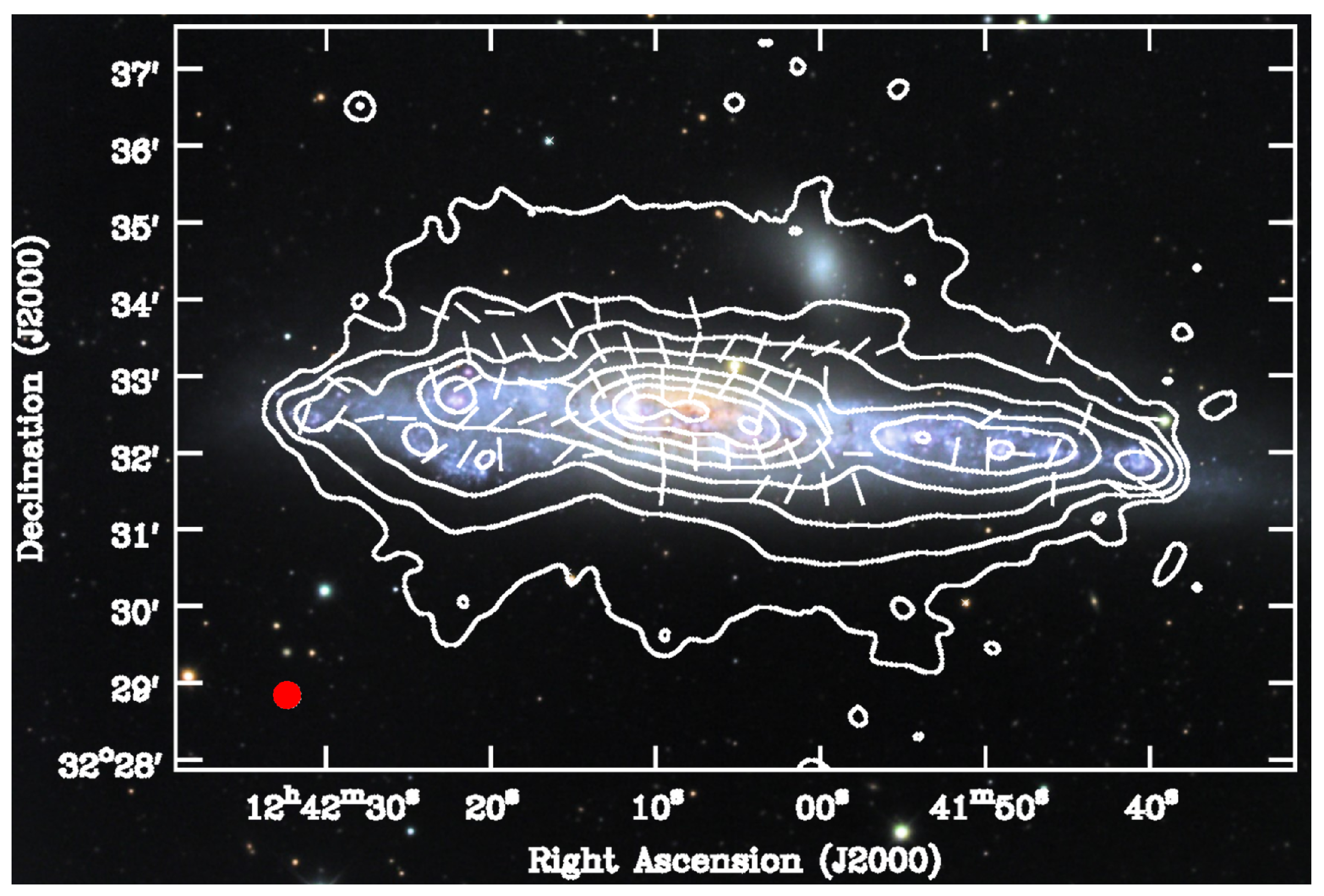
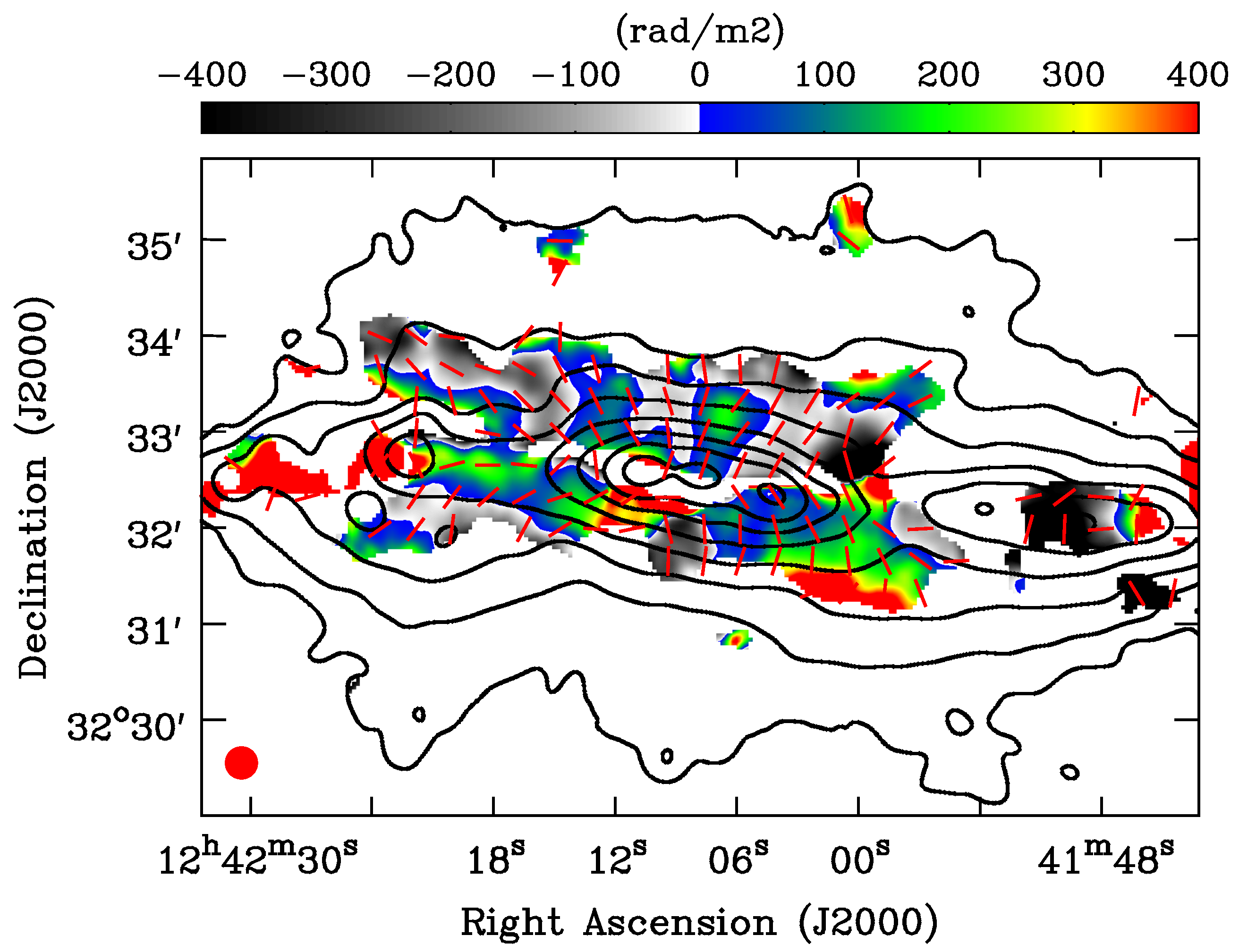
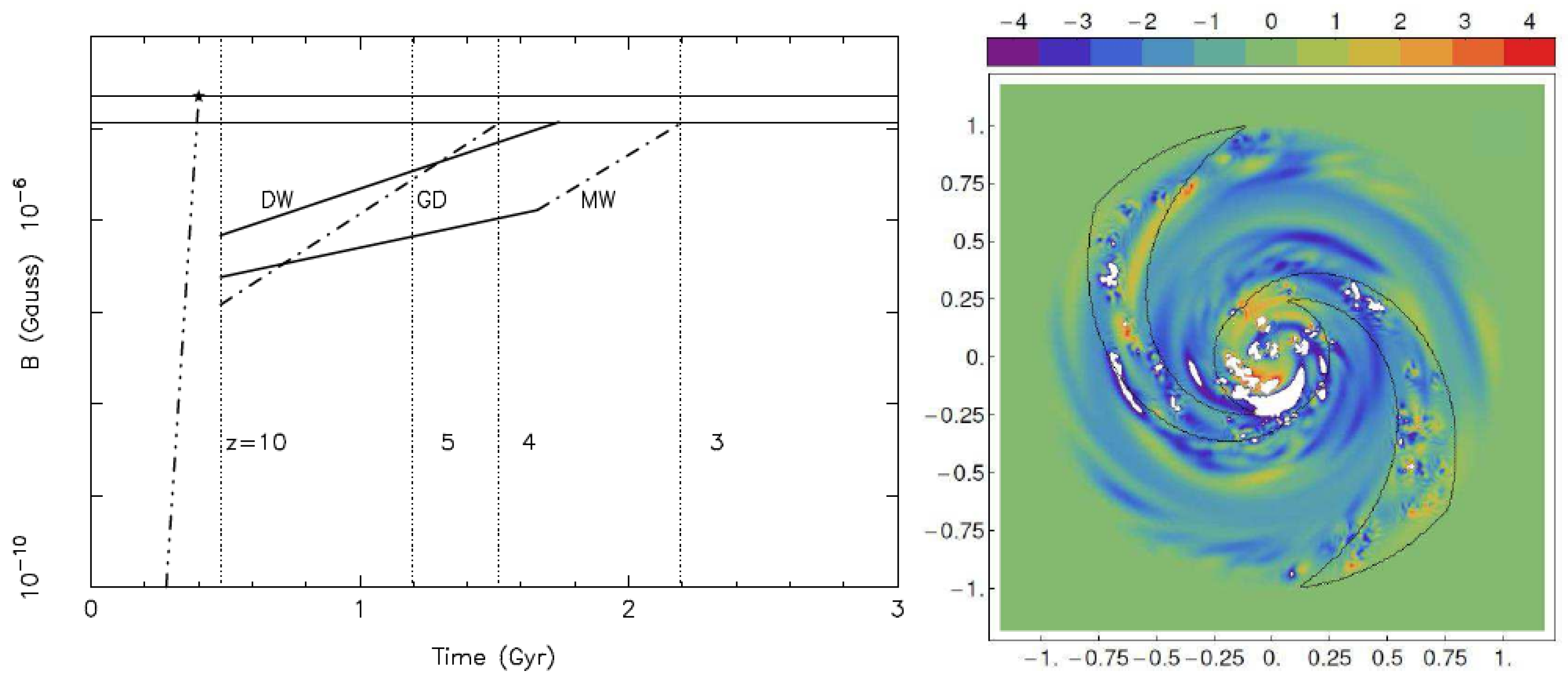
5. Dynamo Action and the Evolution of the Large-Scale Magnetic Field
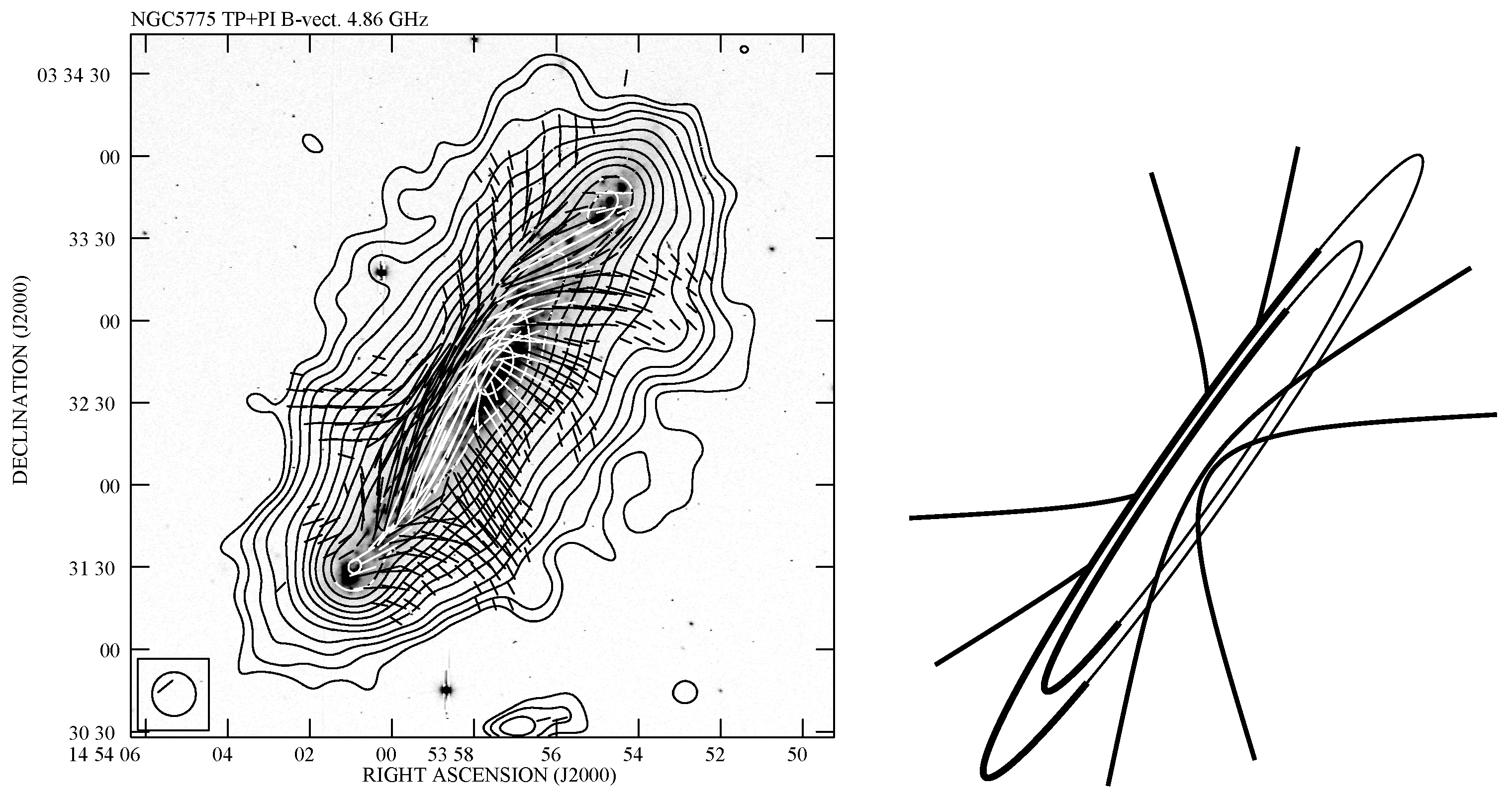
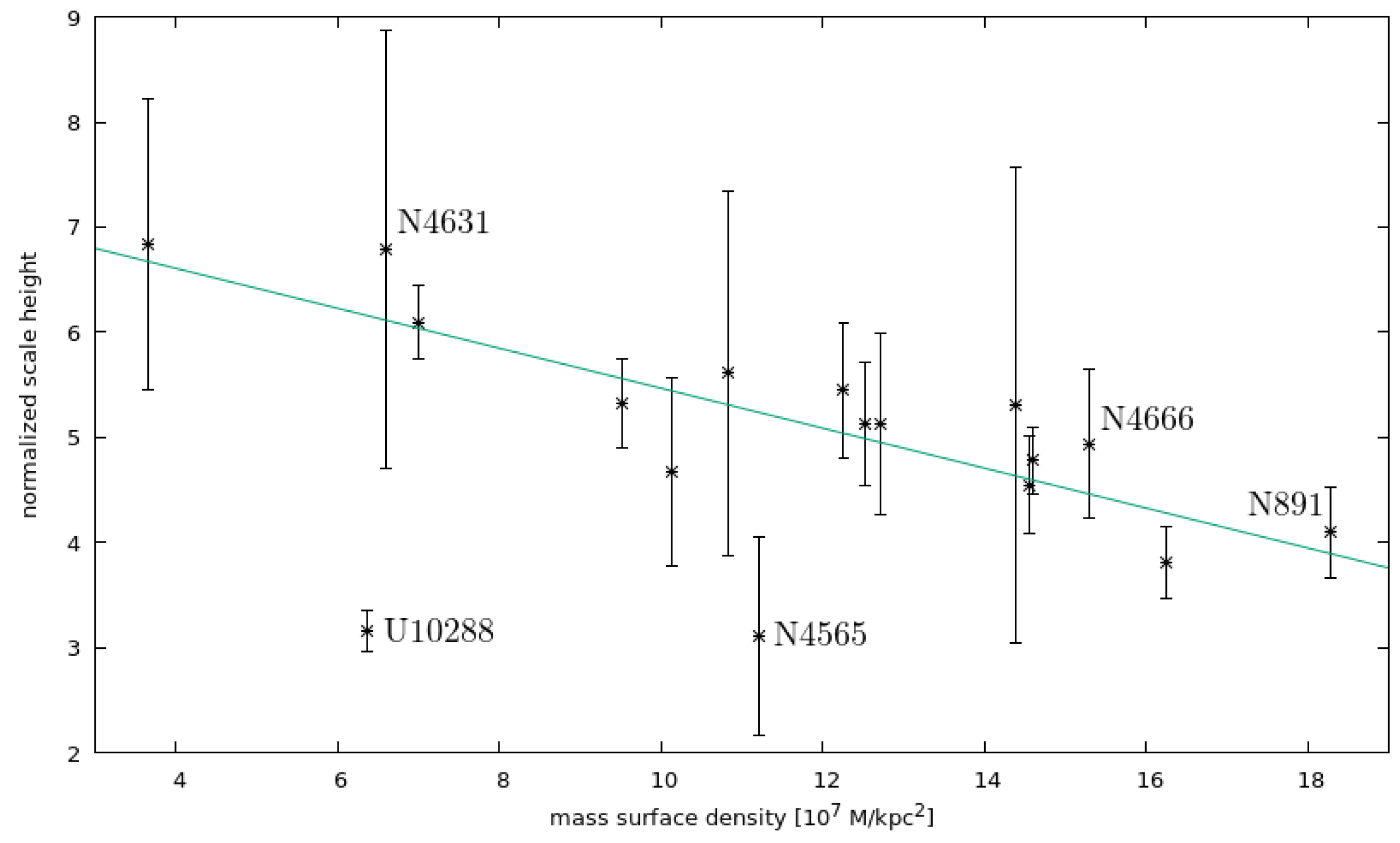
6. Vertical Scale Heights and Galactic Wind
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Avillez, M.A.; Breitschwerdt, D. Global Dynamical Evolution of the ISM in Star Forming Galaxies. I. High Resolution 3D Simulations: Effect of the magnetic Field. Astron. Astrophys. 2019, 436, 585–600. [Google Scholar] [CrossRef]
- Korpi, M.J.; Brandenburg, A.; Shukurov, A.; Tuominen, I.; Nordlund, A. A Supernova-regulated Interstellar Medium: Simulations of the turbulent multiphase Medium. Astrophys. J. 1999, 514, L99–L102. [Google Scholar] [CrossRef]
- Pakmor, R.; Springel, V. Simulations of Magnetic Fields in isolated Disc Galaxies. Mon. Not. R. Astron. Soc. 2013, 432, 176–193. [Google Scholar] [CrossRef]
- Beck, R. Magnetism in the Spiral Galaxy NGC 6946: Magnetic Arms, depolarization Rings, dynamo Modes, and helical Fields. Astron. Astrophys. 2007, 470, 539–556. [Google Scholar] [CrossRef]
- Tabatabaei, F.S.; Krause, M.; Fletcher, A.; Beck, R. High-resolution radio continuum Survey of M 33. III. Magnetic Fields. Astron. Astrophys. 2008, 490, 1005–1017. [Google Scholar] [CrossRef]
- Marinacci, F.; Vogelsberger, M.; Pakmor, V.; Torrey, P.; Springel, V.; Hernquist, L.; Nelson, D.; Weinerger, R.; Pillepich, A.; Naiman, J.; et al. First Results from the IllustrisTNG Simulations: Radio Haloes and magnetic Fields. Mon. Not. R. Astron. Soc. 2018, 480, 5113–5139. [Google Scholar] [CrossRef]
- Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Pakmor, R.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Jenkins, A.; White, S.D.M. The Auriga Project: The Properties and Formation Mechanisms of Disc Galaxies across cosmic Time. Mon. Not. R. Astron. Soc. 2017, 467, 179–207. [Google Scholar] [CrossRef]
- Pakmor, R.; Gómez, F.A.; Grand, R.J.J.; Marinacci, F.; Simpson, C.M.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Guillet, T.; Pfrommer, C.; et al. Magnetic field Formation in the Milky Way like disc Galaxies of the Auriga Project. Mon. Not. R. Astron. Soc. 2017, 469, 3185–3199. [Google Scholar] [CrossRef]
- Burn, B.J. On the Depolarization of discrete Radio Sources by Faraday Dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67–83. [Google Scholar] [CrossRef]
- Sokoloff, D.D.; Bykov, A.A.; Shukurov, A.; Berkhuijsen, E.M.; Beck, R.; Poezd, A.D. Depolarization and Faraday Effects in Galaxies. Mon. Not. R. Astron. Soc. 1998, 299, 189–206. [Google Scholar] [CrossRef]
- Mora, S.C.; Krause, M. Magnetic Field Structure and Halo in NGC 4631. Astron. Astrophys. 2013, 560, A42. [Google Scholar] [CrossRef][Green Version]
- Brentjens, M.A.; de Bruyn, A.G. Faraday Rotation Measure Synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Heald, G.; Braun, R.; Edmonds, R. The Westerbork SINGS Survey. II Polarization, Faraday Rotation, and magnetic Fields. Astron. Astrophys. 2009, 503, 409–435. [Google Scholar] [CrossRef]
- Beck, R.; Krause, M. Revised Equipartition and minimum Energy Formula for magnetic Field Strength Estimates from radio Synchrotron Observations. Astron. Nachr. 2005, 326, 414–427. [Google Scholar] [CrossRef]
- Niklas, S. Eigenschaften von Spiralgalaxien im hochfrequenten Radiokontinuum. Ph.D. Thesis, University Bonn, Bonn, Germany, 1995. [Google Scholar]
- Fletcher, A.; Beck, R.; Shukurov, A.; Berkhuijsen, E.M.; Horrelou, C. Magnetic Fields and spiral Arms in the Galaxy M51. Mon. Not. R. Astron. Soc. 2011, 412, 2396–2416. [Google Scholar] [CrossRef]
- Mulcahy, D.D.; Beck, R.; Heald, G.H. Resolved magnetic Structures in the disk-halo Interface of NGC 628. Astron. Astrophys. 2017, 600, A6. [Google Scholar] [CrossRef]
- Krause, M. High Resolution Observations of the Magnetic Field in IC 342. In The Cosmic Dynamo, Proceedings of IAU Symposium; Cambridge University Press: Cambridge, UK, 1993; pp. 305–310. [Google Scholar]
- Beck, R. Magnetic Fields in the nearby spiral Galaxy IC 342: A multi-frequency radio polarization Study. Astron. Astrophys. 2015, 578, A93. [Google Scholar] [CrossRef]
- Beck, R.; Brandenburg, A.; Moss, D.; Shukurov, A.; Sokoloff, D. Galactic Magnetism: Recent Developments and Perspectives. Annu. Rev. Astron. Astrophys. 1996, 34, 155–206. [Google Scholar] [CrossRef]
- Niklas, S.; Beck, R. A new Approach to the radio-far infrared Correlation for non-calorimeter Galaxies. Astron. Astrophys. 1997, 320, 54–64. [Google Scholar]
- Krause, M. Magnetic Fields and Star Formation in Spiral Galaxies. Rev. Mex. Astron. Astrofis. 2009, 36, 25–29. [Google Scholar]
- Stil, J.M.; Krause, M.; Beck, R.; Taylor, A.R. The integrated Polarization of spiral Galaxy Disks. Astrophys. J. 2009, 693, 1392–1403. [Google Scholar] [CrossRef]
- Chyży, K.T. Magnetic Fields and Gas in the cluster-influenced spiral Galaxy NGC 4254. II. Structures of magnetic Fields. Astron. Astrophys. 2008, 482, 755–769. [Google Scholar] [CrossRef]
- Frick, P.; Stepanov, R.; Beck, R.; Sokoloff, D.; Shukurov, A.; Ehle, M.; Lundgren, A. Magnetic and gaseous spiral Arms in M83. Astron. Astrophys. 2016, 585, A21. [Google Scholar] [CrossRef]
- Berkhuijsen, E.M.; Urbanik, M.; Beck, R.; Han, J.L. Radio Polarization and magnetic Field Structure in M 101. Astron. Astrophys. 2016, 588, A114. [Google Scholar] [CrossRef][Green Version]
- Ruzmaikin, A.A.; Shukurov, A.M.; Sokoloff, D.D. Magnetic Fields of Galaxies; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Seigar, M.S.; Kennefick, D.; Kennefick, J.; Lacy, C.H.S. Discovery of a Relationship between Spiral Arm Morphology and Supermassive Black Hole Mass in Disk Galaxies. Astrophys. J. 2008, 678, L93–L96. [Google Scholar] [CrossRef]
- Soida, M.; Krause, M.; Dettmar, R.-J.; Urbanik, M. The large scale magnetic Field Structure of the Spiral Galaxy NGC 5775. Astron. Astrophys. 2011, 531, A127. [Google Scholar] [CrossRef]
- Mora-Partiarroyo, S.C.; Krause, M.; Basu, A.; Beck, R.; Wiegert, T.; Irwin, J.; Henriksen, R.; Stein, Y.; Vargas, C.J.; Heesen, V.; et al. CHANG-ES XIV: Cosmic-Ray Propagation and Magnetic Field Strengths in the Radio Halo of NGC 4631. Astron. Astrophys. 2019, submitted. [Google Scholar]
- Irwin, J.; Beck, R.; Benjamin, R.A.; Dettmar, R.-J.; English, J.; Heald, G.; Henriksen, R.N.; Johnson, M.; Krause, M.; Li, J.-T.; et al. Continuum Halos in Nearby Galaxies: An EVLA Survey (CHANG-ES). I. Introduction to the Survey. Astron. J. 2012, 144, 43. [Google Scholar] [CrossRef]
- Irwin, J.; Damas-Segovia, A.; Krause, M.; Miskolczi, A.; Li, J.-T.; Stein, Y.; English, J.; Henriksen, R.; Beck, R.; Wiegert, T.; et al. CHANG-ES: XVIII—The CHANG-ES survey and relected results. Galaxies 2019, 7, 42. [Google Scholar] [CrossRef]
- Krause, M.; Mora-Partiarroyo, S.C.; Schmidt, P. Magnetic Fields and CR Propagation in the Halos of Spiral Galaxies. In Proceedings of the Focus Meeting 8 at the XXXth IAU General Assembly, Vienna, Austria, 29–31 August 2018; pp. 127–128. [Google Scholar]
- Mora-Partiarroyo, S.C.; Krause, M.; Basu, A.; Beck, R.; English, J.; Wiegert, T.; Irwin, J.; Henriksen, R.; Stein, Y.; Vargas, C.J.; et al. CHANG-ES XV: Large-Scale Magnetic Field Reversal in the Halo of NGC 4631. Astron. Astrophys. 2019, submitted. [Google Scholar]
- Woodfinden, A.; Henriksen, R.N.; Irwin, J.; Mora-Partiarroyo, S.C. Evolving Galactic Dynamos and Fits to the Reversing Magnetic Field in the Halo of NGC 4631. Mon. Not. R. Astron. Soc. 2019, submitted. [Google Scholar]
- Moss, D.; Sokoloff, D. Magnetic Fields around galactic Discs. Galaxies 2019, 7, 36. [Google Scholar] [CrossRef]
- Seta, A.; Beck, R. Revisiting the Equipatition Assumption in star-forming Galaxies. Galaxies 2019, 7, 45. [Google Scholar] [CrossRef]
- Heesen, V.; Beck, R.; Krause, M.; Dettmar, R.-J. Cosmic Rays and the magnetic Field in the nearby Starburst Galaxy NGC 253. I. The Distribution and Transport of Cosmic Rays. Astron. Astrophys. 2009, 494, 563–577. [Google Scholar] [CrossRef]
- Schmidt, P.; Krause, M.; Heesen, V.; Basu, A.; Beck, R.; Wiegert, T.; Irwin, J.A.; Heald, J.; Rand, R.J.; Li, J.-T.; et al. CHANG-ES XVI: An in-depth View of the Cosmic-Ray Transport in the edge-on Spiral Galaxies NGC 891 and NGC 4565. Astron. Astrophys. 2019. submitted. [Google Scholar]
- Stein, Y.; Dettmar, R.-J.; Irwin, J.; Beck, R.; Weżgowiec, M.; Miskolczi, A.; Krause, M.; Heesen, V.; Wiegert, T.; Heald, G.; et al. CHANG-ES XIII: Transport Processes and the magnetic Fields of NGC 4666—Indication of a reversing Disk magnetic Field. Astron. Astrophys. 2019, 623, A33. [Google Scholar] [CrossRef]
- Stein, Y.; Dettmar, R.-J.; Weżgowiec; Irwin, J.; Beck, R.; Wiegert, T.; Krause, M.; Li, J.-T.; Heesen, V.; Miskolczi, A.; et al. CHANG-ES XIX: The Galaxy NGC 4013—A Diffusion-dominated Radio Halo with Plane-parallel Disk and Vertical Halo Magnetic Fields. Astron. Astrophys. 2019. submitted. [Google Scholar]
- Beck, R.; Poezd, A.D.; Sukurov, A.; Sokoloff, D.D. Dynamos in evolving Galaxies. Astron. Astrophys. 1994, 289, 94–100. [Google Scholar]
- Chamandy, L.; Taylor, A.R. Non-linear galactic Dynamos and the magnetic pitch Angle. Astrophys. J. 2015, 808, 28. [Google Scholar] [CrossRef]
- Fletcher, A. Magnetic Fields in Nearby Galaxies. Dynamoc Interstellar Medium Celebr. Can. Glactic Plane Surv. 2010, 438, 197–210. [Google Scholar]
- Beck, R. Magnetic Fields in spiral Galaxies. Astron. Astrophys. Rev. 2016, 24, 4. [Google Scholar] [CrossRef]
- Arshakian, T.G.; Beck, R.; Krause, M.; Sokoloff, D. Evolution of magnetic Fields in Galaxies and future observational Tests with the Square Kilometre Array. Astron. Astrophys. 2009, 494, 21–32. [Google Scholar] [CrossRef]
- Rodrigues, L.F.S.; Chamandy, L.; Shukurov, A.; Baugh, C.M.; Taylor, A.R. Evolution of galactic magnetic Fields. Mon. Not. R. Astron. Soc. 2019, 483, 2424–2440. [Google Scholar] [CrossRef]
- Moss, D.; Beck, R.; Sokoloff, D.; Stepanov, R.; Krause, M.; Arshakian, T.G. The Relation between magnetic and material Arms in Models for Spiral Galaxies. Astron. Astrophys. 2013, 556, A147. [Google Scholar] [CrossRef]
- Arshakian, T.G.; Stepanov, R.; Beck, R.; Krause, M.; Sokoloff, D. Modeling the total and polarized Emission in evolving Galaxies: “Spotty” magnetic Structures. Astron. Nachr. 2011, 332, 524–536. [Google Scholar] [CrossRef]
- Moss, D.; Stepanov, R.; Arshakian, T.; Beck, R.; Krause, M.; Sokoloff, D. Multiscale magnetic Fields in Spiral Galaxies: Evolution and Reversals. Astron. Astrophys. 2012, 537, A68. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Subramanian, K. Magnetic spiral Arms and galactic Outflows. Mon. Not. R. Astron. Soc. 2015, 446, L6–L10. [Google Scholar] [CrossRef]
- Heesen, V.; Krause, M.; Beck, R.; Adebahr, B.; Bomans, D.J.; Carretti, E.; Dumke, M.; Heald, G.; Irwin, J.; Koribalski, B.; et al. Radio Haloes in nearby Galaxies modelled with 1D Cosmic Ray Transport using SPINNAKER. Mon. Not. R. Astron. Soc. 2018, 476, 158–183. [Google Scholar] [CrossRef]
- Heesen, V.; Dettmar, R.-J.; Krause, M.; Beck, R. Advective and diffusive Cosmic Ray Transport in galactic Haloes. Mon. Not. R. Astron. Soc. 2016, 458, 332–353. [Google Scholar] [CrossRef]
- Dumke, M.; Krause, M. Radio and Polarization Properties in the Disk and Halo of edge-on Spirals. In IAU Colloq. 166: The Lokal Bubble and Beyond; Lecture Notes in Physics; Springer: Berlin, Germany, 1998; pp. 555–558. [Google Scholar]
- Krause, M.; Irwin, J.; Wiegert, T.; Miskoczi, A.; Damas-Segovia, A.; Beck, R.; Li, J.-T.; Heald, G.; Müller, P.; Stein, Y.; et al. CHANG-ES. IX. Radio Scale Heights and Scale Lengths of a consistent Sample of 13 Spiral Galaxies seen edge-on and their Correlations. Astron. Astrophys. 2018, 611, A72. [Google Scholar] [CrossRef]
- Dumke, M.; Krause, M.; Wielebinski, R.; Klein, U. Polarized Radio Emission at 2.8cm from a selected Sample of edge-on Galaxies. Astron. Astrophys. 1995, 302, 691–703. [Google Scholar]
- Müller, P.; Krause, M.; Beck, R. The NOD3 Software Package: A graphical user Interface-supported Reduction Package for Single-Dish Radio Continuum and Polarisation Observations. Astron. Astrophys. 2017, 606, A41. [Google Scholar] [CrossRef]
- Vargas, C.J.; Walterbos, R.A.M.; Rand, R.J.; Stil, J.M.; Krause, M.; Li, J.-T.; Irwin, J. CHANG-ES XVII: Hα Imaging of Nearby Edge-on Galaxies, New SFRs, and an Extreme Star Formation Region—Data Release 2. Astrophys. J. 2019, submitted. [Google Scholar]
- Brandenburg, A.; Donner, K.J.; Moss, D.; Shukurov, A.; Sokoloff, D.; Tuaminen, I. Vertical magnetic Fields above the Discs of Spiral Galaxies. Astron. Astrophys. 1993, 271, 36–50. [Google Scholar]
- Moss, D.; Sokoloff, D.; Beck, R.; Krause, M. Galactic Winds and the Symmetry Properties of galactic magnetic Fields. Astron. Astrophys. 2010, 512, A61. [Google Scholar] [CrossRef]
- Gressel, O.; Elstner, D.; Ziegler, U.; Rüdiger, G. Direct Simulations of a Supernova-driven galactic Dynamo. Astron. Astrophys. 2008, 486, L35–L38. [Google Scholar] [CrossRef]
- Hanasz, M.; Otmianowska-Mazur, K.; Kowal; Lesch, H. Cosmic-Ray-driven Dynamo in galactic Disks. A Parameter Study. Astron. Astrophys. 2009, 498, 335–346. [Google Scholar] [CrossRef]
- Hanasz, M.; Wóltánski, D.; Kowalik, K. Global galactic Dynamo driven by Cosmic Rays and exploding magnetized Stars. Astrophys. J. 2009, 706, L155–L159. [Google Scholar] [CrossRef]
- Sur, S.; Shukurov, A.; Subramanian, K. Galactic Dynamos supported by magnetic Helicity Fluxes. Mon. Not. R. Astron. Soc. 2007, 377, 874–882. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krause, M. Magnetic Fields and Halos in Spiral Galaxies. Galaxies 2019, 7, 54. https://doi.org/10.3390/galaxies7020054
Krause M. Magnetic Fields and Halos in Spiral Galaxies. Galaxies. 2019; 7(2):54. https://doi.org/10.3390/galaxies7020054
Chicago/Turabian StyleKrause, Marita. 2019. "Magnetic Fields and Halos in Spiral Galaxies" Galaxies 7, no. 2: 54. https://doi.org/10.3390/galaxies7020054
APA StyleKrause, M. (2019). Magnetic Fields and Halos in Spiral Galaxies. Galaxies, 7(2), 54. https://doi.org/10.3390/galaxies7020054



