Faraday Rotation of Extended Emission as a Probe of the Large-Scale Galactic Magnetic Field
Abstract
1. Introduction
2. The Data
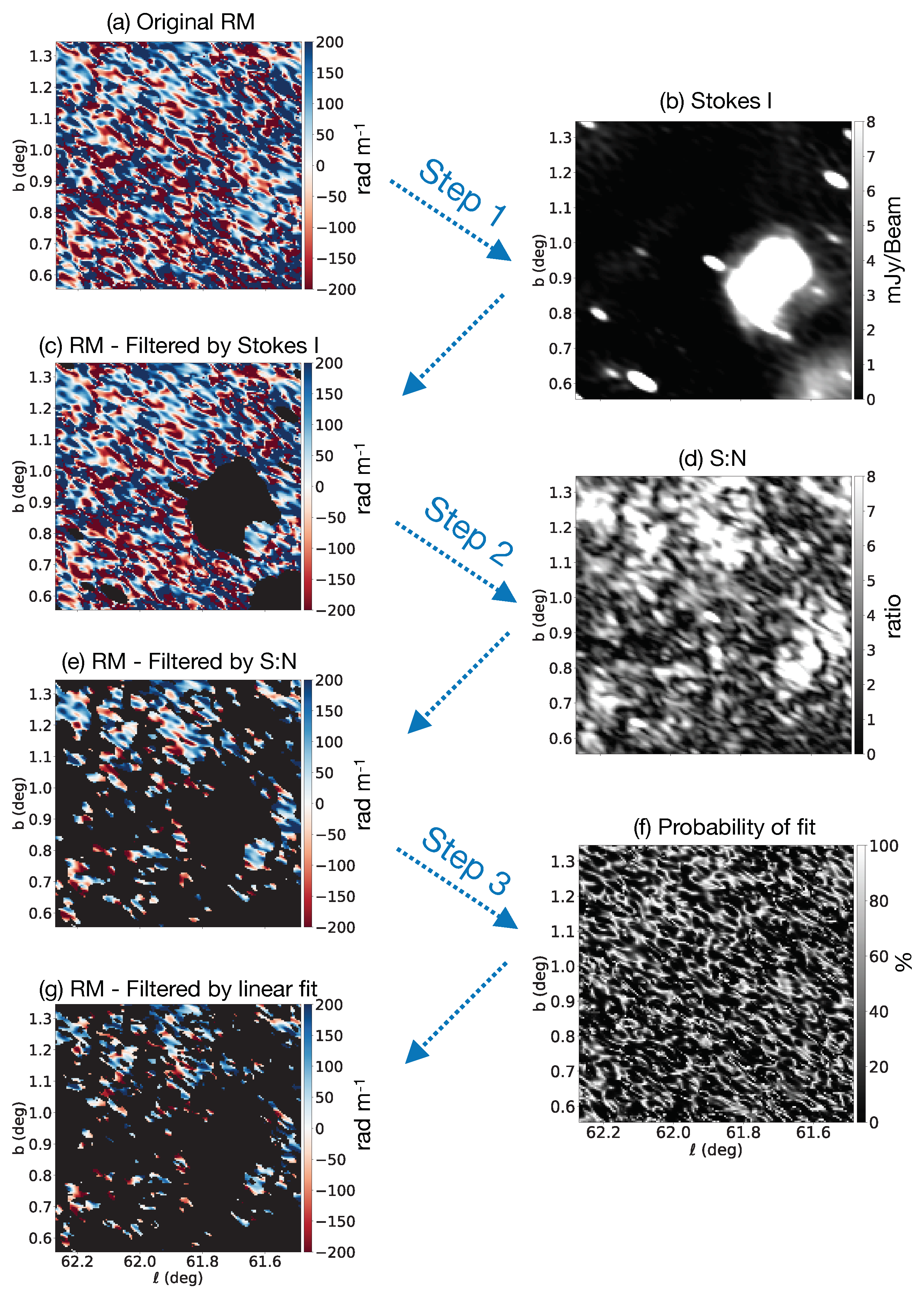
Data Processing
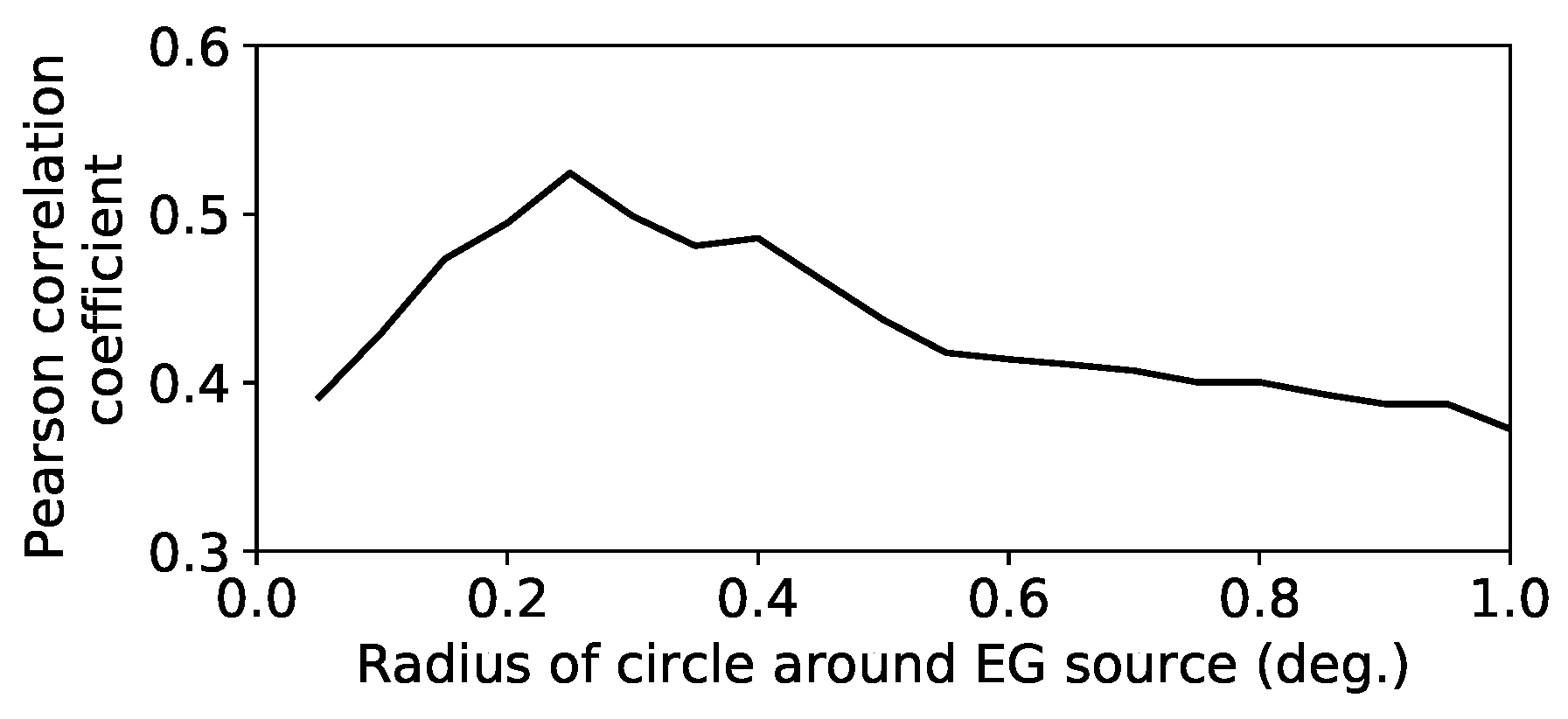
3. Analysis
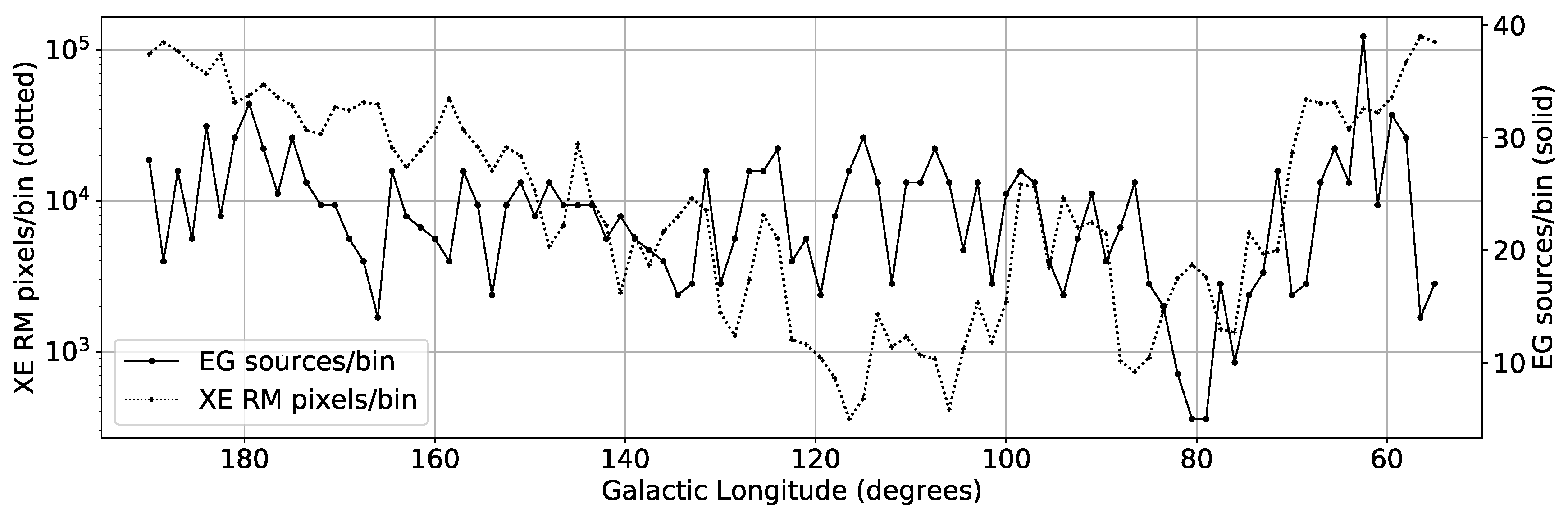
- The intensity of synchrotron emission depends on the component of the magnetic field perpendicular to the LOS, as well as the relativistic electron density in the emitting region. The intensity peaks close to the anticentre, in the Fan region (near ), and falls smoothly toward lower longitudes.
- The synthesized beam of the telescope varies with declination, with a smaller beam having less signal for the same polarised brightness temperature. The beam is smallest at longitude about 120°, corresponding to the highest declination, where there are fewer pixels in the beam to survive the various filters that we have applied.
- The shortest baseline used by the Synthesis Telescope is 12.9 m. At low declinations foreshortening of the baseline extends the sensitivity of the telescope to larger angular structures. Conversely, at high declinations the sensitivity to extended structure is somewhat reduced. The highest declinations correspond to roughly . Although it would be possible to make the sensitivity to extended structures uniform across the dataset by tapering the visibilities of long baselines, doing so would not yield significant gains, since it would correspond to an overall loss of high quality data.
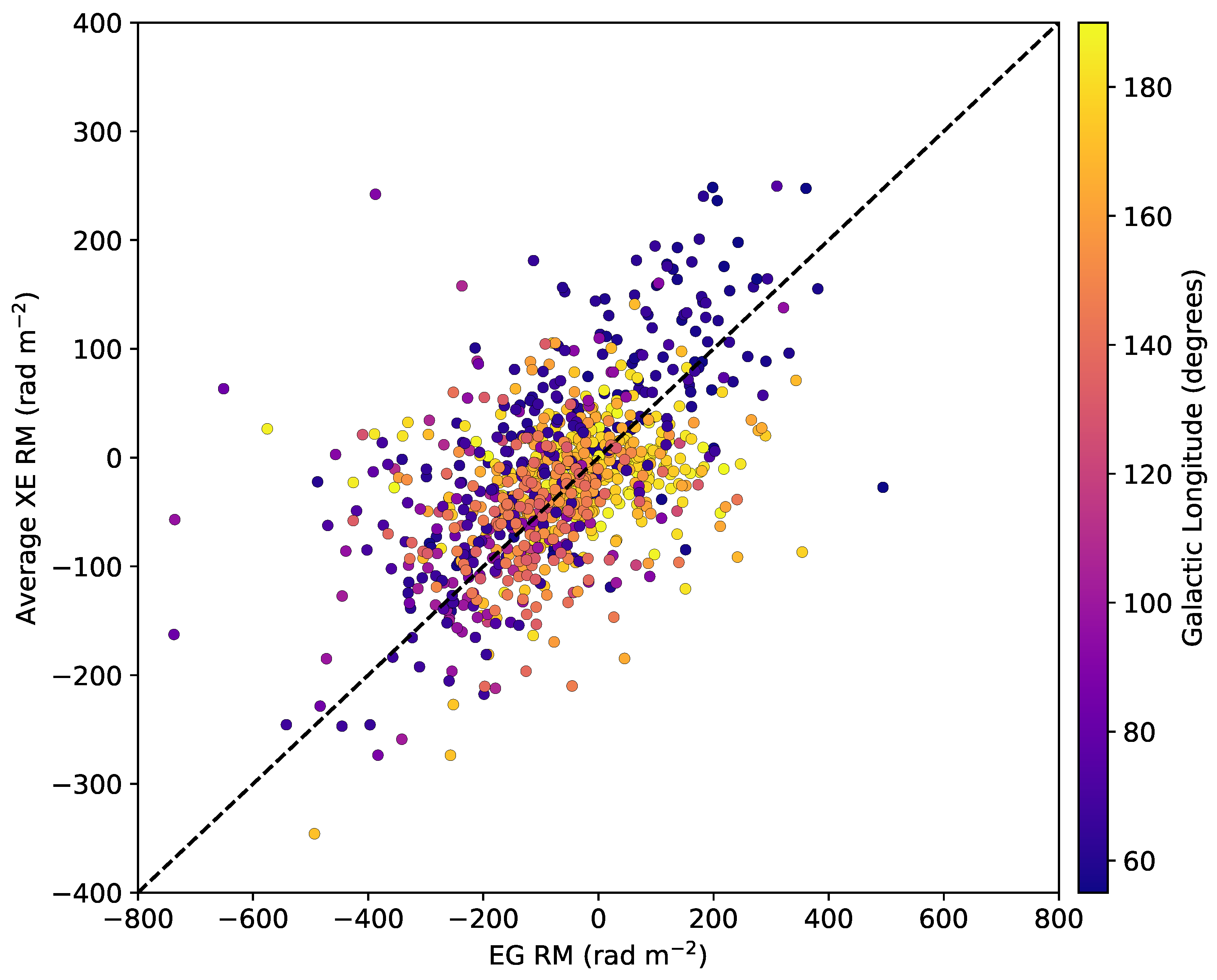
4. Discussion
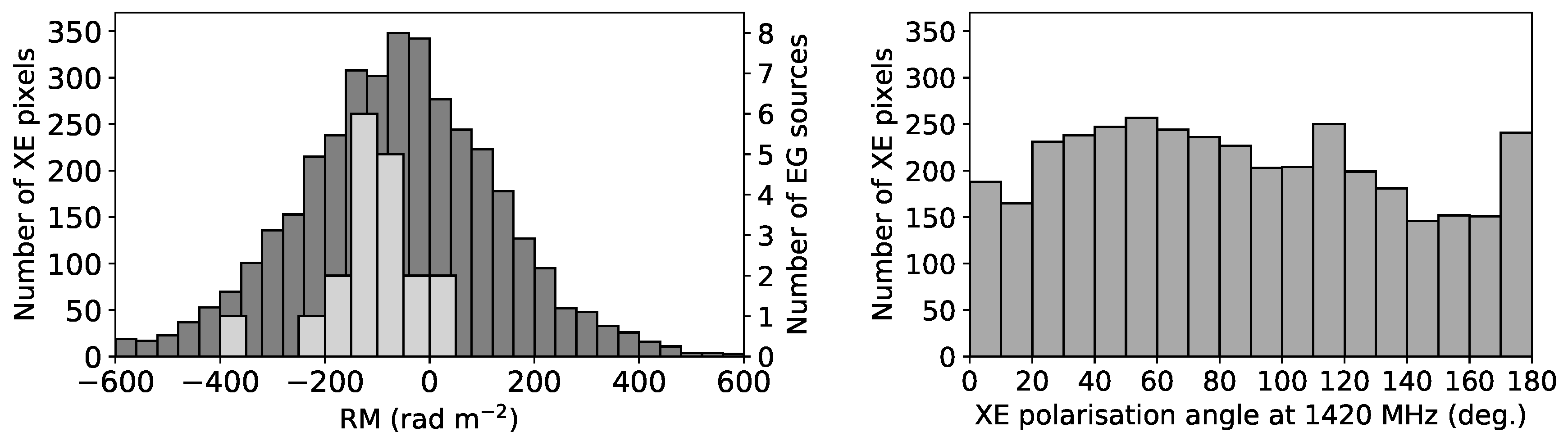
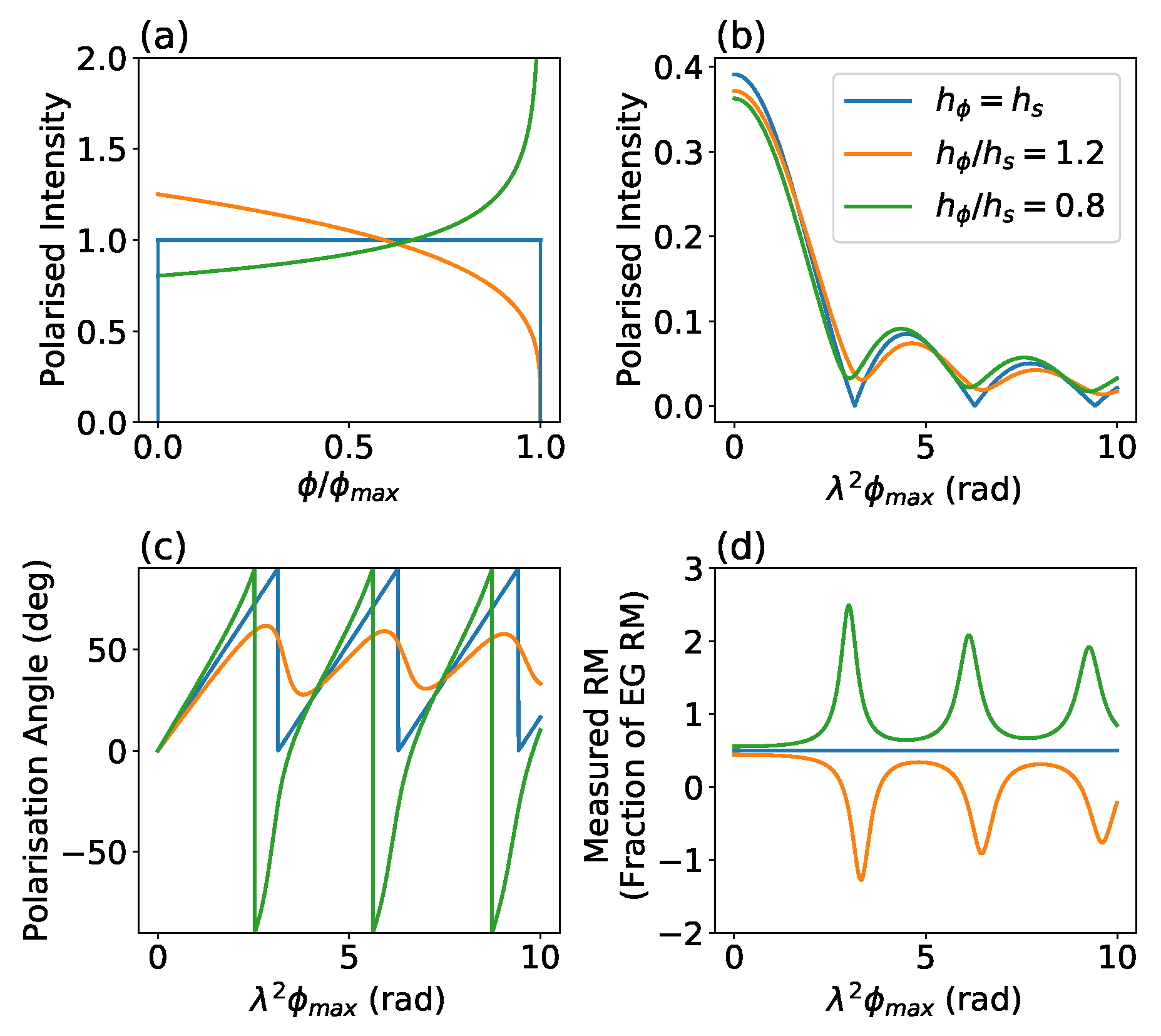
4.1. Polarisation Angles in the XE Data
4.2. ISM Configurations
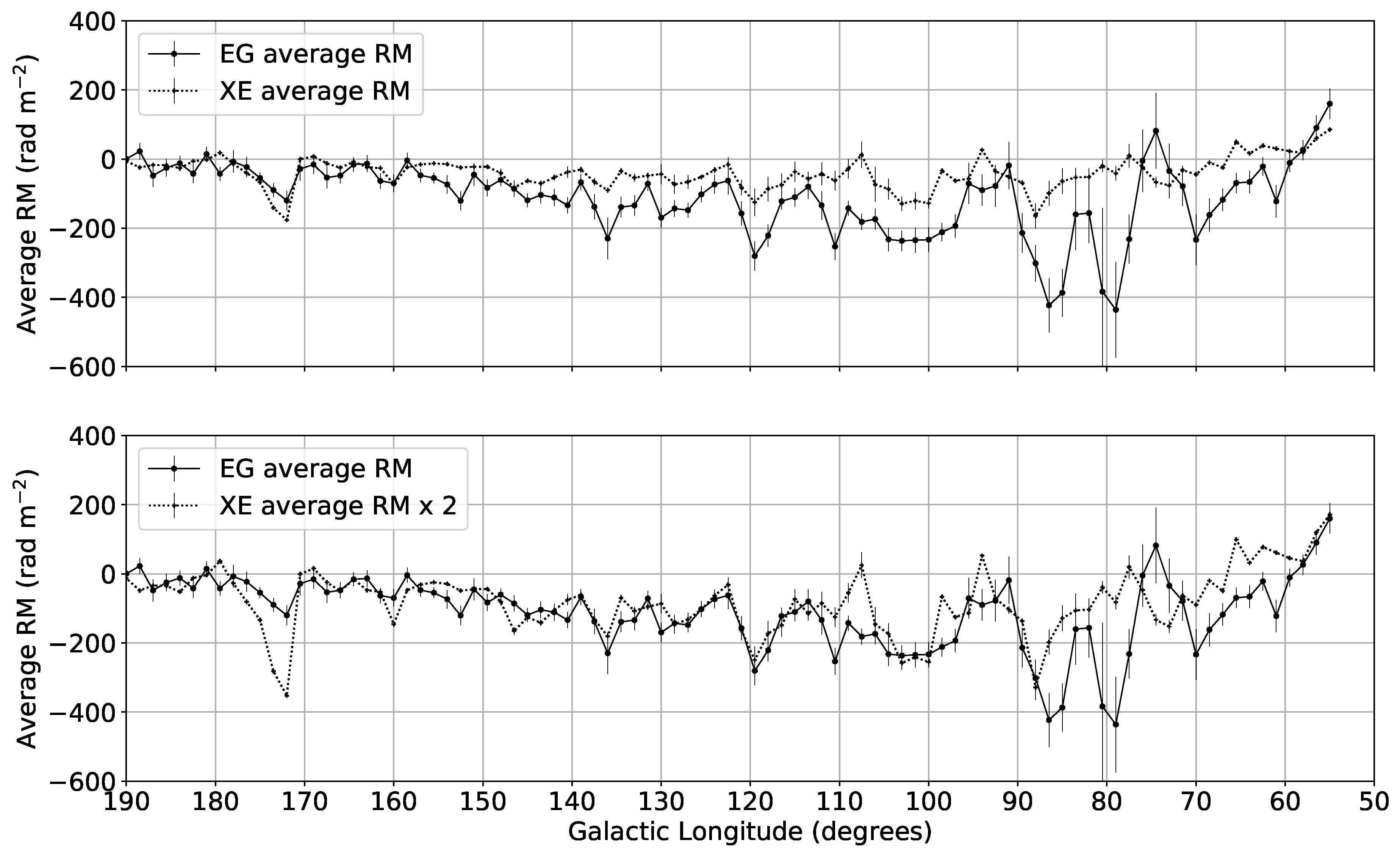
4.3. Regions of Disparity between the XE and EG RMs
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Alfvén, H. Cosmic radiation as an intragalactic phenomenon. Ark. Mat. Astron. Fys. 1937, 27A, 1–5. [Google Scholar]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Hiltner, W.A. Polarization of Radiation from Distant Stars by the Interstellar Medium. Nature 1949, 163, 283. [Google Scholar] [CrossRef]
- Hall, J.S. Observations of the Polarized Light from Stars. Science 1949, 109, 166–167. [Google Scholar] [CrossRef]
- van Loo, S.; Hartquist, T.W.; Falle, S.A.E.G. Magnetic fields and star formation. Astron. Geophys. 2012, 53, 5–31. [Google Scholar] [CrossRef][Green Version]
- Boulares, A.; Cox, D.P. Galactic hydrostatic equilibrium with magnetic tension and cosmic-ray diffusion. Astrophys. J. 1990, 365, 544–558. [Google Scholar] [CrossRef]
- Kim, E.-J.; Olinto, A.V.; Rosner, R. Generation of Density Perturbations by Primordial Magnetic Fields. Astrophys. J. 1996, 468, 28–50. [Google Scholar] [CrossRef]
- Simard-Normandin, M.; Kronberg, P.P. New large-scale magnetic features of the Milky Way. Nature 1979, 279, 115–118. [Google Scholar] [CrossRef]
- Rand, R.J.; Lyne, A.G. New Rotation Measures of Distant Pulsars in the Inner Galaxy and Magnetic Field Reversals. Mon. Not. R. Astron. Soc. 1994, 268, 497–505. [Google Scholar] [CrossRef]
- Brown, J.C.; Taylor, A.R.; Jackel, B.J. Rotation Measures of Compact Sources in the Canadian Galactic Plane Survey. Astrophys. J. Suppl. Ser. 2003, 145, 213–223. [Google Scholar] [CrossRef]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. Astrophys. J. 2009, 702, 1230–1236. [Google Scholar] [CrossRef]
- Jaffe, T.R.; Leahy, J.P.; Banday, A.J.; Leach, S.M.; Lowe, S.R.; Wilkinson, A. Modelling the Galactic magnetic field on the plane in two dimensions. Mon. Not. R. Astron. Soc. 2010, 401, 1013–1028. [Google Scholar] [CrossRef]
- Van Eck, C.L.; Brown, J.C.; Stil, J.M.; Rae, K.; Mao, S.A.; Gaensler, B.M.; Shukurov, A.; Taylor, A.R.; Haverkorn, M.; Kronberg, P.P.; et al. Modeling the Magnetic Field in the Galactic Disk Using New Rotation Measure Observations from the Very Large Array. Astrophys. J. 2011, 728, 97. [Google Scholar] [CrossRef]
- Jansson, R.; Farrar, G.R. A New Model of the Galactic Magnetic Field. Astrophys. J. 2012, 757, 14. [Google Scholar] [CrossRef]
- Gressel, O.; Elstner, D.; Ziegler, U. Towards a hybrid dynamo model for the Milky Way. Astron. Astrophys. 2013, 560, A93. [Google Scholar] [CrossRef]
- Han, J.L.; Manchester, R.N.; van Straten, W.; Demorest, P. Pulsar Rotation Measures and Large-scale Magnetic Field Reversals in the Galactic Disk. Astrophys. J. Suppl. Ser. 2018, 234, 11. [Google Scholar] [CrossRef]
- Thomson, R.C.; Nelson, A.H. The interpretation of pulsar rotation measures and the magnetic field of the galaxy. Mon. Not. R. Astron. Soc. 1980, 191, 863–870. [Google Scholar] [CrossRef]
- Iacobelli, M.; Haverkorn, M.; Katgert, P. Rotation measure synthesis at the 2 m wavelength of the FAN region: Unveiling screens and bubbles. Astron. Astrophys. 2013, 549, A56. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67–83. [Google Scholar] [CrossRef]
- Sokoloff, D.D.; Bykov, A.A.; Shukurov, A.; Berkhuijsen, E.M.; Beck, R.; Poezd, A.D. Depolarization and Faraday effects in galaxies. Mon. Not. R. Astron. Soc. 1998, 299, 189–206. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday rotation measure synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Ordog, A.; Brown, J.C.; Kothes, R.; Landecker, T.L. Three-dimensional structure of the magnetic field in the disk of the Milky Way. Astron. Astrophys. 2017, 603, A15. [Google Scholar] [CrossRef]
- Landecker, T.L.; Reich, W.; Reid, R.I.; Reich, P.; Wolleben, M.; Kothes, R.; Uyanıker, B.; Gray, A.D.; Del Rizzo, D.; Fürst, E.; et al. A Survey of the polarized emission from the Galactic plane at 1420 MHz with arcminute angular resolution. Astron. Astrophys. 2010, 520, A80. [Google Scholar] [CrossRef]
- Brown, J.C. The Magnetic Field in the Outer Galaxy. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2002. [Google Scholar]
- Oppermann, N.; Junklewitz, H.; Robbers, G.; Bell, M.R.; Enßlin, T.A.; Bonafede, A.; Braun, R.; Brown, J.C.; Clarke, T.E.; Feain, I.J.; et al. An improved map of the Galactic Faraday sky. Astron. Astrophys. 2012, 542, A93. [Google Scholar] [CrossRef]
- Uyaniker, B.; Landecker, T.L.; Gray, A.D.; Kothes, R. Radio Polarization from the Galactic Plane in Cygnus. Astrophys. J. 2003, 585, 785–800. [Google Scholar] [CrossRef]
- Sun, X.H.; Reich, W.; Waelkens, A.; Enßlin, T.A. Radio observational constraints on Galactic 3D-emission models. Astron. Astrophys. 2008, 477, 573–592. [Google Scholar] [CrossRef]
- Cordes, J.M.; Lazio, T.J.W. NE2001.I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations. arXiv, 2002; arXiv:astro-ph/0207156. [Google Scholar]
- Kang, J.-H.; Koo, B.-C.; Salter, C. An Old Supernova Remnant within an H II Complex at l ≈173∘: FVW 172.8+1.5. Astron. J. 2012, 143, 75. [Google Scholar] [CrossRef]
- Gao, X.Y.; Reich, W.; Han, J.L.; Sun, X.H.; Wielebinski, R.; Shi, W.B.; Xiao, L.; Reich, P.; Fürst, E.; Chen, M.Z.; et al. A Sino-German λ6 cm polarization survey of the Galactic plane. II. The region from 129° to 230° longitude. Astron. Astrophys. 2010, 515, A64. [Google Scholar] [CrossRef][Green Version]
- Gottschalk, M.; Kothes, R.; Matthews, H.E.; Landecker, T.L.; Dent, W.R.F. The JCMT 12CO(3-2) survey of the Cygnus X region. I. A pathfinder. Astron. Astrophys. 2012, 541, A79. [Google Scholar] [CrossRef]
| 1. | The final filtered XE RM map will be available at the CDS via http://vizier.u-strasbg.fr/viz-bin/VizieR. |
| 2. | The pixels are not independent, because the synthesized beam of the telescope consists of between 9 and 24 pixels in the image, depending on the declination. However, even with this taken into account, we still gain lines of sight in the XE that are missing in the EG source list. |
| 3. | We use the tilde to denote a complex phasor encoding both the polarised intensity and polarisation angle. |

| Overall coverage | |
| Continuum bandwidth | 30 MHz in four bands of 7.5 MHz each |
| Polarisation products | Stokes I, Q, and U |
| Centre frequencies | 1407.2, 1414.1, 1427.7, and 1434.6 MHz |
| Angular resolution | 58″ × 58″ cosec |
| Sensitivity, I | 200 to 400 μJy/beam rms |
| Sensitivity, Q and U | 180 to 260 μJy/beam rms |
| Typical noise in mosaicked images | mK |
| * Sources of single-antenna data | Effelsberg 100-m Telescope and DRAO 26-m Telescope |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ordog, A.; Booth, R.A.; Van Eck, C.L.; Brown, J.-A.C.; Landecker, T.L. Faraday Rotation of Extended Emission as a Probe of the Large-Scale Galactic Magnetic Field. Galaxies 2019, 7, 43. https://doi.org/10.3390/galaxies7020043
Ordog A, Booth RA, Van Eck CL, Brown J-AC, Landecker TL. Faraday Rotation of Extended Emission as a Probe of the Large-Scale Galactic Magnetic Field. Galaxies. 2019; 7(2):43. https://doi.org/10.3390/galaxies7020043
Chicago/Turabian StyleOrdog, Anna, Rebecca A. Booth, Cameron L. Van Eck, Jo-Anne C. Brown, and Thomas L. Landecker. 2019. "Faraday Rotation of Extended Emission as a Probe of the Large-Scale Galactic Magnetic Field" Galaxies 7, no. 2: 43. https://doi.org/10.3390/galaxies7020043
APA StyleOrdog, A., Booth, R. A., Van Eck, C. L., Brown, J.-A. C., & Landecker, T. L. (2019). Faraday Rotation of Extended Emission as a Probe of the Large-Scale Galactic Magnetic Field. Galaxies, 7(2), 43. https://doi.org/10.3390/galaxies7020043





