Thermal Sunyaev–Zel’dovich Effect in the IGM due to Primordial Magnetic Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Formalism of the PMFs
2.2. Matter Density Evolution with PMFs
2.3. Thermal Evolution with PMFs
2.4. CMB Angular Power Spectrum
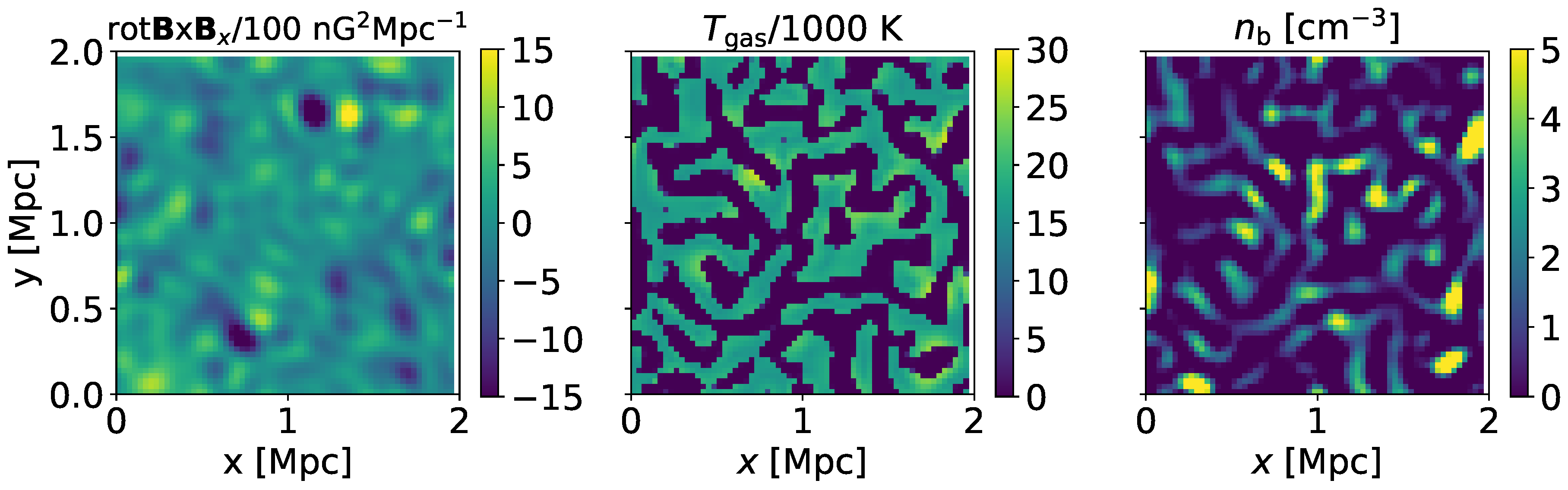
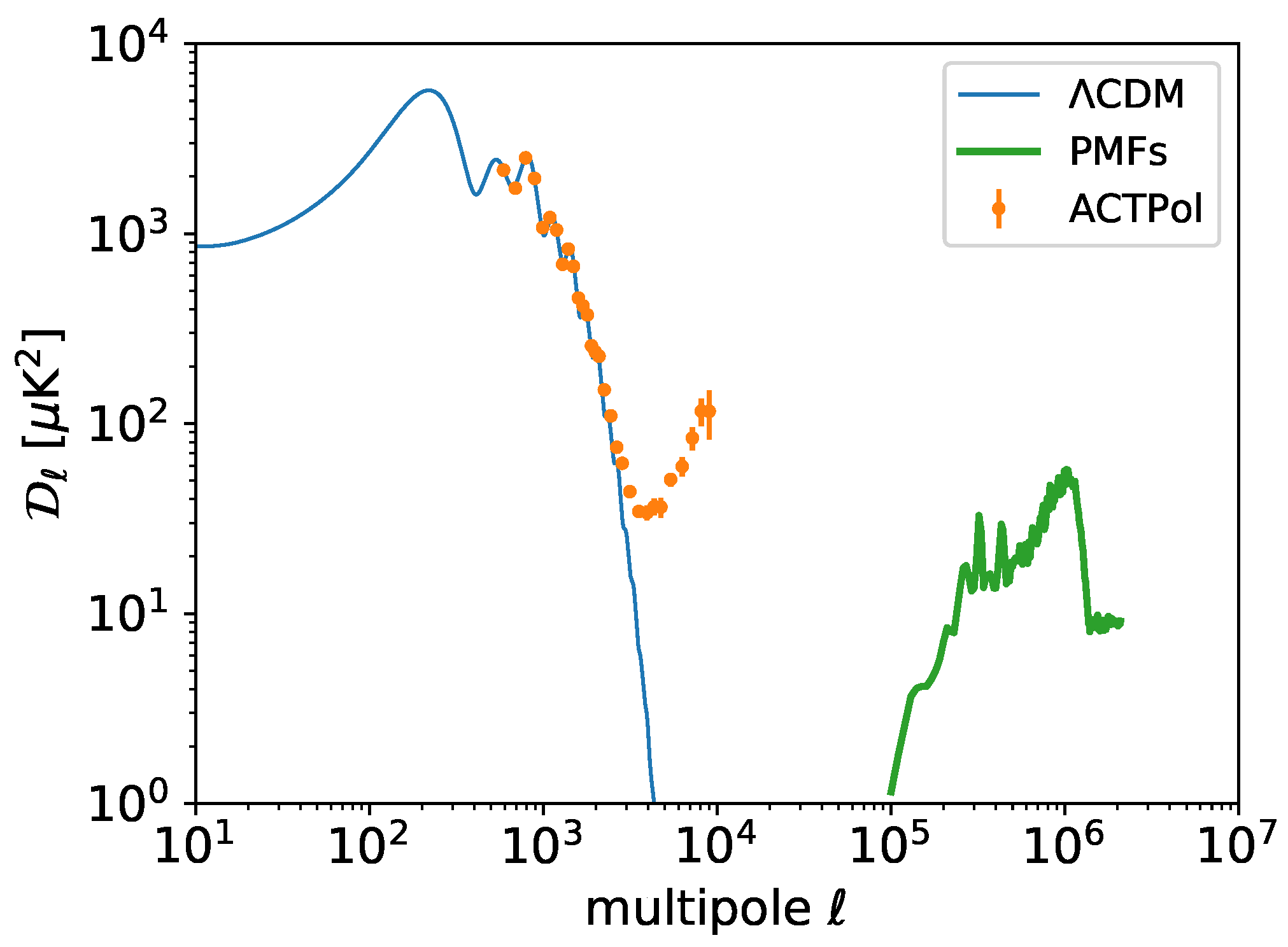
3. Results
4. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| CMB | Cosmic Microwave Background |
| PMF | primordial magnetic field |
| IGM | intergalactic medium |
| tSZ | thermal Sunyaev–Zel’dovich effect |
References
- Connerney, J.E.P. Magnetic fields of the outer planets. J. Geophys. Res. 1993, 98, 18. [Google Scholar] [CrossRef]
- Donati, J.F.; Landstreet, J.D. Magnetic Fields of Nondegenerate Stars. Annu. Rev. Astron. Astrophys. 2009, 47, 333–370. [Google Scholar] [CrossRef]
- Carilli, C.L.; Taylor, G.B. Cluster Magnetic Fields. Annu. Rev. Astron. Astrophys. 2002, 40, 319–348. [Google Scholar] [CrossRef]
- Ando, S.; Kusenko, A. Evidence for Gamma-ray Halos Around Active Galactic Nuclei and the First Measurement of Intergalactic Magnetic Fields. Astrophys. J. Lett. 2010, 722, L39–L44. [Google Scholar] [CrossRef]
- Neronov, A.; Vovk, I. Evidence for Strong Extragalactic Magnetic Fields from Fermi Observations of TeV Blazars. Science 2010, 328, 73–75. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Mori, M.; Ichiki, K.; Inoue, S.; Takami, H. Lower Bounds on Magnetic Fields in Intergalactic 155 Voids from Long-term GeV-TeV Light Curves of the Blazar Mrk 421. Astrophys. J. Lett. 2013, 771, L42. [Google Scholar] [CrossRef]
- Tashiro, H.; Chen, W.; Ferrer, F.; Vachaspati, T. Search for CP violating signature of intergalactic magnetic helicity in the gamma-ray sky. Mon. Not. R. Astron. Soc. Lett. 2014, 445, L41–L45. [Google Scholar] [CrossRef]
- Minoda, T.; Hasegawa, K.; Tashiro, H.; Ichiki, K.; Sugiyama, N. Thermal Sunyaev–Zel’dovich effect in the intergalactic medium with primordial magnetic fields. Phys. Rev. D 2017, 96, 123525. [Google Scholar] [CrossRef]
- Jedamzik, K.; Katalinić, V.; Olinto, A.V. Damping of cosmic magnetic fields. Phys. Rev. D 1998, 57, 3264–3284. [Google Scholar] [CrossRef]
- Subramanian, K.; Barrow, J.D. Magnetohydrodynamics in the early universe and the damping of nonlinear Alfvén waves. Phys. Rev. D 1998, 58, 083502. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; et al. Planck 2015 results. XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 2016, 594, A19. [Google Scholar] [CrossRef]
- Sethi, S.K.; Subramanian, K. Primordial magnetic fields in the post-recombination era and early reionization. Mon. Not. R. Astron. Soc. 2005, 356, 778–788. [Google Scholar] [CrossRef]
- Fukugita, M.; Kawasaki, M. Reionization during Hierarchical Clustering in a Universe Dominated by Cold Dark Matter. Mon. Not. R. Astron. Soc. 1994, 269, 563–578. [Google Scholar] [CrossRef]
- Draine, B.T.; Roberge, W.G.; Dalgarno, A. Magnetohydrodynamic shock waves in molecular clouds. Astrophys. J. 1983, 264, 485–507. [Google Scholar] [CrossRef]
- Seager, S.; Sasselov, D.D.; Scott, D. A New Calculation of the Recombination Epoch. Astrophys. J. Lett. 1999, 523, L1–L5. [Google Scholar] [CrossRef]
- Seager, S.; Sasselov, D.D.; Scott, D. How Exactly Did the Universe Become Neutral? Astrophys. J. Suppl. Ser. 2000, 128, 407–430. [Google Scholar] [CrossRef]
- Chluba, J.; Paoletti, D.; Finelli, F.; Rubiño-Martín, J.A. Effect of primordial magnetic fields on the ionization history. Mon. Not. R. Astron. Soc. 2015, 451, 2244–2250. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. Small-Scale Fluctuations of Relic Radiation. Astrophys. Space Sci. 1970, 7, 3–19. [Google Scholar] [CrossRef]
- Louis, T.; Grace, E.; Hasselfield, M.; Lungu, M.; Maurin, L.; Addison, G.E.; Ade, P.A.R.; Aiola, S.; Allison, R.; Amiri, M.; et al. The Atacama Cosmology Telescope: Two-season ACTPol spectra and parameters. J. Cosmol. Astropart. Phys. 2017, 6, 031. [Google Scholar] [CrossRef]
- Trivedi, P.; Reppin, J.; Chluba, J.; Banerjee, R. Magnetic heating across the cosmological recombination era: Results from 3D MHD simulations. Mon. Not. R. Astron. Soc. 2018, 481, 3401–3422. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minoda, T.; Hasegawa, K.; Tashiro, H.; Ichiki, K.; Sugiyama, N. Thermal Sunyaev–Zel’dovich Effect in the IGM due to Primordial Magnetic Fields. Galaxies 2018, 6, 143. https://doi.org/10.3390/galaxies6040143
Minoda T, Hasegawa K, Tashiro H, Ichiki K, Sugiyama N. Thermal Sunyaev–Zel’dovich Effect in the IGM due to Primordial Magnetic Fields. Galaxies. 2018; 6(4):143. https://doi.org/10.3390/galaxies6040143
Chicago/Turabian StyleMinoda, Teppei, Kenji Hasegawa, Hiroyuki Tashiro, Kiyotomo Ichiki, and Naoshi Sugiyama. 2018. "Thermal Sunyaev–Zel’dovich Effect in the IGM due to Primordial Magnetic Fields" Galaxies 6, no. 4: 143. https://doi.org/10.3390/galaxies6040143
APA StyleMinoda, T., Hasegawa, K., Tashiro, H., Ichiki, K., & Sugiyama, N. (2018). Thermal Sunyaev–Zel’dovich Effect in the IGM due to Primordial Magnetic Fields. Galaxies, 6(4), 143. https://doi.org/10.3390/galaxies6040143




