1. Introduction
About half the stars exceeding the mass of the Sun are binaries, and of these many interact during their lifetime [
1]. Many key astrophysical phenomena occur in binary systems, such as thermonuclear novae, X-ray bursts, type Ia supernovae and merging compact objects as detected by gravitational waves. Despite their importance to fundamental astrophysics, many aspects of binary evolution remain poorly understood.
The evolution of binary stars differs from that of single stars mostly because of mass transfer. In binaries wide enough that one star becomes a giant, yet short enough that the giant cannot fit inside the binary, mass transfer begins when the radius of the giant star exceeds its Roche radius. Because the giant is convective, and likely significantly more massive than its companion, mass transfer is unstable and accelerates. This leads to a common envelope forming around the stars. Drag between the stars and the envelope cause the orbit to decay and, if enough energy is transferred to the envelope, the envelope is ejected [
2]. Stars on the giant branch or asymptotic giant branch (GB or AGB stars) are stripped almost down to their cores, leaving a post-(A)GB binary.
During the common envelope process, tides are expected to be highly efficient and hence the binary that emerges is expected to have little, if any, eccentricity (
). Yet, post-AGB binaries are often highly eccentric, up to
. The source of this eccentricity is unknown but is probably related to a similar phenomena observed in the barium stars which are thought to have involved mass transfer from an AGB star [
3,
4].
Many post-AGB stars have discs, and all those with discs are in binary systems [
5]. Investigations into the link between these discs and their stellar systems’ peculiar eccentricity, based on eccentricity pumping by Lindblad resonances, suggest that the discs can cause the post-AGB systems’ eccentricity if they are sufficiently massive and live for long enough [
6]. Recent ALMA observations, e.g., of IRAS 08544-4431, show that post-AGB discs are mostly Keplerian, have masses of about
, outer diameters of
, angular momenta similar to their parent binary systems (around
), and both slow mass loss from the outer part of the disc and inflow at its inner edge at a rate of about
[
7].
In this work we combine a fast, analytic model of circumbinary discs with a synthetic binary stellar-evolution code to estimate the number of post-(A)GB discs and their properties. We include mass loss from the disc caused by illumination from the central star, ram-stripping by the interstellar medium, and include a viscous-timescale flow onto the central binary. The disc extracts angular momentum from its central binary star system. Resonances excited in the disc pump the central binary’s eccentricity. While our results are preliminary, they show that eccentricity pumping is efficient in some systems, and the discs may live a considerable time.
2. Circumbinary Disc Model
We assume that circular, Keplerian discs form when a common envelope is ejected and some small fraction of the envelope mass,
, is left behind as a disc containing a fraction,
, of the envelope’s angular momentum. The disc thus has mass
and angular momentum
. We assume our discs are thin such that
, where
is the scale height at a radius
R, and have viscous timescales that are short compared to their lifetimes such that they spread instantaneously [
8]. Given that observed discs are mostly cool and neutral (i.e.,
in most of the disc), we fix the opacity to
and assume an
-viscosity model with
.
Given the above simplifications, we write the heat-balance equation in the disc as,
where
is the temperature in the disc mid-plane (cf. [
9] where these terms are derived in detail). The
term is the heating by the post-(A)GB star, which is balanced in equilibrium by visocus heating (
) and re-radiation (
and
). We neglect the impact of mass changes on the heat balance because observed discs have low mass-loss rates (≲
). The terms
,
and
are functions of radius, such that we can rewrite Equation (
1) as,
where
is the surface density at radius
R. At a given radius
R we then choose the largest term in the right hand side of Equation (
2) and set the other terms to zero, allowing a simple solution for
everywhere in the disc (cf. [
10]). Errors in
are up to a factor of 3, hence errors in
T are at most
and typically much less, which is good enough for our purposes.
To verify that we can neglect mass changes, note that the temperature,
, associated with accretion at a rate
at radius
R and binary mass
[
9],
where the gravitational mass is dominated by the binary. Evaluating this yields,
At the inner edges of our discs so is a factor of several smaller than the typical 1000 temperatures we find. The outer edges, at , have which both cooler than the disc and the Cosmic Microwave background so this term can be safely ignored.
We next scale the density and outer radius so that the integrals of mass and angular momentum throughout the disc match
and
respectively, while the inner radius
is fixed by the torque on the disc caused by the inner binary which we take from [
11] with a multiplier of
. Thus, given three constraints—
,
and the inner binary torque—we know
throughout the disc. From this we construct any other required physical quantities, and can integrate these to calculate, for example, the luminosity of the disc. With our chosen torque prescription, our discs’ inner radii are typically around twice the orbital separation, as assumed in other works (e.g., [
12]).
We treat mass loss from the circumbinary disc as a slow phenomenon. At the inner edge of the disc we include mass inflow onto the central binary at the local viscous rate. At the outer edge we strip material when its pressure is less than that of the interstellar medium, assumed to be 3000
where
is the Boltzmann constant. Irradiation by the post-(A)GB star, particularly in X-rays, causes mass loss and we model this with the prescription of [
13]. During most of the disc’s lifetime, the viscous inflow is most important, but X-ray losses dominate when the star transitions to become a hot, young white dwarf and these losses quickly evaporate the disc. Our neglect of mass loss in Equation (
1) is incorrect in this brief phase but because the disc is terminated very rapidly, on timescales of years, such systems will be rarely observed.
The evolution of the binary stars is calculated using
binary_c [
14,
15,
16,
17]. Common envelopes are ejected with the formalism of [
18] using an efficiency
to match observed post-AGB systems with periods between 100 and about
which are observed to have circumbinary discs. The envelope binding energy parameter,
, is fitted to the models of [
19], and
of the envelope’s recombination energy is used to aid ejection. Because typically
during the AGB, such envelopes are nearly unbound and common envelope ejection is efficient with only modest orbital shrinkage.First giant branch stars have
because they are more tightly bound, so their orbits shrink significantly. We also assume that stars exit the common envelope with a small eccentricity,
, to which we apply Lindblad resonance pumping [
6]. If
is less than 1.0, as suggested by e.g., [
20,
21,
22], then more recombination energy can be included to prevent orbital shrinkage. We do not pretend to better understand common envelope evolution with our simple model.
At the end of the common envelope phase our treatment differs from [
18] in that we keep a thin envelope on the (A)GB star such that it just fills its Roche lobe when the envelope is ejected. Typically this is a
–
hydrogen-rich envelope which keeps the star cool (∼
) during the post-(A)GB phase relative to the white dwarf (≳
) it will become. The star continues its nuclear burning which reduces the mass of the envelope. Accretion from the circumbinary disc replenishes the shell and extends the lifetime of the post-(A)GB phase, as we show in the following section.
3. Example System
As an example binary star system we choose an initial primary mass , initial secondary mass , initial separation and metallicity . The separation is chosen such that Roche-lobe overflow is initiated just after the primary starts thermally pulsing on the AGB. Common envelope evolution follows with so the orbit shrinks to . The primary is then a post-AGB star, with an envelope mass of and a main-sequence dwarf companion. The accreted on to the secondary is from the wind of the AGB star prior to common envelope evolution. The orbital period is then about , typical of post-AGB binaries with circumbinary discs. We model circular orbits but our model is equally applicable to initially mildly eccentric binaries. Tides are expected to be efficient as the primary ascends the AGB and will quickly circularize the system. In the following discussion, and the figures, times are measured from the moment the common envelope is ejected.
A circumbinary disc is formed with
and
, giving
and
. Both
and
are chosen to give us a disc with mass and angular momentum similar that of IRAS 08544-4431 [
7] and other post-AGB systems with circumbinary discs (e.g., the Red Rectangle). As the disc evolves, it feeds off the angular momentum of the inner binary, but the total angular momentum gained during its lifetime is small. Mass flows through the inner edge onto the binary at between
(initially) and
, although this does not significantly alter the evolution of the disc. Rather, X-ray driven mass loss, caused by the post-AGB star increasing in temperature at approximately constant luminosity, leads to sudden termination of the disc at
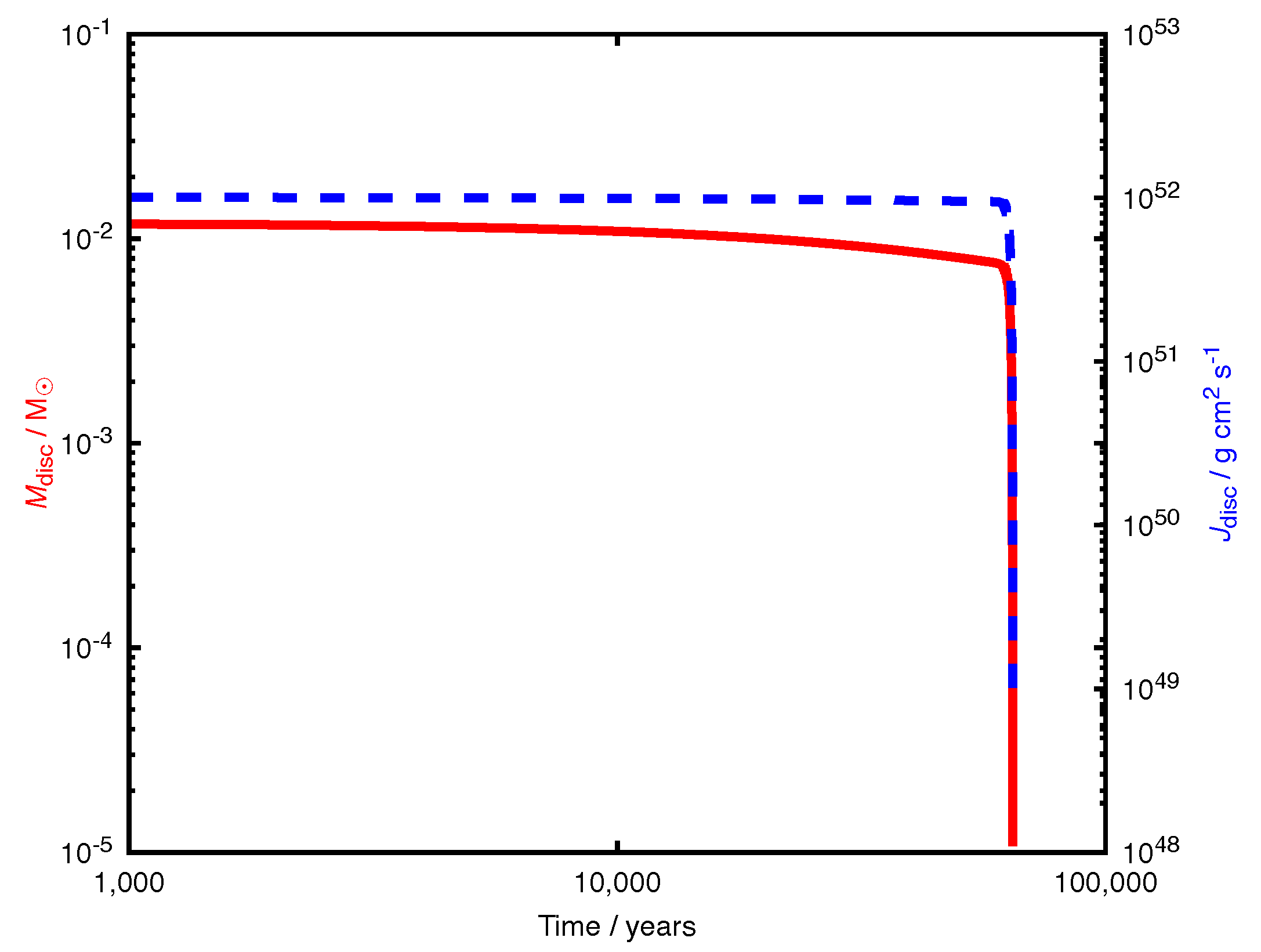
, as shown in
Figure 1.
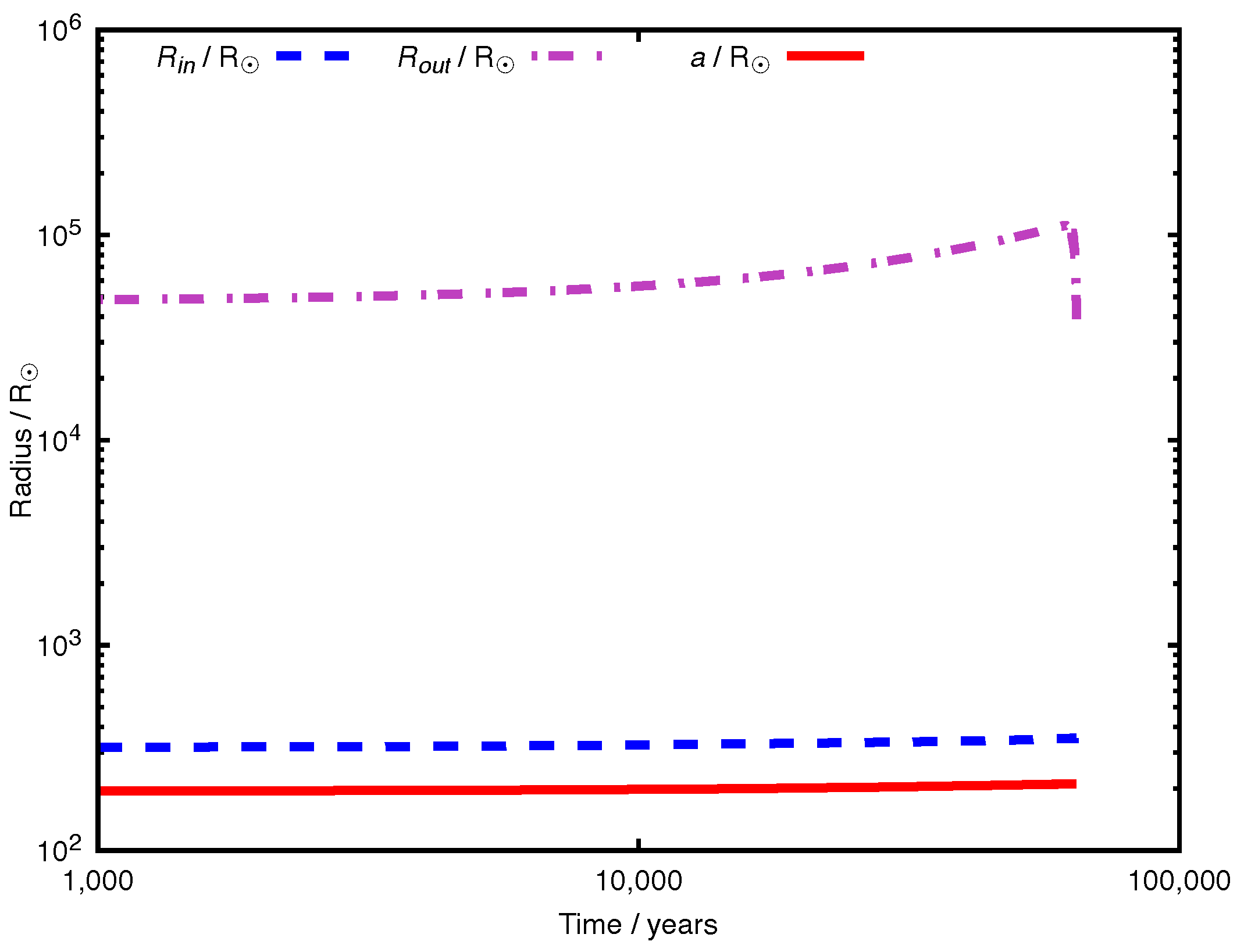
The inner edge of the disc is at
, well outside the inner binary orbit, while the outer edge is at
. The former is set by the applied torque, while the latter is set by the disc angular momentum. Until the disc is evaporated, neither the inner nor outer radius changes significantly.
Figure 2 shows the evolution of said radii.
The eccentricity of the inner binary system is pumped to about by the time the disc is evaporated. This is similar to the eccentricity observed in post-AGB systems, and it is certainly non-zero.
Mass accreted onto the post-AGB star from the inner edge of the disc replenishes its hydrogen-rich envelope, thus cooling the star and prolonging its lifetime. Because our post-AGB star has a core mass of only
, its nuclear burning rate is similar to the disc’s viscous accretion rate. The stellar wind mass loss rate is less than
because we apply the rate of [
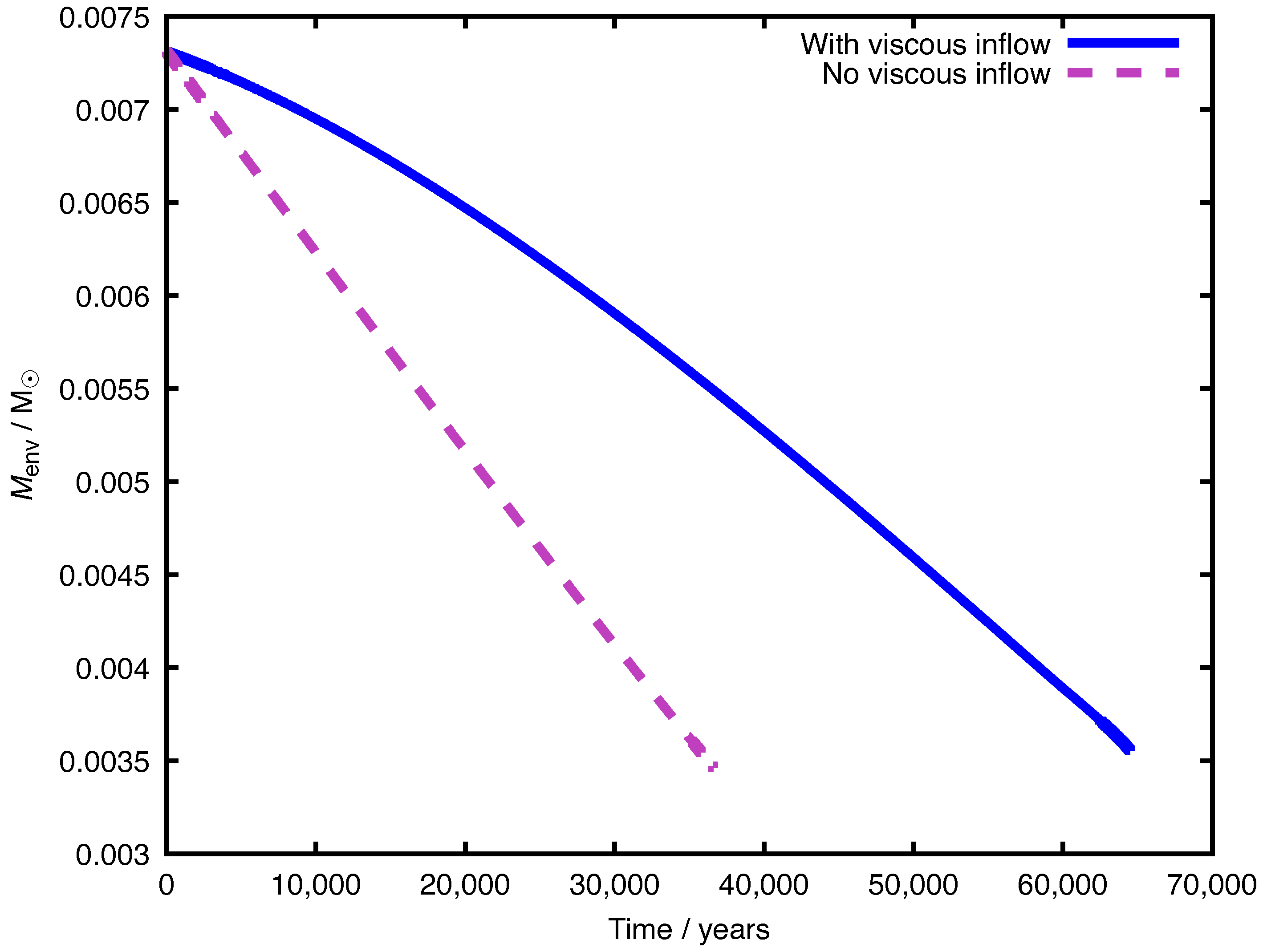
23] in our ignorance of the mechanism of post-AGB wind loss. To test how long accretion extends the post-AGB, we evolved an identical example system but with the inner-edge viscous inflow disabled.
Figure 3 shows that the post-AGB star in the system with accretion lives for an extra
, an approximate doubling of the its post-AGB lifetime. The extra lifetime of such systems may explain why they do not show residual nebulosity from envelope ejection. Observed planetary nebulae, which may be ejected common envelopes, have dynamical timescales of about
. By the time the post-AGB star is hot enough to ionize such envelopes they are likely too diffuse to be observed as planetary nebulae [
24].
4. Stellar Populations and Improved Physics
Our model is simple yet it contains the essential physics of circumbinary discs around post-(A)GB stars. It is also fast enough that we can evolve a typical binary system containing a circumbinary disc in just a few seconds of CPU time. Speed is a an essential requirement of binary population synthesis studies because the parameter space is large. We can explore the consequence of the initial mass and angular momentum of our discs through the input parameters and , and we can estimate the effect of changing uncertain input physics, e.g., a stronger or weaker X-ray wind or binary torque.
We can also model post-first giant branch (helium core) systems and post-early-AGB systems. From an observational point of view, these differ in that their stellar evolution is truncated at an earlier stage than in post-thermally-pulsing-AGB, hence they are dimmer. These systems also overflow their Roche lobes at shorter periods and have more bound envelopes, so their orbits and resultant discs are more compact. Our assumption of constant opacity likely breaks at this point, although our assumed instantaneous viscous spreading of the disc is certainly valid. We are working on improving the model to take this into account.
Our discs are low in mass relative to their stars and we never put more than 10% of the common envelope mass in the disc. The example system we report in
Section 3 has a Toomre
Q parameter of about
[
25] so is not gravitationally unstable. However, this does not preclude the formation of rocks in the disc, after all we know the discs contain small grains which emit in the infra red. In our models we expect a small number of discs to form in systems that exit the red giant branch just before helium ignition. These systems will contain sdB stars rather than white dwarfs, thus stay relatively cool. The relatively low X-ray flux from sdB stars means their discs are not evaporated quickly, at least not by means modelled here, so long-lived discs and the formation of so-called debris, i.e., rocks, in them discs seems quite likely.
The formation of second-generation planets in our discs seems not to be favoured. Our discs live for less than , too short for planet formation in the canonical sense, and our discs are quite warm, hotter than , near the inner edge where they are densest. That said, circumbinary discs have material concentrated in their orbital plane of the system for some time, so if even minor planets survive the common-envelope phase, they could accrete material from the disc. The consequences for the disc may be that it does not survive but this is currently beyond the scope of our model.
Our discs do succeed in pumping the eccentricity of their inner binary, in the case of our example system up to 0.25. In part this is because our discs are, by design, quite massive (about ), but this is to match observed discs such as IRAS 08544-4431, so is reasonable. Circumbinary discs seem to be good candidates to explain the eccentricities of at least some post-mass-transfer objects such as barium stars. We have not yet tested wind mass transfer as a mechanism for disc formation, but this is an obvious extension to our work and likely contributes to the observed population of post-(A)GB binaries.