2. The Fe-Peak Elements
The Fe-peak elements constitute a unique group of ions that are critical in astrophysical applications. These elements, located in the periodic table from Sc (Z = 21) through Zn (Z = 30), provide one of the main keys to our understanding of the early Universe and star formation. Of particular interest are the low ionisation stages of elements such as Fe, Ni, Co, Cr, and Mn, and atomic data for these are essential in the spectral modelling and analysis of myriad astronomical objects. It is very difficult to investigate these ions theoretically because of their open d-shell structures. Describing the target ion is problematic due to the hundreds of strongly coupled energy levels present, the large numbers of coupled channels, and the presence of numerous series of Rydberg resonances converging onto the target state thresholds in the low-energy scattering domain. All of these must be accurately accounted for in any calculation, and the computational effort and capacity required is substantial. To overcome these problems, new parallel versions of the R-matrix computer packages have been developed over the years which can exploit both national and international high-performance computing (HPC) facilities. The Queen’s University team have been involved in the development, testing, and use of these new variants, ensuring that all our atomic calculations are carried out using the most up-to-date software.
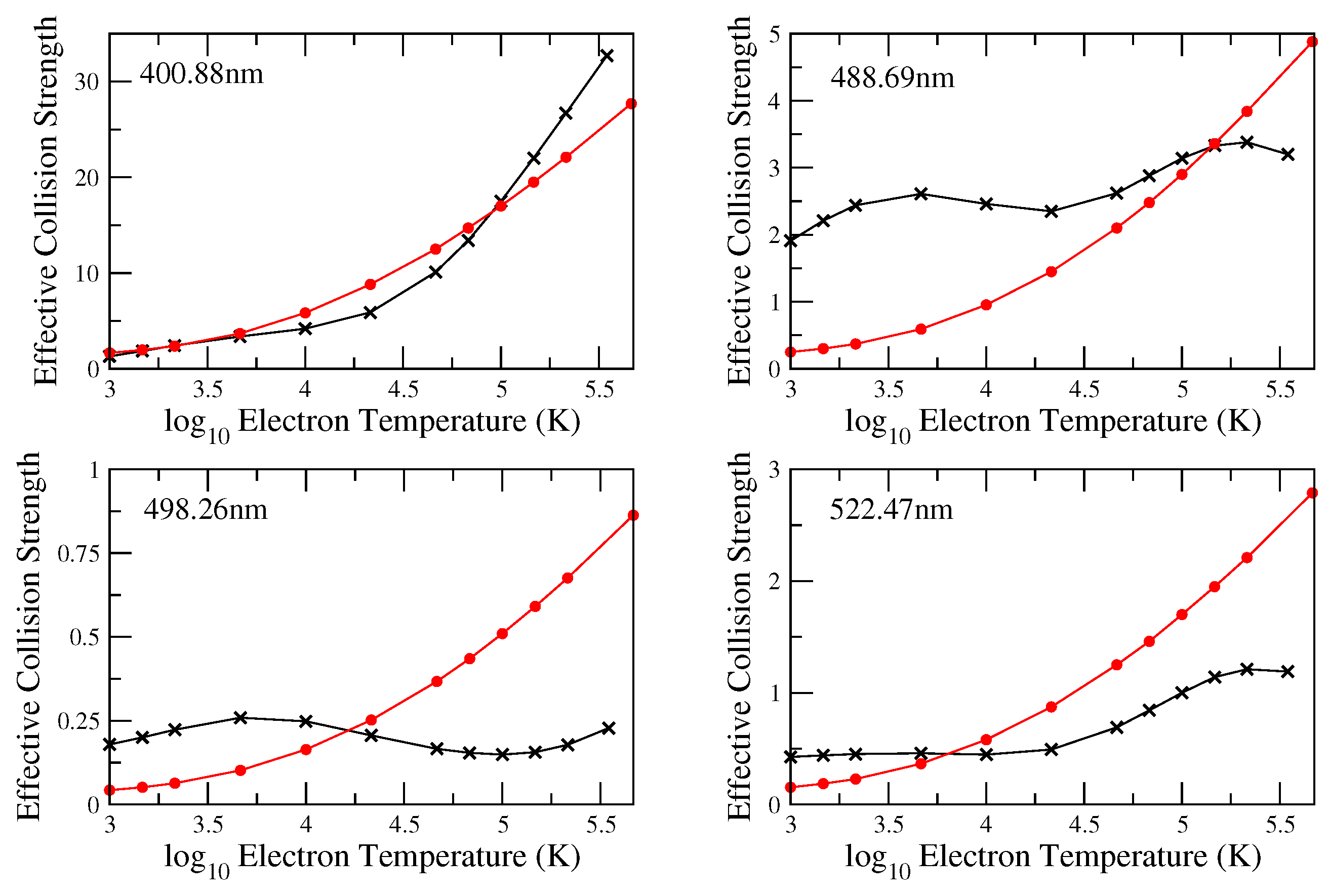
As an indicator of the current capabilities for generating atomic data for these difficult species, we concentrate in this section on discussing the electron-impact excitation of singly ionised iron. Emission and absorption lines of Fe
ii were identified in the spectra of objects as diverse as stars, planetary nebulae, and quasars from the IR to the UV spectra. Over the last thirty years, many theorists have computed atomic data for this ion, with little consensus found among the datasets (see Ramsbottom et al. [
1,
2], and references therein). These series of calculations have grown in complexity and size over the last decade, but no concrete evidence for convergence of the atomic data has been found. As an example, in
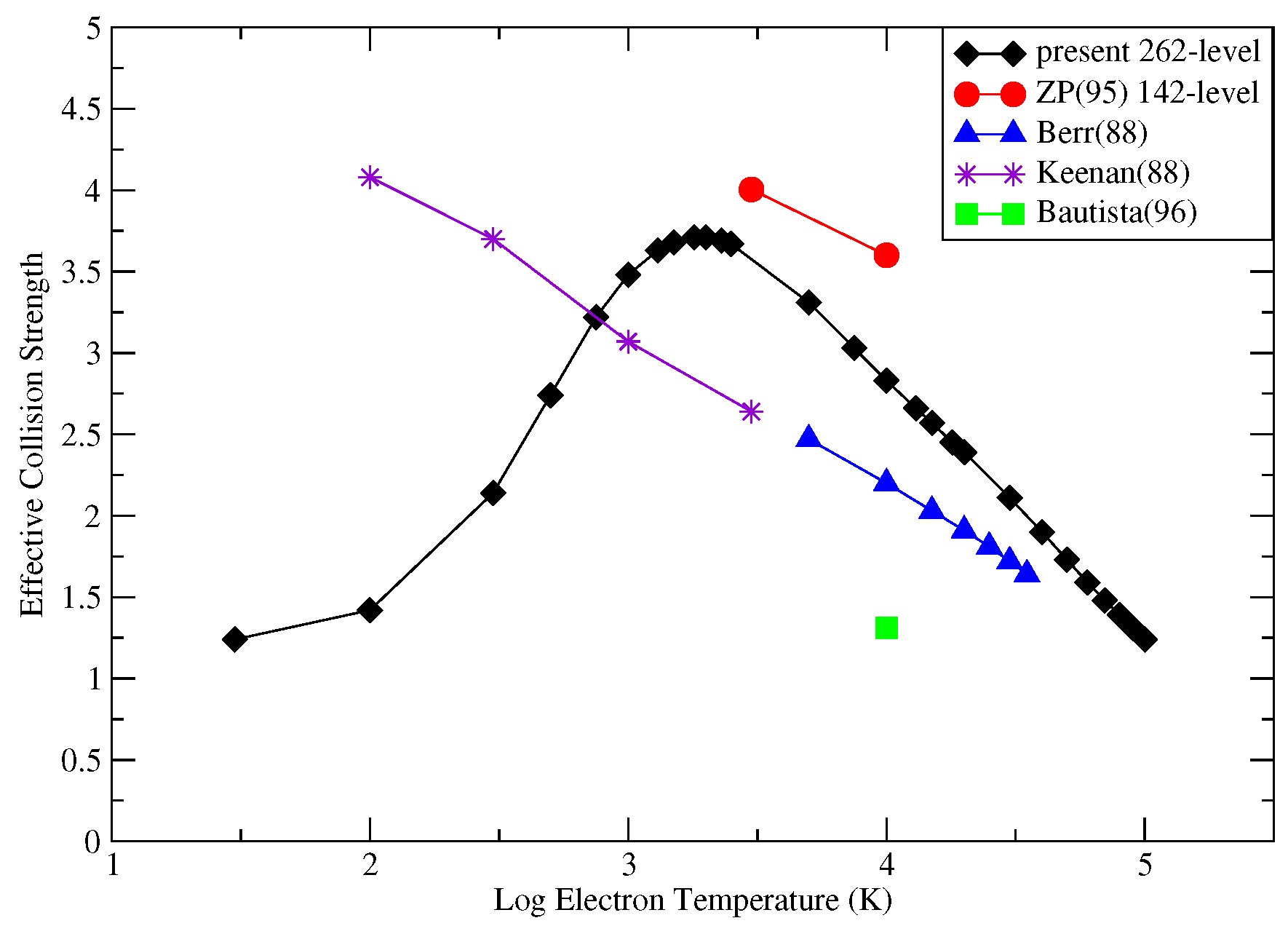
Figure 1 we consider the effective collision strength as a function of electron temperature for the spin-changing forbidden transition from the 3d
64s
6D
ground state of Fe
ii to the first metastable level above the ground state split levels, 3d
7 4F
. This figure is from Ramsbottom et al. [
1] and displays the effective collision strengths generated by theoretical work from 1988 to 2007. The temperature of maximum abundance for Fe
ii in ionisation equilibrium is 10
4 K, and at this temperature there are differences of a factor of 1.6 between the lowest and highest values of effective collision strength in
Figure 1. There is closest agreement at the highest temperatures considered between the Ramsbottom et al. [
1] data (labelled present 262-level) and the much earlier and simpler evaluation of Berrington et al. [
3] (labelled Berr(88)). For temperatures below 1000 K, the uncertainties for all calculations are greatest. The most sophisticated work in this figure is the Breit–Pauli calculation of Ramsbottom et al. [
1], which included 262 individual fine-structure levels corresponding to the 3d
64s, 3d
7, and 3d
64p configurations. Additional correlation effects were accounted for via the inclusion of a
pseudo-orbital.
In an attempt to improve these data and to test their convergence, an additional two substantial evaluations were recently completed by the Belfast group. The first was an extension of the Ramsbottom et al. [
1] Breit–Pauli model by incorporating all levels associated with the additional configurations 3d
54s
2 and 3d
54s4p. This gave rise to an extensive 716 fine-structure level calculation, generating data for over 250,000 individual transitions and dealing with 5076 coupled channels—the largest Fe
ii treatment undertaken to date. To test convergence, we then performed a fully relativistic Dirac Atomic R-matrix calculation (DARC) including the original 262 levels (three configurations) plus a further 17 configurations introduced as CI to provide a more accurate target model. In
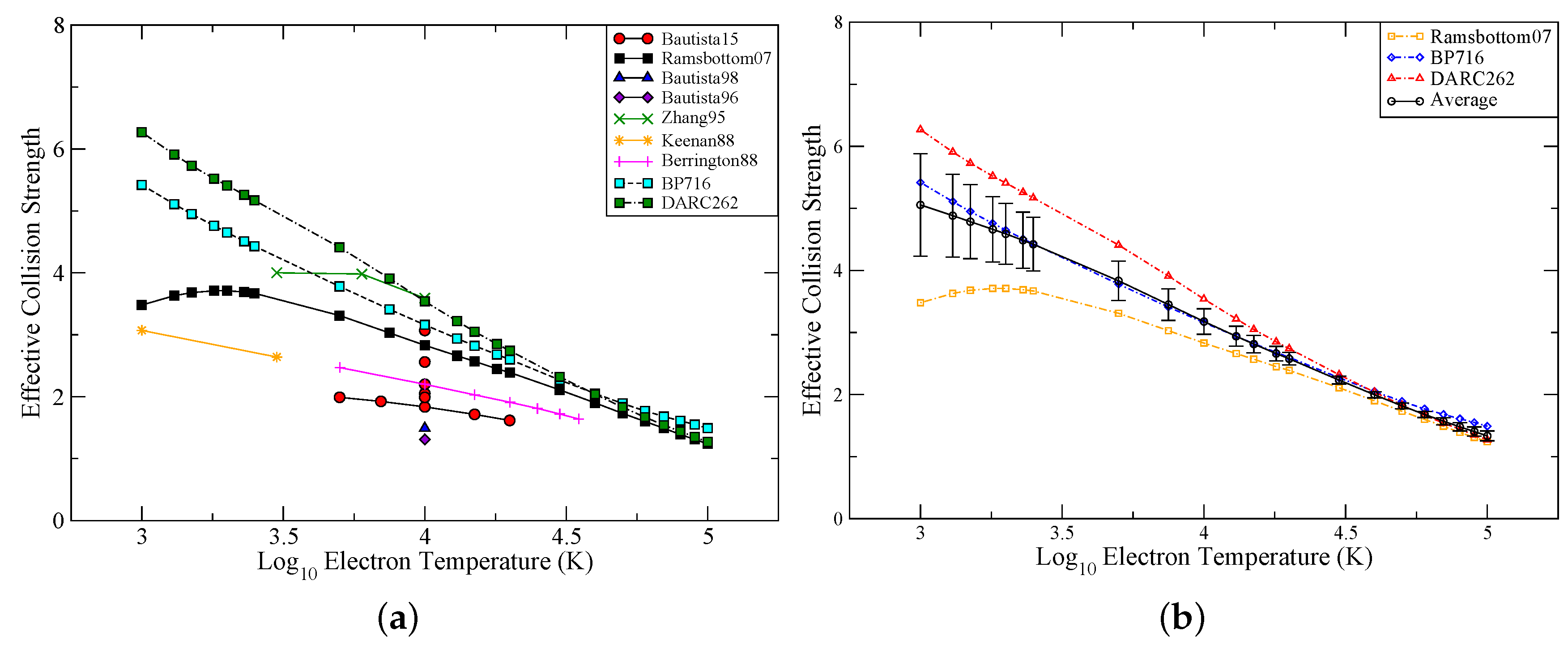
Figure 2a we present the current comparison for the 3d
64s
6D
-3d
7 4F
spin-changing transition, including the new 716 Breit–Pauli and 262 DARC evaluations. Close to the temperature of maximum abundance (10
4 K), the BP-716, DARC-262, and the original data from Ramsbottom et al. [
1] agree within 10%, and substantially better as we moved to higher temperatures. The greatest deviations were evident at the lowest temperatures considered (1000 K), as expected. This is due to the difficulty in accurately positioning the near-degenerate low-lying target state thresholds when adopting relatively few CI terms in the wavefunction description of the target Fe
ii ion. Three very different models using two different techniques are now producing similar effective collision strength values for the first time, across a range of temperatures, indicating that we are achieving near-convergence for this difficult-to-treat (yet vitally important) species. It should be noted that the additional data point at log T = 3.5 K in the work of [
4] originated from an earlier preliminary calculation by the same authors [
5]. The mean of the three largest datasets is plotted in
Figure 2b, and error bars are displayed to indicate their level of accuracy, facilitating future modelling for a wide range of astrophysical objects. Note that a similar picture was found for many other important transitions with regard to comparison, accuracy, convergence, and error prediction. A complete and comprehensive dataset of all effective collision strengths across a range of temperatures will be available from the authors in the near future.
3. Photoionisation Calculations
It is well known that massive stars and supernovae (SNe) play a critical role in the chemical evolution of galaxies. Through spectroscopic analysis, we can deduce important parameters that describe these objects and obtain information on the evolutionary history of the star. Level-resolved photoionisation cross sections are essential data in the modelling codes, and for many abundant ions in SNe (e.g., the Fe-peak elements already mentioned), these cross sections are not available. Difficulties arise in the evaluation of photoionisation cross sections due to the large intermediate dipole data files that need to be stored temporarily during the evaluations, leading to significant IO and memory issues. To overcome some of the computational bottlenecks, the Belfast group has undertaken some developments to the parallel R-matrix codes. The Breit–Pauli and DARC packages both employ two levels of MPI parallelisation. The first level is simply the distribution of distinct partial waves over processors concurrently, while the second level addresses the construction of the Hamiltonian matrix itself. Both the Breit–Pauli and DARC codes assign different numbers of processors to each Hamiltonian construction based upon its dimension. The goal is to reduce IO usage and hold the Hamiltonian matrix in memory.
In
Figure 3 and
Figure 4 we present some examples of the quality of the photoionisation cross sections that can now be produced and the level of agreement that can be achieved when compared with experiment.
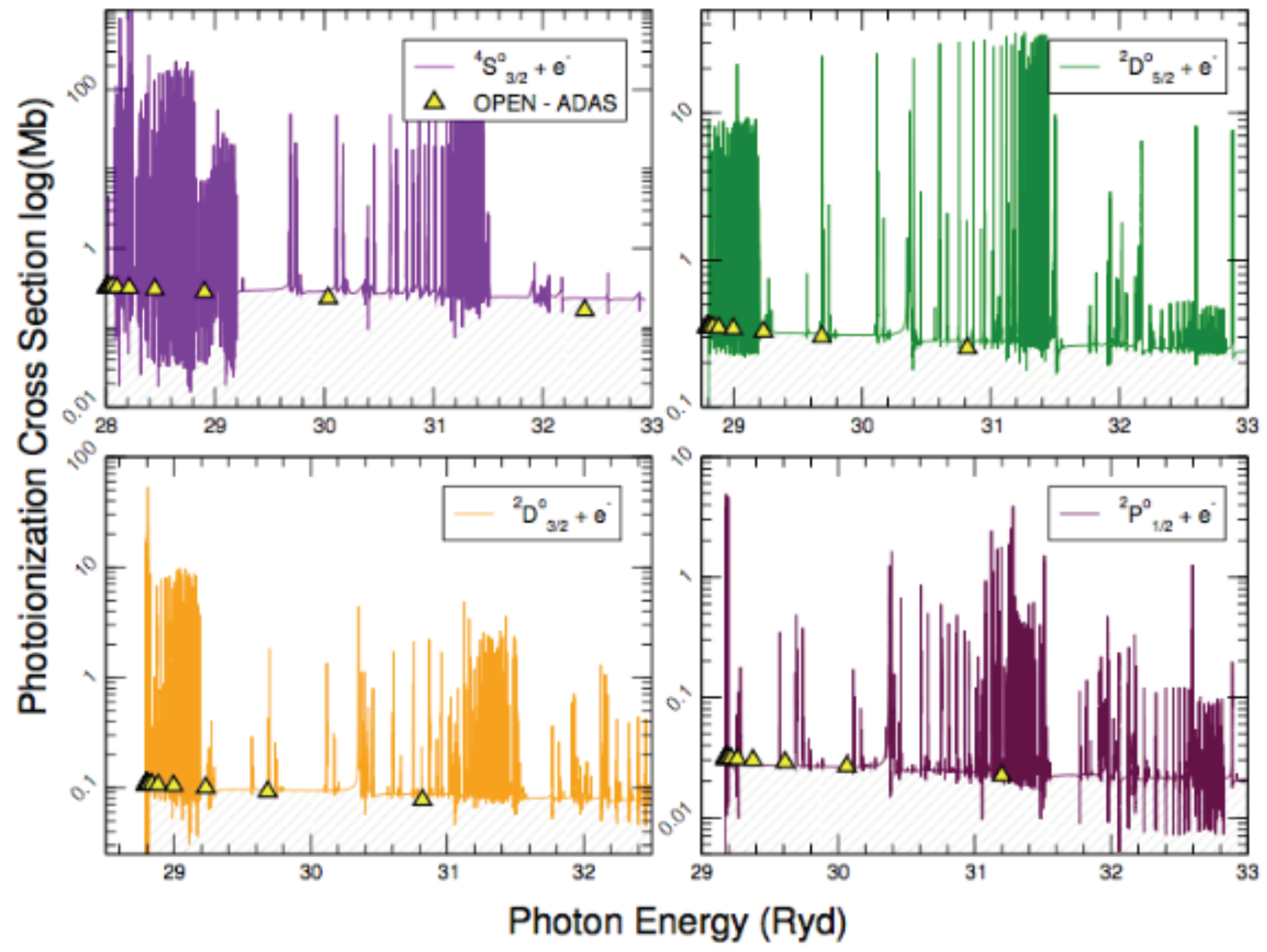
Figure 3 shows partial cross sections for the photoionisation of O-like S
ix from the 2s
22p
4 3P
2 ground state to the four lowest final target levels, 2s
22p
3,
4S
,
2D
, and
2P
; see Tyndall et al. [
10] (
Figure 3 in their paper). Comparisons are provided in the figure with a limited set of resonance-free data obtained from the OPEN-ADAS database [
11]. Excellent agreement was evident for all four partial cross sections at all photon energies, and the Rydberg resonances converging onto the target thresholds were clearly and carefully resolved.
In
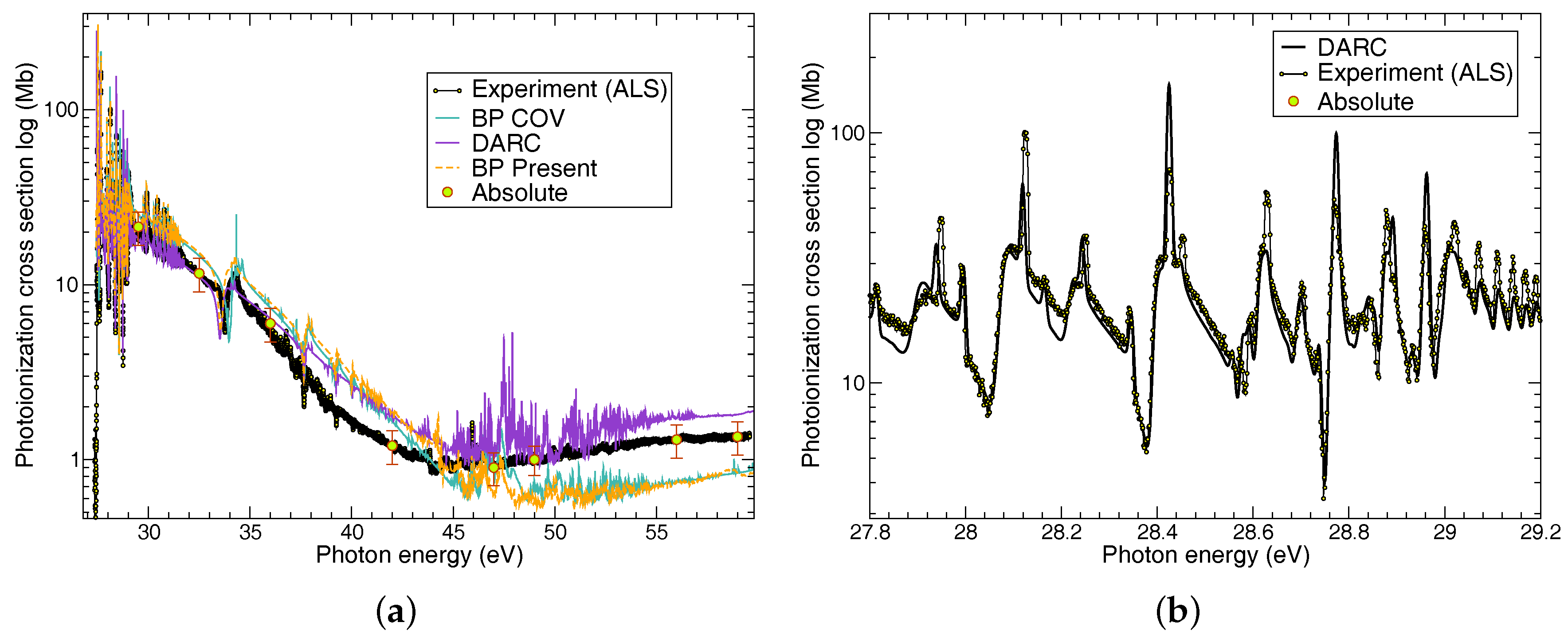
Figure 4a we present the total photoionisation cross section from the initial 3s
23p
5 2P
o ground state of Cl-like Ar
ii from Tyndall et al. [
12] (
Figure 2 in their paper). Two Breit–Pauli calculations as well as a large fully relativistic DARC calculation are shown in the figure and compared with absolute cross sections obtained from the merged beam apparatus at the Advanced Light Source (ALS) at an energy resolution of 10 meV [
13]. In this publication, three sets of data are presented: the experimental measurements, the absolute measurements at the resonance-free regions, and a theoretical Breit–Pauli calculation. All three are presented in
Figure 4 for completeness and compared with the results of [
12]. Excellent agreement was found at all photon energies considered, with particularly good conformity in the low-energy region close to threshold, and in the vicinity of the Cooper minimum around 45 eV. To further emphasize the exceptional quality of the data we can now produce, in
Figure 4b we expand the photon energy region just above threshold, from 27.8–29.2 eV. Exceptional conformity is achieved across this very narrow range, indicating how accurately the theory and numerical methods can mirror the experimental values.
4. Heavier Systems
Atomic data for heavy elements such as tungsten and molybdenum have wide applications in areas such as fusion energy and plasma physics. For example, neutral tungsten is well-known to be the primary candidate for lining the wall of the divertor region of the International Thermonuclear Experimental Reactor (ITER), while neutral molybdenum is extensively used as a plasma facing component (PFC) in tokamaks. Similar to the Fe-peak elements, these complex atoms and ions are very difficult to model due to the presence of a half-open 4d sub-shell in the ground state representation of Mo i, and a half-filled 5d sub-shell in the case of W i. Additional complications arise in the diagnostics due to the misidentification of lines and an absence of classification for many states in the spectral database for these ions. Strong mixing between low-lying levels, of which there are many hundreds, makes it very difficult to model these ions and obtain a reasonable structure representation for use in the collisional calculations.
To allow these substantial projects to be tractable, the computational capacity of the relativistic DARC R-matrix packages needed to be upgraded, and some code development was required. Our recent DARC collisional calculations for neutral heavy systems adopted more extensive large-scale atomic structure models, including up to 25 target configurations, resulting in up to 7825 fine-structure levels and 62,917 relativistic configurations (MXNC). However, integer arrays associated with angular algebra calculations within the DARC codes require dimensions of up to MXNC × (MXNC − 1)—a value which exceeds the capabilities of 4-byte integer precision for MXNC > 46,341. As a result, recent upgrades to our set of DARC codes include the option of modifying all relevant integer values to 8-byte integer precision during calculations, and also leave the 4-byte integer precision of all passing binary files unchanged to interface with other existing R-matrix codes. Additional dimension checks and dynamic array allocations during runtime have also been implemented for angular algebra arrays throughout the DARC codes. This alleviates the need for setting fixed parameters for array allocation prior to compilation, which previously may have resulted in termination at a late point in the calculation if they were not sufficiently large. Now, once the limit of the array dimension is reached, a new routine will employ intrinsic Fortran 2003 subroutine calls to carry out a fast binary allocate/deallocate, recreating the angular algebra array with increased dimensions and preserving the original contents, ultimately minimising the computational cost.
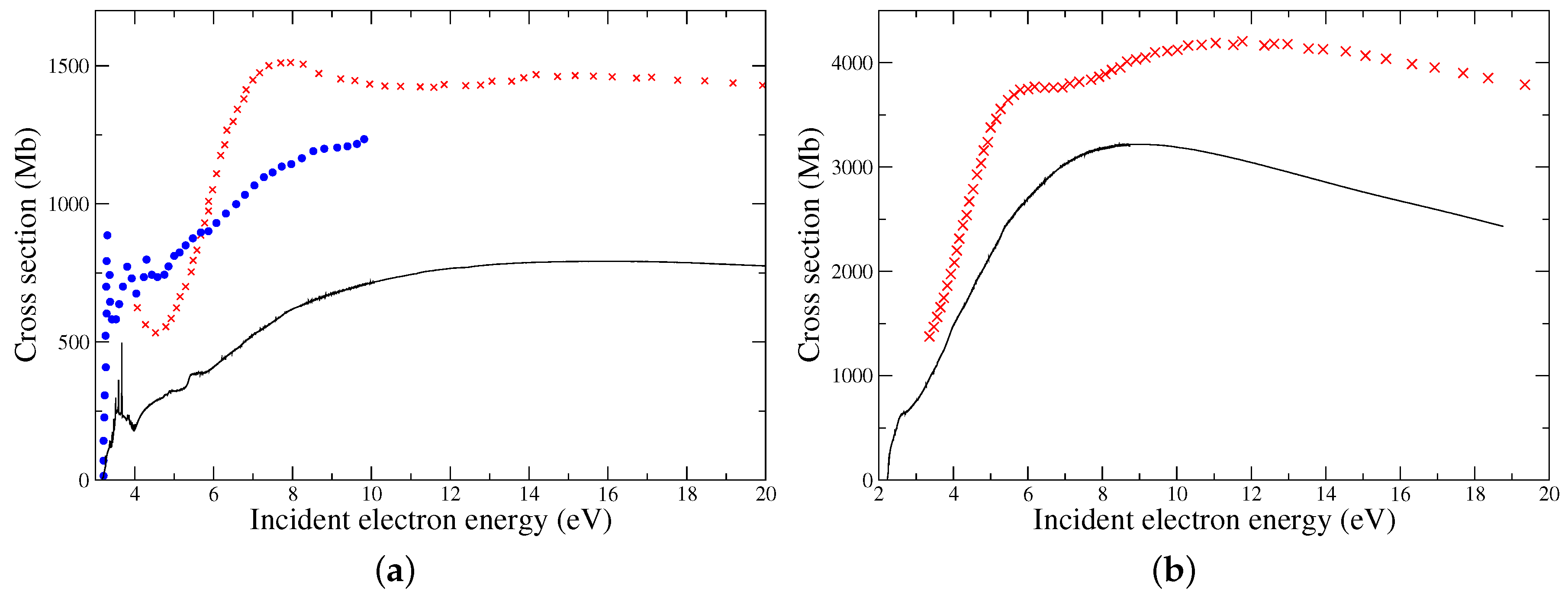
Following these developments, some very impressive atomic data were compiled by the Belfast group for Mo
i and W
i. In
Figure 5a,b we present the electron-impact excitation cross sections for the
a 7S →
z 7P
o (390.3 nm, 386.4 nm, 379.8 nm) and
a 5S →
z 5P
o (557.0 nm, 553.3 nm, 550.6 nm) important diagnostic lines of Mo
i as a function of incident electron energy from Smyth et al. [
14] (Figures 3 and 5 in their paper) and references therein. Comparisons are made with the earlier (and less-sophisticated) work of Badnell et al. [
15] and Bartschat et al. [
16]. It is evident in both figures that the current excitation cross sections were much smaller in magnitude than those previously predicted, although we saw good agreement with regard to shape. To demonstrate the quality and accuracy of this dataset, in
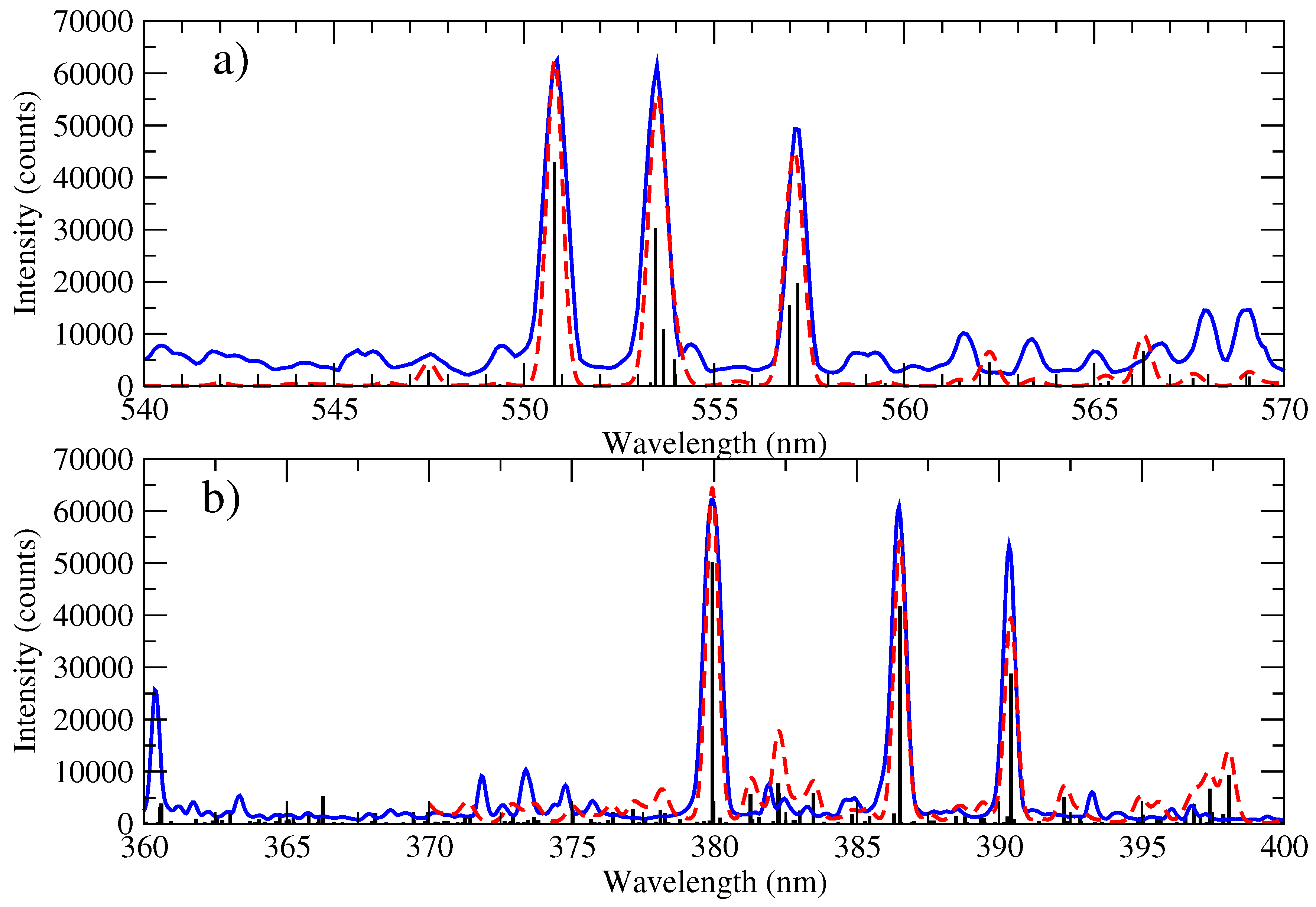
Figure 6 we present the photon emissivity coefficients (PECs) calculated using the improved results in the 379–391 nm and 550–558 nm ranges, and compare with the observed spectrum obtained by the Compact Toroidal Hybrid plasma experiment (CTH) at Auburn University [
17]. A high level of agreement was clearly evident across both wavelength regions, providing support for the accuracy of the atomic data produced.
In
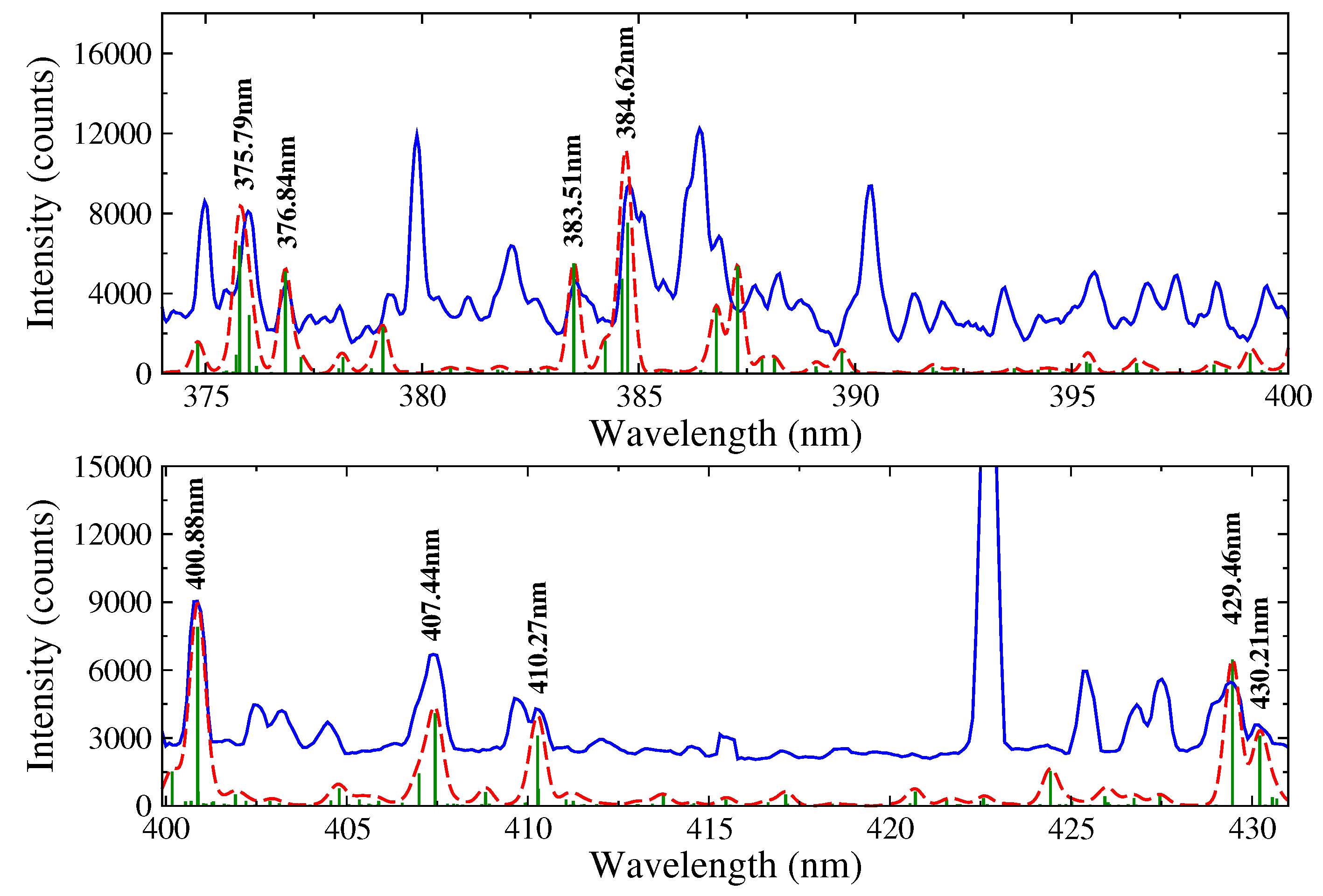
Figure 7 and
Figure 8 we present similar evidence of accuracy and quality for neutral tungsten, with data from Smyth et al. [
18] (Figures 3 and 6 in their paper).
Figure 7 shows effective collision strengths for four diagnostically important transitions in W
i and a comparison with a less-sophisticated plane-wave Born calculation, while
Figure 8 contains the spectrum from the CTH experiment compared with those generated using these new atomic data. Excellent agreement was again evident for the well-known diagnostic lines at 400.88 nm, 410.21 nm, and 430.21 nm, with respect to both magnitude and position. The differing background in the theoretical spectrum and the slight discrepancies in terms of spectral heights of specific lines are due to the atomic structure of the W
i ion. The calculated transition rates were consistently larger than the observed values, thus leading to inflated spectral heights and background.
The remainder of this section concentrates on the structure packages that are currently available for use within the R-matrix framework, and investigates whether one method is more appropriate than another when dealing with these complicated ions. Structure packages considered were the semi-relativistic configuration interaction CIV3 code [
20], the semi-relativistic autostructure (AS) package [
21], and finally the fully-relativistic GRASP structure code [
22]. The first two are commonly used alongside the Breit–Pauli suite of R-matrix codes, and the latter with the DARC packages. In
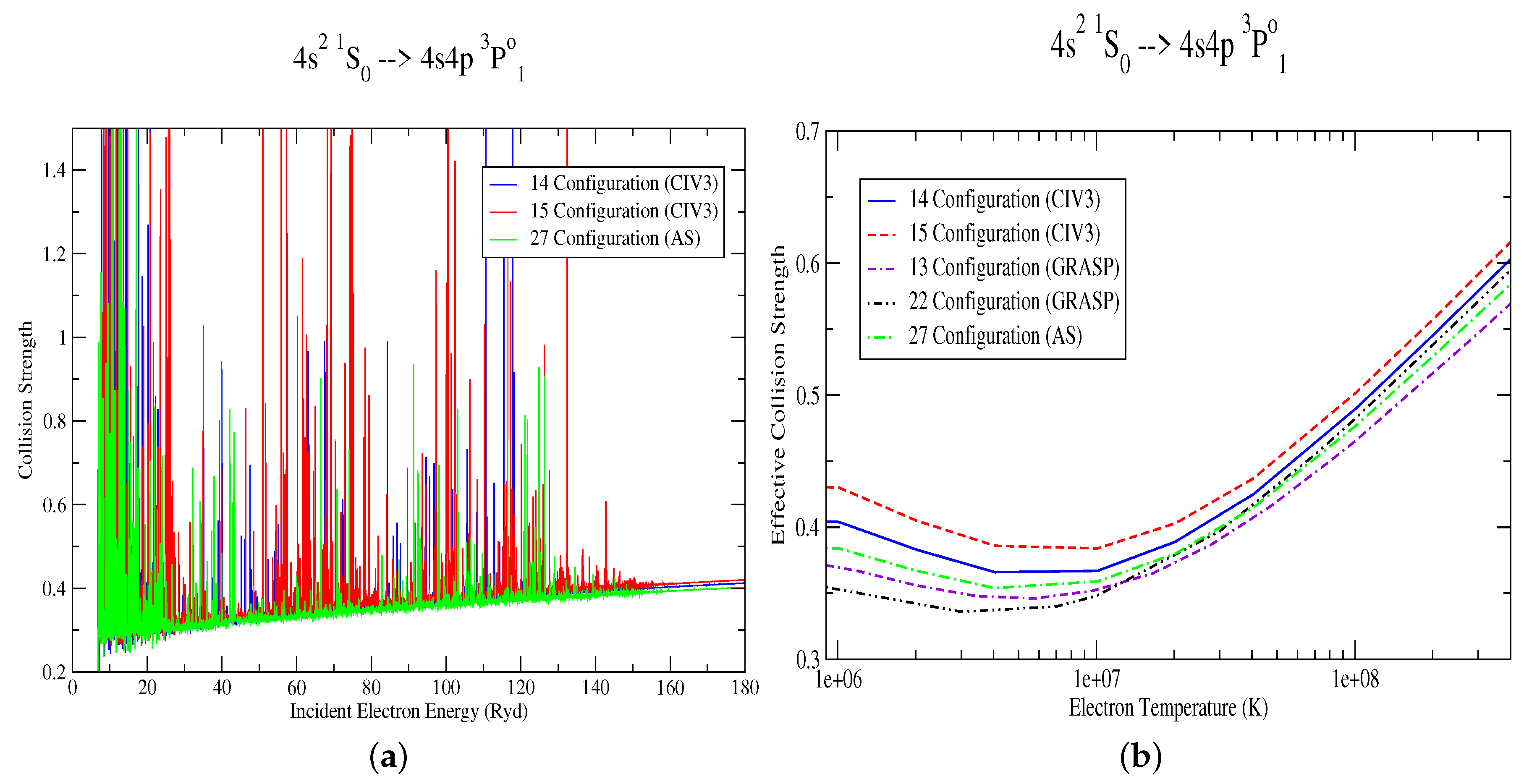
Figure 9a,b we present collision strengths and the corresponding Maxwellian-averaged effective collision strength for the spin-changing 4s
2 1S
0→ 4s4p
3P
forbidden transition in highly ionised W
44+. This important line was reasonably strong, but coupled closely to the
1P
o terms in the expansion and hence correlation and mixing effects will be important. In
Figure 9a three calculations are presented using CIV3 and AS orbital parameters and configuration sets varying in size from 14 to 27. The resonance profiles aligned quite well but differed slightly in position and magnitude at some incident electron energies. This did not appear to significantly affect the corresponding effective collision strengths plotted in
Figure 9b for these three models, and the atomic data were in excellent agreement for all temperatures considered. Both of these structure packages work in a semi-relativistic regime, and for highly ionised heavy systems such as W
44+, relativistic effects become increasingly important. To test this, in
Figure 9b we present the rates produced by a full relativistic GRASP structure treatment with varying size of model from 13 to 22 configurations. At the high temperatures above 10
7 K, all five calculations exhibited excellent agreement, with slightly larger disparities appearing at the lowest temperatures considered (≈10
6 K). Nonetheless, it is very encouraging to see the conformity of the structure and collision codes when treating these highly ionised heavy species, particularly as the orbitals described by the CIV3 and AS packages are not fully relativistic. If computational capacity is not an issue, then a fully relativistic GRASP plus DARC calculation is advisable for these heavy systems. However, it is worth noting that other options are available which can provide suitably accurate data. These data will be useful in applications to magnetically confined fusion plasmas, and will help characterise useful diagnostic lines and identify the influx of potential impurities into the plasma core.
5. Conclusions
In this review publication, the current capabilities of the numerical methods and computer packages which are used systematically in the generation of accurate collisional and radiative atomic data are discussed. Particular emphasis is given to the calculation of electron-impact excitation and photoionisation collisional cross sections for a variety of species important in astrophysical applications. For the critical Fe-peak ion Fe ii, the advances in the quality of the atomic data over the last thirty years was investigated, and it was shown that the latest sophisticated 716-level DARC and BP models produced close-to-converged effective collision strengths, for the first time, for this difficult-to-treat yet vital species. These new data will be applicable in future spectral analyses of a host of astronomical objects.
To investigate the quality of the currently achievable photoionisation data, level-resolved cross sections were presented for two ions: O-like S ix and Cl-like Ar ii. Comparisons were made with experimental observations measured using the merged beam apparatus at the Advanced Light Source (ALS), and the exceptional conformity achieved was emphasised for a very narrow photon energy range. These data will be extremely useful in the spectral modelling and analysis of massive stars and SNe, critical for the chemical evolution of galaxies.
Finally, the computationally challenging heavy systems of Mo i, W i, and W 44+ were investigated. Significant code development of the existing theoretical R-matrix packages was necessary to enable these calculations to be tractable. The quality of the data produced was verified by comparing the theoretical spectra produced with the observed spectra from the CTH experiment at Auburn University. A high level of agreement was found, particularly in the wavelength region of the strongest lines, giving credence to the accuracy of the atomic data adopted in the modelling. These data will be extremely useful in application to magnetically confined fusion plasmas.