R-Matrix Scattering Calculations for Iron-Peak Species: Photoionisation of Fe I and Electron-Impact Excitation of Fe II
Abstract
1. Introduction
2. Results and Discussion
2.1. Target Models
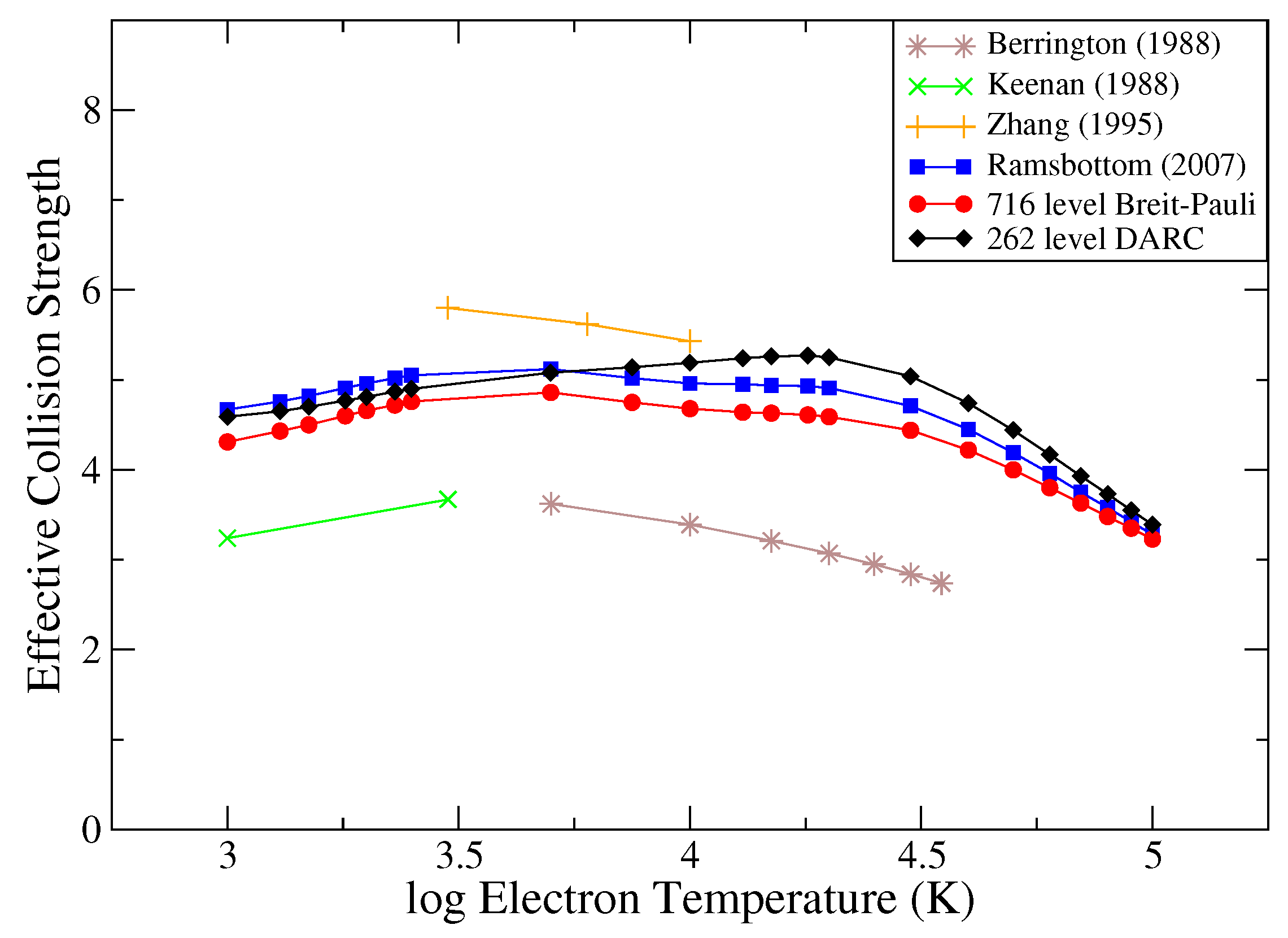
2.2. Fe II Electron-Impact Excitation
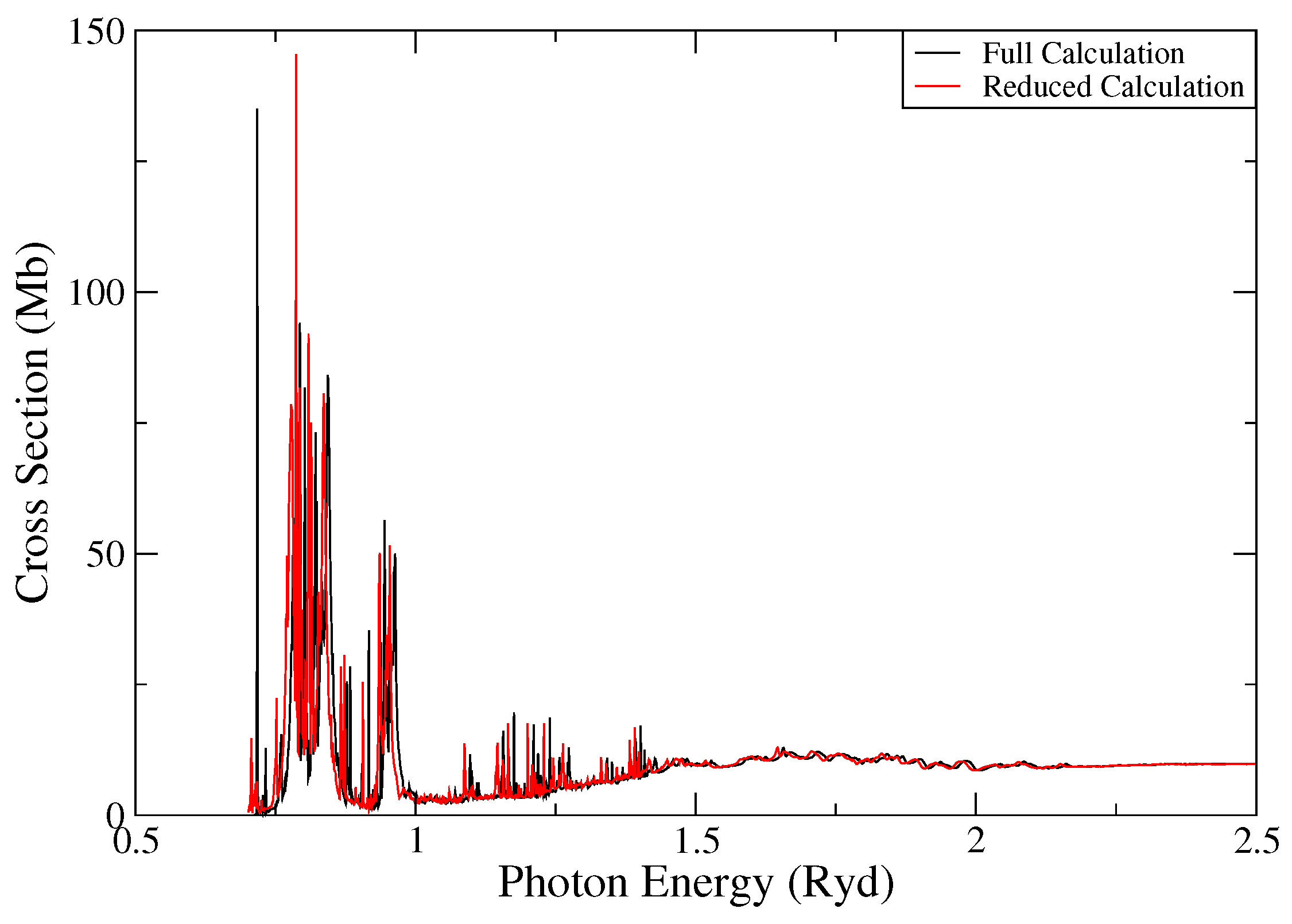
2.3. Fe I Photoionisation
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eriksson, M.; Johansson, S.; Wahlgren, G.M. The nature of ultraviolet spectra of AG Pegasi and other symbiotic stars: locations, origins, and excitation mechanisms of emission lines. Astron. Astrophys. 2006, 451, 157–175. [Google Scholar] [CrossRef]
- Smith, N.; Hartigan, P. Infrared [Fe II] Emission from P Cygni’s Nebula: Atomic Data, Mass, Kinematics, and the 1600 AD Outburst. Astrophys. J. 2006, 638, 1045–1055. [Google Scholar] [CrossRef]
- Nussbaumer, H.; Storey, P.J. Atomic data for Fe II. Astron. Astrophys. 1980, 89, 308–313. [Google Scholar]
- Nussbaumer, H.; Pettini, M.; Storey, P.J. Sextet transitions in Fe II. Astron. Astrophys. 1981, 102, 351–358. [Google Scholar]
- Baluja, K.L.; Hibbert, A.; Mohan, M. Electron impact excitation of Fe II using the R-matrix method. J. Phys. B At. Mol. Phys. 1986, 19, 3613–3623. [Google Scholar] [CrossRef]
- Pradhan, A.K.; Berrington, K.A. R-matrix calculations for electron impact excitation of Fe II: LS coupling and Breit–Pauli approximations. J. Phys. B At. Mol. Phys. 1993, 26, 157–172. [Google Scholar] [CrossRef]
- Ramsbottom, C.A.; Scott, M.P.; Bell, K.L.; Keenan, F.P.; McLaughlin, B.M.; Sunderland, A.G.; Burke, V.M.; Noble, C.J.; Burke, P.G. Electron impact excitation of the iron peak element Fe II. J. Phys. B At. Mol. Phys. 2002, 35, 3451–3477. [Google Scholar] [CrossRef]
- Ramsbottom, C.A.; Noble, C.J.; Burke, V.M.; Scott, M.P.; Burke, P.G. Configuration interaction effects in low-energy electron collisions with Fe II. J. Phys. B At. Mol. Phys. 2004, 37, 3609–3631. [Google Scholar] [CrossRef]
- Ramsbottom, C.A.; Noble, C.J.; Burke, V.M.; Scott, M.P.; Kisielius, R.; Burke, P.G. Electron impact excitation of Fe II: Total LS effective collision strengths. J. Phys. B At. Mol. Phys. 2005, 38, 2999–3014. [Google Scholar] [CrossRef]
- Berrington, K.A.; Burke, P.G.; Hibbert, A.; Mohan, M.; Baluja, K.L. Electron impact excitation of Fe + using the R-matrix method incorporating fine-structure effects. J. Phys. B At. Mol. Phys. 1988, 21, 339–350. [Google Scholar] [CrossRef]
- Zhang, H.L.; Pradhan, A.K. Atomic data from the Iron Project. VI. Collision strengths and rate coefficients for Fe II. Astron. Astrophys. 1995, 293, 953–966. [Google Scholar]
- Bautista, M.A.; Pradhan, A.K. Atomic data from the Iron project. XIII. Electron excitation rates and emissivity ratios for forbidden transitions in NI II and Fe II. Astron. Astrophys. Suppl. 1996, 115, 551–559. [Google Scholar]
- Bautista, M.A.; Pradhan, A.K. Ionization Structure and Spectra of Iron in Gaseous Nebulae. Astrophys. J. 1998, 492, 650–676. [Google Scholar] [CrossRef]
- Bautista, M.A.; Fivet, V.; Ballance, C.; Quinet, P.; Ferland, G.; Mendoza, C.; Kallman, T.R. Atomic Data and Spectral Model for Fe II. Astrophys. J. 2015, 808, 174. [Google Scholar] [CrossRef]
- Ramsbottom, C.A.; Hudson, C.E.; Norrington, P.H.; Scott, M.P. Electron-impact excitation of Fe II*—Collision strengths and effective collision strengths for low-lying fine-structure forbidden transitions. Astron. Astrophys. 2007, 475, 765–769. [Google Scholar] [CrossRef]
- Ramsbottom, C. Electron-impact excitation of Fe II: Effective collision strengths for optically allowed fine-structure transitions. At. Data Nucl. Data Tables 2009, 95, 910–986. [Google Scholar] [CrossRef]
- Dirac R-Matrix Codes. Available online: http://connorb.freeshell.org/ (accessed on 18 June 2018).
- Reilman, R.F.; Manson, S.T. Photoabsorption cross sections for positive atomic ions with Z equal to or less than 30. Astrophys. J. Suppl. Ser. 1979, 40, 815–880. [Google Scholar] [CrossRef]
- Verner, D.; Yakovlev, D.; Band, I.; Trzhaskovskaya, M. Subshell Photoionization Cross Sections and Ionization Energies of Atoms and Ions from He to Zn. At. Data Nucl. Data Tables 1993, 55, 233–280. [Google Scholar] [CrossRef]
- Kelly, H.P. Photoionization Accompanied by Excitation of Fe I. Phys. Rev. A 1972, 6, 1048–1053. [Google Scholar] [CrossRef]
- Kelly, H.P.; Ron, A. Photoionization Cross Section of the Neutral Iron Atom. Phys. Rev. A 1972, 5, 168–176. [Google Scholar] [CrossRef]
- Sawey, P.M.J.; Berrington, K.A. Atomic data for opacity calculations. XV. Fe I-IV. J. Phys. B At. Mol. Phys. 1992, 25, 1451–1466. [Google Scholar] [CrossRef]
- Bautista, M.A. Atomic data from the IRON Project—XX. Photoionization cross sections and oscillator strengths for Fe I. Astron. Astrophys. Suppl. Ser. 1997, 122, 167–176. [Google Scholar] [CrossRef]
- Bautista, M.A.; Pradhan, A.K. Photoionization of neutral iron. J. Phys. B At. Mol. Phys. 1995, 28, L173–L179. [Google Scholar] [CrossRef]
- Sawey, P.M.J.; Berrington, K.A. Resonances due to photoexcitation of the core in the photoionization cross section for excited states of iron. J. Phys. B At. Mol. Phys. 1990, 23, L817–L822. [Google Scholar] [CrossRef]
- Bautista, M.A.; Lind, K.; Bergemann, M. Photoionization and electron impact excitation cross sections for Fe. Astron. Astrophys. 2017, 606, A127. [Google Scholar] [CrossRef]
- Berrington, K.A.; Ballance, C. Double ionization yields from the photoionization of Fe II and Fe I. J. Phys. B At. Mol. Phys. 2001, 34, L383. [Google Scholar] [CrossRef]
- Baluja, K.L.; Butler, K.; Le Bourlot, J.; Zeippen, C.J. Recent radiative and collisional atomic data of astrophysical interest. J. Phys. Colloques 1988, 49, C1-129–C1-132. [Google Scholar] [CrossRef]
- Fivet, V.; Bautista, M.A.; Ballance, C.P. Fine-structure photoionization cross sections of Fe II. J. Phys. B At. Mol. Phys. 2012, 45, 035201. [Google Scholar] [CrossRef]
- Nahar, S.N. Relativistic photoionization cross sections for C II. Phys. Rev. A 2002, 65, 052702. [Google Scholar] [CrossRef]
- Hibbert, A. CIV3—A general program to calculate configuration interaction wave functions and electric-dipole oscillator strengths. Comput. Phys. Commun. 1975, 9, 141–172. [Google Scholar] [CrossRef]
- Dyall, K.; Grant, I.; Johnson, C.; Parpia, F.; Plummer, E. GRASP: A general-purpose relativistic atomic structure program. Comput. Phys. Commun. 1989, 55, 425–456. [Google Scholar] [CrossRef]
- Parpia, F.A.; Grant, I.P. Software for relativistic atomic theory: The GRASP project at Oxford. J. Phys. IV Fr. 1991, 1, C1-33–C1-46. [Google Scholar] [CrossRef]
- NIST. Available online: http://www.nist.gov/pml/data/asd.cfm (accessed on 18th June 2018).
- Keenan, F.P.; Hibbert, A.; Burke, P.G.; Berrington, K.A. Fine-structure populations for the 6D ground state of Fe II. Astrophys. J. 1988, 332, 539–542. [Google Scholar] [CrossRef]
| Term | J | NIST | Breit–Pauli | DARC |
|---|---|---|---|---|
| 3d4s D | 9/2 | 0.00000 | 0.00000 | 0.00000 |
| 3d4s D | 7/2 | 0.00351 | 0.00398 | 0.00323 |
| 3d4s D | 5/2 | 0.00608 | 0.00695 | 0.00562 |
| 3d4s D | 3/2 | 0.00786 | 0.00903 | 0.00728 |
| 3d4s D | 1/2 | 0.00890 | 0.01025 | 0.00825 |
| 3d F | 9/2 | 0.01706 | 0.02786 | 0.01757 |
| 3d F | 7/2 | 0.02215 | 0.03315 | 0.02197 |
| 3d F | 5/2 | 0.02586 | 0.03707 | 0.02523 |
| 3d F | 3/2 | 0.02841 | 0.03977 | 0.02748 |
| 3d4s D | 7/2 | 0.07249 | 0.07232 | 0.10600 |
| 3d4s D | 5/2 | 0.07647 | 0.07694 | 0.10983 |
| 3d4s D | 3/2 | 0.07910 | 0.08005 | 0.11222 |
| 3d4s D | 1/2 | 0.08062 | 0.08186 | 0.11363 |
| 3d P | 5/2 | 0.12279 | 0.14864 | 0.10860 |
| 3d P | 3/2 | 0.12460 | 0.15096 | 0.11062 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smyth, R.T.; Ramsbottom, C.A.; Ballance, C.P. R-Matrix Scattering Calculations for Iron-Peak Species: Photoionisation of Fe I and Electron-Impact Excitation of Fe II. Galaxies 2018, 6, 87. https://doi.org/10.3390/galaxies6030087
Smyth RT, Ramsbottom CA, Ballance CP. R-Matrix Scattering Calculations for Iron-Peak Species: Photoionisation of Fe I and Electron-Impact Excitation of Fe II. Galaxies. 2018; 6(3):87. https://doi.org/10.3390/galaxies6030087
Chicago/Turabian StyleSmyth, Ryan T., Catherine A. Ramsbottom, and Connor P. Ballance. 2018. "R-Matrix Scattering Calculations for Iron-Peak Species: Photoionisation of Fe I and Electron-Impact Excitation of Fe II" Galaxies 6, no. 3: 87. https://doi.org/10.3390/galaxies6030087
APA StyleSmyth, R. T., Ramsbottom, C. A., & Ballance, C. P. (2018). R-Matrix Scattering Calculations for Iron-Peak Species: Photoionisation of Fe I and Electron-Impact Excitation of Fe II. Galaxies, 6(3), 87. https://doi.org/10.3390/galaxies6030087




