Molecular Data Needs for Modelling AGB Stellar Winds and Other Molecular Environments
Abstract
1. Introduction
2. Required Molecular Data
2.1. Radiative Rates
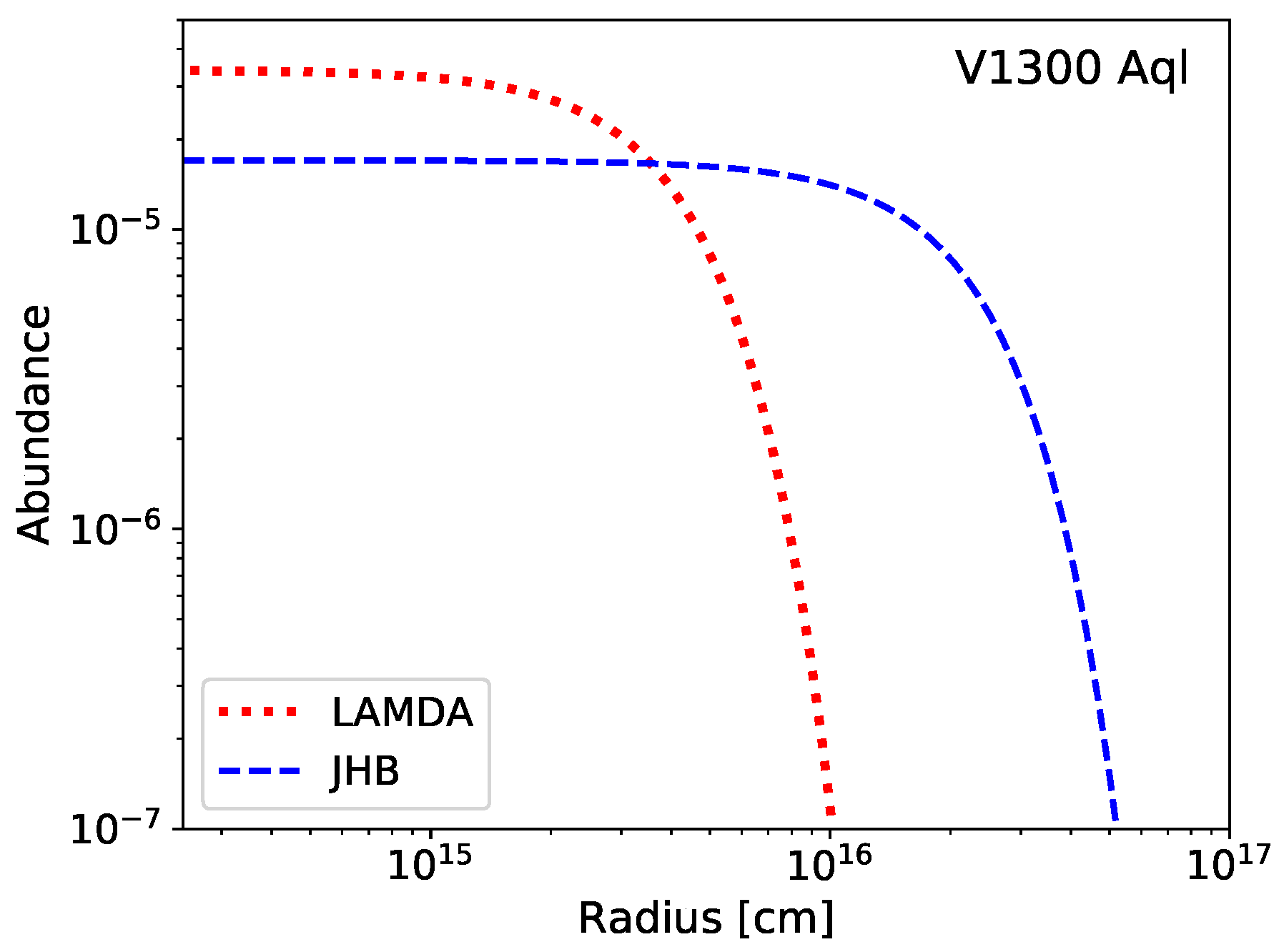
2.2. Collisional Rates
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Asymptotic Giant Branch |
| CDMS | Cologne Database for Molecular Spectroscopy |
| HITRAN | High-Resolution Transmission Molecular Absorption Database |
| ISM | Interstellar Medium |
| JPL | Jet Propulsion Laboratory |
| LAMDA | Leiden Atomic and Molecular Database |
| LTE | Local Thermodynamic Equilibrium |
| NIST | National Institute of Standards and Technology |
| NRAO | National Radio Astronomy Observatory |
| PDR | Photon Dominated Region |
References
- Endres, C.P.; Schlemmer, S.; Schilke, P.; Stutzki, J.; Müller, H.S.P. The Cologne Database for Molecular Spectroscopy, CDMS, in the Virtual Atomic and Molecular Data Centre, VAMDC. J. Mol. Spectrosc. 2016, 327, 95–104. [Google Scholar] [CrossRef]
- Müller, H.S.P.; Thorwirth, S.; Roth, D.A.; Winnewisser, G. The Cologne Database for Molecular Spectroscopy, CDMS. Astron. Astrophys. 2001, 370, L49–L52. [Google Scholar] [CrossRef]
- Müller, H.S.P.; Schlöder, F.; Stutzki, J.; Winnewisser, G. The Cologne Database for Molecular Spectroscopy, CDMS: a useful tool for astronomers and spectroscopists. J. Mol. Struct. 2005, 742, 215–227. [Google Scholar] [CrossRef]
- Höfner, S.; Olofsson, H. Mass loss of stars on the asymptotic giant branch. Mechanisms, models and measurements. Astron. Astrophys. Res. 2018, 26, 1. [Google Scholar] [CrossRef]
- Habing, H.J.; Olofsson, H. (Eds.) Asymptotic Giant Branch Stars; Springer: Berlin, Germany, 2003. [Google Scholar]
- Schöier, F.L.; Ramstedt, S.; Olofsson, H.; Lindqvist, M.; Bieging, J.H.; Marvel, K.B. The abundance of HCN in circumstellar envelopes of AGB stars of different chemical type. Astron. Astrophys. 2013, 550, A78. [Google Scholar] [CrossRef]
- Danilovich, T.; Bergman, P.; Justtanont, K.; Lombaert, R.; Maercker, M.; Olofsson, H.; Ramstedt, S.; Royer, P. Detailed modelling of the circumstellar molecular line emission of the S-type AGB star W Aquilae. Astron. Astrophys. 2014, 569, A76. [Google Scholar] [CrossRef]
- Ramstedt, S.; Olofsson, H. The 12CO/13CO ratio in AGB stars of different chemical type. Connection to the 12C/13C ratio and the evolution along the AGB. Astron. Astrophys. 2014, 566, A145. [Google Scholar] [CrossRef]
- Decin, L.; Richards, A.M.S.; Waters, L.B.F.M.; Danilovich, T.; Gobrecht, D.; Khouri, T.; Homan, W.; Bakker, J.M.; Van de Sande, M.; Nuth, J.A.; et al. Study of the aluminium content in AGB winds using ALMA. Indications for the presence of gas-phase (Al2O3)n clusters. Astron. Astrophys. 2017, 608, A55. [Google Scholar] [CrossRef]
- Schöier, F.L.; Maercker, M.; Justtanont, K.; Olofsson, H.; Black, J.H.; Decin, L.; de Koter, A.; Waters, R. A chemical inventory of the S-type AGB star χ Cygni based on Herschel/HIFI observations of circumstellar line emission. The importance of non-LTE chemical processes in a dynamical region. Astron. Astrophys. 2011, 530, A83. [Google Scholar] [CrossRef]
- Schöier, F.L.; Olofsson, H. Models of circumstellar molecular radio line emission. Mass loss rates for a sample of bright carbon stars. Astron. Astrophys. 2001, 368, 969–993. [Google Scholar] [CrossRef]
- Punzi, K.M.; Hily-Blant, P.; Kastner, J.H.; Sacco, G.G.; Forveille, T. An Unbiased 1.3 mm Emission Line Survey of the Protoplanetary Disk Orbiting LkCa 15. Astrophys. J. 2015, 805, 147. [Google Scholar] [CrossRef]
- Nagy, Z.; Choi, Y.; Ossenkopf-Okada, V.; van der Tak, F.F.S.; Bergin, E.A.; Gerin, M.; Joblin, C.; Röllig, M.; Simon, R.; Stutzki, J. Herschel/HIFI spectral line survey of the Orion Bar. Temperature and density differentiation near the PDR surface. Astron. Astrophys. 2017, 599, A22. [Google Scholar] [CrossRef]
- Barman, T.S.; Konopacky, Q.M.; Macintosh, B.; Marois, C. Simultaneous Detection of Water, Methane, and Carbon Monoxide in the Atmosphere of Exoplanet HR8799b. Astrophys. J. 2015, 804, 61. [Google Scholar] [CrossRef]
- Fortney, J.J.; Robinson, T.D.; Domagal-Goldman, S.; Skålid Amundsen, D.; Brogi, M.; Claire, M.; Crisp, D.; Hebrard, E.; Imanaka, H.; de Kok, R.; et al. The Need for Laboratory Work to Aid in The Understanding of Exoplanetary Atmospheres. arXiv, 2016; arXiv:astro-ph.EP/1602.06305. [Google Scholar]
- Tennyson, J.; Yurchenko, S.N. Laboratory spectra of hot molecules: Data needs for hot super-Earth exoplanets. Mol. Astrophys. 2017, 8, 1–18. [Google Scholar] [CrossRef]
- Roueff, E.; Lique, F. Molecular Excitation in the Interstellar Medium: Recent Advances in Collisional, Radiative, and Chemical Processes. Chem. Rev. 2013, 113, 8906–8938. [Google Scholar] [PubMed]
- Rybicki, G.B.; Hummer, D.G. An accelerated lambda iteration method for multilevel radiative transfer. I-Non-overlapping lines with background continuum. Astron. Astrophys. 1991, 245, 171–181. [Google Scholar]
- Van Zadelhoff, G.J.; Dullemond, C.P.; van der Tak, F.F.S.; Yates, J.A.; Doty, S.D.; Ossenkopf, V.; Hogerheijde, M.R.; Juvela, M.; Wiesemeyer, H.; Schöier, F.L. Numerical methods for non-LTE line radiative transfer: Performance and convergence characteristics. Astron. Astrophys. 2002, 395, 373–384. [Google Scholar]
- Decin, L.; Hony, S.; de Koter, A.; Justtanont, K.; Tielens, A.G.G.M.; Waters, L.B.F.M. Probing the mass-loss history of AGB and red supergiant stars from CO rotational line profiles. I. Theoretical model-Mass-loss history unravelled in VY CMa. Astron. Astrophys. 2006, 456, 549–563. [Google Scholar]
- Ferland, G.J.; Porter, R.L.; van Hoof, P.A.M.; Williams, R.J.R.; Abel, N.P.; Lykins, M.L.; Shaw, G.; Henney, W.J.; Stancil, P.C. The 2013 Release of Cloudy. Rev. Mexi. Astron. Astrofísica 2013, 49, 137–163. [Google Scholar]
- Mihalas, D.; Kunasz, P.B.; Hummer, D.G. Solution of the comoving frame equation of transfer in spherically symmetric flows. I - Computational method for equivalent-two-level-atom source functions. Astrophys. J. 1975, 202, 465–489. [Google Scholar] [CrossRef]
- Yang, B.; Stancil, P.C.; Balakrishnan, N.; Forrey, R.C. Rotational Quenching of CO due to H2 Collisions. Astrophys. J. 2010, 718, 1062–1069. [Google Scholar] [CrossRef]
- Faure, A.; Josselin, E. Collisional excitation of water in warm astrophysical media. I. Rate coefficients for rovibrationally excited states. Astron. Astrophys. 2008, 492, 257–264. [Google Scholar] [CrossRef]
- Pickett, H.M.; Poynter, R.L.; Cohen, E.A.; Delitsky, M.L.; Pearson, J.C.; Müller, H.S.P. Submillimeter, millimeter and microwave spectral line catalog. J. Q. Spectrosc. Radiat. Transf. 1998, 60, 883–890. [Google Scholar] [CrossRef]
- Schmidt, M.R.; He, J.H.; Szczerba, R.; Bujarrabal, V.; Alcolea, J.; Cernicharo, J.; Decin, L.; Justtanont, K.; Teyssier, D.; Menten, K.M.; et al. Herschel/HIFI observations of the circumstellar ammonia lines in IRC+10216. Astron. Astrophys. 2016, 592, A131. [Google Scholar] [CrossRef] [PubMed]
- Buhl, D.; Snyder, L.E.; Lovas, F.J.; Johnson, D.R. Silicon Monoxide: Detection of Maser Emission from the Second Vibrationally Excited State. Astrophys. J. Lett. 1974, 192, L97–L100. [Google Scholar] [CrossRef]
- Desmurs, J.F.; Bujarrabal, V.; Lindqvist, M.; Alcolea, J.; Soria-Ruiz, R.; Bergman, P. SiO masers from AGB stars in the vibrationally excited v = 1, v = 2, and v = 3 states. In Proceedings of the 12th European VLBI Network Symposium and Users Meeting (EVN 2014), Cagliari, Italy, 7–10 October 2014; p. 60. [Google Scholar]
- Ziurys, L.M.; Turner, B.E. Detection of interstellar vibrationally excited HCN. Astrophys. J. Lett. 1986, 300, L19–L23. [Google Scholar] [CrossRef]
- Bieging, J.H. Discovery of Two New HCN Maser Lines in Five Carbon Stars. Astrophys. J. Lett. 2001, 549, L125–L129. [Google Scholar] [CrossRef]
- Menten, K.M.; Wyrowski, F.; Keller, D.; Kamiński, T. Widespread HCN maser emission in carbon-rich evolved stars. arXiv, 2018; arXiv:astro-ph.SR/1803.00943. [Google Scholar] [CrossRef]
- Khouri, T.; Vlemmings, W.H.T.; Ramstedt, S.; Lombaert, R.; Maercker, M.; De Beck, E. ALMA observations of the vibrationally excited rotational CO transition v = 1, J = 3 − 2 towards five AGB stars. Mon. Not. R. Astron. Soc. 2016, 463, L74–L78. [Google Scholar] [CrossRef]
- Justtanont, K.; Khouri, T.; Maercker, M.; Alcolea, J.; Decin, L.; Olofsson, H.; Schöier, F.L.; Bujarrabal, V.; Marston, A.P.; Teyssier, D.; et al. Herschel/HIFI observations of O-rich AGB stars: molecular inventory. Astron. Astrophys. 2012, 537, A144. [Google Scholar] [CrossRef]
- Baudry, A.; Humphreys, E.M.L.; Herpin, F.; Torstensson, K.; Vlemmings, W.H.T.; Richards, A.M.S.; Gray, M.D.; De Breuck, C.; Olberg, M. Vibrationally excited water emission at 658 GHz from evolved stars. Astron. Astrophys. 2018, 609, A25. [Google Scholar] [CrossRef]
- Decin, L.; Richards, A.M.S.; Danilovich, T.; Homan, W.; Nuth, J.A. ALMA spectral line and imaging survey of a low and a high mass-loss rate AGB star between 335 and 362 GHz. Astron. Astrophys. 2018. forthcoming. [Google Scholar] [CrossRef]
- Velilla Prieto, L.; Sánchez Contreras, C.; Cernicharo, J.; Agúndez, M.; Quintana-Lacaci, G.; Bujarrabal, V.; Alcolea, J.; Balança, C.; Herpin, F.; Menten, K.M.; et al. The millimeter IRAM-30 m line survey toward IK Tauri. Astron. Astrophys. 2017, 597, A25. [Google Scholar] [CrossRef] [PubMed]
- Cernicharo, J.; Daniel, F.; Castro-Carrizo, A.; Agundez, M.; Marcelino, N.; Joblin, C.; Goicoechea, J.R.; Guélin, M. Unveiling the Dust Nucleation Zone of IRC+10216 with ALMA. Astrophys. J. Lett. 2013, 778, L25. [Google Scholar] [CrossRef]
- Schöier, F.L.; van der Tak, F.F.S.; van Dishoeck, E.F.; Black, J.H. An atomic and molecular database for analysis of submillimetre line observations. Astron. Astrophys. 2005, 432, 369–379. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Alexander, M.H.; Ba, Y.A.; Balakrishnan, N.; Balança, C.; Ceccarelli, C.; Cernicharo, J.; Daniel, F.; Dayou, F.; Doronin, M.; et al. BASECOL2012: A collisional database repository and web service within the Virtual Atomic and Molecular Data Centre (VAMDC). Astron. Astrophys. 2013, 553, A50. [Google Scholar] [CrossRef]
- Faure, A.; Varambhia, H.N.; Stoecklin, T.; Tennyson, J. Electron-impact rotational and hyperfine excitation of HCN, HNC, DCN and DNC. Mon. Not. R. Astron. Soc. 2007, 382, 840–848. [Google Scholar] [CrossRef]
- Daniel, F.; Faure, A.; Dagdigian, P.J.; Dubernet, M.L.; Lique, F.; Forêts, G.P.d. Collisional excitation of water by hydrogen atoms. Mon. Not. R. Astron. Soc. 2015, 446, 2312–2316. [Google Scholar] [CrossRef]
- Scribano, Y.; Faure, A.; Wiesenfeld, L. Communication: Rotational excitation of interstellar heavy water by hydrogen molecules. J. Chem. Phys. 2010, 133, 231105. [Google Scholar] [CrossRef] [PubMed]
- Dumouchel, F.; Kłos, J.; Toboła, R.; Bacmann, A.; Maret, S.; Hily-Blant, P.; Faure, A.; Lique, F. Fine and hyperfine excitation of NH and ND by He: On the importance of calculating rate coefficients of isotopologues. J. Chem. Phys. 2012, 137, 114306. [Google Scholar] [CrossRef] [PubMed]
- Dubernet, M.L.; Daniel, F.; Grosjean, A.; Faure, A.; Valiron, P.; Wernli, M.; Wiesenfeld, L.; Rist, C.; Noga, J.; Tennyson, J. Influence of a new potential energy surface on the rotational (de)excitation of H2O by H2 at low temperature. Astron. Astrophys. 2006, 460, 323–329. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Daniel, F.; Grosjean, A.; Lin, C.Y. Rotational excitation of ortho-H2O by para-H2 (j2 = 0, 2, 4, 6, 8) at high temperature. Astron. Astrophys. 2009, 497, 911–925. [Google Scholar] [CrossRef]
- Daniel, F.; Dubernet, M.L.; Pacaud, F.; Grosjean, A. Rotational excitation of 20 levels of para-H2O by ortho-H2 (j2 = 1, 3, 5, 7) at high temperature. Astron. Astrophys. 2010, 517, A13. [Google Scholar] [CrossRef]
- Daniel, F.; Dubernet, M.L.; Grosjean, A. Rotational excitation of 45 levels of ortho/para-H2O by excited ortho/para-H2 from 5 K to 1500 K: state-to-state, effective, and thermalized rate coefficients. Astron. Astrophys. 2011, 536, A76. [Google Scholar] [CrossRef]
- Faure, A.; Crimier, N.; Ceccarelli, C.; Valiron, P.; Wiesenfeld, L.; Dubernet, M.L. Quasi-classical rate coefficient calculations for the rotational (de)excitation of H2O by H2. Astron. Astrophys. 2007, 472, 1029–1035. [Google Scholar] [CrossRef]
- Van der Tak, F. Radiative Transfer and Molecular Data for Astrochemistry. In The Molecular Universe (IAU S280); Cernicharo, J., Bachiller, R., Eds.; Cambridge University Press: Cambridge, UK, 2011; Volume 280, pp. 449–460. [Google Scholar]
- Danilovich, T.; Van de Sande, M.; De Beck, E.; Decin, L.; Olofsson, H.; Ramstedt, S.; Millar, T.J. Sulphur-bearing molecules in AGB stars. I. The occurrence of hydrogen sulphide. Astron. Astrophys. 2017, 606, A124. [Google Scholar] [CrossRef]
- Lide, D. CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Viswanathan, R.; Dyke, T.R. Electric dipole moments and nuclear hyperfine interactions for H2S, HDS, and D2S. J. Mol. Spectrosc. 1984, 103, 231–239. [Google Scholar] [CrossRef]
- Jaber Al-Edhari, A.; Ceccarelli, C.; Kahane, C.; Viti, S.; Balucani, N.; Caux, E.; Faure, A.; Lefloch, B.; Lique, F.; Mendoza, E.; et al. History of the solar-type protostar IRAS 16293-2422 as told by the cyanopolyynes. Astron. Astrophys. 2017, 597, A40. [Google Scholar] [CrossRef]
- Agúndez, M.; Cernicharo, J.; Quintana-Lacaci, G.; Castro-Carrizo, A.; Velilla Prieto, L.; Marcelino, N.; Guélin, M.; Joblin, C.; Martín-Gago, J.A.; Gottlieb, C.A.; et al. Growth of carbon chains in IRC +10216 mapped with ALMA. Astron. Astrophys. 2017, 601, A4. [Google Scholar] [CrossRef] [PubMed]
- Faure, A.; Lique, F. The impact of collisional rate coefficients on molecular hyperfine selective excitation. Mon. Not. R. Astron. Soc. 2012, 425, 740–748. [Google Scholar] [CrossRef]
- Keto, E.; Rybicki, G. Modeling Molecular Hyperfine Line Emission. Astrophys. J. 2010, 716, 1315–1322. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 | The NRAO Spectral Line Catalog: www.splatalogue.net. |
| 4 | Lovas/National Institute of Standards and Technology: http://physics.nist.gov/restfreq. |
| 5 | The high-resolution transmission molecular absorption database: http://hitran.org. |
| 6 | High temperature molecular line lists for modelling exoplanet atmospheres: http://exomol.com. |
| 7 | |
| 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danilovich, T.; Decin, L.; Van de Sande, M. Molecular Data Needs for Modelling AGB Stellar Winds and Other Molecular Environments. Galaxies 2018, 6, 86. https://doi.org/10.3390/galaxies6030086
Danilovich T, Decin L, Van de Sande M. Molecular Data Needs for Modelling AGB Stellar Winds and Other Molecular Environments. Galaxies. 2018; 6(3):86. https://doi.org/10.3390/galaxies6030086
Chicago/Turabian StyleDanilovich, Taïssa, Leen Decin, and Marie Van de Sande. 2018. "Molecular Data Needs for Modelling AGB Stellar Winds and Other Molecular Environments" Galaxies 6, no. 3: 86. https://doi.org/10.3390/galaxies6030086
APA StyleDanilovich, T., Decin, L., & Van de Sande, M. (2018). Molecular Data Needs for Modelling AGB Stellar Winds and Other Molecular Environments. Galaxies, 6(3), 86. https://doi.org/10.3390/galaxies6030086




