Surveying Planetary Nebulae Central Stars for Close Binaries: Constraining Evolution of Central Stars Based on Binary Parameters
Abstract
1. Introduction
2. Relationships between Close Binary CSs and Their PNe
2.1. The Connection between Central Binaries and PN Shaping
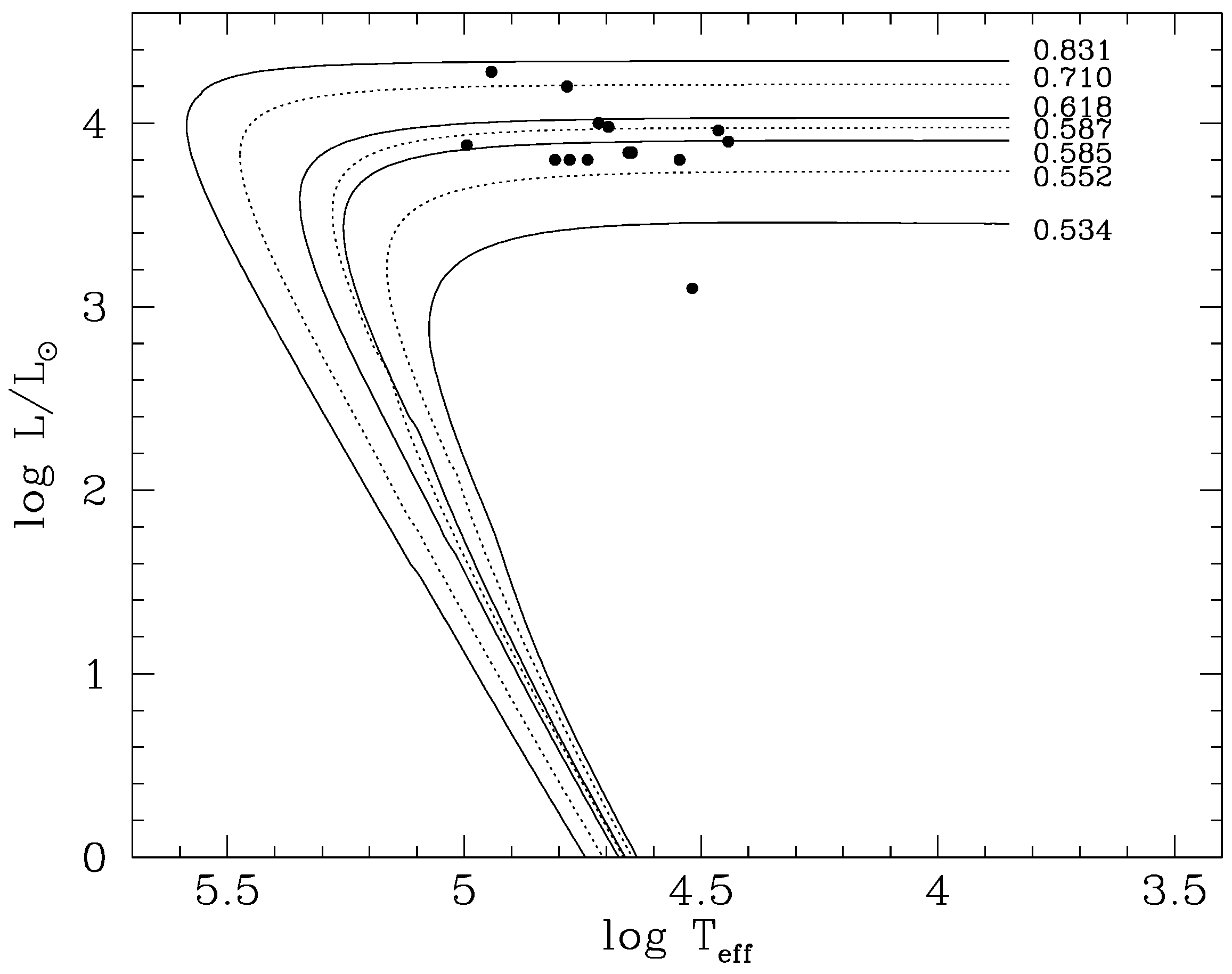
2.2. The CE Phase and Evolution of the CS
2.3. Companions to Binary CSPNe and the Close Binary Fraction
3. The Relationship between PPNe and PNe
4. Discussion
Funding
Conflicts of Interest
References
- Bond, H.E.; Livio, M. Morphologies of Planetary Nebulae Ejected by Close-Binary Nuclei. Astrophys. J. 1990, 355, 568–576. [Google Scholar] [CrossRef]
- Miszalski, B.; Acker, A.; Moffat, A.F.J.; Parker, Q.A.; Udalski, A. Binary planetary nebulae nuclei towards the Galactic bulge. I. Sample discovery, period distribution, and binary fraction. Astron. Astrophys. 2009, 496, 813–825. [Google Scholar] [CrossRef]
- De Marco, O.; Long, J.; Jacoby, G.H.; Hillwig, T.; Kronberger, M.; Howell, S.B.; Reindl, N.; Margheim, S. Identifying close binary central stars of PN with Kepler. Mon. Not. R. Astron. Soc. 2015, 448, 3587–3602. [Google Scholar] [CrossRef]
- Hillwig, T.C. The physical characteristics of binary central stars of planetary nebulae. In Proceedings of the Asymmetric Planetary Nebulae 5 Conference, Bowness-on-Windermere, UK, 20–25 June 2010; p. 275. [Google Scholar]
- Santander-Garcia, M.; Rodríguez-Gil, P.; Jones, D.; Corradi, R.L.M.; Miszalski, B.; Pyrzas, S.; Rubio-Díez, M.M. The binary central stars of PNe with the shortest orbital period. In Proceedings of the Asymmetric Planetary Nebulae 5 Conference, Bowness-on-Windermere, UK, 20–25 June 2010; p. 259. [Google Scholar]
- Douchin, D.; De Marco, O.; Frew, D.J.; Jacoby, G.H.; Jasniewicz, G.; Fitzgerald, M.; Passy, J.C.; Harmer, D.; Hillwig, T.; Moe, M. The binary fraction of planetary nebula central stars-II. A larger sample and improved technique for the infrared excess search. Mon. Not. R. Astron. Soc. 2015, 448, 3132–3155. [Google Scholar] [CrossRef]
- De Marco, O.; Bond, H.E.; Harmer, D.; Fleming, A.J. Indications of a Large Fraction of Spectroscopic Binaries among Nuclei of Planetary Nebulae. Astrophys. J. 2004, 602, L93. [Google Scholar] [CrossRef]
- Jones, D.; Van Winckel, H.; Aller, A.; Exter, K.; De Marco, O. The long-period binary central stars of the planetary nebulae NGC 1514 and LoTr 5. Astron. Astrophys. 2017, 600, L9. [Google Scholar] [CrossRef]
- Kashi, A.; Soker, N. A circumbinary disc in the final stages of common envelope and the core-degenerate scenario for Type Ia supernovae. Mon. Not. R. Astron. Soc. 2011, 417, 1466–1479. [Google Scholar] [CrossRef]
- Paczynski, B. Common Envelope Binaries. Struct. Evol. Close Bin. Syst. 1976, 73, 75. [Google Scholar]
- Bond, H.E.; Liller, W.; Mannery, E.J. UU Sagittae: Eclipsing nucleus of the planetary nebula Abell 63. Astrophys. J. 1978, 223, 252. [Google Scholar] [CrossRef]
- Morris, M. Models for the structure and origin of bipolar nebulae. Astrophys. J. 1981, 249, 572–585. [Google Scholar] [CrossRef]
- Soker, N. Close Stellar Binary Systems by Grazing Envelope Evolution. Astrophys. J. 2015, 800, 114. [Google Scholar] [CrossRef]
- Ivanova, N.; Nandez, J. Planetary Nebulae Embryo after a Common Envelope Event. Galaxies 2018, 6, 75. [Google Scholar] [CrossRef]
- Abu-Backer, A.; Gilkis, A.; Soker, N. Orbital Radius during the Grazing Envelope Evolution. Astrophys. J. 2018, 861, 136. [Google Scholar] [CrossRef]
- Hillwig, T.C.; Jones, D.; De Marco, O.; Bond, H.E.; Margheim, S.; Frew, D. Observational Confirmation of a Link between Common Envelope Binary Interaction and Planetary Nebula Shaping. Astrophys. J. 2016, 832, 125. [Google Scholar] [CrossRef]
- Nordhaus, J. Common Envelope Evolution: Implications for Post-AGB Stars and Planetary Nebulae. In Planetary Nebulae: Multi-Wavelength Probes of Stellar and Galactic Evolution; IAU Symposium; Cambridge University Press: Cambridge, UK, 2017; Volume 323, p. 207. [Google Scholar] [CrossRef]
- Corradi, R.L.M.; García-Rojas, J.; Jones, D.; Rodríguez-Gil, P. Binarity and the Abundance Discrepancy Problem in Planetary Nebulae. Astrophys. J. 2015, 803, 99. [Google Scholar] [CrossRef]
- Jones, D.; Wesson, R.; García-Rojas, J.; Corradi, R.L.M.; Boffin, H.M.J. NGC 6778: Strengthening the link between extreme abundance discrepancy factors and central star binarity in planetary nebulae. Mon. Not. R. Astron. Soc. 2016, 455, 3263–3272. [Google Scholar] [CrossRef]
- García-Rojas, J.; Corradi, R.L.M.; Monteiro, H.; Jones, D.; Rodríguez-Gil, P.; Cabrera-Lavers, A. Imaging the Elusive H-poor Gas in the High adf Planetary Nebula NGC 6778. Astrophys. J. 2016, 824, L27. [Google Scholar] [CrossRef]
- Hall, P.D.; Tout, C.A.; Izzard, R.G.; Keller, D. Planetary nebulae after common-envelope phases initiated by low-mass red giants. Mon. Not. R. Astron. Soc. 2013, 435, 2048–2059. [Google Scholar] [CrossRef]
- Hillwig, T.C.; Frew, D.J.; Reindl, N.; Rotter, H.; Webb, A.; Margheim, S. Binary Central Stars of Planetary Nebulae Discovered through Photometric Variability. V. The Central Stars of HaTr 7 and ESO 330-9. Astrophys. J. 2017, 153, 24. [Google Scholar] [CrossRef]
- Frew, D.J.; Parker, Q.A.; Bojičić, I.S. The Hα surface brightness-radius relation: A robust statistical distance indicator for planetary nebulae. Mon. Not. R. Astron. Soc. 2016, 455, 1459–1488. [Google Scholar] [CrossRef]
- Bond, H.E. Binarity of Central Stars of Planetary Nebulae. arXiv, 1999; arXiv:astro-ph/9909516. [Google Scholar]
- Parthasarathy, M.; Pottasch, S.R. The far-infrared (IRAS) excess in HD 161796 and related stars. Astron. Astrophys. 1986, 154, L16. [Google Scholar]
- Hrivnak, B.J.; Kwok, S.; Volk, K.M. The High-Latitude F Supergiant IRAS 18095+2704: A Proto-Planetary Nebula. Astrophys. J. 1988, 331, 832–837. [Google Scholar] [CrossRef]
- Van der Veen, W.E.C.J.; Habing, H.J.; Geballe, T.R. Objects in transition from the AGB to the planetary nebula stage: New visual and infrared observations. Astron. Astrophys. 1989, 226, 108. [Google Scholar]
- Hrivnak, B.J.; Langill, P.P.; Su, K.Y.L.; Kwok, S. Subarcsecond Optical Imaging of Proto-Planetary Nebulae. Astrophys. J. 1999, 513, 421. [Google Scholar] [CrossRef]
- Ueta, T.; Meixner, M.; Bobrowsky, M. A Hubble Space Telescope Snapshot Survey of Proto-Planetary Nebula Candidates: Two Types of Axisymmetric Reflection Nebulosities. Astrophys. J. 2000, 528, 861. [Google Scholar] [CrossRef]
- Sahai, R. Multi-polar Structures in Young Planetary and Protoplanetary Nebulae. In Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 2003; Volume 209, p. 471. [Google Scholar]
- Hrivnak, B.J. A Search for Binaries in Proto-Planetary Nebulae. In Proceedings of the Asymmetrical Planetary Nebulae IV, La Palma, Spain, 18–22 June 2017. [Google Scholar]
- Hrivnak, B.J.; Van de Steene, G.; Van Winckel, H.; Sperauskas, J.; Bohlender, D.; Lu, W. Where are the Binaries? Results of a Long-term Search for Radial Velocity Binaries in Proto-planetary Nebulae. Astrophys. J. 2017, 846, 96. [Google Scholar] [CrossRef]
- Galaviz, P.; De Marco, O.; Passy, J.-C.; Staff, J.E.; Iaconi, R. Common Envelope Light Curves. I. Grid-code Module Calibration. Astrophys. J. Suppl. Ser. 2017, 229, 36. [Google Scholar] [CrossRef]
- Miller Bertolami, M.M. New Models for the Evolution of Post-Asymptotic Giant Branch Stars and Central Stars of Planetary Nebulae. Astron. Astrophys. 2016, 588, A25. [Google Scholar] [CrossRef]
- Eggleton, P.P. Aproximations to the radii of Roche lobes. Astrophys. J. 1983, 268, 368. [Google Scholar] [CrossRef]
- Rodríguez-Gil, P.; Santander-García, M.; Knigge, C.; Corradi, R.L.M.; Gänsicke, B.T.; Barlow, M.J.; Drake, J.J.; Drew, J.; Miszalski, B.; Napiwotzki, R.; et al. The orbital period of V458 Vulpeculae, a post-double common-envelope nova. Mon. Not. R. Astron. Soc. 2010, 407, L21. [Google Scholar] [CrossRef]
- Tovmassian, G.; Yungelson, L.; Rauch, T.; Suleimanov, V.; Napiwotzki, R.; Stasińska, G.; Tomsick, J.; Wilms, J.; Morisset, C.; Pena, M.; et al. The Double-degenerate Nucleus of the Planetary Nebula TS 01: A Close Binary Evolution Showcase. Astrophys. J. 2010, 714, 178. [Google Scholar] [CrossRef]
- Bruch, A.; Vaz, L.P.R.; Diaz, M.P. An analysis of the light curve of the post common envelope binary MT Serpentis. Astron. Astrophys. 2001, 377, 898–910. [Google Scholar] [CrossRef]
- Shimanskii, V.V.; Borisov, N.V.; Sakhibullin, N.A.; Sheveleva, D.V. MT Ser, a binary blue subdwarf. Astron. Rep. 2008, 52, 479–486. [Google Scholar] [CrossRef]
- Drilling, J.S. LSS 2018: A double-lined spectroscopic binary central star with an extremely large reflection effect. Astrophys. J. 1985, 294, L107. [Google Scholar] [CrossRef]
- Hilditch, R.W.; Harries, T.J.; Hill, G. On the reflection effect in three sdOB binary stars. Mon. Not. R. Astron. Soc. 1996, 279, 1380–1392. [Google Scholar] [CrossRef]
- Afşar, M.; Ibanoglu, C. Two-colour photometry of the binary planetary nebula nuclei UU Sagitte and V477 Lyrae: Oversized secondaries in post-common-envelope binaries. Mon. Not. R. Astron. Soc. 2008, 391, 802–814. [Google Scholar] [CrossRef]
- Hillwig, T.C.; Bond, H.E.; Afşar, M.; De Marco, O. Binary Central Stars of Planetary Nebulae Discovered through Photometric Variability. II. Modeling the Central Stars of NGC 6026 and NGC 6337. Astron. J. 2010, 140, 319. [Google Scholar] [CrossRef]
- Shimanskii, V.V.; Borisov, N.V.; Sakhibullin, N.A.; Surkov, A.E. The Nature of the Unique Precataclysmic Variable V664 Cas with Two-Peaked Balmer Lines in Its Spectrum. Astron. Rep. 2004, 48, 563–576. [Google Scholar] [CrossRef]
- Hillwig, T.C.; Bond, H.E.; Frew, D.J.; Schaub, S.C.; Bodman, E.H.L. Binary Central Stars of Planetary Nebulae Discovered through Photometric Variability. IV. The Central Stars of HaTr 4 and Hf 2-2. Astron. J. 2016, 152, 34. [Google Scholar] [CrossRef]
- Shimanskii, V.V.; Borisov, N.V.; Pozdnyakova, S.A.; Bikmaev, I.F.; Vlasyuk, V.V.; Sakhibullin, N.A.; Spiridonova, O.I. Fundamental parameters of BE UMa revised. Astron. Rep. 2008, 52, 558–575. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Chen, X.; De Marco, O.; Fryer, C.L.; Gaburov, E.; Ge, H.; Glebbeek, E.; Han, Z.; Li, X.D.; et al. Common envelope evolution: Where we stand and how we can move forward. Astron. Astrophys. Rev. 2013, 21, 59. [Google Scholar] [CrossRef]
| PN Name | (days) | () | () | () | Ref. | ||
|---|---|---|---|---|---|---|---|
| V458 Vul | 0.06812255 | 0.58 | 1 | 0.27 | 3.88 | 4.99 | [36] |
| TS 01 | 0.163508 | 0.80 | 0.54 | 0.57 | 4.28 | 4.94 | [37] |
| NGC 6337 | 0.1736133 | 0.56 | 0.35 | 0.53 | 3.80 | 4.81 | [16] |
| Abell 41 | 0.226453066 | 0.56 | 0.56 | 0.61 | 3.80 | 4.78 | [38,39] |
| HaTr 7 | 0.3221246 | 0.56 | 0.14 | 0.88 | 3.80 | 4.74 | [22] |
| DS 1 | 0.35711296 | 0.70 | 0.3 | 0.96 | 4.20 | 4.78 | [40,41] |
| Abell 63 | 0.46506921 | 0.63 | 0.29 | 1.10 | 4.00 | 4.72 | [42] |
| Abell 46 | 0.47172909 | 0.51 | 0.14 | 1.09 | 3.10 | 4.51 | [42] |
| Lo 16 | 0.48626 | 0.6 | 0.4 | 1.08 | 3.98 | 4.69 | in prep |
| NGC 6026 | 0.528086 | 0.57 | 0.57 | 1.09 | 3.84 | 4.65 | [43] |
| HFG 1 | 0.5816475 | 0.57 | 1.09 | 1.13 | 3.84 | 4.65 | [44] |
| Abell 65 | 1.0037577 | 0.56 | 0.22 | 1.79 | 3.80 | 4.54 | [45] |
| LTNF 1 | 2.2911667 | 0.59 | 0.25 | 3.14 | 3.96 | 4.46 | [46] |
| Sp 1 | 2.90611 | 0.58 | 0.48 | 3.45 | 3.90 | 4.44 | [16] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hillwig, T. Surveying Planetary Nebulae Central Stars for Close Binaries: Constraining Evolution of Central Stars Based on Binary Parameters. Galaxies 2018, 6, 85. https://doi.org/10.3390/galaxies6030085
Hillwig T. Surveying Planetary Nebulae Central Stars for Close Binaries: Constraining Evolution of Central Stars Based on Binary Parameters. Galaxies. 2018; 6(3):85. https://doi.org/10.3390/galaxies6030085
Chicago/Turabian StyleHillwig, Todd. 2018. "Surveying Planetary Nebulae Central Stars for Close Binaries: Constraining Evolution of Central Stars Based on Binary Parameters" Galaxies 6, no. 3: 85. https://doi.org/10.3390/galaxies6030085
APA StyleHillwig, T. (2018). Surveying Planetary Nebulae Central Stars for Close Binaries: Constraining Evolution of Central Stars Based on Binary Parameters. Galaxies, 6(3), 85. https://doi.org/10.3390/galaxies6030085





