1. Introduction
The R-matrix method [
1] has provided a large quantity of electron-impact excitation data within various astrophysical databases such as CLOUDY [
2], AtomDB
1, CHIANTI [
3] and Open-ADAS
2. The Fe-peak elements have a nuclear charge that allows us the opportunity to assess this variation between a semi-relativistic Breit–Pauli [
4] and a fully-relativistic Dirac–Coulomb [
5] framework for near-neutral (or low-ionized) systems.
Lowly-charged ions of the iron-peak elements (
,
,
,
) contribute in general significantly to the opacity of the interstellar gas clouds and other astrophysical objects. If the good conditions are given for nickel to be in its atomic form and not to be depleted in grains, then the absorbance lines of its lowly-charged ions will contribute in a significant way to the opacity. Nickel can be important in stellar atmospheres, and models of hot stars in nonlocal thermodynamic equilibrium should take into account these photoionization cross-sections. Photoionization of these species initially in the ground or a low-energy metastable state is the principal process for this opacity. For the correct interpretation of the collected spectra from a variety of astrophysical objects, such as interstellar clouds, nebulae, remains of supernovae or the previously mentioned stellar atmospheres, it is essential to rely on accurate data for the photoionization of ions present in the interstellar clouds. The Opacity Project [
6]
3 represents an international collaboration between research institutions to maintain a large database of opacity tables.
Opacity calculations are also an important part of the CLOUDY software package used in the simulation and interpretation of the spectra collected from interstellar clouds [
2]
4. CLOUDY is extensively used by groups in theoretical astronomy all over the world.
Using as our benchmark system, we assess the variation in the electron-impact excitation and photoionisation rates using a Dirac atomic R-matrix code (DARC). To get the atomic structures to be used in the different calculations as close as possible, we use the same set of configurations in the target configuration interaction (CI) expansions. We discuss issues of convergence in terms of the atomic structure CI and close coupling (CC) expansions with the goal of generating uncertainty information for every transition as a function of electron temperature.
Recent work for a low-ionized iron peak element was performed by Zhang and Pradhan [
7,
8]. They calculated the electron-impact excitation of
. Subsequently, Ramsbottom and co-workers performed several calculations, each with an improved structure of the target [
9,
10,
11]. They included in the expansion orbitals up to
and a total of 113
terms in the close coupling expansion. Other works along the isoelectronic sequences of low-ionized iron peak elements are Zhang and co-workers [
12] for electron-impact excitation of
and Bautista [
13] for electron-impact excitation of
.
Neither the photoionization of , nor the electron-impact excitation of have been previously addressed in the literature with an R-matrix method.
We present preliminary results for the photoionization of and electron-impact excitation of . The definitive results will be ready to be used by any modelling code.
2. Method
We used a fully-relativistic DARC method [
5,
14,
15] to calculate the photoionization of
and electron-impact excitation of
. For the atomic structure of the
target, we used the general relativistic atomic structure package (GRASP) [
16,
17]. We include a set of 23 non-relativistic configurations, distributing the 25 electrons of the target among 13 orbitals:
- Even parity
, , , , , , , , , , , , , ,
- Odd parity
, , , , , , ,
With this configuration set, we obtained a total of 6841 levels. From the total set of target levels, we included the lowest-energy 262 states in the CC expansion. With this basis, we obtained a reasonably complete description of the system within our computational capabilities.
To build the configuration set for the bound states of the initial ion , we added one electron to the previous set for . This led to an enormous amount of configurations and levels and made the calculation impossible even for current supercomputer capabilities. Hence, we simplified the structure cutting the highest-excited configurations from our set.
In addition, we included for each symmetry 20 continuum functions. With this set, we can describe with good accuracy the continuum up to .
As a test of the accuracy of our dataset, we performed two variants of the close coupling calculation. In the first one, we kept the Hamiltonian of the final ion
as theoretically determined by DARC. In the second one, we manually modified the diagonal elements of the Hamiltonian before its diagonalization, to ensure that the energies of the final ion
agreed exactly with the recommended values of the NIST database [
18], and as consequence, the transition wavelengths agreed exactly with the observed ones.
3. Level Energies
As a comparison, we performed a second calculation for the atomic structure of the target using the program
autostructure [
19]. In this calculation, we included exactly the same configuration set as the one with GRASP in order to get an atomic structure as close as possible for both calculations. The scaling parameters obtained with
autostructure after the optimization process were: 1s
; 2s
; 2p
; 3s
; 3p
; 3d
; 4s
; 4p
; 4d
; 5s
; 5p
; 6s
; 6p
.
Table 1 shows a comparison of the level energies with respect to the ground state between both calculations, GRASP and AS, and the recommended values of the NIST data table [
18].
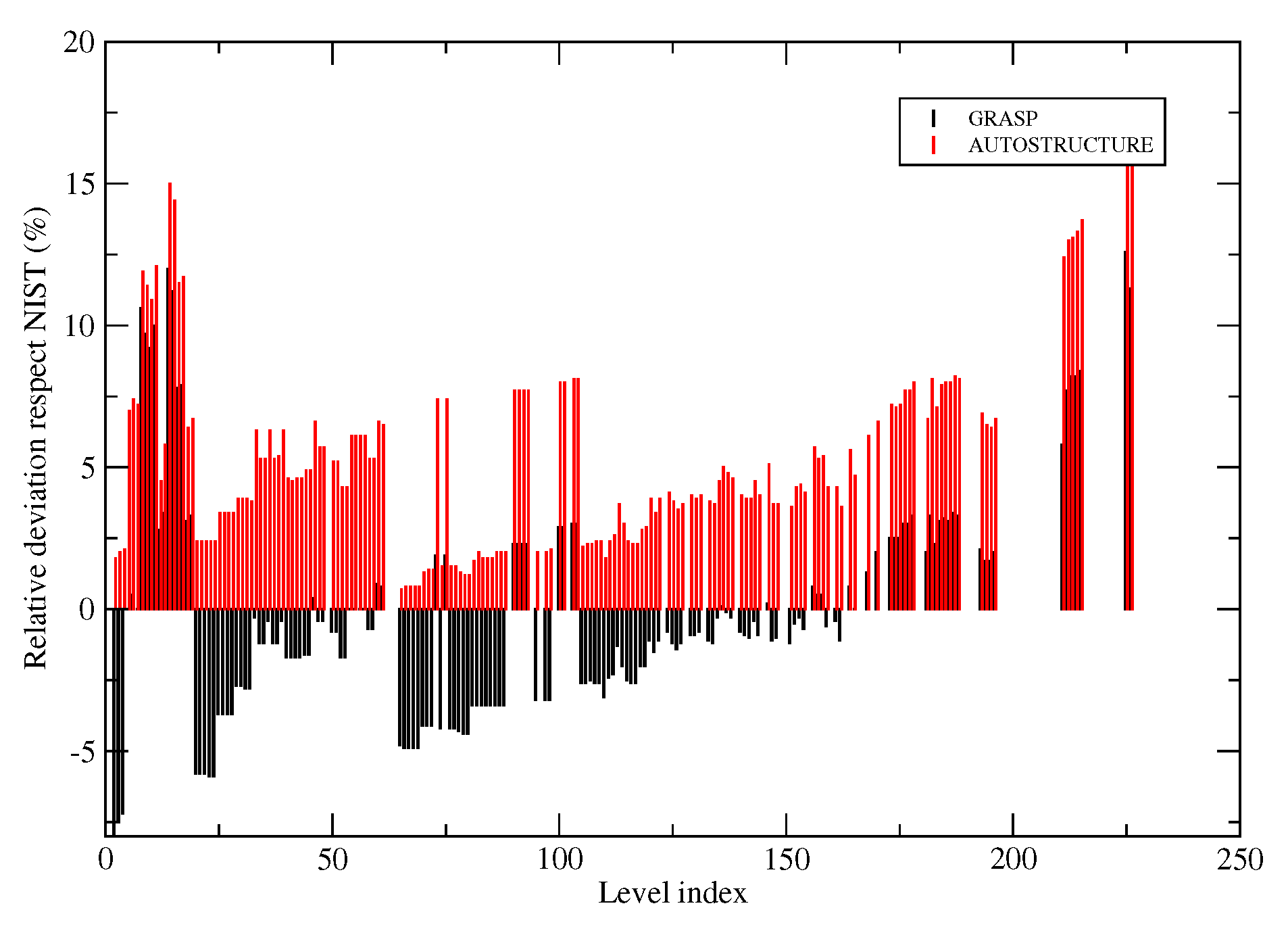
Figure 1 shows the relative deviation in percentage of the calculated excitation energy values of
with GRASP and
autostructure with respect to the recommended data of NIST. In general terms, the relative errors of GRASP and AS were the same order, being the GRASP one slightly smaller. The largest deviation was order
, and this was a quite acceptable limit if we consider the difficulty of the system, with 13 active electrons and an open d shell. Each configuration split into several tens of
levels, and with the present expansion, we obtained a total of 6841 levels. We also obtained a smaller error than the previous works for the isoelectronic system
, of
in
coupling for the one of Pradhan and Berrington [
7] and of
for the one of Ramsbottom et al. [
9].
4. Preliminary Results
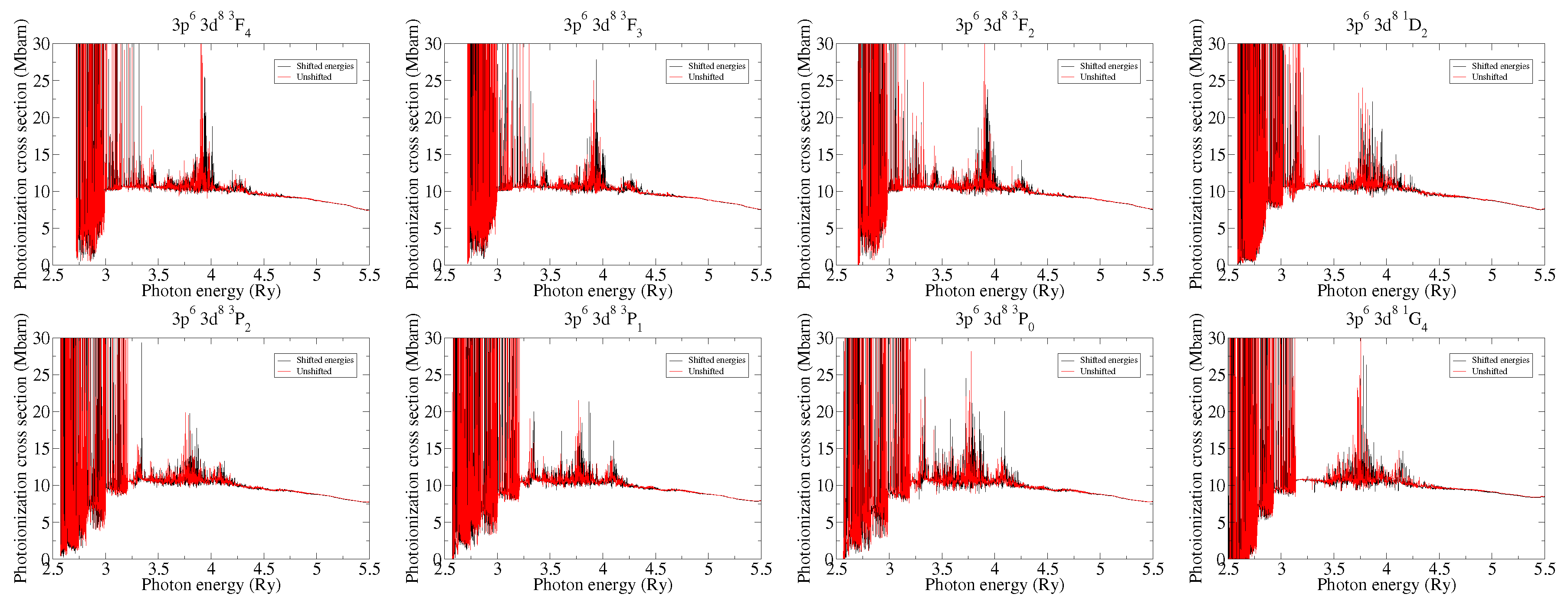
We calculated the photoionization cross-sections of from its ground and the lowest excited initial levels. We included all possible dipole-allowed transitions in the close coupling expansion. The maximum number of channels for any partial wave was 1662.
Figure 2 shows the photoionization cross-sections as a function of the photon energy. We display for each initial level both versions of the calculation, with shifted and unshifted target level energies.
The photoionization cross-sections showed the usual structure. A threshold was present for photon energies below the ionization potential, and in the case of the ground level, its values was . Below the energy threshold for each initial level, the cross-section had a value of zero. For energies above the threshold, there was a resonance structure corresponding with exact excitation energies to bound levels of the ionized species . As expected, the main difference between the shifted and unshifted calculations lied in the position of these resonances, as the level energies of the target had been shifted. On the other hand, the background of the curve was equal in both versions of the calculation. Finally, for photon energies higher than the last excitation energy included in the close coupling expansion, no resonances were present, and the cross-section took a smooth form. Curves for both versions of the calculation were equal in this high-energy region, as it did not depend on the exact position of the target energies.
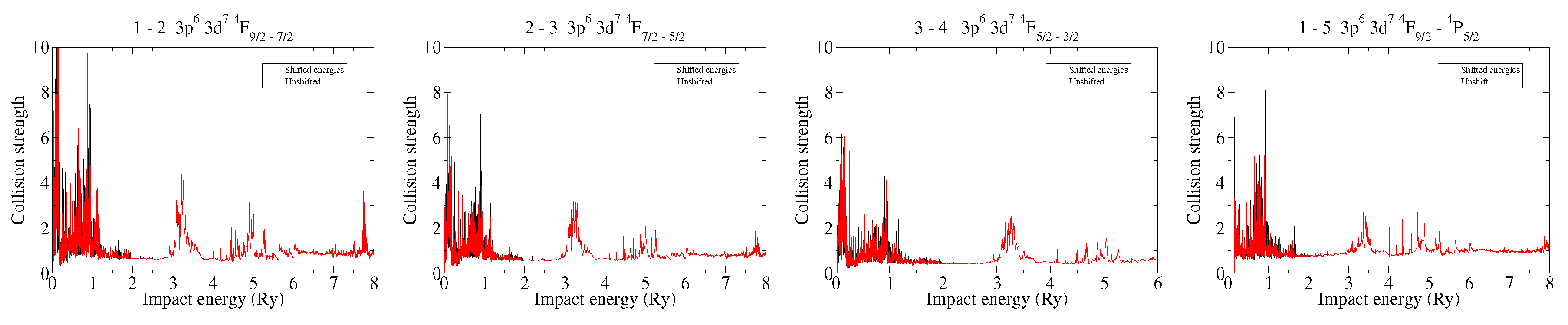
Figure 3 shows the electron-impact excitation of
for some relevant transitions in astrophysical plasma modelling, and
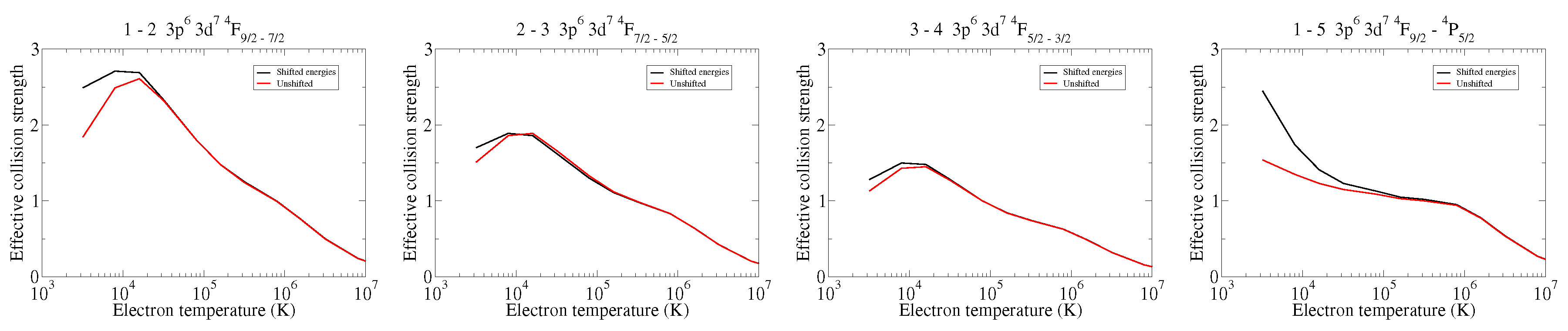
Figure 4 shows the effective collision strength convoluted with a Maxwellian distribution for the same transitions. We also compare both versions of the calculation, with the shifted target energies to the observed values and the unshifted ones.
We also appreciated in the excitation collision strengths the usual resonance structure over a background. The differences between both versions of the calculation lied in the position of the resonances. The effective collision strengths differed mainly at low temperature, where the Maxwellian envelope was narrow and the position of the resonances contributed the most. The peak abundance temperature for
in a local thermodynamical equilibrium collisional plasma had a valued of
[
20,
21]. In the range of the peak-abundance temperature, the difference in the effective collision strengths between both versions of the calculation was practically zero.
As a test of accuracy, we can take the difference between the two versions of the calculation, with shifted and unshifted target energies. To avoid large overestimation in the error due to the position of the resonances in the case of the photoionization, we performed a Gaussian convolution of the cross-sections and calculated the difference in the convoluted results. In the case that the convolution was performed with an envelope width of , the maximum relative difference was order , if we reduce the width to , the maximum difference was order . The maximum differences lied in the resonance region, for photon energy below . In the higher-energy region, the relative difference was below , even for convolution widths below . In the case of the electron-impact excitation, performing the Maxwellian convolution, the largest differences were in the low temperature region. In the worst case, these differences reached .
The principal source of error lied in the atomic structure of the target. To analyse that, we would need to check the results with a different atomic structure, for example performing the CC calculation with the structure obtained with autostructure. That was a problem, which will be treated in a further work. Another source of error in the excitation calculation was the convergence of the expansion in partial waves. We have checked several expansions, including partial waves up to , and and including top-up to J infinity. The largest difference in the collision strengths between the calculations with and without top-up was order , and the largest disparity between the calculations up to and was order , so the calculation was clearly converged in terms of partial wave expansion.
The present results are the first available R-matrix dataset in the literature for the photoionization of and electron-impact excitation of .
5. Conclusions
We presented preliminary results for the photoionisation of and the electron-impact excitation of . We adopt a fully-relativistic Dirac atomic R-matrix code (DARC) with a configuration interaction expansion of the target including a total of 6841 intermediate coupling levels. The 262 lowest levels were included in the close coupling expansion. For each of the two processes, we performed two variations of the calculation. The first one was done without any modification of the Hamiltonian matrix, including the target energies and atomic wave functions, as obtained within GRASP. In the second version, we replaced prior to the diagonalization the calculated energies by the recommended values tabulated in the NIST database. For both processes, the differences between the two calculations performed was negligible with the background cross-section. The main difference remained in the position of the resonances, but after performing a proper convolution, this difference was softened.
Accuracy checks were performed throughout the analysis, and we are confident that the present data represent the best available to date for use by the astrophysics and plasma physics communities. For electron-impact excitation within the levels split from the ground term and Maxwellian temperatures in the range of the peak abundance, we gave a preliminary estimation of the accuracy of present data as . For lower temperatures, such as those in photoionised plasma, where can exist, we estimated the accuracy as . For the photoionization of and photons in the ultraviolet region, we estimated the accuracy of the calculation as . Further calculations and comparison will be carried out in order to limit the accuracy of the present data.
Author Contributions
Conceptualization, L.F.M., C.A.R. and C.P.B.; Methodology, L.F.M., C.A.R. and C.P.B.; Software, L.F.M. and C.P.B.; Validation, L.F.M., C.A.R. and C.P.B.; Formal Analysis, L.F.M.; Investigation, L.F.M.; Resources, C.A.R. and C.P.B.; Data Curation, L.F.M.; Writing—Original Draft Preparation, L.F.M.; Writing—Review & Editing, L.F.M.; Visualization, L.F.M., C.A.R. and C.P.B.; Supervision, C.P.B.; Project Administration, C.A.R. and C.P.B.; Funding Acquisition, C.A.R. and C.P.B.
Funding
This research was funded by the Science and Technology Facilities Council (STFC) of the United Kingdom under the QUB Astronomy Observation and Theory Consolidated Grant number ST/P000312/1.
Acknowledgments
The computation was performed at the supercomputer Hazelhen property of the Höchstleistungsrechner für Wissenschaft und Wirtschaft (Germany) and the Archer property of the Engineering and Physical Science Research Council under the allocation E464-RAMPA.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Burke, P.G. R-Matrix of Atomic Collisions: Application to Atomic, Molecular, and Optical Processes; Springer-Verlag: New-York, NY, USA, 2011. [Google Scholar]
- Ferland, G.J.; Chatzikos, M.; Guzmán, F.; Lykins, M.L.; van Hoof, P.A.M.; Williams, R.J.R.; Abel, N.P.; Badnell, N.R.; Keenan, F.P.; Porter, R.L.; et al. The 2017 Release of Cloudy. arXiv, 2017; arXiv:1705.10877v2. [Google Scholar]
- Landi, E.; Young, P.R.; Dere, K.P.; Del Zanna, G.; Mason, H.E. CHIANTI—An atomic database for emission lines. XIII. Soft X-ray improvements and other changes. Astroph. J. 2013, 763, 86. [Google Scholar] [CrossRef]
- Griffin, D.C.; Badnell, N.R.; Pindzola, M.S. R-matrix electron-impact excitation cross-sections in intermediate coupling: An MQDT transformation approach. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 3713–3727. [Google Scholar] [CrossRef]
- Norrington, P.H.; Grant, I.P. Electron scattering from Ne II using the relativistic R-matrix method. J. Phys. B At. Mol. Phys. 1981, 14, L261–L267. [Google Scholar] [CrossRef]
- The Opacity Project Team. The Opacity Project Vol. 1; Institute of Physics Publications: Bristol, UK, 1995. [Google Scholar]
- Pradhan, A.K.; Berrington, K.A. R-matrix calculations for electron impact excitation of Fe II: LS coupling and Breit–Pauli approximations. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 157. [Google Scholar] [CrossRef]
- Zhang, H.L.; Pradhan, A.K. Atomic data from the Iron Project. VI. Collision strengths and rate coefficients for Fe II. Astron. Astroph. 1995, 293, 953. [Google Scholar]
- Ramsbottom, C.A.; Noble, C.J.; Burke, V.M.; Scott, M.P.; Kisielius, R.; Burke, P.G. Electron impact excitation of Fe II: Total LS effective collision strengths. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2999–3014. [Google Scholar] [CrossRef]
- Ramsbottom, C.A.; Hudson, C.E.; Norrington, P.H.; Scott, M.P. Electron-impact excitation of Fe II: Collision strengths and effective collision strengths for low-lying fine-structure forbidden transitions. Astron. Astroph. 2007, 475, 765–769. [Google Scholar] [CrossRef]
- Ramsbottom, C.A. Electron-impact excitation of Fe II: Effective collision strengths for optically allowed fine-structure transitions. At. Data Nucl. Data Tables 2009, 95, 910–986. [Google Scholar] [CrossRef]
- Zhang, H.L.; Pradhan, A.K. Atomic data from the Iron Project. XXVII. Electron impact excitation collision strengths and rate coefficients for Fe IV. Astron. Astroph. Suppl. Ser. 1997, 126, 373–378. [Google Scholar] [CrossRef]
- Bautista, M.A. Atomic data from the iron project—LV. Electron impact excitation of Ni II. Astron. Astroph. 2004, 420, 763–768. [Google Scholar] [CrossRef]
- Ait-Tahar, S.; Grant, I.P.; Norrington, P.H. Electron scattering by Fe XXII within the Dirac R-matrix approach. Phys. Rev. A 1996, 54, 3984–3989. [Google Scholar] [CrossRef] [PubMed]
- Norrington, P.H.; Grant, I.P. Low-energy electron scattering by Fe XXIII and Fe VII using the Dirac R-matrix method. J. Phys. B At. Mol. Opt. Phys. 1987, 20, 4869–4881. [Google Scholar] [CrossRef]
- Dyall, K.G.; Grant, I.P.; Johnson, C.T.; Parpia, F.A.; Plummer, E.P. GRASP: A general-purpose relativistic atomic structure program. Comput. Phys. Commum. 1989, 55, 425. [Google Scholar] [CrossRef]
- Parpia, F.A.; Fischer, C.F.; Grant, I.P. GRASP92: A package for large-scale relativistic structure calculations. Comput. Phys. Commum. 1996, 94, 249. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.5.6). Available online: https://physics.nist.gov/asd (accessed on 27 June 2018).
- Badnell, N.R. A Breit–Pauli distorted wave implementation for AUTOSTRUCTURE. Comput. Phys. Commum. 2011, 182, 1528–1535. [Google Scholar] [CrossRef]
- Mazzotta, P.; Mazzitelli, G.; Colafrancesco, S.; Vittorio, N. Ionization balance for optically thin plasmas: Rate coefficients for all atoms and ions of the elements H to Ni. Astron. Astroph. Suppl. Ser. 1998, 133, 403–409. [Google Scholar] [CrossRef]
- Bryans, P.; Badnell, N.R.; Gorczyca, T.W.; Laming, J.M.; Mitthumsiri, W.; Savin, D.W. Collisional ionization equilibrium for optically thin plasmas. I. Updated recombination rate coefficients for bare through sodium-like ions. Astroph. J. Suppl. Ser. 2006, 167, 343–356. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).