Abstract
In this paper, we show how baryonic physics can solve the problem of the striking diversity in dwarf galaxy rotation curves shapes. To this aim, we compare the distribution of galaxies of the SPARC sample, in the plane - ( being the galaxy rotation velocity at 2 kpc, and being the outermost one), with that of galaxies that we simulated, taking account of baryonic effects. The scatter in the rotation curves in the - plane, as well as the trend of the SPARC sample, and our simulated galaxy distribution is in good agreement. The solution of the “diversity” problem lies in the ability of the baryonic process to produce non-self-similar haloes, contrary to DM-only simulations. We show also that baryonic effects can reproduce the rotation curves of galaxies such as IC2574, which are characterized by a slow rise in radius. A solution to the diversity problem can be obtained taking the baryon physics effects appropriately into account.
1. Introduction
Among the predictions of the CDM paradigm, agreeing very well with a plethora of observations [1,2,3,4,5,6,7]1, is the forecast that dark matter (DM) haloes have a cuspy density profile, with [10], close to the halo center, given by the so-called Navarro–Frenk–White (NFW) profile [10]. More recent findings confirm this result, albeit with a lower slope for the cusp [11,12]. The rotation curves (RCs) of dwarf galaxies and low-brightness galaxies (LSBs) are usually characterized by a more gentle increase than predicted by the NFW profile. This problem was noticed for the first time more than two decades ago [13,14] and studied in many other papers [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31], and it was recently shown to be present even within clusters of galaxies [32,33,34,35].
From a more general point of view, the cusp/core problem is better defined in terms of the excess of DM predicted in the inner parts of the galaxies compared with the observed inner slope, and it can be connected to the Too-Big-To-Fail problem [36,37,38,39].
While dwarf galaxies usually have cored profiles, a more detailed study shows a significant spread in their RCs and the existence of cuspy dwarfs [19,40,41].
Despite disagreement on the above discrepancy, the inner profiles of several dwarf galaxies or LSBs are clearly not always flat (e.g., [37,40]), and the authors of [42] noticed a clear mass dependence of inner profiles in the THINGS sample. The authors of [43] first predicted such mass dependence by using DM-only simulations. Inner slope dependence on the halo mass and on the ratio , where is the stellar mass, has been shown in more recent studies [27,44,45].
In addition, currently, different techniques (e.g., spherical Jeans equation, multiple stellar populations techniques, and Schwarzschild modeling) applied to those or similar objects sometimes give different results (e.g., the cuspy profile found in [46] in Fornax as well as the cores found in [47,48,49,50]). Finally, discrepancies are evident for larger objects than those MW satellites (e.g., the authors of [51] found in the case of NGC2976, while the authors of [52] found , and the authors of [41] found when stars were used to trace the potential and found when it was the gas).
From the studies discussed above, and several others, results show the existence of a range of profiles and show that no agreement on the exact dark matter slopes [19,40,41] distribution can be reached based on morphologies, despite current improvements in kinematic maps. Namely, despite using the most recent and accurate data (kinematic maps), distinguishing between cusp and cores even in galaxies of the same morphology, and in some case even for the same object, is very complicated. This problem is more evident in dwarf galaxies (see the above citations).
Recently, the authors of [37] quantified this diversity in dwarf galaxy RCs. They compared the circular velocity at 2 kpc , given a fixed maximum in the circular velocity, . The scatter in , in the range 50–250 km/s, spans a factor 3–4.
Several authors proposed solutions to that problem, almost all relying on core formation process due to supernovae feedback (hereafter SNFM). At this point, we want to emphasize that, despite the majority of studies converging on the idea that baryon physics leads to the formation of cores [17,23,24,44,53,54,55], some studies arrive at the opposite conclusion [56,57,58,59]. While this disagreement can be due to different physical processes included in the simulations, it motivates one to be more careful in accepting simulation results. As for the diversity problem, it brings about one question: if the galaxies they formed were as realistic as claimed, why wasn’t the diversity problem seen and solved by the large number of hydro-simulations run in the last decade, especially in the past years, before the authors of [37] pointed it out? Some years before the publication of [37], the problem was discussed and solved by means of baryon physics, using a semi-analytical model in [23]. That core formation model, differently from the SNFM, is related to the exchange of energy and angular momentum (AM) between gas clumps [60] and DM through dynamical friction (dubbed dynamical friction from the baryonic clumps model (DFBC)) [23,24,44,53,61,62,63,64,65,66,67,68,69,70].
However, after the [37] analysis, several authors claimed the problem could be solved by the same simulations, based on the SNFM, that were previously blind to it. In particular, the authors of [71] showed that similar simulations can solve the diversity problem with core formation by baryons, while [37] could not. Even if the core formation scenario through supernovae feedback can solve the diversity problem, such a scenario encounters serious difficulties in explaining the structure of objects such as IC2574 [37,72,73], which displays a core extending to 8 kpc, where there is no star (the ICG2574 half-mass radius is 5 kpc). Problems like this prompted the authors of [73] to explore a solution based on self-interacting dark matter (SIDM): they found that the SIDM alone cannot solve the problem and thus somehow some baryonic physics must be introduced.
In this paper, the distribution of galaxies produced by the DFBC in the -, where is the outermost radius, will be compared, following [37], to the SPARC data [74], a collection of high quality RCs of nearby galaxies.
We expect the mass dependence of the inner structure of the galaxies [75,76], as shown in [44,69], to give rise to a scatter in the - plane. Such scatter is not possible in the CDM scenario, producing self-similar DM haloes.
2. Model and Comparison with Observations
Our study of the diversity problem involved a subsample of the SPARC sample [74], which is a collection of high-quality rotation curves of nearby galaxies, to determine and . The subsample characteristics are described in Section 2.2.
We then simulated 100 galaxies with the DFBC model [53,70], with similar characteristics to our SPARC subsample, and with , in a CDM cosmology according to the [77] parameters. Finally, we compared the SPARC subsample and simulated and , as summarized in the following.
2.1. Model
The model simulating galaxy formation we used has been described in several other papers [23,24,53,69,70]. These are spherical collapse models highly improved over those described by [78,79,80,81,82,83,84] and include the effects of dark energy [85,86,87,88], random angular momentum (e.g., [81,83]) produced by the random motions arising in the collapse phase, ordered angular momentum (e.g., [89,90,91]) arising from tidal torques, adiabatic contraction (e.g., [92,93,94,95]), gas and stellar clumps interactions with DM through dynamical friction [53,61,62,63,64,65,66,67,68], gas cooling, star formation, photoionization, supernova, and AGN feedback ([96,97,98]; see the following).
It follows perturbations of diffuse gas (baryons) and DM, which will give rise to the proto-structure, from the linear to the non-linear phase, through turn-around and collapse. The baryon fraction is set to the “universal baryon fraction” [99] (0.167 in [2].) The baryons collapse compresses DM (adiabatic compression), steepening the DM profile [92,93,95].
If a DM particle is located at a given radius , as follows,
where is the initial dark halo distribution [100], then , the final mass distribution of baryons (e.g., an exponential disk for spirals or a Hernquist configuration ([101,102] for elliptical galaxies)), r, the final radius, and , the final DM distribution, are obtained through solving iteratively Equation (1) [103]. This model can be improved to better reproduce numerical simulations by assuming conservation of the product of the radius by the inside mass for that orbit-averaged radius [93].
Radiative processes form baryon clumps, in turn collapsing towards the center of the galaxy and forming stars. Clumps formation, their life-time, and observation are discussed in [70].
Dynamical friction (DF) between baryons and DM transfers energy and angular momentum (AM) to the DM component [61,62]. This gives rise to a predominantly outwards motion of DM particles, reducing the central density, and transforming the cusp into a core. ([53], Appendix D) describes how DF is taken into account, inserting the DF force in the equation of motion (Equation (A14) [53]) to affect structure formation.
That mechanism, flattening the cusp, is amplified in the case of rotationally supported (spiral) galaxies through the ordered AM, L, acquired by the proto-structure through tidal interactions with neighbors [89,104,105,106], and by random AM, j, originating by the random motions arising in the collapse phase [81].
The “ordered” AM is calculated from evaluating the torque , and integrating it over time ([89], Equation (35); see also Section C2 of [53]). “Random” AM is taken into account by assigning a specific angular momentum at turnaround (for details, see Appendix C2 of [53]).
A classical cooling flow served as a gas cooling mechanism (e.g., [107]) (see Section 2.2.2 of [97]). The inclusion by [96] and ([97], Sections 2.2.2 and 2.2.3) of star formation, reionization and supernovae feedback were replicated. Following [97], reionization reduces the baryon fraction by
with the virial mass and is the “filtering mass” (see [108]). We take the reionization redshift in the range 11.5–15. Our treatment of supernovae feedback also follows [109]. In that stage, each supernova explosion expels gas in successive events, lowering stellar density. The smallest clumps are destroyed by feedback soon after stars are formed from a small part of their mass [68].
AGN quenching becomes important for masses ≃6 [110]. Its feedback was taken into account modifying the [111] model as in Section 2.3 of [98], by forming a Super-Massive-Black-Hole (SMB) when the star density exceeds M/kpc, then accreting mass into it.
Our model demonstrated its robustness in several ways:
- Cusp flattening from DM heating by collapsing baryonic clumps is in agreement with previous studies [61,62,64,65,66,67,68]. In [45], based on Figure 4, a comparison of our model with the SPH simulations of [17] is made.
- Galaxy density profiles correct shape [53,112], and this was found before the [17,113] SPH simulations and before the correct cluster density profiles [24] were predicted, and a series of correlations in cluster observations [34,35] were reobtained [114]. Notice that, concerning correlations in clusters of galaxies, in [6], based on Figures 2–5, we compared the observations found in [35].
- Inner slope dependence on halo mass [44] and on the total baryonic content to total mass ratio [24] were predicted, and were in agreement with [27]. In addition to this dependence, the inner slope was also found to depend on the angular momentum [24]. In [69,70], a comparison of the change of the inner slope with mass with [27] simulations is made. A comparison is also made based on Figures 4 and 5 in [69,70] with respect to the Tully–Fisher, Faber–Jackson, and relationship, with simulations. Finally, the correct DM profile inner slope dependence on the halo mass is explained over 6 orders of magnitude in halo mass, from dwarfs to clusters [23,24,44,53,114], a range that no other model can achieve.
2.2. Observational Data
The choice we made of galaxies observations was a subsample extracted from the Spitzer Photometry & Accurate Rotation Curves (SPARCs) [74]. Spanning large ranges in morphologies, surface brightnesses, and luminosities, and presenting new surface photometry at 3.6 m and high-quality rotation curves from previous studies, the entire sample contains 175 nearby disk galaxies. To minimize the scatter in the baryonic Tully–Fisher relation, the authors of [115] assumed a mass-to-light ratio .
For galaxies, not having a measured point at 2 kpc, we used an interpolation between close bins.
We also applied to the sample the following conditions:
- selecting stellar masses similar to our simulated galaxies, and
- selecting galaxies with inclination >45, which are the most reliable RC data.
3. Results
Once the observed sample and model simulated galaxy populations were determined, we compared their location in the plane . We defined from the relation , which only slightly differs from the Santos–Santos case ([116], Figure 1).
In Figure 1, we compared the SPARC data with the result of our model. The models interpretation of circular velocity are based on the 3D spherical circular velocity approximation (, with r the 3D radius and M (<r) its enclosed mass) in Figure 1a (left panel of Figure 1) and calculated using the disk plane cylindrical gravitational potential (, with R the cylindrical radius and the disk potential, restricted in the galactic plane ) in Figure 1b (right panel of Figure 1). In both panels of Figure 1, the full triangles represent the SPARC sample. The open blue hexagons mark our simulated galaxies, the green line represents the mean trend line, and the dashed line represents the expectation when an NFW profile describes all haloes. The plot shows that the region occupied by the galaxy distributions predicted by our model are in much better agreement with the SPARC galaxy distribution and its scatter than the output of [37].
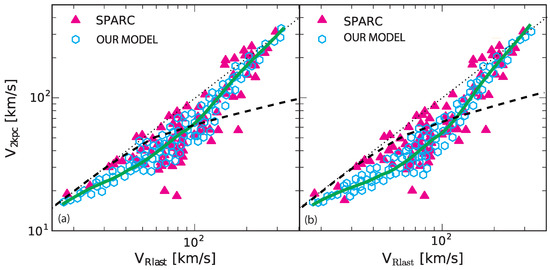
Figure 1.
The prediction from our model and a selection of SPARC data, using (a) (left panel) the spherical circular velocity approximation and (b) (right panel) the disk plane cylindrical gravitational potential approximation. The full triangles represent the SPARC sample, the open blue hexagons represent our simulated galaxies, the green line represents the mean trend line, and the dashed line represents the expectation when an NFW profile describes all haloes.
Notice that the robustness of the quoted results are independent of the choice of inner velocity (here 2 kpc) as we verified, considering smaller radii (1 kpc), and as was checked by ([116], Figure 3).
Denoting as ”outliers” SPARC galaxies having outside the range determined with respect to our model trend line, there are two outliers, namely: IC2574 and UCG05750. The circular-potential velocity definition employed in Figure 1b lowers the trend line, especially in the maximum feedback region, and gives rise to a small increase in scatter. This reintegrates, on the one hand, the outliers IC2574 and UGC05750. Moreover, the error bars on the SPARC galaxies are not shown in the figures, in order to obtain a cleaner plot. Taking account of errors, on average of 5–10 km/s for SPARC, renders even more evident that the galaxies are not outliers.
The successful reproduction of a similar distribution and scatter to SPARC galaxies by our model reflects the ability to model the total and stellar mass dependence of galaxies DM density profile and RCs, as shown in [69]: galaxies with are cored with a very flat profile and inner slope , while galaxies with tend to be more cuspy (larger ) as the feedback mechanism efficiency, producing the cores, is decreased due to the lack of baryon clumps. Conversely, galaxies with also tend to be cuspier. This time the cuspy profiles are produced by the presence of a larger number of stars, which deepens the galactic potential well and opposes the SNFM mechanism.
It is important to notice that our galaxies follow the SPARC trend at km/s, thanks to our accounting of AGN feedback, which counteracts baryon cooling and modifies star formation. In addition, tidal interaction in our model makes it more environment dependent than several hydro-dynamic simulations, in which galaxies are usually isolated.
A recent paper of [116] shows similar results. We want to stress that the method used in the two papers is totally different: simulations [116] vs. a semi-analytic method (this paper). The explanation of the “diversity problem” is related to the interaction of baryon clumps with dark matter and not due to supernovae feedback. Our results are dependent of environment (galaxies are not isolated) and of the effect of AGN feedback, differently from [116]. Those effects change the distribution of galaxies in the - plane. There are also differences in the SPARC sample used. In that of [116], some SPARC galaxies, outliers in their case, were not plotted by the authors.
As previously discussed, IC2574 and UGC05750 are no longer outliers, once calculating in the galactic plane, as can be deduced from the right panel of Figure 1 and from taking into account the errors.
In Figure 2, we showed our model predictions for the case of IC2574 RC. The SPARC RC of IC2574 (dots with error bars) is shown with our simulation’s most similar galaxy RC (solid line). The plot also displays the contribution to the RC coming from stars (the dotted green line), from the gas disk (the dashed orange line), and from the total baryonic mass (the blue line). It shows a good agreement between our calculated RC and the SPARC’s. This is also the case for other galaxy properties, such as the baryonic mass profile (star and gas), and half-mass radius, almost equal to 5 kpc, in very good agreement with the observations (check http://astroweb.cwru.edu/SPARC/).
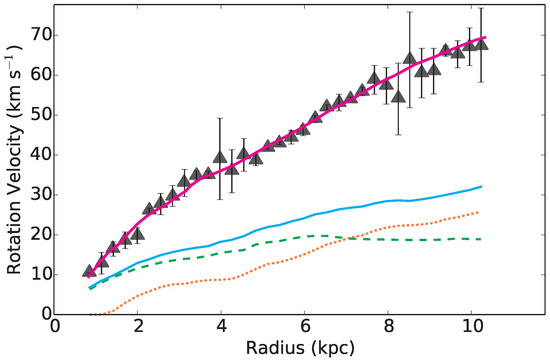
Figure 2.
Rotation curve of IC2574 compared with our results. The SPARC rotation curve of IC2574 is presented as dots with error bars. Our simulations result is represented by the grey solid line, including the RCs from its stars (dotted green line) and the gas disk (dashed orange line) components, summed into the total baryonic mass (blue solid line).
The case of UCG05750 was not plotted since the RC fit using the same correction yields results as good as those for IC2574.
4. Conclusions
In this paper, we studied the problem of the diversity of RC shapes in dwarf galaxies [37]. To this aim, we simulated 100 galaxies with similar characteristics to a subsample of the SPARC compilation and compared the distributions of galaxies of that subsample in the - plane with the simulated galaxies. The distribution scatter and trend show good agreement between the SPARC compilation and our galaxies. However, two outliers are present. Determining the circular velocity in the galactic plane, instead of from the spherical symmetrical evaluation, we showed that the two galaxies are no longer outliers. We also showed how the prediction of our model is in agreement with the observations for one of the outliers, namely IC2574.
Author Contributions
A.D.P. had the idea of the study, and performed the calculations with the help of X.L. M.L.D. wrote the draft.
Funding
This research received no external funding.
Acknowledgments
ADP was supported by the Chinese Academy of Sciences and by the President’s International Fellowship Initiative, grant no. 2017 VMA0044. MLeD acknowledges the financial support by the Lanzhou University starting fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Del Popolo, A. Dark matter, density perturbations, and structure formation. Astron. Rep. 2007, 51, 169–196. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-baryonic dark matter in cosmology. AIP Conf. Proc. 2013, 1548, 2–63. [Google Scholar] [CrossRef]
- Story, K.T.; Reichardt, C.L.; Hou, Z.; Keisler, R.; Aird, K.A.; Benson, B.A.; Bleem, L.E.; Carlstrom, J.E.; Chang, C.L.; Cho, H.-M.; et al. A Measurement of the Cosmic Microwave Background Damping Tail from the 2500-Square-Degree SPT-SZ Survey. Astrophys. J. 2013, 779, 86–104. [Google Scholar] [CrossRef]
- Das, S.; Louis, T.; Nolta, M.R.; Addison, G.E.; Battistelli, E.S.; Bond, J.R.; Calabrese, E.; Crichton, D.; Devlin, M.J.; Dunkley, J.; et al. The Atacama Cosmology Telescope: Temperature and gravitational lensing power spectrum measurements from three seasons of data. J. Cosmol. Astropart. Phys. 2014, 4, 014. [Google Scholar] [CrossRef]
- Del Popolo, A. Nonbaryonic Dark Matter in Cosmology. Int. J. Mod. Phys. D 2014, 23, 30005. [Google Scholar] [CrossRef]
- Planck Collaboration XIII. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Astashenok, A.V.; del Popolo, A. Cosmological measure with volume averaging and the vacuum energy problem. Class. Quantum Gravity 2012, 29, 085014. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Gao, L.; Navarro, J.F.; Cole, S.; Frenk, C.S.; White, S.D.M.; Springel, V.; Jenkins, A.; Neto, A.F. The redshift dependence of the structure of massive Λ cold dark matter haloes. Mon. Not. R. Astron. Soc. 2008, 387, 536–544. [Google Scholar] [CrossRef]
- Navarro, J.F.; Ludlow, A.; Springel, V.; Wang, J.; Vogelsberger, M.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Helmi, A. The diversity and similarity of simulated cold dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 402, 21–34. [Google Scholar] [CrossRef]
- Moore, B. Evidence against dissipation-less dark matter from observations of galaxy haloes. Nature 1994, 370, 629–631. [Google Scholar] [CrossRef]
- Flores, R.A.; Primack, J.R. Observational and theoretical constraints on singular dark matter halos. Astrophys. J. Lett. 1994, 427, L1–L4. [Google Scholar] [CrossRef]
- Burkert, A. The Structure of Dark Matter Halos in Dwarf Galaxies. Astrophys. J. Lett. 1995, 447, L25–L28. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Bosma, A.; McGaugh, S. Simulating observations of dark matter dominated galaxies: Towards the optimal halo profile. Mon. Not. R. Astron. Soc. 2003, 340, 657–678. [Google Scholar] [CrossRef]
- Governato, F.; Brook, C.; Mayer, L.; Brooks, A.; Rhee, G.; Wadsley, J.; Jonsson, P.; Willman, B.; Stinson, G.; Quinn, T.; et al. Bulgeless dwarf galaxies and dark matter cores from supernova-driven outflows. Nature 2010, 463, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Kuzio de Naray, R.; Kaufmann, T. Recovering cores and cusps in dark matter haloes using mock velocity field observations. Mon. Not. R. Astron. Soc. 2011, 414, 3617–3626. [Google Scholar] [CrossRef]
- Oh, S.H.; Brook, C.; Governato, F.; Brinks, E.; Mayer, L.; de Blok, W.J.G.; Brooks, A.; Walter, F. The Central Slope of Dark Matter Cores in Dwarf Galaxies: Simulations versus THINGS. Astrophys. J. 2011, 142, 24. [Google Scholar] [CrossRef]
- Cardone, V.F.; Leubner, M.P.; Del Popolo, A. Spherical galaxy models as equilibrium configurations in non-extensive statistics. Mon. Not. R. Astron. Soc. 2011, 414, 2265–2274. [Google Scholar] [CrossRef]
- Cardone, V.F.; Del Popolo, A.; Tortora, C.; Napolitano, N.R. Secondary infall model and dark matter scaling relations in intermediate-redshift early-type galaxies. Mon. Not. R. Astron. Soc. 2011, 416, 1822–1835. [Google Scholar] [CrossRef]
- Cardone, V.F.; Del Popolo, A. Newtonian acceleration scales in spiral galaxies. Mon. Not. R. Astron. Soc. 2012, 427, 3176–3187. [Google Scholar] [CrossRef]
- Del Popolo, A. Density profile slopes of dwarf galaxies and their environment. Mon. Not. R. Astron. Soc. 2012, 419, 971–984. [Google Scholar] [CrossRef]
- Del Popolo, A. On the density-profile slope of clusters of galaxies. Mon. Not. R. Astron. Soc. 2012, 424, 38–51. [Google Scholar] [CrossRef]
- Del Popolo, A.; Cardone, V.F. Statistical properties of the dark matter haloes of dwarf galaxies and correlations with the environment. Mon. Not. R. Astron. Soc. 2012, 423, 1060–1072. [Google Scholar] [CrossRef]
- Del Popolo, A.; Cardone, V.F.; Belvedere, G. Surface density of dark matter haloes on galactic and cluster scales. Mon. Not. R. Astron. Soc. 2013, 429, 1080–1087. [Google Scholar] [CrossRef]
- Di Cintio, A.; Brook, C.B.; Macciò, A.V.; Stinson, G.S.; Knebe, A.; Dutton, A.A.; Wadsley, J. The dependence of dark matter profiles on the stellar-to-halo mass ratio: A prediction for cusps versus cores. Mon. Not. R. Astron. Soc. 2014, 437, 415–423. [Google Scholar] [CrossRef]
- Del Popolo, A.; Hiotelis, N. Cusps and cores in the presence of galactic bulges. J. Cosmol. Astropart. Phys. 2014, 1, 47. [Google Scholar] [CrossRef]
- Del Popolo, A.; Lima, J.A.S.; Fabris, J.C.; Rodrigues, D.C. A unified solution to the small scale problems of the ΛCDM model. J. Cosmol. Astropart. Phys. 2014, 4, 21. [Google Scholar] [CrossRef]
- Del Popolo, A.; Le Delliou, M. A unified solution to the small scale problems of the ΛCDM model II: Introducing parent-satellite interaction. J. Cosmol. Astropart. Phys. 2014, 12, 51. [Google Scholar] [CrossRef]
- Polisensky, E.; Ricotti, M. Fingerprints of the initial conditions on the density profiles of cold and warm dark matter haloes. Mon. Not. R. Astron. Soc. 2015, 450, 2172–2184. [Google Scholar] [CrossRef]
- Sand, D.J.; Treu, T.; Ellis, R.S. The Dark Matter Density Profile of the Lensing Cluster MS 2137-23: A Test of the Cold Dark Matter Paradigm. Astrophys. J. Lett. 2002, 574, L129–L133. [Google Scholar] [CrossRef]
- Sand, D.J.; Treu, T.; Smith, G.P.; Ellis, R.S. The Dark Matter Distribution in the Central Regions of Galaxy Clusters: Implications for Cold Dark Matter. Astrophys. J. 2004, 604, 88–107. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J.; Nipoti, C.; Richard, J.; Jullo, E. The Density Profiles of Massive, Relaxed Galaxy Clusters. I. The Total Density Over Three Decades in Radius. Astrophys. J. 2013, 765, 24–38. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J. The Density Profiles of Massive, Relaxed Galaxy Clusters. II. Separating Luminous and Dark Matter in Cluster Cores. Astrophys. J. 2013, 765, 25–36. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. 2011, 415, L40–L44. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Fattahi, A.; Frenk, C.S.; Sawala, T.; White, S.D.M.; Bower, R.; Crain, R.A.; Furlong, M.; Schaller, M.; et al. The unexpected diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2015, 452, 3650–3665. [Google Scholar] [CrossRef]
- Papastergis, E.; Giovanelli, R.; Haynes, M.P.; Shankar, F. Is there a “too big to fail” problem in the field? Astron. Astrophys. 2015, 574, A113. [Google Scholar] [CrossRef]
- Del Popolo, A.; Le Delliou, M. Small Scale Problems of the ΛCDM Model: A Short Review. Galaxies 2017, 5, 17. [Google Scholar] [CrossRef]
- Simon, J.D.; Bolatto, A.D.; Leroy, A.; Blitz, L.; Gates, E.L. High-Resolution Measurements of the Halos of Four Dark Matter-Dominated Galaxies: Deviations from a Universal Density Profile. Astrophys. J. 2005, 621, 757–776. [Google Scholar] [CrossRef]
- Adams, J.J.; Simon, J.D.; Fabricius, M.H.; van den Bosch, R.C.E.; Barentine, J.C.; Bender, R.; Gebhardt, K.; Hill, G.J.; Murphy, J.D.; Swaters, R.A.; et al. Dwarf Galaxy Dark Matter Density Profiles Inferred from Stellar and Gas Kinematics. Astrophys. J. 2014, 789, 1–28. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astrophys. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Ricotti, M. Dependence of the inner dark matter profile on the halo mass. Mon. Not. R. Astron. Soc. 2003, 344, 1237–1249. [Google Scholar] [CrossRef]
- Del Popolo, A. On the universality of density profiles. Mon. Not. R. Astron. Soc. 2010, 408, 1808–1817. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-power law behavior of the radial profile of phase-space density of halos. J. Cosmol. Astropart. Phys. 2011, 7, 14. [Google Scholar] [CrossRef]
- Breddels, M.A.; Helmi, A.; van den Bosch, R.C.E.; van de Ven, G.; Battaglia, G. Orbit-based dynamical models of the Sculptor dSph galaxy. Mon. Not. R. Astron. Soc. 2013, 433, 3173–3189. [Google Scholar] [CrossRef]
- Walker, M.G.; Peñarrubia, J. A Method for Measuring (Slopes of) the Mass Profiles of Dwarf Spheroidal Galaxies. Astrophys. J. 2011, 742, 1–19. [Google Scholar] [CrossRef]
- Battaglia, G.; Helmi, A.; Tolstoy, E.; Irwin, M.; Hill, V.; Jablonka, P. The Kinematic Status and Mass Content of the Sculptor Dwarf Spheroidal Galaxy. Astrophys. J. Lett. 2008, 681, L13–L16. [Google Scholar] [CrossRef]
- Agnello, A.; Evans, N.W. A Virial Core in the Sculptor Dwarf Spheroidal Galaxy. Astrophys. J. Lett. 2012, 754, L39. [Google Scholar] [CrossRef]
- Genina, A.; Benítez-Llambay, A.; Frenk, C.S.; Cole, S.; Fattahi, A.; Navarro, J.F.; Oman, K.A.; Sawala, T.; Theuns, T. The core-cusp problem: A matter of perspective. Mon. Not. R. Astron. Soc. 2018, 474, 1398–1411. [Google Scholar] [CrossRef]
- Simon, J.D.; Bolatto, A.D.; Leroy, A.; Blitz, L. High-Resolution Measurements of the Dark Matter Halo of NGC 2976: Evidence for a Shallow Density Profile. Astrophys. J. 2003, 596, 957–981. [Google Scholar] [CrossRef]
- Adams, J.J.; Gebhardt, K.; Blanc, G.A.; Fabricius, M.H.; Hill, G.J.; Murphy, J.D.; van den Bosch, R.C.E.; van de Ven, G. The Central Dark Matter Distribution of NGC 2976. Astrophys. J. 2012, 745, 1–17. [Google Scholar] [CrossRef]
- Del Popolo, A. The Cusp/Core Problem and the Secondary Infall Model. Astrophys. J. 2009, 698, 2093–2113. [Google Scholar] [CrossRef]
- Oñorbe, J.; Boylan-Kolchin, M.; Bullock, J.S.; Hopkins, P.F.; Kerěs, D.; Faucher-Giguère, C.A.; Quataert, E.; Murray, N. Forged in FIRE: Cusps, cores, and baryons in low-mass dwarf galaxies. Mon. Not. R. Astron. Soc. 2015, 454, 2092–2106. [Google Scholar] [CrossRef]
- Read, J.I.; Agertz, O.; Collins, M.L.M. Dark matter cores all the way down. Mon. Not. R. Astron. Soc. 2016, 459, 2573–2590. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Simpson, C.; Jenkins, A. Dwarf galaxies in CDM and SIDM with baryons: Observational probes of the nature of dark matter. Mon. Not. R. Astron. Soc. 2014, 444, 3684–3698. [Google Scholar] [CrossRef]
- González-Samaniego, A.; Colín, P.; Avila-Reese, V.; Rodríguez-Puebla, A.; Valenzuela, O. Simulations of Isolated Dwarf Galaxies Formed in Dark Matter Halos with Different Mass Assembly Histories. Astrophys. J. 2014, 785, 1–15. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Bower, R.G.; Crain, R.A.; Dalla Vecchia, C.; Furlong, M.; Jenkins, A.; McCarthy, I.G.; et al. Bent by baryons: The low-mass galaxy-halo relation. Mon. Not. R. Astron. Soc. 2015, 448, 2941–2947. [Google Scholar] [CrossRef]
- Schaller, M.; Frenk, C.S.; Bower, R.G.; Theuns, T.; Jenkins, A.; Schaye, J.; Crain, R.A.; Furlong, M.; Dalla Vecchia, C.; McCarthy, I.G. Baryon effects on the internal structure of ΛCDM haloes in the EAGLE simulations. Mon. Not. R. Astron. Soc. 2015, 451, 1247–1267. [Google Scholar] [CrossRef]
- Zanella, A.; Daddi, E.; Le Floc’h, E.; Bournaud, F.; Gobat, R.; Valentino, F.; Strazzullo, V.; Cibinel, A.; Onodera, M.; Perret, V.; et al. An extremely young massive clump forming by gravitational collapse in a primordial galaxy. Nature 2015, 521, 54–56. [Google Scholar] [CrossRef] [PubMed]
- El-Zant, A.; Shlosman, I.; Hoffman, Y. Dark Halos: The Flattening of the Density Cusp by Dynamical Friction. Astrophys. J. 2001, 560, 636–643. [Google Scholar] [CrossRef]
- El-Zant, A.A.; Hoffman, Y.; Primack, J.; Combes, F.; Shlosman, I. Flat-cored Dark Matter in Cuspy Clusters of Galaxies. Astrophys. J. Lett. 2004, 607, L75–L78. [Google Scholar] [CrossRef]
- Ma, C.P.; Boylan-Kolchin, M. Are Halos of Collisionless Cold Dark Matter Collisionless? Phys. Rev. Lett. 2004, 93, 021301. [Google Scholar] [CrossRef] [PubMed]
- Romano-Díaz, E.; Shlosman, I.; Hoffman, Y.; Heller, C. Erasing Dark Matter Cusps in Cosmological Galactic Halos with Baryons. Astrophys. J. Lett. 2008, 685, L105–L108. [Google Scholar] [CrossRef]
- Romano-Díaz, E.; Shlosman, I.; Heller, C.; Hoffman, Y. Dissecting Galaxy Formation. I. Comparison between Pure Dark Matter and Baryonic Models. Astrophys. J. 2009, 702, 1250–1267. [Google Scholar] [CrossRef]
- Cole, D.R.; Dehnen, W.; Wilkinson, M.I. Weakening dark matter cusps by clumpy baryonic infall. Mon. Not. R. Astron. Soc. 2011, 416, 1118–1134. [Google Scholar] [CrossRef]
- Inoue, S.; Saitoh, T.R. Cores and revived cusps of dark matter haloes in disc galaxy formation through clump clusters. Mon. Not. R. Astron. Soc. 2011, 418, 2527–2531. [Google Scholar] [CrossRef]
- Nipoti, C.; Binney, J. Early flattening of dark matter cusps in dwarf spheroidal galaxies. Mon. Not. R. Astron. Soc. 2015, 446, 1820–1828. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F. The Cusp/Core problem: Supernovae feedback versus the baryonic clumps and dynamical friction model. Astrophys. Space Sci. 2016, 361, 162. [Google Scholar] [CrossRef]
- Del Popolo, A. On the dark matter haloes inner structure and galaxy morphology. Astrophys. Space Sci. 2016, 361, 222. [Google Scholar] [CrossRef]
- Read, J.I.; Iorio, G.; Agertz, O.; Fraternali, F. Understanding the shape and diversity of dwarf galaxy rotation curves in ΛCDM. Mon. Not. R. Astron. Soc. 2016, 462, 3628–3645. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Sales, L.V.; Fattahi, A.; Frenk, C.S.; Sawala, T.; Schaller, M.; White, S.D.M. Missing dark matter in dwarf galaxies? Mon. Not. R. Astron. Soc. 2016, 460, 3610–3623. [Google Scholar] [CrossRef]
- Creasey, P.; Sameie, O.; Sales, L.V.; Yu, H.B.; Vogelsberger, M.; Zavala, J. Spreading out and staying sharp—Creating diverse rotation curves via baryonic and self-interaction effects. Mon. Not. R. Astron. Soc. 2017, 468, 2283–2295. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astron. J. 2016, 152, 1–14. [Google Scholar] [CrossRef]
- Hiotelis, N.; Del Popolo, A. Anomalous diffusion models for the formation of dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 436, 163–178. [Google Scholar] [CrossRef]
- Hiotelis, N.; Del Popolo, A. On the Reliability of Merger-Trees and the Mass-Growth Histories of Dark Matter Haloes. Astrophys. Space Sci. 2006, 301, 167–177. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Gunn, J.E.; Gott, J.R., III. On the Infall of Matter Into Clusters of Galaxies and Some Effects on Their Evolution. Astrophys. J. 1972, 176, 1–19. [Google Scholar] [CrossRef]
- Bertschinger, E. Self-similar secondary infall and accretion in an Einstein-de Sitter universe. Astrophys. J. Suppl. 1985, 58, 39–65. [Google Scholar] [CrossRef]
- Hoffman, Y.; Shaham, J. Local density maxima—Progenitors of structure. Astrophys. J. 1985, 297, 16–22. [Google Scholar] [CrossRef]
- Ryden, B.S.; Gunn, J.E. Galaxy formation by gravitational collapse. Astrophys. J. 1987, 318, 15–31. [Google Scholar] [CrossRef]
- Ascasibar, Y.; Yepes, G.; Gottlöber, S.; Müller, V. On the physical origin of dark matter density profiles. Mon. Not. R. Astron. Soc. 2004, 352, 1109–1120. [Google Scholar] [CrossRef]
- Williams, L.L.R.; Babul, A.; Dalcanton, J.J. Investigating the Origins of Dark Matter Halo Density Profiles. Astrophys. J. 2004, 604, 18–39. [Google Scholar] [CrossRef]
- Del Popolo, A.; Ercan, E.N.; Xia, Z. Ellipsoidal Collapse and Previrialization. Astron. J. 2001, 122, 487–495. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Extended Spherical Collapse and the Accelerating Universe. Int. J. Mod. Phys. D 2013, 22, 50038. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Spherical collapse model with shear and angular momentum in dark energy cosmologies. Mon. Not. R. Astron. Soc. 2013, 430, 628–637. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Maydanyuk, S.P.; Lima, J.A.S.; Jesus, J.F. Shear and rotation in Chaplygin cosmology. Phys. Rev. D 2013, 87, 043527. [Google Scholar] [CrossRef]
- Pace, F.; Batista, R.C.; Del Popolo, A. Effects of shear and rotation on the spherical collapse model for clustering dark energy. Mon. Not. R. Astron. Soc. 2014, 445, 648–659. [Google Scholar] [CrossRef]
- Ryden, B.S. Galaxy formation—The role of tidal torques and dissipational infall. Astrophys. J. 1988, 329, 589–611. [Google Scholar] [CrossRef]
- Del Popolo, A.; Gambera, M. Substructure effects on the collapse of density perturbations. Astron. Astrophys. 1997, 321, 691–695. [Google Scholar]
- Del Popolo, A.; Gambera, M. Non radial motions and the shapes and the abundance of clusters of galaxies. Astron. Astrophys. 2000, 357, 809–815. [Google Scholar]
- Blumenthal, G.R.; Faber, S.M.; Flores, R.; Primack, J.R. Contraction of dark matter galactic halos due to baryonic infall. Astrophys. J. 1986, 301, 27–34. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Kravtsov, A.V.; Klypin, A.A.; Nagai, D. Response of Dark Matter Halos to Condensation of Baryons: Cosmological Simulations and Improved Adiabatic Contraction Model. Astrophys. J. 2004, 616, 16–26. [Google Scholar] [CrossRef]
- Klypin, A.; Zhao, H.; Somerville, R.S. ΛCDM-based Models for the Milky Way and M31. I. Dynamical Models. Astrophys. J. 2002, 573, 597–613. [Google Scholar] [CrossRef]
- Gustafsson, M.; Fairbairn, M.; Sommer-Larsen, J. Baryonic pinching of galactic dark matter halos. Phys. Rev. D 2006, 74, 123522. [Google Scholar] [CrossRef]
- De Lucia, G.; Helmi, A. The Galaxy and its stellar halo: Insights on their formation from a hybrid cosmological approach. Mon. Not. R. Astron. Soc. 2008, 391, 14–31. [Google Scholar] [CrossRef]
- Li, Y.S.; De Lucia, G.; Helmi, A. On the nature of the Milky Way satellites. Mon. Not. R. Astron. Soc. 2010, 401, 2036–2052. [Google Scholar] [CrossRef]
- Martizzi, D.; Teyssier, R.; Moore, B.; Wentz, T. The effects of baryon physics, black holes and active galactic nucleus feedback on the mass distribution in clusters of galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 3081–3091. [Google Scholar] [CrossRef]
- Komatsu, E.; Dunkley, J.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Limon, M.; Page, L.; et al. Five-Year Wilkinson Microwave Anisotropy Probe Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2009, 180, 330–376. [Google Scholar] [CrossRef]
- Flores, R.; Primack, J.R.; Blumenthal, G.R.; Faber, S.M. Rotation curves from baryonic infall—Dependence on disk-to-halo ratio, initial angular momentum, and core radius, and comparison with data. Astrophys. J. 1993, 412, 443–454. [Google Scholar] [CrossRef]
- Keeton, C.R. Cold Dark Matter and Strong Gravitational Lensing: Concord or Conflict? Astrophys. J. 2001, 561, 46–60. [Google Scholar] [CrossRef]
- Treu, T.; Koopmans, L.V.E. The Internal Structure and Formation of Early-Type Galaxies: The Gravitational Lens System MG 2016+112 at z = 1.004. Astrophys. J. 2002, 575, 87–94. [Google Scholar] [CrossRef]
- Spedicato, E.; Bodon, E.; Del Popolo, A.; Mahdavi-Amiri, N. ABS Methods and ABSPACK for Linear Systems and Optimization: A Review. Q. J. Belg. Fr. Ital. Oper. Res. Soc. 2003, 1, 51–66. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Origin of the Angular Momentum of Galaxies. Astrophys. J. 1969, 155, 393–402. [Google Scholar] [CrossRef]
- White, S.D.M. Angular momentum growth in protogalaxies. Astrophys. J. 1984, 286, 38–41. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Loeb, A. An analytical model for the triaxial collapse of cosmological perturbations. Astrophys. J. 1995, 439, 520–541. [Google Scholar] [CrossRef]
- White, S.D.M.; Frenk, C.S. Galaxy formation through hierarchical clustering. Astrophys. J. 1991, 379, 52–79. [Google Scholar] [CrossRef]
- Kravtsov, A.V.; Gnedin, O.Y.; Klypin, A.A. The Tumultuous Lives of Galactic Dwarfs and the Missing Satellites Problem. Astrophys. J. 2004, 609, 482–497. [Google Scholar] [CrossRef]
- Croton, D.J.; Springel, V.; White, S.D.M.; De Lucia, G.; Frenk, C.S.; Gao, L.; Jenkins, A.; Kauffmann, G.; Navarro, J.F.; Yoshida, N. The many lives of active galactic nuclei: Cooling flows, black holes and the luminosities and colours of galaxies. Mon. Not. R. Astron. Soc. 2006, 365, 11–28. [Google Scholar] [CrossRef]
- Cattaneo, A.; Dekel, A.; Devriendt, J.; Guiderdoni, B.; Blaizot, J. Modelling the galaxy bimodality: Shutdown above a critical halo mass. Mon. Not. R. Astron. Soc. 2006, 370, 1651–1665. [Google Scholar] [CrossRef]
- Booth, C.M.; Schaye, J. Cosmological simulations of the growth of supermassive black holes and feedback from active galactic nuclei: Method and tests. Mon. Not. R. Astron. Soc. 2009, 398, 53–74. [Google Scholar] [CrossRef]
- Del Popolo, A.; Kroupa, P. Density profiles of dark matter haloes on galactic and cluster scales. Astron. Astrophys. 2009, 502, 733–747. [Google Scholar] [CrossRef]
- Governato, F.; Zolotov, A.; Pontzen, A.; Christensen, C.; Oh, S.H.; Brooks, A.M.; Quinn, T.; Shen, S.; Wadsley, J. Cuspy no more: How outflows affect the central dark matter and baryon distribution in Λ cold dark matter galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 1231–1240. [Google Scholar] [CrossRef]
- Del Popolo, A. The flat density profiles of massive, and relaxed galaxy clusters. J. Cosmol. Astropart. Phys. 2014, 7, 1–21. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. The Small Scatter of the Baryonic Tully-Fisher Relation. Astrophys. J. Lett. 2016, 816, L14. [Google Scholar] [CrossRef]
- Santos-Santos, I.M.; Di Cintio, A.; Brook, C.B.; Macciò, A.; Dutton, A.; Domínguez-Tenreiro, R. NIHAO XIV: Reproducing the observed diversity of dwarf galaxy rotation curve shapes in LCDM. Mon. Not. R. Astron. Soc. 2017, 473, 4392–4403. [Google Scholar] [CrossRef]
| 1 | Here, we should recall that, in addition to some small-scale problems, the CDM paradigm entails two unsolved problems: the cosmic coincidence problem, and the cosmological constant problem [8,9]. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).