Searching for Axion-Like Particles with X-ray Polarimeters
Abstract
1. Introduction
2. Axion-Like Particle Phenomenology
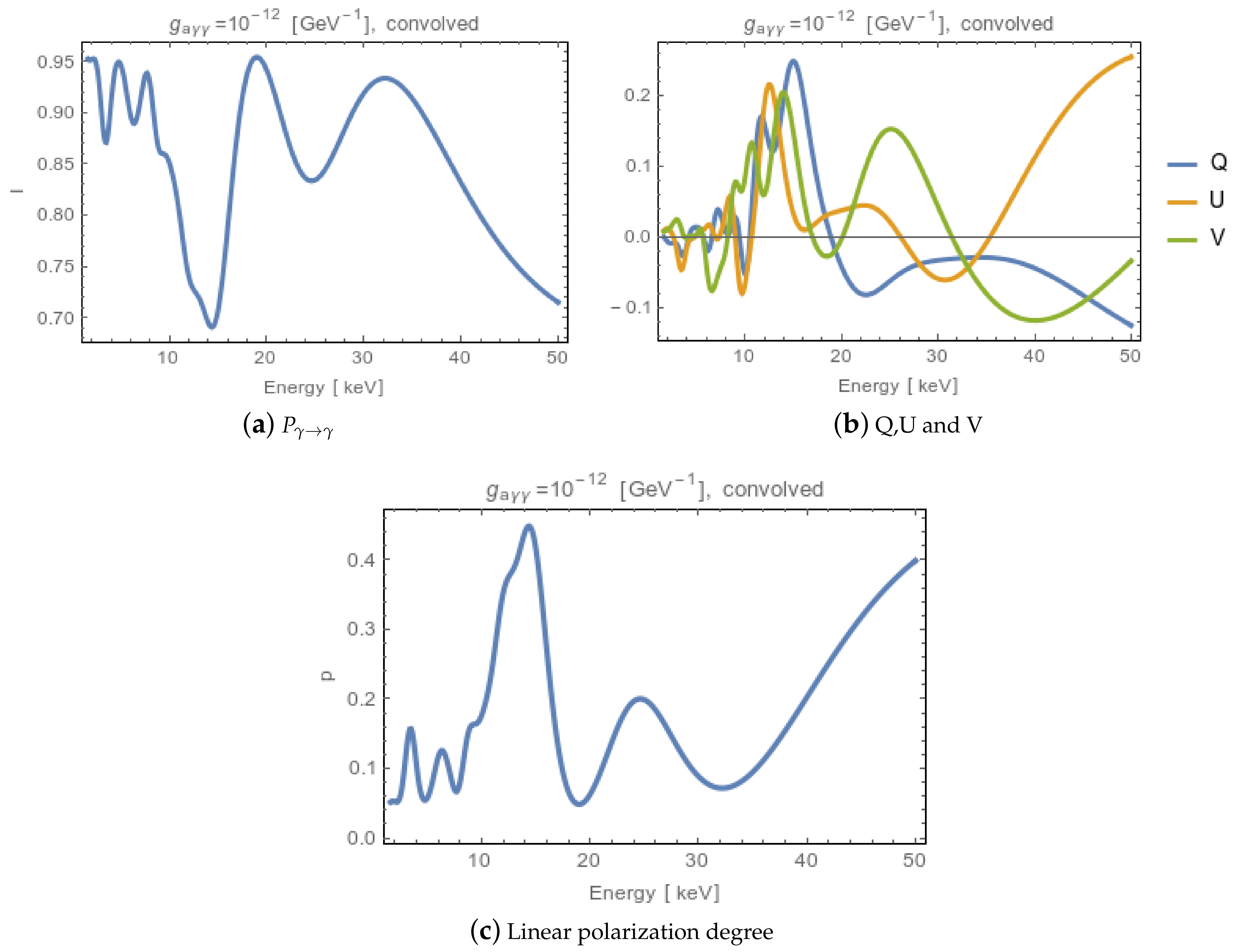
3. Methodology
- The null hypothesis that ALPs exist with coupling or higher to electromagnetism, and mass eV.
- The alternative hypothesis that ALPs with coupling or higher to electromagnetism, and mass eV do not exist.
- Randomly generate 1000 different magnetic field realisations for the line of sight to NGC1275.
- For each , generate the ALP induced linear polarisation and polarisation angle spectra, by numerically propagating the initial photon vector through the cluster.
- From each pair, generate 10 fake data sets by randomly sampling from Equation (6).
- Fit the no ALP constant model to each of the resulting 10,000 fake data sets, and find the corresponding likelihoods .
- If fewer than of the are equal to or higher than (or for the more pessimistic case), is excluded at the confidence level.
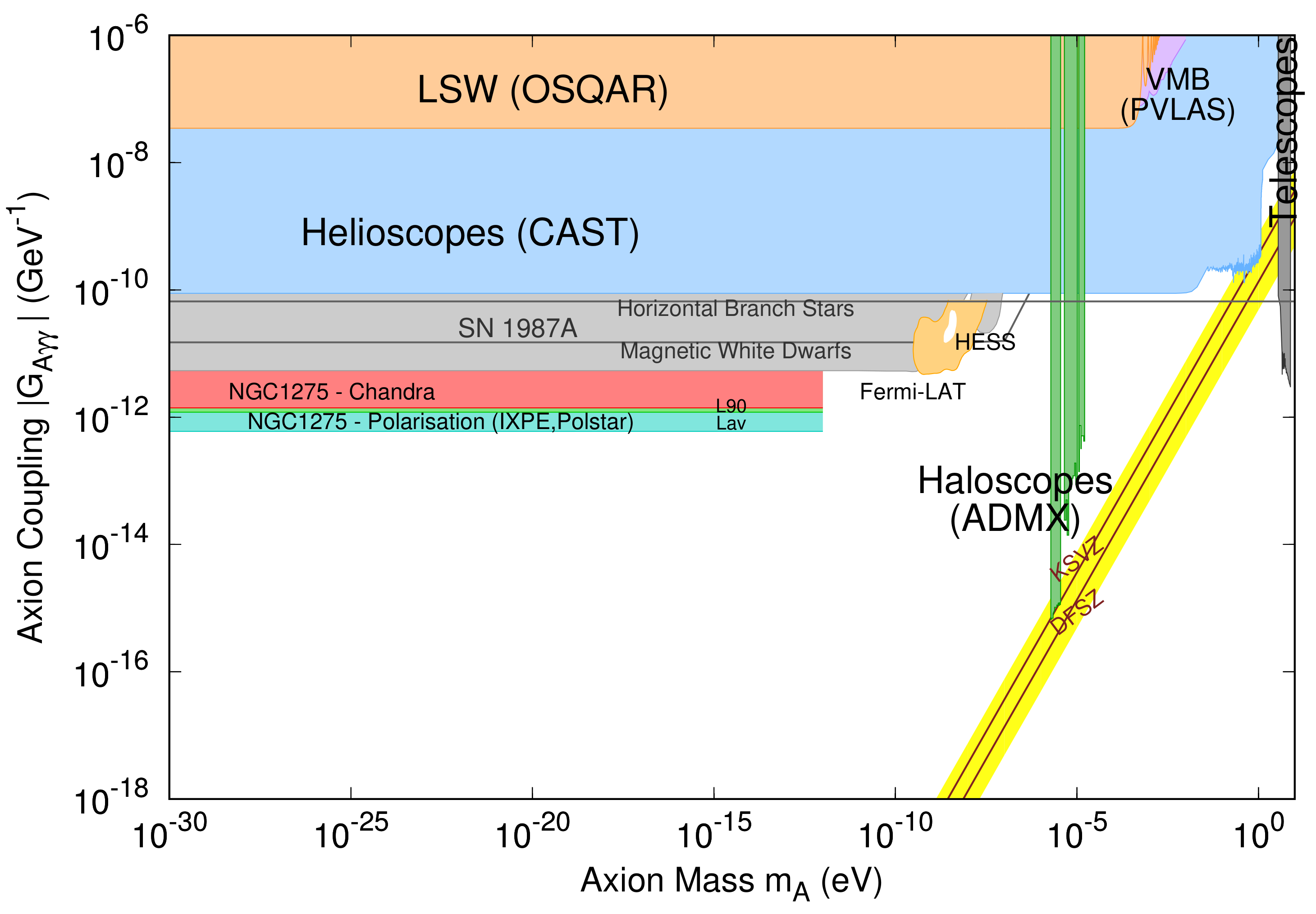
4. Results
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Projected Bounds with a Likelihood Ratio Test
- For each intrinsic source polarisation, simulate 1000 data sets with no ALPs present.
- Simulate transfer matrices for each value of g considered and for 100 different magnetic field configurations .
- For each transfer matrix, find the final spectrum including ALPs for a range of different values for the intrinsic source polarisation degree and angle . We take in steps of and in steps of , and we use an interpolating function derived from this data for the maximisation procedure later on.
- We now fit the spectra with ALPs generated in the previous step to the fake data generated without ALPs. For each set we find the values of and that maximize the likelihood . In each bin k, is the probability of measuring the and values given by , given that the true values are those predicted by an ALP model with parameters . These are calculated from Equation (6). We thus obtain a set of maximised likelihoods .
- For each value of g and each , sort the obtained from different magnetic fields, and select the 95th quantile L value, and the corresponding magnetic field. We thus obtain a set of likelihoods .
- For each , find the value of g, that leads to the maximum .
- We first consider the discovery potential of the data—i.e., the possibility of excluding a null hypothesis of no ALPs. For each , we construct a test statistic .
- We have hence found the distribution of under a null hypothesis of no ALPs. We find the threshold value such that of the are lower than . This value can be used to demonstrate our discovery potential for ALPs, by finding the for some of our fake data with ALPs included. We note that this test statistic does not obey Wilk’s theorem as our hypotheses are not nested.
- We now turn to excluding values of g. Our null hypothesis is now that ALPs exist with some coupling g, and the alternative hypothesis is that . obviously includes the case where ALPs do not exist, but excluding ALPs with should not be possible. Our test statistic for each g is now .
- We take the median value of over the to represent that g. So we now have simply for our test statistic.
- We now need the null distribution of under the hypothesis that ALPs exist with coupling g. Following [40], we assume that and the test statistic for a null hypothesis of no ALPs, above, have the same distribution, and therefore = . In [40], this assumption is tested with simulations for part of the parameter space. We therefore exclude a value of g if .
- For zero intrinsic source polarisation, simulate 10 data sets for each pair, with g running from 1–13 × in steps of and 5 different magnetic field configurations. We therefore have 50 fake data sets for each g.
- Fit each with spectra generated with ALPs of different g, as described in steps 2–7 above. (In this case we use 100 magnetic field configurations rather than 1000 in the interests of computational efficiency.) In this way we calculate a test statistic for each .
- We compare with the calculated in step 8 above. If we may exclude the no ALP hypothesis at the confidence level in that fake data set.
- For each g, we find the proportional of the 50 corresponding fake data sets for each the no ALP hypothesis is excluded.
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. 2012, 716, 30–61. [Google Scholar]
- Patrignani, C.; Agashe, K.; Aielli, G.; Amsler, C.; Antonelli, M.; Asner, D.M.; Baer, H.; Banerjee, S.; Barnett, R.M.; Basaglia, T.; et al. Review of Particle Physics. Chin. Phys. 2016, C40, 100001. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605/R = 4kpc/ to UGC 2885/R = 122 kpc/. Astrophys. J. 1980, 238, 471–487. [Google Scholar] [CrossRef]
- Adam, R.; Ade, P.A.R.; Aghanim, N.; Akrami, Y.; Alves, M.I.R.; Argüeso, F.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; et al. Planck 2015 results. I. Overview of products and scientific results. Astron. Astrophys. 2016, 594, A1. [Google Scholar]
- Randall, S.W.; Markevitch, M.; Clowe, D.; Gonzalez, A.H.; Bradac, M. Constraints on the Self-Interaction Cross-Section of Dark Matter from Numerical Simulations of the Merging Galaxy Cluster 1E 0657-56. Astrophys. J. 2008, 679, 1173–1180. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Anderson, B.; Atwood, W.B.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Searching for Dark Matter Annihilation from Milky Way Dwarf Spheroidal Galaxies with Six Years of Fermi Large Area Telescope Data. Phys. Rev. Lett. 2015, 115, 231301. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; et al. The Fermi Galactic Center GeV Excess and Implications for Dark Matter. Astrophys. J. 2017, 840, 43. [Google Scholar] [CrossRef]
- Conlon, J.P. The QCD axion and moduli stabilisation. J. High Energy Phys. 2006, 2006, 078. [Google Scholar] [CrossRef]
- Svrcek, P.; Witten, E. Axions In String Theory. J. High Energy Phys. 2006, 2006, 051. [Google Scholar] [CrossRef]
- Cicoli, M.; Goodsell, M.; Ringwald, A. The type IIB string axiverse and its low-energy phenomenology. J. High Energy Phys. 2012, 2012, 146. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Raffelt, G.; Stodolsky, L. Mixing of the Photon with Low Mass Particles. Phys. Rev. 1988, 37, 1237–1249. [Google Scholar] [CrossRef]
- Dias, A.G.; Machado, A.C.B.; Nishi, C.C.; Ringwald, A.; Vaudrevange, P. The Quest for an Intermediate-Scale Accidental Axion and Further ALPs. J. High Energy Phys. 2014, 2014, 037. [Google Scholar] [CrossRef]
- Berg, M.; Conlon, J.P.; Day, F.; Jennings, N.; Krippendorf, S.; Powell, A.J.; Rummel, M. Constraints on Axion-Like Particles from X-ray Observations of NGC1275. Astrophys. J. 2017, 847, 101. [Google Scholar] [CrossRef]
- Marsh, M.C.D.; Russell, H.R.; Fabian, A.C.; McNamara, B.P.; Nulsen, P.; Reynolds, C.S. A New Bound on Axion-Like Particles. J. Cosmol. Astropart. Phys. 2017, 2017, 036. [Google Scholar] [CrossRef]
- Conlon, J.P.; Day, F.; Jennings, N.; Krippendorf, S.; Rummel, M. Constraints on Axion-Like Particles from Non-Observation of Spectral Modulations for X-ray Point Sources. J. Cosmol. Astropart. Phys. 2017, 2017, 005. [Google Scholar] [CrossRef][Green Version]
- Chen, L.; Conlon, J.P. Constraints on Massive Axion-Like Particles from X-ray Observations of NGC1275. arXiv, 2017; arXiv:1712.08313v1. [Google Scholar]
- Soffitta, P. IXPE the Imaging X-ray Polarimetry Explorer. Proc. SPIE 2017, 10397, 103970I. [Google Scholar]
- Krawczynski, H.S.; Stern, D.; Harrison, F.A.; Kislat, F.F.; Zajczyk, A.; Beilicke, M.; Hoormann, J.; Guo, Q.; Endsley, R.; Ingram, A.R.; et al. X-ray Polarimetry with the Polarization Spectroscopic Telescope Array (PolSTAR). Astropart. Phys. 2016, 75, 8–28. [Google Scholar] [CrossRef]
- Payez, A.; Cudell, J.R.; Hutsemekers, D. New polarimetric constraints on axion-like particles. J. Cosmol. Astropart. Phys. 2012, 2012, 041. [Google Scholar] [CrossRef][Green Version]
- Govoni, F.; Feretti, L. Magnetic field in clusters of galaxies. Int. J. Mod. Phys. 2004, 13, 1549–1594. [Google Scholar] [CrossRef]
- Brockway, J.W.; Carlson, E.D.; Raffelt, G.G. SN1987A gamma-ray limits on the conversion of pseudoscalars. Phys. Lett. 1996, B383, 439–443. [Google Scholar] [CrossRef]
- Grifols, J.A.; Masso, E.; Toldra, R. Gamma-rays from SN1987A due to pseudoscalar conversion. Phys. Rev. Lett. 1996, 77, 2372–2375. [Google Scholar] [CrossRef] [PubMed]
- Payez, A.; Evoli, C.; Fischer, T.; Giannotti, M.; Mirizzi, A.; Ringwald, A. Revisiting the SN1987A gamma-ray limit on ultralight axion-like particles. J. Cosmol. Astropart. Phys. 2015, 2015, 006. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Conlon, J.P.; Day, F.; Jennings, N.; Krippendorf, S.; Muia, F. Projected bounds on ALPs from Athena. Mon. Not. R. Astron. Soc. 2018, 473, 4932. [Google Scholar] [CrossRef]
- Marin, F.; Dovciak, M.; Muleri, F.; Kislat, F.F.; Krawczynski, H.S. Predicting the X-ray polarization of type-2 Seyfert galaxies. Mon. Not. R. Astron. Soc. 2018, 473, 1286–1316. [Google Scholar] [CrossRef]
- Peterson, B.M. An Introduction to Active Galactic Nuclei; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Marin, F. A compendium of AGN inclinations with corresponding UV/optical continuum polarization measurements. Mon. Not. R. Astron. Soc. 2014, 441, 551–564. [Google Scholar] [CrossRef]
- Kislat, F.; Clark, B.; Beilicke, M.; Krawczynski, H. Analyzing the data from X-ray polarimeters with Stokes parameters. Astropart. Phys. 2015, 68, 45–51. [Google Scholar] [CrossRef]
- Marin, F.; Porquet, D.; Goosmann, R.W.; Dovciak, M.; Muleri, F.; Grosso, N.; Karas, V. Modelling the X-ray polarimetric signatures of complex geometry: the case study of the “changing look” AGN NGC 1365. Mon. Not. R. Astron. Soc. 2013, 436, 1615. [Google Scholar] [CrossRef]
- Churazov, E.; Forman, W.; Jones, C.; Bohringer, H. Xmm-newton observations of the perseus cluster I: The temperature and surface brightness structure. Astrophys. J. 2003, 590, 225–237. [Google Scholar] [CrossRef]
- Taylor, G.B.; Gugliucci, N.E.; Fabian, A.C.; Sanders, J.S.; Gentile, G.; Allen, S.W. Magnetic fields in the center of the perseus cluster. Mon. Not. R. Astron. Soc. 2006, 368, 1500–1506. [Google Scholar] [CrossRef]
- Bonafede, A.; Feretti, L.; Murgia, M.; Govoni, F.; Giovannini, G.; Dallacasa, D.; Dolag, K.; Taylor, G.B. The Coma cluster magnetic field from Faraday rotation measures. Astron. Astrophys. 2010, 513, A30. [Google Scholar] [CrossRef]
- Vacca, V.; Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Perley, R.A.; Taylor, G.B. The intracluster magnetic field power spectrum in A2199. Astron. Astrophys. 2012, 540, A38. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury Press: Duxbury, MA, USA, 2002. [Google Scholar]
- Ajello, M.; Albert, A.; Anderson, B.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. Search for Spectral Irregularities due to Photon—Axionlike-Particle Oscillations with the Fermi Large Area Telescope. Phys. Rev. Lett. 2016, 116, 161101. [Google Scholar] [CrossRef] [PubMed]
- Gill, R.; Heyl, J.S. Constraining the photon-axion coupling constant with magnetic white dwarfs. Phys. Rev. 2011, 84, 08500. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Day, F.; Krippendorf, S. Searching for Axion-Like Particles with X-ray Polarimeters. Galaxies 2018, 6, 45. https://doi.org/10.3390/galaxies6020045
Day F, Krippendorf S. Searching for Axion-Like Particles with X-ray Polarimeters. Galaxies. 2018; 6(2):45. https://doi.org/10.3390/galaxies6020045
Chicago/Turabian StyleDay, Francesca, and Sven Krippendorf. 2018. "Searching for Axion-Like Particles with X-ray Polarimeters" Galaxies 6, no. 2: 45. https://doi.org/10.3390/galaxies6020045
APA StyleDay, F., & Krippendorf, S. (2018). Searching for Axion-Like Particles with X-ray Polarimeters. Galaxies, 6(2), 45. https://doi.org/10.3390/galaxies6020045





