Circular Polarization in Turbulent Blazar Jets
Abstract
:1. Introduction
2. The Full Stokes Equations
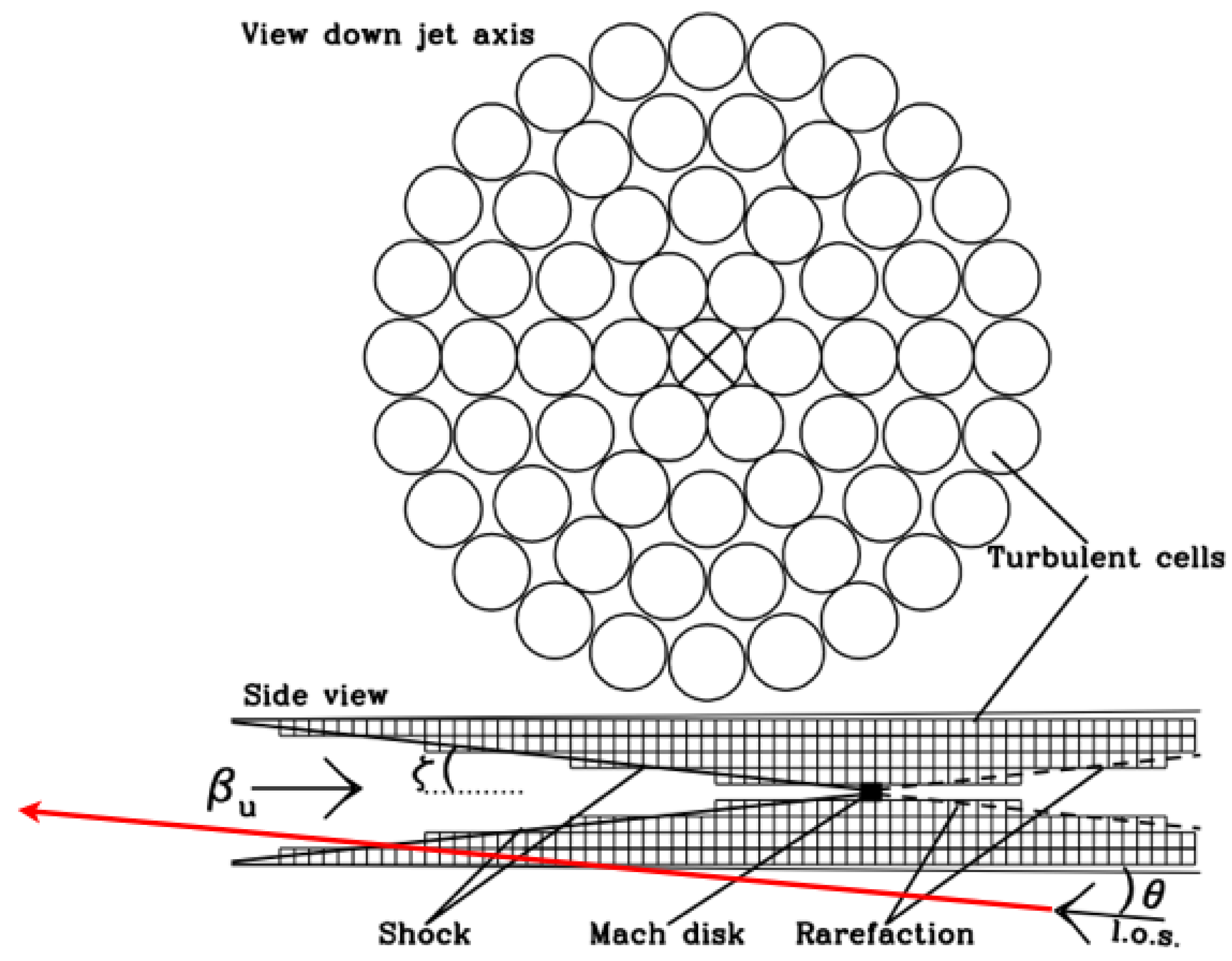
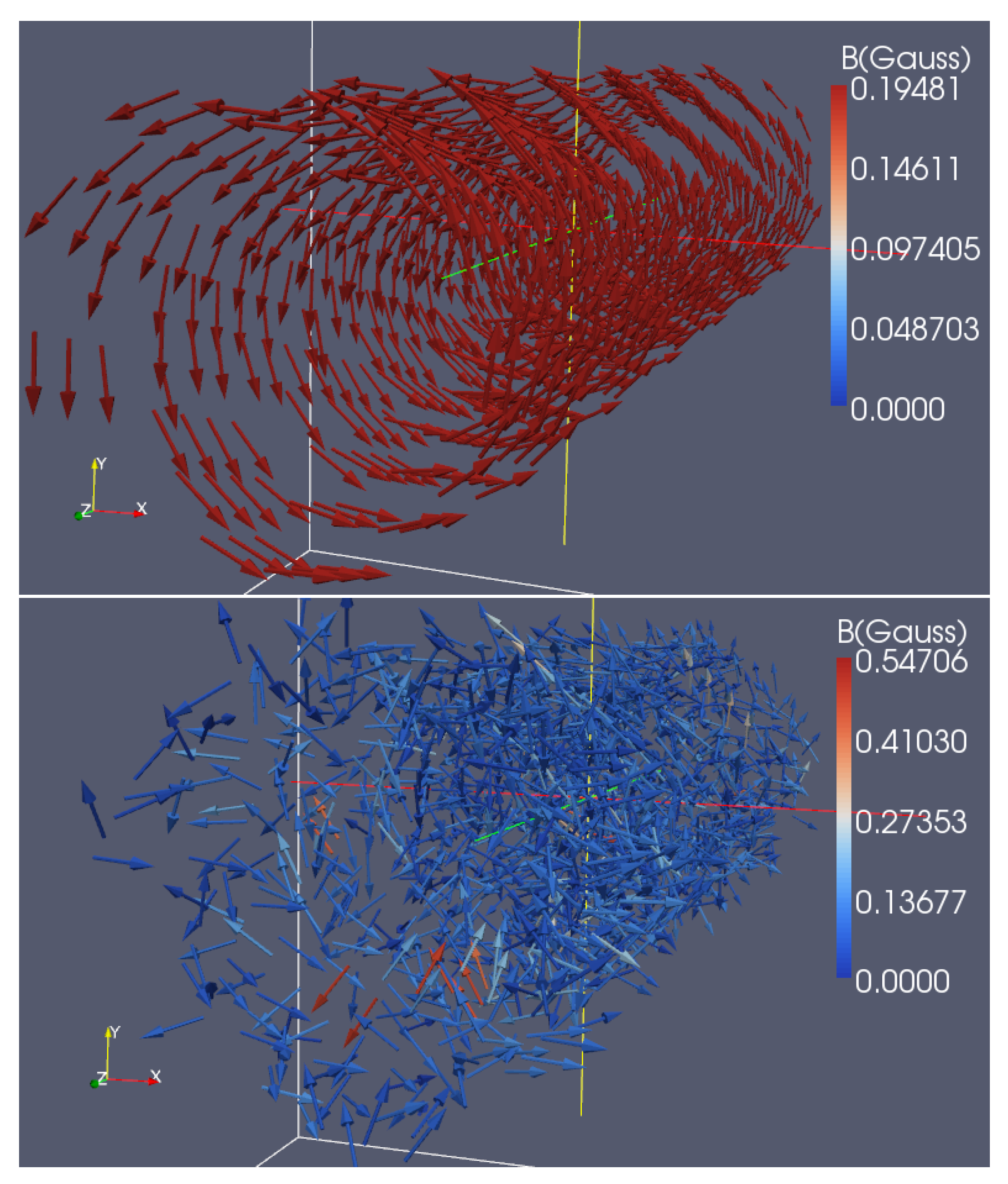
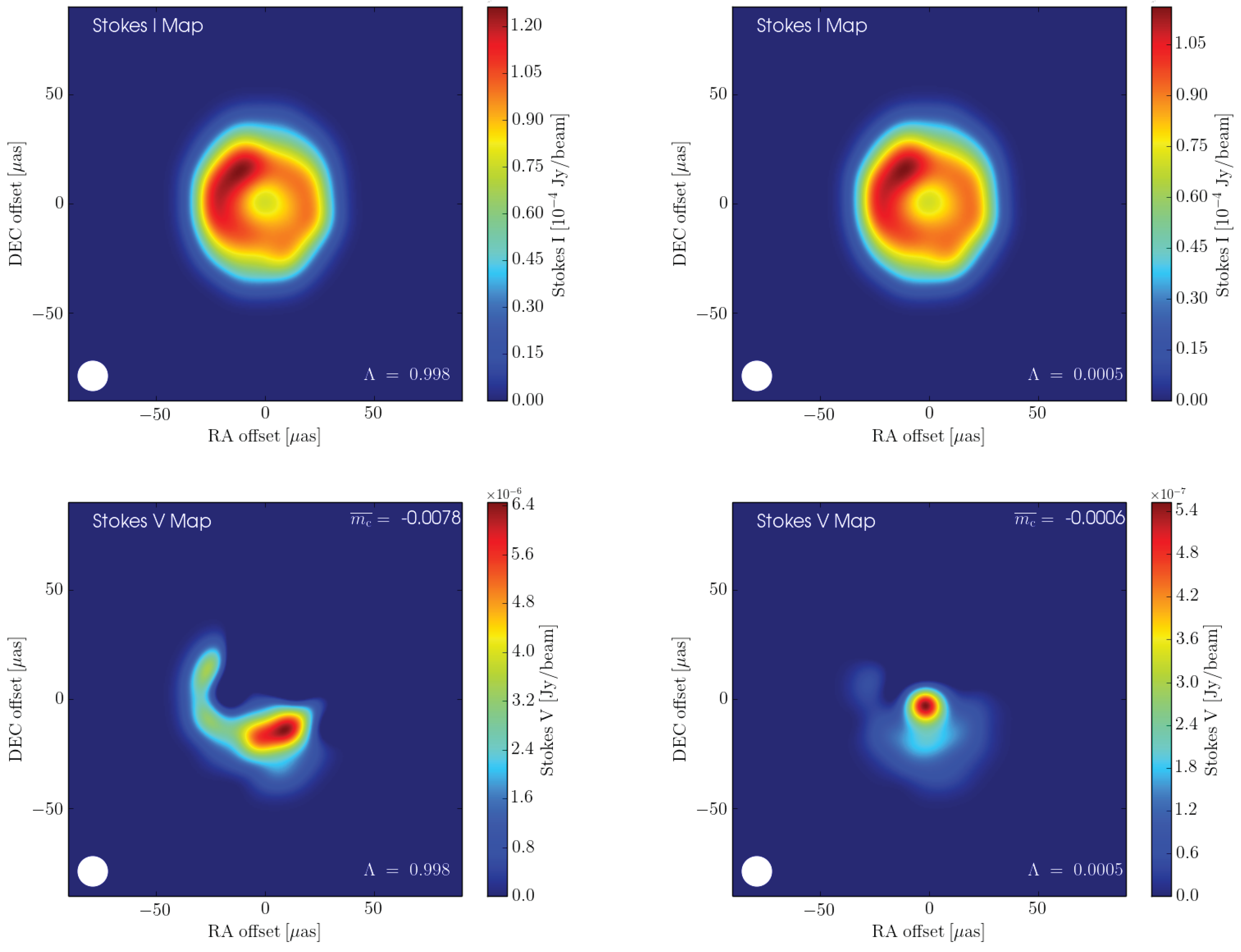
3. Order and Disorder: Turbulence in the Jet
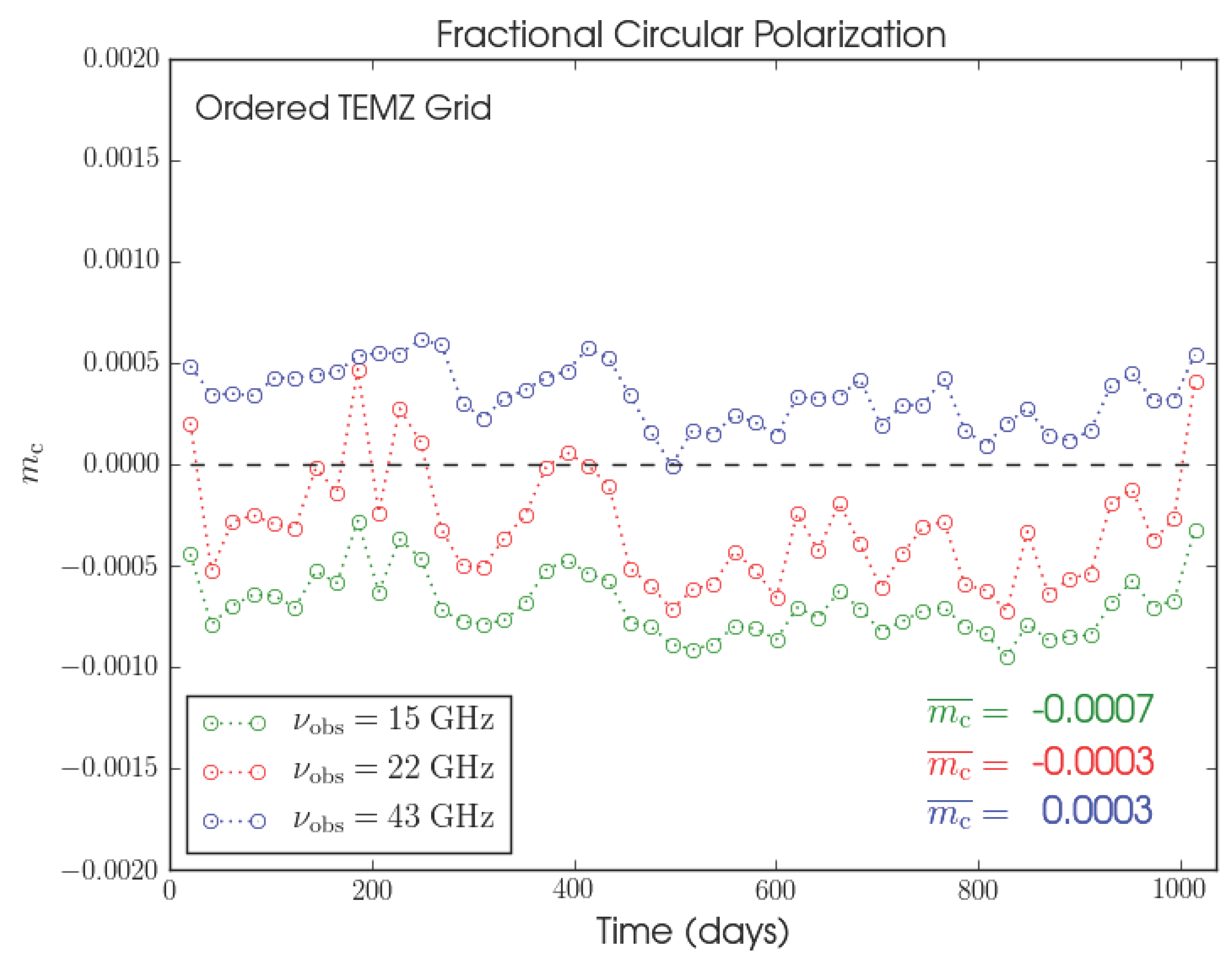
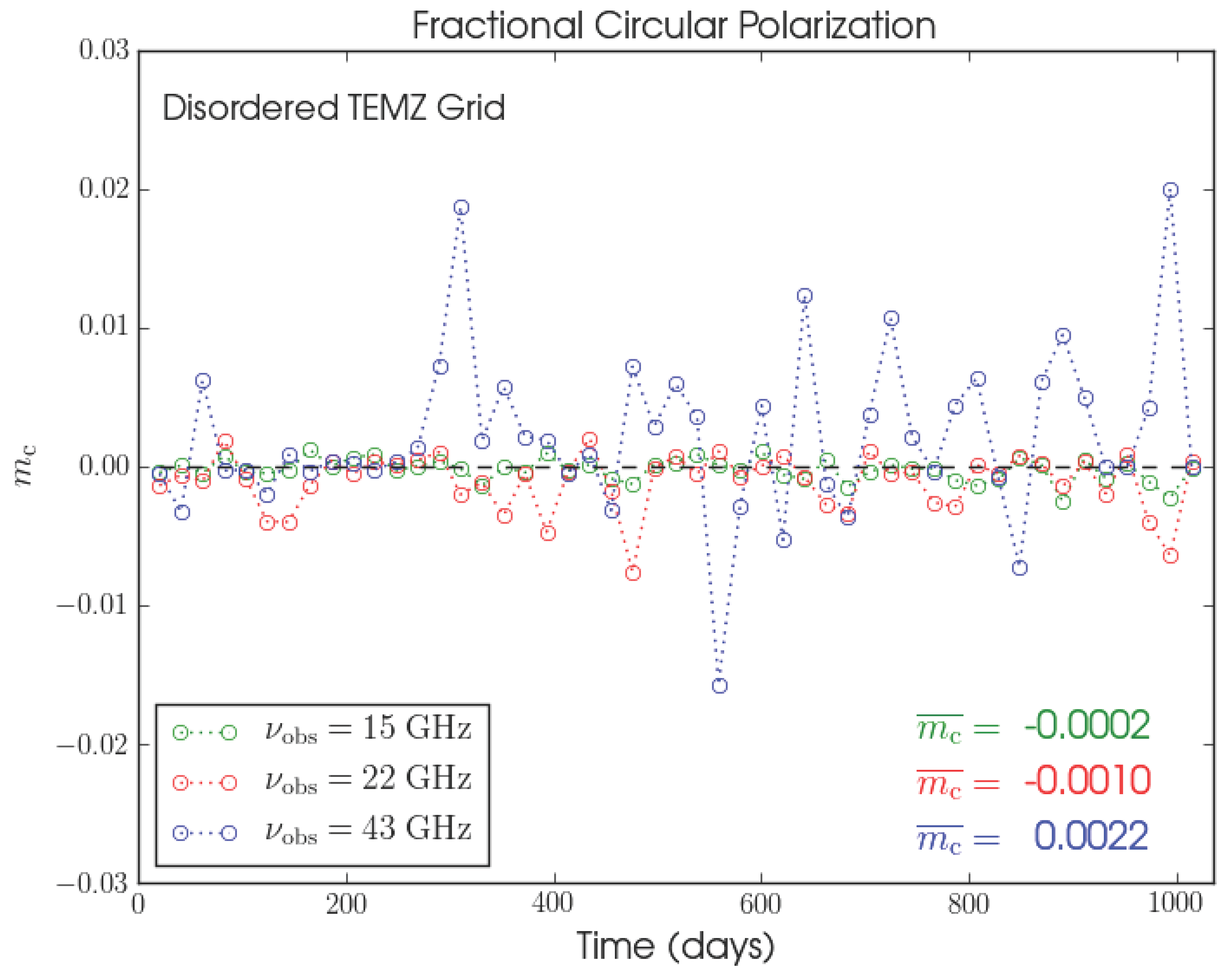
4. Temporal Variability of Circular Polarization
5. Probing the Plasma Content of the Jet
6. Future Research
Conflicts of Interest
References
- Homan, D.C.; Lister, M.L.; Aller, H.D.; Aller, M.F.; Wardle, J.F.C. Full polarization spectra of 3C 279. Astrophys. J. 2009, 696. [Google Scholar] [CrossRef]
- Homan, D.C.; Attridge, J.M.; Wardle, J.F.C. Parsec-scale circular polarization observations of 40 blazars. Astrophys. J. 2001, 556. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, extreme multi-zone model for simulating flux and polarization variability in blazars. Astrophys. J. 2014, 780. [Google Scholar] [CrossRef]
- Macdonald, N.R. Through the Looking Glass: Faraday Conversion in Turbulent Blazar Jets. Galaxies 2016, 4. [Google Scholar] [CrossRef]
- Jones, T.W.; O’Dell, S.L. Transfer of polarized radiation in self-absorbed synchrotron sources. I. Results for a homogeneous source. Astrophys. J. 1977, 214, 522–539. [Google Scholar] [CrossRef]
- Jones, T.W. Polarization as a probe of magnetic field and plasma properties of compact radio sources- Simulation of relativistic jets. Astrophys. J. 1988, 332, 678–695. [Google Scholar] [CrossRef]
- Aller, M.F.; Aller, H.D.; Hughes, P.A. Radio Band Observations of Blazar Variability. J. Astrophys. Astron. 2011, 32. [Google Scholar] [CrossRef]
- Aller, H.D.; Aller, M.F.; Plotkin, R.M. Circular Polarization Variability in Extragalactic Sources on Time Scales of Months to Decades. Astrophys. Space Sci. 2003, 288, 17–28. [Google Scholar] [CrossRef]
- Enßlin, T.A. Does circular polarisation reveal the rotation of quasar engines? Astron. Astrophys. 2003, 401, 499–504. [Google Scholar] [CrossRef]
- Wardle, J.F.C.; Homan, D.C. Theoretical Models for Producing Circularly Polarized Radiation in Extragalactic Radio Sources. Astrophys. Space Sci. 2003, 288, 143–153. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacDonald, N.R. Circular Polarization in Turbulent Blazar Jets. Galaxies 2017, 5, 82. https://doi.org/10.3390/galaxies5040082
MacDonald NR. Circular Polarization in Turbulent Blazar Jets. Galaxies. 2017; 5(4):82. https://doi.org/10.3390/galaxies5040082
Chicago/Turabian StyleMacDonald, Nicholas Roy. 2017. "Circular Polarization in Turbulent Blazar Jets" Galaxies 5, no. 4: 82. https://doi.org/10.3390/galaxies5040082
APA StyleMacDonald, N. R. (2017). Circular Polarization in Turbulent Blazar Jets. Galaxies, 5(4), 82. https://doi.org/10.3390/galaxies5040082



